Hissələr üzrə inteqrasiya metodundan istifadə edərək inteqralları hesablayın. Onlayn kalkulyator Qeyri-müəyyən inteqralı hesablayın (antiderivativ).

Aşağıdakı formula deyilir hissələr düsturu ilə inteqrasiya qeyri-müəyyən inteqralda:

İnteqrasiyanı hissələr düsturu ilə tətbiq etmək üçün inteqranı iki amilə bölmək lazımdır. Onlardan biri ilə işarələnir u, qalanı isə ikinci amilə aiddir və ilə işarələnir dv. Sonra fərqləndirmə yolu ilə tapırıq du və inteqrasiya - funksiyası v. Eyni zamanda, üçün u dv- asanlıqla inteqrasiya oluna bilən inteqranın elə bir hissəsi.

Hissələr üzrə inteqrasiya metodundan nə vaxt istifadə etmək faydalıdır? Sonra nə vaxt inteqral ehtiva edir :

1) - loqarifmik funksiyalar, eləcə də tərs triqonometrik funksiyalar ("qövs" prefiksi ilə), sonra hissələr üzrə inteqrasiyanın uzunmüddətli təcrübəsinə əsaslanaraq bu funksiyalar ilə işarələnir. u;

2) , , - sinus, kosinus və eksponentin vurulması P(x) x-də ixtiyari çoxhədlidir, onda bu funksiyalar ilə işarələnir dv, və çoxhədli keçər u;

3) , , , , bu halda hissələr üzrə inteqrasiya iki dəfə tətbiq edilir.

Birinci halın nümunəsindən istifadə edərək hissələr üzrə inteqrasiya metodunun dəyərini izah edək. Qoy inteqral işarəsi altındakı ifadədə loqarifmik funksiya olsun (bu, 1-ci nümunə olacaq). Hissələr üzrə inteqrasiyadan istifadə edərək, belə bir inteqral yalnız cəbri funksiyaların (əksər hallarda çoxhədli) inteqralının hesablanmasına qədər azaldılır, yəni loqarifmik və ya tərs olmayan triqonometrik funksiya. Dərsin əvvəlində verilmiş hissələrə görə inteqrasiya düsturundan istifadə

birinci hədddə (inteqral olmadan) loqarifmik funksiya, ikinci hədddə isə (inteqral işarəsi altında) loqarifmi olmayan funksiya əldə edirik. Cəbr funksiyasının inteqralı, işarəsi altında loqarifmik və ya tərs triqonometrik funksiyanın ayrıca və ya cəbr əmsalı ilə birlikdə tapıldığı inteqraldan çox sadədir.

Beləliklə, istifadə hissələrin düsturları ilə inteqrasiya inteqrasiya dərhal yerinə yetirilmir: verilmiş inteqralın tapılması digərinin tapılmasına qədər azaldılır. Hissələr üzrə inteqralın düsturunun mənası ondan ibarətdir ki, onun tətbiqi nəticəsində yeni inteqral cədvəlli olur və ya heç olmasa ilkin inteqraldan sadələşir.

Hissələr üzrə inteqrasiya üsulu iki funksiyanın məhsulunu fərqləndirmək üçün düsturun istifadəsinə əsaslanır:

sonra formada yazmaq olar

dərsin əvvəlində verilmişdi.

Funksiyanı inteqrasiya etməklə taparkən v onun üçün sonsuz antitörəmə funksiyalar toplusu alınır. İnteqrasiyanı hissələr düsturu ilə tətbiq etmək üçün onlardan hər hansı birini və buna görə də ixtiyari sabitə uyğun olanı götürə bilərsiniz. İLƏ, sıfıra bərabərdir. Buna görə də funksiyanı taparkən v ixtiyari sabit İLƏ daxil edilməməlidir.

Hissələr üzrə inteqrasiya metodunun çox xüsusi tətbiqi var: inteqral işarəsi altında funksiyaların dərəcəsini azaltmaq lazım olduqda, əks törəmə funksiyaları tapmaq üçün təkrarlanan düsturlar əldə etmək üçün istifadə edilə bilər. Dərəcənin azaldılması, məsələn, sinuslar və kosinuslar kimi funksiyalar üçün ikinci və onların məhsullarından böyük güclərə cədvəl inteqralları olmadıqda lazımdır. Təkrarlanan düstur əvvəlki üzv vasitəsilə ardıcıllığın növbəti üzvünü tapmaq üçün düsturdur. Göstərilən hallar üçün dərəcəni ardıcıl olaraq aşağı salmaqla məqsədə nail olunur. Deməli, əgər inteqral x-in dördüncü dərəcəsinə sindirsə, onda hissələr üzrə inteqral etməklə sinusun üçüncü dərəcəyə inteqralının düsturunu tapmaq olar və s. Bu dərsin son paraqrafı təsvir olunan vəzifəyə həsr edilmişdir.

Parçalar üzrə inteqrasiyanın birlikdə tətbiqi

Nümunə 1. Hissələr üzrə inteqral üsulundan istifadə edərək qeyri-müəyyən inteqralı tapın:

Həll. İnteqral ifadəsində - artıq bildiyimiz kimi, əsaslı şəkildə işarələnə bilən loqarifm. u. Biz inanırıq ki, .

Tapırıq (nəzəri istinad üçün izahatda qeyd olunduğu kimi, biz dərhal birinci hədddə loqarifmik funksiyanı (inteqral olmadan) və ikinci hədddə loqarifmi olmayan funksiyanı (inteqral işarəsi altında) əldə edirik):

Və yenə loqarifm...

Misal 2. Qeyri-müəyyən inteqralı tapın:

Həll. Qoy,.

Loqarifm kvadratda mövcuddur. Bu o deməkdir ki, onu mürəkkəb funksiya kimi fərqləndirmək lazımdır. tapırıq
,
.

Yenə hissələrə görə ikinci inteqralı tapırıq və yuxarıda qeyd olunan üstünlüyü əldə edirik (birinci hədddə (inteqral olmadan) loqarifmik funksiya, ikinci hədddə (inteqral işarəsi altında) bir funksiyası olmayan bir funksiya var. loqarifm).

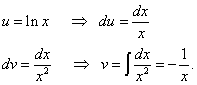
Orijinal inteqralı tapırıq:

Misal 3.

Həll. Arktangent, loqarifm kimi, daha yaxşı ilə işarələnir u. Beləliklə, icazə verin.

Sonra,
.

İnteqrasiyanı hissələr düsturu ilə tətbiq edərək, əldə edirik:

Bir dəyişəni dəyişdirərək ikinci inteqralı tapırıq.

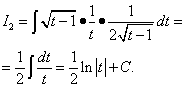
Dəyişənlərə qayıdırıq x, alırıq

.

Orijinal inteqralı tapırıq:

.

Nümunə 4. Hissələr üzrə inteqrasiya üsulundan istifadə edərək qeyri-müəyyən inteqralı tapın:

Həll. Sərgi iştirakçısını ilə işarələmək daha yaxşıdır dv. İnteqrasiyanı iki amilə bölürük. Buna inanaraq

Nümunə 5. Hissələr üzrə inteqrasiya üsulundan istifadə edərək qeyri-müəyyən inteqralı tapın:

.

Həll. Qoy,. Sonra ,.

Hissələr üzrə inteqrasiyadan (1) istifadə edərək tapırıq:

Misal 6. Qeyri-müəyyən inteqralı hissələrə görə inteqrasiya edərək tapın:

Həll. Sinus, eksponensial kimi, rahatlıqla işarələnə bilər dv. Qoy,.

Hissələrə görə inteqrasiya düsturundan istifadə edərək, tapırıq:

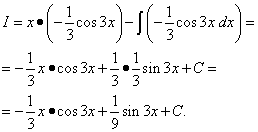
Parçalara görə inteqrasiyanı yenidən birlikdə tətbiq edirik

Misal 10. Qeyri-müəyyən inteqralı hissələrə görə inteqrasiya edərək tapın:

.

Həll. Bütün oxşar hallarda olduğu kimi, kosinusu ilə işarələmək rahatdır dv. , işarə edirik.

Sonra , .

Hissələr üzrə inteqrasiya düsturundan istifadə edərək, əldə edirik:

Biz ikinci terminə hissə-hissə inteqrasiyanı da tətbiq edirik. , işarə edirik.

Bu qeydlərdən istifadə edərək qeyd olunan termini birləşdiririk:

İndi tələb olunan inteqralı tapırıq:

Hissələr üzrə inteqrasiya üsulu ilə həll oluna bilən inteqrallar arasında nəzəri hissədə qeyd olunan üç qrupun heç birinə daxil olmayanlar da var ki, onlar üçün praktikadan məlumdur ki, onlar üçün ilə işarələmək daha yaxşıdır. u, və nə vasitəsilə dv. Buna görə də, bu hallarda, "Hissələr üzrə inteqrasiya metodunun mahiyyəti" bəndində də verilmiş rahatlıq nəzərə alınmalıdır: u diferensiallaşma zamanı çox da mürəkkəbləşməyən inteqralın bir hissəsini götürmək lazımdır, amma dv- asanlıqla inteqrasiya oluna bilən inteqranın elə bir hissəsi. Bu dərsin son nümunəsi məhz belə bir inteqralın həllidir.

Müəyyən bir inteqralla -dən davamlı funksiya f(x) son seqmentdə [ a, b] (burada ) bu seqmentdə onun bəzi antiderivativlərinin artımıdır. (Ümumiyyətlə, qeyri-müəyyən inteqralın mövzusunu təkrarlasanız, başa düşmək nəzərəçarpacaq dərəcədə asanlaşacaq) Bu vəziyyətdə qeyd istifadə olunur.

Aşağıdakı qrafiklərdən göründüyü kimi (antiderivativ funksiyanın artımı ilə göstərilir), müəyyən inteqral müsbət və ya ola bilər mənfi rəqəm (Yuxarı hədddəki antiderivativin dəyəri ilə aşağı hədddəki dəyəri arasındakı fərq kimi hesablanır, yəni. F(b) - F(a)).

Nömrələr a Və b müvafiq olaraq inteqrasiyanın aşağı və yuxarı həddi adlanır və seqment [ a, b] – inteqrasiya seqmenti.

Beləliklə, əgər F(x) – üçün bəzi antitörəmə funksiyası f(x), onda tərifə uyğun olaraq,

(38)

Bərabərlik (38) adlanır Nyuton-Leybnits düsturu . Fərq F(b) – F(a) qısaca belə yazılır:

Buna görə də Nyuton-Leybnits düsturunu belə yazacağıq:

(39)

Sübut edək ki, müəyyən inteqral onu hesablayarkən onun hansı antitörəmə götürülməsindən asılı deyil. Qoy F(x) və F( X) inteqralın ixtiyari antiderivativləridir. Bunlar eyni funksiyanın antitörəmələri olduğundan, onlar sabit terminlə fərqlənirlər: Ф( X) = F(x) + C. Buna görə

Bu müəyyən edir ki, seqmentdə [ a, b] funksiyanın bütün antiderivativlərinin artımları f(x) uyğun gəlir.

Beləliklə, müəyyən inteqralı hesablamaq üçün inteqralın hər hansı bir antitörəməni tapmaq lazımdır, yəni. Əvvəlcə qeyri-müəyyən inteqralı tapmaq lazımdır. Daimi İLƏ sonrakı hesablamalardan xaric edilir. Sonra Nyuton-Leybnits düsturu tətbiq olunur: yuxarı həddin qiyməti antitörəmə funksiyası ilə əvəz olunur. b , daha sonra - aşağı həddinin dəyəri a və fərq hesablanır F(b) - F(a) . Nəticədə alınan ədəd müəyyən inteqral olacaqdır..

At a = b tərifinə görə qəbul edilir

Misal 1.

Həll. Əvvəlcə qeyri-müəyyən inteqralı tapaq:

Nyuton-Leybniz düsturunun antitörəmə tətbiqi

(saat İLƏ= 0), alırıq

Lakin müəyyən inteqralı hesablayarkən əks törəməni ayrıca tapmamaq, inteqralı dərhal (39) şəklində yazmaq daha yaxşıdır.

Misal 2. Müəyyən inteqralı hesablayın

Həll. Formuladan istifadə etməklə

Müəyyən inteqralın xassələri

Teorem 2.Müəyyən inteqralın qiyməti inteqrasiya dəyişəninin təyinatından asılı deyil, yəni.

(40)

Qoy F(x) – üçün antitörəmə f(x). üçün f(t) əks törəmə eyni funksiyadır F(t), burada müstəqil dəyişən yalnız fərqli olaraq təyin olunur. Beləliklə,

(39) düsturu əsasında sonuncu bərabərlik inteqralların bərabərliyini bildirir

Teorem 3.Sabit amili müəyyən inteqralın işarəsindən çıxarmaq olar, yəni.

(41)

Teorem 4.Sonlu sayda funksiyanın cəbri cəminin müəyyən inteqralı bu funksiyaların müəyyən inteqrallarının cəbri cəminə bərabərdir., yəni.

(42)

Teorem 5.Əgər inteqrasiya seqmenti hissələrə bölünürsə, onda bütün seqment üzərində müəyyən inteqral məbləğinə bərabərdir hissələri üzərində müəyyən inteqrallar, yəni. Əgər

(43)

Teorem 6.İnteqrasiya hüdudlarını yenidən təşkil edərkən mütləq dəyər müəyyən inteqral dəyişmir, ancaq onun işarəsi dəyişir, yəni.

(44)

Teorem 7(orta dəyər teoremi). Müəyyən bir inteqral, inteqrasiya seqmentinin uzunluğunun və onun daxilindəki bəzi nöqtədə inteqranın qiymətinin hasilinə bərabərdir., yəni.

(45)

Teorem 8.Əgər inteqrasiyanın yuxarı həddi aşağıdan böyükdürsə və inteqral qeyri-mənfidirsə (müsbət), onda müəyyən inteqral da mənfi deyil (müsbət), yəni. Əgər

Teorem 9.Əgər inteqrasiyanın yuxarı həddi aşağıdan və funksiyalardan böyükdürsə və davamlıdırsa, onda bərabərsizlik

terminə görə inteqrasiya oluna bilər, yəni.

(46)

Müəyyən inteqralın xassələri inteqralların birbaşa hesablanmasını sadələşdirməyə imkan verir.

Misal 5. Müəyyən inteqralı hesablayın

4 və 3-cü teoremlərdən istifadə edərək, antitörəmələri - cədvəl (7) və (6) inteqrallarını taparkən əldə edirik.

Dəyişən yuxarı həddi olan müəyyən inteqral

Qoy f(x) – seqmentdə davamlı [ a, b] funksiyası və F(x) onun antiderivatividir. Müəyyən inteqralı nəzərdən keçirək

(47)

və vasitəsilə t inteqrasiya dəyişəni onu qarışdırmamaq üçün təyin edilir yuxarı həddi. Dəyişən zaman X müəyyən inteqral (47) də dəyişir, yəni. inteqrasiyanın yuxarı həddinin funksiyasıdır X ilə işarə etdiyimiz F(X), yəni.

(48)

funksiyası olduğunu sübut edək F(X) üçün antitörəmədir f(x) = f(t). Doğrudan da, fərqləndirici F(X), alırıq

çünki F(x) – üçün antitörəmə f(x), A F(a) sabit qiymətdir.

Funksiya F(X) – üçün sonsuz sayda antitörəmələrdən biridir f(x), yəni x = a sıfıra düşür. Bu ifadə əgər bərabərlikdə (48) qoysaq əldə edilir x = a və əvvəlki paraqrafın 1-ci teoremindən istifadə edin.

Müəyyən inteqralların hissələr üzrə inteqrasiya üsulu və dəyişənin dəyişdirilməsi üsulu ilə hesablanması.

harada, tərifinə görə, F(x) – üçün antitörəmə f(x). İnteqraldakı dəyişəni dəyişdirsək

onda (16) düsturuna uyğun olaraq yaza bilərik

Bu ifadədə

üçün antitörəmə funksiyası

Əslində, onun törəməsi, görə mürəkkəb funksiyaların diferensiasiya qaydası, bərabərdir

α və β dəyişənin qiymətləri olsun t, bunun üçün funksiya

dəyərlərinə uyğun olaraq qəbul edir a Və b, yəni.

Ancaq Nyuton-Leybniz düsturuna görə fərq F(b) – F(a) var

Hissələr üzrə inteqrasiya üsulu əsasən inteqral müəyyən tipli iki amilin hasilindən ibarət olduqda istifadə olunur. Hissələr üzrə inteqrasiya düsturu belə görünür:

Verilmiş inteqralın hesablanmasını azaltmağa imkan verir
inteqralın hesablanmasına
, bunun bundan daha sadə olduğu ortaya çıxır.

Hissələr üzrə inteqrasiya üsulu ilə hesablanan inteqralların əksəriyyətini üç qrupa bölmək olar:

1. Formanın inteqralları
,
,
, Harada
- çoxhədli,
– sıfıra bərabər olmayan ədəd

Bu halda vasitəsilə çoxhədli işarə edin

.

2. Formanın inteqralları
,
,
,
,
, Harada
- çoxhədli.

Bu halda vasitəsilə
işarələmək
, və inteqralın qalan hissəsi vasitəsilə :

3. Formanın inteqralları
,
, Harada
- nömrələr.

Bu halda vasitəsilə işarələmək
və hissələr düsturu ilə inteqrasiyanı iki dəfə tətbiq edin, nəticədə ilkin inteqrala qayıdın, bundan sonra ilkin inteqral bərabərlikdən ifadə edilir.

Şərh: Bəzi hallarda verilmiş inteqralı tapmaq üçün hissələr üzrə inteqral düsturunu bir neçə dəfə tətbiq etmək lazımdır. Həmçinin, hissələr üzrə inteqrasiya üsulu digər üsullarla birləşdirilir.

Misal 26.

Hissələrə görə metoddan istifadə edərək inteqralları tapın: a)
; b)
.

Həll.

b)

3.1.4. Kəsr-rasional funksiyaların inteqrasiyası

Kəsrə rasional funksiya(rasional kəsr) iki çoxhədlinin nisbətinə bərabər funksiyadır:
, Harada
– dərəcə polinomu
,
– dərəcə polinomu .

Rasional kəsr deyilir düzgün, əgər saydakı çoxhədlinin dərəcəsi məxrəcdəki çoxhədlinin dərəcəsindən kiçikdirsə, yəni.
, əks halda (əgər
) rasional kəsr deyilir səhv.

Hər hansı düzgün olmayan rasional kəsr çoxhədlinin cəmi kimi təqdim edilə bilər
və düzgün rasional kəsr, çoxhədlilərin bölünməsi qaydasına uyğun olaraq payın məxrəcə bölünməsi:

,

Harada
– bütün hissəsi bölmədən, - düzgün rasional kəsr;
- bölmənin qalan hissəsi.

Formanın düzgün rasional kəsrləri:

I. ;

II.
;

III.
;

IV.
,

Harada ,,
,
,,,
– həqiqi ədədlər və
(bunlar. kvadrat üçbucaqlı kəsrlərin III və IV məxrəcində kök yoxdur - diskriminant mənfidir) adlanır sadə rasional kəsrlər I, II, III və IV növləri.

Sadə kəsrlərin inteqrasiyası

Dörd növdən ibarət ən sadə kəsrlərin inteqralları aşağıdakı kimi hesablanır.

mən)
.

II),
.

III) III tipli ən sadə kəsri inteqral etmək üçün məxrəcdə tam kvadrat seçin və əvəz edin
. Əvəz olunduqdan sonra inteqral iki inteqrala bölünür. Birinci inteqral məxrəcin törəməsini paylayıcıda təcrid etməklə hesablanır ki, bu da cədvəlli inteqral verir, ikinci inteqral isə formaya çevrilir.
, çünki
, bu da cədvəlli inteqral verir.

;

IV) IV tipli ən sadə kəsri inteqrasiya etmək üçün məxrəcdə tam kvadrat seçin və əvəz edin
. Əvəz olunduqdan sonra inteqral iki inteqrala bölünür. Birinci inteqral əvəzetmə yolu ilə hesablanır
, ikincisi isə təkrarlama münasibətlərindən istifadə edir.

Misal 27.

Sadə kəsrlərin inteqrallarını tapın:

A)
;
b)
.

Həll.

;
.

V)

A) ;

Məxrəci faktorlara bölünə bilən istənilən düzgün rasional kəsr sadə fraksiyaların cəmi kimi təqdim edilə bilər. Sadə kəsrlərin cəminə parçalanma qeyri-müəyyən əmsallar üsulu ilə həyata keçirilir. Bu aşağıdakı kimidir:
formanın bir hissəsinə uyğun gəlir – məxrəcin hər bir faktoru

məbləğinə uyğun gəlir
;

– məxrəcin hər kvadrat əmsalı
formanın bir hissəsinə uyğun gəlir formanın fraksiyaları

qeyri-müəyyən əmsallar haradadır.

Qeyri-müəyyən əmsalları tapmaq üçün sadə kəsrlərin cəmi şəklində sağ tərəf ümumi məxrəcə gətirilir və çevrilir. Nəticə tənliyin sol tərəfində olduğu kimi eyni məxrəcli kəsrdir. Sonra məxrəclər atılır və saylar bərabərləşdirilir. Nəticə, sol tərəfin məlum əmsalları olan çoxhədli olduğu eyni bərabərlikdir və sağ tərəf– əmsalları qeyri-müəyyən olan çoxhədli.

Naməlum əmsalları təyin etməyin iki yolu var: naməlum əmsallar üsulu və qismən qiymətlər üsulu.

Qeyri-müəyyən əmsallar üsulu.

Çünki çoxhədlilər eyni dərəcədə bərabərdir, onda eyni güclərdə olan əmsallar bərabərdir . Eyni dərəcələrdə əmsalların bərabərləşdirilməsi sol və sağ tərəflərin çoxhədlilərində sistemi əldə edirik xətti tənliklər. Sistemi həll edərkən qeyri-müəyyən əmsalları təyin edirik.

Şəxsi dəyərlər metodu.

Çünki çoxhədlilər eyni şəkildə bərabərdir, onda əvəzedicidir hər hansı bir ədədin sol və sağ tərəflərinə, naməlum əmsallara görə xətti olan həqiqi bərabərlik əldə edirik. Bu qədər dəyərləri əvəz etmək , neçə naməlum əmsal var, xətti tənliklər sistemi alırıq. Əvəzində İstənilən rəqəmləri sol və sağ tərəflərə əvəz edə bilərsiniz, lakin fraksiyaların məxrəclərinin köklərini əvəz etmək daha rahatdır.

Naməlum əmsalların qiymətlərini tapdıqdan sonra orijinal kəsr inteqraldakı sadə fraksiyaların cəmi kimi yazılır və hər bir sadə kəsr üzərində əvvəllər müzakirə olunan inteqrasiya aparılır.

İnteqrasiya sxemi rasional kəsrlər:

1. Əgər inteqral düzgün deyilsə, onda onu çoxhədli və uyğun rasional kəsrin cəmi kimi təqdim etmək lazımdır (yəni, çoxhədli çoxhədlini məxrəc çoxhədli ilə qalığa bölmək). İnteqral düzgündürsə, dərhal diaqramın ikinci nöqtəsinə keçirik.

2. Mümkünsə, düzgün rasional kəsrin məxrəcini çarpazlayın.

3. Qeyri-müəyyən əmsallar üsulundan istifadə edərək düzgün rasional kəsri sadə rasional kəsrlərin cəminə parçalayın.

4. Çoxhədli və sadə kəsrlərin cəmini inteqral edin.

Misal 28.

Rasional kəsrlərin inteqrallarını tapın:

;
;
b)
.

Həll.

;
.

Çünki inteqral düzgün olmayan rasional kəsrdir, onda biz bütün hissəni seçirik, yəni. Gəlin onu çoxhədli və uyğun rasional kəsrin cəmi kimi təsəvvür edək. Küncdən istifadə edərək saydakı çoxhədlini məxrəcdəki çoxhədliyə bölün.

Orijinal inteqral aşağıdakı formanı alacaq:
.

Qeyri-müəyyən əmsallar metodundan istifadə edərək düzgün rasional kəsri sadə kəsrlərin cəminə parçalayaq:

, alırıq:

Xətti tənliklər sistemini həll edərək qeyri-müəyyən əmsalların dəyərlərini alırıq: A = 1; IN = 3.

Sonra tələb olunan genişləndirmə formaya malikdir:
.

=
.

b)
.

.

Məxrəcləri atıb sol və sağ tərəfləri bərabərləşdirək:

Eyni dərəcələrdə əmsalların bərabərləşdirilməsi , sistemi alırıq:

Beş xətti tənlik sistemini həll edərək, müəyyən edilməmiş əmsalları tapırıq:

.

Yaranan genişlənməni nəzərə alaraq orijinal inteqralı tapaq:

.

V)
.

Qeyri-müəyyən əmsallar metodundan istifadə edərək inteqranı (düzgün rasional kəsr) sadə kəsrlərin cəminə genişləndirək. Parçalanmanı formada axtarırıq:

.

Ümumi məxrəcə endirərək, əldə edirik:

Məxrəcləri atıb sol və sağ tərəfləri bərabərləşdirək:

Qeyri-müəyyən əmsalları tapmaq üçün biz qismən dəyər metodunu tətbiq edirik. əlavə edək amillərin yox olduğu qismən dəyərlər, yəni bu dəyərləri son ifadə ilə əvəz edirik və üç tənlik alırıq:

;
;

;
;

;
.

Sonra tələb olunan genişləndirmə formaya malikdir:

Yaranan genişlənməni nəzərə alaraq orijinal inteqralı tapaq:

Verilmiş X intervalında diferensiallana bilən F(x) funksiyası adlanır funksiyanın əks törəməsi f(x) və ya f(x) inteqralı, əgər hər x ∈X üçün aşağıdakı bərabərlik olarsa:

F " (x) = f(x). (8.1)

Verilmiş funksiya üçün bütün əks törəmələrin tapılması onun adlanır inteqrasiya. Qeyri-müəyyən inteqral funksiya f(x) verilmiş intervalda X f(x) funksiyası üçün bütün əks törəmə funksiyaların çoxluğudur; təyinat -

Əgər F(x) f(x) funksiyasının hansısa əks törəməsidirsə, onda ∫ f(x)dx = F(x) + C, (8.2)

burada C ixtiyari sabitdir.

İnteqrallar cədvəli

Birbaşa tərifdən əsas xüsusiyyətləri əldə edirik yox müəyyən inteqral və cədvəlli inteqralların siyahısı:

1) d∫f(x)dx=f(x)

2)∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Cədvəl inteqrallarının siyahısı

1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sin x + C

7. = arktan x + C

8. = arcsin x + C

10. = - ctg x + C

Dəyişən dəyişdirmə

Bir çox funksiyaları inteqrasiya etmək üçün dəyişən dəyişdirmə metodundan və ya istifadə edin əvəzetmələr, inteqralları cədvəl formasına endirməyə imkan verir.

Əgər f(z) funksiyası [α,β] üzərində kəsilməzdirsə, z =g(x) funksiyası davamlı törəmə və α ≤ g(x) ≤ β olur, onda

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

Üstəlik, sağ tərəfdəki inteqrasiyadan sonra z=g(x) əvəzi aparılmalıdır.

Bunu sübut etmək üçün orijinal inteqralı aşağıdakı formada yazmaq kifayətdir:

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Məsələn:

Parçalar üzrə inteqrasiya üsulu

u = f(x) və v = g(x) funksiyaları davamlı olan funksiyalar olsun. Sonra işə görə,

d(uv))= udv + vdu və ya udv = d(uv) - vdu.

d(uv) ifadəsi üçün antitörəmə açıq-aydın uv olacaq, ona görə də düstur belədir:

∫ udv = uv - ∫ vdu (8.4.)

Bu düstur qaydanı ifadə edir hissələri ilə inteqrasiya. udv=uv"dx ifadəsinin vdu=vu"dx ifadəsinin inteqrasiyasına gətirib çıxarır.

Məsələn, ∫xcosx dx tapmaq istəyirsən. Gəlin u = x, dv = cosxdx qoyaq, ona görə də du=dx, v=sinx. Sonra

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

Parçalar üzrə inteqrasiya qaydası dəyişənlərin əvəzlənməsindən daha məhdud əhatə dairəsinə malikdir. Lakin inteqralların bütün sinifləri var, məsələn,

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax və başqaları, hissələr üzrə inteqrasiyadan istifadə etməklə dəqiq hesablanır.

Müəyyən inteqral

Müəyyən inteqral anlayışı aşağıdakı kimi təqdim olunur. F(x) funksiyası intervalda təyin olunsun. [a,b] seqmentini bölək n a= x 0 nöqtələri üzrə hissələr< x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i =x i - x i-1. f(ξ i)Δ x i formasının cəminə deyilir inteqral cəmi, və onun λ = maxΔx i → 0-dakı həddi, əgər mövcuddursa və sonludursa, adlanır. müəyyən inteqral f(x) funksiyaları aüçün b və təyin olunur:

F(ξ i)Δx i (8.5).

Bu halda f(x) funksiyası çağırılır intervalda inteqral oluna bilir, a və b ədədləri çağırılır inteqralın aşağı və yuxarı hədləri.

Müəyyən bir inteqral üçün aşağıdakı xüsusiyyətlər doğrudur:

4), (k = const, k∈R);

5)

6)

7) f(ξ)(b-a) (ξ∈).

Son əmlak deyilir orta dəyər teoremi.

f(x) üzərində davamlı olsun. Onda bu seqmentdə qeyri-müəyyən inteqral var

∫f(x)dx = F(x) + C

və baş verir Nyuton-Leybnits düsturu, müəyyən inteqralı qeyri-müəyyən inteqrala bağlayan:

F(b) - F(a). (8.6)

Həndəsi şərh: müəyyən inteqral yuxarıdan y=f(x) əyrisi, x = a və x = b düz xətləri və oxun seqmenti ilə məhdudlaşan əyrixətti trapezoidin sahəsidir. öküz.

Yanlış inteqrallar

Sonsuz həddi olan inteqrallara və kəsikli (məhdudiyyətsiz) funksiyaların inteqrallarına deyilir. sənin deyil. Birinci növ düzgün olmayan inteqrallar - Bunlar sonsuz intervalda olan inteqrallardır və aşağıdakı kimi müəyyən edilir:

(8.7)

Əgər bu hədd mövcuddursa və sonludursa, ona deyilir f(x)-in konvergent yanlış inteqralı[a,+ ∞) intervalında və f(x) funksiyası çağırılır sonsuz intervalda inteqral oluna bilir[a,+ ∞). Əks halda, inteqral deyilir mövcud deyil və ya ayrılır.

(-∞,b] və (-∞, + ∞) intervalları üzrə uyğun olmayan inteqrallar oxşar şəkildə təyin olunur:

Sərhədsiz funksiyanın inteqralı anlayışını müəyyən edək. Əgər f(x) bütün qiymətlər üçün davamlıdırsa x f(x)-in sonsuz kəsilməyə malik olduğu c nöqtəsi istisna olmaqla, seqment ikinci növ düzgün olmayan inteqral f(x) a-dan b-ə qədər məbləğ deyilir:

əgər bu məhdudiyyətlər mövcuddursa və sonludursa. Təyinat:

İnteqral hesablamaların nümunələri

Misal 3.30.∫dx/(x+2) hesablayın.

Həll. t = x+2, sonra dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.

Misal 3.31. ∫ tgxdx tapın.

Həll.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. t=cosx olsun, onda ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Misal3.32 . ∫dx/sinx tapın

Həll.

Misal3.33. tap .

Həll. = .

Misal3.34 . ∫arctgxdx tapın.

Həll. Gəlin hissələrə görə inteqrasiya edək. u=arctgx, dv=dx kimi işarə edək. Onda du = dx/(x 2 +1), v=x, buradan ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; çünki
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Misal3.35 . ∫lnxdx hesablayın.

Həll.İnteqrasiyanı hissələr düsturu ilə tətbiq edərək, əldə edirik:
u=lnx, dv=dx, du=1/x dx, v=x. Onda ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Misal3.36 . ∫e x sinxdx hesablayın.

Həll. u = e x, dv = sinxdx, sonra du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx işarə edək. ∫e x cosxdx inteqralını da hissələrə görə inteqral edirik: u = e x , dv = cosxdx, du=e x dx, v=sinx. Bizdə:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx münasibətini əldə etdik, ondan 2∫e x sinx dx = - e x cosx + e x sinx + C.

Misal 3.37. J = ∫cos(lnx)dx/x hesablayın.

Həll. dx/x = dlnx olduğundan, J= ∫cos(lnx)d(lnx). lnx-i t ilə əvəz edərək J = ∫ costdt = sint + C = sin(lnx) + C inteqralına gəlirik.

Misal 3.38 . J = hesablayın.

Həll.= d(lnx) olduğunu nəzərə alaraq lnx = t əvəz edirik. Sonra J = .

Misal 3.39 . J = inteqralını hesablayın .

Həll. Bizdə: . Buna görə =
=
=.

belə daxil edildi: sqrt(tan(x/2)).

Nəticə pəncərəsində yuxarı sağ küncdəki Addımları göstər düyməsini sıxsanız, ətraflı bir həll əldə edəcəksiniz.
.

Hissələr üzrə inteqrasiya düsturu belə görünür:
Hissələr üzrə inteqrasiya üsulu bu düsturun tətbiqindən ibarətdir. Praktiki tətbiqdə qeyd etmək lazımdır ki, u və v inteqrasiya dəyişəninin funksiyalarıdır. İnteqrasiya dəyişəni x kimi təyin edilsin (inteqral qeydinin sonunda d diferensial işarəsindən sonrakı simvol). Onda u və v x funksiyalarıdır: u(x) və v(x) .
, .
Sonra
.

Və hissələr üzrə inteqrasiya düsturu formasını alır:
,
onlardan birini u kimi işarə edirik: g(x) = u, digəri üçün isə inteqral hesablanmalıdır (daha dəqiq desək, əks törəmə tapılmalıdır):
, onda dv = f(x) dx .

Bəzi hallarda f(x) = 1 .
,
Yəni inteqralda

g(x) = u, x = v qoya bilərik.

CV
;
.

Beləliklə, bu üsulda hissələrə görə inteqrasiya düsturu yadda saxlanılmalı və iki formada tətbiq edilməlidir:

Hissələr üzrə inteqrasiya yolu ilə hesablanmış inteqrallar

Loqarifmləri və tərs triqonometrik (hiperbolik) funksiyaları ehtiva edən inteqrallar

Loqarifmləri və tərs triqonometrik və ya hiperbolik funksiyaları ehtiva edən inteqrallar çox vaxt hissələrlə inteqrasiya olunur. Bu zaman loqarifm və ya tərs triqonometrik (hiperbolik) funksiyaları ehtiva edən hissə u, qalan hissəsi dv ilə işarələnir.
, , , , , , .

Hissələr üzrə inteqrasiya üsulu ilə hesablanan belə inteqralların nümunələri:

Çoxhədli və sin x, cos x və ya e x hasilini ehtiva edən inteqrallar
, , ,
Hissələr düsturundan istifadə edərək formanın inteqralları tapılır: burada P(x) x-də çoxhədlidir.İnteqrasiya zamanı P(x) polinomu u ilə, e ax dx, çünki ax dx və ya

günah ax dx
, , .

- dv vasitəsilə.

Bu cür inteqralların nümunələri:

Hissələr üzrə inteqrasiya metodundan istifadə etməklə inteqralların hesablanması nümunələri

Loqarifmləri və tərs triqonometrik funksiyaları ehtiva edən inteqralların nümunələri

Misal

İnteqralı hesablayın:
Ətraflı həll Burada inteqral loqarifmi ehtiva edir. Əvəzetmələrin edilməsi,
u = ln x.
Hissələr üzrə inteqrasiya üsulu bu düsturun tətbiqindən ibarətdir. Praktiki tətbiqdə qeyd etmək lazımdır ki, u və v inteqrasiya dəyişəninin funksiyalarıdır. İnteqrasiya dəyişəni x kimi təyin edilsin (inteqral qeydinin sonunda d diferensial işarəsindən sonrakı simvol). Onda u və v x funksiyalarıdır: u(x) və v(x) .
,
.

dv = x
.
Hissələr üzrə inteqrasiya üsulu bu düsturun tətbiqindən ibarətdir. Praktiki tətbiqdə qeyd etmək lazımdır ki, u və v inteqrasiya dəyişəninin funksiyalarıdır. İnteqrasiya dəyişəni x kimi təyin edilsin (inteqral qeydinin sonunda d diferensial işarəsindən sonrakı simvol). Onda u və v x funksiyalarıdır: u(x) və v(x) .
.
2 dx

Qalan inteqralı hesablayırıq:

Hesablamaların sonunda C sabitini əlavə etmək lazımdır, çünki qeyri-müəyyən inteqral bütün antiderivativlərin çoxluğudur. O, həmçinin aralıq hesablamalara əlavə edilə bilər, lakin bu, yalnız hesablamaları çətinləşdirir.

.

Daha qısa həll

Həllini daha qısa versiyada təqdim edə bilərsiniz. Bunun üçün u və v ilə əvəzləmələr etmək lazım deyil, lakin siz amilləri qruplaşdıra və ikinci formada hissələr düsturuna görə inteqrasiyanı tətbiq edə bilərsiniz.

Hissələr üzrə inteqrasiya metodundan istifadə etməklə inteqralların hesablanması nümunələri

Loqarifmləri və tərs triqonometrik funksiyaları ehtiva edən inteqralların nümunələri
.

Cavab verin

Çoxhədli və sin x, cos x və ya ex hasilini ehtiva edən inteqral nümunələri
Həll.

Diferensial işarəsi altında eksponent təqdim edək:
.
e - x dx = - e - x d(-x) = - d(e - x)
.
.
.
Gəlin hissələrə görə inteqrasiya edək.