SYSTÉM HOMOGENNÍCH LINEÁRNÍCH ROVNIC

Systém homogenní lineární rovnice nazývaný systém formuláře

Je jasné, že v tomto případě , protože všechny prvky jednoho ze sloupců v těchto determinantech se rovnají nule.

Protože neznámé se nalézají podle vzorců , pak v případě, kdy Δ ≠ 0, má systém jedinečné nulové řešení X = y = z= 0. V mnoha problémech je však zajímavá otázka, zda má homogenní systém jiná řešení než nula.

Teorém. Aby lineární systém homogenní rovnice měl nenulové řešení, je nutné a postačující, aby Δ ≠ 0.

Pokud je tedy determinant Δ ≠ 0, pak má systém jedinečné řešení. Je-li Δ ≠ 0, pak má soustava lineárních homogenních rovnic nekonečný počet řešení.

Příklady.

Vlastní vektory a vlastní hodnoty matice

Nechť je dána čtvercová matice , X– nějaký maticový sloupec, jehož výška se shoduje s řádem matice A. .

V mnoha úlohách musíme uvažovat rovnici pro X

kde λ je určité číslo. Je jasné, že pro libovolné λ má tato rovnice nulové řešení.

Číslo λ, pro které má tato rovnice nenulová řešení, se nazývá vlastní hodnota matrice A, A X neboť takové λ se říká vlastní vektor matrice A.

Pojďme najít vlastní vektor matice A. Protože E∙X = X, pak lze maticovou rovnici přepsat jako nebo . V rozšířené formě lze tuto rovnici přepsat jako systém lineárních rovnic. Opravdu .

A proto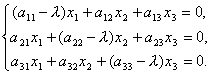

Získali jsme tedy systém homogenních lineárních rovnic pro určení souřadnic x 1, x 2, x 3 vektor X. Aby systém měl nenulová řešení, je nutné a postačující, aby determinant systému byl roven nule, tzn.

Toto je rovnice 3. stupně pro λ. Jmenuje se to charakteristická rovnice matrice A a slouží k určení vlastních hodnot λ.

Každé vlastní číslo λ odpovídá vlastnímu vektoru X, jehož souřadnice jsou určeny ze systému při odpovídající hodnotě λ.

Příklady.

VEKTOROVÁ ALGEBRA. KONCEPCE VEKTORU

Při studiu různých odvětví fyziky existují veličiny, které jsou zcela určeny uvedením jejich číselných hodnot, například délka, plocha, hmotnost, teplota atd. Takové veličiny se nazývají skalární. Kromě nich však existují ještě veličiny, k jejichž určení je kromě číselné hodnoty nutné znát i jejich směr v prostoru, například sílu působící na těleso, rychlost a zrychlení kulovnice. tělo, když se pohybuje v prostoru, napětí magnetické pole v daném bodě prostoru atd. Takové veličiny se nazývají vektorové veličiny.

Uveďme striktní definici.

Režie segmentu Nazvěme segment, podle jehož konců je známo, který z nich je první a který druhý.

Vektor nazývaný směrovaný segment mající určitou délku, tzn. Jedná se o úsek určité délky, ve kterém je jeden z bodů, který jej omezuje, považován za začátek a druhý za konec. Li A- začátek vektoru, B je jeho konec, pak se vektor značí symbolem navíc se vektor často značí jedním písmenem. Na obrázku je vektor označen úsečkou a jeho směr šipkou.

Modul nebo délka Vektor se nazývá délka směrovaného segmentu, který jej definuje. Označeno || nebo ||.

Jako vektory zařadíme i tzv. nulový vektor, jehož začátek a konec se shodují. Je určeno. Nulový vektor nemá konkrétní směr a jeho modul je nula ||=0.

Vektory se nazývají kolineární, pokud jsou umístěny na stejné linii nebo na rovnoběžných liniích. Navíc, pokud jsou vektory a ve stejném směru, napíšeme opak.

Nazývají se vektory umístěné na přímkách rovnoběžných se stejnou rovinou koplanární.

Tyto dva vektory se nazývají rovnat se, pokud jsou kolineární, mají stejný směr a jsou stejně dlouhé. V tomto případě píšou.

Z definice rovnosti vektorů vyplývá, že vektor může být transportován rovnoběžně sám se sebou, přičemž jeho počátek je umístěn v libovolném bodě prostoru.

Například.

LINEÁRNÍ OPERACE S VEKTORY

1. Násobení vektoru číslem.

   Součin vektoru a čísla λ je nový vektor takový, že:

   Součin vektoru a čísla λ se značí .

   

   Například, existuje vektor nasměrovaný stejným směrem jako vektor a má poloviční délku než vektor.

   Uvedená operace má následující vlastnosti:

2. Vektorové sčítání.

   Nechť a být dva libovolné vektory. Vezměme si libovolný bod Ó a zkonstruovat vektor. Poté od bodu A vektor necháme stranou. Zavolá se vektor spojující začátek prvního vektoru s koncem druhého množství těchto vektorů a je označen .

   

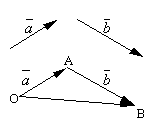
   Formulovaná definice sčítání vektorů se nazývá pravidlo rovnoběžníku, protože stejný součet vektorů lze získat následovně. Odložme od věci Ó vektory a . Na těchto vektorech sestrojme rovnoběžník OABC. Od vektorů pak vektor, což je úhlopříčka rovnoběžníku vytaženého z vrcholu Ó, bude zjevně součtem vektorů.

   

   Je snadné zkontrolovat následující vlastnosti sčítání vektorů.

3. Vektorový rozdíl.

   Nazývá se vektor kolineární k danému vektoru, stejně dlouhý a opačně orientovaný naproti vektor pro vektor a je označeno . Opačný vektor lze považovat za výsledek vynásobení vektoru číslem λ = –1: .

Vlastní čísla (čísla) a vlastní vektory.
Příklady řešení

Buď sám sebou

Z obou rovnic vyplývá, že .

Tak si to řekněme: .

Jako výsledek: – druhý vlastní vektor.

zopakujme důležité bodyřešení:

– výsledný systém určitě má společné rozhodnutí(rovnice jsou lineárně závislé);

– „y“ vybereme tak, aby bylo celé číslo a první souřadnice „x“ byla celá, kladná a co nejmenší.

– zkontrolujeme, zda konkrétní řešení vyhovuje každé rovnici soustavy.

Odpovědět .

Středně pokročilí " kontrolní body“ byl zcela dostačující, takže kontrola rovnosti je v zásadě zbytečná.

V různých zdrojích informací jsou souřadnice vlastních vektorů často zapsány nikoli ve sloupcích, ale v řádcích, například: (a abych byl upřímný, sám jsem zvyklý je zapisovat do řádků). Tato možnost je přijatelná, ale ve světle tématu lineární transformace technicky pohodlnější použití sloupcové vektory.

Možná se vám řešení zdálo velmi dlouhé, ale to jen proto, že jsem velmi podrobně komentoval první příklad.

Příklad 2

Matice

Pojďme trénovat sami! Přibližná ukázka závěrečného úkolu na konci lekce.

Někdy musíte udělat dodatečný úkol, jmenovitě:

napsat kanonický maticový rozklad

co to je?

Pokud vlastní vektory matice tvoří základ, pak to může být reprezentováno jako:

Kde je matice složená ze souřadnic vlastních vektorů, – úhlopříčka matice s odpovídajícími vlastními hodnotami.

Tento rozklad matice se nazývá kanonický nebo úhlopříčka.

Podívejme se na matici prvního příkladu. Jeho vlastní vektory lineárně nezávislé(nekolineární) a tvoří základ. Vytvořme matici jejich souřadnic:

Na hlavní úhlopříčka matrice v příslušném pořadí jsou umístěny vlastní hodnoty a zbývající prvky se rovnají nule:
– Ještě jednou zdůrazňuji důležitost pořadí: „dva“ odpovídá 1. vektoru a nachází se tedy v 1. sloupci, „tři“ – 2. vektoru.

Podle na obvyklý algoritmus nález inverzní matice nebo Gauss-Jordanova metoda shledáváme . Ne, to není překlep! - před vámi je vzácná událost, jako je zatmění Slunce, kdy se opak shodoval s původní maticí.

Zbývá zapsat kanonický rozklad matice:

Systém lze řešit pomocí elementárních transformací ak nim se uchýlíme v následujících příkladech tato metoda. Ale zde „školní“ metoda funguje mnohem rychleji. Z 3. rovnice vyjádříme: – dosadíme do druhé rovnice:

Protože první souřadnice je nulová, získáme z každé rovnice systém, z něhož vyplývá, že .

A znovu věnujte pozornost povinné přítomnosti lineárního vztahu. Pokud se získá jen triviální řešení , pak buď bylo nesprávně nalezeno vlastní číslo, nebo byl systém zkompilován/vyřešen s chybou.

Kompaktní souřadnice udávají hodnotu

Vlastní vektor:

A ještě jednou zkontrolujeme, že řešení bylo nalezeno splňuje každou rovnici systému. V dalších odstavcích a v navazujících úkolech doporučuji toto přání brát jako povinné pravidlo.

2) Pro vlastní hodnotu pomocí stejného principu získáme následující systém:

Z 2. rovnice soustavy vyjádříme: – dosadíme do třetí rovnice:

Protože souřadnice „zeta“ je rovna nule, získáme z každé rovnice systém, který následuje lineární závislost.

Nechat

Kontrola, že řešení splňuje každou rovnici systému.

Vlastní vektor je tedy: .

3) A konečně, systém odpovídá vlastní hodnotě:

Druhá rovnice vypadá nejjednodušší, tak ji vyjádřeme a dosaďte do 1. a 3. rovnice:

Vše je v pořádku – vznikla lineární závislost, kterou dosadíme do výrazu:

V důsledku toho byly „x“ a „y“ vyjádřeny prostřednictvím „z“: . V praxi není nutné dosahovat přesně takových vztahů, v některých případech je vhodnější vyjádřit jak prostřednictvím, tak i prostřednictvím . Nebo dokonce „vlak“ - například „X“ přes „I“ a „I“ přes „Z“

Tak si to řekněme:

Zkontrolujeme, že řešení bylo nalezeno splňuje každou rovnici systému a zapisuje třetí vlastní vektor

Odpovědět: vlastní vektory:

Geometricky tyto vektory definují tři různé prostorové směry ("Tam a zase zpátky"), podle kterého lineární transformace transformuje nenulové vektory (vlastní vektory) na kolineární vektory.

Pokud podmínka vyžadovala nalezení kanonického rozkladu, pak je to zde možné, protože různá vlastní čísla odpovídají různým lineárně nezávislým vlastním vektorům. Vytvoření matrice z jejich souřadnic, diagonální matice z relevantní vlastní hodnoty a najít inverzní matice .

Pokud podle podmínky potřebujete napsat lineární transformační matice na bázi vlastních vektorů, pak uvedeme odpověď ve tvaru . Je v tom rozdíl a ten rozdíl je podstatný! Protože tato matice je maticí „de“.

Problém s více jednoduché výpočty Pro nezávislé rozhodnutí:

Příklad 5

Najděte vlastní vektory lineární transformace dané maticí

Při hledání vlastních čísel se snažte nezajít až k polynomu 3. stupně. Vaše systémová řešení se navíc mohou lišit od mých řešení – zde není jistota; a vektory, které najdete, se mohou lišit od vzorových vektorů až do proporcionality jejich příslušných souřadnic. Například a. Je estetičtější prezentovat odpověď ve formuláři, ale je v pořádku, když se zastavíte u druhé možnosti. Všechno však má rozumné meze, verze už nevypadá moc dobře.

Přibližná závěrečná ukázka zadání na konci lekce.

Jak vyřešit problém v případě více vlastních čísel?

Obecný algoritmus zůstává stejný, ale má své vlastní charakteristiky a je vhodné ponechat některé části řešení v přísnějším akademickém stylu:

Příklad 6

Najděte vlastní čísla a vlastní vektory

Řešení

Samozřejmě, pojďme psát velkými písmeny báječný první sloupec:

A po rozkladu kvadratický trinom podle násobitelů:

V důsledku toho jsou získány vlastní hodnoty, z nichž dvě jsou násobky.

Pojďme najít vlastní vektory:

1) Pojďme se vypořádat s osamělým vojákem podle „zjednodušeného“ schématu:

Z posledních dvou rovnic je jasně patrná rovnost, která by se samozřejmě měla dosadit do 1. rovnice soustavy:

Lepší kombinaci nenajdete:
Vlastní vektor:

2-3) Nyní odstraníme několik strážců. V v tomto případě mohlo by to vyjít buď dva nebo jeden vlastní vektor. Bez ohledu na násobnost kořenů dosadíme hodnotu do determinantu která nám přináší další homogenní soustava lineárních rovnic:

Vlastní vektory jsou přesně vektory
základní systém řešení

Ve skutečnosti jsme během celé lekce nedělali nic jiného, ​​než že jsme nacházeli vektory základního systému. Jen tento termín nebyl prozatím nijak zvlášť vyžadován. Mimochodem ti šikovní studenti, kterým uniklo téma v maskáčích homogenní rovnice, bude nucen ji nyní kouřit.

Jedinou akcí bylo odstranění přebytečných řádků. Výsledkem je matice jedna po třech s formálním „krokem“ uprostřed.
– základní proměnná, – volné proměnné. Existují tedy dvě volné proměnné, existují také dva vektory základního systému.

Vyjádřeme základní proměnnou pomocí volných proměnných: . Nulový multiplikátor před „X“ mu umožňuje nabývat absolutně jakýchkoli hodnot (což je jasně viditelné ze systému rovnic).

V kontextu tohoto problému je vhodnější napsat obecné řešení nikoli do řádku, ale do sloupce:

Pár odpovídá vlastnímu vektoru:
Pár odpovídá vlastnímu vektoru:

Poznámka : sofistikovaní čtenáři mohou tyto vektory vybrat ústně – jednoduše analýzou systému , ale jsou zde potřeba určité znalosti: existují tři proměnné, system matrix rank- jeden, což znamená základní rozhodovací systém sestává ze 3 – 1 = 2 vektorů. Nalezené vektory jsou však dobře viditelné i bez této znalosti, čistě na intuitivní úrovni. V tomto případě bude třetí vektor zapsán ještě „krásněji“: . Upozorňuji vás však, že v jiném příkladu nemusí být jednoduchý výběr možný, a proto je doložka určena zkušeným lidem. Navíc, proč nevzít, řekněme, jako třetí vektor? Koneckonců, jeho souřadnice také splňují každou rovnici systému a vektory lineárně nezávislé. Tato možnost je v zásadě vhodná, ale „křivá“, protože „jiný“ vektor je lineární kombinací vektorů základního systému.

Odpovědět: vlastní čísla: , vlastní vektory:

Podobný příklad pro nezávislé řešení:

Příklad 7

Najděte vlastní čísla a vlastní vektory

Přibližná ukázka finálního návrhu na konci lekce.

Je třeba poznamenat, že v 6. i 7. příkladu se získá trojice lineárně nezávislých vlastních vektorů, a proto je původní matice reprezentovatelná v kanonickém rozkladu. Ale takové maliny se nestávají ve všech případech:

Příklad 8

Řešení: Vytvořme a vyřešme charakteristickou rovnici:

Rozšiřme determinant v prvním sloupci:

Provádíme další zjednodušení podle uvažované metody, vyhýbáme se polynomu 3. stupně:

– vlastní hodnoty.

Pojďme najít vlastní vektory:

1) S kořenem nejsou žádné potíže:

Nebuďte překvapeni, kromě stavebnice se používají také proměnné - zde není žádný rozdíl.

Z 3. rovnice ji vyjádříme a dosadíme do 1. a 2. rovnice:

Z obou rovnic vyplývá:

Nechte tedy:

2-3) Pro více hodnot dostaneme systém .

Zapišme si matici systému a pomocí elementárních transformací ji uveďme do stupňovité podoby:

www.stránka vám umožní najít. Místo provede výpočet. Během několika sekund server nabídne správné řešení. Charakteristická rovnice pro matici bude algebraický výraz, zjištěné pravidlem pro výpočet determinantu matrice matrice, zatímco podél hlavní úhlopříčky budou rozdíly v hodnotách diagonálních prvků a proměnné. Při počítání charakteristická rovnice pro matici online, každý prvek matrice budou násobeny odpovídajícími dalšími prvky matrice. Najít v režimu online možné pouze pro čtverec matrice. Nálezová operace charakteristická rovnice pro matici online redukuje na výpočet algebraického součtu součinu prvků matrice v důsledku nalezení determinantu matrice, pouze za účelem určení charakteristická rovnice pro matici online. Tato operace zaujímá v teorii zvláštní místo matrice, umožňuje najít vlastní čísla a vektory pomocí kořenů. Úkol najít charakteristická rovnice pro matici online sestává z množících se prvků matrice následuje sečtení těchto produktů podle určitého pravidla. www.stránka najde charakteristická rovnice pro matici daný rozměr v režimu online. Výpočet charakteristická rovnice pro matici online vzhledem k jeho rozměru se jedná o nalezení polynomu s číselnými nebo symbolickými koeficienty, nalezenými podle pravidla pro výpočet determinantu matrice- jako součet součinů odpovídajících prvků matrice, pouze za účelem určení charakteristická rovnice pro matici online. Hledání polynomu vzhledem k proměnné pro kvadratiku matrice, jako definice charakteristická rovnice pro matici, teoreticky běžné matrice. Význam kořenů polynomu charakteristická rovnice pro matici online používá se k určení vlastních vektorů a vlastních hodnot pro matrice. Navíc pokud je determinant matrice bude tedy rovna nule charakteristická rovnice matice bude stále existovat, na rozdíl od opačného matrice. Aby bylo možné počítat charakteristická rovnice pro matici nebo najít několik najednou matice charakteristické rovnice, musíte strávit spoustu času a úsilí, zatímco náš server najde během několika sekund charakteristická rovnice pro matici online. V tomto případě odpověď na nalezení charakteristická rovnice pro matici online budou správné a s dostatečnou přesností, i když čísla při nálezu charakteristická rovnice pro matici online bude iracionální. Na stránce www.stránka v prvcích jsou povoleny znaky matrice, to je charakteristická rovnice pro matici online lze při výpočtu reprezentovat v obecné symbolické formě charakteristická rovnice matice online. Získanou odpověď je užitečné zkontrolovat při řešení problému hledání charakteristická rovnice pro matici online pomocí webu www.stránka. Při provádění operace výpočtu polynomu - charakteristická rovnice matice, musíte být při řešení tohoto problému opatrní a extrémně soustředění. Naše stránky vám zase pomohou zkontrolovat vaše rozhodnutí o tématu charakteristická rovnice matice online. Pokud nemáte čas na dlouhé kontroly vyřešených problémů, tak www.stránka bude jistě pohodlným nástrojem pro kontrolu při hledání a výpočtu charakteristická rovnice pro matici online.

Vlastní vektor čtvercové matice je ten, který po vynásobení danou maticí vede ke kolineárnímu vektoru. Jednoduše řečeno, při vynásobení matice vlastním vektorem zůstane tento stejný, ale vynásobený určitým číslem.

Definice

Vlastní vektor je nenulový vektor V, který se po vynásobení čtvercovou maticí M sám zvětší o nějaké číslo λ. V algebraickém zápisu to vypadá takto:

M × V = λ × V,

kde λ je vlastní hodnota matice M.

Uvažujme číselný příklad. Pro usnadnění záznamu budou čísla v matici oddělena středníkem. Mějme matici:

• M = 0; 4;
• 6; 10.

Vynásobme to sloupcovým vektorem:

• V = -2;

Když vynásobíme matici sloupcovým vektorem, dostaneme také sloupcový vektor. Přísný matematický jazyk Vzorec pro násobení matice 2 × 2 sloupcovým vektorem by vypadal takto:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 znamená prvek matice M umístěný v prvním řádku a prvním sloupci a M22 znamená prvek umístěný v druhém řádku a druhém sloupci. Pro naši matici se tyto prvky rovnají M11 = 0, M12 = 4, M21 = 6, M22 10. Pro sloupcový vektor se tyto hodnoty rovnají V11 = –2, V21 = 1. Podle tohoto vzorce dostaneme následující výsledek součinu čtvercové matice vektorem:

• M x V = 0 x (-2) + (4) x (1) = 4;
• 6 x (-2) + 10 x (1) = -2.

Pro usnadnění zapišme sloupcový vektor do řádku. Čtvercovou matici jsme tedy vynásobili vektorem (-2; 1), čímž jsme získali vektor (4; -2). Je zřejmé, že se jedná o stejný vektor vynásobený λ = -2. Lambda v tomto případě označuje vlastní hodnotu matice.

Vlastní vektor matice je kolineární vektor, to znamená objekt, který po vynásobení maticí nemění svou polohu v prostoru. Pojem kolinearity ve vektorové algebře je podobný termínu rovnoběžnosti v geometrii. V geometrické interpretaci jsou kolineární vektory rovnoběžné směrované segmenty různých délek. Od dob Euklida víme, že jedna přímka má nekonečně mnoho rovnoběžných přímek, takže je logické předpokládat, že každá matice má nekonečný počet vlastních vektorů.

Z předchozího příkladu je zřejmé, že vlastní vektory mohou být (-8; 4) a (16; -8) a (32, -16). To vše jsou kolineární vektory odpovídající vlastní hodnotě λ = -2. Při vynásobení původní matice těmito vektory stejně skončíme s vektorem, který se od originálu liší 2x. Proto je při řešení úloh hledání vlastního vektoru nutné hledat pouze lineárně nezávislé vektorové objekty. Nejčastěji pro matici n × n existuje n počet vlastních vektorů. Naše kalkulačka je určena pro analýzu čtvercových matic druhého řádu, takže téměř vždy výsledek najde dva vlastní vektory, kromě případů, kdy se shodují.

Ve výše uvedeném příkladu jsme předem znali vlastní vektor původní matice a jasně určili číslo lambda. V praxi se však vše děje naopak: nejprve se najdou vlastní čísla a teprve potom vlastní vektory.

Algoritmus řešení

Podívejme se znovu na původní matici M a pokusme se najít oba její vlastní vektory. Matrix tedy vypadá takto:

• M = 0; 4;
• 6; 10.

Nejprve musíme určit vlastní hodnotu λ, což vyžaduje výpočet determinantu následující matice:

• (0 - λ); 4;
• 6; (10 - λ).

Tato matice se získá odečtením neznámého λ od prvků na hlavní diagonále. Determinant se určí pomocí standardního vzorce:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Protože náš vektor musí být nenulový, přijmeme výslednou rovnici jako lineárně závislou a srovnáme náš determinant detA s nulou.

(0 − λ) × (10 − λ) − 24 = 0

Otevřeme závorky a získáme charakteristickou rovnici matice:

λ 2 − 10λ − 24 = 0

To je standardní kvadratická rovnice, kterou je potřeba řešit přes diskriminant.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

Kořen diskriminantu je sqrt(D) = 14, tedy λ1 = -2, λ2 = 12. Nyní pro každou hodnotu lambda potřebujeme najít vlastní vektor. Vyjádřeme systémové koeficienty pro λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

V tomto vzorci je E matice identity. Na základě výsledné matice vytvoříme soustavu lineárních rovnic:

2x + 4 roky = 6x + 12 let,

kde x a y jsou prvky vlastního vektoru.

Sesbírejme všechna X nalevo a všechna Y napravo. Pochopitelně - 4x = 8 let. Vydělte výraz -4 a dostanete x = –2y. Nyní můžeme určit první vlastní vektor matice s libovolnými hodnotami neznámých (pamatujte na nekonečno lineárně závislých vlastních vektorů). Vezměme y = 1, pak x = –2. Proto první vlastní vektor vypadá jako V1 = (–2; 1). Vraťte se na začátek článku. Byl to tento vektorový objekt, kterým jsme vynásobili matici, abychom demonstrovali koncept vlastního vektoru.

Nyní najdeme vlastní vektor pro λ = 12.

• M - X x E = -12; 4
• 6; -2.

Vytvořme stejný systém lineárních rovnic;

• -12x + 4y = 6x − 2y
• -18x = -6 let
• 3x = y.

Nyní vezmeme x = 1, tedy y = 3. Druhý vlastní vektor tedy vypadá jako V2 = (1; 3). Při vynásobení původní matice daným vektorem bude výsledkem vždy stejný vektor vynásobený 12. Zde algoritmus řešení končí. Nyní víte, jak ručně určit vlastní vektor matice.

• determinant;
• stopa, tedy součet prvků na hlavní diagonále;
• rank, tedy maximální počet lineárně nezávislých řádků/sloupců.

Program pracuje podle výše uvedeného algoritmu a maximálně zkracuje proces řešení. Je důležité upozornit, že v programu je lambda označena písmenem „c“. Podívejme se na číselný příklad.

Příklad, jak program funguje

Zkusme určit vlastní vektory pro následující matici:

• M = 5; 13;
• 4; 14.

Zadejme tyto hodnoty do buněk kalkulačky a získáme odpověď v následujícím tvaru:

• Pořadí matice: 2;
• Maticový determinant: 18;
• Maticová stopa: 19;
• Výpočet vlastního vektoru: c 2 − 19,00c + 18,00 (charakteristická rovnice);
• Výpočet vlastního vektoru: 18 (první hodnota lambda);
• Výpočet vlastního vektoru: 1 (druhá hodnota lambda);
• Soustava rovnic pro vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
• Soustava rovnic pro vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
• Vlastní vektor 1: (1; 1);
• Vlastní vektor 2: (-3,25; 1).

Tak jsme získali dva lineárně nezávislé vlastní vektory.

Závěr

Lineární algebra a analytická geometrie jsou standardními předměty pro každého prváka v oboru strojírenství. Velké množství vektorů a matic je děsivé a v tak těžkopádných výpočtech je snadné udělat chybu. Náš program umožní studentům zkontrolovat své výpočty nebo automaticky vyřešit problém s nalezením vlastního vektoru. V našem katalogu jsou další kalkulačky lineární algebry, použijte je při studiu nebo práci.

Diagonální matice mají nejjednodušší strukturu. Nabízí se otázka, zda je možné najít základ, ve kterém by matice lineárního operátoru měla diagonální tvar. Takový základ existuje.
Nechť je nám dán lineární prostor R n a v něm působící lineární operátor A; v tomto případě operátor A vezme R n do sebe, tedy A:R n → R n .

Definice. Nenulový vektor se nazývá vlastní vektor operátoru A, pokud se operátor A převede na kolineární vektor, tzn. Číslo λ se nazývá vlastní hodnota nebo vlastní hodnota operátoru A, odpovídající vlastnímu vektoru.
Všimněme si některých vlastností vlastních čísel a vlastních vektorů.
1. Libovolná lineární kombinace vlastních vektorů operátor A odpovídající stejnému vlastnímu číslu λ je vlastní vektor se stejným vlastním číslem.
2. Vlastní vektory operátor A s párově odlišnými vlastními hodnotami λ 1 , λ 2 , …, λ m jsou lineárně nezávislé.
3. Jestliže vlastní čísla λ 1 =λ 2 = λ m = λ, pak vlastní číslo λ odpovídá nejvýše m lineárně nezávislých vlastních vektorů.

Pokud tedy existuje n lineárně nezávislých vlastních vektorů , odpovídající různým vlastním číslům λ 1, λ 2, ..., λ n, pak jsou lineárně nezávislé, proto je lze brát jako základ prostoru R n. Nalezněme tvar matice lineárního operátoru A na základě jeho vlastních vektorů, pro které budeme s operátorem A jednat na vektorech báze: Pak .
Matice lineárního operátoru A má tedy na základě svých vlastních vektorů diagonální tvar a vlastní hodnoty operátoru A jsou podél úhlopříčky.
Existuje jiný základ, ve kterém má matice diagonální tvar? Odpověď na tuto otázku dává následující věta.

Teorém. Matice lineárního operátoru A v bázi (i = 1..n) má diagonální tvar právě tehdy, když všechny vektory báze jsou vlastními vektory operátoru A.

Pravidlo pro hledání vlastních čísel a vlastních vektorů

Nechť je dán vektor , kde x 1 , x 2 , …, x n jsou souřadnice vektoru vzhledem k bázi a je vlastním vektorem lineárního operátoru A odpovídajícím vlastnímu číslu λ, tzn. Tento vztah lze zapsat v maticové formě

. (*)

Rovnici (*) lze považovat za rovnici pro hledání a , to znamená, že nás zajímají netriviální řešení, protože vlastní vektor nemůže být nula. Je známo, že netriviální řešení homogenní soustavy lineárních rovnic existují právě tehdy, když det(A - λE) = 0. Aby tedy λ bylo vlastní hodnotou operátoru A, je nutné a postačující, aby det(A - λE ) = 0.
Pokud je rovnice (*) napsána podrobně v souřadnicovém tvaru, získáme soustavu lineárních homogenních rovnic:

(1)
Kde - lineární operátorová matice.

Soustava (1) má nenulové řešení, pokud je její determinant D roven nule

Dostali jsme rovnici pro hledání vlastních čísel.
Tato rovnice se nazývá charakteristická rovnice a její levá strana- charakteristický polynom matice (operátor) A. Pokud charakteristický polynom nemá reálné kořeny, pak matice A nemá vlastní vektory a nelze ji redukovat do diagonální formy.
Nechť λ 1, λ 2, …, λ n jsou skutečné kořeny charakteristické rovnice a mezi nimi mohou být násobky. Dosazením těchto hodnot do systému (1) najdeme vlastní vektory.

Příklad 12. Lineární operátor A působí v R 3 podle zákona, kde x 1, x 2, .., x n jsou souřadnice vektoru v zákl. , , . Najděte vlastní čísla a vlastní vektory tohoto operátoru.
Řešení. Sestavíme matici tohoto operátoru:
.
Vytváříme systém pro určování souřadnic vlastních vektorů:

Sestavíme charakteristickou rovnici a vyřešíme ji:

.
λ 1,2 = -1, λ 3 = 3.
Dosazením λ = -1 do systému máme:
nebo
Protože , pak existují dvě závislé proměnné a jedna volná proměnná.
Nechť x 1 je tedy volná neznámá Tento systém vyřešíme jakýmkoliv způsobem a najdeme obecné řešení tohoto systému: Základní systémřešení se skládá z jednoho řešení, protože n - r = 3 - 2 = 1.
Množina vlastních vektorů odpovídajících vlastnímu číslu λ = -1 má tvar: , kde x 1 je libovolné číslo jiné než nula. Vyberme jeden vektor z této množiny, například dosadíme x 1 = 1: .
Podobně zjistíme, že vlastní vektor odpovídá vlastnímu číslu λ = 3: .
V prostoru R 3 se základna skládá ze tří lineárně nezávislých vektorů, ale dostali jsme pouze dva lineárně nezávislé vlastní vektory, z nichž základ v R 3 nelze poskládat. V důsledku toho nemůžeme matici A lineárního operátoru redukovat na diagonální tvar.

Příklad 13. Daná matrice .
1. Dokažte, že vektor je vlastním vektorem matice A. Najděte vlastní hodnotu odpovídající tomuto vlastnímu vektoru.
2. Najděte základ, ve kterém má matice A diagonální tvar.
Řešení.
1. Jestliže , pak je vlastní vektor

.
Vektor (1, 8, -1) je vlastní vektor. Vlastní číslo λ = -1.
Matice má diagonální tvar v bázi skládající se z vlastních vektorů. Jeden z nich je slavný. Pojďme najít zbytek.
Hledáme vlastní vektory ze systému:

Charakteristická rovnice: ;
(3 + A)[-2(2-A)(2+A)+3] = 0; (3+A)(A2-1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Pojďme najít vlastní vektor odpovídající vlastnímu číslu λ = -3:

Hodnost matice této soustavy je dvě a rovná se počtu neznámých, takže tato soustava má pouze nulové řešení x 1 = x 3 = 0. x 2 zde může být cokoliv jiného než nula, například x 2 = 1. Vektor (0 ,1,0) je tedy vlastní vektor odpovídající λ = -3. Pojďme zkontrolovat:
.
Je-li λ = 1, získáme soustavu
Hodnost matice je dvě. Poslední rovnici škrtneme.
Nechť x 3 je volná neznámá. Potom x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Za předpokladu x 3 = 1 máme (-3,-9,1) - vlastní vektor odpovídající vlastnímu číslu λ = 1. Zkontrolujte:

.
Protože jsou vlastní čísla skutečná a odlišná, vektory jim odpovídající jsou lineárně nezávislé, takže je lze vzít jako základ v R 3 . Tedy v zákl , , matice A má tvar:
.
Ne každou matici lineárního operátoru A:R n → R n lze redukovat na diagonální tvar, protože pro některé lineární operátory Lineárně nezávislých vlastních vektorů může být méně než n. Pokud je však matice symetrická, pak kořen charakteristické rovnice násobnosti m odpovídá přesně m lineárně nezávislým vektorům.

Definice. Symetrická matice je čtvercová matice, ve které jsou prvky symetrické kolem hlavní diagonály stejné, tj.
Poznámky. 1. Všechny vlastní hodnoty symetrické matice jsou reálné.
2. Vlastní vektory symetrické matice odpovídající párově různým vlastním číslům jsou ortogonální.
Jako jednu z mnoha aplikací studovaného aparátu považujeme problém určení typu křivky druhého řádu.