Fisherovo kritérium
Fisherovo kritérium se používá k testování hypotézy, že rozptyly dvou obecné populace, distribuované podle normálního zákona. Je to parametrické kritérium.
Fisherův F test se nazývá variační poměr, protože je tvořen jako poměr dvou nezaujatých odhadů rozptylů, které se porovnávají.
Nechť získají dva vzorky jako výsledek pozorování. Od nich odchylky a 
mít 
A 
stupně svobody. Budeme předpokládat, že první vzorek je odebrán z populace s rozptylem 
, a druhý je z běžné populace s rozptylem 
. Je předložena nulová hypotéza o rovnosti dvou rozptylů, tzn. H0: 
nebo . Pro zamítnutí této hypotézy je nutné prokázat významnost rozdílu na dané hladině významnosti 
.
Hodnota kritéria se vypočítá pomocí vzorce:
Je zřejmé, že pokud jsou rozptyly stejné, bude hodnota kritéria rovna jedné. V ostatních případech bude větší (menší) než jedna.
Test má Fisherovo rozdělení 
. Fisherův test - dvoustranný test a nulová hypotéza 
zamítnuta ve prospěch alternativy 
Pokud . Tady kde 
– objem prvního a druhého vzorku.
Systém STATISTICA implementuje jednostranný Fisherův test, tzn. jako kvalita se vždy bere maximální rozptyl. V tomto případě je nulová hypotéza zamítnuta ve prospěch alternativního if.
Příklad
Nechť je úkol nastaven tak, aby porovnal efektivitu výuky dvou skupin žáků. Úroveň úspěchu charakterizuje úroveň řízení procesu učení a rozptylem je kvalita řízení učení, stupeň organizace procesu učení. Oba ukazatele jsou nezávislé a obecný případ je třeba posuzovat společně. Úroveň studijního výkonu (matematické očekávání) každé skupiny studentů je charakterizována aritmetickými průměry 
a , a kvalita je charakterizována odpovídajícími výběrovými rozptyly odhadů: a . Při hodnocení úrovně aktuálního výkonu se ukázalo, že u obou studentů byla stejná: 
= = 4,0. Vzorové odchylky: 
A 
. Počty stupňů volnosti odpovídající těmto odhadům: 
A 
. Odtud pro stanovení rozdílů v efektivitě učení můžeme využít stabilitu akademického výkonu, tzn. Pojďme si hypotézu otestovat.
Pojďme počítat 
(v čitateli by měl být velký rozptyl), . Podle tabulek ( STATISTIKA –
PravděpodobnostRozděleníKalkulačka)
zjistíme , což je méně než vypočítané, proto by měla být nulová hypotéza zamítnuta ve prospěch alternativy. Tento závěr nemusí výzkumníka uspokojit, protože ho zajímá skutečná hodnota poměru 
(v čitateli máme vždy velký rozptyl). Při kontrole jednostranného kritéria dostaneme, že je menší než výše vypočítaná hodnota. Nulová hypotéza tedy musí být zamítnuta ve prospěch alternativy.
Fisherův test v programu STATISTICA v prostředí Windows
Pro příklad testování hypotézy (Fisherovo kritérium) použijeme (vytvoříme) soubor se dvěma proměnnými (fisher.sta):
Rýže. 1. Tabulka se dvěma nezávislými proměnnými
K otestování hypotézy je nutné v základní statistice ( ZákladníStatistikaaTabulky) vyberte t-test pro nezávislé proměnné. ( t-test, nezávislý, podle proměnných).
Rýže. 2. Testování parametrických hypotéz
Po výběru proměnných a stisknutí klávesy souhrn Vypočítají se hodnoty směrodatných odchylek a Fisherovo kritérium. Kromě toho je stanovena hladina významnosti p, ve kterém je rozdíl nepatrný.
Rýže. 3. Výsledky testování hypotéz (F-test)
Použitím PravděpodobnostKalkulačka a nastavením hodnot parametrů můžete sestavit graf Fisherova rozdělení s označenou vypočítanou hodnotou.
Rýže. 4. Oblast přijetí (zamítnutí) hypotézy (F-kritérium)
Prameny.
Testování hypotéz o vztahu mezi dvěma rozptyly
URL: /tryfonov3/terms3/testdi.htm
Přednáška 6. :8080/resources/math/mop/lections/lection_6.htm
F – Fisherovo kritérium
URL: /home/portal/applications/Multivariatadvisor/F-Fisher/F-Fisheer.htm
Teorie a praxe pravděpodobnostního statistického výzkumu.
URL: /active/referats/read/doc-3663-1.html
F – Fisherovo kritérium
Fisherovo kritérium umožňuje porovnat výběrové rozptyly dvou nezávislých vzorků. Chcete-li vypočítat F emp, musíte najít poměr rozptylů dvou vzorků tak, aby větší rozptyl byl v čitateli a menší ve jmenovateli. Vzorec pro výpočet Fisherova kritéria je:
kde jsou rozptyly prvního a druhého vzorku.
Protože podle podmínek kritéria musí být hodnota čitatele větší nebo rovna hodnotě jmenovatele, bude hodnota F emp vždy větší nebo rovna jedné.
Počet stupňů volnosti se také určuje jednoduše:
k 1 =n l - 1 pro první vzorek (tj. pro vzorek, jehož rozptyl je větší) a k 2 = n 2 - 1 pro druhý vzorek.
V příloze 1 jsou kritické hodnoty Fisherova kritéria zjištěny hodnotami k 1 (horní řádek tabulky) a k 2 (levý sloupec tabulky).
Pokud t em >t crit, pak je přijata nulová hypotéza, jinak je přijata alternativa.
Příklad 3 Testování probíhalo ve dvou třetích třídách duševní vývoj deset studentů na testu TURMSH. Získané průměrné hodnoty se významně nelišily, ale psychologa zajímá otázka, zda existují rozdíly ve stupni homogenity ukazatelů duševního rozvoje mezi třídami.
Řešení. Pro Fisherův test je nutné porovnat rozptyly skóre testu v obou třídách. Výsledky testu jsou uvedeny v tabulce:
Tabulka 3.
|
Student č. |
První stupeň |
Druhá třída |
Po výpočtu rozptylů pro proměnné X a Y získáme:
s X 2 =572,83; s y 2 =174,04
Potom pomocí vzorce (8) pro výpočet pomocí Fisherova F kritéria zjistíme:
Podle tabulky z Přílohy 1 pro kritérium F se stupni volnosti v obou případech rovnými k = 10 - 1 = 9 zjistíme F crit = 3,18 (<3.29), следовательно, в терминах статистических гипотез можно утверждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.
6.2 Neparametrické testy
Porovnáním okem (procentuálně) výsledků před a po jakémkoli dopadu dospívá výzkumník k závěru, že pokud jsou pozorovány rozdíly, pak existuje rozdíl ve srovnávaných vzorcích. Tento přístup je kategoricky nepřijatelný, protože pro procenta není možné určit úroveň spolehlivosti v rozdílech. Procenta sama o sobě neumožňují vyvodit statisticky spolehlivé závěry. K prokázání účinnosti jakékoli intervence je nutné identifikovat statisticky významný trend ve vychýlení (posunu) ukazatelů. K řešení takových problémů může výzkumník použít řadu diskriminačních kritérií. Níže budeme zvažovat neparametrické testy: znaménkový test a chí-kvadrát test.
)Výpočet kritéria φ*
1. Určete hodnoty atributu, které budou kritériem pro rozdělení subjektů na ty, které „mají vliv“ a ty, které „nemají vliv“. Pokud je charakteristika měřena kvantitativně, použijte k nalezení optimálního separačního bodu kritérium λ.
2. Nakreslete čtyřbuněčnou (synonymum: čtyřpolní) tabulku se dvěma sloupci a dvěma řádky. První sloupec je „existuje účinek“; druhý sloupec - „žádný účinek“; první řádek shora - 1 skupina (ukázka); druhý řádek - skupina 2 (ukázka).
4. Spočítejte počet subjektů v prvním vzorku, kteří nemají „žádný účinek“ a zadejte toto číslo do pravé horní buňky tabulky. Vypočítejte součet dvou horních buněk. Měl by se shodovat s počtem předmětů v první skupině.
6. Spočítejte počet subjektů ve druhém vzorku, kteří nemají „žádný účinek“ a zadejte toto číslo do pravé dolní buňky tabulky. Vypočítejte součet dvou spodních buněk. Měl by se shodovat s počtem subjektů ve druhé skupině (vzorku).
7. Určete procento subjektů, které „mají vliv“, vztažením jejich počtu k celkovému počtu subjektů v dané skupině (vzorku). Výsledná procenta zapište do levé horní a levé dolní buňky tabulky do závorek, aby nedošlo k jejich záměně s absolutními hodnotami.
8. Zkontrolujte, zda se jedno z porovnávaných procent rovná nule. Pokud je tomu tak, zkuste to změnit posunutím bodu oddělení skupiny jedním nebo druhým směrem. Pokud to není možné nebo nežádoucí, opusťte kritérium φ* a použijte kritérium χ2.
9. Určete podle tabulky. XII Příloha 1 úhly φ pro každé z porovnávaných procent.
kde: φ1 - úhel odpovídající většímu procentu;
φ2 - úhel odpovídající menšímu procentu;
N1 - počet pozorování ve vzorku 1;
N2 - počet pozorování ve vzorku 2.
11. Porovnejte získanou hodnotu φ* s kritickými hodnotami: φ* ≤1,64 (p<0,05) и φ* ≤2,31 (р<0,01).
Pokud φ*emp ≤φ*cr. H0 je zamítnuto.
V případě potřeby určete přesnou hladinu významnosti výsledného φ*emp podle tabulky. XIII Příloha 1.
Tato metoda je popsána v mnoha příručkách (Plokhinsky N.A., 1970; Gubler E.V., 1978; Ivanter E.V., Korosov A.V., 1992 atd.) Tento popis je založen na verzi metody, která byla vyvinuta a prezentována E.V. Gubler.
Účel kritéria φ*
Fisherovo kritérium je určeno k porovnání dvou vzorků podle četnosti výskytu efektu (ukazatele), který je pro výzkumníka zajímavý. Čím je větší, tím jsou rozdíly spolehlivější.
Popis kritéria
Kritérium hodnotí spolehlivost rozdílů mezi těmi procentuálními podíly dvou vzorků, ve kterých byl zaznamenán pro nás zajímavý efekt (ukazatel). Obrazně řečeno porovnáme 2 nejlepší kousky nakrájené ze 2 koláčů a rozhodneme, který je skutečně větší.
Podstatou Fisherovy úhlové transformace je převod procent na hodnoty středového úhlu, které se měří v radiánech. Větší procento bude odpovídat většímu úhlu φ a menší procento bude odpovídat menšímu úhlu, ale vztahy zde nejsou lineární:
kde P je procento vyjádřené ve zlomcích jednotky (viz obr. 5.1).
S rostoucím nesouladem mezi úhly φ 1 a φ 2 a zvýšením počtu vzorků se hodnota kritéria zvyšuje. Čím větší je hodnota φ*, tím je pravděpodobnější, že rozdíly jsou významné.
Hypotézy
H 0 : Podíl osob, ve kterých se studovaný efekt projevuje, jich ve vzorku 1 není více než ve vzorku 2.
H 1 : Podíl jedinců, kteří vykazují studovaný účinek, je větší ve vzorku 1 než ve vzorku 2.
Grafické znázornění kritéria φ*
Metoda úhlové transformace je poněkud abstraktnější než ostatní kritéria.
Vzorec, kterým se řídí E.V. Gubler při výpočtu hodnot φ, předpokládá, že 100 % tvoří úhel φ=3,142, tedy zaokrouhlenou hodnotu π=3,14159... To nám umožňuje prezentovat porovnávané vzorky ve formě dva půlkruhy, z nichž každý symbolizuje 100 % populace svého vzorku. Procenta subjektů s „efektem“ budou reprezentována jako sektory tvořené středovými úhly φ. Na Obr. Obrázek 5.2 ukazuje dva půlkruhy ilustrující příklad 1. V prvním vzorku vyřešilo problém 60 % subjektů. Toto procento odpovídá úhlu φ=1,772. Ve druhém vzorku problém vyřešilo 40 % subjektů. Toto procento odpovídá úhlu φ =1,369.
Kritérium φ* nám umožňuje určit, zda je jeden z úhlů skutečně statisticky významně lepší než druhý pro dané velikosti vzorku.
Omezení kritéria φ*
1. Žádný z porovnávaných poměrů by neměl být nulový. Formálně neexistují žádné překážky pro aplikaci metody φ v případech, kdy je podíl pozorování v jednom ze vzorků roven 0. V těchto případech se však výsledek může ukázat jako neoprávněně nafouknutý (Gubler E.V., 1978, s. 86).
2. Horní v kritériu φ není žádné omezení - vzorky mohou být libovolně velké.
Dolní limit - 2 pozorování v jednom ze vzorků. Je však třeba dodržet následující poměry v počtu dvou vzorků:
a) pokud má jeden vzorek pouze 2 pozorování, pak druhý musí mít alespoň 30:
b) má-li jeden ze vzorků pouze 3 pozorování, pak druhý musí mít alespoň 7:
c) pokud má jeden ze vzorků pouze 4 pozorování, pak druhý musí mít alespoň 5:
d) vn 1 , n 2 ≥ 5 Jakékoli srovnání je možné.
V zásadě je možné porovnávat i vzorky, které tuto podmínku nesplňují, např. relacín 1 =2, n 2 = 15, ale v těchto případech nebude možné identifikovat významné rozdíly.
Kritérium φ* nemá žádná další omezení.
Podívejme se na několik příkladů pro ilustraci možnostíkritérium φ*.
Příklad 1: porovnání vzorků podle kvalitativně definované charakteristiky.
Příklad 2: porovnání vzorků podle kvantitativně naměřené charakteristiky.
Příklad 3: porovnání vzorků podle úrovně a rozložení charakteristiky.
Příklad 4: Použití kritéria φ* v kombinaci s kritériemX Kolmogorov-Smirnov s cílem dosáhnout co nejpřesnějšího výsledku.
Příklad 1 - porovnání vzorků podle kvalitativně stanovené charakteristiky
Při tomto použití kritéria porovnáváme procento subjektů v jednom vzorku charakterizovaném určitou kvalitou s procentem subjektů v jiném vzorku charakterizovaném stejnou kvalitou.
Řekněme, že nás zajímá, zda se dvě skupiny studentů liší v úspěšnosti při řešení nového experimentálního problému. V první skupině 20 lidí se s tím vyrovnalo 12 lidí a ve druhém vzorku 25 lidí - 10. V prvním případě bude procento těch, kteří problém vyřešili, 12/20 · 100 %=60 %, a ve druhém 10/25·100 %= 40 %. Liší se tato procenta významně vzhledem k údajům?n 1 An 2 ?
Zdálo by se, že i „od oka“ lze určit, že 60 % je výrazně vyšší než 40 %. Nicméně, ve skutečnosti, tyto rozdíly, s ohledem na datan 1 , n 2 nespolehlivý.
Pojďme to zkontrolovat. Vzhledem k tomu, že nás zajímá fakt řešení problému, budeme úspěch při řešení experimentálního problému považovat za „efekt“ a neúspěch při jeho řešení za absenci účinku.
Pojďme formulovat hypotézy.
H 0 : Podíl osobV první skupině nebylo více lidí, kteří splnili úkol, než ve skupině druhé.
H 1 : Podíl lidí, kteří dokončili úkol v první skupině, je větší než ve skupině druhé.
Nyní sestavíme takzvanou čtyřbuňkovou nebo čtyřpolní tabulku, což je vlastně tabulka empirických frekvencí pro dvě hodnoty atributu: „existuje účinek“ - „není žádný účinek“.
Tabulka 5.1
Čtyřbuňková tabulka pro výpočet kritéria při porovnání dvou skupin subjektů podle procenta těch, kteří problém vyřešili.
Skupiny | „Existuje efekt“: problém vyřešen | "Žádný efekt": problém není vyřešen | Množství |
||||
Množství předměty | % podíl | Množství předměty | % podíl | ||||
1 skupina | (60%) | (40%) | |||||
2. skupina | (40%) | (60%) | |||||
Množství | |||||||
V tabulce se čtyřmi buňkami jsou zpravidla sloupce „Existuje efekt“ a „Žádný efekt“ označeny nahoře a řádky „Skupina 1“ a „Skupina 2“ jsou vlevo. Ve skutečnosti jsou do srovnání zahrnuta pouze pole (buňky) A a B, tedy procenta ve sloupci „Existuje účinek“.
Podle tabulky.XIIPříloha 1 určuje hodnoty φ odpovídající procentuálním podílům v každé ze skupin.
Nyní vypočítejme empirickou hodnotu φ* pomocí vzorce:
kde φ 1 - úhel odpovídající většímu % podílu;
φ 2 - úhel odpovídající menšímu % podílu;
n 1 - počet pozorování ve vzorku 1;
n 2 - počet pozorování ve vzorku 2.
V tomto případě:
Podle tabulky.XIIIV příloze 1 určíme, jaká hladina významnosti odpovídá φ* em=1,34:
p=0,09
Je také možné stanovit kritické hodnoty φ* odpovídající úrovním akceptovaným v psychologii statistická významnost:
Postavme „osu významu“.
Získaná empirická hodnota φ* je v pásmu nevýznamnosti.
Odpovědět: H 0 přijato. Procento lidí, kteří dokončili úkolPROTIv první skupině ne více než ve skupině druhé.
Lze pouze sympatizovat s výzkumníkem, který považuje rozdíly 20 % a dokonce 10 % za významné, aniž bychom ověřovali jejich spolehlivost pomocí kritéria φ*. V tomto případě by například byly významné pouze rozdíly alespoň 24,3 %.
Zdá se, že při srovnání dvou vzorků na jakémkoli kvalitativním základě nás kritérium φ může spíše mrzet než těšit. Co se zdálo významné, nemusí být ze statistického hlediska tak významné.
Fisherovo kritérium má mnohem více příležitostí potěšit výzkumníka, když porovnáváme dva vzorky podle kvantitativně naměřených charakteristik a můžeme měnit „účinek“.
Příklad 2 - porovnání dvou vzorků podle kvantitativně naměřené charakteristiky
Při tomto použití kritéria porovnáváme procento subjektů v jednom vzorku, kteří dosahují určité úrovně hodnoty atributu, s procentem subjektů, které této úrovně dosahují v jiném vzorku.
Ve studii G. A. Tlegenové (1990) bylo ze 70 mladých studentů odborných škol ve věku 14 až 16 let na základě výsledků vybráno 10 subjektů s vysokým skóre na škále Agrese a 11 subjektů s nízkým skóre na škále Agrese. průzkumu pomocí Freiburského osobnostního dotazníku. Je třeba zjistit, zda se skupiny agresivních a neagresivních mladých mužů liší ve vzdálenosti, kterou si spontánně zvolí v rozhovoru se spolužákem. Údaje G. A. Tlegenové jsou uvedeny v tabulce. 5.2. Můžete si všimnout, že agresivní mladí muži častěji volí vzdálenost 50cm nebo i méně, zatímco neagresivní chlapci častěji volí vzdálenost větší než 50 cm.
Nyní můžeme považovat vzdálenost 50 cm za kritickou a předpokládat, že pokud je vzdálenost zvolená subjektem menší nebo rovna 50 cm, pak „existuje účinek“, a pokud je vybraná vzdálenost větší než 50 cm, pak "nemá žádný účinek." Vidíme, že ve skupině agresivních mladých mužů je účinek pozorován u 7 z 10, tj. v 70 % případů a ve skupině neagresivních mladých mužů - u 2 z 11, tj. v 18,2 % případů. . Tato procenta lze porovnat pomocí metody φ* a stanovit významnost rozdílů mezi nimi.
Tabulka 5.2
Ukazatele vzdálenosti (v cm) zvolené agresivními a neagresivními mladými muži v rozhovoru se spolužákem (podle G.A. Tlegenové, 1990)
Skupina 1: chlapci s vysokým skóre na škále agreseFPI- R (n 1 =10) | Skupina 2: chlapci s nízkými hodnotami na škále agreseFPI- R (n 2 =11) |
|||
DC m ) | % podíl | DC M ) | % podíl |
|
"Jíst Účinek" d≤ 50 cm | ||||
18,2% |
||||
"Ne účinek" d>50 cm | ||||
80 QO | 81,8% |
|||
Množství | 100% | 100% |
||
Průměrný | 5b:o | 77.3 | ||
Pojďme formulovat hypotézy.
H 0 d ≤ 50 cm, ve skupině agresivních chlapců není více než ve skupině neagresivních chlapců.
H 1 : Podíl lidí, kteří volí vzdálenostd≤ 50 cm, více ve skupině agresivních mladých mužů než ve skupině neagresivních mladých mužů. Nyní si postavme tzv. čtyřbuňkový stůl.
Tabulka 53
Čtyřčlánková tabulka pro výpočet φ* kritéria při porovnávání skupin agresivních (nf=10) a neagresivní mladí muži (n2=11)
Skupiny | "Existuje efekt": d≤50 | "Žádný efekt." d>50 | Množství |
||||
Počet předmětů | (% podíl) | Počet předmětů | (% podíl) | ||||
Skupina 1 - agresivní mladí muži | (70%) | (30%) | |||||
Skupina 2 - neagresivní mladí muži | (180%) | (81,8%) | |||||
Součet | |||||||
Podle tabulky.XIIPříloha 1 určuje hodnoty φ odpovídající procentuálnímu podílu „efektu“ v každé ze skupin.
Získaná empirická hodnota φ* je v pásmu významnosti.
Odpovědět: H 0 odmítl. PřijatoH 1 . Podíl lidí, kteří volí při rozhovoru vzdálenost menší nebo rovnou 50 cm, je větší ve skupině agresivních mladých mužů než ve skupině neagresivních mladých mužů
Na základě získaných výsledků můžeme usoudit, že agresivnější mladí muži volí častěji vzdálenost menší než půl metru, zatímco neagresivní mladí muži častěji vzdálenost větší než půl metru. Vidíme, že agresivní mladí muži skutečně komunikují na pomezí intimní (0-46 cm) a osobní zóny (od 46 cm). Pamatujeme si však, že intimní vzdálenost mezi partnery je výsadou nejen blízkých, dobrých vztahů, aleAboj z ruky do ruky (halaE. T., 1959).
Příklad 3 - porovnání vzorků podle úrovně a rozložení charakteristiky.
V tomto případě použití můžeme nejprve otestovat, zda se skupiny liší v úrovních nějakého znaku, a poté porovnat distribuci znaku ve dvou vzorcích. Takový úkol může být relevantní při analýze rozdílů v rozsahu nebo tvaru distribuce hodnocení získaných subjekty pomocí jakékoli nové techniky.
Ve studii R. T. Chirkiny (1995) byl poprvé použit dotazník zaměřený na zjišťování tendence potlačovat z paměti fakta, jména, záměry a způsoby jednání z důvodu osobních, rodinných a profesních komplexů. Dotazník byl vytvořen za účasti E.V. Sidorenka na základě materiálů z knihy 3. Freud „Psychopatologie každodenního života“. Pomocí tohoto dotazníku byl vyšetřen vzorek 50 studentů Pedagogického institutu, svobodní, bezdětní, ve věku 17 až 20 let, a dále metodou Menester-Corzini k identifikaci intenzity pocitu osobní nedostatečnosti,nebo"komplex méněcennosti" (ManažerG. J., CorsiniR. J., 1982).
Výsledky průzkumu jsou uvedeny v tabulce. 5.4.
Dá se říci, že existuje nějaký významný vztah mezi indikátorem represivní energie, diagnostikovaným pomocí dotazníku, a indikátory intenzity pocitu vlastní nedostatečnosti?
Tabulka 5.4
Ukazatele intenzity pocitů osobní nedostatečnosti ve skupinách žáků s vysokou (nj=18) a nízká (n2=24) energie posunutí
Skupina 1: vytěsňovací energie od 19 do 31 bodů (n 1 =181 | Skupina 2: vytěsňovací energie od 7 do 13 bodů (n 2 =24) |
|
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30; 30 50; 50 60; 60 | 0; 0 5; 5; 5; 5 10; 10; 10; 10; 10; 10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30 |
|
Množství Průměrný | 26,11 | 15,42 |
Navzdory skutečnosti, že průměrná hodnota ve skupině s energičtější represí je vyšší, je v ní také pozorováno 5 nulových hodnot. Porovnáme-li histogramy rozložení hodnocení ve dvou vzorcích, odhalí se mezi nimi nápadný kontrast (obr. 5.3).
Pro porovnání dvou distribucí bychom mohli použít testχ 2 nebo kritériumλ , ale k tomu bychom museli rozšířit řady a navíc v obou vzorcíchn <30.
Kritérium φ* nám umožní zkontrolovat vliv nesouladu mezi dvěma distribucemi pozorovanými v grafu, pokud souhlasíme s předpokladem, že „existuje efekt“, pokud indikátor pocitů nedostatečnosti bude buď velmi nízký (0), nebo naopak , velmi vysoké hodnoty (S30) a že „nemá žádný efekt“, pokud indikátor pocitů nedostatečnosti nabývá průměrných hodnot, od 5 do 25.
Pojďme formulovat hypotézy.
H 0 : Extrémní hodnoty indexu deficitu (buď 0 nebo 30 nebo více) ve skupině s energičtější represí nejsou častější než ve skupině s méně energickou represí.
H 1 : Extrémní hodnoty indexu deficitu (buď 0 nebo 30 nebo více) ve skupině s energičtější represí jsou častější než ve skupině s méně energickou represí.
Vytvořme čtyřčlánkovou tabulku vhodnou pro další výpočet kritéria φ*.
Tabulka 5.5
Čtyřčlánková tabulka pro výpočet kritéria φ* při porovnání skupin s vyšší a nižší represivní energií na základě poměru indikátorů nedostatečnosti
Skupiny | „Existuje účinek“: indikátor nedostatku je 0 nebo >30 | „Žádný efekt“: index selhání od 5 do 25 | Množství |
||
(88,9%) | (11,1%) | ||||
(33,3%) | (66,7%) | ||||
Množství | |||||
Podle tabulky.XIIV příloze 1 určíme hodnoty φ odpovídající porovnávaným procentům:
Vypočítejme empirickou hodnotu φ*:
Kritické hodnoty φ* pro libovolnén 1 , n 2 , jak si pamatujeme z předchozího příkladu, jsou:
StůlXIIIPříloha 1 nám umožňuje přesněji určit hladinu významnosti získaného výsledku: Str<0,001.
Odpovědět: H 0 odmítl. PřijatoH 1 . Extrémní hodnoty indexu deficitu (buď 0 nebo 30 nebo více) se ve skupině s větší represivní energií vyskytují častěji než ve skupině s menší represivní energií.
Takže subjekty s větší represivní energií mohou mít jak velmi vysoké (30 a více), tak velmi nízké (nulové) indikátory pocitu vlastní nedostatečnosti. Dá se předpokládat, že potlačují jak svou nespokojenost, tak potřebu úspěchu v životě. Tyto předpoklady vyžadují další testování.
Získaný výsledek bez ohledu na jeho interpretaci potvrzuje schopnosti kritéria φ* při posuzování rozdílů ve tvaru rozložení znaku ve dvou vzorcích.
V původním vzorku bylo 50 lidí, ale 8 z nich bylo vyloučeno z úvahy s průměrným skóre na indexu represivní anergie (14-15). Jejich ukazatele intenzity pocitů nedostatečnosti jsou rovněž průměrné: 6 hodnot po 20 bodech a 2 hodnoty po 25 bodech.
Výkonné schopnosti kritéria φ* lze ověřit potvrzením zcela jiné hypotézy při analýze materiálů tohoto příkladu. Můžeme například dokázat, že ve skupině s větší represivní energií je míra insuficience stále vyšší, a to i přes paradoxní charakter jejího rozložení v této skupině.
Pojďme formulovat nové hypotézy.
H 0 Nejvyšší hodnoty indexu deficitu (30 a více) ve skupině s větší represivní energií nejsou častější než ve skupině s menší represivní energií.
H 1 : Nejvyšší hodnoty indexu deficitu (30 a více) ve skupině s větší represivní energií se vyskytují častěji než ve skupině s menší represivní energií. Vytvořme čtyřpolní tabulku pomocí dat v tabulce. 5.4.
Tabulka 5.6
Čtyřčlánková tabulka pro výpočet kritéria φ* při porovnání skupin s větší a menší represivní energií podle úrovně indikátoru nedostatečnosti
Skupiny | Indikátor selhání „Existuje účinek“* je větší nebo roven 30 | „Žádný efekt“: míra selhání je nižší 30 | Množství |
||
Skupina 1 - s větší výtlakovou energií | (61,1%) | (38.9%) | |||
Skupina 2 - s nižší výtlakovou energií | (25.0%) | (75.0%) | |||
Množství | |||||
Podle tabulky.XIIIV příloze 1 stanovíme, že tento výsledek odpovídá hladině významnosti p = 0,008.
Odpovědět: Ale to se odmítá. PřijatoHj: Nejvyšší ukazatele nedostatku (30 a více bodů) ve skupiněSs větší výtlakovou energií se vyskytují častěji než ve skupině s menší výtlakovou energií (p = 0,008).
Takže jsme to mohli dokázatPROTIskupinaSpři energičtější represi převažují extrémní hodnoty indikátoru nedostatečnosti a skutečnost, že tento indikátor překračuje své hodnotydosáhnepřesně v této skupině.
Nyní bychom se mohli pokusit dokázat, že ve skupině s vyšší represivní energií jsou nižší hodnoty indexu insuficience častější, přestože průměrná hodnotaPROTI tato skupina má více (26,11 oproti 15,42 ve skupiněS menší výtlak).
Pojďme formulovat hypotézy.
H 0 : Nejnižší míry nedostatku (nula) ve skupiněS represe s větší energií nejsou častější než ve skupiněS menší výtlačná energie.
H 1 : Vyskytuje se nejnižší míra nedostatku (nula).PROTI skupina s větší represivní energií častěji než ve skupiněS méně energická represe. Seskupíme data do nové tabulky se čtyřmi buňkami.
Tabulka 5.7
Čtyřčlánková tabulka pro porovnání skupin s různou represivní energií na základě četnosti nulových hodnot indikátoru nedostatku
Skupiny | "Existuje efekt": indikátor selhání je 0 | "Žádný účinek" nedostatečnosti | indikátor není roven 0 | Množství |
|
Skupina 1 - s větší výtlakovou energií | (27,8%) | (72,2%) | |||
1 skupina - s menší výtlačnou energií | (8,3%) | (91,7%) | |||
Množství | |||||
Určíme hodnoty φ a vypočítáme hodnotu φ*:
Odpovědět: H 0 odmítl. Nejnižší indexy insuficience (nula) ve skupině s větší represivní energií jsou častější než ve skupině s menší represivní energií (p<0,05).
Celkově lze získané výsledky považovat za důkaz částečné shody pojmů komplex u S. Freuda a A. Adlera.
Je významné, že mezi indikátorem represivní energie a indikátorem intenzity pocitu vlastní nedostatečnosti ve vzorku jako celku byla získána pozitivní lineární korelace (p = +0,491, p<0,01). Как мы можем убедиться, применение критерия φ* позволяет проникнуть в более тонкие и содержательно значимые соотношения между этими двумя показателями.
Příklad 4 - použití kritéria φ* v kombinaci s kritériem λ Kolmogorov-Smirnov s cílem dosáhnout maxima přesnývýsledek
Pokud jsou vzorky porovnávány podle jakýchkoli kvantitativně měřených ukazatelů, vzniká problém s identifikací distribučního bodu, který lze použít jako kritický bod při rozdělování všech subjektů na ty, které „mají efekt“ a ty, které „nemají efekt“.
V zásadě bod, ve kterém bychom rozdělili skupinu na podskupiny, kde je efekt a kde efekt není, lze zvolit zcela libovolně. Můžeme se zajímat o jakýkoli efekt, a proto můžeme oba vzorky kdykoli rozdělit na dvě části, pokud to dává nějaký smysl.
Pro maximalizaci síly φ* testu je však nutné vybrat bod, ve kterém jsou rozdíly mezi oběma porovnávanými skupinami největší. Nejpřesněji to můžeme udělat pomocí algoritmu pro výpočet kritériaλ , což vám umožní detekovat bod maximální nesrovnalosti mezi dvěma vzorky.
Možnost kombinace kritérií φ* aλ popsal E.V. Gubler (1978, s. 85-88). Pokusme se tuto metodu použít při řešení následujícího problému.
Ve společné studii M.A. Kurochkina, E.V. Sidorenko a Yu.A. Churakov (1992) ve Spojeném království provedl průzkum mezi anglickými praktickými lékaři ve dvou kategoriích: a) lékaři, kteří podporovali reformu medicíny a již přeměnili své přijímací kanceláře na fondy s vlastním rozpočtem; b) lékaři, jejichž ordinace dosud nemají vlastní finanční prostředky a jsou zcela zajišťovány státním rozpočtem. Dotazníky byly zaslány vzorku 200 lékařů, reprezentativních pro běžnou populaci anglických lékařů z hlediska zastoupení lidí různého pohlaví, věku, délky služby a místa výkonu práce - ve velkých městech nebo v provinciích.
Na dotazník odpovědělo 78 lékařů, z toho 50 pracovalo v čekárnách s prostředky a 28 z čekáren bez prostředků. Každý z lékařů měl předpovědět, jaký bude podíl přijetí s finančními prostředky v příštím roce 1993. Na tuto otázku odpovědělo pouze 70 lékařů ze 78, kteří zaslali odpovědi. Rozdělení jejich předpovědí je uvedeno v tabulce. 5.8 zvlášť pro skupinu lékařů s finančními prostředky a skupinu lékařů bez finančních prostředků.
Liší se nějak prognózy lékařů s finančními prostředky a lékařů bez prostředků?
Tabulka 5.8
Rozdělení prognóz praktických lékařů o tom, jaký bude podíl pohotovostí s finančními prostředky v roce 1993
Předpokládaný podíl | |||
přijímací místnosti s finančními prostředky | lékaři s fondem (n 1 =45) | lékaři bez fondu (n 2 =25) | Množství |
1. od 0 do 20 % | 4 | 5 | 9 |
2. od 21 do 40 % | 15 | A | 26 |
3. od 41 do 60 % | 18 | 5 | 23 |
4. od 61 do 80 % | 7 | 4 | A |
5. od 81 do 100 % | 1 | 0 | 1 |
Množství | 45 | 25 | 70 |
Pojďme určit bod maximálního nesouladu mezi dvěma distribucemi odezvy pomocí Algoritmu 15 z článku 4.3 (viz Tabulka 5.9).
Tabulka 5.9
Výpočet maximálního rozdílu akumulovaných frekvencí v rozdělení prognóz lékařů dvou skupin
Předpokládaný podíl přijetí s finančními prostředky (%) | Empirické frekvence volby pro danou kategorii odezvy | Empirické frekvence | Kumulativní empirické četnosti | Rozdíl (d) |
|||
lékaři s fondem(n 1 =45) | lékaři bez fondu (n 2 =25) | F* uh 1 | F* a2 | ∑F* e1 | ∑F* a1 |
||
1. od 0 do 20 % 2. od 21 do 40 % 3. od 41 do 60 % 4. od 61 do 80 % 5. od 81 do 100 % | 4 15 18 7 1 | 5 11 5 4 0 | 0,089 0,333 0,400 0,156 0,022 | 0,200 0,440 0,200 0,160 0 | 0,089 0,422 0,822 0,978 1,000 | 0,200 0,640 0,840 1,000 1,000 | 0111 0,218 0,018 0,022 0 |
Maximální zjištěný rozdíl mezi dvěma akumulovanými empirickými frekvencemi je0,218.
Ukazuje se, že tento rozdíl je kumulován ve druhé kategorii prognózy. Zkusme použít horní hranici této kategorie jako kritérium pro rozdělení obou vzorků do podskupiny, kde „existuje efekt“ a podskupiny, kde „není žádný efekt“. Budeme předpokládat, že existuje „efekt“, pokud daný lékař predikuje 41 až 100 % přijetí s finančními prostředky v1993 roce a že „nemá žádný efekt“, pokud daný lékař předpovídá 0 až 40 % přijetí s finančními prostředky v1993 rok. Kombinujeme kategorie předpovědí 1 a 2 na jedné straně a kategorie předpovědí 3, 4 a 5 na straně druhé. Výsledné rozdělení prognóz je uvedeno v tabulce. 5.10.
Tabulka 5.10
Distribuce prognóz pro lékaře s finančními prostředky a lékaře bez prostředků
Předpokládaný podíl přijetí s finančními prostředky (%1 | Empirické frekvence pro výběr dané kategorie předpovědi | Množství |
|
lékaři s fondem(n 1 =45) | lékaři bez fondu(n 2 =25) |
||
1. od 0 do 40 % | 19 | 16 | 35 |
2. od 41 do 100 % | 26 | 9 | 35 |
Množství | 45 | 25 | 70 |
Výslednou tabulku (tab. 5.10) můžeme použít k testování různých hypotéz porovnáním dvou libovolných jejích buněk. Pamatujeme si, že se jedná o tzv. čtyřbuňkovou neboli čtyřpolní tabulku.
Zde nás zajímá, zda lékaři, kteří již mají finanční prostředky, předpovídají v budoucnu větší růst tohoto hnutí než lékaři, kteří prostředky nemají. Podmínečně proto považujeme za „účinek“, když prognóza spadá do kategorie od 41 do 100 %. Abychom zjednodušili výpočty, musíme nyní otočit stůl o 90° ve směru hodinových ručiček. Můžete to dokonce udělat doslova otočením knihy spolu se stolem. Nyní můžeme přejít k pracovnímu listu pro výpočet kritéria φ* – Fisherova úhlová transformace.
Stůl 5.11
Čtyřbuňková tabulka pro výpočet Fisherova φ* testu k identifikaci rozdílů v prognózách dvou skupin praktických lékařů
Skupina | Existuje efekt – předpověď od 41 do 100 % | Žádný efekt – předpověď od 0 do 40 % | Celkový |
jáskupina - lékaři, kteří vzali fond | 26 (57.8%) | 19 (42.2%) | 45 |
IIskupina - lékaři, kteří fond nevzali | 9 (36.0%) | 16 (64.0%) | 25 |
Celkový | 35 | 35 | 70 |
Pojďme formulovat hypotézy.
H 0 : Podíl osobpredikce rozložení prostředků na 41%-100% všech lékařských ordinací, ve skupině lékařů s finančními prostředky není více než ve skupině lékařů bez prostředků.
H 1 : Podíl lidí predikujících rozložení prostředků na 41 %-100 % všech přijatých je větší ve skupině lékařů s finančními prostředky než ve skupině lékařů bez prostředků.
Určení hodnot φ 1 a φ 2 podle tabulkyXIIDodatek 1. Připomeňme, že φ 1 je vždy úhel odpovídající většímu procentu.
Nyní určíme empirickou hodnotu kritéria φ*:
Podle tabulky.XIIIV příloze 1 určíme, jaké hladině významnosti tato hodnota odpovídá: p = 0,039.
Pomocí stejné tabulky v příloze 1 můžete určit kritické hodnoty kritéria φ*:
Odpovědět: Ale je zamítnuto (p=0,039). Podíl lidí předpovídajících rozložení prostředků na41-100 % všech přijetí ve skupině lékařů, kteří fond odebírali, převyšuje tento podíl ve skupině lékařů, kteří fond neodebírali.
Jinými slovy, lékaři, kteří již pracují ve svých čekárnách se samostatným rozpočtem, předpovídají v letošním roce širší rozšíření této praxe než lékaři, kteří s přechodem na samostatný rozpočet dosud nesouhlasili. Existuje několik interpretací tohoto výsledku. Dá se například předpokládat, že lékaři v každé skupině podvědomě považují své chování za typičtější. To může také znamenat, že lékaři, kteří již přijali samofinancování, mají tendenci zveličovat rozsah tohoto hnutí, protože potřebují zdůvodnit své rozhodnutí. Zjištěné rozdíly mohou znamenat i něco, co je zcela mimo rámec otázek položených ve studii. Například, že činnost lékařů pracujících na nezávislý rozpočet přispívá k vyostření rozdílů v pozicích obou skupin. Byli aktivnější, když souhlasili s převzetím finančních prostředků, byli aktivnější, když si dali tu práci a odpověděli na poštovní dotazník; jsou aktivnější, když předpovídají, že ostatní lékaři budou aktivnější při získávání finančních prostředků.
Tak či onak si můžeme být jisti, že zjištěná míra statistických rozdílů je pro tato reálná data maximální možná. Stanovili jsme pomocí kritériaλ bod maximální divergence mezi dvěma distribucemi a právě v tomto bodě byly vzorky rozděleny na dvě části.
Vaše značka.
Funkce FISCHER vrací Fisherovu transformaci argumentů na X . Tato transformace vytváří funkci, která má spíše normální než šikmé rozdělení. FISCHERova funkce slouží k testování hypotézy pomocí korelačního koeficientu.
Popis funkce FISCHER v Excelu
Při práci s touto funkcí musíte nastavit hodnotu proměnné. Okamžitě stojí za zmínku, že existují situace, ve kterých tato funkce nepřinese výsledky. To je možné, pokud proměnná:
- není číslo. V takové situaci funkce FISCHER vrátí chybovou hodnotu #HODNOTA!;
- má hodnotu buď menší než -1 nebo větší než 1. V tomto případě funkce FISCHER vrátí chybovou hodnotu #NUM!.
Rovnice, která se používá k matematickému popisu FISCHERovy funkce, je:
Z"=1/2*ln(1+x)/(1-x)
Podívejme se na použití této funkce pomocí 3 konkrétních příkladů.
Odhad vztahu mezi ziskem a náklady pomocí funkce FISHER
Příklad 1. Na základě údajů o činnosti komerčních organizací je třeba provést posouzení vztahu mezi ziskem Y (miliony rublů) a náklady X (miliony rublů) použitými na vývoj produktu (uvedeno v tabulce 1).
Tabulka 1 – Počáteční údaje:
| № | X | Y |
| 1 | 210 000 000,00 RUR | 95 000 000,00 RUR |
| 2 | 1 068 000 000,00 RUB | 76 000 000,00 RUR |
| 3 | 1 005 000 000,00 RUB | 78 000 000,00 RUR |
| 4 | 610 000 000,00 RUR | 89 000 000,00 RUR |
| 5 | 768 000 000,00 RUR | 77 000 000,00 RUR |
| 6 | 799 000 000,00 RUR | 85 000 000,00 RUR |
Schéma řešení takových problémů je následující:
- Vypočteno lineární koeficient korelace r xy ;
- Významnost lineárního korelačního koeficientu se kontroluje na základě Studentova t-testu. V tomto případě je předložena a testována hypotéza, že korelační koeficient je roven nule. K testování této hypotézy se používá t-statistika. Pokud se hypotéza potvrdí, má t-statistika Studentovo rozdělení. Je-li vypočtená hodnota t p > t cr, pak je hypotéza zamítnuta, což ukazuje na významnost lineárního korelačního koeficientu, a tedy statistickou významnost vztahu mezi X a Y;
- Pro statisticky významný lineární korelační koeficient se stanoví intervalový odhad.
- Intervalový odhad pro lineární korelační koeficient je určen na základě inverzní Fisherovy z-transformace;
- Vypočte se směrodatná chyba lineárního korelačního koeficientu.
Výsledky řešení tohoto problému pomocí funkcí používaných v Excelu ukazuje obrázek 1.
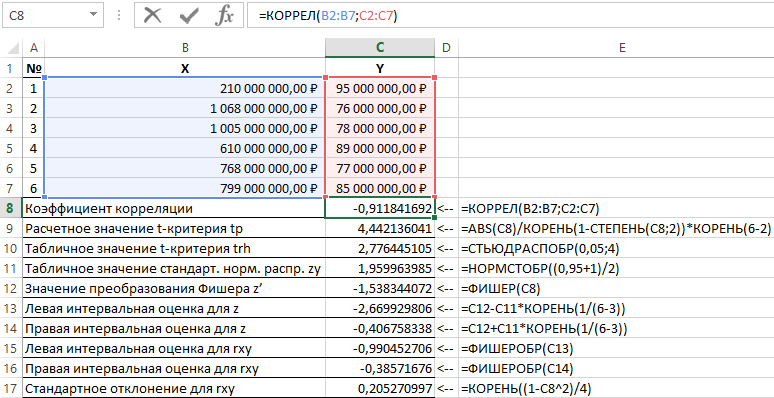
Obrázek 1 – Příklad výpočtů.
| Ne. | Název indikátoru | Výpočtový vzorec |
| 1 | Korelační koeficient | =CORREL(B2:B7;C2:C7) |
| 2 | Vypočtená hodnota t-testu tp | =ABS(C8)/SQRT(1-POWER(C8,2))*SQRT(6-2) |
| 3 | Tabulková hodnota t-testu trh | =STUDISCOVER(0,05;4) |
| 4 | Tabulková hodnota normy normální distribuce z y | =NORMSINV((0,95+1)/2) |
| 5 | Hodnota Fisherovy transformace z | =FISHER(C8) |
| 6 | Levý odhad intervalu pro z | =C12-C11*ROOT(1/(6-3)) |
| 7 | Pravý odhad intervalu pro z | =C12+C11*ROOT(1/(6-3)) |
| 8 | Levý odhad intervalu pro rxy | =FISHEROBR(C13) |
| 9 | Pravý odhad intervalu pro rxy | =FISHEROBR(C14) |
| 10 | Směrodatná odchylka pro rxy | =ROOT((1-C8^2)/4) |
S pravděpodobností 0,95 tedy lineární korelační koeficient leží v rozmezí od (–0,386) do (–0,990) se směrodatnou chybou 0,205.
Kontrola statistické významnosti regrese pomocí funkce FASTER
Příklad 2: Testování statistické významnosti rovnice vícenásobná regrese Pomocí Fisherova F testu vyvodte závěry.
Pro kontrolu významnosti rovnice jako celku předkládáme hypotézu H 0 o statistické nevýznamnosti koeficientu determinace a opačnou hypotézu H 1 o statistické významnosti koeficientu determinace:
H1: R2 ≠ 0.
Otestujme hypotézy pomocí Fisherova F testu. Ukazatele jsou uvedeny v tabulce 2.
Tabulka 2 - Počáteční údaje
K tomu použijeme funkci v Excelu:
RYCHLEJŠÍ (α;p;n-p-1)
- α je pravděpodobnost spojená s daným rozdělením;
- p a n jsou čitatel a jmenovatel stupňů volnosti.
Když víme, že α = 0,05, p = 2 an = 53, získáme pro F krit následující hodnotu (viz obrázek 2).
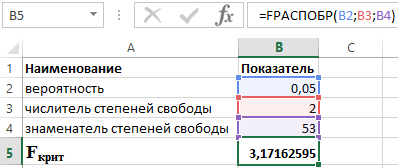
Obrázek 2 – Příklad výpočtů.
Můžeme tedy říci, že F vypočteno > F kritické. V důsledku toho je přijata hypotéza H 1 o statistické významnosti koeficientu determinace.
Výpočet hodnoty korelačního ukazatele v Excelu
Příklad 3. Použití údajů od 23 podniků o: X je cena produktu A, tisíc rublů; Y je zisk obchodního podniku, miliony rublů; studuje se jejich závislost. Školní známka regresní model dal následující: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Jaký korelační ukazatel lze z těchto údajů určit? Vypočítejte hodnotu korelačního ukazatele a pomocí Fisherova kritéria vyvodte závěr o kvalitě regresního modelu.
Určíme F krit z výrazu:
F vypočteno = R2 /23*(1-R2)
kde R je koeficient determinace rovný 0,67.
Vypočtená hodnota F calc = 46.
Pro stanovení F kritu použijeme Fisherovo rozdělení (viz obrázek 3).
Obrázek 3 – Příklad výpočtů.
Výsledný odhad regresní rovnice je tedy spolehlivý.
Význam vícenásobné regresní rovnice jako celku i v párové regresi se hodnotí pomocí Fisherova kritéria:
,
(2.22)
Kde 
– faktor součet čtverců na stupeň volnosti; 
– zbytkový součet čtverců na stupeň volnosti; 
– koeficient (index) vícenásobného určení; 
– počet parametrů pro proměnné 
(PROTI lineární regrese se shoduje s počtem faktorů zahrnutých v modelu); 
– počet pozorování.
Posuzuje se významnost nejen rovnice jako celku, ale i faktoru dodatečně zahrnutého do regresního modelu. Potřeba takového hodnocení je dána tím, že ne každý faktor zahrnutý v modelu může významně zvýšit podíl vysvětlené variace ve výsledném znaku. Pokud je navíc v modelu více faktorů, lze je do modelu zadávat v různých posloupnostech. Vzhledem ke korelaci mezi faktory může být významnost stejného faktoru různá v závislosti na posloupnosti jeho zavádění do modelu. Měřítkem pro posouzení zahrnutí faktoru do modelu je soukromé 
-kritérium, tj. 
.
Soukromé 
-kritérium je založeno na porovnání nárůstu rozptylu faktorů vlivem dodatečně zařazeného faktoru se zbytkovým rozptylem na jeden stupeň volnosti pro regresní model jako celek. V obecný pohled pro faktor 
soukromé 
-kritérium bude určeno jako
,
(2.23)
Kde 
– koeficient vícenásobného určení pro model s úplnou sadou faktorů, 
– stejný ukazatel, ale bez zahrnutí faktoru do modelu 
,
– počet pozorování, 
– počet parametrů v modelu (bez volného termínu).
Skutečná hodnota kvocientu 
- kritérium je porovnáno s tabulkou na hladině významnosti 
a počet stupňů volnosti: 1 a 
. Pokud je skutečná hodnota 
přesahuje 
, pak dodatečné zahrnutí faktoru 
do modelu je statisticky zdůvodněn a čistý regresní koeficient 
v faktoru 
statisticky významný. Pokud je skutečná hodnota 
je menší než tabulková hodnota, pak další zahrnutí faktoru do modelu 
nezvyšuje významně podíl vysvětlené variace ve znaku 
, proto je nevhodné jej zařazovat do modelu; Regresní koeficient pro tento faktor je v tomto případě statisticky nevýznamný.
Pro dvoufaktorovou rovnici kvocienty 
-kritéria mají tvar:
,
. (2.23a)
Použití soukromé 
-kritérium, lze zkontrolovat významnost všech regresních koeficientů za předpokladu, že každý odpovídající faktor 
vstoupil do vícenásobné regresní rovnice jako poslední.
-Studentský test pro vícenásobnou regresní rovnici.
Soukromé 
-kritérium hodnotí význam čistých regresních koeficientů. Znát velikost 
, je možné určit 
-kritérium pro regresní koeficient at 
-m faktor, 
, jmenovitě:
.
(2.24)
Posouzení významnosti čistých regresních koeficientů podle 
-Studentův t-test lze provést bez výpočtu dílčího 
-kritéria. V tomto případě, stejně jako v párové regresi, se pro každý faktor použije vzorec:
,
(2.25)
Kde 
– čistý regresní koeficient u faktoru 
,
– střední kvadratická (směrodatná) chyba regresního koeficientu 
.
Pro vícenásobnou regresní rovnici lze střední čtvercovou chybu regresního koeficientu určit podle následujícího vzorce:
,
(2.26)
Kde 
,
– směrodatná odchylka pro charakteristiku 
,
– koeficient determinace pro vícenásobnou regresní rovnici, 
– koeficient determinace pro závislost faktoru 
se všemi ostatními faktory v rovnici vícenásobné regrese; 
– počet stupňů volnosti pro zbytkový součet kvadrátů odchylek.
Jak vidíte, abyste mohli použít tento vzorec, potřebujete mezifaktorovou korelační matici a výpočet odpovídajících koeficientů determinace pomocí ní 
. Takže k rovnici 
posouzení významnosti regresních koeficientů 
,
,
zahrnuje výpočet tří koeficientů určování mezifaktorů: 
,
,
.
Vztah mezi ukazateli parciální korelační koeficient, parciální 
-kritéria a 
-Studentův t-test pro čisté regresní koeficienty lze použít v postupu výběru faktoru. Eliminaci faktorů při konstrukci regresní rovnice eliminační metodou lze prakticky provádět nejen parciálními korelačními koeficienty s vyloučením v každém kroku faktoru s nejmenší nevýznamnou hodnotou parciálního korelačního koeficientu, ale také hodnotami 
A 
.
Soukromé 
-kritérium je široce používáno při konstrukci modelu pomocí metody zahrnutí proměnných a metody postupné regrese.
