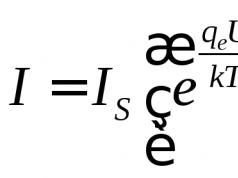Determinantes y sus propiedades. Determinantes de segundo orden y sus propiedades.

LECCIÓN 2

2.1 DETERMINANTES DE SEGUNDO ORDEN

Determinante de segundo orden(correspondiente a esta matriz

) se llama número

Ejemplo1: Calculemos el determinante de la matriz.

Ejemplo 2. Calcular determinantes de segundo orden:

2(-4) - 5(-3) = -8 + 15 = 7

=

2.2 DETERMINANTES DE TERCER ORDEN

Sea una matriz cuadrada de tercer orden:

A=

Determinante (o determinante) de tercer orden correspondiente a una matriz dada es el número

detA = =

Ejemplo 3

Primera solución:

La fórmula es larga y es fácil equivocarse por descuido. ¿Cómo evitar errores molestos? Para ello se inventó un segundo método de cálculo del determinante, que en realidad coincide con el primero. Se llama método Sarrus o método de “tiras paralelas”. La conclusión es que a la derecha del determinante, asigne la primera y segunda columnas y dibuje líneas cuidadosamente con un lápiz:

Los multiplicadores ubicados en las diagonales "rojas" se incluyen en la fórmula con un signo "más". Los multiplicadores ubicados en las diagonales "azules" se incluyen en la fórmula con un signo menos:

Ejemplo 3

Segunda solución:

Compara las dos soluciones. Es fácil ver que esto es LO MISMO, solo que en el segundo caso los factores de la fórmula están ligeramente reorganizados y, lo más importante, la probabilidad de cometer un error es mucho menor.

Ejemplo 4

Calcule el determinante de tercer orden:

Ejemplo 5

Calcular el determinante de tercer orden.

PRÁCTICA 2

TAREA N 1, Eso…

Solución:

Eso

Por condición , Entonces

TAREA N 2Tema: Determinantes de segundo orden Si el determinante de segundo orden

, Eso…

Solución:

En nuestro caso tenemos

Por condición , Entonces

TAREA N 3

Tema: Determinantes de segundo orden Si el determinante de segundo orden

, Eso…

Solución: Dado que el determinante de segundo orden es igual al número obtenido por la regla:

Eso

Por condición , Entonces

TAREA N° 4Tema: Determinantes de segundo orden Si el determinante es de segundo orden, entonces...

Solución: Te recordamos que el determinante de segundo orden es igual al número obtenido por la regla:

En nuestro caso tenemos

Por condición , Entonces

TAREA N° 5Tema: Determinantes de tercer orden El valor del determinante de tercer orden se puede calcular utilizando la "regla de los triángulos", que se indica esquemáticamente en las figuras. Entonces el determinante es...

Solución:

TAREA N 6

Tema: Determinantes de tercer orden El valor del determinante de tercer orden se puede calcular utilizando la "regla de los triángulos", que se indica esquemáticamente en las figuras. Entonces el determinante es...

Solución: Determinante de tercer orden igual a la suma seis términos, de los cuales tres se toman con el signo “+” y tres con el signo “-”. La regla para calcular términos con el signo "+" se muestra esquemáticamente en la Fig. 1. Uno de los términos es igual al producto de los elementos del determinante que se encuentran en la diagonal principal. Cada uno de los otros dos se encuentra como el producto de los elementos que se encuentran en paralelo a esta diagonal, con la adición de un tercer factor desde la esquina opuesta del determinante. Los términos con el signo “-” se obtienen de la misma forma, pero con respecto a la segunda diagonal (Fig. 2). Entonces

TRABAJO INDEPENDIENTE 2

TAREA N 1Tema: Determinantes de segundo orden Si el determinante de segundo orden , Eso…

Conferencia 2.clasificados

Determinantes de segundo orden

Determinantes de tercer orden

Complementos algebraicos y menores

Expandiendo el determinante por fila o columna

Propiedades de los determinantes

matriz inversa

Propiedades de una matriz inversa

1. Determinantes de segundo orden

Se introduce el concepto de determinante. solo para matriz cuadrada.

Determinante es un número que se calcula según ciertas reglas. orden determinante es el orden de la matriz cuadrada. Si se utilizaron paréntesis para especificar matrices, en la teoría de los determinantes se utilizan paréntesis rectos.

Asociamos cada matriz cuadrada a un número determinado, al que llamaremos determinante de la matriz, e indicar la regla para su cálculo. Designaciones :

.

Ejemplo 1.
.

2. Determinantes de tercer orden

Cada producto no contiene números de una columna o una fila.

Demos un diagrama para recordar el orden de obtención de los términos en el determinante.

El producto de los números en una diagonal se toma con el signo “+” (esta es la diagonal principal de la matriz) y en la otra, con el signo opuesto.

Ejemplo 2.

3. Complementos algebraicos y menores

Para calcular determinantes de orden mayor que tres se utilizan otros métodos de cálculo.

Ejemplo 3. Menor
determinante Hay.

.

Es útil recordar que
Y
.

Ejemplo 4. En el ejemplo 3, la suma algebraica

4. Expansión del determinante en una fila o columna.

Cálculo del determinante El orden se puede reducir al cálculo de los determinantes del orden.
utilizando las siguientes fórmulas.

Este número es igual a la suma de los productos. elementos cualquier th lineas en sus complementos algebraicos.

Ejemplo 5. Calcular el determinante de tercer orden.
expansión a lo largo de la primera fila.

Solución

Este número es igual a la suma de los productos de los elementos de cualquier ª columna sobre ellos sumas algebraicas.

Independientemente del método de descomposición, siempre se obtiene la misma respuesta.

5. Propiedades de los determinantes

1. Al transponer una matriz cuadrada su determinante no cambia:
.

Conclusión. Las propiedades de los determinantes formulados para filas también son válidas para columnas.

2. Al reorganizar dos cuerdas (columnas) el determinante cambia de signo al contrario. Por ejemplo,
.

3. El determinante es cero. , Si:

a) tiene una fila (columna) cero
;

b) tiene filas (columnas) proporcionales (idénticas)
.

4. Factor común en fila (columna) se puede sacar como signo determinante. Por ejemplo,
.

5. El determinante no cambia. , si sumas (restas) los elementos correspondientes de otra fila a los elementos de una fila, multiplicados por cualquier número.

Por ejemplo,
.

6. Si en el determinante cada el elemento de la fila es la suma dos términos, entonces este determinante es igual a la suma de dos determinantes:

.

7. Determinante del producto de dos matrices cuadradas del mismo orden es igual al producto de los determinantes de estas matrices:

.

8. Determinante de una matriz triangular cuadrada igual al producto de los elementos de la diagonal principal:

.

6. Matriz inversa

En lugar de la operación de división matricial, se introduce el concepto. matriz inversa.

Denotado por matriz inversa
, eso es .

La analogía con los números es obvia: para el número 2, el número ½ es el inverso, ya que
. Por eso la matriz inversa de A se denota
.

Teorema “Condición necesaria y suficiente para la existencia matriz inversa». Para que una matriz cuadrada tenía una matriz inversa
, es necesario y suficiente que el determinante de la matriz no era igual a cero.

Regla para encontrar la matriz inversa

0) Veamos si la matriz es cuadrada. Si no, entonces la matriz inversa no existe; si es cuadrado, vaya al paso 1.

1) Calcular el determinante de la matriz.
: si no es cero, entonces existe la matriz inversa:
; si es igual a cero, entonces no hay matriz inversa.

2) Para cada elemento de la matriz calculamos su complemento algebraico .

3) Confeccionamos una matriz de sumas algebraicas, que luego transponemos:
.

4) Cada elemento de la matriz.
dividir por el determinante :
Obtenemos la matriz inversa de ésta.

7. Encontrar la matriz inversa para matrices de segundo orden

Ejemplo 6. Dada una matriz
. Encuentra la matriz inversa.

Solución.

Examen. Asegurémonos de que realmente se haya encontrado la matriz inversa. Encontremos el producto de matrices. Y
.

8. Propiedades de la matriz inversa

1.
,

donde A y B son matrices cuadradas no singulares del mismo orden.

2.
.

3.
.

4.
.

Preguntas de seguridad

¿Qué es un determinante de segundo orden?

¿Cómo calcular el determinante de tercer orden?

¿Cómo calcular el determinante de tercer orden usando la regla del triángulo?

¿Cuál es el complemento algebraico de un elemento de un determinante? Dé ejemplos de determinantes de segundo y tercer orden.

Escribe expansiones del determinante de tercer orden sobre elementos de una fila arbitraria y una columna arbitraria.

Lección practica

Sujeto: Cálculo de determinantes.

Objetivos: h fortalecer los conceptos de determinantes y sus propiedades, para formar y consolidar habilidades y habilidades calcular determinantes de segundo y tercer orden; Desarrollar la capacidad de resumir los conocimientos adquiridos, realizar análisis y comparaciones, promover el desarrollo. pensamiento lógico; cultivar en los estudiantes una actitud consciente hacia el proceso de aprendizaje.

I. Principios teóricos generales

Un determinante de segundo orden es un número.

Un determinante de tercer orden es un número.

Propiedades de los determinantes

Propiedad 1.
El determinante no cambiará si todas las filas se reemplazan por las columnas correspondientes y viceversa.

Propiedad 2.
Cuando se intercambian dos filas o columnas cualesquiera, el determinante cambia de signo.

Propiedad 3.
Un determinante es igual a cero si tiene dos filas (columnas) iguales.

Propiedad 4.
Un factor común a todos los elementos de una fila o columna se puede tomar más allá del signo determinante.

Propiedad 5.
Si los elementos correspondientes de otra fila o columna se suman a los elementos de una fila o columna, el determinante no cambiará.

Corolario de las propiedades 4 y 5: Si sumas a los elementos de una fila o columna los elementos correspondientes de otra fila o columna, multiplicados por un número determinado, entonces el determinante no cambiará.

Preguntas de seguridad:

1.Dar la definición de matriz.
2. ¿Qué significa el símbolo? ?
3. ¿Qué matriz se llama transpuesta con respecto a la matriz A?
4. ¿Qué matriz se llama cuadrado de orden n?
5. Defina un determinante de segundo orden.

6. Dé la definición de determinante de tercer orden.

7. ¿Cuál es el determinante de una matriz transpuesta?

8. ¿Cómo cambiará el valor del determinante si se intercambian 2 filas (columnas) en la matriz?

9. ¿Es posible sacar el factor común de una fila o columna del signo determinante?

10.¿Cuál es el determinante si todos los elementos de una determinada fila (columna) son iguales a 0?

11. ¿A qué equivale el determinante si tiene dos filas (columnas) idénticas?

12. Formule una regla para calcular el determinante de segundo orden.

13. Formule una regla para calcular el determinante de tercer orden.

II . Formación de habilidades y destrezas.

Ejemplo 1. Tu numeras el determinante : a) según la regla del triángulo b) según la regla de Sarrus;

c) por el método de expansión por elementos de la primera fila

Solución:

b) sumar las dos primeras columnas y calcular el producto de tres elementos a lo largo de la diagonal principal y paralelo a ella con signo (+), y luego a lo largo de la diagonal secundaria y paralelo a ella con signo (-):

obtenemos:

Ejemplo 2. Calcular determinante de dos maneras: usando la expansión de la primera fila y la regla del triángulo.

Solución:

Ejemplo 3. Calcula el determinante usando las propiedades:

III .Refuerzo del material estudiado.

N° 1. Calcular determinantes:

№ 2. Resuelve las ecuaciones:

No. 4. Calcule los determinantes utilizando las propiedades:

1 .
. 2.
. 3.
. 4 .
.

Literatura

1. Pismenny, D. T. Apuntes de conferencias sobre matemáticas superiores: un curso completo de D. T. Pismenny. – 9ª ed. – M.: Iris-press, 2009. 608 p.: enfermo. – ( Educación superior).

2. Lungu, K. N. Colección de problemas de matemáticas superiores. 1er año / K. N. Lungu, D. T. Pismenny, S. N. Fedin, Yu A. Shevchenko. – 7ª ed. – M.: Iris-press, 2008. 576 págs.: – (Educación superior).

En la práctica, un investigador a menudo tiene que lidiar con cantidades desconocidas interconectadas por ciertas dependencias predeterminadas que pueden expresarse mediante cualquier fórmula. Si se cumplen una serie de condiciones:

1. los coeficientes en las fórmulas son constantes,
2. las incógnitas se incluyen en las fórmulas solo en primer grado,
3. no hay obras entre las propias incógnitas,

entonces tales dependencias se llaman lineales.

Ejemplo. En el laboratorio, 10 muestras tienen un peso total de 280 g. Encuentre el peso promedio de una muestra si el recipiente pesa 15 g.

Solución. Para responder la pregunta, usaremos una ecuación simple:

denotando por x el peso promedio de una muestra. La solución a la ecuación compilada será 26,5 g.

Ejemplo. En el laboratorio, 10 muestras recibidas del primer departamento y 10 muestras recibidas del segundo departamento tienen un peso total de 280 g, y 5 muestras del primer conjunto y 2 muestras del segundo conjunto tienen un peso total de 128 g. el peso promedio de las muestras en cada conjunto.

Solución. Para responder a la pregunta, creemos dos ecuaciones, denotando con x el peso promedio de la muestra de roca 1 y con y el peso promedio de la muestra de roca 2.

10x+10y=280; 5x+2y=128,

resolviendo los cuales juntos, obtenemos x=24 g; y=4g.

En ambos ejemplos considerados, estábamos tratando con dependencias lineales: en el primer caso – con lineal ecuación, y en el segundo – con lineal sistema de ecuaciones.

Reemplacemos los coeficientes con letras y obtengamos sistema lineal ecuaciones:

Definición 1. Matriz llamaremos a cualquier tabla rectangular formada por números un ij

Definición 2. Elementos un ij a partir de los cuales se compone la matriz se llaman elementos de esta matriz

Definición 3. Determinante de segundo orden o determinante, correspondiente a la matriz (1.2) llamemos al numero D tal que

(1.3)

El determinante se denota con las letras D o y escrito.

Cabe señalar que aunque el determinante es un número, por definición 3, pero hasta que se encuentre su valor en forma de un número singular (usando la fórmula 1.2 o algún otro método válido), se escribe en forma de tabla. Entonces podemos decir, por ejemplo, sobre reorganizar filas o columnas en esta tabla. En este caso, habría que decir “el determinante correspondiente a la matriz”. Pero en la práctica, por razones de simplicidad, generalmente se omite la segunda parte de esta frase y luego solo queda una palabra: determinante. Para distinguir lo que se quiere decir: el determinante mismo en forma de tabla o su valor encontrado, en el segundo caso se utiliza la palabra determinante. Por lo tanto, si dicen, por ejemplo, "el número de filas en el determinante...", entonces se refieren al determinante correspondiente a la matriz, pero aún no calculado a un solo número. Y, si dicen determinante, quieren decir que este determinante está representado singular, calculado mediante fórmula o de alguna otra forma aceptable.

Ejemplo. Dado un sistema de ecuaciones

Componga la matriz del sistema y calcule el determinante.

Solución. De coeficientes del sistema creemos una matriz: y su correspondiente determinante

Realicemos cálculos usando la fórmula (2), obtenemos

Definición 4. El número de filas (o columnas) del determinante se llama por el orden del determinante

En el ejemplo, se calculó el determinante de segundo orden.

Los determinantes tienen las siguientes propiedades.

Propiedad 1. El determinante no cambiará si sus filas se reemplazan por columnas y viceversa.

Mostrémoslo. Sea un determinante de segundo orden.

Reemplacemos las filas con columnas y calculemos nuevamente el determinante resultante.

Comparando D con D* podemos ver que D = D* .

Definición 5. La operación de sustituir filas por columnas (o viceversa) en un determinante se llama transposición.

Propiedad 2. Cuando se reordenan dos filas o columnas, el determinante cambia de signo.

Verificaremos esta propiedad usando un ejemplo, como para la propiedad 1. Sea el determinante dado

Intercambiemos las columnas y calculemos el determinante resultante.

Comparando los resultados, estamos convencidos de que el determinante efectivamente ha cambiado de signo. Intercambiemos ahora las líneas y verifiquemos nuevamente la validez de esta propiedad.

Determinante una matriz cuadrada es un número que se calcula de la siguiente manera:

a) Si el orden de una matriz cuadrada es 1, es decir consta de 1 número, entonces el determinante es igual a este número;

b) Si el orden de una matriz cuadrada es 2, es decir consta de 4 números, entonces el determinante es igual a la diferencia entre el producto de los elementos de la diagonal principal y el producto de los elementos de la diagonal secundaria;

c) Si el orden de una matriz cuadrada es 3, es decir consta de 9 números, entonces el determinante es igual a la suma de los productos de los elementos de la diagonal principal y dos triángulos paralelos a esta diagonal, de donde la suma de los productos de los elementos de la diagonal secundaria y dos triángulos paralelos a esta diagonal se le resta.

Ejemplos

Propiedades de los determinantes

1. El determinante no cambiará si las filas se reemplazan por columnas y las columnas por filas.

1. Un determinante que tiene 2 series idénticas es igual a cero.
2. El factor común de cualquier fila (fila o columna) del determinante se puede sacar del signo del determinante.

4. Al reorganizar dos series paralelas, el determinante cambia de signo al opuesto

5. Si los elementos de cualquier serie de un determinante son la suma de dos términos, entonces el determinante se puede expandir a la suma de dos determinantes correspondientes.

6. El determinante no cambiará si los elementos correspondientes de una serie paralela se suman a los elementos de una serie, multiplicados por cualquier número.

Elemento menor del determinante y su complemento algebraico

Elemento menor a IJ El determinante de orden n es un determinante de orden n-1 que se obtiene del original tachando la fila i y la columna j.

Complemento algebraico del elemento a IJ determinante es su menor multiplicado por (-1) i+ j

Ejemplo

matriz inversa

La matriz se llama no degenerado, si su determinante no es igual a cero, en caso contrario, la matriz se llama singular

La matriz se llama unión, si consta de los complementos algebraicos correspondientes y se transpone

La matriz se llama contrarrestar a una matriz dada si su producto es igual a la matriz identidad del mismo orden que la matriz dada

Teorema sobre la existencia de una matriz inversa

Cualquier matriz no singular tiene una inversa igual a la matriz de unión dividida por el determinante de esta matriz

Algoritmo para encontrar la matriz inversa A

1. Calcular determinante

1. Transponer matriz

1. Construya una matriz de unión, calcule todos los complementos algebraicos de la matriz transpuesta

1. Usa la fórmula:

Matriz menor es un determinante que consta de elementos ubicados en la intersección de k filas y k columnas seleccionadas de una matriz dada de tamaño mxn

rango de matriz es el orden más alto de la matriz menor que es distinto de cero

Notación r(A), rangoA

Rango es igual al número de filas distintas de cero de la matriz de pasos.

Ejemplo

Sistemas ecuaciones lineales.

Un sistema de ecuaciones lineales que contiene m ecuaciones yn incógnitas se llama sistema de la forma

donde estan los numeros a IJ - coeficientes del sistema, números b i - términos libres

Formulario de grabación matricial sistemas de ecuaciones lineales

Solución del sistema Se llaman n valores de incógnitas c 1, c 2,…, c n, al sustituirlos en el sistema, todas las ecuaciones del sistema se convierten en verdaderas igualdades. La solución del sistema se puede escribir como un vector columna.

El sistema de ecuaciones se llama articulación, si tiene al menos una solución, y no conjunto, si no hay soluciones.

Teorema de Kronecker-Capelli

Un sistema LU es consistente si y sólo si el rango de la matriz principal es igual al rango de la matriz extendida

Métodos para resolver un sistema LU.

1. método de gauss(usando transformaciones elementales, reduzca la matriz extendida a una matriz de pasos y luego a una canónica)

Las transformaciones elementales incluyen:

Reorganizar filas (columnas)

Sumar a una fila (columna) otra, multiplicada por un número distinto de 0.

Creemos una matriz extendida:

Seleccionemos el elemento principal en la primera columna y la primera fila, elemento 1, y llamémoslo principal. La línea que contiene el elemento principal no cambiará. Restablezcamos los elementos debajo de la diagonal principal. Para hacer esto, agregue la primera línea a la segunda línea, multiplicada por (-2). Sumamos la primera línea a la tercera línea, multiplicada por (-1), obtenemos:

Intercambiemos la segunda y tercera línea. Tacha mentalmente la primera columna y la primera fila y continúa el algoritmo para la matriz restante. A la tercera línea le sumamos la 2da, multiplicada por 5.

Llevamos la matriz extendida a una forma escalonada. Volviendo a las ecuaciones del sistema, comenzando desde la última línea y subiendo, determinamos las incógnitas una por una.

2. método matricial (AX=B, A -1 AX=A -1 B, X=A -1 B; matriz inversa a la matriz principal multiplicada por la columna de términos libres)

3. El método de Cramer.

La solución del sistema se encuentra mediante la fórmula:

¿Dónde está el determinante de la matriz principal modificada, en la que la i-ésima columna se cambia a una columna de términos libres, y es el determinante principal, formado por los coeficientes de las incógnitas?

Vectores.

Vector es un segmento dirigido

Cualquier vector viene dado por la longitud (módulo) y la dirección.

Designación: o

donde A es el comienzo del vector, B es el final del vector y es la longitud del vector.

Clasificación de vectores

vector cero es un vector cuya longitud es cero

vector unitario es un vector cuya longitud es igual a uno

Vectores iguales– estos son dos vectores que tienen la misma longitud y dirección

Vectores opuestos– estos son dos vectores cuyas longitudes son iguales y direcciones opuestas

Vectores colineales– estos son dos vectores que se encuentran en la misma recta o en rectas paralelas

Codireccional Los vectores son dos vectores colineales con la misma dirección.

dirigido opuestamente los vectores son dos vectores colineales con direcciones opuestas

coplanar Los vectores son tres vectores que se encuentran en el mismo plano o en planos paralelos.

Sistema rectangular Las coordenadas en un plano son dos líneas mutuamente perpendiculares con una dirección y origen seleccionados, con la línea horizontal llamada eje de abscisas y la línea vertical llamada eje de ordenadas.

A cada punto de un sistema de coordenadas rectangular le asignamos dos números: abscisa y ordenada.

Sistema rectangular Las coordenadas en el espacio son tres líneas rectas mutuamente perpendiculares con una dirección y origen elegidos, mientras que la línea recta horizontal dirigida hacia nosotros se llama eje de abscisas, la línea recta horizontal dirigida a nuestra derecha es el eje de ordenadas y la línea recta vertical. Dirigido hacia arriba se llama eje de aplicación.

A cada punto de un sistema de coordenadas rectangular le asignamos tres números: abscisa, ordenada y aplicación.