Definición 7.1. El conjunto de todos los puntos del plano para los cuales la suma de las distancias a dos puntos fijos F 1 y F 2 es un valor constante dado se llama elipse.
La definición de elipse da el siguiente método de construcción geométrica. Fijamos dos puntos F 1 y F 2 en el plano y denotamos un valor constante no negativo por 2a. Sea la distancia entre los puntos F 1 y F 2 2c. Imaginemos que un hilo inextensible de longitud 2a se fija en los puntos F 1 y F 2, por ejemplo, utilizando dos agujas. Está claro que esto sólo es posible para a ≥ c. Después de tirar del hilo con un lápiz, dibuje una línea que será una elipse (Fig. 7.1).
Entonces, el conjunto descrito no está vacío si a ≥ c. Cuando a = c, la elipse es un segmento con extremos F 1 y F 2, y cuando c = 0, es decir Si los puntos fijos especificados en la definición de elipse coinciden, se trata de una circunferencia de radio a. Descartando estos casos degenerados, asumiremos además, como regla, que a > c > 0.
Los puntos fijos F 1 y F 2 en la definición 7.1 de la elipse (ver Fig. 7.1) se denominan focos de elipse, la distancia entre ellos, indicada por 2c, - longitud focal, y los segmentos F 1 M y F 2 M que conectan un punto arbitrario M en la elipse con sus focos son radios focales.
La forma de la elipse está completamente determinada por la distancia focal |F 1 F 2 | = 2c y parámetro a, y su posición en el plano: un par de puntos F 1 y F 2.
De la definición de elipse se desprende que es simétrica con respecto a la recta que pasa por los focos F 1 y F 2, así como con respecto a la recta que divide el segmento F 1 F 2 por la mitad y es perpendicular a él. (Figura 7.2, a). Estas líneas se llaman ejes de elipse. El punto O de su intersección es el centro de simetría de la elipse y se llama centro de la elipse, y los puntos de intersección de la elipse con los ejes de simetría (puntos A, B, C y D en la Fig. 7.2, a) - vértices de la elipse.
El numero a se llama semieje mayor de la elipse, y b = √(a 2 - c 2) - es eje menor. Es fácil ver que para c > 0, el semieje mayor a es igual a la distancia desde el centro de la elipse a aquellos de sus vértices que están en el mismo eje que los focos de la elipse (vértices A y B en la Fig. 7.2, a), y el semieje menor b es igual a la distancia desde la elipse central a sus otros dos vértices (vértices C y D en la Fig. 7.2, a).
Ecuación de elipse. Consideremos una elipse en el plano con focos en los puntos F 1 y F 2, eje mayor 2a. Sea 2c la distancia focal, 2c = |F 1 F 2 |
Elijamos un sistema de coordenadas rectangular Oxy en el plano de modo que su origen coincida con el centro de la elipse y sus focos estén en eje x(Figura 7.2, b). Este sistema de coordenadas se llama canónico para la elipse en cuestión, y las variables correspondientes son canónico.
En el sistema de coordenadas seleccionado, los focos tienen coordenadas F 1 (c; 0), F 2 (-c; 0). Usando la fórmula para la distancia entre puntos, escribimos la condición |F 1 M| + |F 2 M| = 2a en coordenadas:
√((x - c) 2 + y 2) + √((x + c) 2 + y 2) = 2a. (7.2)
Esta ecuación es inconveniente porque contiene dos radicales cuadrados. Así que transformémoslo. Traslademos el segundo radical de la ecuación (7.2) a lado derecho y cuadrarlo:
(x - c) 2 + y 2 = 4a 2 - 4a√((x + c) 2 + y 2) + (x + c) 2 + y 2.
Después de abrir los paréntesis y traer términos similares, obtenemos
√((x + c) 2 + y 2) = a + εx
donde ε = c/a. Repetimos la operación de elevar al cuadrado para eliminar el segundo radical: (x + c) 2 + y 2 = a 2 + 2εax + ε 2 x 2, o, teniendo en cuenta el valor del parámetro ε ingresado, (a 2 - c 2 ) x 2 / a 2 + y 2 = a 2 - c 2. Dado que a 2 - c 2 = b 2 > 0, entonces
x 2 /a 2 + y 2 /b 2 = 1, a > b > 0. (7.4)
La ecuación (7.4) se satisface con las coordenadas de todos los puntos que se encuentran en la elipse. Pero al derivar esta ecuación, se utilizaron transformaciones no equivalentes de la ecuación original (7.2): dos elevaciones al cuadrado que eliminan los radicales cuadrados. Cuadrar una ecuación es una transformación equivalente si ambos lados tienen cantidades con el mismo signo, pero no verificamos esto en nuestras transformaciones.
Podemos evitar comprobar la equivalencia de transformaciones si tenemos en cuenta lo siguiente. Un par de puntos F 1 y F 2, |F 1 F 2 | = 2c, en el plano se define una familia de elipses con focos en estos puntos. Cada punto del plano, excepto los puntos del segmento F 1 F 2, pertenece a alguna elipse de la familia indicada. En este caso no se cruzan dos elipses, ya que la suma de los radios focales determina de forma inequívoca una elipse determinada. Entonces, la familia descrita de elipses sin intersecciones cubre todo el plano, excepto los puntos del segmento F 1 F 2. Consideremos un conjunto de puntos cuyas coordenadas satisfacen la ecuación (7.4) con un valor dado del parámetro a. ¿Se puede distribuir este conjunto entre varias elipses? Algunos de los puntos del conjunto pertenecen a una elipse con semieje mayor a. Sea un punto en este conjunto situado sobre una elipse con semieje mayor a. Entonces las coordenadas de este punto obedecen a la ecuación
aquellos. las ecuaciones (7.4) y (7.5) tienen soluciones generales. Sin embargo, es fácil verificar que el sistema
para ã ≠ a no tiene soluciones. Para hacer esto, basta con excluir, por ejemplo, x de la primera ecuación:
que después de transformaciones conduce a la ecuación
que no tiene soluciones para ã ≠ a, ya que . Entonces, (7.4) es la ecuación de una elipse con semieje mayor a > 0 y semieje menor b =√(a 2 - c 2) > 0. Se llama ecuación de elipse canónica.
Vista de elipse. El método geométrico para construir una elipse discutido anteriormente da una idea suficiente de apariencia elipse. Pero la forma de la elipse también se puede estudiar utilizando su ecuación canónica (7.4). Por ejemplo, es posible, asumiendo y ≥ 0, expresar y a través de x: y = b√(1 - x 2 /a 2) y, habiendo estudiado esta función, construir su gráfica. Hay otra forma de construir una elipse. Un círculo de radio a con centro en el origen del sistema de coordenadas canónico de la elipse (7.4) se describe mediante la ecuación x 2 + y 2 = a 2. Si se comprime con un coeficiente a/b > 1 a lo largo eje y, entonces obtienes una curva que se describe mediante la ecuación x 2 + (ya/b) 2 = a 2, es decir, una elipse.
Observación 7.1. Si el mismo círculo se comprime con un coeficiente a/b
Excentricidad de elipse. La relación entre la distancia focal de una elipse y su eje mayor se llama excentricidad de la elipse y denotado por ε. Para una elipse dada
ecuación canónica (7.4), ε = 2c/2a = c/a. Si en (7.4) los parámetros a y b están relacionados por la desigualdad a
Cuando c = 0, cuando la elipse se convierte en un círculo, y ε = 0. En otros casos, 0
La ecuación (7.3) es equivalente a la ecuación (7.4), ya que las ecuaciones (7.4) y (7.2) son equivalentes. Por tanto, la ecuación de la elipse también es (7.3). Además, la relación (7.3) es interesante porque proporciona una fórmula simple y libre de radicales para la longitud |F 2 M| uno de los radios focales del punto M(x; y) de la elipse: |F 2 M| = a + εx.
Se puede obtener una fórmula similar para el segundo radio focal a partir de consideraciones de simetría o repitiendo cálculos en los que, antes de elevar al cuadrado la ecuación (7.2), el primer radical se transfiere al lado derecho y no el segundo. Entonces, para cualquier punto M(x; y) en la elipse (ver Fig. 7.2)
|F 1 M | = a - εx, |F 2 M| = a + εx, (7.6)
y cada una de estas ecuaciones es una ecuación de una elipse.
Ejemplo 7.1. Encontremos la ecuación canónica de una elipse con semieje mayor 5 y excentricidad 0,8 y construyámosla.
Conociendo el semieje mayor de la elipse a = 5 y la excentricidad ε = 0,8, encontraremos su semieje menor b. Dado que b = √(a 2 - c 2), y c = εa = 4, entonces b = √(5 2 - 4 2) = 3. Entonces la ecuación canónica tiene la forma x 2 /5 2 + y 2 /3 2 = 1. Para construir una elipse, es conveniente dibujar un rectángulo con centro en el origen del sistema de coordenadas canónico, cuyos lados sean paralelos a los ejes de simetría de la elipse e iguales a sus ejes correspondientes (Fig. 7.4). Este rectángulo se cruza con
los ejes de la elipse en sus vértices A(-5; 0), B(5; 0), C(0; -3), D(0; 3), y la propia elipse está inscrita en él. En la figura. 7.4 también muestra los focos F 1.2 (±4; 0) de la elipse.
Propiedades geométricas de la elipse. Reescribamos la primera ecuación en (7.6) como |F 1 M| = (a/ε - x)ε. Tenga en cuenta que el valor a/ε - x para a > c es positivo, ya que el foco F 1 no pertenece a la elipse. Este valor representa la distancia a la línea vertical d: x = a/ε desde el punto M(x; y) que se encuentra a la izquierda de esta línea. La ecuación de la elipse se puede escribir como
|F 1 M|/(a/ε - x) = ε
Esto significa que esta elipse consta de aquellos puntos M(x; y) del plano para los cuales la relación entre la longitud del radio focal F 1 M y la distancia a la línea recta d es un valor constante igual a ε (Fig. 7.5).
La línea recta d tiene un "doble": una línea recta vertical d, simétrica a d con respecto al centro de la elipse, que viene dada por la ecuación x = -a/ε. Con respecto a d, la elipse se describe en. de la misma manera que con respecto a d. Ambas líneas d y d" se llaman directrices de la elipse. Las directrices de la elipse son perpendiculares al eje de simetría de la elipse en el que se encuentran sus focos y están espaciadas del centro de la elipse a una distancia a/ε = a 2 /c (ver Fig. 7.5).
La distancia p desde la directriz al foco más cercano a ella se llama parámetro focal de la elipse. Este parámetro es igual a
p = a/ε - c = (a 2 - c 2)/c = b 2 /c
La elipse tiene otra propiedad geométrica importante: los radios focales F 1 M y F 2 M forman ángulos iguales con la tangente a la elipse en el punto M (figura 7.6).
Esta propiedad tiene una clara significado fisico. Si se coloca una fuente de luz en el foco F 1, entonces el rayo que emerge de este foco, después de la reflexión en la elipse, irá a lo largo del segundo radio focal, ya que después de la reflexión formará el mismo ángulo con la curva que antes de la reflexión. Así, todos los rayos que emergen del foco F 1 se concentrarán en el segundo foco F 2 y viceversa. Según esta interpretación, esta propiedad se llama propiedad óptica de la elipse.
Definición. Una elipse es el lugar geométrico de puntos en un plano, la suma de las distancias de cada uno de los cuales a dos puntos dados de este plano, llamados focos, es un valor constante (siempre que este valor sea mayor que la distancia entre los focos). .
Denotamos los focos a través de la distancia entre ellos - a través de , y un valor constante, igual a la cantidad distancias desde cada punto de la elipse hasta los focos, pasando (según la condición).
Construyamos un sistema de coordenadas cartesiano de modo que los focos estén en el eje de abscisas y el origen de las coordenadas coincida con la mitad del segmento (Fig. 44). Entonces los focos tendrán las siguientes coordenadas: foco izquierdo y foco derecho. Derivemos la ecuación de la elipse en el sistema de coordenadas que hemos elegido. Para ello, considere un punto arbitrario de la elipse. Por definición de elipse, la suma de las distancias desde este punto a los focos es igual a:
Usando la fórmula para la distancia entre dos puntos, obtenemos por tanto
Para simplificar esta ecuación, la escribimos en la forma
Luego elevando al cuadrado ambos lados de la ecuación obtenemos
o, después de obvias simplificaciones:
Ahora elevamos nuevamente al cuadrado ambos lados de la ecuación, después de lo cual tenemos:
o, después de transformaciones idénticas:
Dado que, según la condición de la definición de elipse, el número es positivo. Introduzcamos la notación
Entonces la ecuación tomará la siguiente forma:
Según la definición de elipse, las coordenadas de cualquiera de sus puntos satisfacen la ecuación (26). Pero la ecuación (29) es consecuencia de la ecuación (26). En consecuencia, también lo satisfacen las coordenadas de cualquier punto de la elipse.
Se puede demostrar que las coordenadas de los puntos que no se encuentran en la elipse no satisfacen la ecuación (29). Por tanto, la ecuación (29) es la ecuación de una elipse. Se llama ecuación canónica de la elipse.
Establezcamos la forma de la elipse usando su ecuación canónica.
En primer lugar, prestemos atención al hecho de que esta ecuación contiene solo grados pares x e y. Esto significa que si algún punto pertenece a una elipse, entonces también contiene un punto simétrico con el punto relativo al eje de abscisas y un punto simétrico con el punto relativo al eje de ordenadas. Por tanto, la elipse tiene dos ejes de simetría mutuamente perpendiculares, que en nuestro sistema de coordenadas elegido coinciden con los ejes de coordenadas. De ahora en adelante llamaremos a los ejes de simetría de la elipse ejes de la elipse y al punto de su intersección centro de la elipse. El eje en el que se ubican los focos de la elipse (en en este caso eje x) se llama eje focal.
Primero determinemos la forma de la elipse en el primer cuarto. Para hacer esto, resolvamos la ecuación (28) para y:
Es obvio que aquí, ya que y toma valores imaginarios. A medida que aumenta de 0 a a, y disminuye de b a 0. La parte de la elipse que se encuentra en el primer cuarto será un arco delimitado por los puntos B (0; b) y que se encuentra en los ejes de coordenadas (Fig. 45). Usando ahora la simetría de la elipse, llegamos a la conclusión de que la elipse tiene la forma que se muestra en la Fig. 45.
Los puntos de intersección de la elipse con los ejes se denominan vértices de la elipse. De la simetría de la elipse se deduce que, además de los vértices, la elipse tiene dos vértices más (ver Fig. 45).
Los segmentos y los vértices opuestos que conectan la elipse, así como sus longitudes, se denominan ejes mayor y menor de la elipse, respectivamente. Los números a y b se denominan semiejes mayor y menor de la elipse, respectivamente.
La relación entre la mitad de la distancia entre los focos y el semieje mayor de la elipse se llama excentricidad de la elipse y generalmente se denota con la letra:
Dado que , la excentricidad de la elipse es menor que la unidad: La excentricidad caracteriza la forma de la elipse. De hecho, de la fórmula (28) se deduce que cuanto menor es la excentricidad de la elipse, menos difiere su semieje menor b del semieje mayor a, es decir, menos alargada es la elipse (a lo largo del eje focal).
En el caso límite, el resultado es un círculo de radio a: , o . Al mismo tiempo, los focos de la elipse parecen fusionarse en un punto: el centro del círculo. La excentricidad del círculo es cero:
La conexión entre la elipse y el círculo se puede establecer desde otro punto de vista. Demostremos que una elipse con semiejes a y b puede considerarse como una proyección de un círculo de radio a.
Consideremos dos planos P y Q, que forman entre sí un ángulo a, para el cual (Fig. 46). Construyamos un sistema de coordenadas en el plano P, y en el plano Q un sistema Oxy con un origen común O y un eje de abscisas común coincidente con la línea de intersección de los planos. Considere un círculo en el plano P.
con centro en el origen y radio igual a a. Sea un punto elegido arbitrariamente en el círculo, sea su proyección sobre el plano Q y sea la proyección del punto M sobre el eje Ox. Demostremos que el punto se encuentra en una elipse con semiejes a y b.
Curvas de segundo orden en un plano hay líneas definidas por ecuaciones en las que las coordenadas variables incógnita Y y están contenidos en el segundo grado. Estos incluyen la elipse, la hipérbola y la parábola.
La forma general de la ecuación de la curva de segundo orden es la siguiente:
Dónde A, B, C, D, E, F- números y al menos uno de los coeficientes A, B, C no igual a cero.
Al resolver problemas con curvas de segundo orden, las ecuaciones canónicas de elipse, hipérbola y parábola se consideran con mayor frecuencia. Es fácil pasar a ellos desde las ecuaciones generales; a esto se dedicará el ejemplo 1 de problemas con elipses.
Elipse dada por la ecuación canónica
Definición de elipse. Una elipse es el conjunto de todos los puntos del plano para los cuales la suma de las distancias a los puntos llamados focos es un valor constante mayor que la distancia entre los focos.
Los focos se indican como en la siguiente figura.
La ecuación canónica de una elipse tiene la forma:
Dónde a Y b (a > b) - las longitudes de los semiejes, es decir, la mitad de las longitudes de los segmentos cortados por la elipse en los ejes de coordenadas.
La línea recta que pasa por los focos de la elipse es su eje de simetría. Otro eje de simetría de una elipse es una línea recta que pasa por el medio de un segmento perpendicular a este segmento. Punto ACERCA DE la intersección de estas líneas sirve como centro de simetría de la elipse o simplemente como centro de la elipse.
El eje de abscisas de la elipse se cruza en los puntos ( a, ACERCA DE) Y (- a, ACERCA DE), y el eje de ordenadas está en puntos ( b, ACERCA DE) Y (- b, ACERCA DE). Estos cuatro puntos se llaman vértices de la elipse. El segmento entre los vértices de la elipse en el eje x se llama eje mayor y en el eje de ordenadas, eje menor. Sus segmentos desde la cima hasta el centro de la elipse se llaman semiejes.
Si a = b, entonces la ecuación de la elipse toma la forma . Esta es la ecuación de un círculo con radio. a, y el círculo es caso especial elipse. Se puede obtener una elipse a partir de un círculo de radio. a, si lo comprimes en a/b veces a lo largo del eje Oye .
Ejemplo 1. Comprueba si una recta dada por una ecuación general es 
, elipse.
Solución. Hacemos transformaciones ecuación general. Usamos la transferencia del término libre al lado derecho, la división término por término de la ecuación por el mismo número y la reducción de fracciones:
Respuesta. La ecuación obtenida como resultado de las transformaciones es la ecuación canónica de la elipse. Por tanto, esta recta es una elipse.
Ejemplo 2. Componga la ecuación canónica de una elipse si sus semiejes son 5 y 4, respectivamente.
Solución. Observamos la fórmula de la ecuación canónica de una elipse y la sustituimos: el semieje mayor es a= 5, el semieje menor es b= 4 . Obtenemos la ecuación canónica de la elipse:
Puntos y , indicados en verde en el eje mayor, donde
son llamados engaños.
llamado excentricidad elipse.
Actitud b/a caracteriza el “achatamiento” de la elipse. Cuanto menor es esta relación, más se alarga la elipse a lo largo del eje mayor. Sin embargo, el grado de alargamiento de una elipse se expresa más a menudo mediante la excentricidad, cuya fórmula se proporciona anteriormente. Para diferentes elipses, la excentricidad varía de 0 a 1, siendo siempre menor que la unidad.
Ejemplo 3. Componga la ecuación canónica de la elipse si la distancia entre los focos es 8 y el eje mayor es 10.
Solución. Saquemos algunas conclusiones simples:
Si el eje mayor es igual a 10, entonces su mitad, es decir, el semieje a = 5 ,
Si la distancia entre los focos es 8, entonces el número do de las coordenadas focales es igual a 4.
Sustituimos y calculamos:
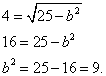
El resultado es la ecuación canónica de la elipse:
Ejemplo 4. Componga la ecuación canónica de una elipse si su eje mayor es 26 y su excentricidad es .
Solución. Como se deduce tanto del tamaño del eje mayor como de la ecuación de excentricidad, el semieje mayor de la elipse a= 13. De la ecuación de excentricidad expresamos el número. do, necesario para calcular la longitud del semieje menor:
.
Calculamos el cuadrado de la longitud del semieje menor:
Redactamos la ecuación canónica de la elipse:
Ejemplo 5. Determine los focos de la elipse dada por la ecuación canónica.
Solución. Encuentra el número do, que determina las primeras coordenadas de los focos de la elipse:
.
Obtenemos los focos de la elipse:
Ejemplo 6. Los focos de la elipse están ubicados en el eje. Buey simétricamente respecto al origen. Componga la ecuación canónica de la elipse si:
1) la distancia entre los focos es 30 y el eje mayor es 34
2) eje menor 24, y uno de los focos está en el punto (-5; 0)
3) excentricidad, y uno de los focos está en el punto (6; 0)
Sigamos resolviendo problemas de elipse juntos.
Si es un punto arbitrario de la elipse (indicado en verde en la parte superior derecha de la elipse en el dibujo) y es la distancia a este punto desde los focos, entonces las fórmulas para las distancias son las siguientes:
Para cada punto perteneciente a la elipse, la suma de las distancias a los focos es un valor constante igual a 2 a.
Rectas definidas por ecuaciones
son llamados directoras elipse (en el dibujo hay líneas rojas a lo largo de los bordes).
De las dos ecuaciones anteriores se deduce que para cualquier punto de la elipse
,
donde y son las distancias de este punto a las directivas y .
Ejemplo 7. Dada una elipse. Escribe una ecuación para sus directivas.
Solución. Observamos la ecuación de la directriz y encontramos que necesitamos encontrar la excentricidad de la elipse, es decir Tenemos todos los datos para ello. Calculamos:
.
Obtenemos la ecuación de las directivas de la elipse:
Ejemplo 8. Componga la ecuación canónica de una elipse si sus focos son puntos y sus directrices son rectas.
Conferencias sobre álgebra y geometría. Semestre 1.
Conferencia 15. Elipse.
Capítulo 15. Elipse.
cláusula 1. Definiciones básicas.
Definición. Una elipse es el GMT de un avión, la suma de las distancias a dos puntos fijos del avión, llamados focos, es un valor constante.
Definición. La distancia desde un punto arbitrario M del plano hasta el foco de la elipse se llama radio focal del punto M.
Designaciones: 
– focos de la elipse, 
– radios focales del punto M.
Según la definición de elipse, un punto M es un punto de una elipse si y sólo si 
– valor constante. Esta constante suele denotarse como 2a:
.
(1)
Tenga en cuenta que 
.
Por definición de elipse, sus focos son puntos fijos, por lo que la distancia entre ellos también es un valor constante para una elipse determinada.
Definición. La distancia entre los focos de la elipse se llama distancia focal.
Designación: 
.
De un triangulo 
resulta que 
, es decir.
.
Denotemos por b el número igual a 
, es decir.
.
(2)
Definición. Actitud
(3)
se llama excentricidad de la elipse.
Introduzcamos un sistema de coordenadas en este plano, que llamaremos canónico para la elipse.
Definición. El eje sobre el que se encuentran los focos de la elipse se llama eje focal.
Construyamos un PDSC canónico para la elipse, consulte la Fig. 2.
Seleccionamos el eje focal como eje de abscisas y dibujamos el eje de ordenadas que pasa por el medio del segmento. 
perpendicular al eje focal.
Entonces los focos tienen coordenadas. 
,
.
cláusula 2. Ecuación canónica de una elipse.
Teorema. En el sistema de coordenadas canónico de una elipse, la ecuación de la elipse tiene la forma:
.
(4)
Prueba. Realizamos la prueba en dos etapas. En la primera etapa, demostraremos que las coordenadas de cualquier punto que se encuentre en la elipse satisfacen la ecuación (4). En la segunda etapa demostraremos que cualquier solución a la ecuación (4) da las coordenadas de un punto que se encuentra en la elipse. De aquí se deduce que la ecuación (4) se satisface con aquellos y sólo aquellos puntos del plano de coordenadas que se encuentran en la elipse. De esto y de la definición de la ecuación de una curva se deduce que la ecuación (4) es una ecuación de una elipse.
1) Sea el punto M(x, y) un punto de la elipse, es decir la suma de sus radios focales es 2a:
.
Usemos la fórmula para la distancia entre dos puntos en el plano de coordenadas y usemos esta fórmula para encontrar los radios focales de un punto dado M:
,
, de donde obtenemos:
Movamos una raíz al lado derecho de la igualdad y la elevamos al cuadrado:
Reduciendo obtenemos:
Presentamos otros similares, reducimos a 4 y eliminamos el radical:
.
cuadratura
Abra los corchetes y acorte 
:
donde obtenemos:
Usando la igualdad (2), obtenemos:
.
Dividiendo la última igualdad por 
, obtenemos igualdad (4), etc.
2) Sea ahora un par de números (x, y) que satisfagan la ecuación (4) y sea M(x, y) el punto correspondiente en el plano coordenado Oxy.
Luego de (4) se sigue:
.
Sustituimos esta igualdad en la expresión de los radios focales del punto M:
.
Aquí usamos la igualdad (2) y (3).
De este modo, 
. Asimismo, 
.
Ahora observe que de la igualdad (4) se sigue que
o 
etc. 
, entonces la desigualdad sigue:
.
De aquí se deduce, a su vez, que
o 
Y
,
.
(5)
De las igualdades (5) se deduce que 
, es decir. el punto M(x, y) es un punto de la elipse, etc.
El teorema ha sido demostrado.
Definición. La ecuación (4) se llama ecuación canónica de la elipse.
Definición. Los ejes de coordenadas canónicos de una elipse se denominan ejes principales de la elipse.
Definición. El origen del sistema de coordenadas canónico de una elipse se llama centro de la elipse.
cláusula 3. Propiedades de la elipse.
Teorema. (Propiedades de una elipse).
1. En el sistema de coordenadas canónico de una elipse, todo
los puntos de la elipse están en el rectángulo
,
.
2. Los puntos se encuentran en
3. Una elipse es una curva que es simétrica con respecto a
sus ejes principales.
4. El centro de la elipse es su centro de simetría.
Prueba. 1, 2) Se sigue inmediatamente de la ecuación canónica de la elipse.
3, 4) Sea M(x, y) un punto arbitrario de la elipse. Entonces sus coordenadas satisfacen la ecuación (4). Pero entonces las coordenadas de los puntos también satisfacen la ecuación (4) y, por tanto, son puntos de la elipse, de donde se derivan los enunciados del teorema.
El teorema ha sido demostrado.
Definición. La cantidad 2a se llama eje mayor de la elipse, la cantidad a se llama semieje mayor de la elipse.
Definición. La cantidad 2b se llama eje menor de la elipse, la cantidad b se llama semieje menor de la elipse.
Definición. Los puntos de intersección de una elipse con sus ejes principales se denominan vértices de la elipse.
Comentario. Una elipse se puede construir de la siguiente manera. En el avión, "clavamos un clavo en los puntos focales" y les sujetamos un trozo de hilo. 
. Luego cogemos un lápiz y lo usamos para estirar el hilo. Luego movemos la mina del lápiz a lo largo del plano, asegurándonos de que el hilo quede tenso.
De la definición de excentricidad se deduce que
Fijemos el número a y dirijamos el número c a cero. Entonces en 
,
Y 
. En el límite llegamos
o 
– ecuación de un círculo.
Dirigámonos ahora 
. Entonces 
,
y vemos que en el límite la elipse degenera en un segmento de recta 
en la notación de la Figura 3.
cláusula 4. Ecuaciones paramétricas de la elipse.
Teorema. Dejar 
– números reales arbitrarios. Entonces el sistema de ecuaciones
,
(6)
son ecuaciones paramétricas de una elipse en el sistema de coordenadas canónico de la elipse.
Prueba. Basta demostrar que el sistema de ecuaciones (6) es equivalente a la ecuación (4), es decir tienen el mismo conjunto de soluciones.
1) Sea (x, y) una solución arbitraria del sistema (6). Divide la primera ecuación por a, la segunda por b, eleva al cuadrado ambas ecuaciones y suma:
.
Aquellos. cualquier solución (x, y) del sistema (6) satisface la ecuación (4).
2) Por el contrario, sea el par (x, y) una solución de la ecuación (4), es decir,
.
De esta igualdad se deduce que el punto con coordenadas 
se encuentra en un círculo de radio unitario con centro en el origen, es decir es un punto en un círculo trigonométrico al que corresponde un cierto ángulo 
:
De la definición de seno y coseno se deduce inmediatamente que
,
, Dónde 
, de lo que se deduce que el par (x, y) es una solución al sistema (6), etc.
El teorema ha sido demostrado.
Comentario. Se puede obtener una elipse como resultado de una "compresión" uniforme de un círculo de radio a hacia el eje de abscisas.
Dejar 
– ecuación de una circunferencia con centro en el origen. La “compresión” de un círculo al eje de abscisas no es más que una transformación del plano coordenado, realizada según la siguiente regla. A cada punto M(x, y) le asociamos un punto en el mismo plano 
, Dónde 
,
– relación de compresión.
Con esta transformación, cada punto del círculo "hace una transición" a otro punto del plano, que tiene la misma abscisa, pero una ordenada más pequeña. Expresemos la ordenada antigua de un punto a través de la nueva:
y sustituimos círculos en la ecuación:
.
De aquí obtenemos:
.
(7)
De ello se deduce que si antes de la transformación de “compresión” el punto M(x, y) estaba en el círculo, es decir sus coordenadas satisfacían la ecuación del círculo, luego después de la transformación de "compresión" este punto se "transformó" en el punto 
, cuyas coordenadas satisfacen la ecuación de elipse (7). Si queremos obtener la ecuación de una elipse con semieje menor b, entonces debemos tomar el factor de compresión.
.
cláusula 5. Tangente a una elipse.
Teorema. Dejar 
– punto arbitrario de la elipse
.
Entonces la ecuación de la tangente a esta elipse en el punto 
tiene la forma:
.
(8)
Prueba. Basta considerar el caso en el que el punto de tangencia se encuentra en el primer o segundo cuarto del plano de coordenadas: 
. La ecuación de la elipse en el semiplano superior tiene la forma:
.
(9)
Usemos la ecuación tangente a la gráfica de la función. 
en el punto 
:
Dónde 
– el valor de la derivada de una función dada en un punto 
. La elipse en el primer cuarto se puede considerar como una gráfica de la función (8). Encontremos su derivada y su valor en el punto de tangencia:
,
. Aquí aprovechamos el hecho de que el punto tangente 
es un punto de la elipse y por lo tanto sus coordenadas satisfacen la ecuación de la elipse (9), es decir
.
Sustituimos el valor encontrado de la derivada en la ecuación tangente (10):
,
donde obtenemos:
De esto se desprende:
Dividamos esta igualdad por 
:
.
Queda por señalar que 
, porque punto 
pertenece a la elipse y sus coordenadas satisfacen su ecuación.
La ecuación tangente (8) se demuestra de manera similar en el punto de tangencia que se encuentra en el tercer o cuarto cuarto del plano de coordenadas.
Y finalmente, podemos verificar fácilmente que la ecuación (8) da la ecuación tangente en los puntos 
,
:
o 
, Y 
o 
.
El teorema ha sido demostrado.
cláusula 6. Propiedad especular de una elipse.
Teorema. La tangente a la elipse tiene ángulos iguales con los radios focales del punto de tangencia.
Dejar 
– punto de contacto, 
,
– radios focales del punto de tangencia, P y Q – proyecciones de focos sobre la tangente trazada a la elipse en el punto 
.
El teorema establece que
.
(11)
Esta igualdad puede interpretarse como la igualdad de los ángulos de incidencia y reflexión de un rayo de luz desde una elipse liberada de su foco. Esta propiedad se llama propiedad especular de la elipse:
Un rayo de luz liberado desde el foco de la elipse, después de reflejarse en el espejo de la elipse, pasa a través de otro foco de la elipse.
Prueba del teorema. Para demostrar la igualdad de los ángulos (11), demostramos la similitud de los triángulos. 
Y 
, en el que las partes 
Y 
será similar. Como los triángulos son rectángulos, basta con demostrar la igualdad.
Una elipse es el lugar geométrico de puntos en un plano, la suma de las distancias de cada uno de ellos a dos puntos dados F_1, y F_2 es un valor constante (2a) mayor que la distancia (2c) entre estos puntos dados(Figura 3.36, a). Esta definición geométrica expresa propiedad focal de una elipse.
Propiedad focal de una elipse
Los puntos F_1 y F_2 se llaman focos de la elipse, la distancia entre ellos 2c=F_1F_2 es la distancia focal, la O media del segmento F_1F_2 es el centro de la elipse, el número 2a es la longitud del eje mayor de la elipse (en consecuencia, el número a es el semieje mayor de la elipse). Los segmentos F_1M y F_2M que conectan un punto arbitrario M de la elipse con sus focos se denominan radios focales del punto M. El segmento que une dos puntos de una elipse se llama cuerda de la elipse.
La relación e=\frac(c)(a) se llama excentricidad de la elipse. De la definición (2a>2c) se deduce que 0\leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр O совпадают, и эллипс является окружностью радиуса a (рис.3.36,6).
Definición geométrica de elipse, que expresa su propiedad focal, es equivalente a su definición analítica: la recta dada por la ecuación canónica de la elipse:
De hecho, introduzcamos un sistema de coordenadas rectangular (figura 3.36c). Tomamos el centro O de la elipse como origen del sistema de coordenadas; tomamos la línea recta que pasa por los focos (eje focal o primer eje de la elipse) como eje de abscisas (la dirección positiva es del punto F_1 al punto F_2); tomemos una línea recta perpendicular al eje focal y que pasa por el centro de la elipse (el segundo eje de la elipse) como eje de ordenadas (la dirección en el eje de ordenadas se elige de modo que el sistema de coordenadas rectangular Oxy sea el correcto) .
Creemos una ecuación para la elipse usando su definición geométrica, que expresa la propiedad focal. En el sistema de coordenadas seleccionado, determinamos las coordenadas de los focos. F_1(-c,0),~F_2(c,0). Para un punto arbitrario M(x,y) perteneciente a la elipse, tenemos:
\vline\,\overrightarrow(F_1M)\,\vline\,+\vline\,\overrightarrow(F_2M)\,\vline\,=2a.
Escribiendo esta igualdad en forma de coordenadas, obtenemos:
\sqrt((x+c)^2+y^2)+\sqrt((x-c)^2+y^2)=2a.
Movemos el segundo radical hacia el lado derecho, elevamos al cuadrado ambos lados de la ecuación y llevamos términos similares:
(x+c)^2+y^2=4a^2-4a\sqrt((x-c)^2+y^2)+(x-c)^2+y^2~\Leftrightarrow ~4a\sqrt((x-c )^2+y^2)=4a^2-4cx.
Dividiendo por 4 elevamos al cuadrado ambos lados de la ecuación:
a^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^ 2=a^2(a^2-c^2).
habiendo designado b=\sqrt(a^2-c^2)>0, obtenemos b^2x^2+a^2y^2=a^2b^2. Dividiendo ambos lados por a^2b^2\ne0, llegamos a ecuación canónica elipse:
\frac(x^2)(a^2)+\frac(y^2)(b^2)=1.
Por tanto, el sistema de coordenadas elegido es canónico.
Si los focos de la elipse coinciden, entonces la elipse es un círculo (Fig. 3.36,6), ya que a=b. En este caso, cualquier sistema de coordenadas rectangular con origen en el punto será canónico. O\equiv F_1\equiv F_2, y la ecuación x^2+y^2=a^2 es la ecuación de un círculo con centro en el punto O y radio igual a a.
Al razonar en orden inverso, se puede demostrar que todos los puntos cuyas coordenadas satisfacen la ecuación (3.49), y sólo ellos, pertenecen al lugar geométrico de puntos llamado elipse. En otras palabras, la definición analítica de una elipse es equivalente a su definición geométrica, que expresa la propiedad focal de la elipse.
Propiedad directora de una elipse
Las directivas de una elipse son dos líneas rectas que corren paralelas al eje de ordenadas del sistema de coordenadas canónico a la misma distancia \frac(a^2)(c) de él. En c=0, cuando la elipse es un círculo, no hay directivas (podemos suponer que las directivas están en el infinito).
Elipse con excentricidad 0
De hecho, por ejemplo, para el foco F_2 y la directriz d_2 (Fig. 3.37,6) la condición \frac(r_2)(\rho_2)=e se puede escribir en forma de coordenadas:
\sqrt((x-c)^2+y^2)=e\cdot\!\left(\frac(a^2)(c)-x\right)
Deshacerse de la irracionalidad y reemplazar e=\frac(c)(a),~a^2-c^2=b^2, llegamos a la ecuación de elipse canónica (3.49). Se puede realizar un razonamiento similar para el foco F_1 y el director. d_1\dos puntos\frac(r_1)(\rho_1)=e.
Ecuación de una elipse en un sistema de coordenadas polares.
La ecuación de la elipse en el sistema de coordenadas polares F_1r\varphi (Fig. 3.37, cy 3.37 (2)) tiene la forma
r=\frac(p)(1-e\cdot\cos\varphi)
donde p=\frac(b^2)(a) es el parámetro focal de la elipse.
De hecho, elijamos el foco izquierdo F_1 de la elipse como polo del sistema de coordenadas polares y el rayo F_1F_2 como eje polar (figura 3.37, c). Entonces, para un punto arbitrario M(r,\varphi), según la definición geométrica (propiedad focal) de una elipse, tenemos r+MF_2=2a. Expresamos la distancia entre los puntos M(r,\varphi) y F_2(2c,0) (ver):
\begin(alineado)F_2M&=\sqrt((2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0))=\\ &=\sqrt(r^2- 4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2).\end(alineado)
Por lo tanto, en forma de coordenadas, la ecuación de la elipse F_1M+F_2M=2a tiene la forma
r+\sqrt(r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2)=2\cdot a.
Aislamos el radical, elevamos al cuadrado ambos lados de la ecuación, dividimos por 4 y presentamos términos similares:
r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac(c)(a)\cdot\cos \varphi\right)\!\cdot r=a^2-c^2.
Expresa el radio polar r y haz el reemplazo. e=\frac(c)(a),~b^2=a^2-c^2,~p=\frac(b^2)(a):
r=\frac(a^2-c^2)(a\cdot(1-e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(b^2)(a\cdot(1) -e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(p)(1-e\cdot\cos\varphi),
Q.E.D.
Significado geométrico de los coeficientes en la ecuación de la elipse.
Encontremos los puntos de intersección de la elipse (ver figura 3.37a) con los ejes de coordenadas (vértices de la elipse). Sustituyendo y=0 en la ecuación, encontramos los puntos de intersección de la elipse con el eje de abscisas (con el eje focal): x=\pm a. Por tanto, la longitud del segmento del eje focal contenido dentro de la elipse es igual a 2a. Este segmento, como se señaló anteriormente, se llama eje mayor de la elipse y el número a es el semieje mayor de la elipse. Sustituyendo x=0, obtenemos y=\pm b. Por tanto, la longitud del segmento del segundo eje de la elipse contenido dentro de la elipse es igual a 2b. Este segmento se llama eje menor de la elipse y el número b es el semieje menor de la elipse.
En realidad, b=\sqrt(a^2-c^2)\leqslant\sqrt(a^2)=a, y la igualdad b=a se obtiene sólo en el caso c=0, cuando la elipse es un círculo. Actitud k=\frac(b)(a)\leqslant1 se llama relación de compresión de elipse.
Notas 3.9
1. Las rectas x=\pm a,~y=\pm b limitan el rectángulo principal en el plano de coordenadas, dentro del cual hay una elipse (ver Fig. 3.37, a).
2. Una elipse se puede definir como el lugar geométrico de los puntos obtenidos al comprimir un círculo a su diámetro.
De hecho, supongamos que la ecuación de un círculo en el sistema de coordenadas rectangular Oxy tenga la forma x^2+y^2=a^2. Cuando se comprime en el eje x con un coeficiente de 0 \begin(casos)x"=x,\\y"=k\cdot y.\end(casos) Sustituyendo los círculos x=x" e y=\frac(1)(k)y" en la ecuación, obtenemos la ecuación para las coordenadas de la imagen M"(x",y") del punto M(x,y) ) : (x")^2+(\left(\frac(1)(k)\cdot y"\right)\^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} ya que b=k\cdot a . Esta es la ecuación canónica de la elipse. 3. Los ejes de coordenadas (del sistema de coordenadas canónico) son los ejes de simetría de la elipse (llamados ejes principales de la elipse), y su centro es el centro de simetría. En efecto, si el punto M(x,y) pertenece a la elipse. entonces los puntos M"(x,-y) y M""(-x,y), simétricos al punto M con respecto a los ejes de coordenadas, también pertenecen a la misma elipse. 4. De la ecuación de la elipse en el sistema de coordenadas polares. r=\frac(p)(1-e\cos\varphi)(ver Fig. 3.37, c), se aclara el significado geométrico del parámetro focal: esta es la mitad de la longitud de la cuerda de la elipse que pasa a través de su foco perpendicular al eje focal (r=p en \varphi=\frac(\pi)(2)). 5. La excentricidad e caracteriza la forma de la elipse, es decir, la diferencia entre la elipse y el círculo. Cuanto mayor es e, más alargada es la elipse, y cuanto más cerca está e de cero, más cerca está la elipse de un círculo (figura 3.38a). De hecho, teniendo en cuenta que e=\frac(c)(a) y c^2=a^2-b^2 , obtenemos e^2=\frac(c^2)(a^2)=\frac(a^2-b^2)(a^2)=1-(\left(\frac(a)(b)\right )\^2=1-k^2,
!} donde k es la relación de compresión de la elipse, 0 6. Ecuación \frac(x^2)(a^2)+\frac(y^2)(b^2)=1 en un 7. Ecuación \frac((x-x_0)^2)(a^2)+\frac((y-y_0)^2)(b^2)=1,~a\geqslant b define una elipse con centro en el punto O"(x_0,y_0), cuyos ejes son paralelos a los ejes de coordenadas (Fig. 3.38, c). Esta ecuación se reduce a la canónica mediante traslación paralela (3.36). Cuando a=b=R la ecuación (x-x_0)^2+(y-y_0)^2=R^2 describe un círculo de radio R con centro en el punto O"(x_0,y_0) . Ecuación paramétrica de elipse en el sistema de coordenadas canónico tiene la forma \begin(cases)x=a\cdot\cos(t),\\ y=b\cdot\sin(t),\end(cases)0\leqslant t<2\pi.
De hecho, sustituyendo estas expresiones en la ecuación (3.49), llegamos a la identidad trigonométrica principal \cos^2t+\sin^2t=1. Ejemplo 3.20. dibujar una elipse \frac(x^2)(2^2)+\frac(y^2)(1^2)=1 en el sistema de coordenadas canónico Oxy. Encuentre los semiejes, la distancia focal, la excentricidad, la relación de compresión, el parámetro focal y las ecuaciones de directriz. Solución. Comparando la ecuación dada con la canónica, determinamos los semiejes: a=2 - semieje mayor, b=1 - semieje menor de la elipse. Construimos el rectángulo principal con lados 2a=4,~2b=2 con el centro en el origen (figura 3.39). Teniendo en cuenta la simetría de la elipse, la encajamos en el rectángulo principal. Si es necesario, determine las coordenadas de algunos puntos de la elipse. Por ejemplo, sustituyendo x=1 en la ecuación de la elipse, obtenemos \frac(1^2)(2^2)+\frac(y^2)(1^2)=1 \quad \Leftrightarrow \quad y^2=\frac(3)(4) \quad \Leftrightarrow \ quad y=\pm\frac(\sqrt(3))(2). Por tanto, puntos con coordenadas \left(1;\,\frac(\sqrt(3))(2)\right)\!,~\left(1;\,-\frac(\sqrt(3))(2)\right)- pertenecen a la elipse. Calcular la relación de compresión k=\frac(b)(a)=\frac(1)(2); longitud focal 2c=2\sqrt(a^2-b^2)=2\sqrt(2^2-1^2)=2\sqrt(3); excentricidad e=\frac(c)(a)=\frac(\sqrt(3))(2); parámetro focal p=\frac(b^2)(a)=\frac(1^2)(2)=\frac(1)(2). Componemos las ecuaciones de directriz: x=\pm\frac(a^2)(c)~\Leftrightarrow~x=\pm\frac(4)(\sqrt(3)).Ecuación paramétrica de elipse
