Calcular integrales utilizando el método de integración por partes. Calculadora en línea Calcula la integral indefinida (antiderivada)

La siguiente fórmula se llama fórmula de integración por partes en la integral indefinida:

Para aplicar la fórmula de integración por partes, el integrando debe dividirse en dos factores. Uno de ellos se denota por tu, y el resto se refiere al segundo factor y se denota por dv. Luego por diferenciación encontramos du e integración - función v. Al mismo tiempo, para tu dv- una parte del integrando que pueda integrarse fácilmente.

¿Cuándo es beneficioso utilizar el método de integración por partes? Entonces cuando el integrando contiene :

1) - funciones logarítmicas, así como funciones trigonométricas inversas (con el prefijo "arco"), luego, según la experiencia a largo plazo de integración por partes, estas funciones se denotan por tu;

2) , , - seno, coseno y exponente multiplicado por PAG(X) es un polinomio arbitrario en x, entonces estas funciones se denotan por dv, y el polinomio es a través de tu;

3) , , , , en este caso la integración por partes se aplica dos veces.

Expliquemos el valor del método de integración por partes usando el ejemplo del primer caso. Deje que la expresión bajo el signo integral contenga una función logarítmica (este será el ejemplo 1). Al utilizar la integración por partes, dicha integral se reduce a calcular la integral de funciones algebraicas únicamente (la mayoría de las veces un polinomio), es decir, que no contienen una función logarítmica o inversa. Funcion trigonometrica. Usando la fórmula de integración por partes dada al comienzo de la lección

obtenemos en el primer término (sin integral) una función logarítmica, y en el segundo término (bajo el signo de integral) una función que no contiene logaritmo. La integral de una función algebraica es mucho más simple que la integral bajo cuyo signo se encuentra una función logarítmica o trigonométrica inversa por separado o junto con un factor algebraico.

Así, utilizando fórmulas de integración por partes la integración no se realiza de inmediato: encontrar una integral dada se reduce a encontrar otra. El significado de la fórmula de integración por partes es que como resultado de su aplicación, la nueva integral resulta tabular o al menos se vuelve más simple que la original.

El método de integración por partes se basa en el uso de la fórmula para derivar el producto de dos funciones:

entonces se puede escribir en la forma

que se dio al comienzo de la lección.

Al encontrar integrando la función v para ello se obtiene un conjunto infinito de funciones antiderivadas. Para aplicar la fórmula de integración por partes se puede tomar cualquiera de ellas, y por tanto la que corresponda a una constante arbitraria CON, igual a cero. Por lo tanto, al encontrar la función v Constante arbitraria CON no se debe ingresar.

El método de integración por partes tiene una aplicación muy especial: se puede utilizar para derivar fórmulas recurrentes para encontrar funciones antiderivadas cuando es necesario reducir el grado de funciones bajo el signo integral. Es necesario reducir el grado cuando no hay integrales tabulares para, por ejemplo, funciones como senos y cosenos a potencias mayores que el segundo y sus productos. Una fórmula recurrente es una fórmula para encontrar el siguiente miembro de una secuencia a través del miembro anterior. Para los casos indicados, el objetivo se consigue bajando sucesivamente el grado. Entonces, si el integrando es un seno elevado a la cuarta potencia de x, entonces integrando por partes puedes encontrar una fórmula para la integral del seno elevado a la tercera potencia, y así sucesivamente. El último párrafo de esta lección está dedicado a la tarea descrita.

Aplicando la integración por partes juntas

Ejemplo 1. Encuentra la integral indefinida usando el método de integración por partes.:

Solución. En la expresión integrando, el logaritmo, que, como ya sabemos, puede denotarse razonablemente por tu. Creemos que , .

Encontramos (como ya se mencionó en la explicación de la referencia teórica, inmediatamente obtenemos una función logarítmica en el primer término (sin integral), y una función que no contiene un logaritmo en el segundo término (bajo el signo de integral): ):

Y de nuevo el logaritmo...

Ejemplo 2. Encuentra la integral indefinida:

Solución. Dejar , .

El logaritmo está presente en el cuadrado. Esto significa que debe diferenciarse como una función compleja. Encontramos
,
.

Volvemos a encontrar la segunda integral por partes y obtenemos la ventaja ya mencionada (en el primer término (sin la integral) hay una función logarítmica, y en el segundo término (bajo el signo de integral) hay una función que no contiene una logaritmo).

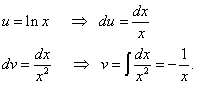
Encontramos la integral original:

Ejemplo 3.

Solución. El arcotangente, al igual que el logaritmo, se denota mejor por tu. Entonces deja , .

Entonces ,
.

Aplicando la fórmula de integración por partes obtenemos:

Encontramos la segunda integral cambiando una variable.

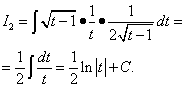
Volviendo a la variable X, obtenemos

.

Encontramos la integral original:

.

Ejemplo 4. Encuentra la integral indefinida usando el método de integración por partes.:

Solución. Es mejor denotar el exponente por dv. Dividimos el integrando en dos factores. Creyendo que

Ejemplo 5. Encuentra la integral indefinida usando el método de integración por partes.:

.

Solución. Dejar , . Entonces , .

Usando la fórmula de integración por partes (1), encontramos:

Ejemplo 6. Encuentra la integral indefinida por integración por partes:

Solución. El seno, al igual que el exponencial, puede denotarse convenientemente por dv. Dejar , .

Usando la fórmula de integración por partes encontramos:

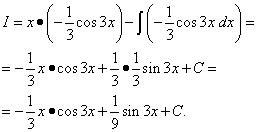
Volvemos a aplicar la integración por partes juntas

Ejemplo 10. Encuentra la integral indefinida por integración por partes:

.

Solución. Como en todos los casos similares, conviene denotar el coseno como dv. Denotamos , .

Entonces , .

Usando la fórmula de integración por partes obtenemos:

También aplicamos la integración por partes al segundo término. Denotamos , .

Usando estas notaciones integramos el término mencionado:

Ahora encontramos la integral requerida:

Entre las integrales que se pueden resolver mediante el método de integración por partes, también se encuentran aquellas que no están incluidas en ninguno de los tres grupos mencionados en la parte teórica, para las cuales se sabe por la práctica que es mejor denotar por tu, y a través de qué dv. Por lo tanto, en estos casos es necesario utilizar la consideración de conveniencia, también dada en el párrafo “La esencia del método de integración por partes”: para tu se debe tomar una parte del integrando que no se vuelva mucho más complicada durante la diferenciación, pero dv- una parte del integrando que pueda integrarse fácilmente. El último ejemplo de esta lección es la solución de tal integral.

Por una integral definida de función continua F(X) en el segmento final [ a, b] (donde ) es el incremento de algunas de sus antiderivadas en este segmento. (En general, la comprensión será notablemente más fácil si repites el tema de la integral indefinida) En este caso, se utiliza la notación

Como se puede ver en los gráficos siguientes (el incremento de la función antiderivada se indica con ), la integral definida puede ser positiva o numero negativo (Se calcula como la diferencia entre el valor de la antiderivada en el límite superior y su valor en el límite inferior, es decir, como F(b) - F(a)).

Números a Y b se denominan límites inferior y superior de integración, respectivamente, y el segmento [ a, b] – segmento de integración.

Así, si F(X) – alguna función antiderivada para F(X), entonces, según la definición,

(38)

La igualdad (38) se llama Fórmula de Newton-Leibniz . Diferencia F(b) – F(a) se escribe brevemente de la siguiente manera:

Por tanto, escribiremos la fórmula de Newton-Leibniz así:

(39)

Demostremos que la integral definida no depende de qué antiderivada del integrando se tome al calcularla. Dejar F(X) y F( X) son antiderivadas arbitrarias del integrando. Como son antiderivadas de la misma función, se diferencian por un término constante: Ф( X) = F(X) + C. Es por eso

Esto establece que en el segmento [ a, b] incrementos de todas las antiderivadas de la función F(X) emparejar.

Por tanto, para calcular una integral definida, es necesario encontrar cualquier antiderivada del integrando, es decir Primero necesitas encontrar la integral indefinida. Constante CON excluidos de los cálculos posteriores. Luego se aplica la fórmula de Newton-Leibniz: el valor del límite superior se sustituye en la función antiderivada b , además - el valor del límite inferior a y se calcula la diferencia F(b) - F(a) . El número resultante será una integral definida..

En a = b por definición aceptado

Ejemplo 1.

Solución. Primero, encontremos la integral indefinida:

Aplicando la fórmula de Newton-Leibniz a la antiderivada

(en CON= 0), obtenemos

Sin embargo, al calcular una integral definida, es mejor no encontrar la primitiva por separado, sino escribir inmediatamente la integral en la forma (39).

Ejemplo 2. Calcular integral definida

Solución. Usando la fórmula

Propiedades de la integral definida

Teorema 2.El valor de la integral definida no depende de la designación de la variable de integración., es decir.

(40)

Dejar F(X) – antiderivada para F(X). Para F(t) la antiderivada es la misma función F(t), en el que la variable independiente sólo se designa de forma diferente. Por eso,

Según la fórmula (39), la última igualdad significa la igualdad de las integrales.

Teorema 3.El factor constante se puede sacar del signo de la integral definida., es decir.

(41)

Teorema 4.La integral definida de una suma algebraica de un número finito de funciones es igual a la suma algebraica de integrales definidas de estas funciones, es decir.

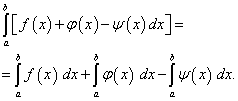(42)

Teorema 5.Si el segmento de integración se divide en partes, entonces la integral definida sobre todo el segmento igual a la suma integrales definidas sobre sus partes, es decir. Si

(43)

Teorema 6.Al reordenar los límites de la integración valor absoluto la integral definida no cambia, solo cambia su signo, es decir.

(44)

Teorema 7(teorema del valor medio). Una integral definida es igual al producto de la longitud del segmento de integración por el valor del integrando en algún punto dentro de él., es decir.

(45)

Teorema 8.Si el límite superior de integración es mayor que el inferior y el integrando no es negativo (positivo), entonces la integral definida también es no negativa (positiva), es decir Si

Teorema 9.Si el límite superior de integración es mayor que el inferior y las funciones y son continuas, entonces la desigualdad

se puede integrar término por término, es decir.

(46)

Las propiedades de la integral definida permiten simplificar el cálculo directo de integrales.

Ejemplo 5. Calcular integral definida

Usando los teoremas 4 y 3, y al encontrar antiderivadas - integrales de tabla (7) y (6), obtenemos

Integral definida con límite superior variable

Dejar F(X) – continua en el segmento [ a, b] función, y F(X) es su antiderivada. Considere la integral definida

(47)

y mediante t la variable de integración está designada para no confundirla con limite superior. cuando cambia X la integral definida (47) también cambia, es decir es una función del límite superior de integración X, que denotamos por F(X), es decir.

(48)

Demostremos que la función F(X) es una antiderivada de F(X) = F(t). En efecto, diferenciando F(X), obtenemos

porque F(X) – antiderivada para F(X), A F(a) es un valor constante.

Función F(X) – una del número infinito de antiderivadas para F(X), es decir, el que X = a va a cero. Esta afirmación se obtiene si en igualdad (48) ponemos X = a y utilice el Teorema 1 del párrafo anterior.

Cálculo de integrales definidas por el método de integración por partes y el método de cambio de variable

donde, por definición, F(X) – antiderivada para F(X). Si cambiamos la variable en el integrando

entonces, de acuerdo con la fórmula (16), podemos escribir

en esta expresión

función antiderivada para

De hecho, su derivada, según regla de diferenciación de funciones complejas, es igual

Sean α y β los valores de la variable t, para lo cual la función

toma valores en consecuencia a Y b, es decir.

Pero, según la fórmula de Newton-Leibniz, la diferencia F(b) – F(a) Hay

El método de integración por partes se utiliza principalmente cuando el integrando está formado por el producto de dos factores de un determinado tipo. La fórmula de integración por partes queda así:

Permite reducir el cálculo de una integral dada.
al cálculo de la integral
, que resulta ser más simple que este.

La mayoría de las integrales calculadas por el método de integración por partes se pueden dividir en tres grupos:

1. Integrales de la forma
,
,
, Dónde
– polinomio,
– un número distinto de cero

En este caso, a través de denotar un polinomio

.

2. Integrales de la forma
,
,
,
,
, Dónde
– polinomio.

En este caso, a través de
denotar
, y el resto del integrando a través :

3. Integrales de la forma
,
, Dónde
– números.

En este caso, a través de denotar
y aplicar la fórmula de integración por partes dos veces, volviendo como resultado a la integral original, luego de lo cual la integral original se expresa a partir de la igualdad.

Comentario: En algunos casos, para encontrar una integral dada, se debe aplicar varias veces la fórmula de integración por partes. Además, el método de integración por partes se combina con otros métodos.

Ejemplo 26.

Encuentra integrales usando el método por partes: a)
; b)
.

Solución.

b)

3.1.4. Integración de funciones racionales fraccionarias

Función racional fraccionaria(fracción racional) es una función igual a la razón de dos polinomios:
, Dónde
– polinomio de grado
,
– polinomio de grado .

La fracción racional se llama correcto, si el grado del polinomio en el numerador es menor que el grado del polinomio en el denominador, es decir
, de lo contrario (si
) la fracción racional se llama equivocado.

Cualquier fracción racional impropia se puede representar como la suma de un polinomio.
y correcto fracción racional, dividiendo el numerador por el denominador según la regla de división de polinomios:

,

Dónde
– Toda una parte de la división, – fracción racional propia,
- resto de la división.

Fracciones racionales propias de la forma:

I. ;

II.
;

III.
;

IV.
,

Dónde ,,
,
,,,
– números reales y
(aquellos. trinomio cuadrático en el denominador III y IV de las fracciones no tiene raíces - el discriminante es negativo) se llaman fracciones racionales simples I, II, III y IV tipos.

Integrando fracciones simples

Las integrales de las fracciones más simples de cuatro tipos se calculan de la siguiente manera.

I)
.

II),
.

III) Para integrar la fracción más simple del tipo III, seleccione un cuadrado completo en el denominador y reemplace
. Después de la sustitución, la integral se divide en dos integrales. La primera integral se calcula aislando la derivada del denominador en el numerador, lo que da una integral tabular, y la segunda integral se convierte a la forma
, porque
, que también da la integral tabular.

;

IV) Para integrar la fracción más simple del tipo IV, seleccione un cuadrado completo en el denominador y reemplace
. Después de la sustitución, la integral se divide en dos integrales. La primera integral se calcula por sustitución.
, y el segundo usando relaciones de recurrencia.

Ejemplo 27.

Encuentra integrales de fracciones simples:

A)
; b)
; V)
.

Solución.

A)
.

Cualquier fracción racional propia cuyo denominador pueda factorizarse puede representarse como una suma de fracciones simples. La descomposición en suma de fracciones simples se realiza mediante el método de coeficientes indefinidos. Es el siguiente:

corresponde a una fracción de la forma ;

– cada factor del denominador
corresponde a la cantidad fracciones de la forma

corresponde a una fracción de la forma
;

– cada factor cuadrado del denominador
corresponde a la cantidad fracciones de la forma

¿Dónde están los coeficientes indeterminados?

Para encontrar coeficientes indefinidos, el lado derecho en forma de suma de fracciones simples se lleva a un denominador común y se transforma. El resultado es una fracción con el mismo denominador que en el lado izquierdo de la ecuación. Luego se descartan los denominadores y se igualan los numeradores. El resultado es una igualdad idéntica en la que el lado izquierdo es un polinomio con coeficientes conocidos, y parte derecha– un polinomio con coeficientes indeterminados.

Hay dos formas de determinar coeficientes desconocidos: el método de coeficientes desconocidos y el método de valores parciales.

Método de coeficientes indeterminados.

Porque polinomios son idénticamente iguales, entonces los coeficientes a las mismas potencias son iguales . Igualar coeficientes en los mismos grados en los polinomios de los lados izquierdo y derecho, obtenemos el sistema ecuaciones lineales. Al resolver el sistema, determinamos los coeficientes inciertos.

Método de valores privados.

Porque los polinomios son idénticamente iguales, entonces, sustituyendo a los lados izquierdo y derecho de cualquier número, obtenemos una igualdad verdadera, lineal con respecto a los coeficientes desconocidos. Sustituyendo tantos valores , cuántos coeficientes desconocidos hay, obtenemos un sistema de ecuaciones lineales. En lugar de Puedes sustituir cualquier número en los lados izquierdo y derecho, pero es más conveniente sustituir las raíces de los denominadores de fracciones.

Después de encontrar los valores de los coeficientes desconocidos, la fracción original se escribe como una suma de fracciones simples en el integrando y se realiza la integración discutida anteriormente sobre cada fracción simple.

Esquema de integración fracciones racionales:

1. Si el integrando es impropio, entonces es necesario presentarlo como la suma de un polinomio y una fracción racional propia (es decir, dividir el polinomio del numerador por el polinomio del denominador con un resto). Si el integrando es correcto pasamos inmediatamente al segundo punto del diagrama.

2. Factoriza el denominador de una fracción racional propia, si es posible.

3. Descomponer una fracción racional propia en la suma de fracciones racionales simples utilizando el método de coeficientes indefinidos.

4. Integrar la suma resultante de las fracciones polinómicas y simples.

Ejemplo 28.

Encuentra integrales de fracciones racionales:

A)
; b)
; V)
.

Solución.

A)
.

Porque el integrando es una fracción racional impropia, entonces seleccionamos la parte entera, es decir Imaginémoslo como la suma de un polinomio y una fracción racional propia. Divide el polinomio en el numerador por el polinomio en el denominador usando una esquina.

La integral original tomará la forma:
.

Descompongamos una fracción racional propia en una suma de fracciones simples usando el método de coeficientes indefinidos:

, obtenemos:

Resolviendo el sistema de ecuaciones lineales, obtenemos los valores de los coeficientes inciertos: A = 1; EN = 3.

Entonces la expansión requerida tiene la forma:
.

=
.

b)
.

.

Descartemos los denominadores e igualemos los lados izquierdo y derecho:

Igualar coeficientes en los mismos grados , obtenemos el sistema:

Resolviendo un sistema de cinco ecuaciones lineales, encontramos los coeficientes indeterminados:

.

Encontremos la integral original, teniendo en cuenta la expansión resultante:

.

V)
.

Expandamos el integrando (fracción racional propia) en una suma de fracciones simples usando el método de coeficientes indefinidos. Buscamos descomposición en la forma:

.

Reduciendo a un denominador común, obtenemos:

Descartemos los denominadores e igualemos los lados izquierdo y derecho:

Para encontrar coeficientes inciertos, aplicamos el método del valor parcial. agreguemos valores parciales, en los que los factores desaparecen, es decir, sustituimos estos valores en la última expresión y obtenemos tres ecuaciones:

;
;

;
;

;
.

Entonces la expansión requerida tiene la forma:

Encontremos la integral original, teniendo en cuenta la expansión resultante:

Una función F(x) derivable en un intervalo dado X se llama antiderivada de la función f(x), o la integral de f(x), si para todo x ∈X se cumple la siguiente igualdad:

F " (x) = f(x). (8.1)

Encontrar todas las primitivas de una función dada se llama integración. Función integral indefinida f(x) en un intervalo dado X es el conjunto de todas las funciones antiderivadas para la función f(x); designación -

Si F(x) es alguna primitiva de la función f(x), entonces ∫ f(x)dx = F(x) + C, (8.2)

donde C es una constante arbitraria.

Tabla de integrales

Directamente de la definición obtenemos las propiedades principales. No integral definida y una lista de integrales tabulares:

1) d∫f(x)dx=f(x)

2)∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Lista de integrales tabulares

1. ∫x m dx = x m+1 /(m + 1) +C; (metro ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sen x + C

7. = arctan x + C

8. = arcosen x + C

10. = - ctg x + C

Reemplazo de variables

Para integrar muchas funciones, utilice el método de reemplazo de variables o sustituciones, permitiéndole reducir integrales a forma tabular.

Si la función f(z) es continua en [α,β], la función z =g(x) tiene una derivada continua y α ≤ g(x) ≤ β, entonces

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

Además, después de la integración en el lado derecho, se debe realizar la sustitución z=g(x).

Para demostrarlo basta escribir la integral original en la forma:

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Por ejemplo:

Método de integración por partes.

Sean u = f(x) y v = g(x) funciones que tienen continuidad. Entonces, según el trabajo,

d(uv))= udv + vdu o udv = d(uv) - vdu.

Para la expresión d(uv), la antiderivada obviamente será uv, por lo que la fórmula es válida:

∫ udv = uv - ∫ vdu (8.4.)

Esta fórmula expresa la regla. integración por partes. Lleva la integración de la expresión udv=uv"dx a la integración de la expresión vdu=vu"dx.

Supongamos, por ejemplo, que desea encontrar ∫xcosx dx. Pongamos u = x, dv = cosxdx, entonces du=dx, v=senx. Entonces

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

La regla de integración por partes tiene un alcance más limitado que la sustitución de variables. Pero hay clases enteras de integrales, por ejemplo,

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax y otros, que se calculan precisamente mediante integración por partes.

Integral definida

El concepto de integral definida se presenta a continuación. Definamos una función f(x) en un intervalo. Dividamos el segmento [a,b] en norte partes por puntos a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x yo =x yo - x yo-1. Una suma de la forma f(ξ i)Δ x i se llama suma integral, y su límite en λ = maxΔx i → 0, si existe y es finito, se llama integral definida funciones f(x) de a antes b y se designa:

F(ξ i)Δx i (8.5).

La función f(x) en este caso se llama integrable en el intervalo, los números a y b se llaman límites inferior y superior de la integral.

Las siguientes propiedades son verdaderas para una integral definida:

4), (k = constante, k∈R);

5)

6)

7) f(ξ)(b-a) (ξ∈).

La última propiedad se llama teorema del valor medio.

Sea f(x) continua en . Entonces en este segmento hay una integral indefinida.

∫f(x)dx = F(x) + C

y tiene lugar Fórmula de Newton-Leibniz, conectando la integral definida con la integral indefinida:

F(b) - F(a). (8.6)

Interpretación geométrica: la integral definida es el área de un trapezoide curvilíneo delimitado desde arriba por la curva y=f(x), las rectas x = a y x = b y un segmento del eje Buey.

Integrales impropias

Las integrales con límites infinitos y las integrales de funciones discontinuas (ilimitadas) se denominan no el tuyo. Integrales impropias del primer tipo - estas son integrales en un intervalo infinito, definido de la siguiente manera:

(8.7)

Si este límite existe y es finito, entonces se llama integral impropia convergente de f(x) en el intervalo [a,+ ∞), y la función f(x) se llama integrable en un intervalo infinito[a,+ ∞). En caso contrario, se dice que la integral es no existe o diverge.

Las integrales impropias en los intervalos (-∞,b] y (-∞, + ∞) se definen de manera similar:

Definamos el concepto de integral de una función ilimitada. Si f(x) es continua para todos los valores X segmento, excepto por el punto c, en el cual f(x) tiene una discontinuidad infinita, entonces Integral impropia del segundo tipo de f(x) que van de a a b la cantidad se llama:

si estos límites existen y son finitos. Designación:

Ejemplos de cálculos integrales

Ejemplo 3.30. Calcular ∫dx/(x+2).

Solución. Denotemos t = x+2, entonces dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.

Ejemplo 3.31. Encuentre ∫ tgxdx.

Solución.∫ tgxdx = ∫senx/cosxdx = - ∫dcosx/cosx. Sea t=cosx, entonces ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Ejemplo3.32 . Encuentra ∫dx/senx

Solución.

Ejemplo3.33. Encontrar .

Solución. = .

Ejemplo3.34 . Encuentre ∫arctgxdx.

Solución. Integramos por partes. Denotemos u=arctgx, dv=dx. Entonces du = dx/(x 2 +1), v=x, de donde ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; porque
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Ejemplo3.35 . Calcula ∫lnxdx.

Solución. Aplicando la fórmula de integración por partes obtenemos:
u=lnx, dv=dx, du=1/x dx, v=x. Entonces ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Ejemplo3.36 . Calcula ∫e x senxdx.

Solución. Denotemos u = e x, dv = sinxdx, luego du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. También integramos la integral ∫e x cosxdx por partes: u = e x , dv = cosxdx, du=e x dx, v=sinx. Tenemos:
∫ e x cosxdx = e x senx - ∫ e x senxdx. Obtuvimos la relación ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, de la cual 2∫e x sinx dx = - e x cosx + e x sinx + C.

Ejemplo 3.37. Calcular J = ∫cos(lnx)dx/x.

Solución. Dado que dx/x = dlnx, entonces J= ∫cos(lnx)d(lnx). Reemplazando lnx por t, llegamos a la integral de tabla J = ∫ costdt = sint + C = sin(lnx) + C.

Ejemplo 3.38 . Calcule J = .

Solución. Considerando que = d(lnx), sustituimos lnx = t. Entonces J = .

Ejemplo 3.39 . Calcular la integral J = .

Solución. Tenemos: . Por lo tanto =
=
=. ingresado así: sqrt(tan(x/2)).

Y si en la ventana de resultados haces clic en Mostrar pasos en la esquina superior derecha, obtendrás una solución detallada.

La fórmula de integración por partes queda así:
.

El método de integración por partes consiste en aplicar esta fórmula. En la aplicación práctica, vale la pena señalar que u y v son funciones de la variable de integración. Sea la variable de integración designada como x (el símbolo después del signo diferencial d al final de la notación integral). Entonces u y v son funciones de x: u(x) y v(x).
Entonces
, .
Y la fórmula de integración por partes toma la forma:
.

Es decir, la función integrando debe consistir en el producto de dos funciones:
,
uno de los cuales denotamos como u: g(x) = u, y para el otro hay que calcular la integral (más precisamente, hay que encontrar la antiderivada):
, entonces dv = f(x) dx .

En algunos casos f(x) = 1 . Es decir, en la integral
,
podemos poner g(x) = u, x = v .

Resumen

Entonces, en este método, la fórmula de integración por partes debe recordarse y aplicarse de dos formas:
;
.

Integrales calculadas por integración por partes

Integrales que contienen logaritmos y funciones trigonométricas (hiperbólicas) inversas

Las integrales que contienen logaritmos y funciones trigonométricas o hiperbólicas inversas suelen integrarse por partes. En este caso, la parte que contiene el logaritmo o las funciones trigonométricas inversas (hiperbólicas) se denota por u, la parte restante por dv.

A continuación se muestran ejemplos de integrales que se calculan mediante el método de integración por partes:
, , , , , , .

Integrales que contienen el producto de un polinomio y sen x, cos x o e x

Usando la fórmula de integración por partes, se encuentran integrales de la forma:
, , ,
donde P(x) es un polinomio en x. Al integrar, el polinomio P(x) se denota por u, y e ax dx, porque hacha dx o pecado hacha dx- vía dv.

A continuación se muestran ejemplos de tales integrales:
, , .

Ejemplos de cálculo de integrales utilizando el método de integración por partes.

Ejemplos de integrales que contienen logaritmos y funciones trigonométricas inversas

Ejemplo

Calcula la integral:

Solución detallada

Aquí el integrando contiene un logaritmo. Hacer sustituciones
tu = en x,
dv=x 2 dx.
Entonces
,
.

Calculamos la integral restante:
.
Entonces
.
Al final de los cálculos es necesario sumar la constante C, ya que la integral indefinida es el conjunto de todas las primitivas. También podría agregarse en cálculos intermedios, pero esto sólo desordenaría los cálculos.

Solución más corta

Puede presentar la solución en una versión más corta. Para hacer esto, no necesitas hacer sustituciones con u y v, pero puedes agrupar los factores y aplicar la fórmula de integración por partes en la segunda forma.

.

Respuesta

Ejemplos de integrales que contienen el producto de un polinomio y sen x, cos x o ex

Ejemplo

Calcula la integral:
.

Solución

Introduzcamos el exponente bajo el signo diferencial:
mi - x dx = - mi - x d(-x) = - d(e - x).

Integramos por partes.
.
También utilizamos el método de integración por partes.
.
.
.
Finalmente lo tenemos.