Definīcija. Lai funkcija f(x) ir definēta kādā intervālā un x 0 ir punkts šajā intervālā. Ja , tad f(x) tiek uzskatīts par nepārtrauktu punktā x 0 .
No definīcijas izriet, ka par nepārtrauktību var runāt tikai attiecībā uz tiem punktiem, kuros ir definēts f(x) (definējot funkcijas robežu, šāds nosacījums netika izvirzīts). Nepārtrauktām funkcijām , tas ir, darbības f un lim ir maināmas. Attiecīgi divām funkcijas robežas definīcijām punktā var dot divas nepārtrauktības definīcijas - “sekvenču valodā” un “nevienādību valodā” (ε-δ valodā). Ieteicams to darīt pašam.
Praktiskai lietošanai dažreiz ir ērtāk definēt nepārtrauktību pieauguma valodā.
Vērtību Δx=x-x 0 sauc par argumenta pieaugumu, un Δy=f(x)-f(x 0) ir funkcijas pieaugums, pārejot no punkta x 0 uz punktu x.
Definīcija. Ļaujiet f(x) definēt punktā x 0 . Funkciju f(x) sauc par nepārtrauktu punktā x 0, ja bezgalīgi mazs argumenta pieaugums šajā punktā atbilst bezgalīgi mazam funkcijas pieaugumam, tas ir, Δy→0 Δx→0.

1. piemērs. Pierādīt, ka funkcija y=sinx ir nepārtraukta jebkurai x vērtībai.
Risinājums. Lai x 0 ir patvaļīgs punkts. Piešķirot tam pieaugumu Δx, iegūstam punktu x=x 0 +Δx. Tad . Mēs saņemam .
Definīcija. Funkciju y=f(x) sauc par nepārtrauktu punktā x 0 labajā (kreisajā pusē), ja
.
Nepārtraukta funkcija iekšējā punktā būs nepārtraukta gan pa labi, gan pa kreisi. Ir arī otrādi: ja funkcija ir nepārtraukta punktā pa kreisi un pa labi, tad tā būs nepārtraukta šajā punktā. Tomēr funkcija var būt nepārtraukta tikai vienā pusē. Piemēram, priekš , , f(1)=1, tāpēc šī funkcija ir nepārtraukta tikai kreisajā pusē (šīs funkcijas grafiku sk. iepriekš 5.7.2. punktā).
Definīcija. Funkciju sauc par nepārtrauktu kādā intervālā, ja tā ir nepārtraukta katrā šī intervāla punktā.
Jo īpaši, ja intervāls ir segments, tad tā galos tiek nozīmēta vienpusēja nepārtrauktība.

Nepārtraukto funkciju īpašības

1. Visas elementārās funkcijas ir nepārtrauktas savā definīcijas jomā.
2. Ja f(x) un φ(x), kas doti noteiktā intervālā, ir nepārtraukti šī intervāla punktā x 0, tad arī funkcijas būs nepārtrauktas šajā punktā.
3. Ja y=f(x) ir nepārtraukts punktā x 0 no X, un z=φ(y) ir nepārtraukts attiecīgajā punktā y 0 =f(x 0) no Y, tad sarežģīta funkcija z=φ(f(x)) būs nepārtraukts punktā x 0 .

Funkciju pārtraukumi un to klasifikācija

Funkcijas f(x) nepārtrauktības zīme punktā x 0 ir vienādība, kas nozīmē trīs nosacījumu esamību:
1) f(x) ir definēts punktā x 0 ;
2) ;
3) .
Ja tiek pārkāpta vismaz viena no šīm prasībām, tad x 0 sauc par funkcijas pārtraukuma punktu. Citiem vārdiem sakot, pārtraukuma punkts ir punkts, kurā šī funkcija nav nepārtraukta. No pārtraukuma punktu definīcijas izriet, ka funkcijas pārtraukuma punkti ir:
a) punkti, kas pieder funkcijas definīcijas jomai, kurā f(x) zaudē nepārtrauktības īpašību,
b) punkti, kas neietilpst f(x) definīcijas apgabalā un ir divu funkcijas definīcijas apgabala intervālu blakus punkti.
Piemēram, funkcijai punkts x=0 ir pārtraukuma punkts, jo funkcija šajā punktā nav definēta, un funkcija ir pārtraukums punktā x=1, kas atrodas blakus diviem f(x) definīcijas apgabala intervāliem (-∞,1) un (1,∞), un tā neeksistē.

Pārtraukuma punktiem tiek pieņemta šāda klasifikācija.
1) Ja punktā x 0 ir galīgi Un , bet f(x 0 +0)≠f(x 0 -0), tad tiek izsaukts x 0 pirmā veida pārtraukuma punkts , un tiek saukts funkciju lēciens .

2. piemērs. Apsveriet funkciju
Funkciju var lauzt tikai punktā x=2 (citos punktos tā ir nepārtraukta kā jebkurš polinoms).
Mēs atradīsim , . Tā kā vienpusējās robežas ir ierobežotas, bet nav viena ar otru vienādas, tad punktā x=2 funkcijai ir pirmā veida pārtraukums. ievērojiet, tas , tāpēc funkcija šajā punktā ir nepārtraukta labajā pusē (2. att.).
2) Otrā veida pārtraukumu punkti tiek saukti punkti, kuros vismaz viena no vienpusējām robežām ir vienāda ar ∞ vai neeksistē.

3. piemērs. Funkcija y=2 1/x ir nepārtraukta visām x vērtībām, izņemot x=0. Atradīsim vienpusējus ierobežojumus: , , tāpēc x=0 ir otrā veida pārtraukuma punkts (3. att.).
3) Tiek izsaukts punkts x=x 0 noņemams pārtraukuma punkts , ja f(x 0 +0)=f(x 0 -0)≠f(x 0).
Mēs “likvidēsim” atstarpi tādā nozīmē, ka pietiek ar funkcijas vērtību mainīt (pārdefinēt vai no jauna definēt) šajā brīdī, iestatot , un funkcija kļūs nepārtraukta punktā x 0 .
4. piemērs. Ir zināms, ka , un šī robeža nav atkarīga no tā, kā x tiecas uz nulli. Bet funkcija punktā x=0 nav definēta. Ja funkciju pārdefinējam, iestatot f(0)=1, tad šajā punktā tā izrādās nepārtraukta (citos punktos tā ir nepārtraukta kā nepārtraukto funkciju sinx un x koeficients).
5. piemērs. Pārbaudiet funkcijas nepārtrauktību .
Risinājums. Funkcijas y=x 3 un y=2x ir definētas un nepārtrauktas visur, arī norādītajos intervālos. Apskatīsim intervālu x=0 savienojuma punktu:
, , . Mēs iegūstam, ka , kas nozīmē, ka punktā x=0 funkcija ir nepārtraukta.
Definīcija. Funkciju, kas ir nepārtraukta intervālā, izņemot ierobežotu skaitu pirmā veida pārtraukumu punktu vai noņemamu pārtraukumu, šajā intervālā sauc par nepārtrauktu.

Nepārtrauktu funkciju piemēri

1. piemērs. Funkcija ir definēta un nepārtraukti ieslēgta (-∞,+∞), izņemot punktu x=2. Noteiksim pārtraukuma veidu. Tāpēc ka Un , tad punktā x=2 ir otrā veida pārtraukums (6. att.).
2. piemērs. Funkcija ir definēta un nepārtraukta visiem x, izņemot x=0, kur saucējs ir nulle. Atradīsim vienpusējas robežas punktā x=0:
Vienpusējās robežas ir ierobežotas un dažādas, tāpēc x=0 ir pirmā veida pārtraukuma punkts (7. att.).
3. piemērs. Nosakiet, kādos punktos un kāda veida pārrāvumi ir funkcijai
Šī funkcija ir definēta [-2,2]. Tā kā x 2 un 1/x ir nepārtraukti attiecīgi intervālos [-2,0] un , pārtraukums var rasties tikai intervālu krustpunktā, tas ir, punktā x=0. Tā kā , tad x=0 ir otrā veida pārtraukuma punkts.

4. piemērs. Vai ir iespējams novērst funkciju nepilnības:
A) punktā x=2;
b) punktā x=2;
V) punktā x=1?
Risinājums. Attiecībā uz piemēru a) uzreiz var teikt, ka pārrāvumu f(x) punktā x=2 nevar novērst, jo šajā punktā ir bezgalīgas vienpusējas robežas (skat. 1. piemēru).
b) Funkcijai g(x), lai gan tai ir noteiktas vienpusējas robežas punktā x=2

(,),

bet tie nesakrīt, tāpēc arī plaisu nevar novērst.
c) Funkcijai φ(x) pārtraukuma punktā x=1 ir vienādas vienpusējas galīgas robežas: . Tāpēc atstarpi var novērst, atkārtoti definējot funkciju pie x=1, f(1)=2 vietā liekot f(1)=1.

5. piemērs. Parādiet, ka Dirihleta funkcija

pārtraukts katrā skaitliskās ass punktā.
Risinājums. Lai x 0 ir jebkurš punkts no (-∞,+∞). Jebkurā tās apkaimē ir gan racionāli, gan neracionāli punkti. Tas nozīmē, ka jebkurā x 0 apkārtnē funkcijai būs vērtības, kas vienādas ar 0 un 1. Šajā gadījumā nevar būt funkcijas ierobežojums punktā x 0 ne pa kreisi, ne pa labi, kas nozīmē ka Dirihlē funkcijai ir otrā veida pārtraukumi katrā reālās ass punktā.

6. piemērs. Atrodiet funkciju pārtraukuma punktus

un noteikt to veidu.
Risinājums. Punkti, par kuriem ir aizdomas par lūzumu, ir punkti x 1 =2, x 2 =5, x 3 =3.
Punktā x 1 =2 f(x) ir otrā veida pārtraukums, jo
.
Punkts x 2 =5 ir nepārtrauktības punkts, jo funkcijas vērtību šajā punktā un tā tuvumā nosaka otrā rinda, nevis pirmā: .
Apskatīsim punktu x 3 = 3: , , no kā izriet, ka x=3 ir pirmā veida pārtraukuma punkts.

Priekš neatkarīgs lēmums.
Pārbaudiet nepārtrauktības funkcijas un nosakiet pārtraukuma punktu veidu:
1) ; Atbilde: x=-1 – noņemamā pārtraukuma punkts;
2) ; Atbilde: Otrā veida pārtraukums punktā x=8;
3) ; Atbilde: Pirmā veida pārtraukums pie x=1;
4)
Atbilde: Punktā x 1 =-5 ir noņemama sprauga, pie x 2 =1 ir otrā veida sprauga un punktā x 3 =0 ir pirmā veida atstarpe.
5) Kā jāizvēlas skaitlis A, lai funkcija

būtu nepārtraukts pie x=0?
Atbilde: A=2.
6) Vai ir iespējams izvēlēties skaitli A, lai funkcija

būtu nepārtraukts pie x=2?
Atbilde: nē.

Funkcijas nepārtrauktība punktā. Funkcija y = f(x ) sauc par iepriekšēju

saraustīts punktā x 0, ja:

1) šī funkcija ir definēta kādā punkta apkārtnē x 0 ;

2) ir limits f(x);

→ x 0

3) šis limits vienāds ar vērtību funkcijas punktā x 0, t.i. limf (x )= f (x 0 ) .
		x → x0
Pēdējais nosacījums ir līdzvērtīgs nosacījumam lim		y = 0, kur x = x − x 0 – kad
	x → 0
argumenta rotācija, y = f (x 0 +	x )− f (x 0 ) – funkcijas palielinājums, atbilstošs
argumenta palielināšana	x, t.i. funkciju	f(x) ir nepārtraukts pie x 0

tad un tikai tad, ja šajā brīdī bezgalīgi mazs argumenta pieaugums atbilst bezgalīgi mazam funkcijas pieaugumam.

Vienvirziena nepārtrauktība. Funkciju y = f (x) sauc par nepārtrauktu

pa kreisi punktāx 0, ja tas ir definēts kādā pusintervālā (a ;x 0 ]

un lim f (x) = f (x 0).

x→ x0–0

Tiek uzskatīts, ka funkcija y = f (x) ir taisni nepārtraukta punktā x 0, ja tā ir op-

ir sadalīts noteiktā pusintervālā [ x 0 ;a ) un limf (x )= f (x 0 ) .

x → x0 + 0

Funkcija y = f(x)		nepārtraukts punktā x 0			tad un tikai tad, kad viņa
nepārtraukts
lim f (x) = limf (x) = limf (x) = f (x 0).
x → x0 + 0	x→ x0–0	x → x0

Funkcijas nepārtrauktība komplektā. Tiek izsaukta funkcija y = f (x).

nepārtraukti filmēšanas laukumā X, ja tas ir nepārtraukts katrā šīs kopas punktā. Turklāt, ja funkcija ir definēta skaitliskās ass noteikta intervāla beigās, tad nepārtrauktība šajā punktā tiek saprasta kā nepārtrauktība labajā vai kreisajā pusē. Jo īpaši funkciju y = f (x) sauc par ne-

segmentā pārtraukts [a; b] ja viņa

1) nepārtraukts katrā intervāla punktā(a;b) ;

2) ir taisni nepārtraukts punktā a;

3) punktā ir atstāts nepārtraukts b.

Funkciju pārtraukuma punkti. Punktu x 0, kas pieder funkcijas y = f (x) definīcijas apgabalam vai ir šīs jomas robežpunkts, sauc

šīs funkcijas pārtraukuma punkts, iff(x) šajā punktā nav nepārtraukts.

Pārtraukuma punkti ir sadalīti pirmā un otrā veida pārtraukuma punktos:

1) Ja ir galīgas robežas lim f (x )= f (x 0 − 0) un

x→ x0–0

	f (x) = f (x 0 + 0), un ne visi trīs skaitļi ir f (x 0 - 0), f (x 0 + 0),		f (x 0 ) ir vienādi
x → x0 + 0
savā starpā, tad x 0		sauc par pirmā veida pārtraukuma punktu.
	Jo īpaši, ja funkcijas kreisā un labā robeža punktā x 0		vienāds starp
	sevi, bet	nav vienādi ar funkcijas vērtību šajā brīdī:

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , tad x 0 sauc par noņemamu pārtraukuma punktu.

Šajā gadījumā, iestatot f (x 0 )= A, varat modificēt funkciju punktā x 0

lai tas kļūtu nepārtraukts ( no jauna definējiet funkciju pēc nepārtrauktības). Atšķirību f (x 0 + 0)− f (x 0 − 0) sauc funkcijas lēciens punktā x 0 .

Funkciju lēciens noņemamajā pārtraukuma punktā ir nulle.

2) Tiek izsaukti pārrāvuma punkti, kas nav pirmā veida pārtraukumu punkti otrā veida pārtraukuma punkti. Otrā veida pārtraukuma punktos vismaz viena no vienpusējām robežām f (x 0 − 0) un f (x 0 + 0) neeksistē vai ir bezgalīga.

Punktā nepārtrauktu funkciju īpašības.

		f(x)	un g (x) ir nepārtraukti punktā x 0, tad funkcijas
f(x)±g(x),	f(x)g(x) un	f(x)	(kur g (x)≠ 0) ir arī nepārtraukti punktā x.
		g(x)

2) Ja funkcija u (x) ir nepārtraukta punktā x 0 un funkcija f (u) ir nepārtraukta

punktā u 0 = u (x 0), tad kompleksā funkcija f (u (x)) ir nepārtraukta punktā x 0.

3) Visas pamata elementārās funkcijas (c, x a, a x, loga x, sinx, cosx, tgx, ctgx, secx, cosecx, arcsinx, arccosx, arctgx, arcctgx) ir nepārtrauktas katrā.

līdz to definīcijas jomām.

No īpašībām 1)–3) izriet, ka visas elementārās funkcijas (funkcijas, kas iegūtas no pamatelementārajām funkcijām, izmantojot ierobežotu skaitu aritmētisko darbību un kompozīcijas operāciju) arī ir nepārtrauktas katrā to definīcijas jomas punktā.

Intervālā nepārtrauktu funkciju īpašības.

1) (starpvērtības teorēma) Ļaujiet definēt funkciju f(x).

ir nepārtraukts segmentā [a;b]. Tad jebkuram ciparam C

starp skaitļiem f (a) un f (b), (f (a)< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (Bolcāno-Košī teorēma

segmentā [a;b] ir pārtraukts un tā galos iegūst dažādu zīmju vērtības.

Tad ir vismaz viens punkts x 0 [ a ; b ], lai f (x 0 )= 0 .

3) (1 Veierštrāsa teorēma) Lai funkcija f (x) ir definēta un

saplēsts uz segmenta [a;b]. Tad šī funkcija šajā segmentā ir ierobežota.

4) (2 Veierštrāsa teorēma) Lai funkcija f (x) ir definēta un

skriešanās uz segmentu		[a;b] . Tad šī funkcija sasniedz intervālu [ a ; b ]
labākais		vismazāk	vērtības, t.i.	pastāvēt
x1, x2 [a; b] ,		jebkuram	punkti x [a;b]	godīgi	nevienlīdzības

f (x 1 ) ≤ f ( x ) ≤ f ( x 2 ) .

Piemērs 5.17. Izmantojot nepārtrauktības definīciju, pierādiet, ka funkcija y = 3x 2 + 2x − 5 ir nepārtraukta patvaļīgā skaitļu taisnes punktā x 0.

Risinājums: 1. metode: lai x 0 ir patvaļīgs punkts uz skaitļa ass. tu-

Vispirms mēs aprēķinām funkcijas f (x) robežu kā x → x 0, izmantojot teorēmas par funkciju summas un reizinājuma robežu:

lim f (x ) = lim (3x 2 + 2x - 5) = 3 (limx )2 + 2 limx - 5 = 3x 2							− 5.
x → x0	x → x0	x → x0	x → x0
Tad mēs aprēķinām funkcijas vērtību punktā x:f (x)= 3x 2							− 5 .
Salīdzinot iegūtos rezultātus, mēs redzam				lim f (x)= f (x 0), kas saskaņā ar
				x → x0

definīcija un nozīmē aplūkojamās funkcijas nepārtrauktību punktā x 0.

2. metode: ļaujiet		x – argumenta pieaugums punktāx 0. Atradīsim korespondenci
atbilstošs	pieaugums			y = f(x0 + x) − f(x0 ) =
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x − 5)
6 x x+ (x) 2	2x = (6x + 2)x + (x)2.
Tagad aprēķināsim funkcijas pieauguma robežu, kad pieaug arguments
		tiecas

	y = lim (6x + 2)		x + (x )2 = (6x + 2) lim		x + (limx)2 = 0.
x → 0	x → 0			x → 0	x → 0

Tādējādi lim y = 0, kas pēc definīcijas nozīmē nepārtrauktību

x → 0

funkcijas jebkuram x 0 R .

Piemērs 5.18. Atrodiet funkcijas f (x) pārtraukuma punktus un nosakiet to veidu. IN

Noņemamas pārtraukuma gadījumā definējiet funkciju pēc nepārtrauktības:

1) f (x) = 1− x 2 pie x< 3;

5x, ja x ≥ 3

2) f(x)= x 2 + 4 x + 3;

x+1

	f(x)=
		x4 (x−2)
	f(x)= arktāns
			(x–5)

Risinājums: 1) Šīs funkcijas definīcijas domēns ir viss skaitlis

y ass (−∞ ;+∞ ) . Intervālos (−∞ ;3) ,(3;+∞ ) funkcija ir nepārtraukta. Pārtraukums ir iespējams tikai punktā x = 3, kurā mainās funkcijas analītiskā specifikācija.

Norādītajā punktā atradīsim funkcijas vienpusējās robežas:

f (3− 0) = lim (1− x 2 ) = 1− 9 = 8;

x →3 −0

f (3+0)= lim 5x = 15.

x →3 +0

Mēs redzam, ka kreisā un labā robeža ir ierobežota, tāpēc x = 3
plīsums I			f(x). Funkcija pāriet uz
f (3+ 0)− f (3− 0)= 15−8= 7 .
		f (3)= 5 3= 15= f (3+ 0) , tātad punktā		x = 3

f(x) ir taisni nepārtraukts.

2) Funkcija ir nepārtraukta visā skaitļu rindā, izņemot punktu x = − 1, kurā tas nav definēts. Pārveidosim izteiksmi f (x), paplašinot skaitītāju

frakcijas faktoros:		f(x)=			4 x +3			(x + 1) (x + 3)	X + 3, ja x ≠ – 1.
					x+1			x+1
Atradīsim funkcijas vienpusējās robežas punktā x = − 1:
	f(x)=lim	f (x ) = lim (x + 3) = 2 .
x →−1−0	x →−1 +0		x →−1

Mēs noskaidrojām, ka funkcijas kreisās un labās robežas pētāmajā punktā pastāv, ir ierobežotas un viena ar otru vienādas, tāpēc x = − 1 ir noņemams punkts

taisne y = x + 3 ar “caurdurtu” punktu M (− 1;2) . Lai funkcija kļūtu pastāvīga

pārtraukts, mums vajadzētu likt f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 .

Tādējādi, tālāk definējot f (x) pēc nepārtrauktības punktā x = − 1, mēs ieguvām funkciju f * (x)= x + 3 ar definīcijas apgabalu (−∞ ;+∞ ).

3) Šī funkcija definēts un nepārtraukts ikvienam x izņemot punktus

x = 0,x = 2, kurā daļdaļas saucējs kļūst par nulle.

Apsveriet punktu x = 0:

Tā kā pietiekami mazā nulles apkārtnē funkcija aizņem tikai

	negatīvām vērtībām, tad f (− 0)= lim			= −∞ = f (+0)	Tie. punkts
			(x–2)
	x →−0
	x = 0 ir otrā veida funkcijas pārtraukuma punkts		f(x).

Tagad apsveriet punktu x = 2:

Funkcija ņem negatīvas vērtības tuvu pa kreisi no aplūkotā

	punkts un pozitīvie ir labajā pusē, tāpēc				f (2−0)=			= −∞,
							x4 (x−2)
						x →2 -0
	f (2+0)= lim			= +∞ . Tāpat kā iepriekšējā gadījumā, punktā x = 2
			(x–2)
	x →2 +0

cijai nav ne kreisās, ne labās robežas, t.i. šajā brīdī cieš no II tipa plīsuma.

x = 5.

f (5− 0) = lim arktāns

π ,f (5+ 0)= lim arktāns

x = 5

(x–5)

(x–5)

x →5 −0

x →5 +0

ka plīsums

f (5+ 0)− f (5− 0)=

π − (−

π )= π (skat. 5.2. att.).

Problēmas, kas jārisina patstāvīgi

5.174. Izmantojot tikai definīciju, pierādiet funkcijas f (x) nepārtrauktību

katrs punkts x 0 R :

a) f(x) = c= const;		b) f (x) = x;
c) f (x) = x 3;		d) f (x) = 5x 2 - 4x + 1;
e) f (x) = sinx.
5.175. Pierādiet, ka funkcija	f(x) = x2	1, ja x ≥ 0,	ir nepārtraukti ieslēgts
		1 pie x< 0
visa skaitļa līnija. Izveidojiet šīs funkcijas grafiku.
5.176. Pierādiet, ka funkcija	f(x) = x2	1, ja x ≥ 0,	nav nepārtraukts
		0 pie x< 0

punktā x = 0, bet ir taisni nepārtraukts šajā punktā. Grafiksējiet funkciju f(x).

saraustīts punktā x =

Bet šajā brīdī tas ir nepārtraukts kreisajā pusē. Izveidojiet grafiku

funkcijas f(x).

5.178. Grafika funkcijas

a) y =

x+1

b) y= x+

x+1

x+1

x+1

Kuri no nepārtrauktības nosacījumiem šo funkciju pārtraukuma punktos ir izpildīti un kuri nav izpildīti?

5.179. Norādiet funkcijas pārtraukuma punktu

grēks x		Ja x ≠ 0
		pie x = 0

Kuri no nepārtrauktības nosacījumiem šajā brīdī ir izpildīti un kuri nav izpildīti?

Definīcija funkciju pārtraukuma punkti un to veidi ir funkcijas nepārtrauktības tēmas turpinājums. Pretstatā kontinuitātes jēdzienam sniegts arī vizuāls (grafisks) funkcijas pārtraukuma punktu nozīmes skaidrojums. Mācīsimies atrast funkcijas pārtraukuma punktus un noteikt to veidus. Un mūsējie mums to palīdzēs uzticīgi draugi- kreisās un labās robežas, ko parasti sauc par vienpusējām robežām. Ja kādam ir kādas bailes no vienpusējiem ierobežojumiem, mēs tās drīz kliedēsim.

Grafika punkti, kas nav saistīti viens ar otru, tiek saukti funkciju pārtraukuma punkti . Šādas funkcijas grafiks, kas cieš no pārtraukuma punktā x=2 - - attēlā zemāk.

Iepriekš minētā vispārinājums ir šāda definīcija. Ja funkcija punktā nav nepārtraukta, tad tai šajā punktā ir pārtraukums un pats punkts tiek saukts pārtraukuma punkts . Traucējumi ir pirmā un otrā veida .

Lai noteiktu pārtraukuma punktu veidi (rakstzīmes). funkcijas ir jāatrod ar pārliecību robežas, tāpēc ir ieteicams atvērt atbilstošo nodarbību jaunā logā. Bet saistībā ar pārtraukuma punktiem mums ir kaut kas jauns un svarīgs - vienpusīgas (kreisās un labās) robežas. Kopumā tie ir rakstīti (labais ierobežojums) un (kreisais ierobežojums). Tāpat kā ierobežojumu gadījumā, lai atrastu funkcijas robežu, funkcijas izteiksmē X ir jāaizstāj ar X. Bet, iespējams, jūs jautāsiet, kā atšķirsies labās un kreisās robežas, ja labās puses gadījumā kaut kas tiek pievienots X, bet tas ir nulle, bet kreisā gadījumā kaut kas tiek atņemts no X, bet šis kaut kas - arī nulle? Un tev būs taisnība. Vairumā gadījumu.

Bet praksē, meklējot funkcijas pārtraukuma punktus un nosakot to veidu, ir divi tipiski gadījumi, kad labās un kreisās robežas nav vienādas:

• funkcijai ir divas vai vairākas izteiksmes atkarībā no skaitļu līnijas daļas, kurai pieder x (šīs izteiksmes parasti raksta cirtainās iekavās pēc f(x)= );
• aizvietojot to, uz ko X ir tendence, mēs iegūstam daļskaitli, kuras saucējā paliek vai nu plus nulle (+0) vai mīnus nulle (-0), un tāpēc šāda daļa nozīmē vai nu plus bezgalību vai mīnus bezgalību, un tās ir pilnīgi dažādas lietas.

Pirmā veida pārtraukumu punkti

Pirmā veida pārtraukuma punkts: funkcijai ir gan galīga (t.i., nav vienāda ar bezgalību) kreisā robeža, gan galīga labā robeža, bet funkcija nav definēta punktā vai arī kreisā un labā robeža ir atšķirīga (nav vienāda).

Pirmā veida noņemamā pārtraukuma punkts. Kreisā un labā robeža ir vienāda. Šajā gadījumā ir iespējams sīkāk definēt funkciju punktā. Funkcijas definēšana punktā, vienkārši runājot, nozīmē nodrošināt punktu savienojumu, starp kuriem ir punkts, kurā kreisā un labā robeža ir vienāda ar otru. Šajā gadījumā savienojumam ir jāatspoguļo tikai viens punkts, kurā jāatrod funkcijas vērtība.

1. piemērs. Nosakiet funkcijas pārtraukuma punktu un pārtraukuma punkta veidu (raksturu).

Otrā veida pārtraukumu punkti

Otrā veida lūzuma punkts: punkts, kurā vismaz viena no robežām (pa kreisi vai pa labi) ir bezgalīga (vienāda ar bezgalību).

3. piemērs.

Risinājums. No izteiksmes jaudai plkst e ir skaidrs, ka funkcija nav definēta punktā. Šajā brīdī atradīsim funkcijas kreiso un labo robežu:

Viena no robežām ir vienāda ar bezgalību, tāpēc punkts ir otrā veida pārtraukuma punkts. Funkcijas grafiks ar pārtraukuma punktu ir zem piemēra.

Funkcijas pārtraukuma punktu atrašana var būt vai nu neatkarīgs uzdevums, vai tā daļa Pilnu funkciju izpēte un grafiku veidošana .

4. piemērs. Nosakiet funkcijas pārtraukuma punktu un funkcijas pārtraukuma punkta veidu (raksturu).

Risinājums. No jaudas izteiksmes pie 2 ir skaidrs, ka funkcija nav definēta punktā. Šajā brīdī atradīsim funkcijas kreiso un labo robežu.

Noņemama sprauga.

Definīcija. Punkts a sauc par funkcijas noņemamo pārtraukuma punktu y=f(x), ja funkcijas robeža f(x) pastāv šajā brīdī, bet punktā a funkciju f(x) vai nu nav definēts, vai tam ir privāta nozīme f(a), atšķiras no limita f(x)šajā brīdī.

Piemērs. Piemēram, funkcija

ir punktā x=0 labojama sprauga. Patiešām, šīs funkcijas ierobežojošā vērtība punktā x=0 ir vienāds ar 1. Daļējā vērtība ir vienāda ar 2.

Ja funkcija f(x) ir punktā a noņemamu spraugu, tad šo atstarpi var novērst, nemainot funkcijas vērtības citos punktos, izņemot a. Lai to izdarītu, pietiek ar funkcijas vērtību ievietot punktā a vienāds ar tā robežvērtību šajā brīdī. Tātad, iepriekš aplūkotajā piemērā ir pietiekami ievietot f(0)=1 un tad , t.i. funkciju f(x) punktā kļūs nepārtraukts x=0.

Pirmā veida traucējumi.

Definīcija. Punkts a tiek saukts par pirmā veida pārtraukuma punktu, ja šajā punktā funkcija f(x) ir ierobežotas, bet nevienlīdzīgas labās un kreisās robežas

Sniegsim dažus piemērus.

Piemērs. Funkcija y=sgn x ir punktā x=0 pirmā veida plīsums. Patiešām, un tādējādi šīs robežas nav vienādas viena ar otru.

Piemērs. Funkcija , definēts visur, izņemot punktu x=1, ir pie punkta x=1 pirmā veida plīsums. Patiešām, .

Otrā veida traucējumi.

Definīcija. Punkts a tiek saukts par otrā veida pārtraukuma punktu, ja šajā punktā funkcija f(x) nav vismaz viena no vienpusējām robežām vai ja vismaz viena no vienpusējām robežām ir bezgalīga.

Piemērs. Funkcija f(x)=iedegums x, acīmredzot, katrā punktā ir otrā veida pārtraukums x k =π/2+π k, k=0, ± 1, ± 2,…, jo katrā šādā punktā

Piemērs. Funkcijai punktā ir otrā veida pārtraukums x=0, jo šajā brīdī tai nav ne labās, ne kreisās robežas.

Funkcijas nepārtrauktība segmentā

Definīcija. Funkcija noteikta intervālā un nepārtrauktu katrā tā punktā sauc par nepārtrauktu šajā segmentā.

Turklāt saskaņā ar nepārtrauktību punktā a tiek saprasts kā nepārtrauktība labajā pusē un ar nepārtrauktību punktā b- nepārtrauktība kreisajā pusē.

Mēs teiksim, ka funkcija y=f(x), kas definēts komplektā (x) sasniedz savu augšējo (apakšējo) malu uz tā , ja šāds punkts pastāv x 0 ∈(x), Kas f(x 0)=β (f(x 0)=α).

[Veijerštrass] Teorēma. Katra intervāla nepārtraukta funkcija ir ierobežota un sasniedz savu augšējo un apakšējo robežu.

Teorēma [Bolcāno-Košī]. Ja funkcija y=f(x) nepārtraukti segmentā Un f(a)=A, f(b)=B, tad jebkuram C, noslēgts starp A Un B, ir tāds punkts ξ∈ , Kas f(ξ)=C.

Citiem vārdiem sakot, funkcija, kas nepārtraukta intervālā, ņemot jebkuras divas vērtības, ņem arī jebkuru vērtību, kas atrodas starp tām.

Sekas. Ja funkcija ir nepārtraukta segmentā un tā galos iegūst dažādu zīmju vērtības, tad šajā segmentā ir vismaz viens punkts, kurā funkcija pazūd.

Sekas. Ļaujiet funkcijai y=f(x) nepārtraukti segmentā Un , . Pēc tam funkcija f(x)ņem visas vērtības no segmenta un tikai šīs vērtības.

Tādējādi visas funkcijas vērtību kopa, kas ir dota un nepārtraukta noteiktā segmentā, ir arī segments.

Funkciju nepārtrauktība. Lūzuma punkti.

Vērsis iet, šūpojas, nopūšas, ejot:
- Ak, dēlis beidzas, tagad es nokritīšu!

Šajā nodarbībā aplūkosim funkcijas nepārtrauktības jēdzienu, pārrāvumu punktu klasifikāciju un izplatītu praktisku problēmu. funkciju nepārtrauktības pētījumi. Pēc paša tēmas nosaukuma daudzi intuitīvi uzmin, kas tiks apspriests, un domā, ka materiāls ir diezgan vienkāršs. Tā ir patiesība. Bet tieši vienkārši uzdevumi visbiežāk tiek sodīti par nolaidību un paviršu pieeju to risināšanai. Tāpēc es iesaku ļoti rūpīgi izpētīt rakstu un aptvert visus smalkumus un paņēmienus.

Kas jums jāzina un jāprot? Ne pārāk. Lai labi apgūtu stundu, jums ir jāsaprot, kas tas ir funkcijas robeža. Lasītāji ar zems līmenis pietiek ar sagatavošanos, lai saprastu rakstu Funkciju ierobežojumi. Risinājumu piemēri un skatīties ģeometriskā nozīme ierobežojums rokasgrāmatā Elementāro funkciju grafiki un īpašības. Ir arī ieteicams iepazīties ar grafu ģeometriskās transformācijas, jo praksē vairumā gadījumu ir jākonstruē zīmējums. Izredzes visiem ir optimistiskas, un pat pilna tējkanna tuvākās stundas vai divu laikā pati tiks galā ar uzdevumu!

Funkciju nepārtrauktība. Pārtraukuma punkti un to klasifikācija

Funkcijas nepārtrauktības jēdziens

Apskatīsim kādu funkciju, kas ir nepārtraukta visā skaitļu rindā:

Vai, precīzāk sakot, mūsu funkcija ir nepārtraukta ieslēgta (reālo skaitļu kopa).

Kāds ir "filistiešu" nepārtrauktības kritērijs? Acīmredzot grafiks nepārtraukta funkcija var zīmēt, nepaceļot zīmuli no papīra.

Šajā gadījumā ir skaidri jānošķir divi vienkārši jēdzieni: funkcijas domēns Un funkciju nepārtrauktība. IN vispārējs gadījums tas nav viens un tas pats. Piemēram:

Šī funkcija ir definēta visā skaitļu rindā, tas ir, for visi Vārda “x” nozīmei ir sava “y” nozīme. Jo īpaši, ja , tad . Ņemiet vērā, ka otram punktam ir pieturzīmes, jo pēc funkcijas definīcijas argumenta vērtībai ir jāatbilst vienīgā lieta funkcijas vērtība. Tādējādi domēns mūsu funkcija: .

Tomēr šī funkcija nav ieslēgta nepārtraukti! Ir pilnīgi skaidrs, ka tajā brīdī viņa cieš plaisa. Arī termins ir diezgan saprotams un vizuāls, tiešām, šeit zīmulis tik un tā būs jānorauj no papīra. Nedaudz vēlāk apskatīsim pārtraukuma punktu klasifikāciju.

Funkcijas nepārtrauktība punktā un intervālā

Konkrētā matemātiskā uzdevumā mēs varam runāt par funkcijas nepārtrauktību punktā, funkcijas nepārtrauktību intervālā, pusintervālu vai funkcijas nepārtrauktību segmentā. Tas ir, nav "vienkāršas nepārtrauktības"– funkcija var būt nepārtraukta KAUT KUR. Un visa pārējā pamatelements ir funkciju nepārtrauktība punktā .

Teorija matemātiskā analīze sniedz funkcijas nepārtrauktības definīciju punktā, izmantojot “delta” un “epsilon” apkaimes, taču praksē tiek izmantota cita definīcija, kurai mēs pievērsīsim īpašu uzmanību.

Vispirms atcerēsimies vienpusējas robežas kas ielauzās mūsu dzīvē pirmajā nodarbībā par funkciju grafikiem. Apsveriet ikdienas situāciju:

Ja tuvojamies asij punktam pa kreisi(sarkanā bultiņa), tad atbilstošās “spēļu” vērtības virzīsies pa asi līdz punktam (sārtināta bultiņa). Matemātiski šis fakts tiek fiksēts, izmantojot kreisās puses ierobežojums:

Pievērsiet uzmanību ierakstam (kreisajā pusē ir uzraksts “x mēdz ka ka”). “Piedeva” “mīnus nulle” simbolizē , būtībā tas nozīmē, ka mēs tuvojamies skaitlim no kreisās puses.

Tāpat, ja tuvojaties punktam “ka” pa labi(zilā bultiņa), tad “spēles” sasniegs tādu pašu vērtību, bet gar zaļo bultiņu un labās puses ierobežojums tiks formatēts šādi:

"Piedeva" simbolizē , un ieraksts skan: “x mēdz ka labajā pusē”.

Ja vienpusējās robežas ir galīgas un vienādas(kā mūsu gadījumā): , tad teiksim, ka ir VISPĀRĒJS ierobežojums. Tas ir vienkārši, vispārējais ierobežojums ir mūsu "parastais" funkcijas robeža, vienāds ar ierobežotu skaitli.

Ņemiet vērā, ka, ja funkcija nav definēta pie (punkcija melns punkts uz grafika filiāles), tad iepriekš minētie aprēķini paliek spēkā. Kā jau vairākas reizes tika atzīmēts, jo īpaši rakstā par bezgalīgi mazām funkcijām, izteicieni nozīmē, ka "x" bezgala tuvu tuvojas punktam, kamēr NAV SVARĪGI, neatkarīgi no tā, vai funkcija pati par sevi ir definēta noteiktā punktā vai nē. Labs piemērs parādīsies nākamajā rindkopā, kad funkcija tiks analizēta.

Definīcija: funkcija ir nepārtraukta punktā, ja funkcijas robeža dotajā punktā ir vienāda ar funkcijas vērtību šajā punktā: .

Definīcija ir detalizēti aprakstīta šādiem nosacījumiem:

1) Funkcijai jābūt definētai punktā, tas ir, vērtībai ir jāpastāv.

2) Jābūt vispārīgam funkcijas ierobežojumam. Kā minēts iepriekš, tas nozīmē vienpusēju ierobežojumu esamību un vienlīdzību: .

3) Funkcijas robežai dotajā punktā jābūt vienādai ar funkcijas vērtību šajā punktā: .

Ja tiek pārkāpts vismaz viens no trim nosacījumiem, tad funkcija zaudē nepārtrauktības īpašību punktā .

Funkcijas nepārtrauktība intervālā ir formulēts ģeniāli un ļoti vienkārši: funkcija ir nepārtraukta intervālā, ja tā ir nepārtraukta katrā noteiktā intervāla punktā.

Jo īpaši daudzas funkcijas ir nepārtrauktas bezgalīgā intervālā, tas ir, reālo skaitļu kopā. Šī ir lineāra funkcija, polinomi, eksponenciāls, sinuss, kosinuss utt. Un kopumā jebkura elementāra funkcija nepārtraukti uz tās definīcijas joma, piemēram, logaritmiskā funkcija ir nepārtraukta intervālā . ES ceru šobrīd jums ir diezgan labs priekšstats par to, kā izskatās galveno funkciju grafiki. Vairāk Detalizēta informācija no to nepārtrauktības var secināt laipns cilvēks ar uzvārdu Fihtengolts.

Ar funkcijas nepārtrauktību segmentā un pusintervāliem viss arī nav grūti, taču par to ir pareizāk runāt klasē par funkcijas minimālo un maksimālo vērtību atrašanu segmentā, bet pagaidām par to neuztraucamies.

Pārtraukuma punktu klasifikācija

Funkciju aizraujošā dzīve ir bagāta ar visādiem īpašiem punktiem, un pārtraukuma punkti ir tikai viena no viņu biogrāfijas lappusēm.

Piezīme : katram gadījumam es pakavēšos pie elementāra punkta: lūzuma punkts vienmēr ir viens punkts– nav “vairākas breikbumbas pēc kārtas”, tas ir, nav tādas lietas kā “breika intervāls”.

Šie punkti savukārt ir sadalīti divās daļās lielas grupas: pirmā veida plīsumi Un otrā veida plīsumi. Katram spraugas veidam ir savs īpašības ko mēs tagad apskatīsim:

Pirmā veida pārtraukuma punkts

Ja kādā punktā tiek pārkāpts nepārtrauktības nosacījums un vienpusējas robežas ierobežots , tad to sauc pirmā veida pārtraukuma punkts.

Sāksim ar visoptimistiskāko gadījumu. Pēc sākotnējās nodarbības idejas es gribēju pastāstīt teoriju “in vispārējs skats”, bet, lai demonstrētu materiāla realitāti, es pieņēmu iespēju ar konkrētiem varoņiem.

Tas ir skumji, piemēram, jaunlaulāto fotogrāfija uz Mūžīgās liesmas fona, taču šāds kadrs ir vispārpieņemts. Attēlosim funkcijas grafiku zīmējumā:


Šī funkcija ir nepārtraukta visā skaitļu rindā, izņemot punktu. Un patiesībā saucējs nevar būt vienāds ar nulli. Taču saskaņā ar limita nozīmi mēs varam bezgala tuvu tuvojieties “nullei” gan no kreisās, gan no labās puses, tas ir, pastāv vienpusējas robežas un, protams, tās sakrīt:
(Nepārtrauktības nosacījums Nr. 2 ir izpildīts).

Bet funkcija šajā punktā nav definēta, tāpēc tiek pārkāpts nepārtrauktības nosacījums Nr. 1, un šajā punktā funkcijai ir pārtraukums.

Šāda veida pārtraukums (ar esošo vispārējais ierobežojums) tiek saukti labojama sprauga. Kāpēc noņemams? Tā kā funkcija var pārdefinēt lūzuma punktā:

Vai tas izskatās dīvaini? Var būt. Bet šāds funkciju apzīmējums ne ar ko nav pretrunā! Tagad plaisa ir novērsta un visi ir laimīgi:


Veiksim formālu pārbaudi:

2) – ir vispārējs ierobežojums;
3)

Tādējādi ir izpildīti visi trīs nosacījumi, un funkcija ir nepārtraukta punktā saskaņā ar funkcijas nepārtrauktības definīciju punktā.

Tomēr matan nīdēji var definēt funkciju sliktā veidā, piemēram :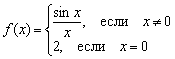


Interesanti, ka šeit ir izpildīti pirmie divi nepārtrauktības nosacījumi:
1) – funkcija ir definēta noteiktā punktā;
2) – ir vispārējs ierobežojums.

Bet trešā robeža nav pārkāpta: , tas ir, funkcijas robeža punktā nav vienāds noteiktas funkcijas vērtība noteiktā punktā.

Tādējādi kādā brīdī funkcija cieš no pārtraukuma.

Tiek saukts otrs, skumjākais gadījums pirmā veida plīsums ar lēcienu. Un skumjas izraisa vienpusīgas robežas, kas ierobežots un atšķirīgs. Piemērs ir parādīts stundas otrajā zīmējumā. Šāda plaisa parasti rodas, kad pa daļām definētas funkcijas, kas jau ir minēti rakstā par grafu transformācijām.

Apsveriet funkciju pa daļām un mēs pabeigsim tā zīmējumu. Kā izveidot grafiku? Ļoti vienkārši. Pusintervālā mēs uzzīmējam parabolas fragmentu ( zaļa krāsa), uz intervāla – taisnes nogrieznis (sarkans) un pusintervālā – taisne ( Zilā krāsa).

Turklāt nevienlīdzības dēļ vērtība tiek noteikta kvadrātiskā funkcija(zaļš punkts), un nevienlīdzības dēļ vērtība tiek noteikta lineārā funkcija(zils punkts):

Sarežģītākajā gadījumā jums vajadzētu ķerties pie katras diagrammas daļas pa punktiem (skatiet pirmo nodarbība par funkciju grafikiem).

Tagad mūs interesēs tikai punkts. Pārbaudīsim to nepārtrauktības nodrošināšanai:

2) Aprēķināsim vienpusējās robežas.

Kreisajā pusē ir sarkanas līnijas segments, tāpēc kreisās puses ierobežojums ir:

Labajā pusē ir zila taisna līnija un labās puses robeža:

Rezultātā saņēmām galīgi skaitļi, un viņi nav vienāds. Tā kā vienpusējās robežas ierobežots un atšķirīgs: , tad mūsu funkcija tolerē pirmā veida pārtraukums ar lēcienu.

Loģiski, ka plaisu nevar novērst - funkciju tiešām nevar tālāk definēt un “salīmēt kopā”, kā iepriekšējā piemērā.

Otrā veida pārtraukumu punkti

Parasti visi pārējie pārrāvuma gadījumi tiek gudri klasificēti šajā kategorijā. Es neuzskaitīšu visu, jo praksē jūs saskarsities ar 99% problēmu bezgalīga plaisa– ja kreilis vai labrocis, un biežāk, abas robežas ir bezgalīgas.

Un, protams, visredzamākā aina ir hiperbola nulles punktā. Šeit abas vienpusējās robežas ir bezgalīgas: , tāpēc funkcijai punktā ir otrā veida pārtraukums.

Es cenšos savus rakstus aizpildīt ar pēc iespējas dažādāku saturu, tāpēc apskatīsim vēl nesastaptas funkcijas grafiku:

saskaņā ar standarta shēmu:

1) Funkcija šajā brīdī nav definēta, jo saucējs iet uz nulli.

Protams, mēs varam uzreiz secināt, ka funkcijai ir pārtraukums punktā, taču būtu labi klasificēt pārtraukuma raksturu, ko bieži pieprasa nosacījums. Priekš šī:

Atgādināšu, ka ar ierakstīšanu mēs domājam bezgala mazs negatīvs skaitlis , un zem ieraksta - bezgalīgi mazs pozitīvs skaitlis.

Vienpusējās robežas ir bezgalīgas, kas nozīmē, ka funkcijai punktā ir 2. veida pārtraukums. Y ass ir vertikālā asimptote grafikam.

Nereti pastāv abas vienpusējas robežas, taču tikai viena no tām ir bezgalīga, piemēram:

Šis ir funkcijas grafiks.

Mēs pārbaudām nepārtrauktības punktu:

1) Funkcija šobrīd nav definēta.

2) Aprēķināsim vienpusējās robežas:

Par šādu vienpusēju robežu aprēķināšanas metodi runāsim pēdējos divos lekcijas piemēros, lai gan daudzi lasītāji jau visu ir redzējuši un uzminējuši.

Kreisās puses robeža ir ierobežota un vienāda ar nulli (mēs “neejam uz pašu punktu”), bet labās puses robeža ir bezgalīga un grafa oranžais zars tuvojas bezgalīgi tuvu savam vertikālā asimptote, kas dots ar vienādojumu (melna punktēta līnija).

Tātad funkcija cieš otrā veida pārtraukums punktā.

Kas attiecas uz 1. veida pārtraukumu, funkciju var definēt pašā pārtraukuma punktā. Piemēram, gabalveida funkcijai Jūtieties brīvi ievietot melnu treknu punktu koordinātu sākumā. Labajā pusē ir hiperbolas atzars, un labās puses robeža ir bezgalīga. Es domāju, ka gandrīz ikvienam ir priekšstats par to, kā izskatās šī diagramma.

Ko visi ļoti gaidīja:

Kā pārbaudīt funkcijas nepārtrauktību?

Funkcijas nepārtrauktības izpēte punktā tiek veikta saskaņā ar jau izveidotu rutīnas shēmu, kas sastāv no trīs nepārtrauktības nosacījumu pārbaudes:

1. piemērs

Izpētīt funkciju

Risinājums:

1) Vienīgais darbības jomas punkts ir tas, kur funkcija nav definēta.

2) Aprēķināsim vienpusējās robežas:

Vienpusējās robežas ir ierobežotas un vienādas.

Tādējādi brīdī, kad funkcija cieš no noņemama pārtraukuma.

Kā izskatās šīs funkcijas grafiks?

Es gribētu vienkāršot , un šķiet, ka tiek iegūta parasta parabola. BET sākotnējā funkcija nav definēta punktā, tāpēc ir nepieciešama šāda klauzula:

Izveidosim zīmējumu:

Atbilde: funkcija ir nepārtraukta visā skaitļu rindā, izņemot punktu, kurā tai ir noņemams pārtraukums.

Funkciju var tālāk definēt labā vai ne tik labā veidā, bet atkarībā no nosacījuma tas nav nepieciešams.

Jūs sakāt, ka tas ir tāls piemērs? Nepavisam. Praksē tas ir noticis desmitiem reižu. Gandrīz visi vietnes uzdevumi nāk no reāla neatkarīga darba un testiem.

Atbrīvosimies no mūsu iecienītākajiem moduļiem:

2. piemērs

Izpētīt funkciju nepārtrauktībai. Nosakiet funkciju pārtraukumu raksturu, ja tādi pastāv. Izpildi zīmējumu.

Risinājums: Nez kāpēc studenti baidās un viņiem nepatīk funkcijas ar moduli, lai gan tajās nav nekā sarežģīta. Mēs jau nodarbībā nedaudz pieskārāmies šādām lietām. Grafu ģeometriskās transformācijas. Tā kā modulis nav negatīvs, tas tiek paplašināts šādi: , kur “alfa” ir kāda izteiksme. IN šajā gadījumā, un mūsu funkcija ir jāraksta pa daļām: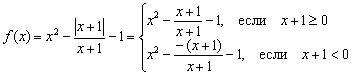

Bet abu gabalu daļas jāsamazina par . Samazinājums, tāpat kā iepriekšējā piemērā, nenotiks bez sekām. Sākotnējā funkcija šajā punktā nav definēta, jo saucējs iet uz nulli. Tāpēc sistēmai papildus jānorāda nosacījums un jāpadara stingra pirmā nevienlīdzība:

Tagad par ĻOTI NODERĪGA uzņemšana risinājumus: pirms uzdevuma pabeigšanas uz melnraksta ir izdevīgi izveidot zīmējumu (neatkarīgi no tā, vai to prasa nosacījumi vai nē). Tas palīdzēs, pirmkārt, uzreiz saskatīt nepārtrauktības un pārtraukuma punktus, un, otrkārt, tas 100% pasargās jūs no kļūdām, atrodot vienpusējas robežas.

Taisīsim zīmējumu. Saskaņā ar mūsu aprēķiniem, pa kreisi no punkta ir nepieciešams uzzīmēt parabolas fragmentu (zilā krāsā), bet pa labi - parabolas gabalu (sarkanā krāsā), savukārt funkcija nav definēta pie punkta. pats punkts:

Ja rodas šaubas, ņemiet dažas x vērtības un pievienojiet tās funkcijai (atceroties, ka modulis iznīcina iespējamo mīnusa zīmi) un pārbaudiet grafiku.

Pārbaudīsim nepārtrauktības funkciju analītiski:

1) Funkcija punktā nav definēta, tāpēc uzreiz varam teikt, ka tā tajā nav nepārtraukta.

2) Noskaidrosim pārtraukuma raksturu; lai to izdarītu, mēs aprēķinām vienpusējas robežas:

Vienpusējās robežas ir ierobežotas un dažādas, kas nozīmē, ka funkcija cieš no 1. veida pārtraukuma ar lēcienu punktā . Vēlreiz ņemiet vērā, ka, atrodot robežas, nav nozīmes tam, vai funkcija pārtraukuma punktā ir definēta vai nē.

Tagad atliek tikai pārnest zīmējumu no uzmetuma (tas tapa it kā ar pētījumu palīdzību ;-)) un izpildīt uzdevumu:

Atbilde: funkcija ir nepārtraukta visā skaitļu rindā, izņemot punktu, kurā tā cieš no pirmā veida pārtraukuma ar lēcienu.

Dažreiz tiem ir nepieciešama papildu norāde par pārtraukuma lēcienu. To aprēķina vienkārši - no labās robežas jums ir jāatņem kreisais ierobežojums: , tas ir, pārtraukuma punktā mūsu funkcija nolēca par 2 vienībām uz leju (kā norāda mīnusa zīme).

3. piemērs

Izpētīt funkciju nepārtrauktībai. Nosakiet funkciju pārtraukumu raksturu, ja tādi pastāv. Izveidojiet zīmējumu.

Šis ir piemērs, ko varat atrisināt pašam, risinājuma paraugs nodarbības beigās.

Pāriesim pie vispopulārākās un izplatītākās uzdevuma versijas, kad funkcija sastāv no trim daļām:

4. piemērs

Pārbaudiet funkcijas nepārtrauktību un izveidojiet funkcijas grafiku .

Risinājums: ir skaidrs, ka visas trīs funkcijas daļas ir nepārtrauktas atbilstošajos intervālos, tāpēc atliek pārbaudīt tikai divus “savienojuma” punktus starp daļām. Vispirms izveidosim uzmetumu, raksta pirmajā daļā es pietiekami detalizēti komentēju būvniecības tehniku. Vienīgais ir tas, ka mums rūpīgi jāievēro mūsu vienskaitļa punkti: nevienlīdzības dēļ vērtība pieder taisnei (zaļš punkts), un nevienlīdzības dēļ vērtība pieder parabolai (sarkanais punkts):


Nu principā viss skaidrs =) Atliek tikai noformēt lēmumu. Katram no diviem “savienošanās” punktiem mēs parasti pārbaudām 3 nepārtrauktības nosacījumus:

es) Mēs pārbaudām nepārtrauktības punktu

1)

Vienpusējās robežas ir ierobežotas un dažādas, kas nozīmē, ka funkcija cieš no 1. veida pārtraukuma ar lēcienu punktā .

Aprēķināsim pārtraukuma lēcienu kā starpību starp labo un kreiso robežu:
, tas ir, grafiks pacēlās par vienu vienību uz augšu.

II) Mēs pārbaudām nepārtrauktības punktu

1) – funkcija ir definēta noteiktā punktā.

2) Atrodiet vienpusējus ierobežojumus:

– vienpusējās robežas ir ierobežotas un vienādas, kas nozīmē, ka pastāv vispārēja robeža.

3) – funkcijas robeža punktā ir vienāda ar šīs funkcijas vērtību noteiktā punktā.

Pēdējā posmā mēs pārnesam zīmējumu uz galīgo versiju, pēc kura ievietojam pēdējo akordu:

Atbilde: funkcija ir nepārtraukta visā skaitļu rindā, izņemot punktu, kurā tā cieš no pirmā veida pārtraukuma ar lēcienu.

5. piemērs

Pārbaudiet funkcijas nepārtrauktību un izveidojiet tās grafiku .

Šis ir piemērs, ko varat atrisināt pašam, īss risinājums un aptuvenu uzdevuma paraugu nodarbības beigās.

Jums var rasties iespaids, ka vienā brīdī funkcijai ir jābūt nepārtrauktai, bet citā vietā ir jābūt pārtraukumam. Praksē tas ne vienmēr notiek. Centieties neatstāt novārtā atlikušos piemērus - būs vairākas interesantas un svarīgas funkcijas:

6. piemērs

Dota funkcija . Izpētiet nepārtrauktības funkciju punktos. Izveidojiet grafiku.

Risinājums: un atkal nekavējoties izpildiet zīmējumu uz melnraksta:

Šī grafika īpatnība ir tāda, ka pa daļām funkciju nosaka abscisu ass vienādojums. Šis apgabals ir uzzīmēts šeit zaļš, un piezīmju grāmatiņā tas parasti ir izcelts treknrakstā ar vienkāršu zīmuli. Un, protams, neaizmirstiet par mūsu auniem: vērtība pieder pieskares zaram (sarkans punkts), un vērtība pieder taisnei.

No zīmējuma viss ir skaidrs - funkcija ir nepārtraukta pa visu skaitļu līniju, atliek tikai formalizēt risinājumu, kas tiek pilnībā automatizēts burtiski pēc 3-4 līdzīgiem piemēriem:

es) Mēs pārbaudām nepārtrauktības punktu

1) – funkcija ir definēta noteiktā punktā.

2) Aprēķināsim vienpusējās robežas:

, kas nozīmē, ka pastāv vispārējs ierobežojums.

Katram gadījumam atgādināšu kādu triviālu faktu: konstantes robeža ir vienāda ar pašu konstanti. Šajā gadījumā nulles robeža ir vienāda ar pašu nulli (kreisās puses robeža).

3) – funkcijas robeža punktā ir vienāda ar šīs funkcijas vērtību noteiktā punktā.

Tādējādi funkcija ir nepārtraukta punktā saskaņā ar funkcijas nepārtrauktības definīciju punktā.

II) Mēs pārbaudām nepārtrauktības punktu

1) – funkcija ir definēta noteiktā punktā.

2) Atrodiet vienpusējus ierobežojumus:

Un šeit – viena robeža ir vienāda ar pašu vienību.

– ir vispārējs ierobežojums.

3) – funkcijas robeža punktā ir vienāda ar šīs funkcijas vērtību noteiktā punktā.

Tādējādi funkcija ir nepārtraukta punktā saskaņā ar funkcijas nepārtrauktības definīciju punktā.

Kā parasti, pēc izpētes mēs pārnesam savu zīmējumu uz galīgo versiju.

Atbilde: funkcija ir nepārtraukta punktos.

Lūdzu, ņemiet vērā, ka situācijā, kad mums nekas netika jautāts par visas funkcijas izpēti nepārtrauktībai, un tiek uzskatīts, ka tā ir laba matemātiskā forma, lai formulētu precīzi un skaidri atbildi uz uzdoto jautājumu. Starp citu, ja nosacījums neprasa izveidot grafiku, tad jums tas ir jādara visas tiesības neveidojiet to (lai gan skolotājs var piespiest jūs to darīt vēlāk).

Neliels matemātisks “mēles griezējs”, lai to atrisinātu pats:

7. piemērs

Dota funkcija . Izpētiet nepārtrauktības funkciju punktos. Klasificējiet pārtraukuma punktus, ja tādi ir. Izpildi zīmējumu.

Pamēģini pareizi “izrunāt” visus “vārdus” =) Un uzzīmē grafiku precīzāk, precizitāte, tas visur nebūs lieki;-)

Kā atceraties, es rekomendēju uzreiz pabeigt zīmējumu kā melnrakstu, taču ik pa laikam nākas saskarties ar piemēriem, kur uzreiz nevar saprast, kā izskatās grafiks. Tāpēc atsevišķos gadījumos ir izdevīgi vispirms atrast vienpusējas robežas un tikai tad, pamatojoties uz pētījumu, attēlot zarus. Pēdējos divos piemēros mēs arī apgūsim paņēmienu dažu vienpusēju ierobežojumu aprēķināšanai:

8. piemērs

Pārbaudiet funkcijas nepārtrauktību un izveidojiet tās shematisko grafiku.

Risinājums: sliktie punkti ir acīmredzami: (samazina eksponenta saucēju līdz nullei) un (samazina visas daļas saucēju līdz nullei). Nav skaidrs, kā izskatās šīs funkcijas grafiks, kas nozīmē, ka vispirms ir labāk veikt kādu pētījumu.