Liczba, która jest ułamkiem dziesiętnym. Zapis dziesiętny liczby ułamkowej

W tym samouczku przyjrzymy się każdej z tych operacji osobno.

Treść lekcji

Dodawanie ułamków dziesiętnych

Jak wiemy, ułamek dziesiętny składa się z liczby całkowitej i części ułamkowej. Podczas dodawania ułamków dziesiętnych części całkowite i ułamkowe dodawane są oddzielnie.

Na przykład dodajmy ułamki dziesiętne 3,2 i 5,3. Wygodniej jest dodawać ułamki dziesiętne w kolumnie.

Zapiszmy najpierw te dwa ułamki w kolumnie, tak aby części całkowite znajdowały się pod liczbami całkowitymi, a ułamki pod ułamkami. W szkole ten wymóg nazywa się „przecinek pod przecinkiem”.

Zapiszmy ułamki w kolumnie tak, aby przecinek znalazł się pod przecinkiem:

Zaczynamy dodawać części ułamkowe: 2 + 3 = 5. Piątkę wpisujemy w części ułamkowej naszej odpowiedzi:

Teraz dodajemy całe części: 3 + 5 = 8. W całej części naszej odpowiedzi wpisujemy ósemkę:

Teraz oddzielamy całą część od części ułamkowej przecinkiem. Aby to zrobić, ponownie postępujemy zgodnie z regułą „przecinek pod przecinkiem”:

Otrzymaliśmy odpowiedź 8,5. Zatem wyrażenie 3,2 + 5,3 równa się 8,5

Tak naprawdę nie wszystko jest tak proste, jak się wydaje na pierwszy rzut oka. Istnieją również pułapki, o których teraz porozmawiamy.

Miejsca po przecinku

Ułamki dziesiętne, podobnie jak zwykłe liczby, mają swoje własne cyfry. Są to miejsca dziesiątych, setnych i tysięcznych. W tym przypadku cyfry zaczynają się po przecinku.

Pierwsza cyfra po przecinku odpowiada za miejsce dziesiętne, druga cyfra po przecinku za miejsce setne, zaś trzecia cyfra po przecinku za miejsce tysięczne.

Miejsca w ułamkach dziesiętnych zawierają pewne przydatna informacja. W szczególności informują, ile części dziesiętnych, setnych i tysięcznych mieści się w ułamku dziesiętnym.

Rozważmy na przykład ułamek dziesiętny 0,345

Pozycja, w której znajduje się trójka, nazywa się dziesiąte miejsce

Pozycja, w której znajduje się czwórka, nazywa się setne miejsce

Pozycja, w której znajduje się piątka, nazywa się tysięczne miejsce

Spójrzmy na ten rysunek. Widzimy, że na dziesiątym miejscu jest trójka. Oznacza to, że w ułamku dziesiętnym 0,345 znajdują się trzy dziesiąte.

Jeśli dodamy ułamki zwykłe, otrzymamy pierwotny ułamek dziesiętny 0,345

Widać, że na początku otrzymaliśmy odpowiedź, ale przeliczyliśmy ją na ułamek dziesiętny i otrzymaliśmy 0,345.

Dodając ułamki dziesiętne, przestrzegaj tych samych zasad i reguł, co przy dodawaniu zwykłych liczb. Dodawanie ułamków dziesiętnych odbywa się za pomocą cyfr: dziesiąte dodaje się do dziesiątych, setne do setnych, tysięczne do tysięcznych.

Dlatego dodając ułamki dziesiętne, musisz przestrzegać reguły „przecinek pod przecinkiem”. Przecinek pod przecinkiem określa kolejność dodawania dziesiątych do dziesiątych, setnych do setnych, tysięcznych do tysięcznych.

Przykład 1. Znajdź wartość wyrażenia 1,5 + 3,4

Najpierw dodajemy części ułamkowe 5 + 4 = 9. W części ułamkowej naszej odpowiedzi piszemy dziewięć:

Teraz dodajemy części całkowite 1 + 3 = 4. Czwórkę wpisujemy w części całkowitej naszej odpowiedzi:

Teraz oddzielamy całą część od części ułamkowej przecinkiem. Aby to zrobić, ponownie stosujemy zasadę „przecinek pod przecinkiem”:

Otrzymaliśmy odpowiedź 4,9. Oznacza to, że wartość wyrażenia 1,5 + 3,4 wynosi 4,9

Przykład 2. Znajdź wartość wyrażenia: 3,51 + 1,22

To wyrażenie zapisujemy w kolumnie, przestrzegając zasady „przecinek pod przecinkiem”.

Najpierw dodajemy część ułamkową, czyli setne części 1+2=3. W setnej części naszej odpowiedzi piszemy trójkę:

Teraz dodaj części dziesiąte 5+2=7. W dziesiątej części naszej odpowiedzi wpisujemy siódemkę:

Teraz dodajemy całe części 3+1=4. Czwórkę piszemy w całej części naszej odpowiedzi:

Całą część od części ułamkowej oddzielamy przecinkiem, zachowując zasadę „przecinek pod przecinkiem”:

Odpowiedź jaką otrzymaliśmy to 4,73. Oznacza to, że wartość wyrażenia 3,51 + 1,22 wynosi 4,73

3,51 + 1,22 = 4,73

Podobnie jak w przypadku zwykłych liczb, podczas dodawania ułamków dziesiętnych, . W takim przypadku w odpowiedzi zapisuje się jedną cyfrę, a resztę przenosi się na następną cyfrę.

Przykład 3. Znajdź wartość wyrażenia 2,65 + 3,27

Zapisujemy to wyrażenie w kolumnie:

Dodaj części setne 5+7=12. Liczba 12 nie zmieści się w setnej części naszej odpowiedzi. Dlatego w części setnej zapisujemy liczbę 2 i przenosimy jednostkę do kolejnej cyfry:

Teraz dodajemy dziesiąte części 6+2=8 plus jednostkę otrzymaną z poprzedniej operacji i otrzymujemy 9. Liczbę 9 wpisujemy w dziesiątej części naszej odpowiedzi:

Teraz dodajemy całe części 2+3=5. W części całkowitej naszej odpowiedzi wpisujemy cyfrę 5:

Odpowiedź jaką otrzymaliśmy to 5,92. Oznacza to, że wartość wyrażenia 2,65 + 3,27 wynosi 5,92

2,65 + 3,27 = 5,92

Przykład 4. Znajdź wartość wyrażenia 9,5 + 2,8

Zapisujemy to wyrażenie w kolumnie

Dodajemy części ułamkowe 5 + 8 = 13. Liczba 13 nie zmieści się w części ułamkowej naszej odpowiedzi, więc najpierw zapisujemy liczbę 3 i przenosimy jednostkę do następnej cyfry, a raczej przenosimy ją do część całkowita:

Teraz dodajemy części całkowite 9+2=11 plus jednostkę otrzymaną z poprzedniej operacji i otrzymujemy 12. Liczbę 12 wpisujemy w części całkowitej naszej odpowiedzi:

Oddziel część całą od części ułamkowej przecinkiem:

Otrzymaliśmy odpowiedź 12.3. Oznacza to, że wartość wyrażenia 9,5 + 2,8 wynosi 12,3

9,5 + 2,8 = 12,3

Podczas dodawania ułamków dziesiętnych liczba cyfr po przecinku w obu ułamkach musi być taka sama. Jeśli nie ma wystarczającej liczby liczb, te miejsca w części ułamkowej są wypełniane zerami.

Przykład 5. Znajdź wartość wyrażenia: 12,725 + 1,7

Zanim zapiszemy to wyrażenie w kolumnie, sprawmy, aby liczba cyfr po przecinku w obu ułamkach była taka sama. Ułamek dziesiętny 12,725 ma trzy cyfry po przecinku, ale ułamek 1,7 ma tylko jedną. Oznacza to, że we frakcji 1,7 należy dodać na końcu dwa zera. Następnie otrzymujemy ułamek 1,700. Teraz możesz zapisać to wyrażenie w kolumnie i rozpocząć obliczenia:

Dodaj części tysięczne 5+0=5. W tysięcznej części naszej odpowiedzi wpisujemy cyfrę 5:

Dodaj części setne 2+0=2. W setnej części naszej odpowiedzi zapisujemy cyfrę 2:

Dodaj części dziesiąte 7+7=14. Liczba 14 nie zmieści się w jednej dziesiątej naszej odpowiedzi. Dlatego najpierw zapisujemy liczbę 4 i przenosimy jednostkę do następnej cyfry:

Teraz dodajemy części całkowite 12+1=13 plus jednostkę otrzymaną z poprzedniej operacji i otrzymujemy 14. Liczbę 14 wpisujemy w części całkowitej naszej odpowiedzi:

Oddziel część całą od części ułamkowej przecinkiem:

Otrzymaliśmy odpowiedź 14 425. Oznacza to, że wartość wyrażenia 12,725+1,700 wynosi 14,425

12,725+ 1,700 = 14,425

Odejmowanie ułamków dziesiętnych

Odejmując ułamki dziesiętne należy zachować takie same zasady jak przy dodawaniu: „przecinek pod przecinkiem” i „równą liczbę cyfr po przecinku”.

Przykład 1. Znajdź wartość wyrażenia 2,5 - 2,2

To wyrażenie zapisujemy w kolumnie, przestrzegając zasady „przecinek pod przecinkiem”:

Obliczamy część ułamkową 5−2=3. W dziesiątej części naszej odpowiedzi wpisujemy cyfrę 3:

Obliczamy część całkowitą 2−2=0. W części całkowitej naszej odpowiedzi zapisujemy zero:

Oddziel część całą od części ułamkowej przecinkiem:

Otrzymaliśmy odpowiedź 0,3. Oznacza to, że wartość wyrażenia 2,5 − 2,2 jest równa 0,3

2,5 − 2,2 = 0,3

Przykład 2. Znajdź wartość wyrażenia 7,353 - 3,1

To wyrażenie ma inną liczbę miejsc po przecinku. Ułamek 7,353 ma trzy cyfry po przecinku, ale ułamek 3,1 ma tylko jedną. Oznacza to, że we ułamku 3.1 należy dodać na końcu dwa zera, aby liczba cyfr w obu ułamkach była taka sama. Wtedy otrzymamy 3100.

Teraz możesz zapisać to wyrażenie w kolumnie i obliczyć:

Otrzymaliśmy odpowiedź 4253. Oznacza to, że wartość wyrażenia 7,353 - 3,1 jest równa 4,253

7,353 — 3,1 = 4,253

Podobnie jak w przypadku zwykłych liczb, czasami będziesz musiał pożyczyć jedną z sąsiedniej cyfry, jeśli odejmowanie stanie się niemożliwe.

Przykład 3. Znajdź wartość wyrażenia 3,46 - 2,39

Odejmij setne części 6-9. Nie możesz odjąć liczby 9 od liczby 6. Dlatego musisz pożyczyć cyfrę od sąsiedniej cyfry. Pożyczając jedynkę z sąsiedniej cyfry, liczba 6 zamienia się w liczbę 16. Teraz możesz obliczyć setne części 16−9=7. W setnej części naszej odpowiedzi wpisujemy siódemkę:

Teraz odejmujemy dziesiątki. Ponieważ na dziesiątym miejscu zajęliśmy jedną jednostkę, znajdująca się tam liczba zmniejszyła się o jedną jednostkę. Innymi słowy, na miejscu dziesiątym nie znajduje się teraz liczba 4, ale liczba 3. Obliczmy dziesiąte części 3−3=0. W dziesiątej części naszej odpowiedzi zapisujemy zero:

Teraz odejmujemy całe części 3−2=1. W części całkowitej naszej odpowiedzi zapisujemy jedynkę:

Oddziel część całą od części ułamkowej przecinkiem:

Otrzymaliśmy odpowiedź 1.07. Oznacza to, że wartość wyrażenia 3,46−2,39 jest równa 1,07

3,46−2,39=1,07

Przykład 4. Znajdź wartość wyrażenia 3−1,2

W tym przykładzie odejmuje się ułamek dziesiętny od liczby całkowitej. Zapiszmy to wyrażenie w kolumnie, aby cała część ułamek dziesiętny 1,23 okazał się liczbą 3

Teraz sprawmy, aby liczba cyfr po przecinku była taka sama. Aby to zrobić, po liczbie 3 stawiamy przecinek i dodajemy jedno zero:

Teraz odejmujemy dziesiąte: 0-2. Nie możesz odjąć liczby 2 od zera, dlatego musisz pożyczyć jedynkę od sąsiedniej cyfry. Pożyczając jedynkę od sąsiedniej cyfry, 0 zamienia się w liczbę 10. Teraz możesz obliczyć dziesiąte części 10−2=8. W dziesiątej części naszej odpowiedzi wpisujemy ósemkę:

Teraz odejmujemy całe części. Poprzednio cyfra 3 znajdowała się w całości, ale my wzięliśmy z niej jedną jednostkę. W rezultacie zamieniło się w liczbę 2. Dlatego od 2 odejmujemy 1. 2−1=1. W części całkowitej naszej odpowiedzi zapisujemy jedynkę:

Oddziel część całą od części ułamkowej przecinkiem:

Odpowiedź jaką otrzymaliśmy to 1,8. Oznacza to, że wartość wyrażenia 3−1,2 wynosi 1,8

Mnożenie ułamków dziesiętnych

Mnożenie ułamków dziesiętnych jest proste, a nawet przyjemne. Aby pomnożyć ułamki dziesiętne, mnożysz je jak zwykłe liczby, ignorując przecinki.

Po otrzymaniu odpowiedzi należy oddzielić całą część od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w obu ułamkach, a następnie policzyć tę samą liczbę cyfr od prawej strony w odpowiedzi i postawić przecinek.

Przykład 1. Znajdź wartość wyrażenia 2,5 × 1,5

Pomnóżmy te ułamki dziesiętne jak zwykłe liczby, ignorując przecinki. Aby zignorować przecinki, możesz tymczasowo wyobrazić sobie, że są one całkowicie nieobecne:

Mamy 375. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamkach 2,5 i 1,5. Pierwszy ułamek ma jedną cyfrę po przecinku, drugi ułamek również ma jedną cyfrę. W sumie dwie liczby.

Wracamy do liczby 375 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć dwie cyfry po prawej stronie i postawić przecinek:

Otrzymaliśmy odpowiedź 3,75. Zatem wartość wyrażenia 2,5 × 1,5 wynosi 3,75

2,5 × 1,5 = 3,75

Przykład 2. Znajdź wartość wyrażenia 12,85 × 2,7

Pomnóżmy te ułamki dziesiętne, ignorując przecinki:

Otrzymaliśmy 34695. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamkach 12,85 i 2,7. Ułamek 12,85 ma dwie cyfry po przecinku, a ułamek 2,7 ma jedną cyfrę – w sumie trzy cyfry.

Wracamy do numeru 34695 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć trzy cyfry od prawej strony i postawić przecinek:

Otrzymaliśmy odpowiedź 34 695. Zatem wartość wyrażenia 12,85 × 2,7 wynosi 34,695

12,85 × 2,7 = 34,695

Mnożenie ułamka dziesiętnego przez liczbę zwykłą

Czasami pojawiają się sytuacje, gdy trzeba pomnożyć ułamek dziesiętny przez liczbę zwykłą.

Aby pomnożyć ułamek dziesiętny i liczbę, mnożysz je bez zwracania uwagi na przecinek w miejscu dziesiętnym. Po otrzymaniu odpowiedzi należy oddzielić całą część od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamku dziesiętnym, a następnie policzyć tę samą liczbę cyfr od prawej strony w odpowiedzi i postawić przecinek.

Na przykład pomnóż 2,54 przez 2

Pomnóż ułamek dziesiętny 2,54 przez zwykłą liczbę 2, ignorując przecinek:

Otrzymaliśmy liczbę 508. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamku 2,54. Ułamek 2,54 ma dwie cyfry po przecinku.

Wracamy do numeru 508 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć dwie cyfry po prawej stronie i postawić przecinek:

Otrzymaliśmy odpowiedź 5.08. Zatem wartość wyrażenia 2,54 × 2 wynosi 5,08

2,54 × 2 = 5,08

Mnożenie ułamków dziesiętnych przez 10, 100, 1000

Mnożenie ułamków dziesiętnych przez 10, 100 lub 1000 odbywa się w taki sam sposób, jak mnożenie ułamków dziesiętnych przez liczby zwykłe. Należy wykonać mnożenie, nie zwracając uwagi na przecinek w ułamku dziesiętnym, następnie w odpowiedzi oddzielić część całą od części ułamkowej, licząc od prawej strony tyle cyfr, ile było cyfr po przecinku.

Na przykład pomnóż 2,88 przez 10

Pomnóż ułamek dziesiętny 2,88 przez 10, ignorując przecinek w ułamku dziesiętnym:

Mamy 2880. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamku 2,88. Widzimy, że ułamek 2,88 ma dwie cyfry po przecinku.

Wracamy do liczby 2880 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć dwie cyfry po prawej stronie i postawić przecinek:

Otrzymaliśmy odpowiedź 28,80. Odrzućmy ostatnie zero i otrzymajmy 28,8. Oznacza to, że wartość wyrażenia 2,88×10 wynosi 28,8

2,88 × 10 = 28,8

Istnieje drugi sposób mnożenia ułamków dziesiętnych przez 10, 100, 1000. Ta metoda jest znacznie prostsza i wygodniejsza. Polega na przesunięciu przecinka w prawo o tyle cyfr, ile jest zer w współczynniku.

Na przykład rozwiążmy w ten sposób poprzedni przykład 2,88×10. Nie podając żadnych obliczeń, od razu patrzymy na współczynnik 10. Interesuje nas, ile jest w nim zer. Widzimy, że jest w nim jedno zero. Teraz w ułamku 2,88 przesuwamy przecinek w prawo o jedną cyfrę, otrzymujemy 28,8.

2,88 × 10 = 28,8

Spróbujmy pomnożyć 2,88 przez 100. Od razu patrzymy na współczynnik 100. Interesuje nas, ile jest w nim zer. Widzimy, że są w nim dwa zera. Teraz w ułamku 2,88 przesuwamy przecinek w prawo o dwie cyfry, otrzymujemy 288

2,88 × 100 = 288

Spróbujmy pomnożyć 2,88 przez 1000. Od razu patrzymy na współczynnik 1000. Interesuje nas, ile jest w nim zer. Widzimy, że są w nim trzy zera. Teraz we ułamku 2,88 przesuwamy przecinek w prawo o trzy cyfry. Nie ma tam trzeciej cyfry, więc dodajemy kolejne zero. W rezultacie otrzymujemy 2880.

2,88 × 1000 = 2880

Mnożenie ułamków dziesiętnych przez 0,1 0,01 i 0,001

Mnożenie ułamków dziesiętnych przez 0,1, 0,01 i 0,001 działa w taki sam sposób, jak mnożenie ułamka dziesiętnego przez ułamek dziesiętny. Należy pomnożyć ułamki zwykłe jak liczby, a w odpowiedzi postawić przecinek, licząc po prawej stronie tyle cyfr, ile jest cyfr po przecinku w obu ułamkach.

Na przykład pomnóż 3,25 przez 0,1

Mnożymy te ułamki jak zwykłe liczby, ignorując przecinki:

Mamy 325. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamkach 3,25 i 0,1. Ułamek 3,25 ma dwie cyfry po przecinku, a ułamek 0,1 ma jedną cyfrę. Razem trzy liczby.

Wracamy do liczby 325 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć trzy cyfry od prawej i postawić przecinek. Po odliczeniu trzech cyfr stwierdzamy, że liczby się wyczerpały. W takim przypadku musisz dodać jedno zero i dodać przecinek:

Otrzymaliśmy odpowiedź 0,325. Oznacza to, że wartość wyrażenia 3,25 × 0,1 wynosi 0,325

3,25 × 0,1 = 0,325

Istnieje drugi sposób mnożenia ułamków dziesiętnych przez 0,1, 0,01 i 0,001. Ta metoda jest znacznie prostsza i wygodniejsza. Polega na przesunięciu przecinka w lewo o tyle cyfr, ile jest zer w współczynniku.

Na przykład rozwiążmy w ten sposób poprzedni przykład 3,25 × 0,1. Nie podając żadnych obliczeń, od razu patrzymy na mnożnik 0,1. Interesuje nas, ile jest w nim zer. Widzimy, że jest w nim jedno zero. Teraz w ułamku 3,25 przesuwamy przecinek w lewo o jedną cyfrę. Przesuwając przecinek o jedną cyfrę w lewo, widzimy, że przed trójką nie ma już więcej cyfr. W takim przypadku dodaj jedno zero i wstaw przecinek. Wynik to 0,325

3,25 × 0,1 = 0,325

Spróbujmy pomnożyć 3,25 przez 0,01. Natychmiast patrzymy na mnożnik 0,01. Interesuje nas, ile jest w nim zer. Widzimy, że są w nim dwa zera. Teraz w ułamku 3,25 przesuwamy przecinek w lewo o dwie cyfry, otrzymujemy 0,0325

3,25 × 0,01 = 0,0325

Spróbujmy pomnożyć 3,25 przez 0,001. Natychmiast patrzymy na mnożnik 0,001. Interesuje nas, ile jest w nim zer. Widzimy, że są w nim trzy zera. Teraz w ułamku 3,25 przesuwamy przecinek w lewo o trzy cyfry, otrzymujemy 0,00325

3,25 × 0,001 = 0,00325

Nie myl mnożenia ułamków dziesiętnych przez 0,1, 0,001 i 0,001 z mnożeniem przez 10, 100, 1000. Częsty błąd większość ludzi.

Przy mnożeniu przez 10, 100, 1000 przecinek dziesiętny przesuwa się w prawo o tę samą liczbę cyfr, ile jest zer w mnożniku.

A przy mnożeniu przez 0,1, 0,01 i 0,001 przecinek dziesiętny przesuwa się w lewo o tę samą liczbę cyfr, ile jest zer w mnożniku.

Jeśli na początku trudno jest to zapamiętać, możesz zastosować pierwszą metodę, w której mnożenie wykonuje się jak w przypadku zwykłych liczb. W odpowiedzi będziesz musiał oddzielić część całą od części ułamkowej, licząc po prawej stronie tyle cyfr, ile jest cyfr po przecinku w obu ułamkach.

Dzielenie mniejszej liczby przez większą liczbę. Poziom zaawansowany.

Na jednej z poprzednich lekcji powiedzieliśmy, że dzieląc mniejszą liczbę przez większą liczbę, otrzymujemy ułamek, którego licznik jest dzielną, a mianownik jest dzielnikiem.

Na przykład, aby podzielić jedno jabłko między dwa, musisz wpisać 1 (jedno jabłko) w liczniku i wpisać 2 (dwóch przyjaciół) w mianowniku. W rezultacie otrzymujemy ułamek . Oznacza to, że każdy przyjaciel otrzyma jabłko. Innymi słowy, pół jabłka. Ułamek jest odpowiedzią na problem „Jak podzielić jedno jabłko na dwa”

Okazuje się, że możesz rozwiązać ten problem dalej, dzieląc 1 przez 2. Przecież linia ułamkowa w dowolnym ułamku oznacza dzielenie, dlatego ten podział jest dozwolony w ułamku. Ale jak? Przyzwyczailiśmy się, że dywidenda jest zawsze większa niż dzielnik. Ale wręcz przeciwnie, dywidenda jest mniejsza niż dzielnik.

Wszystko stanie się jasne, jeśli przypomnimy sobie, że ułamek oznacza miażdżenie, dzielenie, dzielenie. Oznacza to, że urządzenie można podzielić na dowolną liczbę części, a nie tylko na dwie części.

Dzieląc mniejszą liczbę przez większą liczbę, otrzymujesz ułamek dziesiętny, którego częścią całkowitą jest 0 (zero). Część ułamkowa może być dowolna.

Podzielmy więc 1 przez 2. Rozwiążmy ten przykład za pomocą rogu:

Jednego nie da się całkowicie podzielić na dwa. Jeśli zadasz pytanie „Ile dwójek jest w jednym” , wówczas odpowiedzią będzie 0. Dlatego w ilorazie piszemy 0 i stawiamy przecinek:

Teraz jak zwykle mnożymy iloraz przez dzielnik, aby otrzymać resztę:

Nadszedł moment, w którym jednostkę można podzielić na dwie części. Aby to zrobić, dodaj kolejne zero po prawej stronie wynikowego:

Otrzymaliśmy 10. Podzielmy 10 przez 2 i otrzymamy 5. Piątkę zapisujemy w części ułamkowej naszej odpowiedzi:

Teraz usuwamy ostatnią resztę, aby zakończyć obliczenia. Pomnóż 5 przez 2, aby otrzymać 10

Otrzymaliśmy odpowiedź 0,5. Zatem ułamek wynosi 0,5

Połówkę jabłka można również zapisać przy użyciu ułamka dziesiętnego 0,5. Jeśli dodamy te dwie połówki (0,5 i 0,5), ponownie otrzymamy oryginalne całe jabłko:

Ten punkt można również zrozumieć, jeśli wyobrazisz sobie, jak 1 cm jest podzielony na dwie części. Jeśli podzielisz 1 centymetr na 2 części, otrzymasz 0,5 cm

Przykład 2. Znajdź wartość wyrażenia 4:5

Ile piątek jest w czwórce? Zupełnie nie. W iloraz wpisujemy 0 i stawiamy przecinek:

Mnożymy 0 przez 5, otrzymujemy 0. Pod czwórką piszemy zero. Natychmiast odejmij to zero od dywidendy:

Teraz zacznijmy dzielić (dzielić) cztery na 5 części. Aby to zrobić, dodaj zero po prawej stronie 4 i podziel 40 przez 5, otrzymamy 8. W iloraz zapisujemy osiem.

Uzupełniamy przykład, mnożąc 8 przez 5, aby otrzymać 40:

Otrzymaliśmy odpowiedź 0,8. Oznacza to, że wartość wyrażenia 4:5 wynosi 0,8

Przykład 3. Znajdź wartość wyrażenia 5: 125

Ile liczb jest 125 w pięciu? Zupełnie nie. W iloraz wpisujemy 0 i stawiamy przecinek:

Mnożymy 0 przez 5, otrzymujemy 0. Pod piątką piszemy 0. Natychmiast odejmij 0 od pięciu

Teraz zacznijmy dzielić (dzielić) tę piątkę na 125 części. Aby to zrobić, napiszemy zero po prawej stronie tej piątki:

Podziel 50 przez 125. Ile liczb wynosi 125 w liczbie 50? Zupełnie nie. Zatem w ilorazie ponownie piszemy 0

Pomnóż 0 przez 125, otrzymamy 0. Zapisz to zero pod 50. Natychmiast odejmij 0 od 50

Teraz podziel liczbę 50 na 125 części. Aby to zrobić, zapisujemy kolejne zero po prawej stronie 50:

Podziel 500 przez 125. Ile liczb 125 znajduje się w liczbie 500? W liczbie 500 znajdują się cztery liczby 125. Zapisz cztery w iloraz:

Uzupełniamy przykład, mnożąc 4 przez 125, aby otrzymać 500

Otrzymaliśmy odpowiedź 0,04. Oznacza to, że wartość wyrażenia 5:125 wynosi 0,04

Dzielenie liczb bez reszty

Zatem postawmy przecinek po jednostce ilorazu, sygnalizując w ten sposób, że dzielenie części całkowitych zostało zakończone i przechodzimy do części ułamkowej:

Dodajmy zero do reszty 4

Teraz podziel 40 przez 5, otrzymamy 8. W iloraz zapisujemy osiem:

40−40=0. Zostało nam 0. Oznacza to, że podział jest całkowicie zakończony. Dzielenie 9 przez 5 daje ułamek dziesiętny 1,8:

9: 5 = 1,8

Przykład 2. Podziel 84 przez 5 bez reszty

Najpierw podziel 84 przez 5 jak zwykle z resztą:

Prywatnie zostało nas 16, zostały jeszcze 4. Teraz podzielmy tę resztę przez 5. W iloraz wstaw przecinek i dodaj 0 do reszty 4

Teraz dzielimy 40 przez 5, otrzymujemy 8. Ósemkę zapisujemy w iloraz po przecinku:

i uzupełnij przykład, sprawdzając, czy jest jeszcze reszta:

Dzielenie ułamka dziesiętnego przez liczbę zwykłą

Jak wiemy, ułamek dziesiętny składa się z liczby całkowitej i części ułamkowej. Dzieląc ułamek dziesiętny przez liczbę zwykłą, najpierw musisz:

• podziel całą część ułamka dziesiętnego przez tę liczbę;
• po podzieleniu całej części należy natychmiast wstawić przecinek w iloraz i kontynuować obliczenia jak przy normalnym dzieleniu.

Na przykład podziel 4,8 przez 2

Zapiszmy ten przykład w rogu:

Teraz podzielmy całą część przez 2. Cztery podzielone przez dwa równa się dwa. W iloraz piszemy dwa i natychmiast stawiamy przecinek:

Teraz mnożymy iloraz przez dzielnik i sprawdzamy, czy z dzielenia zostanie reszta:

4-4=0. Reszta wynosi zero. Nie zapisujemy jeszcze zera, ponieważ rozwiązanie nie jest ukończone. Następnie kontynuujemy obliczenia jak przy zwykłym dzieleniu. Odejmij 8 i podziel przez 2

8: 2 = 4. Czwórkę zapisujemy w ilorazu i natychmiast mnożymy przez dzielnik:

Otrzymaliśmy odpowiedź 2,4. Wartość wyrażenia 4,8:2 wynosi 2,4

Przykład 2. Znajdź wartość wyrażenia 8,43: 3

Podziel 8 przez 3, otrzymamy 2. Natychmiast postaw przecinek po 2:

Teraz mnożymy iloraz przez dzielnik 2 × 3 = 6. Sześć zapisujemy pod ósmą i znajdujemy resztę:

Podziel 24 przez 3, otrzymamy 8. W iloraz zapisujemy osiem. Natychmiast pomnóż go przez dzielnik, aby znaleźć resztę dzielenia:

24-24=0. Reszta wynosi zero. Nie zapisujemy jeszcze zera. Odejmujemy ostatnie trzy z dywidendy i dzielimy przez 3, otrzymujemy 1. Natychmiast pomnóż 1 przez 3, aby zakończyć ten przykład:

Odpowiedź jaką otrzymaliśmy to 2,81. Oznacza to, że wartość wyrażenia 8,43:3 wynosi 2,81

Dzielenie ułamka dziesiętnego przez ułamek dziesiętny

Aby podzielić ułamek dziesiętny przez ułamek dziesiętny, należy przesunąć przecinek dziesiętny w dywidendzie i dzielniku w prawo o tę samą liczbę cyfr, ile jest po przecinku w dzielniku, a następnie podzielić przez zwykłą liczbę.

Na przykład podziel 5,95 przez 1,7

Zapiszmy to wyrażenie z rogiem

Teraz w dzielnej i dzielniku przesuwamy przecinek w prawo o tę samą liczbę cyfr, ile jest po przecinku w dzielniku. Dzielnik ma jedną cyfrę po przecinku. Oznacza to, że w dzielnej i dzielniku musimy przesunąć przecinek w prawo o jedną cyfrę. Przenosimy:

Po przesunięciu przecinka w prawo o jedną cyfrę, ułamek dziesiętny 5,95 stał się ułamkiem 59,5. A ułamek dziesiętny 1,7 po przesunięciu przecinka w prawo o jedną cyfrę zamienił się w zwykłą liczbę 17. I już wiemy, jak podzielić ułamek dziesiętny przez liczbę zwykłą. Dalsze obliczenia nie są trudne:

Przecinek przesunięto w prawo, aby ułatwić dzielenie. Jest to dozwolone, ponieważ przy mnożeniu lub dzieleniu dywidendy i dzielnika przez tę samą liczbę iloraz się nie zmienia. Co to znaczy?

To jest jeden z ciekawe funkcje dział. Nazywa się to właściwością ilorazu. Rozważ wyrażenie 9: 3 = 3. Jeśli w tym wyrażeniu dywidenda i dzielnik zostaną pomnożone lub podzielone przez tę samą liczbę, wówczas iloraz 3 nie ulegnie zmianie.

Pomnóżmy dzielną i dzielnik przez 2 i zobaczmy, co z tego wyjdzie:

(9 × 2): (3 × 2) = 18: 6 = 3

Jak widać na przykładzie, iloraz się nie zmienił.

To samo dzieje się, gdy przesuwamy przecinek w dzielnej i dzielniku. W poprzednim przykładzie, gdzie podzieliliśmy 5,91 przez 1,7, przesunęliśmy przecinek w dzielnej i dzielniku o jedną cyfrę w prawo. Po przesunięciu przecinka ułamek 5,91 został przekształcony na ułamek 59,1, a ułamek 1,7 na zwykłą liczbę 17.

W rzeczywistości w tym procesie nastąpiło pomnożenie przez 10. Tak to wyglądało:

5,91 × 10 = 59,1

Dlatego liczba cyfr po przecinku w dzielniku określa, przez co zostanie pomnożona dywidenda i dzielnik. Innymi słowy, liczba cyfr po przecinku w dzielniku określi, o ile cyfr w dzielnej, a w dzielniku przecinek dziesiętny zostanie przesunięty w prawo.

Dzielenie ułamka dziesiętnego przez 10, 100, 1000

Dzielenie ułamka dziesiętnego przez 10, 100 lub 1000 odbywa się w taki sam sposób jak . Na przykład podziel 2,1 przez 10. Rozwiąż ten przykład, używając narożnika:

Ale jest drugi sposób. Jest lżejszy. Istota tej metody polega na tym, że przecinek w dzielnej przesuwa się w lewo o tyle cyfr, ile jest zer w dzielniku.

Rozwiążmy w ten sposób poprzedni przykład. 2.1: 10. Patrzymy na dzielnik. Interesuje nas, ile jest w nim zer. Widzimy, że jest jedno zero. Oznacza to, że w dywidendzie 2,1 należy przesunąć przecinek w lewo o jedną cyfrę. Przesuwamy przecinek w lewo o jedną cyfrę i widzimy, że nie ma już więcej cyfr. W takim przypadku dodaj kolejne zero przed liczbą. W rezultacie otrzymujemy 0,21

Spróbujmy podzielić 2,1 przez 100. W 100 są dwa zera. Oznacza to, że w dywidendzie 2.1 musimy przesunąć przecinek w lewo o dwie cyfry:

2,1: 100 = 0,021

Spróbujmy podzielić 2,1 przez 1000. W 1000 są trzy zera. Oznacza to, że w dywidendzie 2.1 należy przesunąć przecinek w lewo o trzy cyfry:

2,1: 1000 = 0,0021

Dzielenie ułamka dziesiętnego przez 0,1, 0,01 i 0,001

Dzielenie ułamka dziesiętnego przez 0,1, 0,01 i 0,001 odbywa się w taki sam sposób jak . W dzielnej i dzielniku należy przesunąć przecinek w prawo o tyle cyfr, ile jest po przecinku w dzielniku.

Na przykład podzielmy 6,3 przez 0,1. Na początek przesuńmy przecinki w dzielnej i dzielniku w prawo o tyle cyfr, ile jest w dzielniku po przecinku. Dzielnik ma jedną cyfrę po przecinku. Oznacza to, że przecinki w dzielnej i dzielniku przesuwamy w prawo o jedną cyfrę.

Po przesunięciu przecinka w prawo o jedną cyfrę, ułamek dziesiętny 6,3 staje się zwykłą liczbą 63, a ułamek dziesiętny 0,1 po przesunięciu przecinka w prawo o jedną cyfrę zamienia się w jeden. A dzielenie 63 przez 1 jest bardzo proste:

Oznacza to, że wartość wyrażenia 6,3: 0,1 wynosi 63

Ale jest drugi sposób. Jest lżejszy. Istota tej metody polega na tym, że przecinek w dzielnej przesuwa się w prawo o tyle cyfr, ile jest zer w dzielniku.

Rozwiążmy w ten sposób poprzedni przykład. 6,3: 0,1. Spójrzmy na dzielnik. Interesuje nas, ile jest w nim zer. Widzimy, że jest jedno zero. Oznacza to, że w dywidendzie 6,3 należy przesunąć przecinek w prawo o jedną cyfrę. Przesuń przecinek w prawo o jedną cyfrę i uzyskaj 63

Spróbujmy podzielić 6,3 przez 0,01. Dzielnik liczby 0,01 ma dwa zera. Oznacza to, że w dywidendzie 6,3 musimy przesunąć przecinek w prawo o dwie cyfry. Ale w dywidendzie jest tylko jedna cyfra po przecinku. W takim przypadku musisz dodać kolejne zero na końcu. W rezultacie otrzymujemy 630

Spróbujmy podzielić 6,3 przez 0,001. Dzielnik liczby 0,001 ma trzy zera. Oznacza to, że w dywidendzie 6,3 musimy przesunąć przecinek w prawo o trzy cyfry:

6,3: 0,001 = 6300

Zadania do samodzielnego rozwiązania

Czy podobała Ci się lekcja?
Dołączć do naszego Nowa grupa VKontakte i zacznij otrzymywać powiadomienia o nowych lekcjach

Poświęcimy ten materiał tak ważnemu tematowi, jak ułamki dziesiętne. Najpierw zdefiniujmy podstawowe definicje, podamy przykłady i zatrzymajmy się nad zasadami zapisu dziesiętnego, a także czym są cyfry ułamków dziesiętnych. Następnie wyróżniamy główne typy: ułamki skończone i nieskończone, okresowe i nieokresowe. W końcowej części pokażemy, jak na osi współrzędnych rozmieszczone są punkty odpowiadające liczbom ułamkowym.

Yandex.RTB R-A-339285-1

Co to jest zapis dziesiętny liczb ułamkowych

Tak zwaną notację dziesiętną liczb ułamkowych można stosować zarówno w przypadku liczb naturalnych, jak i ułamkowych. Wygląda jak zestaw dwóch lub więcej liczb z przecinkiem między nimi.

Aby oddzielić część całkowitą od części ułamkowej, potrzebny jest przecinek dziesiętny. Z reguły ostatnią cyfrą ułamka dziesiętnego nie jest zero, chyba że przecinek dziesiętny pojawia się bezpośrednio po pierwszym zera.

Jakie są przykłady liczb ułamkowych w zapisie dziesiętnym? Może to być 34, 21, 0, 35035044, 0, 0001, 11 231 552, 9 itd.

W niektórych podręcznikach zamiast przecinka można spotkać kropkę (5,67, 6789, 1011 itd.) Ta opcja jest uważana za równoważną, ale jest bardziej typowa dla źródeł anglojęzycznych.

Definicja ułamków dziesiętnych

Bazując na powyższej koncepcji zapisu dziesiętnego, możemy sformułować następującą definicję ułamków dziesiętnych:

Definicja 1

Ułamki dziesiętne reprezentują liczby ułamkowe w zapisie dziesiętnym.

Dlaczego musimy zapisywać ułamki zwykłe w tej formie? Daje nam to pewne zalety w stosunku do zwykłych, na przykład bardziej zwarty zapis, szczególnie w przypadkach, gdy w mianowniku znajduje się 1000, 100, 10 itd. Lub liczba mieszana. Przykładowo zamiast 6 10 możemy podać 0,6, zamiast 25 10000 – 0,0023, zamiast 512 3 100 – 512,03.

Jak poprawnie przedstawić ułamki zwykłe z dziesiątkami, setkami, tysiącami w mianowniku w formie dziesiętnej, omówimy w osobnym materiale.

Jak poprawnie czytać ułamki dziesiętne

Istnieją pewne zasady czytania zapisów dziesiętnych. Zatem te ułamki dziesiętne, które odpowiadają ich zwykłym zwykłym odpowiednikom, czyta się prawie w ten sam sposób, ale z dodatkiem na początku słów „zero dziesiątych”. Zatem wpis 0, 14, który odpowiada 14 100, jest odczytywany jako „punkt zerowy czternaście setnych”.

Jeśli ułamek dziesiętny można skojarzyć z liczbą mieszaną, wówczas odczytuje się go w taki sam sposób, jak tę liczbę. Jeśli więc mamy ułamek 56 002, który odpowiada 56 2 1000, czytamy ten wpis jako „pięćdziesiąt sześć i dwie tysięczne”.

Znaczenie cyfry w ułamku dziesiętnym zależy od tego, gdzie się ona znajduje (tak samo jak w przypadku liczb naturalnych). Zatem w ułamku dziesiętnym 0,7 siedem to dziesiąte części, w 0,0007 jest to dziesięć tysięcznych, a w ułamku 70 000,345 oznacza to siedem dziesiątek tysięcy pełnych jednostek. Zatem w ułamkach dziesiętnych istnieje również pojęcie wartości miejsca.

Nazwy cyfr znajdujących się przed przecinkiem dziesiętnym są podobne do tych, które występują w liczbach naturalnych. Nazwy tych, które znajdują się później, są wyraźnie przedstawione w tabeli:

Spójrzmy na przykład.

Przykład 1

Mamy ułamek dziesiętny 43 098. Ma czwórkę na miejscu dziesiątek, trójkę na miejscu jedności, zero na miejscu dziesiątym, 9 na miejscu setnym i 8 na miejscu tysięcznym.

Zwyczajowo rozróżnia się szeregi ułamków dziesiętnych według pierwszeństwa. Jeśli będziemy poruszać się po liczbach od lewej do prawej, to przejdziemy od cyfr najbardziej znaczących do najniższych. Okazuje się, że setki są starsze niż dziesiątki, a części na milion są młodsze niż setne. Jeśli weźmiemy końcowy ułamek dziesiętny, który przytoczyliśmy jako przykład powyżej, wówczas najwyższa lub najwyższa cyfra w nim będzie miejscem setek, a najniższa lub najniższa cyfra będzie miejscem 10-tysięcznych.

Dowolny ułamek dziesiętny można rozwinąć na pojedyncze cyfry, czyli przedstawić jako sumę. Czynność tę wykonuje się w taki sam sposób, jak w przypadku liczby naturalne.

Przykład 2

Spróbujmy rozwinąć ułamek 56, 0455 na cyfry.

Dostaniemy:

56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005

Jeśli pamiętamy właściwości dodawania, możemy przedstawić ten ułamek w innych formach, na przykład jako sumę 56 + 0, 0455 lub 56, 0055 + 0, 4 itd.

Co to są końcowe ułamki dziesiętne?

Wszystkie ułamki, o których mówiliśmy powyżej, są skończone miejsca dziesiętne. Oznacza to, że liczba cyfr po przecinku jest skończona. Wyprowadźmy definicję:

Definicja 1

Końcowe ułamki dziesiętne to rodzaj ułamka dziesiętnego, który ma skończoną liczbę miejsc po przecinku.

Przykładami takich ułamków mogą być 0, 367, 3, 7, 55, 102567958, 231 032, 49 itd.

Dowolny z tych ułamków można zamienić albo na liczbę mieszaną (jeżeli wartość ich części ułamkowej jest różna od zera), albo na ułamek wspólny(z zerową częścią całkowitą). Jak to się robi, poświęciliśmy osobny artykuł. Tutaj podamy tylko kilka przykładów: na przykład możemy zredukować końcowy ułamek dziesiętny 5, 63 do postaci 5 63 100, a 0, 2 odpowiada 2 10 (lub dowolnemu innemu ułamkowi mu równemu, np. na przykład 4 20 lub 1 5.)

Ale proces odwrotny, tj. zapisanie ułamka zwykłego w formie dziesiętnej nie zawsze jest możliwe. Zatem 5 13 nie można zastąpić ułamkiem równym o mianowniku 100, 10 itd., co oznacza, że ​​​​nie można z niego uzyskać końcowego ułamka dziesiętnego.

Główne rodzaje nieskończonych ułamków dziesiętnych: ułamki okresowe i nieokresowe

Wskazaliśmy powyżej, że ułamki skończone są tak zwane, ponieważ mają skończoną liczbę cyfr po przecinku. Może jednak być nieskończony, w takim przypadku same ułamki również będą nazywane nieskończonymi.

Definicja 2

Nieskończone ułamki dziesiętne to takie, które mają nieskończoną liczbę cyfr po przecinku.

Oczywiście takich liczb po prostu nie da się zapisać w całości, dlatego wskazujemy tylko część z nich, a następnie dodajemy wielokropek. Znak ten wskazuje na nieskończoną kontynuację ciągu miejsc dziesiętnych. Przykłady nieskończonych ułamków dziesiętnych to 0, 143346732…, ​​​​3, 1415989032…, 153, 0245005…, 2, 66666666666…, 69, 748768152…. itp.

„Ogon” takiego ułamka może zawierać nie tylko pozornie losowe ciągi liczb, ale ciągłe powtarzanie ten sam znak lub grupę znaków. Ułamki zwykłe z liczbami naprzemiennymi po przecinku nazywane są okresowymi.

Definicja 3

Okresowe ułamki dziesiętne to nieskończone ułamki dziesiętne, w których jedna cyfra lub grupa kilku cyfr powtarza się po przecinku. Powtarzająca się część nazywana jest okresem ułamka.

Na przykład dla ułamka 3, 444444…. kropką będzie cyfra 4, a dla 76 134134134134... - grupa 134.

Jaka jest minimalna liczba znaków, jaką można pozostawić w zapisie ułamka okresowego? W przypadku ułamków okresowych wystarczy wpisać cały okres raz w nawiasach. Zatem ułamek 3, 444444…. Poprawne byłoby zapisanie tego jako 3, (4) i 76, 134134134134... – jako 76, (134).

Ogólnie wpisy z kilkoma kropkami w nawiasach będą miały dokładnie to samo znaczenie: na przykład ułamek okresowy 0,677777 jest taki sam jak 0,6 (7) i 0,6 (77) itd. Dopuszczalne są także rekordy w postaci 0, 67777 (7), 0, 67 (7777) itp.

Aby uniknąć błędów, wprowadzamy jednolitość zapisu. Zgódźmy się zapisać tylko jedną kropkę (najkrótszy możliwy ciąg liczb), najbliższy przecinkowi dziesiętnemu i ująć ją w nawiasy.

Oznacza to, że dla powyższego ułamka głównym wpisem będzie 0, 6 (7) i na przykład w przypadku ułamka 8, 9134343434, zapiszemy 8, 91 (34).

Jeśli w mianowniku ułamka zwykłego znajdują się czynniki pierwsze, które nie są równe 5 i 2, to po przeliczeniu na zapis dziesiętny uzyskają one ułamki nieskończone.

W zasadzie dowolny ułamek skończony możemy zapisać jako okresowy. Aby to zrobić, wystarczy dodać nieskończoną liczbę zer po prawej stronie. Jak to wygląda na nagraniu? Powiedzmy, że mamy końcowy ułamek 45, 32. W formie okresowej będzie wyglądać jak 45, 32 (0). Ta akcja jest możliwa, ponieważ dodanie zer po prawej stronie dowolnego ułamka dziesiętnego daje ułamek równy mu.

Szczególną uwagę należy zwrócić na ułamki okresowe o okresie 9, na przykład 4, 89 (9), 31, 6 (9). Są alternatywnym zapisem ułamków podobnych z okresem 0, dlatego często są zastępowane podczas zapisywania ułamków zwykłych z kropką zerową. W takim przypadku do wartości następnej cyfry dodaje się jedynkę, a w nawiasach podaje się (0). Równość otrzymanych liczb można łatwo sprawdzić, przedstawiając je w postaci ułamków zwykłych.

Na przykład ułamek 8, 31 (9) można zastąpić odpowiednią ułamkiem 8, 32 (0). Lub 4, (9) = 5, (0) = 5.

Nieskończone dziesiętne ułamki okresowe odnoszą się do liczby wymierne. Innymi słowy, każdy ułamek okresowy można przedstawić jako ułamek zwykły i odwrotnie.

Istnieją również ułamki zwykłe, które nie mają nieskończenie powtarzającej się sekwencji po przecinku. W tym przypadku nazywane są one ułamkami nieokresowymi.

Definicja 4

Nieokresowe ułamki dziesiętne obejmują te nieskończone ułamki dziesiętne, które nie zawierają kropki po przecinku, tj. powtarzająca się grupa liczb.

Czasami ułamki nieokresowe wyglądają bardzo podobnie do ułamków okresowych. Na przykład 9, 03003000300003... na pierwszy rzut oka wydaje się jednak, że ma kropkę szczegółowa analiza miejsc po przecinku potwierdza, że ​​jest to nadal ułamek nieokresowy. Z takimi liczbami trzeba być bardzo ostrożnym.

Ułamki nieokresowe są klasyfikowane jako liczby niewymierne. Nie są one konwertowane na ułamki zwykłe.

Podstawowe operacje na ułamkach dziesiętnych

Na ułamkach dziesiętnych można wykonywać następujące operacje: porównywanie, odejmowanie, dodawanie, dzielenie i mnożenie. Przyjrzyjmy się każdemu z nich osobno.

Porównywanie ułamków dziesiętnych można sprowadzić do porównywania ułamków zwykłych odpowiadających pierwotnym ułamkom dziesiętnym. Jednak nieskończonych ułamków nieokresowych nie można sprowadzić do tej postaci, a zamiana ułamków dziesiętnych na zwykłe jest często pracochłonnym zadaniem. Jak możemy szybko wykonać czynność porównawczą, jeśli zajdzie taka potrzeba podczas rozwiązywania problemu? Wygodnie jest porównywać ułamki dziesiętne według cyfr w taki sam sposób, w jaki porównujemy liczby naturalne. Tej metodzie poświęcimy osobny artykuł.

Aby dodać niektóre ułamki dziesiętne do innych, wygodnie jest zastosować metodę dodawania kolumn, tak jak w przypadku liczb naturalnych. Aby dodać okresowe ułamki dziesiętne, należy je najpierw zastąpić zwykłymi i policzyć zgodnie ze standardowym schematem. Jeżeli zgodnie z warunkami zadania musimy dodać nieskończone ułamki nieokresowe, to musimy je najpierw zaokrąglić do określonej cyfry, a następnie dodać. Im mniejsza cyfra, do której zaokrąglimy, tym większa będzie dokładność obliczeń. Do odejmowania, mnożenia i dzielenia nieskończonych ułamków konieczne jest również wstępne zaokrąglenie.

Znalezienie różnicy między ułamkami dziesiętnymi jest odwrotnością dodawania. Zasadniczo za pomocą odejmowania możemy znaleźć liczbę, której suma z ułamkiem, który odejmujemy, da nam ułamek, który minimalizujemy. Porozmawiamy o tym bardziej szczegółowo w osobnym artykule.

Mnożenie ułamków dziesiętnych odbywa się w taki sam sposób, jak w przypadku liczb naturalnych. Nadaje się do tego również metoda obliczania kolumn. Ponownie redukujemy to działanie za pomocą ułamków okresowych do mnożenia ułamków zwykłych zgodnie z już zbadanymi zasadami. Jak pamiętamy, ułamki nieskończone należy zaokrąglić przed obliczeniami.

Proces dzielenia ułamków dziesiętnych jest odwrotnością mnożenia. Przy rozwiązywaniu problemów korzystamy również z obliczeń kolumnowych.

Można ustalić dokładną zgodność pomiędzy końcowym ułamkiem dziesiętnym a punktem na osi współrzędnych. Zastanówmy się, jak zaznaczyć na osi punkt, który będzie dokładnie odpowiadał wymaganemu ułamkowi dziesiętnemu.

Badaliśmy już, jak konstruować punkty odpowiadające ułamkom zwykłym, ale ułamki dziesiętne można sprowadzić do tej postaci. Na przykład ułamek wspólny 14 10 jest taki sam jak 1, 4, więc odpowiedni punkt zostanie usunięty z początku w kierunku dodatnim o dokładnie tę samą odległość:

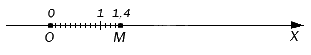
Możesz obejść się bez zastępowania ułamka dziesiętnego zwykłym, ale jako podstawę użyj metody rozwijania cyframi. Jeśli więc będziemy musieli zaznaczyć punkt, którego współrzędna będzie równa 15, 4008, to najpierw przedstawimy tę liczbę jako sumę 15 + 0, 4 +, 0008. Na początek odłóżmy 15 całych segmentów jednostkowych w kierunku dodatnim od początku odliczania, następnie 4 dziesiąte jednego segmentu, a następnie 8 dziesięciotysięcznych jednego segmentu. W rezultacie otrzymujemy punkt współrzędnych odpowiadający ułamkowi 15, 4008.

W przypadku nieskończonej części dziesiętnej lepiej zastosować tę metodę, ponieważ pozwala ona zbliżyć się do żądanego punktu tak blisko, jak chcesz. W niektórych przypadkach możliwe jest skonstruowanie dokładnej zgodności z nieskończonym ułamkiem na osi współrzędnych: na przykład 2 = 1, 41421. . . , a ułamek ten można powiązać z punktem na promieniu współrzędnych, oddalonym od 0 o długość przekątnej kwadratu, którego bok będzie równy jednemu segmentowi jednostkowemu.

Jeśli nie znajdziemy punktu na osi, ale odpowiadający mu ułamek dziesiętny, wówczas czynność tę nazywa się dziesiętnym pomiarem odcinka. Zobaczmy, jak zrobić to poprawnie.

Powiedzmy, że musimy przejść od zera do ponad ten punkt na osi współrzędnych (lub zbliżyć się jak najbliżej w przypadku ułamka nieskończonego). Aby to zrobić, stopniowo przesuwamy segmenty jednostkowe od początku, aż dotrzemy do pożądanego punktu. Po całych segmentach, jeśli to konieczne, odmierzamy dziesiąte, setne i mniejsze ułamki, aby dopasowanie było jak najdokładniejsze. W rezultacie otrzymaliśmy ułamek dziesiętny odpowiadający dany punkt na osi współrzędnych.

Powyżej pokazaliśmy rysunek z punktem M. Spójrz na to jeszcze raz: aby dostać się do tego punktu, musisz zmierzyć jeden segment jednostkowy i jego cztery dziesiąte od zera, ponieważ ten punkt odpowiada ułamkowi dziesiętnemu 1, 4.

Jeśli nie możemy dojść do punktu w procesie pomiaru dziesiętnego, oznacza to, że odpowiada on nieskończonej części dziesiętnej.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Zdarza się, że dla wygody obliczeń trzeba zamienić ułamek zwykły na dziesiętny i odwrotnie. Porozmawiamy o tym, jak to zrobić w tym artykule. Przyjrzyjmy się zasadom konwersji ułamków zwykłych na ułamki dziesiętne i odwrotnie, a także podaj przykłady.

Yandex.RTB R-A-339285-1

Rozważymy zamianę ułamków zwykłych na dziesiętne, zachowując określoną kolejność. Najpierw przyjrzyjmy się, jak ułamki zwykłe o mianowniku będącym wielokrotnością 10 są zamieniane na ułamki dziesiętne: 10, 100, 1000 itd. Ułamki zwykłe o takich mianownikach są w rzeczywistości bardziej uciążliwym zapisem ułamków dziesiętnych.

Następnie przyjrzymy się, jak zamienić ułamki zwykłe o dowolnym mianowniku, a nie tylko wielokrotnościach 10, na ułamki dziesiętne. Należy pamiętać, że podczas konwersji ułamków zwykłych na ułamki dziesiętne uzyskuje się nie tylko skończone ułamki dziesiętne, ale także nieskończone okresowe ułamki dziesiętne.

Zacznijmy!

Tłumaczenie ułamków zwykłych o mianownikach 10, 100, 1000 itd. do ułamków dziesiętnych

Po pierwsze, powiedzmy, że niektóre ułamki zwykłe wymagają pewnego przygotowania przed konwersją do postaci dziesiętnej. Co to jest? Przed liczbą w liczniku należy dodać tyle zer, aby liczba cyfr w liczniku była równa liczbie zer w mianowniku. Na przykład w przypadku ułamka 3100 liczbę 0 należy dodać raz na lewo od 3 w liczniku. Frakcja 610 zgodnie z zasadą podaną powyżej nie wymaga modyfikacji.

Spójrzmy na jeszcze jeden przykład, po którym sformułujemy regułę, która będzie szczególnie wygodna w użyciu na początku, podczas gdy nie ma dużego doświadczenia w konwertowaniu ułamków. Zatem ułamek 1610000 po dodaniu zer w liczniku będzie wyglądał jak 001510000.

Jak przekonwertować ułamek zwykły o mianowniku 10, 100, 1000 itd. do dziesiętnego?

Zasada zamiany ułamków zwykłych zwykłych na dziesiętne

1. Zapisz 0 i wstaw po nim przecinek.
2. Liczbę zapisujemy z licznika, który otrzymaliśmy po dodaniu zer.

Przejdźmy teraz do przykładów.

Przykład 1: Konwersja ułamków zwykłych na dziesiętne

Zamieńmy ułamek zwykły 39 100 na ułamek dziesiętny.

Najpierw patrzymy na ułamek i widzimy, że nie ma potrzeby wykonywania żadnych działań przygotowawczych - liczba cyfr w liczniku pokrywa się z liczbą zer w mianowniku.

Zgodnie z zasadą zapisujemy 0, stawiamy po nim kropkę dziesiętną i zapisujemy liczbę z licznika. Otrzymujemy ułamek dziesiętny 0,39.

Spójrzmy na rozwiązanie innego przykładu na ten temat.

Przykład 2. Zamiana ułamków zwykłych na dziesiętne

Zapiszmy ułamek 105 10000000 jako ułamek dziesiętny.

Liczba zer w mianowniku wynosi 7, a licznik ma tylko trzy cyfry. Dodajmy jeszcze 4 zera przed liczbą w liczniku:

0000105 10000000

Teraz zapisujemy 0, stawiamy po nim kropkę dziesiętną i zapisujemy liczbę z licznika. Otrzymujemy ułamek dziesiętny 0,0000105.

Ułamki uwzględnione we wszystkich przykładach są zwykłymi ułamkami właściwymi. Ale jak zamienić ułamek niewłaściwy na dziesiętny? Powiedzmy od razu, że nie ma potrzeby przygotowania z dodawaniem zer dla takich ułamków. Sformułujmy regułę.

Zasada zamiany zwykłych ułamków niewłaściwych na dziesiętne

1. Zapisz liczbę znajdującą się w liczniku.
2. Przecinkiem dziesiętnym oddzielamy po prawej stronie tyle cyfr, ile jest zer w mianowniku ułamka pierwotnego.

Poniżej znajduje się przykład użycia tej reguły.

Przykład 3. Konwersja ułamków zwykłych na dziesiętne

Zamieńmy ułamek 56888038009 100000 ze zwykłego ułamka nieregularnego na dziesiętny.

Najpierw zapiszmy liczbę z licznika:

Teraz po prawej stronie oddzielamy pięć cyfr przecinkiem (liczba zer w mianowniku wynosi pięć). Otrzymujemy:

Kolejne pytanie, które naturalnie się pojawia, brzmi: jak zamienić liczbę mieszaną na ułamek dziesiętny, jeśli mianownikiem jej części ułamkowej jest liczba 10, 100, 1000 itd. Aby zamienić taką liczbę na ułamek dziesiętny, możesz skorzystać z poniższej reguły.

Zasada zamiany liczb mieszanych na dziesiętne

1. W razie potrzeby przygotowujemy część ułamkową liczby.
2. Zapisujemy całą część pierwotnej liczby i stawiamy po niej przecinek.
3. Liczbę z licznika części ułamkowej zapisujemy wraz z dodanymi zerami.

Spójrzmy na przykład.

Przykład 4: Konwersja liczb mieszanych na dziesiętne

Zamieńmy liczbę mieszaną 23 17 10000 na ułamek dziesiętny.

W części ułamkowej mamy wyrażenie 17 10000. Przygotujmy go i dodajmy jeszcze dwa zera po lewej stronie licznika. Otrzymujemy: 0017 10000.

Teraz zapisujemy całą część liczby i stawiamy po niej przecinek: 23, . .

Po przecinku zapisz liczbę z licznika wraz z zerami. Otrzymujemy wynik:

23 17 10000 = 23 , 0017

Zamiana ułamków zwykłych na ułamki okresowe skończone i nieskończone

Oczywiście można konwertować na ułamki dziesiętne i zwykłe o mianowniku różnym od 10, 100, 1000 itd.

Często ułamek można łatwo sprowadzić do nowego mianownika, a następnie zastosować regułę przedstawioną w pierwszym akapicie tego artykułu. Na przykład wystarczy pomnożyć licznik i mianownik ułamka 25 przez 2 i otrzymamy ułamek 410, który łatwo przeliczyć na postać dziesiętną 0,4.

Jednak ta metoda konwersji ułamka zwykłego na dziesiętny nie zawsze może być zastosowana. Poniżej zastanowimy się, co zrobić, jeśli nie można zastosować rozważanej metody.

Całkowicie nowym sposobem zamiany ułamka zwykłego na dziesiętny jest podzielenie licznika przez mianownik za pomocą kolumny. Ta operacja jest bardzo podobna do dzielenia liczb naturalnych przez kolumnę, ale ma swoje własne cechy.

Licznik podczas dzielenia jest reprezentowany jako ułamek dziesiętny - po prawej stronie ostatnia cyfra Licznik poprzedza się przecinkiem i dodaje się zera. W otrzymanym ilorazie kropkę dziesiętną umieszcza się, gdy kończy się dzielenie części całkowitej licznika. Jak dokładnie działa ta metoda, stanie się jasne po zapoznaniu się z przykładami.

Przykład 5. Konwersja ułamków zwykłych na dziesiętne

Zamieńmy ułamek zwykły 621 4 na postać dziesiętną.

Przedstawmy liczbę 621 z licznika jako ułamek dziesiętny, dodając kilka zer po przecinku. 621 = 621,00

Teraz podzielmy 621,00 przez 4 za pomocą kolumny. Pierwsze trzy kroki dzielenia będą takie same jak przy dzieleniu liczb naturalnych i otrzymamy.

Kiedy dochodzimy do przecinka w dzielnej, a reszta jest różna od zera, stawiamy przecinek w ilorazu i kontynuujemy dzielenie, nie zwracając już uwagi na przecinek w dywidendzie.

W rezultacie otrzymujemy ułamek dziesiętny 155, 25, który jest wynikiem odwrócenia ułamka zwykłego 621 4

621 4 = 155 , 25

Spójrzmy na inny przykład wzmocnienia materiału.

Przykład 6. Konwersja ułamków zwykłych na dziesiętne

Odwróćmy ułamek zwykły 21 800.

Aby to zrobić, podziel ułamek 21 000 na kolumnę przez 800. Dzielenie całej części zakończy się na pierwszym etapie, więc zaraz po nim stawiamy przecinek w ilorazu i kontynuujemy dzielenie, nie zwracając uwagi na przecinek w dzielnej, aż do momentu, gdy otrzymamy resztę równą zero.

W rezultacie otrzymaliśmy: 21 800 = 0,02625.

Co jednak, jeśli przy dzieleniu nadal nie otrzymamy reszty równej 0. W takich przypadkach dzielenie można kontynuować w nieskończoność. Jednakże, począwszy od pewnego etapu, pozostałości będą powtarzane okresowo. W związku z tym liczby w ilorazu zostaną powtórzone. Oznacza to, że ułamek zwykły jest zamieniany na dziesiętny nieskończony ułamek okresowy. Zilustrujmy to przykładem.

Przykład 7. Zamiana ułamków zwykłych na dziesiętne

Zamieńmy ułamek zwykły 19 44 na ułamek dziesiętny. Aby to zrobić, wykonujemy dzielenie według kolumn.

Widzimy, że podczas dzielenia powtarzają się reszty 8 i 36. W tym przypadku liczby 1 i 8 powtarzają się w ilorazie. Jest to okres w ułamku dziesiętnym. Podczas nagrywania liczby te są umieszczane w nawiasach.

W ten sposób pierwotny ułamek zwykły zostaje przekształcony w nieskończony okresowy ułamek dziesiętny.

19 44 = 0 , 43 (18) .

Zobaczmy nieredukowalny ułamek zwykły. Jaką formę przyjmie? Które ułamki zwykłe zamienia się na skończone ułamki dziesiętne, a które na nieskończone ułamki okresowe?

Załóżmy najpierw, że jeśli ułamek można sprowadzić do jednego z mianowników 10, 100, 1000..., to będzie on miał postać końcowego ułamka dziesiętnego. Aby ułamek został zredukowany do jednego z tych mianowników, jego mianownik musi być dzielnikiem co najmniej jednej z liczb 10, 100, 1000 itd. Z zasad rozkładania liczb na czynniki pierwsze wynika, że ​​dzielnikiem liczb jest 10, 100, 1000 itd. musi, po rozłożeniu na czynniki pierwsze, zawierać tylko liczby 2 i 5.

Podsumujmy co zostało powiedziane:

1. Ułamek zwykły można sprowadzić do ułamka dziesiętnego, jeśli jego mianownik można rozłożyć na czynniki pierwsze 2 i 5.
2. Jeżeli oprócz liczb 2 i 5 w rozwinięciu mianownika znajdują się inne liczby pierwsze, ułamek jest redukowany do postaci nieskończonej okresowej części dziesiętnej.

Podajmy przykład.

Przykład 8. Konwersja ułamków zwykłych na dziesiętne

Który z tych ułamków 47 20, 7 12, 21 56, 31 17 zamienia się na końcowy ułamek dziesiętny, a który tylko na okresowy. Odpowiedzmy na to pytanie bez bezpośredniej konwersji ułamka zwykłego na dziesiętny.

Ułamek 47 20, jak łatwo zauważyć, mnożąc licznik i mianownik przez 5, redukuje się do nowego mianownika 100.

47 20 = 235 100. Z tego wnioskujemy, że ułamek ten jest konwertowany na końcowy ułamek dziesiętny.

Rozłożenie mianownika ułamka na czynniki daje 12 = 2 · 2 · 3. Ponieważ czynnik pierwszy 3 różni się od 2 i 5, ułamka tego nie można przedstawić jako skończonego ułamka dziesiętnego, ale będzie on miał postać nieskończonego ułamka okresowego.

Najpierw należy zmniejszyć ułamek 21 56. Po redukcji przez 7 otrzymujemy ułamek nieredukowalny 3 8, którego mianownik jest rozkładany na czynniki w celu uzyskania 8 = 2 · 2 · 2. Jest to zatem końcowy ułamek dziesiętny.

W przypadku ułamka 31 17 mianownikiem jest sama liczba pierwsza 17. W związku z tym ułamek ten można przekształcić w nieskończony okresowy ułamek dziesiętny.

Ułamka zwykłego nie można zamienić na nieskończony i nieokresowy ułamek dziesiętny

Powyżej mówiliśmy tylko o skończonych i nieskończonych ułamkach okresowych. Ale czy każdy zwykły ułamek można przekształcić w nieskończony ułamek nieokresowy?

Odpowiadamy: nie!

Ważny!

Podczas konwersji ułamka nieskończonego na ułamek dziesiętny wynikiem jest albo skończona liczba dziesiętna, albo nieskończona okresowa liczba dziesiętna.

Reszta dzielenia jest zawsze mniejsza od dzielnika. Innymi słowy, zgodnie z twierdzeniem o podzielności, jeśli podzielimy jakąś liczbę naturalną przez liczbę q, to ​​reszta z dzielenia w żadnym wypadku nie może być większa niż q-1. Po zakończeniu podziału możliwa jest jedna z następujących sytuacji:

1. Otrzymujemy resztę równą 0 i na tym dzielenie się kończy.
2. Otrzymujemy resztę, która jest powtarzana przy kolejnym dzieleniu, w wyniku czego otrzymujemy nieskończony ułamek okresowy.

Nie ma innej możliwości zamiany ułamka zwykłego na dziesiętny. Powiedzmy również, że długość okresu (liczba cyfr) nieskończonego ułamka okresowego jest zawsze mniejsza niż liczba cyfr w mianowniku odpowiedniego ułamka zwykłego.

Zamiana ułamków dziesiętnych na ułamki zwykłe

Teraz czas przyjrzeć się odwrotnemu procesowi zamiany ułamka dziesiętnego na ułamek zwykły. Sformułujmy regułę tłumaczenia, która obejmuje trzy etapy. Jak zamienić ułamek dziesiętny na ułamek zwykły?

Zasada zamiany ułamków dziesiętnych na zwykłe

1. W liczniku zapisujemy liczbę z pierwotnego ułamka dziesiętnego, odrzucając przecinek i wszystkie zera po lewej stronie, jeśli występują.
2. W mianowniku zapisujemy jedynkę i tyle zer, ile jest cyfr po przecinku w pierwotnym ułamku dziesiętnym.
3. Jeśli to konieczne, zmniejsz powstałą ułamek zwykły.

Rozważmy aplikację tej zasady z przykładami.

Przykład 8. Zamiana ułamków dziesiętnych na zwykłe

Wyobraźmy sobie liczbę 3,025 jako ułamek zwykły.

1. Do licznika wpisujemy sam ułamek dziesiętny, odrzucając przecinek: 3025.
2. W mianowniku piszemy jeden, a po nim trzy zera - dokładnie tyle cyfr zawiera się w pierwotnym ułamku po przecinku: 3025 1000.
3. Powstały ułamek 3025 1000 można zmniejszyć o 25, otrzymując: 3025 1000 = 121 40.

Przykład 9. Konwersja ułamków dziesiętnych na ułamki zwykłe

Zamieńmy ułamek 0,0017 z dziesiętnego na zwykły.

1. W liczniku zapisujemy ułamek 0, 0017, odrzucając przecinek i zera po lewej stronie. Okazuje się, że będzie to 17.
2. W mianowniku zapisujemy jedynkę, a po niej cztery zera: 17 10000. Ułamek ten jest nieredukowalny.

Jeśli ułamek dziesiętny ma część całkowitą, wówczas taki ułamek można natychmiast przekształcić w liczbę mieszaną. Jak to zrobić?

Sformułujmy jeszcze jedną zasadę.

Zasada zamiany ułamków dziesiętnych na liczby mieszane.

1. Liczbę przed przecinkiem ułamkowym zapisuje się jako część całkowitą liczby mieszanej.
2. W liczniku zapisujemy liczbę po przecinku ułamka zwykłego, odrzucając zera po lewej stronie, jeśli takie istnieją.
3. Do mianownika części ułamkowej dodajemy jeden i tyle zer, ile jest cyfr po przecinku w części ułamkowej.

Weźmy przykład

Przykład 10. Konwersja ułamka dziesiętnego na liczbę mieszaną

Wyobraźmy sobie ułamek 155, 06005 jako liczbę mieszaną.

1. Liczbę 155 zapisujemy jako część całkowitą.
2. W liczniku zapisujemy liczby po przecinku, odrzucając zero.
3. W mianowniku zapisujemy jeden i pięć zer

Nauczmy się liczby mieszanej: 155 6005 100000

Część ułamkową można zmniejszyć o 5. Skracamy go i otrzymujemy efekt końcowy:

155 , 06005 = 155 1201 20000

Zamiana nieskończonych okresowych ułamków dziesiętnych na ułamki zwykłe

Spójrzmy na przykłady zamiany okresowych ułamków dziesiętnych na ułamki zwykłe. Zanim zaczniemy, wyjaśnijmy: każdy okresowy ułamek dziesiętny można zamienić na ułamek zwykły.

Najprostszy przypadek ma miejsce, gdy okres ułamka wynosi zero. Ułamek okresowy z kropką zerową zastępuje się końcowym ułamkiem dziesiętnym, a proces odwracania takiego ułamka sprowadza się do odwracania końcowego ułamka dziesiętnego.

Przykład 11. Konwersja okresowego ułamka dziesiętnego na ułamek zwykły

Odwróćmy ułamek okresowy 3, 75 (0).

Eliminując zera po prawej stronie, otrzymujemy końcowy ułamek dziesiętny 3,75.

Przekształcając ten ułamek na ułamek zwykły za pomocą algorytmu omówionego w poprzednich akapitach, otrzymujemy:

3 , 75 (0) = 3 , 75 = 375 100 = 15 4 .

A co jeśli okres ułamka jest różny od zera? Część okresową należy traktować jako sumę wyrazów postępu geometrycznego, który maleje. Wyjaśnijmy to na przykładzie:

0 , (74) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .

Istnieje wzór na sumę wyrazów nieskończonego malejącego postępu geometrycznego. Jeśli pierwszym wyrazem ciągu jest b, a mianownik q jest taki, że 0< q < 1 , то сумма равна b 1 - q .

Przyjrzyjmy się kilku przykładom wykorzystania tej formuły.

Przykład 12. Konwersja okresowego ułamka dziesiętnego na ułamek zwykły

Mamy ułamek okresowy 0, (8) i musimy go zamienić na zwykły.

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . .

Tutaj mamy nieskończone zmniejszanie postęp geometryczny z pierwszym wyrazem 0, 8 i mianownikiem 0, 1.

Zastosujmy wzór:

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 - 0 , 1 = 0 , 8 0 , 9 = 8 9

Jest to wymagany ułamek zwykły.

Aby skonsolidować materiał, rozważ inny przykład.

Przykład 13. Konwersja okresowego ułamka dziesiętnego na ułamek zwykły

Odwróćmy ułamek 0, 43 (18).

Najpierw zapisujemy ułamek jako sumę nieskończoną:

0 , 43 (18) = 0 , 43 + (0 , 0018 + 0 , 000018 + 0 , 00000018 . .)

Spójrzmy na terminy w nawiasach. Ten postęp geometryczny można przedstawić w następujący sposób:

0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 - 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .

Wynik dodajemy do ułamka końcowego 0, 43 = 43 100 i otrzymujemy wynik:

0 , 43 (18) = 43 100 + 18 9900

Po dodaniu tych ułamków i skróceniu otrzymujemy ostateczną odpowiedź:

0 , 43 (18) = 19 44

Na zakończenie tego artykułu powiemy, że nieokresowych nieskończonych ułamków dziesiętnych nie można przekształcić w ułamki zwykłe.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Ten artykuł jest o miejsca dziesiętne. Tutaj zrozumiemy zapis dziesiętny liczb ułamkowych, wprowadzimy pojęcie ułamka dziesiętnego i podamy przykłady ułamków dziesiętnych. Następnie porozmawiamy o cyfrach ułamków dziesiętnych i podamy nazwy cyfr. Następnie skupimy się na nieskończonych ułamkach dziesiętnych, porozmawiajmy o ułamkach okresowych i nieokresowych. Następnie wymienimy podstawowe operacje na ułamkach dziesiętnych. Podsumowując, ustalmy położenie ułamków dziesiętnych na belce współrzędnych.

Nawigacja strony.

Zapis dziesiętny liczby ułamkowej

Czytanie ułamków dziesiętnych

Powiedzmy kilka słów o zasadach czytania ułamków dziesiętnych.

Ułamki dziesiętne, które odpowiadają właściwym ułamkom zwykłym, czyta się w taki sam sposób, jak te ułamki zwykłe, z tym że najpierw dodaje się tylko „liczbę całkowitą zero”. Na przykład ułamek dziesiętny 0,12 odpowiada ułamkowi zwykłemu 12/100 (czytaj „dwanaście setnych”), dlatego 0,12 odczytuje się jako „przecinek zerowy dwanaście setnych”.

Ułamki dziesiętne odpowiadające liczbom mieszanym czyta się dokładnie tak samo, jak liczby mieszane. Na przykład ułamek dziesiętny 56,002 odpowiada liczbie mieszanej, więc ułamek dziesiętny 56,002 odczytuje się jako „pięćdziesiąt sześć przecinek dwie tysięczne”.

Miejsca po przecinku

Zapisując ułamki dziesiętne, a także zapisując liczby naturalne, znaczenie każdej cyfry zależy od jej położenia. Rzeczywiście liczba 3 w ułamku dziesiętnym 0,3 oznacza trzy dziesiąte, w ułamku dziesiętnym 0,0003 - trzy dziesięciotysięczne, a w ułamku dziesiętnym 30 000,152 - trzy dziesiątki tysięcy. Więc możemy porozmawiać miejsca dziesiętne, a także o cyfrach liczb naturalnych.

Nazwy cyfr ułamka dziesiętnego aż do kropki dziesiętnej całkowicie pokrywają się z nazwami cyfr liczb naturalnych. Nazwy miejsc dziesiętnych po przecinku można zobaczyć w poniższej tabeli.

Na przykład w ułamku dziesiętnym 37,051 cyfra 3 znajduje się na miejscu dziesiątek, 7 na miejscu jedności, 0 na miejscu dziesiątym, 5 na miejscu setnym, a 1 na miejscu tysięcznym.

Miejsca w ułamkach dziesiętnych również różnią się priorytetem. Jeśli zapisując ułamek dziesiętny będziemy przechodzić od cyfry do cyfry od lewej do prawej, to będziemy się przesuwać seniorzy Do stopnie juniorskie. Na przykład miejsce setek jest starsze niż miejsce dziesiątych, a miejsce milionów jest niższe niż miejsce setne. W danym końcowym ułamku dziesiętnym możemy mówić o cyfrach większych i mniejszych. Na przykład w ułamku dziesiętnym 604.9387 starszy (najwyższy) to miejsce jest miejscem setek i junior (najniższy)- cyfra dziesięciotysięczna.

W przypadku ułamków dziesiętnych następuje rozwinięcie do cyfr. Przypomina to rozwinięcie liczb naturalnych na cyfry. Na przykład rozwinięcie liczby 45,6072 do miejsc dziesiętnych wygląda następująco: 45,6072=40+5+0,6+0,007+0,0002. A właściwości dodawania z rozkładu ułamka dziesiętnego na cyfry pozwalają przejść do innych reprezentacji tego ułamka dziesiętnego, na przykład 45,6072=45+0,6072 lub 45,6072=40,6+5,007+0,0002 lub 45,6072= 45,0072+ 0,6.

Kończenie ułamków dziesiętnych

Do tego momentu mówiliśmy jedynie o ułamkach dziesiętnych, w których zapisie po przecinku znajduje się skończona liczba cyfr. Takie ułamki nazywane są skończonymi ułamkami dziesiętnymi.

Definicja.

Kończenie ułamków dziesiętnych- Są to ułamki dziesiętne, których zapisy zawierają skończoną liczbę znaków (cyfr).

Oto kilka przykładów końcowych ułamków dziesiętnych: 0,317, 3,5, 51,1020304958, 230 032,45.

Jednak nie każdy ułamek można przedstawić jako ułamek dziesiętny. Na przykład ułamka 5/13 nie można zastąpić ułamkiem równym o jednym z mianowników 10, 100, ... dlatego nie można go przekształcić w końcowy ułamek dziesiętny. Porozmawiamy o tym więcej w części teoretycznej, zamieniając ułamki zwykłe na dziesiętne.

Nieskończone ułamki dziesiętne: ułamki okresowe i ułamki nieokresowe

Zapisując ułamek dziesiętny po przecinku, można założyć możliwość nieskończonej liczby cyfr. W tym przypadku rozważymy tak zwane nieskończone ułamki dziesiętne.

Definicja.

Nieskończone ułamki dziesiętne- Są to ułamki dziesiętne, które zawierają nieskończoną liczbę cyfr.

Jest oczywiste, że nie możemy zapisać nieskończonych ułamków dziesiętnych w pełnej formie, dlatego w ich zapisie ograniczamy się tylko do pewnej skończonej liczby cyfr po przecinku i stawiamy wielokropek wskazujący nieskończenie ciągły ciąg cyfr. Oto kilka przykładów nieskończonych ułamków dziesiętnych: 0,143940932…, 3,1415935432…, 153,02003004005…, 2,111111111…, 69,74152152152….

Jeśli przyjrzysz się uważnie dwóm ostatnim nieskończonym ułamkom dziesiętnym, to w ułamku 2,111111111... wyraźnie widać powtarzającą się w nieskończoność liczbę 1, a w ułamku 69,74152152152... zaczynając od trzeciego miejsca po przecinku, powtarzającą się grupę liczb 1, 5 i 2 są wyraźnie widoczne. Takie nieskończone ułamki dziesiętne nazywane są okresowymi.

Definicja.

Okresowe ułamki dziesiętne(lub po prostu frakcje okresowe) to nieskończone ułamki dziesiętne, przy zapisie których, zaczynając od określonego miejsca po przecinku, powtarza się w nieskończoność pewna liczba lub grupa liczb, co nazywa się okres ułamka.

Na przykład okres ułamka okresowego 2,111111111... to cyfra 1, a okres ułamka 69,74152152152... to grupa cyfr postaci 152.

Dla nieskończonych okresowych ułamków dziesiętnych jest to akceptowane specjalny kształt dokumentacja. Dla skrócenia zgodziliśmy się na jednorazowe zapisanie kropki, umieszczając ją w nawiasie. Na przykład ułamek okresowy 2,111111111... jest zapisywany jako 2,(1) , a ułamek okresowy 69,74152152152... jest zapisywany jako 69,74(152) .

Warto zauważyć, że dla tego samego okresowego ułamka dziesiętnego można określić różne okresy. Na przykład okresowy ułamek dziesiętny 0,73333... można uznać za ułamek 0,7(3) z okresem 3, a także jako ułamek 0,7(33) z okresem 33 i tak dalej 0,7(333), 0,7 (3333), ... Możesz także spojrzeć na ułamek okresowy 0,73333 ... w ten sposób: 0,733 (3) lub w ten sposób 0,73 (333) itd. Tutaj, aby uniknąć dwuznaczności i rozbieżności, zgodzimy się uznać za okres ułamka dziesiętnego najkrótszy ze wszystkich możliwych ciągów powtarzających się cyfr, zaczynając od pozycji najbliższej przecinkowi dziesiętnemu. Oznacza to, że za okres ułamka dziesiętnego 0,73333... będziemy uważać ciąg jednej cyfry 3, a okresowość zaczyna się od drugiej pozycji po przecinku, czyli 0,73333...=0,7(3). Inny przykład: ułamek okresowy 4,7412121212... ma okres 12, okresowość zaczyna się od trzeciej cyfry po przecinku, czyli 4,7412121212...=4,74(12).

Nieskończone dziesiętne ułamki okresowe otrzymuje się poprzez przekształcenie na ułamki dziesiętne zwykłych ułamków, których mianowniki zawierają czynniki pierwsze inne niż 2 i 5.

Warto tutaj wspomnieć o ułamkach okresowych z okresem 9. Podajmy przykłady takich ułamków: 6,43(9) , 27,(9) . Ułamki te są kolejnym zapisem ułamków okresowych z okresem 0 i zwykle są zastępowane ułamkami okresowymi z okresem 0. W tym celu okres 9 zastępuje się okresem 0, a wartość kolejnej największej cyfry zwiększa się o jeden. Na przykład ułamek o okresie 9 w postaci 7,24(9) zastępuje się ułamkiem okresowym o okresie 0 w postaci 7,25(0) lub równym końcowym ułamkiem dziesiętnym 7,25. Inny przykład: 4,(9)=5,(0)=5. Równość ułamka z okresem 9 i odpowiadającego mu ułamka z okresem 0 można łatwo ustalić po zastąpieniu tych ułamków dziesiętnych równymi ułamkami zwykłymi.

Na koniec przyjrzyjmy się bliżej nieskończonym ułamkom dziesiętnym, które nie zawierają nieskończenie powtarzającej się sekwencji cyfr. Nazywa się je nieokresowymi.

Definicja.

Niepowtarzające się ułamki dziesiętne(lub po prostu frakcje nieokresowe) to nieskończone ułamki dziesiętne bez kropki.

Czasami ułamki nieokresowe mają postać podobną do ułamków okresowych, np. 8.02002000200002... jest ułamkiem nieokresowym. W takich przypadkach należy szczególnie uważać, aby zauważyć różnicę.

Należy zauważyć, że ułamki nieokresowe nie są konwertowane na ułamki zwykłe; nieskończone nieokresowe ułamki dziesiętne reprezentują liczby niewymierne.

Operacje na ułamkach dziesiętnych

Jedną z operacji na ułamkach dziesiętnych jest porównywanie, definiuje się także cztery podstawowe funkcje arytmetyczne operacje na ułamkach dziesiętnych: dodawanie, odejmowanie, mnożenie i dzielenie. Rozważmy osobno każdą z akcji z ułamkami dziesiętnymi.

Porównanie ułamków dziesiętnych zasadniczo opiera się na porównaniu ułamków zwykłych odpowiadających porównywanym ułamkom dziesiętnym. Jednak zamiana ułamków dziesiętnych na ułamki zwykłe jest procesem dość pracochłonnym, a nieskończonych ułamków nieokresowych nie można przedstawić jako ułamka zwykłego, dlatego wygodnie jest zastosować porównanie ułamków dziesiętnych w oparciu o miejsca. Porównanie miejsc ułamków dziesiętnych jest podobne do porównywania liczb naturalnych. Aby uzyskać bardziej szczegółowe informacje, zalecamy przestudiowanie artykułu: porównanie ułamków dziesiętnych, reguły, przykłady, rozwiązania.

Przejdźmy dalej Następna akcja - mnożenie ułamków dziesiętnych. Mnożenie skończonych ułamków dziesiętnych odbywa się analogicznie do odejmowania ułamków dziesiętnych, zasady, przykłady, rozwiązania mnożenia przez kolumnę liczb naturalnych. W przypadku ułamków okresowych mnożenie można sprowadzić do mnożenia ułamków zwykłych. Z kolei mnożenie nieskończonych nieokresowych ułamków dziesiętnych po ich zaokrągleniu sprowadza się do mnożenia skończonych ułamków dziesiętnych. Polecamy do dalszego przestudiowania materiał w artykule: mnożenie ułamków dziesiętnych, zasady, przykłady, rozwiązania.

Miejsca dziesiętne na promieniu współrzędnych

Istnieje zgodność jeden do jednego między kropkami i miejscami dziesiętnymi.

Zastanówmy się, jak zbudowane są punkty na promieniu współrzędnych, które odpowiadają danemu ułamkowi dziesiętnemu.

Możemy zastąpić skończone ułamki dziesiętne i nieskończone okresowe ułamki dziesiętne równymi ułamkami zwykłymi, a następnie skonstruować odpowiednie ułamki zwyczajne na promieniu współrzędnych. Na przykład ułamek dziesiętny 1,4 odpowiada ułamkowi zwykłemu 14/10, więc punkt o współrzędnej 1,4 jest usuwany od początku w kierunku dodatnim o 14 segmentów równych jednej dziesiątej segmentu jednostkowego.

Ułamki dziesiętne można zaznaczyć na promieniu współrzędnych, zaczynając od rozłożenia danego ułamka dziesiętnego na cyfry. Przykładowo, musimy zbudować punkt o współrzędnych 16.3007, ponieważ 16.3007=16+0.3+0.0007, to możemy dojść do tego punktu układając kolejno 16 odcinków jednostkowych od początku współrzędnych, 3 odcinki o długości równej jednej dziesiątej jednostki i 7 odcinków, których długość jest równa dziesięciotysięcznej części jednostkowej.

Ta metoda konstruowania liczb dziesiętnych na promieniu współrzędnych pozwala zbliżyć się tak blisko punktu odpowiadającego nieskończonej części dziesiętnej.

Czasami możliwe jest dokładne wykreślenie punktu odpowiadającego nieskończonej części dziesiętnej. Na przykład, , to ten nieskończony ułamek dziesiętny 1,41421... odpowiada punktowi na promieniu współrzędnych, oddalonym od początku współrzędnych o długość przekątnej kwadratu o boku 1 odcinka jednostkowego.

Odwrotny proces uzyskiwania ułamka dziesiętnego odpowiadającego danemu punktowi na promieniu współrzędnych to tzw dziesiętna miara segmentu. Zastanówmy się, jak to się robi.

Niech naszym zadaniem będzie dotarcie od początku do zadanego punktu na linii współrzędnych (lub dotarcie do niego w nieskończoność, jeśli nie możemy się do niego dostać). Dzięki dziesiętnemu pomiarowi odcinka możemy kolejno odsunąć od początku dowolną liczbę segmentów jednostkowych, następnie segmenty, których długość jest równa jednej dziesiątej jednostki, następnie odcinki, których długość jest równa setnej części jednostki itp. Zapisując liczbę odłożonych odcinków każdej długości, otrzymujemy ułamek dziesiętny odpowiadający danemu punktowi na promieniu współrzędnych.

Przykładowo, aby dostać się do punktu M na powyższym rysunku, należy odłożyć 1 odcinek jednostkowy i 4 odcinki, których długość jest równa jednej dziesiątej jednostki. Zatem punkt M odpowiada ułamkowi dziesiętnemu 1,4.

Oczywiste jest, że punkty promienia współrzędnych, do których nie można dotrzeć w procesie pomiaru dziesiętnego, odpowiadają nieskończonym ułamkom dziesiętnym.

Bibliografia.

• Matematyka: podręcznik dla 5 klasy. ogólne wykształcenie instytucje / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - wyd. 21, skreślone. - M.: Mnemosyne, 2007. - 280 s.: il. ISBN 5-346-00699-0.
• Matematyka. Klasa 6: edukacyjna. dla edukacji ogólnej instytucje / [N. Tak, Vilenkin i inni]. - wyd. 22, wyd. - M.: Mnemosyne, 2008. - 288 s.: il. ISBN 978-5-346-00897-2.
• Algebra: podręcznik dla 8 klasy. ogólne wykształcenie instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2008. - 271 s. : chory. - ISBN 978-5-09-019243-9.
• Gusiew V. A., Mordkovich A. G. Matematyka (podręcznik dla rozpoczynających naukę w technikach): Proc. zasiłek.- M.; Wyższy szkoła, 1984.-351 s., il.

Powiedzieliśmy już, że istnieją ułamki zwykły I dziesiętny. NA ten moment Przestudiowaliśmy trochę ułamki zwykłe. Dowiedzieliśmy się, że istnieją ułamki regularne i niewłaściwe. Dowiedzieliśmy się również, że ułamki zwykłe można zmniejszać, dodawać, odejmować, mnożyć i dzielić. Dowiedzieliśmy się również, że istnieją tak zwane liczby mieszane, które składają się z liczby całkowitej i części ułamkowej.

Nie zbadaliśmy jeszcze w pełni ułamków zwykłych. Istnieje wiele subtelności i szczegółów, o których należy porozmawiać, ale dzisiaj zaczniemy się uczyć dziesiętny ułamki zwykłe, ponieważ często trzeba łączyć ułamki zwykłe i dziesiętne. Oznacza to, że przy rozwiązywaniu problemów należy używać obu rodzajów ułamków.

Ta lekcja może wydawać się skomplikowana i zagmatwana. To całkiem normalne. Tego rodzaju lekcje wymagają studiowania, a nie powierzchownego przeglądania.

Treść lekcji

Wyrażanie wielkości w formie ułamkowej

Czasami wygodnie jest pokazać coś w formie ułamkowej. Na przykład jedna dziesiąta decymetra jest zapisana w następujący sposób:

Wyrażenie to oznacza, że ​​jeden decymetr podzielono na dziesięć części i z tych dziesięciu części wzięto jedną część:

Jak widać na rysunku, jedna dziesiąta decymetra to jeden centymetr.

Rozważ następujący przykład. Pokaż 6 cm i kolejne 3 mm w centymetrach w formie ułamkowej.

Musisz więc wyrazić 6 cm i 3 mm w centymetrach, ale w formie ułamkowej. Mamy już 6 całych centymetrów:

ale pozostały jeszcze 3 milimetry. Jak pokazać te 3 milimetry i w centymetrach? Na ratunek przychodzą frakcje. 3 milimetry to trzecia część centymetra. Trzecia część centymetra jest zapisywana jako cm

Ułamek oznacza, że ​​jeden centymetr podzielono na dziesięć równych części i z tych dziesięciu części pobrano trzy części (trzy z dziesięciu).

W rezultacie mamy sześć pełnych centymetrów i trzy dziesiąte centymetra:

W tym przypadku 6 pokazuje liczbę pełnych centymetrów, a ułamek pokazuje liczbę ułamkowych centymetrów. Ułamek ten odczytuje się jako „sześć przecinek trzy centymetry”.

Ułamki zwykłe, których mianownik zawiera liczby 10, 100, 1000, można zapisać bez mianownika. Najpierw napisz całą część, a następnie licznik części ułamkowej. Część całkowitą oddziela się od licznika części ułamkowej przecinkiem.

Na przykład napiszmy to bez mianownika. Aby to zrobić, najpierw zapiszmy całą część. Częścią całkowitą jest liczba 6. Najpierw zapisujemy tę liczbę:

Całość jest nagrana. Zaraz po napisaniu całej części stawiamy przecinek:

A teraz zapisujemy licznik części ułamkowej. W liczbie mieszanej licznikiem części ułamkowej jest liczba 3. Trójkę po przecinku piszemy:

Dowolna liczba przedstawiona w tej formie nazywana jest dziesiętny.

Dlatego możesz pokazać 6 cm i kolejne 3 mm w centymetrach, używając ułamka dziesiętnego:

6,3cm

Będzie to wyglądać tak:

W rzeczywistości ułamki dziesiętne to to samo, co zwykłe ułamki zwykłe i liczby mieszane. Osobliwością takich ułamków jest to, że w mianowniku ich części ułamkowej znajdują się liczby 10, 100, 1000 lub 10000.

Podobnie jak liczba mieszana, ułamek dziesiętny składa się z części całkowitej i części ułamkowej. Na przykład w liczbie mieszanej część całkowita wynosi 6, a część ułamkowa to .

W ułamku dziesiętnym 6,3 częścią całkowitą jest liczba 6, a częścią ułamkową jest licznik ułamka, czyli liczba 3.

Zdarza się również, że ułamki zwykłe w mianowniku, w których liczby 10, 100, 1000 są podane bez części całkowitej. Na przykład podaje się ułamek bez części całkowitej. Aby zapisać taki ułamek jako ułamek dziesiętny, należy najpierw wpisać 0, następnie postawić przecinek i wpisać licznik ułamka. Ułamek zwykły bez mianownika zapisuje się następująco:

Czyta się jak „zero przecinek pięć”.

Zamiana liczb mieszanych na dziesiętne

Kiedy piszemy liczby mieszane bez mianownika, w ten sposób konwertujemy je na ułamki dziesiętne. Konwertując ułamki zwykłe na dziesiętne, musisz wiedzieć kilka rzeczy, o których teraz porozmawiamy.

Po zapisaniu całej części należy policzyć liczbę zer w mianowniku części ułamkowej, ponieważ liczba zer części ułamkowej i liczba cyfr po przecinku w ułamku dziesiętnym musi być równa To samo. Co to znaczy? Rozważ następujący przykład:

Najpierw

I możesz od razu zapisać licznik części ułamkowej i ułamek dziesiętny jest gotowy, ale zdecydowanie musisz policzyć liczbę zer w mianowniku części ułamkowej.

Zatem liczymy liczbę zer w części ułamkowej liczby mieszanej. W mianowniku części ułamkowej jest jedno zero. Oznacza to, że w ułamku dziesiętnym po przecinku będzie jedna cyfra i cyfra ta będzie licznikiem części ułamkowej liczby mieszanej, czyli liczbą 2

Zatem po przeliczeniu na ułamek dziesiętny liczba mieszana staje się 3,2.

Ten ułamek dziesiętny brzmi następująco:

„Trzy punkty dwa”

„Dziesiątki”, ponieważ liczba 10 należy do części ułamkowej liczby mieszanej.

Przykład 2. Zamień liczbę mieszaną na dziesiętną.

Zapisz całą część i wstaw przecinek:

I można od razu zapisać licznik części ułamkowej i otrzymać ułamek dziesiętny 5,3, ale zasada mówi, że po przecinku powinno być tyle cyfr, ile jest zer w mianowniku części ułamkowej liczby mieszanej. I widzimy, że mianownik części ułamkowej ma dwa zera. Oznacza to, że nasz ułamek dziesiętny musi mieć dwie cyfry po przecinku, a nie jedną.

W takich przypadkach licznik części ułamkowej należy nieco zmodyfikować: dodać zero przed licznikiem, czyli przed liczbą 3

Teraz możesz zamienić tę liczbę mieszaną na ułamek dziesiętny. Zapisz całą część i wstaw przecinek:

I zapisz licznik części ułamkowej:

Ułamek dziesiętny 5,03 odczytuje się w następujący sposób:

„Pięć punkt trzy”

„Setki”, ponieważ w mianowniku części ułamkowej liczby mieszanej znajduje się liczba 100.

Przykład 3. Zamień liczbę mieszaną na dziesiętną.

Z poprzednich przykładów dowiedzieliśmy się, że aby pomyślnie zamienić liczbę mieszaną na ułamek dziesiętny, liczba cyfr w liczniku ułamka i liczba zer w mianowniku ułamka muszą być takie same.

Przed zamianą liczby mieszanej na ułamek dziesiętny należy nieco zmodyfikować jej część ułamkową, a mianowicie upewnić się, że liczba cyfr w liczniku części ułamkowej i liczba zer w mianowniku części ułamkowej są równe To samo.

Przede wszystkim patrzymy na liczbę zer w mianowniku części ułamkowej. Widzimy, że są trzy zera:

Naszym zadaniem jest uporządkowanie trzech cyfr w liczniku części ułamkowej. Mamy już jedną cyfrę - jest to liczba 2. Pozostaje dodać jeszcze dwie cyfry. Będą to dwa zera. Dodaj je przed liczbą 2. W rezultacie liczba zer w mianowniku i liczba cyfr w liczniku będą takie same:

Teraz możesz zacząć konwertować tę liczbę mieszaną na ułamek dziesiętny. Najpierw zapisujemy całą część i stawiamy przecinek:

i natychmiast zapisz licznik części ułamkowej

3,002

Widzimy, że liczba cyfr po przecinku i liczba zer w mianowniku części ułamkowej liczby mieszanej są takie same.

Ułamek dziesiętny 3,002 odczytuje się w następujący sposób:

„Trzy i pół tysięczne”

„Tysięczne”, ponieważ w mianowniku części ułamkowej liczby mieszanej znajduje się liczba 1000.

Zamiana ułamków zwykłych na dziesiętne

Ułamki zwykłe o mianownikach 10, 100, 1000 lub 10000 można również konwertować na ułamki dziesiętne. Ponieważ ułamek zwykły nie ma części całkowitej, najpierw wpisz 0, następnie wstaw przecinek i zapisz licznik części ułamkowej.

Tutaj również liczba zer w mianowniku i liczba cyfr w liczniku muszą być takie same. Dlatego należy zachować ostrożność.

Przykład 1.

Brakuje całej części, dlatego najpierw wpisujemy 0 i stawiamy przecinek:

Teraz patrzymy na liczbę zer w mianowniku. Widzimy, że jest jedno zero. A licznik ma jedną cyfrę. Oznacza to, że możesz bezpiecznie kontynuować ułamek dziesiętny, wpisując cyfrę 5 po przecinku

W powstałym ułamku dziesiętnym 0,5 liczba cyfr po przecinku i liczba zer w mianowniku ułamka są takie same. Oznacza to, że ułamek jest poprawnie przetłumaczony.

Ułamek dziesiętny 0,5 odczytuje się w następujący sposób:

„Piąty punkt zerowy”

Przykład 2. Zamień ułamek zwykły na dziesiętny.

Brakuje całej części. Najpierw piszemy 0 i stawiamy przecinek:

Teraz patrzymy na liczbę zer w mianowniku. Widzimy, że są dwa zera. A licznik ma tylko jedną cyfrę. Aby liczba cyfr i liczba zer były takie same, dodaj jedno zero w liczniku przed liczbą 2. Wtedy ułamek przyjmie postać . Teraz liczba zer w mianowniku i liczba cyfr w liczniku są takie same. Możesz więc kontynuować ułamek dziesiętny:

W powstałym ułamku dziesiętnym 0,02 liczba cyfr po przecinku i liczba zer w mianowniku ułamka są takie same. Oznacza to, że ułamek jest poprawnie przetłumaczony.

Ułamek dziesiętny 0,02 odczytuje się w następujący sposób:

„Przecinek zerowy dwa.”

Przykład 3. Zamień ułamek zwykły na dziesiętny.

Wpisz 0 i wstaw przecinek:

Teraz liczymy liczbę zer w mianowniku ułamka. Widzimy, że jest pięć zer, a licznik ma tylko jedną cyfrę. Aby liczba zer w mianowniku była taka sama, jak liczba cyfr w liczniku, należy dodać cztery zera w liczniku przed liczbą 5:

Teraz liczba zer w mianowniku i liczba cyfr w liczniku są takie same. Możemy więc kontynuować ułamek dziesiętny. Wpisz licznik ułamka zwykłego po przecinku

W powstałym ułamku dziesiętnym 0,00005 liczba cyfr po przecinku i liczba zer w mianowniku ułamka są takie same. Oznacza to, że ułamek jest poprawnie przetłumaczony.

Ułamek dziesiętny 0,00005 odczytuje się w następujący sposób:

„Przecinek zerowy pięćset tysięcznych”.

Zamiana ułamków niewłaściwych na dziesiętne

Ułamek niewłaściwy to ułamek, w którym licznik jest większy od mianownika. Istnieją ułamki niewłaściwe, których mianownikiem są liczby 10, 100, 1000 lub 10000. Takie ułamki można zamienić na ułamki dziesiętne. Ale przed zamianą na ułamek dziesiętny takie ułamki należy rozdzielić na część całkowitą.

Przykład 1.

Ułamek jest ułamkiem niewłaściwym. Aby zamienić taki ułamek na ułamek dziesiętny, należy najpierw zaznaczyć całą jego część. Przypomnijmy sobie jak wyodrębnić całą część ułamków niewłaściwych. Jeśli zapomniałeś, radzimy wrócić do niego i przestudiować go.

Podkreślmy więc całą część w ułamku niewłaściwym. Przypomnijmy, że ułamek oznacza dzielenie - w w tym przypadku dzieląc liczbę 112 przez liczbę 10

Spójrzmy na ten obrazek i złóżmy nową liczbę mieszaną, jak zestaw konstrukcyjny dla dzieci. Liczba 11 będzie częścią całkowitą, liczba 2 będzie licznikiem części ułamkowej, a liczba 10 będzie mianownikiem części ułamkowej.

Mamy liczbę mieszaną. Zamieńmy to na ułamek dziesiętny. I już wiemy, jak zamienić takie liczby na ułamki dziesiętne. Najpierw zapisz całą część i wstaw przecinek:

Teraz liczymy liczbę zer w mianowniku części ułamkowej. Widzimy, że jest jedno zero. A licznik części ułamkowej ma jedną cyfrę. Oznacza to, że liczba zer w mianowniku części ułamkowej i liczba cyfr w liczniku części ułamkowej są takie same. Daje nam to możliwość natychmiastowego zapisania licznika części ułamkowej po przecinku:

W powstałym ułamku dziesiętnym 11,2 liczba cyfr po przecinku i liczba zer w mianowniku ułamka są takie same. Oznacza to, że ułamek jest poprawnie przetłumaczony.

Oznacza to, że po przeliczeniu na ułamek dziesiętny ułamek niewłaściwy otrzymuje wartość 11,2.

Ułamek dziesiętny 11,2 odczytuje się w następujący sposób:

„Jedenaście punkt dwa”.

Przykład 2. Zamień ułamek niewłaściwy na dziesiętny.

Jest to ułamek niewłaściwy, ponieważ licznik jest większy od mianownika. Można go jednak przekonwertować na ułamek dziesiętny, ponieważ w mianowniku znajduje się liczba 100.

Najpierw wybierzmy całą część tego ułamka. Aby to zrobić, podziel 450 przez 100 narożnikiem:

Zbierzmy nową liczbę mieszaną - otrzymamy . Wiemy już, jak zamienić liczby mieszane na ułamki dziesiętne.

Zapisz całą część i wstaw przecinek:

Teraz liczymy liczbę zer w mianowniku części ułamkowej i liczbę cyfr w liczniku części ułamkowej. Widzimy, że liczba zer w mianowniku i liczba cyfr w liczniku są takie same. Daje nam to możliwość natychmiastowego zapisania licznika części ułamkowej po przecinku:

W powstałym ułamku dziesiętnym 4,50 liczba cyfr po przecinku i liczba zer w mianowniku ułamka są takie same. Oznacza to, że ułamek jest poprawnie przetłumaczony.

Oznacza to, że po przeliczeniu na ułamek dziesiętny ułamek niewłaściwy otrzymuje wartość 4,50.

Podczas rozwiązywania problemów, jeśli na końcu ułamka dziesiętnego znajdują się zera, można je odrzucić. W naszej odpowiedzi usuńmy także zero. Wtedy otrzymamy 4,5

To jedna z interesujących rzeczy związanych z ułamkami dziesiętnymi. Polega to na tym, że zera znajdujące się na końcu ułamka nie nadają temu ułamkowi żadnej wagi. Innymi słowy, miejsca po przecinku 4,50 i 4,5 są równe. Postawmy między nimi znak równości:

4,50 = 4,5

Powstaje pytanie: dlaczego tak się dzieje? W końcu 4,50 i 4,5 wyglądają jak różne ułamki. Cały sekret tkwi w podstawowej właściwości ułamków, którą badaliśmy wcześniej. Spróbujemy udowodnić, dlaczego ułamki dziesiętne 4,50 i 4,5 są równe, ale po przestudiowaniu następnego tematu, który nazywa się „przeliczaniem ułamka dziesiętnego na liczbę mieszaną”.

Konwersja ułamka dziesiętnego na liczbę mieszaną

Dowolny ułamek dziesiętny można zamienić z powrotem na liczbę mieszaną. Aby to zrobić, wystarczy umieć czytać ułamki dziesiętne. Na przykład przekonwertujmy 6,3 na liczbę mieszaną. 6,3 to sześć i trzy punkty. Najpierw zapisujemy sześć liczb całkowitych:

i obok trzech dziesiątych:

Przykład 2. Zamień liczbę dziesiętną 3,002 na liczbę mieszaną

3,002 to trzy całe i dwie tysięczne. Najpierw zapisujemy trzy liczby całkowite

a obok piszemy dwie tysięczne:

Przykład 3. Zamień liczbę dziesiętną 4,50 na liczbę mieszaną

4,50 to cztery i pół pięćdziesiąt. Zapisz cztery liczby całkowite

i następne pięćdziesiąt setnych:

Przy okazji przypomnijmy sobie ostatni przykład z poprzedniego tematu. Powiedzieliśmy, że liczby dziesiętne 4,50 i 4,5 są równe. Powiedzieliśmy również, że zero można odrzucić. Spróbujmy udowodnić, że ułamki dziesiętne 4,50 i 4,5 są równe. Aby to zrobić, zamieniamy oba ułamki dziesiętne na liczby mieszane.

Po przeliczeniu na liczbę mieszaną liczba dziesiętna 4,50 staje się , a liczba dziesiętna 4,5

Mamy dwie liczby mieszane i . Zamieńmy te liczby mieszane na ułamki niewłaściwe:

Teraz mamy dwa ułamki i . Czas przypomnieć sobie podstawową własność ułamka, która mówi, że gdy mnożymy (lub dzielimy) licznik i mianownik ułamka przez tę samą liczbę, wartość ułamka się nie zmienia.

Podzielmy pierwszy ułamek przez 10

Mamy i to jest drugi ułamek. Oznacza to, że oba są sobie równe i mają tę samą wartość:

Spróbuj użyć kalkulatora, aby podzielić najpierw 450 przez 100, a następnie 45 przez 10. To będzie zabawne.

Zamiana ułamka dziesiętnego na ułamek zwykły

Każdy ułamek dziesiętny można zamienić z powrotem na ułamek zwykły. Aby to zrobić, wystarczy umieć czytać ułamki dziesiętne. Na przykład zamieńmy 0,3 na ułamek zwykły. 0,3 to zero przecinek trzy. Najpierw zapisujemy zero liczb całkowitych:

i obok trzech dziesiątych 0. Zero nie jest tradycyjnie zapisywane, więc ostateczną odpowiedzią nie będzie 0, ale po prostu .

Przykład 2. Zamień ułamek dziesiętny 0,02 na ułamek zwykły.

0,02 to zero przecinek dwa. Nie zapisujemy zera, więc od razu zapisujemy dwie setne

Przykład 3. Zamień 0,00005 na ułamek

0,00005 to zero przecinek pięć. Nie zapisujemy zera, więc od razu zapisujemy pięćset tysięcznych

Czy podobała Ci się lekcja?
Dołącz do naszej nowej grupy VKontakte i zacznij otrzymywać powiadomienia o nowych lekcjach