Oczekiwanie i wariancja to najczęściej stosowane cechy liczbowe zmienna losowa. Charakteryzują najważniejsze cechy rozkładu: jego położenie i stopień rozproszenia. W wielu praktycznych problemach pełna, wyczerpująca charakterystyka zmiennej losowej – prawo dystrybucji – albo w ogóle nie może zostać uzyskana, albo w ogóle nie jest potrzebna. W takich przypadkach ogranicza się do przybliżonego opisu zmiennej losowej za pomocą charakterystyk numerycznych.

Wartość oczekiwana jest często nazywana po prostu średnią wartością zmiennej losowej. Rozproszenie zmiennej losowej jest cechą dyspersji, rozproszenia zmiennej losowej wokół jej oczekiwań matematycznych.

Oczekiwanie dyskretnej zmiennej losowej

Przyjrzyjmy się koncepcji oczekiwań matematycznych, opierając się najpierw na mechanicznej interpretacji rozkładu dyskretnej zmiennej losowej. Niech masa jednostkowa zostanie rozłożona pomiędzy punktami osi x X1 , X 2 , ..., X N, a każdemu punktowi materialnemu odpowiada masa P1 , P 2 , ..., P N. Należy wybrać jeden punkt na osi odciętych, charakteryzujący położenie całego układu punktów materialnych, z uwzględnieniem ich mas. Naturalnym jest, że za taki punkt przyjmuje się środek masy układu punktów materialnych. Jest to średnia ważona zmiennej losowej X, do której odcięta jest każdy punkt XI wchodzi z „wagą” równą odpowiedniemu prawdopodobieństwu. Uzyskana w ten sposób średnia wartość zmiennej losowej X nazywa się jego oczekiwaniem matematycznym.

Matematyczne oczekiwanie dyskretnej zmiennej losowej jest sumą iloczynów wszystkich jej możliwych wartości i prawdopodobieństw tych wartości:

Przykład 1. Zorganizowano loterię, w której wygrywają obie strony. Wygranych jest 1000, z czego 400 to 10 rubli. 300 - 20 rubli za sztukę. 200 - 100 rubli za sztukę. i 100 - 200 rubli za sztukę. Co średni rozmiar wygrana dla tych, którzy kupili jeden los?

Rozwiązanie. Średnie wygrane znajdziemy, jeśli całkowita kwota wygrane, które są równe 10*400 + 20*300 + 100*200 + 200*100 = 50 000 rubli, podziel przez 1000 (całkowita kwota wygranych). Następnie otrzymujemy 50000/1000 = 50 rubli. Jednak wyrażenie służące do obliczenia średnich wygranych można przedstawić w następującej formie:

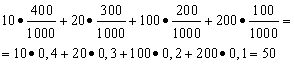
Z drugiej strony w tych warunkach zwycięska wielkość jest zmienną losową, która może przyjmować wartości 10, 20, 100 i 200 rubli. z prawdopodobieństwem równym odpowiednio 0,4; 0,3; 0,2; 0,1. Dlatego oczekiwana średnia wypłata równa sumie iloczyny wielkości wygranych i prawdopodobieństwa ich otrzymania.

Przykład 2. Wydawca podjął decyzję o wydaniu nowej książki. Planuje sprzedać książkę za 280 rubli, z czego sam otrzyma 200, 50 – księgarnia i 30 – autor. Tabela zawiera informacje o kosztach wydania książki i prawdopodobieństwie sprzedaży określonej liczby egzemplarzy książki.

Znajdź oczekiwany zysk wydawcy.

Rozwiązanie. Zmienna losowa „zysk” jest równa różnicy między przychodem ze sprzedaży a kosztem kosztów. Na przykład, jeśli sprzedanych zostanie 500 egzemplarzy książki, dochód ze sprzedaży wyniesie 200 * 500 = 100 000, a koszt publikacji to 225 000 rubli. Tym samym wydawcy grozi strata w wysokości 125 000 rubli. Poniższa tabela podsumowuje oczekiwane wartości zmiennej losowej – zysk:

Numer	Zysk XI	Prawdopodobieństwo PI	XI P I
500	-125000	0,20	-25000
1000	-50000	0,40	-20000
2000	100000	0,25	25000
3000	250000	0,10	25000
4000	400000	0,05	20000
Całkowity:		1,00	25000

W ten sposób otrzymujemy wartość oczekiwana zyski wydawcy:

.

Przykład 3. Prawdopodobieństwo trafienia jednym strzałem P= 0,2. Określ zużycie pocisków, które zapewniają matematyczną oczekiwaną liczbę trafień równą 5.

Rozwiązanie. Z tego samego matematycznego wzoru oczekiwań, którego używaliśmy do tej pory, wyrażamy X- zużycie powłoki:

.

Przykład 4. Określ oczekiwanie matematyczne zmiennej losowej X liczba trafień trzema strzałami, jeżeli prawdopodobieństwo trafienia przy każdym strzale P = 0,4 .

Wskazówka: znajdź prawdopodobieństwo wartości zmiennych losowych według Wzór Bernoulliego .

Właściwości oczekiwań matematycznych

Rozważmy właściwości oczekiwań matematycznych.

Właściwość 1. Matematyczne oczekiwanie na stałą wartość jest równe tej stałej:

Własność 2. Stały współczynnik można wyjąć z matematycznego znaku oczekiwania:

Własność 3. Oczekiwanie matematyczne sumy (różnicy) zmiennych losowych jest równe sumie (różnicy) ich oczekiwań matematycznych:

Właściwość 4. Oczekiwanie matematyczne iloczynu zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych:

Własność 5. Jeśli wszystkie wartości zmiennej losowej X zmniejszyć (zwiększyć) o tę samą liczbę Z, to jego oczekiwanie matematyczne zmniejszy się (zwiększy) o tę samą liczbę:

Kiedy nie możesz ograniczyć się tylko do oczekiwań matematycznych

W większości przypadków jedynie oczekiwanie matematyczne nie jest w stanie w wystarczającym stopniu scharakteryzować zmiennej losowej.

Niech zmienne losowe X I Y wynikają z następujących praw dystrybucji:

Oznaczający X	Prawdopodobieństwo
-0,1	0,1
-0,01	0,2
0	0,4
0,01	0,2
0,1	0,1

Oznaczający Y	Prawdopodobieństwo
-20	0,3
-10	0,1
0	0,2
10	0,1
20	0,3

Oczekiwania matematyczne tych wielkości są takie same – równe zeru:

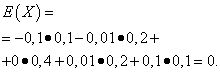
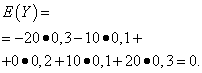
Jednak ich schematy dystrybucji są różne. Losowa wartość X może przyjmować jedynie wartości niewiele różniące się od oczekiwań matematycznych oraz zmienną losową Y może przyjmować wartości znacznie odbiegające od oczekiwań matematycznych. Podobny przykład: średnia pensja nie pozwala ocenić środek ciężkości wysoko i nisko opłacani pracownicy. Innymi słowy, na podstawie oczekiwań matematycznych nie można ocenić, jakie odchylenia od nich, przynajmniej średnio, są możliwe. Aby to zrobić, musisz znaleźć wariancję zmiennej losowej.

Wariancja dyskretnej zmiennej losowej

Zmienność Dyskretna zmienna losowa X nazywa się oczekiwaniem matematycznym kwadratu jego odchylenia od oczekiwania matematycznego:

Odchylenie standardowe zmiennej losowej X wartość arytmetyczną pierwiastka kwadratowego z jej wariancji nazywa się:

.

Przykład 5. Obliczanie wariancji i odchyleń standardowych zmiennych losowych X I Y, których prawa dystrybucji podano w tabelach powyżej.

Rozwiązanie. Matematyczne oczekiwania zmiennych losowych X I Y, jak stwierdzono powyżej, są równe zeru. Zgodnie ze wzorem dyspersji przy mi(X)=mi(y)=0 otrzymujemy:

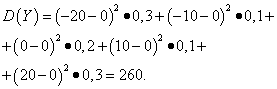
Następnie odchylenia standardowe zmiennych losowych X I Y makijaż

.

Zatem przy tych samych oczekiwaniach matematycznych wariancja zmiennej losowej X bardzo mała, ale zmienna losowa Y- istotne. Jest to konsekwencja różnic w ich rozmieszczeniu.

Przykład 6. Inwestor posiada 4 alternatywne projekty inwestycyjne. Tabela podsumowuje oczekiwany zysk w tych projektach z odpowiednim prawdopodobieństwem.

Projekt 1	Projekt 2	Projekt 3	Projekt 4
500, P=1	1000, P=0,5	500, P=0,5	500, P=0,5
	0, P=0,5	1000, P=0,25	10500, P=0,25
		0, P=0,25	9500, P=0,25

Znajdź matematyczne oczekiwanie, wariancję i odchylenie standardowe dla każdej alternatywy.

Rozwiązanie. Pokażmy, jak obliczane są te wartości dla 3. alternatywy:

Tabela podsumowuje znalezione wartości dla wszystkich alternatyw.

Wszystkie alternatywy mają te same oczekiwania matematyczne. Oznacza to, że w dłuższej perspektywie wszyscy mają takie same dochody. Odchylenie standardowe można interpretować jako miarę ryzyka – im jest ono wyższe, tym większe ryzyko inwestycji. Inwestor, który nie chce dużego ryzyka, wybierze projekt 1, ponieważ ma najmniejsze odchylenie standardowe (0). Jeśli inwestor woli ryzyko i wysokie zyski w krótkim czasie, to wybierze projekt z największym odchylenie standardowe- projekt 4.

Właściwości dyspersyjne

Przedstawmy właściwości dyspersji.

Właściwość 1. Wariancja stałej wartości wynosi zero:

Własność 2. Stały współczynnik można usunąć ze znaku dyspersji podnosząc go do kwadratu:

.

Własność 3. Wariancja zmiennej losowej jest równa matematycznemu oczekiwaniu kwadratu tej wartości, od którego odejmuje się kwadrat matematycznego oczekiwania samej wartości:

,

Gdzie .

Właściwość 4. Wariancja sumy (różnicy) zmiennych losowych jest równa sumie (różnicy) ich wariancji:

Przykład 7. Wiadomo, że dyskretna zmienna losowa X przyjmuje tylko dwie wartości: −3 i 7. Ponadto znane jest oczekiwanie matematyczne: mi(X) = 4 . Znajdź wariancję dyskretnej zmiennej losowej.

Rozwiązanie. Oznaczmy przez P prawdopodobieństwo, z jakim zmienna losowa przyjmuje wartość X1 = −3 . Następnie prawdopodobieństwo wartości X2 = 7 będzie 1- P. Wyprowadźmy równanie na oczekiwanie matematyczne:

mi(X) = X 1 P + X 2 (1 − P) = −3P + 7(1 − P) = 4 ,

gdzie otrzymujemy prawdopodobieństwa: P= 0,3 i 1 − P = 0,7 .

Prawo rozkładu zmiennej losowej:

X	−3	7
P	0,3	0,7

Wariancję tej zmiennej losowej obliczamy korzystając ze wzoru z własności 3 dyspersji:

D(X) = 2,7 + 34,3 − 16 = 21 .

Znajdź samodzielnie matematyczne oczekiwanie zmiennej losowej, a następnie spójrz na rozwiązanie

Przykład 8. Dyskretna zmienna losowa X przyjmuje tylko dwie wartości. Przyjmuje większą z wartości 3 z prawdopodobieństwem 0,4. Ponadto znana jest wariancja zmiennej losowej D(X) = 6 . Znajdź matematyczne oczekiwanie zmiennej losowej.

Przykład 9. W urnie znajduje się 6 kul białych i 4 czarne. Z urny wylosowano 3 kule. Liczba białych kul wśród wylosowanych kul jest dyskretną zmienną losową X. Znajdź matematyczne oczekiwanie i wariancję tej zmiennej losowej.

Rozwiązanie. Losowa wartość X może przyjmować wartości 0, 1, 2, 3. Z odpowiednich prawdopodobieństw można obliczyć reguła mnożenia prawdopodobieństwa. Prawo rozkładu zmiennej losowej:

X	0	1	2	3
P	1/30	3/10	1/2	1/6

Stąd matematyczne oczekiwanie tej zmiennej losowej:

M(X) = 3/10 + 1 + 1/2 = 1,8 .

Wariancja danej zmiennej losowej wynosi:

D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .

Oczekiwanie i wariancja ciągłej zmiennej losowej

W przypadku ciągłej zmiennej losowej mechaniczna interpretacja oczekiwań matematycznych zachowa to samo znaczenie: środek masy jednostki masy rozłożonej w sposób ciągły na osi x z gęstością F(X). W przeciwieństwie do dyskretnej zmiennej losowej, której argumentem jest funkcja XI zmienia się gwałtownie; w przypadku ciągłej zmiennej losowej argument zmienia się w sposób ciągły. Ale matematyczne oczekiwanie ciągłej zmiennej losowej jest również powiązane z jej średnią wartością.

Aby znaleźć matematyczne oczekiwanie i wariancję ciągłej zmiennej losowej, należy znaleźć całki oznaczone . Jeśli podana jest funkcja gęstości ciągłej zmiennej losowej, to wchodzi ona bezpośrednio do całki. Jeśli podana jest funkcja rozkładu prawdopodobieństwa, to różniczkując ją, musisz znaleźć funkcję gęstości.

Nazywa się ją średnią arytmetyczną wszystkich możliwych wartości ciągłej zmiennej losowej oczekiwanie matematyczne, oznaczone lub .

Rozwiązanie.

Jako miarę rozproszenia wartości zmiennych losowych stosujemy dyspersja

Dyspersja (słowo dyspersja oznacza „rozpraszanie”) jest miara rozproszenia wartości zmiennych losowych w stosunku do oczekiwań matematycznych. Dyspersja to matematyczne oczekiwanie kwadratu odchylenia zmiennej losowej od jej oczekiwań matematycznych

Jeśli zmienna losowa jest dyskretna i ma nieskończony, ale przeliczalny zbiór wartości, to

jeśli szereg po prawej stronie równości jest zbieżny.

Właściwości dyspersji.

• 1. Wariancja stałej wartości wynosi zero
• 2. Wariancja sumy zmiennych losowych jest równa sumie wariancji
• 3. Ze znaku kwadratu dyspersji można odjąć stały współczynnik

Wariancja różnicy zmiennych losowych jest równa sumie wariancji

Właściwość ta jest konsekwencją właściwości drugiej i trzeciej. Różnice mogą się tylko sumować.

Wygodnie jest obliczyć dyspersję za pomocą wzoru, który można łatwo uzyskać, korzystając z właściwości dyspersji

Wariancja jest zawsze dodatnia.

Różnica jest wymiar kwadratowy wymiar samej zmiennej losowej, co nie zawsze jest wygodne. Dlatego ilość

Odchylenie standardowe(odchylenie standardowe lub standard) zmiennej losowej to wartość arytmetyczna pierwiastka kwadratowego jej wariancji

Rzuć dwie monety o nominałach 2 i 5 rubli. Jeśli moneta wyląduje jako herb, wówczas przyznawane jest zero punktów, a jeśli wyląduje jako liczba, to liczba punktów równa nominałowi monety. Znajdź matematyczne oczekiwanie i wariancję liczby punktów.

Rozwiązanie. Znajdźmy najpierw rozkład zmiennej losowej X – liczbę punktów. Wszystkie kombinacje - (2;5),(2;0),(0;5),(0;0) - są jednakowo prawdopodobne, a prawo podziału jest następujące:

Wartość oczekiwana:

Wariancję znajdujemy za pomocą wzoru

dlaczego obliczamy

Przykład 2.

Znajdź nieznane prawdopodobieństwo R, matematyczne oczekiwanie i wariancja dyskretnej zmiennej losowej, dany stół rozkłady prawdopodobieństwa

Znajdujemy matematyczne oczekiwanie i wariancję:

M(X) = 00,0081 + 10,0756 + 20,2646 + 3 0,4116 + +40,2401=2,8

Aby obliczyć dyspersję, używamy wzoru (19.4)

D(X) = 020 ,0081 + 120,0756 + 220,2646 + 320,4116 + 420,2401 - 2,82 = 8,68 -

Przykład 3. Dwóch równie silnych zawodników organizuje turniej, który trwa albo do pierwszego zwycięstwa jednego z nich, albo do rozegrania pięciu partii. Prawdopodobieństwo wygrania jednej partii przez każdego ze zawodników wynosi 0,3, a prawdopodobieństwo remisu wynosi 0,4. Znajdź prawo dystrybucji, oczekiwanie matematyczne i rozrzut liczby rozegranych partii.

Rozwiązanie. Losowa wartość X- liczba rozegranych gier przyjmuje wartości od 1 do 5, tj.

Określmy prawdopodobieństwo zakończenia meczu. Mecz zakończy się w pierwszym secie, jeżeli któryś z zawodników tej drużyny zwycięży. Prawdopodobieństwo wygranej wynosi

R(1) = 0,3+0,3 =0,6.

Jeśli był remis (prawdopodobieństwo remisu wynosi 1 - 0,6 = 0,4), mecz jest kontynuowany. Mecz zakończy się drugą partią, jeśli pierwsza zakończyła się remisem, a druga wygrana. Prawdopodobieństwo

R(2) = 0,4 0,6=0,24.

Podobnie mecz zakończy się trzecią partią, jeśli były dwa remisy z rzędu i znowu ktoś wygrał

R(3) = 0,4 0,4 0,6 = 0,096. R(4)= 0,4 0,4 0,4 0,6=0,0384.

Piąta gra jest ostatnią w dowolnej wersji.

R(5)= 1 - (R(1)+R(2)+R(3)+R(4)) = 0,0256.

Umieśćmy wszystko w tabeli. Prawo rozkładu zmiennej losowej „liczba wygranych gier” ma postać

Wartość oczekiwana

Wariancję obliczamy korzystając ze wzoru (19.4)

Standardowe rozkłady dyskretne.

Rozkład dwumianowy. Zastosujmy schemat eksperymentalny Bernoulliego: N identyczne niezależne eksperymenty, w każdym z nich zdarzenie A mogą występować ze stałym prawdopodobieństwem P i nie pojawi się z prawdopodobieństwem

(patrz wykład 18).

Liczba wystąpień zdarzenia A w tych N eksperymentów istnieje dyskretna zmienna losowa X, których możliwe wartości to:

0; 1; 2; ... ;M; ... ; N.

Prawdopodobieństwo wystąpienia M zdarzenia A w określonej serii N eksperymenty i prawo rozkładu takiej zmiennej losowej podaje wzór Bernoulliego (patrz wykład 18)

Charakterystyka numeryczna zmiennej losowej X rozdzielone zgodnie z prawem dwumianu:

Jeśli N jest świetny (), to kiedy formuła (19.6) wchodzi do formuły

oraz tabelaryczną funkcję Gaussa (tabela wartości funkcji Gaussa znajduje się na końcu wykładu 18).

W praktyce często nie samo prawdopodobieństwo wystąpienia jest istotne. M wydarzenia A w konkretnym serialu od N eksperymentów i prawdopodobieństwa zdarzenia A nie mniej się pojawi

razy i nie więcej niż razy, tj. prawdopodobieństwo, że X przyjmie wartości

Aby to zrobić, musimy podsumować prawdopodobieństwa

Jeśli N jest świetny (), to kiedy formuła (19.9) zamienia się w formułę przybliżoną

funkcja tabelaryczna. Tabele znajdują się na końcu wykładu 18.

Korzystając z tabel, należy to wziąć pod uwagę

Przykład 1. Samochód zbliżający się do skrzyżowania może z równym prawdopodobieństwem kontynuować jazdę dowolną z trzech dróg: A, B lub C. Do skrzyżowania zbliża się pięć samochodów. Znajdź średnią liczbę samochodów, które będą podróżować drogą A i prawdopodobieństwo, że drogą B pojadą trzy samochody.

Rozwiązanie. Liczba samochodów przejeżdżających każdą drogą jest zmienną losową. Jeśli założymy, że wszystkie samochody zbliżające się do skrzyżowania jadą niezależnie od siebie, to ta zmienna losowa rozkłada się zgodnie z prawem dwumianu z

N= 5 i P = .

Zatem średnia liczba samochodów, które pojadą drogą A, jest zgodna ze wzorem (19,7)

i pożądane prawdopodobieństwo przy

Przykład 2. Prawdopodobieństwo awarii urządzenia podczas każdego testu wynosi 0,1. Przeprowadzono 60 testów urządzenia. Jakie jest prawdopodobieństwo, że awaria urządzenia nastąpi: a) 15 razy; b) nie więcej niż 15 razy?

A. Ponieważ liczba testów wynosi 60, używamy wzoru (19.8)

Zgodnie z tabelą 1 załącznika do wykładu 18 znajdujemy

B. Używamy wzoru (19.10).

Zgodnie z tabelą 2 załącznika do wykładu 18

• - 0,495
• 0,49995

rozkład Poissona) prawo rzadkich zdarzeń). Jeśli N duży i R mały () i produkt itp zachowuje stałą wartość, którą oznaczamy przez l,

wówczas wzór (19.6) staje się wzorem Poissona

Prawo rozkładu Poissona ma postać:

Oczywiście definicja prawa Poissona jest poprawna, ponieważ główna właściwość szeregu dystrybucyjnego

Gotowe, ponieważ suma serii

Rozszerzenie szeregowe funkcji w

Twierdzenie. Matematyczne oczekiwanie i wariancja zmiennej losowej o rozkładzie zgodnym z prawem Poissona pokrywają się i są równe parametrowi tego prawa, tj.

Dowód.

Przykład. Aby promować swoje produkty na rynku, firma umieszcza ulotki w skrzynkach pocztowych. Dotychczasowe doświadczenia pokazują, że w przybliżeniu w jednym przypadku na 2000 następuje zamówienie. Znajdź prawdopodobieństwo, że po umieszczeniu 10 000 ogłoszeń wpłynie co najmniej jedno zamówienie, średnią liczbę otrzymanych zamówień i wariancję liczby otrzymanych zamówień.

Rozwiązanie. Tutaj

Prawdopodobieństwo, że dotrze co najmniej jedno zamówienie, zostanie znalezione na podstawie prawdopodobieństwa wydarzenie przeciwne, tj.

Losowy przepływ wydarzeń. Strumień zdarzeń to sekwencja zdarzeń, które występują w losowych momentach. Typowe przykłady przepływami są awarie w sieciach komputerowych, połączenia w centralach telefonicznych, potoki zapytań o naprawę sprzętu itp.

Przepływ wydarzenia to tzw stacjonarny, jeżeli prawdopodobieństwo, że określona liczba zdarzeń mieści się w przedziale czasu o długości, zależy tylko od długości tego przedziału i nie zależy od położenia przedziału czasu na osi czasu.

Warunek stacjonarności jest spełniony przez przepływ żądań, których charakterystyki probabilistyczne nie zależą od czasu. W szczególności przepływ stacjonarny charakteryzuje się stałą gęstością (średnią liczbą żądań w jednostce czasu). W praktyce często zdarzają się strumienie wniosków, które (przynajmniej przez ograniczony okres czasu) można uznać za stacjonarne. Na przykład przepływ połączeń w miejskiej centrali telefonicznej w okresie od 12 do 13 godzin można uznać za telefon stacjonarny. Tego samego przepływu w ciągu całej doby nie można już uznać za stacjonarny (w nocy natężenie połączeń jest znacznie mniejsze niż w ciągu dnia).

Przepływ zdarzenia nazywane są strumieniem bez żadnych następstw, jeżeli dla dowolnych nienakładających się okresów liczba zdarzeń przypadających na jeden z nich nie zależy od liczby zdarzeń przypadających na pozostałe.

Warunek braku następstw – najbardziej istotny dla najprostszego przepływu – oznacza, że ​​aplikacje wchodzą do systemu niezależnie od siebie. Na przykład potok pasażerów wchodzących na stację metra można uznać za przepływ bez następstw, ponieważ przyczyny, które zdecydowały o przybyciu konkretnego pasażera w takim, a nie innym momencie, z reguły nie są powiązane z podobnymi powodami dla innych pasażerów . Jednakże warunek braku następstw można łatwo naruszyć w wyniku pojawienia się takiej zależności. Na przykład potoku pasażerów opuszczających stację metra nie można już uważać za przepływ bez skutków ubocznych, ponieważ momenty wyjścia pasażerów przybywających tym samym pociągiem są od siebie zależne.

Przepływ wydarzenia to tzw zwykły, jeżeli prawdopodobieństwo wystąpienia dwóch lub więcej zdarzeń w krótkim odstępie czasu t jest znikome w porównaniu z prawdopodobieństwem wystąpienia jednego zdarzenia (w tym względzie prawo Poissona nazywa się prawem rzadkich zdarzeń).

Warunek zwyczajności oznacza, że ​​zamówienia przychodzą pojedynczo, a nie w parach, trójkach itp. Odchylenie wariancji Rozkład Bernoulliego

Na przykład przepływ klientów wchodzących do salonu fryzjerskiego można uznać za niemal zwyczajny. Jeśli w przepływie nadzwyczajnym wnioski przychodzą tylko parami, tylko trojaczkami itd., to nadzwyczajny przepływ można łatwo sprowadzić do zwykłego; Aby to zrobić, wystarczy zamiast strumienia pojedynczych żądań rozważyć strumień par, trojaczków itp. Będzie to trudniejsze, jeśli każde żądanie może losowo okazać się podwójne, potrójne itp. Wtedy trzeba radzić sobie ze strumieniem nie jednorodnych, ale heterogenicznych zdarzeń.

Jeśli strumień zdarzeń ma wszystkie trzy właściwości (tj. stacjonarny, zwyczajny i nie ma następstw), wówczas nazywany jest prostym (lub stacjonarnym strumieniem Poissona). Nazwa „Poissona” wynika z faktu, że jeśli zostaną spełnione wymienione warunki, liczba zdarzeń przypadających na dowolny ustalony przedział czasu zostanie rozłożona na Prawo Poissona

Oto średnia liczba zdarzeń A, pojawiające się w jednostce czasu.

Prawo to jest jednoparametrowe, tj. aby to ustawić, wystarczy znać tylko jeden parametr. Można wykazać, że oczekiwanie i wariancja w prawie Poissona są liczbowo równe:

Przykład. Załóżmy, że w środku dnia roboczego średnia liczba żądań wynosi 2 na sekundę. Jakie jest prawdopodobieństwo, że 1) w ciągu sekundy nie wpłynie żaden wniosek, 2) w ciągu dwóch sekund wpłynie 10 wniosków?

Rozwiązanie. Ponieważ zasadność zastosowania prawa Poissona nie budzi wątpliwości i podany jest jego parametr (= 2), rozwiązanie problemu sprowadza się do zastosowania wzoru Poissona (19.11)

1) T = 1, M = 0:

2) T = 2, M = 10:

Prawo duże liczby. Matematyczną podstawą tego, że wartości zmiennej losowej skupiają się wokół pewnych stałych wartości, jest prawo wielkich liczb.

Historycznie rzecz biorąc, pierwszym sformułowaniem prawa wielkich liczb było twierdzenie Bernoulliego:

„Przy nieograniczonym wzroście liczby identycznych i niezależnych eksperymentów n częstotliwość występowania zdarzenia A zbiega się prawdopodobieństwem z jego prawdopodobieństwem”, tj.

gdzie jest częstością występowania zdarzenia A w n eksperymentach,

W istocie wyrażenie (19.10) oznacza, że ​​przy dużej liczbie eksperymentów częstotliwość występowania zdarzenia A może zastąpić nieznane prawdopodobieństwo tego zdarzenia, a im większa liczba przeprowadzonych eksperymentów, tym p* jest bliższe p. Ciekawy fakt historyczny. K. Pearson rzucił monetą 12 000 razy, a jego herb wypadł 6019 razy (częstotliwość 0,5016). Rzucając 24 000 razy tą samą monetą, otrzymał 12 012 herbów, czyli: częstotliwość 0,5005.

Najważniejszą formą prawa wielkich liczb jest twierdzenie Czebyszewa: przy nieograniczonym wzroście liczby niezależnych eksperymentów o skończonej wariancji i przeprowadzonych w identycznych warunkach, średnia arytmetyczna zaobserwowanych wartości zmiennej losowej zbiega się z prawdopodobieństwem do jej oczekiwań matematycznych. W formie analitycznej twierdzenie to można zapisać w następujący sposób:

Oprócz podstawowego znaczenia teoretycznego twierdzenie Czebyszewa ma również ważne zastosowania praktyczne, na przykład w teorii pomiaru. Po wykonaniu n pomiarów określonej wielkości X, uzyskaj różne, niepasujące wartości X 1, X 2, ..., xn. Dla przybliżonej wartości mierzonej wielkości X przyjąć średnią arytmetyczną zaobserwowanych wartości

W której, Im więcej eksperymentów zostanie przeprowadzonych, tym dokładniejszy będzie wynik. Faktem jest, że rozproszenie ilości maleje wraz ze wzrostem liczby przeprowadzanych eksperymentów, ponieważ

D(X 1) = D(X 2)=…= D(xn) D(X) , To

Z zależności (19.13) wynika, że ​​nawet przy dużej niedokładności przyrządów pomiarowych (duża wartość), zwiększając liczbę pomiarów, można uzyskać wynik z dowolnie dużą dokładnością.

Korzystając ze wzoru (19.10) można znaleźć prawdopodobieństwo, że częstotliwość statystyczna odbiega od prawdopodobieństwa o nie więcej niż

Przykład. Prawdopodobieństwo zdarzenia w każdej próbie wynosi 0,4. Ile testów należy przeprowadzić, aby z prawdopodobieństwem nie mniejszym niż 0,8 oczekiwać, że względna częstotliwość zdarzenia będzie odbiegać od prawdopodobieństwa w wartości bezwzględnej o mniej niż 0,01?

Rozwiązanie. Według wzoru (19.14)

dlatego zgodnie z tabelą istnieją dwa zastosowania

stąd, N 3932.

W poprzednim przedstawiliśmy szereg wzorów, które pozwalają znaleźć charakterystyki liczbowe funkcji, gdy znane są prawa rozkładu argumentów. Jednak w wielu przypadkach, aby znaleźć numeryczne charakterystyki funkcji, nie jest konieczna nawet znajomość praw rozkładu argumentów, wystarczy znać tylko niektóre ich charakterystyki liczbowe; jednocześnie zasadniczo obejdziemy się bez żadnych praw podziału. Wyznaczanie cech liczbowych funkcji na podstawie zadanych cech liczbowych argumentów jest szeroko stosowane w teorii prawdopodobieństwa i może znacznie uprościć rozwiązanie szeregu problemów. Większość tych uproszczonych metod dotyczy funkcji liniowych; jednakże niektóre elementarne funkcje nieliniowe również pozwalają na podobne podejście.

W niniejszym artykule przedstawimy szereg twierdzeń o numerycznych charakterystykach funkcji, które razem reprezentują bardzo prosty aparat do obliczania tych charakterystyk, mający zastosowanie w szerokim zakresie warunków.

1. Matematyczne oczekiwanie wartości nielosowej

Sformułowana właściwość jest dość oczywista; można to udowodnić, uznając zmienną nielosową za specjalny rodzaj losowości z jedynką możliwe znaczenie z prawdopodobieństwem jedno; wówczas zgodnie z ogólnym wzorem na oczekiwanie matematyczne:

.

2. Wariancja wielkości nielosowej

Jeśli jest to wartość nielosowa, to

3. Podstawienie znaku oczekiwania matematycznego wartością nielosową

, (10.2.1)

oznacza to, że wartość nielosową można przyjąć jako znak oczekiwań matematycznych.

Dowód.

a) Dla ilości nieciągłych

b) Dla ilości ciągłych

.

4. Podstawienie znaku rozproszenia i odchylenia standardowego wartością nielosową

Jeśli jest wielkością nielosową i jest losowa, to

, (10.2.2)

to znaczy, że nielosową wartość można usunąć ze znaku rozproszenia, podnosząc go do kwadratu.

Dowód. Z definicji wariancji

Konsekwencja

,

to znaczy, że wartość nielosową można usunąć ze znaku odchylenia standardowego przez jego wartość bezwzględną. Dowód uzyskujemy wyciągając pierwiastek kwadratowy ze wzoru (10.2.2) i biorąc pod uwagę, że r.s.o. - wartość znacząco dodatnia.

5. Matematyczne oczekiwanie sumy zmiennych losowych

Udowodnijmy, że dla dowolnych dwóch zmiennych losowych i

to znaczy, że matematyczne oczekiwanie sumy dwóch zmiennych losowych jest równe sumie ich matematycznych oczekiwań.

Właściwość ta znana jest jako twierdzenie o dodawaniu oczekiwań matematycznych.

Dowód.

a) Niech będzie układem nieciągłych zmiennych losowych. Zastosuj do sumy zmiennych losowych ogólna formuła(10.1.6) dla matematycznego oczekiwania funkcji dwóch argumentów:

.

Ho reprezentuje nic innego jak całkowite prawdopodobieństwo, że ilość przyjmie wartość:

;

stąd,

.

Udowodnimy to podobnie

,

i twierdzenie zostało udowodnione.

b) Niech będzie układem ciągłych zmiennych losowych. Według wzoru (10.1.7)

. (10.2.4)

Przekształćmy pierwszą z całek (10.2.4):

;

podobnie

,

i twierdzenie zostało udowodnione.

Należy szczególnie zaznaczyć, że twierdzenie o dodawaniu oczekiwań matematycznych obowiązuje dla dowolnych zmiennych losowych – zarówno zależnych, jak i niezależnych.

Twierdzenie o dodawaniu oczekiwań matematycznych jest uogólniane na dowolną liczbę terminów:

, (10.2.5)

to znaczy, że matematyczne oczekiwanie sumy kilku zmiennych losowych jest równe sumie ich matematycznych oczekiwań.

Aby to udowodnić, wystarczy zastosować metodę indukcji zupełnej.

6. Oczekiwanie matematyczne funkcja liniowa

Rozważmy funkcję liniową kilku losowych argumentów:

gdzie są współczynnikami nielosowymi. Udowodnijmy to

, (10.2.6)

tj. matematyczne oczekiwanie funkcji liniowej jest równe tej samej funkcji liniowej oczekiwań matematycznych argumentów.

Dowód. Korzystając z twierdzenia o dodawaniu m.o. oraz zasadę umieszczania nielosowej wielkości poza znakiem m.o, otrzymujemy:

.

7. Wyśwodctę sumę zmiennych losowych

Wariancja sumy dwóch zmiennych losowych jest równa sumie ich wariancji plus dwukrotność momentu korelacji:

Dowód. Oznaczmy

Zgodnie z twierdzeniem o dodawaniu oczekiwań matematycznych

Przejdźmy od zmiennych losowych do odpowiednich zmiennych wyśrodkowanych. Odejmując równość (10.2.9) wyraz po wyrazie od równości (10.2.8), otrzymujemy:

Z definicji wariancji

co było do okazania

Wzór (10.2.7) na wariancję sumy można uogólnić na dowolną liczbę wyrazów:

, (10.2.10)

gdzie jest moment korelacji wielkości, znak pod sumą oznacza, że ​​sumowanie rozciąga się na wszystkie możliwe kombinacje parami zmiennych losowych .

Dowód jest podobny do poprzedniego i wynika ze wzoru na kwadrat wielomianu.

Wzór (10.2.10) można zapisać w innej formie:

, (10.2.11)

gdzie podwójna suma rozciąga się na wszystkie elementy macierzy korelacji układu wielkości , zawierający zarówno momenty korelacji, jak i wariancje.

Jeśli wszystkie zmienne losowe , zawarte w systemie, są nieskorelowane (tzn. gdy ), wzór (10.2.10) przyjmuje postać:

, (10.2.12)

to znaczy wariancja sumy nieskorelowanych zmiennych losowych jest równa sumie wariancji składników.

Stanowisko to znane jest jako twierdzenie o dodawaniu wariancji.

8. Wariancja funkcji liniowej

Rozważmy funkcję liniową kilku zmiennych losowych.

gdzie są ilościami nielosowymi.

Udowodnijmy, że dyspersja tej funkcji liniowej wyraża się wzorem

, (10.2.13)

gdzie jest momentem korelacji wielkości , .

Dowód. Wprowadźmy oznaczenie:

. (10.2.14)

Stosując wzór (10.2.10) na rozproszenie sumy na prawą stronę wyrażenia (10.2.14) i biorąc pod uwagę, że , otrzymujemy:

gdzie jest moment korelacji wielkości:

.

Obliczmy ten moment. Mamy:

;

podobnie

Podstawiając to wyrażenie do (10.2.15) otrzymujemy wzór (10.2.13).

W szczególnym przypadku, gdy wszystkie ilości są nieskorelowane, wzór (10.2.13) przyjmuje postać:

, (10.2.16)

to znaczy wariancja funkcji liniowej nieskorelowanych zmiennych losowych jest równa sumie iloczynów kwadratów współczynników i wariancji odpowiednich argumentów.

9. Matematyczne oczekiwanie iloczynu zmiennych losowych

Oczekiwanie matematyczne iloczynu dwóch zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych plus moment korelacji:

Dowód. Zaczniemy od definicji momentu korelacji:

Przekształćmy to wyrażenie, korzystając z właściwości oczekiwań matematycznych:

co jest oczywiście równoważne formule (10.2.17).

Jeżeli zmienne losowe nie są ze sobą skorelowane, wówczas wzór (10.2.17) przyjmuje postać:

to znaczy, że matematyczne oczekiwanie iloczynu dwóch nieskorelowanych zmiennych losowych jest równe iloczynowi ich matematycznych oczekiwań.

Stanowisko to znane jest jako twierdzenie o mnożeniu oczekiwań matematycznych.

Wzór (10.2.17) to nic innego jak wyrażenie drugiego mieszanego momentu centralnego układu poprzez drugi mieszany moment moment początkowy i oczekiwania matematyczne:

. (10.2.19)

Wyrażenie to jest często stosowane w praktyce przy obliczaniu momentu korelacji w ten sam sposób, w jaki dla jednej zmiennej losowej wariancję często oblicza się na podstawie drugiego momentu początkowego i oczekiwania matematycznego.

Twierdzenie o mnożeniu oczekiwań matematycznych uogólnia się na dowolną liczbę czynników, tylko w tym przypadku do jego zastosowania nie wystarczy, że wielkości są nieskorelowane, ale wymagane jest, aby pewne wyższe momenty mieszane, których liczba zależy na liczbie terminów w produkcie znikają. Warunki te są z pewnością spełnione, jeśli zmienne losowe zawarte w iloczynie są niezależne. W tym przypadku

, (10.2.20)

to znaczy matematyczne oczekiwanie iloczynu niezależnych zmiennych losowych jest równe iloczynowi ich matematycznych oczekiwań.

Twierdzenie to można łatwo udowodnić poprzez indukcję zupełną.

10. Wariancja iloczynu niezależnych zmiennych losowych

Udowodnimy to dla wielkości niezależnych

Dowód. Oznaczmy . Z definicji wariancji

Ponieważ ilości są niezależne i

Gdy są niezależne, ilości są również niezależne; stąd,

,

Ale nie ma nic więcej niż drugi początkowy moment wielkości i dlatego wyraża się poprzez rozproszenie:

;

podobnie

.

Podstawiając te wyrażenia do wzoru (10.2.22) i sprowadzając podobne wyrazy, dochodzimy do wzoru (10.2.21).

W przypadku mnożenia wyśrodkowanych zmiennych losowych (zmiennych z oczekiwaniami matematycznymi równymi zero) wzór (10.2.21) przyjmuje postać:

, (10.2.23)

to znaczy wariancja iloczynu niezależnych wyśrodkowanych zmiennych losowych jest równa iloczynowi ich wariancji.

11. Wyższe momenty sumy zmiennych losowych

W niektórych przypadkach konieczne jest obliczenie największych momentów sumy niezależnych zmiennych losowych. Udowodnimy pewne powiązane tu zależności.

1) Jeżeli wielkości są niezależne, to

Dowód.

skąd, zgodnie z twierdzeniem o mnożeniu oczekiwań matematycznych

Ale pierwszym centralnym momentem dowolnej wielkości jest zero; dwa środkowe człony znikają, a wzór (10.2.24) zostaje udowodniony.

Relację (10.2.24) można łatwo uogólnić poprzez indukcję do dowolnej liczby niezależnych terminów:

. (10.2.25)

2) Czwarty moment centralny sumy dwóch niezależnych zmiennych losowych wyraża się wzorem

gdzie są wariancje ilości i .

Dowód jest całkowicie podobny do poprzedniego.

Stosując metodę indukcji zupełnej łatwo udowodnić uogólnienie wzoru (10.2.26) na dowolną liczbę niezależnych wyrazów.