Dom Ból zęba Rozwinięcie funkcji okresowej w trygonometryczny szereg Fouriera. Rozwinięcie szeregu Fouriera w cosinusach

Ból zęba

Rozwinięcie funkcji okresowej w trygonometryczny szereg Fouriera. Rozwinięcie szeregu Fouriera w cosinusach

Które są już dość nudne. I czuję, że nadszedł moment, w którym ze strategicznych zasobów teorii należy wydobyć nowe konserwy. Czy można w jakiś inny sposób rozwinąć tę funkcję w szereg? Na przykład wyrazić odcinek linii prostej za pomocą sinusów i cosinusów? Wydaje się to niewiarygodne, ale tak pozornie odległe funkcje mogą być
„zjednoczenie”. Oprócz znanych stopni z teorii i praktyki istnieją inne podejścia do rozwijania funkcji w szereg.

Na tej lekcji poznamy trygonometrię. niedaleko Fouriera, poruszymy kwestię jego zbieżności i sumy oraz oczywiście przeanalizujemy liczne przykłady rozwinięcia funkcji w szereg Fouriera. Szczerze chciałem nazwać artykuł „Seria Fouriera dla opornych”, ale byłoby to nieszczere, ponieważ rozwiązanie problemów wymagałoby znajomości innych gałęzi analizy matematycznej i pewnego doświadczenia praktycznego. Dlatego preambuła będzie przypominać szkolenie astronautów =)

Po pierwsze, powinieneś podejść do badania materiałów stronicowych w doskonałej formie. Śpiący, wypoczęty i trzeźwy. Bez mocnych emocji w związku ze złamaną łapką chomika i obsesyjne myśli o trudach życia ryby akwariowe. Jednakże szereg Fouriera nie jest trudny do zrozumienia zadania praktyczne wymagają po prostu wzmożonej koncentracji uwagi – idealnie byłoby, gdybyś całkowicie odciął się od bodźców zewnętrznych. Sytuację pogarsza fakt, że nie ma łatwego sposobu sprawdzenia rozwiązania i odpowiedzi. Dlatego jeśli Twoje zdrowie jest poniżej średniej, lepiej zrobić coś prostszego. Czy to prawda?

Po drugie, przed lotem w kosmos musisz przestudiować tablicę przyrządów statek kosmiczny. Zacznijmy od wartości funkcji, które należy kliknąć na maszynie:

Dla dowolnej wartości przyrodniczej:

1) . Rzeczywiście, sinusoida „zszywa” oś x przez każde „pi”:
. W przypadku ujemnych wartości argumentu wynik będzie oczywiście taki sam: .

2) . Ale nie wszyscy o tym wiedzieli. Cosinus „pi” jest odpowiednikiem „migacza”:

Argument negatywny nie zmienia sprawy: .

Być może to wystarczy.

I po trzecie, kochany korpusie kosmonautów, trzeba umieć... integrować się.
W szczególności śmiało podejmuj funkcję pod znak różniczkowy, całkuj przez części i bądź w zgodzie ze wzorem Newtona-Leibniza. Rozpocznijmy ważne ćwiczenia przed lotem. Kategorycznie nie radzę go pomijać, aby później nie zgiąć się w nieważkości:

Przykład 1

Oblicz całki oznaczone

gdzie bierze walory przyrodnicze.

Rozwiązanie: Całkowanie odbywa się po zmiennej „x” i na tym etapie zmienną dyskretną „en” traktuje się jako stałą. We wszystkich całkach podstawiamy funkcję pod znak różniczkowy:

Krótka wersja rozwiązania, na którą warto celować, wygląda następująco:

Przyzwyczajmy się do tego:

Pozostałe cztery punkty robisz sam. Staraj się podejść do zadania sumiennie i zapisz całki w skrócie. Przykładowe rozwiązania na końcu lekcji.

Po wykonaniu ćwiczeń JAKOŚĆ zakładamy skafandry kosmiczne
i szykuję się do startu!

Rozwinięcie funkcji w szereg Fouriera na przedziale

Rozważmy pewną funkcję zdefiniowaną przynajmniej w przedziale (i ewentualnie w większym przedziale). Jeśli funkcja ta jest całkowalna na przedziale, to można ją rozwinąć w trygonometryczny szereg Fouriera:
, gdzie znajdują się tzw Współczynniki Fouriera.

W tym przypadku liczbę nazywa się okresem rozkładu, a liczbę nazywa się półokresem rozkładu.

Jest oczywiste, że w ogólnym przypadku szereg Fouriera składa się z sinusów i cosinusów:

Rzeczywiście, napiszmy to szczegółowo:

Wyraz zerowy szeregu zwykle zapisuje się w postaci .

Współczynniki Fouriera oblicza się za pomocą następujących wzorów:

Doskonale rozumiem, że osoby rozpoczynające naukę tematu nadal nie są pewne nowych terminów: okres rozkładu, półcykl, Współczynniki Fouriera itp. Nie panikuj, to nie jest porównywalne z ekscytacją przed wyjazdem w przestrzeń kosmiczną. Rozumiemy wszystko w poniższym przykładzie, przed wykonaniem którego logiczne jest zadanie palących pytań praktycznych:

Co musisz zrobić w poniższych zadaniach?

Rozwiń funkcję w szereg Fouriera. Dodatkowo często trzeba zobrazować wykres funkcji, wykres sumy szeregu, sumy częściowej, a w przypadku wyrafinowanych fantazji profesorskich zrobić coś innego.

Jak rozwinąć funkcję w szereg Fouriera?

Zasadniczo musisz znaleźć Współczynniki Fouriera, czyli ułożyć i obliczyć trzy całki oznaczone.

Proszę przepisać do zeszytu ogólną postać szeregu Fouriera i trzy działające wzory. Bardzo się cieszę, że niektórzy odwiedzający witrynę realizują swoje dziecięce marzenie o zostaniu astronautą na moich oczach =)

Przykład 2

Rozwiń funkcję w szereg Fouriera na przedziale. Skonstruuj wykres, wykres sumy szeregu i sumy częściowej.

Rozwiązanie: Pierwsza część zadania polega na rozwinięciu funkcji w szereg Fouriera.

Początek jest standardowy, koniecznie zapisz, że:

W tym zadaniu okres ekspansji jest półokresowy.

Rozwińmy funkcję w szereg Fouriera na przedziale:

Stosując odpowiednie wzory, znajdujemy Współczynniki Fouriera. Teraz musisz skomponować i obliczyć trzy całki oznaczone. Dla wygody ponumeruję punkty:

1) Pierwsza całka jest najprostsza, wymaga jednak również gałek ocznych:

2) Skorzystaj z drugiej formuły:

Całka ta jest dobrze znana i jest rozpatrywana w częściach:

Przy znalezieniu wykorzystano metodę subsumowania funkcji pod znak różniczkowy.

W rozważanym zadaniu wygodniej jest od razu zastosować wzór na całkowanie przez części w całce oznaczonej :

Kilka uwag technicznych. Po pierwsze, po zastosowaniu wzoru całe wyrażenie należy ująć w duże nawiasy, ponieważ przed całką pierwotną znajduje się stała. Nie straćmy jej! Nawiasy można rozwinąć w dowolnym dalszym kroku; zrobiłem to w ostateczności. W pierwszym „kawałku” Przy podstawiewaniu zachowujemy szczególną ostrożność; jak widać, stała nie jest używana, a granice całkowania są podstawiane do iloczynu. Ta czynność jest zaznaczona w nawiasach kwadratowych. Cóż, całkę drugiego „fragmentu” wzoru z zadania szkoleniowego znasz ;-)

A co najważniejsze – ekstremalna koncentracja!

3) Szukamy trzeciego współczynnika Fouriera:

Otrzymuje się krewną poprzedniej całki, którą można również całkować przez części:

Ten przypadek jest trochę bardziej skomplikowany, dalsze kroki opiszę krok po kroku:

(1) Całe wyrażenie ujęliśmy w duże nawiasy. Nie chciałem wydawać się nudny, zbyt często tracą stałość.

(2) W w tym przypadku Natychmiast otworzyłem te duże nawiasy. Szczególna uwaga Poświęcamy się pierwszemu „kawałkowi”: ciągłemu dymieniu na uboczu i nie uczestniczeniu w zastępowaniu granic integracji ( i ) w produkcie. Ze względu na bałagan w zapisie ponownie zaleca się podkreślenie tej akcji nawiasami kwadratowymi. Z drugim „kawałkiem” wszystko jest prostsze: tutaj ułamek pojawił się po otwarciu dużych nawiasów, a stała - w wyniku całkowania znanej całki ;-)

(3) Przekształcenia przeprowadzamy w nawiasach kwadratowych, a w prawej całce podstawiamy granice całkowania.

(4) Z nawiasów kwadratowych usuwamy „migające światło”: , a następnie otwieramy nawiasy wewnętrzne: .

(5) Usuwamy 1 i –1 w nawiasach i dokonujemy ostatecznych uproszczeń.

Wreszcie znaleziono wszystkie trzy współczynniki Fouriera:

Podstawmy je do wzoru :

Jednocześnie nie zapomnij podzielić na pół. W ostatnim kroku stała („minus dwa”), która nie zależy od „en”, jest wyjmowana poza sumę.

W ten sposób otrzymaliśmy rozwinięcie funkcji w szereg Fouriera na przedziale:

Przeanalizujmy zagadnienie zbieżności szeregu Fouriera. Wyjaśnię w szczególności teorię Twierdzenie Dirichleta, dosłownie „na palcach”, więc jeśli potrzebujesz ścisłych sformułowań, zapoznaj się z podręcznikiem analiza matematyczna (na przykład 2. tom Bohana lub 3. tom Fichtenholtza, ale jest to trudniejsze).

Druga część problemu wymaga narysowania wykresu, wykresu sumy szeregu i wykresu sumy częściowej.

Wykres funkcji to zwykła linia prosta na płaszczyźnie, narysowana czarną linią przerywaną:

Obliczmy sumę szeregu. Jak wiadomo, szeregi funkcyjne zbiegają się do funkcji. W naszym przypadku skonstruowany szereg Fouriera dla dowolnej wartości „x” zbiegnie się do funkcji, która jest pokazana na czerwono. Ta funkcja w punktach ma nieciągłości pierwszego rodzaju, ale jest w nich również zdefiniowany (czerwone kropki na rysunku)

Zatem: . Łatwo zauważyć, że funkcja zauważalnie różni się od pierwotnej, dlatego we wpisie Zamiast znaku równości używana jest tylda.

Przeanalizujmy algorytm wygodny do konstruowania sumy szeregu.

W przedziale środkowym szereg Fouriera zbiega się z samą funkcją (środkowy czerwony segment pokrywa się z czarną przerywaną linią funkcji liniowej).

Porozmawiajmy teraz trochę o naturze rozważanego rozwinięcia trygonometrycznego. Szereg Fouriera uwzględnione są tylko funkcje okresowe (stała, sinus i cosinus), a więc suma szeregu jest także funkcją okresową.

Co to oznacza w naszym konkretnym przykładzie? A to oznacza, że suma szeregu – jest z pewnością okresowy i czerwony odcinek przedziału musi być powtarzany w nieskończoność po lewej i prawej stronie.

Myślę, że znaczenie wyrażenia „okres rozkładu” stało się wreszcie jasne. Krótko mówiąc, za każdym razem sytuacja się powtarza.

W praktyce zwykle wystarcza przedstawienie trzech okresów rozkładu, jak pokazano na rysunku. Cóż, a także „pniaki” sąsiednich okresów - aby było jasne, że wykres trwa.

Szczególnie interesujące są punkty nieciągłości pierwszego rodzaju. W takich punktach szereg Fouriera zbiega się do izolowanych wartości, które znajdują się dokładnie w środku „skoku” nieciągłości (czerwone kropki na rysunku). Jak znaleźć rzędne tych punktów? Najpierw znajdźmy rzędną „górnego piętra”: w tym celu obliczamy wartość funkcji w skrajnym na prawo punkcie środkowego okresu rozbudowy: . Aby obliczyć rzędną „dolnego piętra”, najłatwiej jest skorzystać z ekstremum lewa wartość z tego samego okresu: . Rzędną wartości średniej jest średnia arytmetyczna sumy „góry i dołu”: . Przyjemnym faktem jest to, że podczas konstruowania rysunku od razu zobaczysz, czy środek jest obliczony poprawnie, czy niepoprawnie.

Skonstruujmy sumę cząstkową szeregu i jednocześnie powtórzmy znaczenie terminu „zbieżność”. Motyw znany jest także z lekcji o sumie szeregu liczbowego. Opiszmy szczegółowo nasze bogactwo:

Aby utworzyć sumę częściową, musisz napisać zero + dwa kolejne wyrazy szeregu. To jest,

Rysunek przedstawia wykres funkcji zielony i jak widać dość szczelnie „owija” całą ilość. Jeśli weźmiemy pod uwagę częściową sumę pięciu wyrazów serii, wówczas wykres tej funkcji jeszcze dokładniej przybliży czerwone linie, jeśli będzie sto wyrazów, wówczas „zielony wąż” faktycznie całkowicie połączy się z czerwonymi segmentami, itp. Zatem szereg Fouriera zbiega się do swojej sumy.

Warto zauważyć, że każda suma częściowa jest funkcją ciągłą, ale suma całkowita szeregu jest nadal nieciągła.

W praktyce nie jest tak rzadkością konstruowanie wykresu sumy częściowej. Jak to zrobić? W naszym przypadku konieczne jest rozważenie funkcji na odcinku, obliczenie jej wartości na końcach odcinka i w punktach pośrednich (im więcej punktów uwzględnisz, tym dokładniejszy będzie wykres). Następnie należy zaznaczyć te punkty na rysunku i dokładnie narysować wykres na okresie, a następnie „odtworzyć” go na sąsiednie przedziały. Jak inaczej? Przecież aproksymacja to także funkcja okresowa... ...w pewnym sensie jej wykres przypomina mi płynny rytm serca na wyświetlaczu urządzenia medycznego.

Wykonanie konstrukcji oczywiście nie jest zbyt wygodne, ponieważ trzeba zachować szczególną ostrożność, zachowując dokładność nie mniejszą niż pół milimetra. Zadowolę jednak czytelników, którzy nie radzą sobie z rysowaniem - w „prawdziwym” problemie nie zawsze konieczne jest wykonanie rysunku; w około 50% przypadków konieczne jest rozwinięcie funkcji w szereg Fouriera i to wszystko .

Po ukończeniu rysunku wykonujemy zadanie:

Odpowiedź :

W wielu problemach funkcja cierpi na nieciągłość pierwszego rodzaju już w okresie rozwinięcia:

Przykład 3

Rozwiń funkcję podaną na przedziale w szereg Fouriera. Narysuj wykres funkcji i sumy całkowitej szeregu.

Proponowana funkcja jest określona fragmentarycznie (i uwaga, tylko w segmencie) i cierpi na nieciągłość pierwszego rodzaju w punkcie . Czy można obliczyć współczynniki Fouriera? Bez problemu. Zarówno lewa, jak i prawa strona funkcji są całkowalne na swoich przedziałach, dlatego całki w każdym z trzech wzorów należy przedstawić jako sumę dwóch całek. Zobaczmy na przykład, jak to się robi dla zerowego współczynnika:

Druga całka okazała się równa zeru, co zmniejszyło pracę, ale nie zawsze tak jest.

Pozostałe dwa współczynniki Fouriera opisano podobnie.

Jak pokazać sumę szeregu? Na lewym przedziale rysujemy odcinek prosty, a na przedziale odcinek prosty (pogrubioną czcionką zaznaczamy odcinek osi). Oznacza to, że w przedziale rozwinięcia suma szeregu pokrywa się z funkcją wszędzie z wyjątkiem trzech „złych” punktów. W punkcie nieciągłości funkcji szereg Fouriera zbiega się do izolowanej wartości, która znajduje się dokładnie w środku „skoku” nieciągłości. Nietrudno to dostrzec ustnie: granica lewa: , granica prawa: i oczywiście współrzędna środka wynosi 0,5.

Ze względu na okresowość sumy obraz należy „pomnożyć” na sąsiednie okresy, w szczególności to samo należy przedstawić w odstępach i . Jednocześnie w punktach szereg Fouriera zbiegnie się do wartości mediany.

Tak naprawdę nie ma tu nic nowego.

Spróbuj sam poradzić sobie z tym zadaniem. Przybliżona próbka ostatecznego projektu i rysunek na końcu lekcji.

Rozwinięcie funkcji w szereg Fouriera w dowolnym okresie

Dla dowolnego okresu rozwinięcia, gdzie „el” jest dowolną liczbą dodatnią, wzory na szereg Fouriera i współczynniki Fouriera wyróżniają się nieco bardziej skomplikowanym argumentem dla sinusa i cosinusa:

Jeśli , to otrzymamy wzory przedziałów, od których zaczęliśmy.

Algorytm i zasady rozwiązania problemu są całkowicie zachowane, ale wzrasta złożoność techniczna obliczeń:

Przykład 4

Rozwiń funkcję w szereg Fouriera i wykreśl sumę.

Rozwiązanie: właściwie analogia do przykładu nr 3 z nieciągłością pierwszego rodzaju w punkcie. W tym zadaniu okres ekspansji jest półokresowy. Funkcja jest zdefiniowana tylko na połowie przedziału, ale to nie zmienia sprawy - ważne jest, aby oba elementy funkcji były całkowalne.

Rozwińmy tę funkcję w szereg Fouriera:

Ponieważ funkcja jest nieciągła w początku, każdy współczynnik Fouriera należy oczywiście zapisać jako sumę dwóch całek:

1) Napiszę pierwszą całkę tak szczegółowo, jak to możliwe:

2) Uważnie przyglądamy się powierzchni Księżyca:

Całkę drugą obliczamy przez części:

Na co powinniśmy zwrócić szczególną uwagę po otwarciu kontynuacji rozwiązania gwiazdką?

Po pierwsze, nie tracimy pierwszej całki , gdzie natychmiast stosujemy znak różniczkowy. Po drugie, nie zapomnij o niefortunnej stałej przed dużymi nawiasami i nie myl znaków podczas korzystania ze wzoru . Duże zamki są nadal wygodniejsze do otwarcia od razu w następnym kroku.

Reszta jest kwestią techniki; trudności mogą wynikać jedynie z niewystarczającego doświadczenia w rozwiązywaniu całek.

Tak, nie bez powodu oburzyli się wybitni koledzy francuskiego matematyka Fouriera - jak on odważył się układać funkcje w szeregi trygonometryczne?! =) Swoją drogą, chyba każdego interesuje praktyczne znaczenie danego zadania. Nad tym pracował sam Fourier model matematyczny przewodność cieplną, a następnie serię nazwaną jego imieniem zaczęto wykorzystywać do badania wielu procesów okresowych, które są widoczne i niewidoczne w otaczającym świecie. Teraz, nawiasem mówiąc, złapałem się na myśli, że nieprzypadkowo porównałem wykres drugiego przykładu z okresowym rytmem serca. Zainteresowani mogą zapoznać się z praktycznym zastosowaniem Transformata Fouriera w źródłach zewnętrznych. ...Chociaż lepiej tego nie robić - zostanie zapamiętane jako Pierwsza Miłość =)

3) Biorąc pod uwagę wielokrotnie wspominane słabe ogniwa, spójrzmy na trzeci współczynnik:

Całkujmy przez części:

Podstawmy znalezione współczynniki Fouriera do wzoru , nie zapominając o podzieleniu współczynnika zerowego na pół:

Narysujmy sumę szeregu. Powtórzmy krótko procedurę: konstruujemy linię prostą na przedziale i prostą na przedziale. Jeżeli wartość „x” wynosi zero, stawiamy punkt w środku „skoku” luki i „replikujemy” wykres dla sąsiednich okresów:

Na „skrzyżowaniach” okresów suma będzie również równa środkom „skoku” luki.

Gotowy. Przypomnę, że sama funkcja jest pod warunkiem określonym tylko w połowie przedziału i oczywiście pokrywa się z sumą szeregu na przedziałach

Odpowiedź :

Czasami funkcja podana fragmentarycznie jest ciągła w okresie ekspansji. Najprostszy przykład: . Rozwiązanie (patrz Bohan tom 2) tak samo jak w dwóch poprzednich przykładach: pomimo ciągłości funkcji w punkcie, każdy współczynnik Fouriera wyraża się jako sumę dwóch całek.

W przedziale ekspansji może występować więcej punktów nieciągłości I rodzaju i/lub punktów „łącznych” grafu (dwa, trzy i ogólnie dowolne finał ilość). Jeśli funkcja jest całkowalna w każdej części, to można ją również rozwinąć w szereg Fouriera. Ale z praktycznego doświadczenia nie pamiętam tak okrutnej rzeczy. Istnieją jednak zadania trudniejsze niż te właśnie rozważone, a na końcu artykułu znajdują się linki do szeregów Fouriera o zwiększonej złożoności dla każdego.

Tymczasem zrelaksujmy się, odchylmy w fotelach i kontemplujmy niekończące się przestrzenie gwiazd:

Przykład 5

Rozwiń funkcję w szereg Fouriera na przedziale i wykreśl sumę szeregu.

W tym zadaniu funkcja jest ciągła w połowie przedziału rozwinięcia, co upraszcza rozwiązanie. Wszystko jest bardzo podobne do przykładu nr 2. Ze statku kosmicznego nie ma ucieczki - musisz zdecydować =) Przybliżony przykładowy projekt na końcu lekcji, w załączeniu harmonogram.

Rozwinięcie funkcji parzystych i nieparzystych w szereg Fouriera

W przypadku funkcji parzystych i nieparzystych proces rozwiązywania problemu jest zauważalnie uproszczony. I oto dlaczego. Wróćmy do rozwinięcia funkcji w szereg Fouriera o okresie „dwa pi” i dowolny okres „dwa el” .

Załóżmy, że nasza funkcja jest parzysta. Jak widać, ogólny wyraz szeregu zawiera parzyste cosinusy i nieparzyste sinusy. A jeśli rozwijamy funkcję PARZYSTĄ, to po co nam nieparzyste sinusy?! Zresetujmy niepotrzebny współczynnik: .

Zatem funkcję parzystą można rozszerzyć na szereg Fouriera tylko w cosinusach:

Ponieważ całki funkcji parzystych po segmencie całkowania symetrycznym względem zera można podwoić, pozostałe współczynniki Fouriera również są uproszczone.

Dla luki:

Dla dowolnego przedziału:

Przykłady podręczników, które można znaleźć w prawie każdym podręczniku analizy matematycznej, obejmują rozwinięcia funkcji parzystych . Ponadto spotkałem się z nimi kilka razy w mojej osobistej praktyce:

Przykład 6

Funkcja jest podana. Wymagany:

1) rozwiń funkcję w szereg Fouriera z kropką , gdzie jest dowolną liczbą dodatnią;

2) zapisz rozwinięcie przedziału, skonstruuj funkcję i wykreśl sumę całkowitą szeregu.

Rozwiązanie: w pierwszym akapicie zaproponowano rozwiązanie problemu w widok ogólny i jest to bardzo wygodne! Jeśli zajdzie taka potrzeba, po prostu zastąp swoją wartość.

1) W tym zadaniu okres ekspansji jest półokresowy. Podczas dalsze działania, w szczególności podczas całkowania, „el” jest uważane za stałą

Funkcja jest parzysta, co oznacza, że można ją rozwinąć w szereg Fouriera tylko w cosinusach: .

Szukamy współczynników Fouriera za pomocą wzorów . Zwróć uwagę na ich bezwarunkowe zalety. Po pierwsze, integracja odbywa się po dodatnim segmencie rozbudowy, co oznacza, że bezpiecznie pozbywamy się modułu , biorąc pod uwagę tylko „X” z dwóch elementów. Po drugie, integracja jest zauważalnie uproszczona.

Dwa:

Całkujmy przez części:

Zatem:
, natomiast stała , która nie zależy od „en”, jest pobierana poza sumą.

Odpowiedź :

2) Zapiszmy rozwinięcie przedziału, w tym celu w ogólna formuła zastąpić pożądana wartość pół cyklu:

Szeregi Fouriera to reprezentacja dowolnej funkcji z określonym okresem w postaci szeregu. Ogólnie rozwiązanie to nazywa się rozkładem elementu wzdłuż podstawy ortogonalnej. Rozbudowa funkcji na szereg Fouriera jest dość potężnym narzędziem do rozwiązywania różnych problemów ze względu na właściwości tej transformacji podczas całkowania, różniczkowania, a także przesuwania wyrażeń za pomocą argumentu i splotu.

Osoba nieobeznana z wyższą matematyką, a także z pracami francuskiego naukowca Fouriera, najprawdopodobniej nie zrozumie, czym są te „serie” i do czego są potrzebne. Tymczasem ta transformacja została dość zintegrowana z naszym życiem. Używają go nie tylko matematycy, ale także fizycy, chemicy, lekarze, astronomowie, sejsmolodzy, oceanografowie i wielu innych. Przyjrzyjmy się także bliżej pracom wielkiego francuskiego naukowca, który dokonał odkrycia wyprzedzającego swoją epokę.

Człowiek i transformata Fouriera

Jedną z metod (obok analizy i innych) są szeregi Fouriera. Proces ten zachodzi za każdym razem, gdy osoba słyszy dźwięk. Nasze ucho automatycznie dokonuje transformacji cząstki elementarne w ośrodku elastycznym ułożone są w rzędach (wzdłuż widma) kolejne wartości poziomu głośności dla tonów o różnej wysokości. Następnie mózg przekształca te dane w znane nam dźwięki. Wszystko to dzieje się samoistnie bez naszego pragnienia i świadomości, ale aby zrozumieć te procesy, studiowanie wyższej matematyki zajmie kilka lat.

Więcej o transformacie Fouriera

Transformatę Fouriera można przeprowadzić metodami analitycznymi, numerycznymi i innymi. Szereg Fouriera odnosi się do numerycznej metody rozkładu wszelkich procesów oscylacyjnych - od pływów oceanicznych i fal świetlnych po cykle aktywności Słońca (i innych obiektów astronomicznych). Korzystając z tych technik matematycznych, można analizować funkcje, przedstawiając dowolne procesy oscylacyjne jako serię składowych sinusoidalnych, które poruszają się od minimum do maksimum i odwrotnie. Transformata Fouriera jest funkcją opisującą fazę i amplitudę sinusoid odpowiadających określonej częstotliwości. Proces ten można wykorzystać do rozwiązywania bardzo złożonych równań opisujących procesy dynamiczne powstające pod wpływem ciepła, światła lub energia elektryczna. Szeregi Fouriera umożliwiają także wyodrębnienie składowych stałych w złożonych sygnałach oscylacyjnych, co pozwala na prawidłową interpretację obserwacji eksperymentalnych uzyskanych w medycynie, chemii i astronomii.

Tło historyczne

Założycielem tej teorii jest francuski matematyk Jean Baptiste Joseph Fourier. Transformacja ta została później nazwana jego imieniem. Początkowo naukowiec wykorzystał swoją metodę do badania i wyjaśniania mechanizmów przewodnictwa cieplnego - rozprzestrzeniania się ciepła w ciała stałe. Fourier zasugerował, że początkowy nieregularny rozkład można rozłożyć na proste sinusoidy, z których każda będzie miała własne minimum i maksimum temperatury, a także własną fazę. W takim przypadku każdy taki składnik będzie mierzony od minimum do maksimum i odwrotnie. Funkcja matematyczna opisująca górny i dolny szczyt krzywej, a także fazę każdej z harmonicznych, nazywa się transformacją Fouriera wyrażenia rozkładu temperatury. Autor teorii zebrał funkcja ogólna rozkład, który jest trudny do opisania matematycznie, do bardzo wygodnego szeregu cosinus i sinus, które razem dają pierwotny rozkład.

Zasada transformacji i poglądy współczesnych

Współcześni naukowcowi – czołowi matematycy początku XIX wieku – nie akceptowali tej teorii. Głównym zarzutem było twierdzenie Fouriera, że funkcję nieciągłą, opisującą linię prostą lub nieciągłą krzywą, można przedstawić jako sumę wyrażeń sinusoidalnych, które są ciągłe. Jako przykład rozważ krok Heaviside'a: jego wartość wynosi zero na lewo od nieciągłości i jeden na prawo. Funkcja ta opisuje zależność prądu elektrycznego od zmiennej tymczasowej, gdy obwód jest zamknięty. Współcześni ówczesnej teorii nigdy nie spotkali się z podobną sytuacją, w której wyrażenie nieciągłe byłoby opisywane przez kombinację ciągłych, zwyczajnych funkcji, takich jak wykładnicza, sinusoidalna, liniowa lub kwadratowa.

Co zmyliło francuskich matematyków w związku z teorią Fouriera?

Przecież jeśli matematyk miał rację w swoich twierdzeniach, to sumując nieskończony trygonometryczny szereg Fouriera, można uzyskać dokładną reprezentację wyrażenia krokowego, nawet jeśli ma wiele podobnych kroków. Na początku XIX wieku takie stwierdzenie wydawało się absurdalne. Jednak pomimo wszystkich wątpliwości wielu matematyków rozszerzyło zakres badań tego zjawiska, wykraczając poza badanie przewodności cieplnej. Jednak większość naukowców nadal dręczyła pytanie: „Czy suma szeregu sinusoidalnego może się zbiegać dokładna wartość funkcja nieciągła?

Zbieżność szeregu Fouriera: przykład

Kwestia zbieżności pojawia się, gdy konieczne jest zsumowanie nieskończonego szeregu liczb. Aby zrozumieć to zjawisko, rozważmy klasyczny przykład. Czy kiedykolwiek uda ci się dotrzeć do ściany, jeśli każdy kolejny stopień będzie o połowę mniejszy od poprzedniego? Załóżmy, że jesteś dwa metry od celu, pierwszy krok prowadzi do połowy, następny do trzech czwartych, a po piątym pokonasz prawie 97 procent drogi. Jednak niezależnie od tego, ile kroków wykonasz, nie osiągniesz zamierzonego celu w ścisłym sensie matematycznym. Za pomocą obliczeń numerycznych można udowodnić, że ostatecznie możliwe jest zbliżenie się na określoną odległość. Dowód ten jest równoznaczny z wykazaniem, że suma połowy, jednej czwartej itd. będzie dążyć do jedności.

Kwestia konwergencji: drugie przyjście lub urządzenie Lorda Kelvina

Zagadnienie to zostało ponownie podniesione pod koniec XIX wieku, kiedy próbowano wykorzystać szeregi Fouriera do przewidywania intensywności pływów. W tym czasie Lord Kelvin wynalazł urządzenie, które było analogiem urządzenie komputerowe, co pozwoliło marynarzom wojskowym i handlowym na śledzenie tego naturalnego zjawiska. Mechanizm ten wyznaczał zestawy faz i amplitud na podstawie tabeli wysokości pływów i odpowiadających im punktów czasowych, dokładnie mierzonych w danym porcie przez cały rok. Każdy parametr był składową sinusoidalną wyrażenia wysokości pływu i był jednym ze składników regularnych. Pomiary zostały wprowadzone do przyrządu obliczeniowego Lorda Kelvina, który zsyntetyzował krzywą prognozującą wysokość wody w funkcji czasu na następny rok. Bardzo szybko podobne krzywe zostały sporządzone dla wszystkich portów świata.

A co jeśli proces zostanie zakłócony przez funkcję nieciągłą?

W tamtym czasie wydawało się oczywiste, że predyktor fal pływowych z dużą liczbą elementów zliczających może obliczyć dużą liczbę faz i amplitud, a tym samym zapewnić dokładniejsze przewidywania. Okazało się jednak, że tego wzorca nie obserwuje się w przypadkach, gdy wyrażenie pływowe, które należy zsyntetyzować, zawierało ostry skok, czyli było nieciągłe. Jeżeli do urządzenia wprowadzone zostaną dane z tabeli momentów czasowych, wówczas oblicza ono kilka współczynników Fouriera. Pierwotna funkcja zostaje przywrócona dzięki składowym sinusoidalnym (zgodnie ze znalezionymi współczynnikami). Rozbieżność pomiędzy wyrazem oryginalnym i zrekonstruowanym można zmierzyć w dowolnym miejscu. Dokonując wielokrotnych obliczeń i porównań widać, że wartość największego błędu nie maleje. Są one jednak zlokalizowane w obszarze odpowiadającym punktowi nieciągłości, a w każdym innym punkcie dążą do zera. W 1899 roku wynik ten został teoretycznie potwierdzony przez Joshuę Willarda Gibbsa z Uniwersytetu Yale.

Zbieżność szeregu Fouriera i rozwój matematyki w ogóle

Analiza Fouriera nie ma zastosowania do wyrażeń zawierających nieskończoną liczbę impulsów w określonym przedziale. Ogólnie rzecz biorąc, szereg Fouriera, jeśli pierwotna funkcja jest reprezentowana przez wynik rzeczywistego wymiar fizyczny, zawsze zbiegają się. Pytania o zbieżność tego procesu dla określonych klas funkcji doprowadziły do powstania nowych gałęzi matematyki, na przykład teorii funkcji uogólnionych. Kojarzona jest z takimi nazwiskami jak L. Schwartz, J. Mikusiński i J. Temple. W ramach tej teorii jest to jasne i precyzyjne podstawa teoretyczna pod takimi wyrażeniami, jak funkcja delta Diraca (opisuje obszar pojedynczego obszaru skupiony w nieskończenie małym sąsiedztwie punktu) i „krok” Heaviside’a. Dzięki tej pracy szeregi Fouriera znalazły zastosowanie do rozwiązywania równań i problemów obejmujących intuicyjne pojęcia: ładunek punktowy, masa punktowa, dipole magnetyczne i obciążenie skupione na belce.

Metoda Fouriera

Szereg Fouriera, zgodnie z zasadami interferencji, rozpoczyna się od rozkładu form złożonych na prostsze. Na przykład zmianę przepływu ciepła tłumaczy się jego przejściem przez różne przeszkody wykonane z materiału termoizolacyjnego o nieregularnym kształcie lub zmianą powierzchni ziemi - trzęsieniem ziemi, zmianą orbity ciało niebieskie- wpływ planet. Z reguły takie równania opisujące proste układy klasyczne można łatwo rozwiązać dla każdej pojedynczej fali. Fourier to pokazał proste rozwiązania można również podsumować, aby uzyskać rozwiązania bardziej złożonych problemów. Z matematycznego punktu widzenia szeregi Fouriera są techniką przedstawiania wyrażenia jako sumy harmonicznych – cosinusa i sinusa. Dlatego tę analizę zwana także analizą harmoniczną.

Szereg Fouriera - technika idealna przed „erą komputerów”

Przed stworzeniem sprzęt komputerowy Technika Fouriera była najlepszą bronią w arsenale naukowców podczas pracy z falową naturą naszego świata. Szereg Fouriera złożona forma pozwala Ci decydować nie tylko proste zadania, które nadają się do bezpośredniego zastosowania praw mechaniki Newtona, ale także podstawowych równań. Większość odkryć nauki Newtona w XIX wieku była możliwa jedynie dzięki technice Fouriera.

Dzisiejszy szereg Fouriera

Wraz z rozwojem komputerów transformaty Fouriera osiągnęły jakościowo nowy poziom. Technika ta jest mocno zakorzeniona w prawie wszystkich obszarach nauki i technologii. Przykładem jest cyfrowy dźwięk i obraz. Jego realizacja stała się możliwa dopiero dzięki teorii opracowanej przez francuskiego matematyka na początku XIX wieku. Tym samym szereg Fouriera w złożonej formie umożliwił dokonanie przełomu w badaniu przestrzeni kosmicznej. Ponadto wpłynął na badania fizyki materiałów półprzewodnikowych i plazmy, akustyki mikrofalowej, oceanografii, radaru i sejsmologii.

Trygonometryczny szereg Fouriera

W matematyce szereg Fouriera jest sposobem przedstawiania wartości dowolnych złożone funkcje suma prostszych. W przypadki ogólne liczba takich wyrażeń może być nieskończona. Co więcej, im bardziej ich liczba jest brana pod uwagę w obliczeniach, tym dokładniejszy jest wynik końcowy. Najczęściej stosowany jako pierwotniak funkcje trygonometryczne cosinus lub sinus. W tym przypadku szeregi Fouriera nazywane są trygonometrycznymi, a rozwiązanie takich wyrażeń nazywa się rozwinięciem harmonicznym. Ta metoda gra ważną rolę w matematyce. Przede wszystkim szereg trygonometryczny umożliwia przedstawianie i badanie funkcji. Jest to główny aparat teorii. Ponadto pozwala rozwiązać szereg problemów z fizyki matematycznej. Wreszcie teoria ta przyczyniła się do rozwoju i powołała do życia szereg bardzo ważnych działów nauka matematyczna(teoria całek, teoria funkcji okresowych). Ponadto posłużył jako punkt wyjścia do opracowania kolejnych funkcji zmiennej rzeczywistej, a także położył podwaliny pod analizę harmoniczną.

Szereg Fouriera funkcji okresowych o okresie 2π.

Szereg Fouriera pozwala nam badać funkcje okresowe poprzez rozkład ich na składowe. Typowe są prądy i napięcia przemienne, przemieszczenia, prędkość i przyspieszenie mechanizmów korbowych oraz fale akustyczne praktyczne przykłady zastosowanie funkcji okresowych w obliczeniach inżynierskich.

Rozwinięcie szeregu Fouriera opiera się na założeniu, że wszystkie funkcje mające znaczenie praktyczne w przedziale -π ≤x≤ π można wyrazić w postaci zbieżnego szeregu trygonometrycznego (szereg uważa się za zbieżny, jeśli ciąg sum cząstkowych składający się z jego wyrazów zbiega się):

Standardowy (=zwykły) zapis poprzez sumę sinx i cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

gdzie a o, a 1, a 2,...,b 1,b 2,.. są stałymi rzeczywistymi, tj.

Gdzie dla zakresu od -π do π współczynniki szeregu Fouriera oblicza się korzystając ze wzorów:

Współczynniki a o , a n i b n nazywane są współczynnikami Fouriera, a jeśli można je znaleźć, to szereg (1) nazywa się szeregiem Fouriera odpowiadającym funkcji f (x). Dla szeregu (1) człon (a 1 cosx+b 1 sinx) nazywany jest pierwszą lub podstawową harmoniczną,

Innym sposobem napisania szeregu jest użycie relacji acosx+bsinx=csin(x+α)

f(x)=a o +c 1 grzech(x+α 1)+c 2 grzech(2x+α 2)+...+c n grzech(nx+α n)

Gdzie a o jest stałą, c 1 = (a 1 2 + b 1 2) 1/2, c n = (a n 2 + b n 2) 1/2 to amplitudy różnych składowych i jest równe a n = arctg a n /b rz.

Dla szeregu (1) wyraz (a 1 cosx+b 1 sinx) lub c 1 sin(x+α 1) nazywany jest pierwszą lub podstawową harmoniczną (a 2 cos2x+b 2 sin2x) lub c 2 sin(2x +α 2) zwana drugą harmoniczną i tak dalej.

Dokładne przedstawienie złożonego sygnału wymaga zwykle nieskończonej liczby terminów. Jednak w wielu praktycznych problemach wystarczy wziąć pod uwagę tylko kilka pierwszych terminów.

Szereg Fouriera funkcji nieokresowych o okresie 2π.

Rozwinięcie funkcji nieokresowych.

Jeżeli funkcja f(x) jest nieokresowa, oznacza to, że nie można jej rozwinąć w szereg Fouriera dla wszystkich wartości x. Możliwe jest jednak zdefiniowanie szeregu Fouriera reprezentującego funkcję w dowolnym zakresie szerokości 2π.

Mając funkcję nieokresową, można skonstruować nową funkcję, wybierając wartości f(x) z pewnego zakresu i powtarzając je poza tym zakresem w odstępach co 2π. Ponieważ nowa funkcja jest okresowa z okresem 2π, można ją rozwinąć w szereg Fouriera dla wszystkich wartości x. Na przykład funkcja f(x)=x nie jest okresowa. Jeśli jednak zajdzie potrzeba rozwinięcia go w szereg Fouriera w przedziale od o do 2π, to poza tym przedziałem konstruowana jest funkcja okresowa o okresie 2π (jak pokazano na poniższym rysunku).

Dla funkcji nieokresowych, takich jak f(x)=x, suma szeregu Fouriera jest równa wartości f(x) we wszystkich punktach danego zakresu, ale nie jest równa f(x) dla punktów poza zasięgiem. Aby znaleźć szereg Fouriera funkcji nieokresowej w zakresie 2π, stosuje się ten sam wzór na współczynniki Fouriera.

Funkcje parzyste i nieparzyste.

Mówią, że funkcja y=f(x) jest nawet jeśli f(-x)=f(x) dla wszystkich wartości x. Wykresy funkcji parzystych są zawsze symetryczne względem osi Y (czyli są odbiciami lustrzanymi). Dwa przykłady funkcji parzystych: y=x2 i y=cosx.

Mówi się, że funkcja y=f(x) jest nieparzysta, jeśli f(-x)=-f(x) dla wszystkich wartości x. Wykresy funkcji nieparzystych są zawsze symetryczne względem początku.

Wiele funkcji nie jest ani parzystych, ani nieparzystych.

Rozwinięcie szeregu Fouriera w cosinusach.

Szereg Fouriera parzystej funkcji okresowej f(x) z okresem 2π zawiera tylko wyrazy cosinus (tj. żadnych wyrazów sinusoidalnych) i może zawierać człon stały. Stąd,

gdzie są współczynniki szeregu Fouriera,

Szereg Fouriera nieparzystej funkcji okresowej f(x) o okresie 2π zawiera tylko wyrazy z sinusami (to znaczy nie zawiera wyrazów z cosinusami).

Stąd,

gdzie są współczynniki szeregu Fouriera,

Szereg Fouriera w połowie cyklu.

Jeśli funkcja jest zdefiniowana dla zakresu, powiedzmy od 0 do π, a nie tylko od 0 do 2π, można ją rozwinąć w szereg tylko w sinusach lub tylko w cosinusach. Powstały szereg Fouriera nazywany jest półcyklowym szeregiem Fouriera.

Jeżeli chcemy otrzymać półcykliczne rozwinięcie Fouriera cosinusów funkcji f(x) w zakresie od 0 do π, to musimy skonstruować parzystą funkcję okresową. Na ryc. Poniżej znajduje się funkcja f(x)=x zbudowana na przedziale od x=0 do x=π. Od nawet funkcjonować symetrycznie względem osi f(x), narysuj linię AB, jak pokazano na ryc. poniżej. Jeśli założymy, że poza rozpatrywanym przedziałem uzyskano trójkątny kształt jest okresowy z okresem 2π, wówczas końcowy wykres wygląda tak, jak pokazano. na ryc. poniżej. Ponieważ musimy uzyskać rozwinięcie Fouriera w cosinusach, jak poprzednio, obliczamy współczynniki Fouriera a o i an

Jeśli chcesz otrzymać półcykliczne rozwinięcie Fouriera w zakresie sinusów funkcji f(x) w zakresie od 0 do π, musisz skonstruować nieparzystą funkcję okresową. Na ryc. Poniżej znajduje się funkcja f(x)=x zbudowana na przedziale od x=0 do x=π. Ponieważ funkcja nieparzysta jest symetryczna względem początku, konstruujemy linię CD, jak pokazano na ryc. Jeśli założymy, że poza rozpatrywanym przedziałem powstały sygnał piłokształtny jest okresowy z okresem 2π, to końcowy wykres ma postać pokazaną na rys. Ponieważ musimy uzyskać rozwinięcie Fouriera półcyklu w postaci sinusów, tak jak poprzednio, obliczamy współczynnik Fouriera. B

Szereg Fouriera dla dowolnego przedziału.

Rozwinięcie funkcji okresowej o okres L.

Funkcja okresowa f(x) powtarza się, gdy x wzrasta o L, tj. f(x+L)=f(x). Przejście z rozważanych wcześniej funkcji o okresie 2π do funkcji o okresie L jest dość proste, ponieważ można tego dokonać poprzez zmianę zmiennej.

Aby znaleźć szereg Fouriera funkcji f(x) w przedziale -L/2≤x≤L/2, wprowadzamy nową zmienną u tak, aby funkcja f(x) miała okres 2π względem u. Jeżeli u=2πx/L, to x=-L/2 dla u=-π i x=L/2 dla u=π. Niech także f(x)=f(Lu/2π)=F(u). Szereg Fouriera F(u) ma postać

(Granice całkowania można zastąpić dowolnym przedziałem o długości L, na przykład od 0 do L)

Szereg Fouriera na półcyklu dla funkcji określonych w przedziale L≠2π.

Dla podstawienia u=πх/L przedział od x=0 do x=L odpowiada przedziałowi od u=0 do u=π. W związku z tym funkcję można rozwinąć w szereg tylko w cosinusach lub tylko w sinusach, tj. w szereg Fouriera w połowie cyklu.

Rozwinięcie cosinusa w zakresie od 0 do L ma postać

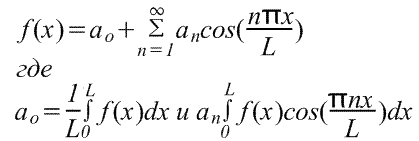
Funkcje, rozkładając je na składowe. Prądy i napięcia przemienne, przemieszczenia, prędkości i przyspieszenia mechanizmów korbowych oraz fale akustyczne są typowymi praktycznymi przykładami wykorzystania funkcji okresowych w obliczeniach inżynierskich.

Standardowy (=zwykły) zapis poprzez sumę sinx i cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

gdzie a o, a 1, a 2,...,b 1,b 2,.. są stałymi rzeczywistymi, tj.

Gdzie dla zakresu od -π do π współczynniki szeregu Fouriera oblicza się korzystając ze wzorów:

Innym sposobem napisania szeregu jest użycie relacji acosx+bsinx=csin(x+α)

f(x)=a o +c 1 grzech(x+α 1)+c 2 grzech(2x+α 2)+...+c n grzech(nx+α n)

Gdzie a o jest stałą, c 1 = (a 1 2 + b 1 2) 1/2, c n = (a n 2 + b n 2) 1/2 to amplitudy różnych składowych i jest równe a n = arctg a n /b rz.

Dla szeregu (1) wyraz (a 1 cosx+b 1 sinx) lub c 1 sin(x+α 1) nazywany jest pierwszą lub podstawową harmoniczną (a 2 cos2x+b 2 sin2x) lub c 2 sin(2x +α 2) zwana drugą harmoniczną i tak dalej.

Dokładne przedstawienie złożonego sygnału wymaga zwykle nieskończonej liczby terminów. Jednak w wielu praktycznych problemach wystarczy wziąć pod uwagę tylko kilka pierwszych terminów.

Szereg Fouriera funkcji nieokresowych o okresie 2π. Rozwinięcie funkcji nieokresowych w szereg Fouriera.

Funkcje parzyste i nieparzyste.

Mówi się, że funkcja y=f(x) jest nieparzysta, jeśli f(-x)=-f(x) dla wszystkich wartości x. Wykresy funkcji nieparzystych są zawsze symetryczne względem początku.

Wiele funkcji nie jest ani parzystych, ani nieparzystych.

Rozwinięcie szeregu Fouriera w cosinusach.

Szereg Fouriera parzystej funkcji okresowej f(x) z okresem 2π zawiera tylko wyrazy cosinus (tj. żadnych wyrazów sinusoidalnych) i może zawierać człon stały. Stąd,

gdzie są współczynniki szeregu Fouriera,

Szereg Fouriera nieparzystej funkcji okresowej f(x) o okresie 2π zawiera tylko wyrazy z sinusami (to znaczy nie zawiera wyrazów z cosinusami).

Stąd,

gdzie są współczynniki szeregu Fouriera,

Szereg Fouriera w połowie cyklu.

Jeżeli chcemy otrzymać półcykliczne rozwinięcie Fouriera cosinusów funkcji f(x) w zakresie od 0 do π, to musimy skonstruować parzystą funkcję okresową. Na ryc. Poniżej znajduje się funkcja f(x)=x zbudowana na przedziale od x=0 do x=π. Ponieważ funkcja parzysta jest symetryczna względem osi f(x), rysujemy linię AB, jak pokazano na ryc. poniżej. Jeśli założymy, że poza rozpatrywanym przedziałem otrzymany kształt trójkąta jest okresowy z okresem 2π, to końcowy wykres wygląda następująco: na ryc. poniżej. Ponieważ musimy uzyskać rozwinięcie Fouriera w cosinusach, jak poprzednio, obliczamy współczynniki Fouriera a o i an

Jeśli chcesz uzyskać funkcje f(x) w zakresie od 0 do π, musisz skonstruować nieparzystą funkcję okresową. Na ryc. Poniżej znajduje się funkcja f(x)=x zbudowana na przedziale od x=0 do x=π. Ponieważ funkcja nieparzysta jest symetryczna względem początku, konstruujemy linię CD, jak pokazano na ryc. Jeśli założymy, że poza rozpatrywanym przedziałem powstały sygnał piłokształtny jest okresowy z okresem 2π, to końcowy wykres ma postać pokazaną na rys. Ponieważ musimy uzyskać rozwinięcie Fouriera półcyklu w postaci sinusów, tak jak poprzednio, obliczamy współczynnik Fouriera. B

Szereg Fouriera dla dowolnego przedziału.

Rozwinięcie funkcji okresowej o okres L.

Gdzie są współczynniki szeregu Fouriera,

Częściej jednak powyższy wzór skutkuje zależnością od x. Ponieważ u=2πx/L, oznacza to du=(2π/L)dx, a granice całkowania wynoszą od -L/2 do L/2 zamiast - π do π. W związku z tym szereg Fouriera zależności od x ma postać

gdzie w przedziale od -L/2 do L/2 są współczynniki szeregu Fouriera,

(Granice całkowania można zastąpić dowolnym przedziałem o długości L, na przykład od 0 do L)

Szereg Fouriera na półcyklu dla funkcji określonych w przedziale L≠2π.

Rozwinięcie cosinusa w zakresie od 0 do L ma postać

Jak wstawić wzory matematyczne do serwisu?

Jeśli kiedykolwiek będziesz musiał dodać jedną lub dwie formuły matematyczne do strony internetowej, najłatwiej to zrobić w sposób opisany w artykule: formuły matematyczne można łatwo wstawić na stronę w postaci obrazów, które są automatycznie generowane przez Wolfram Alpha . Oprócz prostoty, ta uniwersalna metoda pomoże poprawić widoczność witryny w wyszukiwarki. Działa od dawna (i myślę, że będzie działać wiecznie), ale jest już moralnie przestarzały.

Jeśli regularnie korzystasz z formuł matematycznych na swojej stronie, to polecam skorzystać z MathJax – specjalnej biblioteki JavaScript, która wyświetla notację matematyczną w przeglądarkach internetowych przy użyciu znaczników MathML, LaTeX lub ASCIIMathML.

Istnieją dwa sposoby rozpoczęcia korzystania z MathJax: (1) za pomocą prostego kodu możesz szybko podłączyć do swojej witryny skrypt MathJax, który zostanie automatycznie załadowany ze zdalnego serwera w odpowiednim czasie (lista serwerów); (2) pobierz skrypt MathJax ze zdalnego serwera na swój serwer i podłącz go do wszystkich stron swojej witryny. Druga metoda - bardziej złożona i czasochłonna - przyspieszy ładowanie stron Twojej witryny, a jeśli z jakiegoś powodu nadrzędny serwer MathJax stanie się chwilowo niedostępny, nie będzie to miało żadnego wpływu na Twoją witrynę. Pomimo tych zalet wybrałem pierwszą metodę, ponieważ jest prostsza, szybsza i nie wymaga umiejętności technicznych. Podążaj za moim przykładem, a już za 5 minut będziesz mógł korzystać ze wszystkich funkcji MathJax na swojej stronie.

Możesz połączyć skrypt biblioteki MathJax ze zdalnym serwerem, korzystając z dwóch opcji kodu pobranych z głównej witryny MathJax lub ze strony dokumentacji:

Jedną z tych opcji kodu należy skopiować i wkleić do kodu swojej strony internetowej, najlepiej pomiędzy tagami i/lub bezpośrednio po tagu. Według pierwszej opcji MathJax ładuje się szybciej i mniej spowalnia stronę. Ale druga opcja automatycznie monitoruje i ładuje najnowsze wersje MathJax. Jeśli wstawisz pierwszy kod, będzie on wymagał okresowej aktualizacji. Jeśli wstawisz drugi kod, strony będą ładować się wolniej, ale nie będziesz musiał stale monitorować aktualizacji MathJax.

Najłatwiej połączyć się z MathJax w Bloggerze lub WordPressie: w panelu sterowania witryny dodaj widżet przeznaczony do wstawiania kodu JavaScript innej firmy, skopiuj do niego pierwszą lub drugą wersję kodu pobierania przedstawionego powyżej i umieść widżet bliżej na początek szablonu (nawiasem mówiąc, nie jest to wcale konieczne, ponieważ skrypt MathJax jest ładowany asynchronicznie). To wszystko. Teraz poznaj składnię znaczników MathML, LaTeX i ASCIIMathML, a będziesz gotowy do wstawiania formuł matematycznych na stronach internetowych swojej witryny.

Każdy fraktal jest skonstruowany według pewnej reguły, którą konsekwentnie stosuje się nieograniczoną liczbę razy. Każdy taki moment nazywany jest iteracją.

Iteracyjny algorytm konstruowania gąbki Mengera jest dość prosty: oryginalny sześcian o boku 1 jest podzielony płaszczyznami równoległymi do jego ścian na 27 równych sześcianów. Usuwa się z niego jedną środkową kostkę i 6 sąsiadujących z nią kostek. Rezultatem jest zestaw składający się z pozostałych 20 mniejszych kostek. Robiąc to samo z każdą z tych kostek, otrzymamy zestaw składający się z 400 mniejszych kostek. Kontynuując ten proces w nieskończoność, otrzymujemy gąbkę Mengera.