Definicja 7.1. Nazywa się zbiór wszystkich punktów na płaszczyźnie, dla których suma odległości do dwóch stałych punktów F 1 i F 2 jest daną stałą wartością elipsa.
Definicja elipsy podaje następujący sposób jej geometrycznej konstrukcji. Naprawiamy dwa punkty F 1 i F 2 na płaszczyźnie i oznaczamy nieujemną stałą wartość przez 2a. Niech odległość między punktami F 1 i F 2 będzie wynosić 2c. Wyobraźmy sobie, że nierozciągliwa nić o długości 2a jest zamocowana w punktach F 1 i F 2, na przykład za pomocą dwóch igieł. Jest oczywiste, że jest to możliwe tylko dla a ≥ c. Po przeciągnięciu nici ołówkiem narysuj linię, która będzie elipsą (ryc. 7.1).
Zatem opisywany zbiór nie jest pusty, jeśli a ≥ c. Gdy a = c, elipsa jest odcinkiem o końcach F 1 i F 2, a gdy c = 0, tj. Jeżeli punkty stałe określone w definicji elipsy pokrywają się, jest to okrąg o promieniu a. Pomijając te zdegenerowane przypadki, założymy dalej z reguły, że a > c > 0.
Nazywa się punkty stałe F 1 i F 2 w definicji 7.1 elipsy (patrz ryc. 7.1) ogniska elipsy, odległość między nimi, oznaczona jako 2c, - długość ogniskowa, a odcinki F 1 M i F 2 M łączące dowolny punkt M na elipsie z jej ogniskami to promienie ogniskowe.
O kształcie elipsy całkowicie decyduje ogniskowa |F 1 F 2 | = 2c i parametr a oraz jego położenie na płaszczyźnie - para punktów F 1 i F 2.
Z definicji elipsy wynika, że jest ona symetryczna względem linii przechodzącej przez ogniska F 1 i F 2, a także względem linii dzielącej odcinek F 1 F 2 na pół i jest do niej prostopadła (ryc. 7.2, a). Linie te nazywane są osie elipsy. Punkt O ich przecięcia jest środkiem symetrii elipsy i nazywa się to środek elipsy oraz punkty przecięcia elipsy z osiami symetrii (punkty A, B, C i D na ryc. 7.2, a) - wierzchołki elipsy.
Nazywa się liczbę a półoś wielka elipsy i b = √(a 2 - c 2) - jego oś mała. Łatwo zauważyć, że dla c > 0 półoś wielka a jest równa odległości od środka elipsy do tych jej wierzchołków, które leżą na tej samej osi z ogniskami elipsy (wierzchołki A i B na ryc. 7.2, a), a półoś mała b jest równa odległości od środkowej elipsy do jej dwóch pozostałych wierzchołków (wierzchołki C i D na ryc. 7.2, a).
Równanie elipsy. Rozważmy elipsę na płaszczyźnie z ogniskami w punktach F 1 i F 2, oś główna 2a. Niech 2c będzie ogniskową, 2c = |F 1 F 2 |
Wybierzmy na płaszczyźnie prostokątny układ współrzędnych Oxy tak, aby jego początek pokrywał się ze środkiem elipsy, a jego ogniska znajdowały się na oś x(ryc. 7.2, b). Taki układ współrzędnych nazywa się kanoniczny dla danej elipsy i odpowiadające jej zmienne kanoniczny.
W wybranym układzie współrzędnych ogniska mają współrzędne F 1 (c; 0), F 2 (-c; 0). Korzystając ze wzoru na odległość punktów zapisujemy warunek |F 1 M| + |F 2 M| = 2a we współrzędnych:
√((x - do) 2 + y 2) + √((x + do) 2 + y 2) = 2a. (7.2)
Równanie to jest niewygodne, ponieważ zawiera dwa pierwiastki kwadratowe. Więc przekształćmy to. Przesuńmy drugi pierwiastek w równaniu (7.2) do prawa strona i wyprostuj to:
(x - do) 2 + y 2 = 4a 2 - 4a√((x + do) 2 + y 2) + (x + do) 2 + y 2.
Po otwarciu nawiasów i wprowadzeniu podobnych terminów otrzymujemy
√((x + c) 2 + y 2) = a + εx
gdzie ε = c/a. Powtarzamy operację kwadratury, aby usunąć drugi rodnik: (x + c) 2 + y 2 = a 2 + 2εax + ε 2 x 2 lub, biorąc pod uwagę wartość wprowadzonego parametru ε, (a 2 - c 2 ) x 2 / za 2 + y 2 = za 2 - do 2 . Skoro a 2 - do 2 = b 2 > 0, zatem
x 2 /a 2 + y 2 /b 2 = 1, a > b > 0. (7.4)
Równanie (7.4) jest spełnione przez współrzędne wszystkich punktów leżących na elipsie. Ale przy wyprowadzaniu tego równania zastosowano nierównoważne przekształcenia pierwotnego równania (7.2) - dwa kwadraty, które usuwają rodniki kwadratowe. Podniesienie równania do kwadratu jest przekształceniem równoważnym, jeśli obie strony mają wielkości o tym samym znaku, ale nie sprawdzaliśmy tego w naszych przekształceniach.
Sprawdzania równoważności przekształceń możemy uniknąć, jeśli uwzględnimy poniższe. Para punktów F 1 i F 2, |F 1 F 2 | = 2c, na płaszczyźnie definiuje rodzinę elips z ogniskami w tych punktach. Każdy punkt płaszczyzny, za wyjątkiem punktów odcinka F 1 F 2, należy do jakiejś elipsy wskazanej rodziny. W tym przypadku żadne dwie elipsy nie przecinają się, ponieważ suma promieni ogniskowych jednoznacznie określa konkretną elipsę. Zatem opisana rodzina elips bez przecięć obejmuje całą płaszczyznę, z wyjątkiem punktów odcinka F 1 F 2. Rozważmy zbiór punktów, których współrzędne spełniają równanie (7.4) przy danej wartości parametru a. Czy ten zbiór można rozłożyć na kilka elips? Niektóre punkty zbioru należą do elipsy z półosią wielką a. Niech w tym zbiorze będzie punkt leżący na elipsie z półosią wielką a. Wtedy współrzędne tego punktu są zgodne z równaniem
te. równania (7.4) i (7.5) mają rozwiązania ogólne. Łatwo jednak sprawdzić, czy system
dla ã ≠ a nie ma rozwiązań. Aby to zrobić, wystarczy wykluczyć np. x z pierwszego równania:
co po przekształceniach prowadzi do równania
który nie ma rozwiązań dla ã ≠ a, ponieważ . Zatem (7.4) jest równaniem elipsy, w której półoś wielka a > 0 i półoś mała b =√(a 2 - c 2) > 0. Nazywa się to kanoniczne równanie elipsy.
Widok elipsy. Omówiona powyżej geometryczna metoda konstruowania elipsy daje wystarczające pojęcie wygląd elipsa. Ale kształt elipsy można również zbadać za pomocą jej równania kanonicznego (7.4). Można na przykład, zakładając y ≥ 0, wyrazić y przez x: y = b√(1 - x 2 /a 2) i po przestudiowaniu tej funkcji zbudować jej wykres. Istnieje inny sposób skonstruowania elipsy. Okrąg o promieniu a ze środkiem w początku kanonicznego układu współrzędnych elipsy (7.4) opisuje równanie x 2 + y 2 = a 2. Jeśli jest skompresowany ze współczynnikiem a/b > 1 wzdłuż oś y, wówczas otrzymasz krzywą opisaną równaniem x 2 + (ya/b) 2 = a 2, tj. elipsę.
Uwaga 7.1. Jeśli ten sam okrąg zostanie skompresowany przez współczynnik a/b
Ekscentryczność elipsy. Nazywa się stosunek ogniskowej elipsy do jej głównej osi ekscentryczność elipsy i oznaczone przez ε. Dla danej elipsy
równanie kanoniczne (7.4), ε = 2c/2a = c/a. Jeżeli w (7.4) parametry aib są powiązane nierównością a
Gdy c = 0, gdy elipsa zamienia się w okrąg, oraz ε = 0. W pozostałych przypadkach 0
Równanie (7.3) jest równoważne równaniu (7.4), ponieważ równania (7.4) i (7.2) są równoważne. Dlatego równanie elipsy ma również postać (7.3). Dodatkowo zależność (7.3) jest interesująca, ponieważ daje prosty, bezrodnikowy wzór na długość |F 2 M| jeden z ogniskowych promieni punktu M(x; y) elipsy: |F 2 M| = a + εx.
Podobny wzór na drugi promień ogniskowy można otrzymać z rozważań o symetrii lub powtarzając obliczenia, w których przed podniesieniem równania (7.2) do prawej strony przenosi się pierwszy rodnik, a nie drugi. Zatem dla dowolnego punktu M(x; y) na elipsie (patrz rys. 7.2)
|F 1 M | = a - εx, |F 2 M| = a + εx, (7.6)
a każde z tych równań jest równaniem elipsy.
Przykład 7.1. Znajdźmy równanie kanoniczne elipsy z półosią wielką 5 i mimośrodem 0,8 i skonstruujmy je.
Znając półoś wielką elipsy a = 5 i mimośród ε = 0,8, znajdziemy jej półoś małą b. Ponieważ b = √(a 2 - c 2) i c = εa = 4, to b = √(5 2 - 4 2) = 3. Zatem równanie kanoniczne ma postać x 2 /5 2 + y 2 /3 2 = 1. Aby skonstruować elipsę, wygodnie jest narysować prostokąt ze środkiem w początku kanonicznego układu współrzędnych, którego boki są równoległe do osi symetrii elipsy i równe odpowiadającym jej osiom (ryc. 7.4). Ten prostokąt przecina się z
osie elipsy w jej wierzchołkach A(-5; 0), B(5; 0), C(0; -3), D(0; 3), a sama elipsa jest w nią wpisana. Na ryc. 7.4 pokazuje także ogniska F 1.2 (±4; 0) elipsy.
Właściwości geometryczne elipsy. Przepiszemy pierwsze równanie z (7.6) jako |F 1 M| = (a/ε - x)ε. Należy zauważyć, że wartość a/ε - x dla a > c jest dodatnia, ponieważ ognisko F 1 nie należy do elipsy. Wartość ta reprezentuje odległość do linii pionowej d: x = a/ε od punktu M(x; y) leżącego na lewo od tej linii. Równanie elipsy można zapisać jako
|F 1 M|/(a/ε - x) = ε
Oznacza to, że na tę elipsę składają się te punkty M(x, y) płaszczyzny, dla których stosunek długości promienia ogniskowego F 1 M do odległości od prostej d jest wartością stałą równą ε (rys. 7.5).
Linia prosta d ma „podwójną” - pionową linię prostą d, symetryczną do d w stosunku do środka elipsy, co jest określone równaniem x = -a/ε. W odniesieniu do d elipsa jest opisana w w taki sam sposób, jak w przypadku d. Obie linie d i d” są wywoływane kierownice elipsy. Kierownice elipsy są prostopadłe do osi symetrii elipsy, na której znajdują się jej ogniska, i są oddalone od środka elipsy w odległości a/ε = a 2 /c (patrz rys. 7.5).
Nazywa się odległość p od kierownicy do najbliższego jej ogniska parametr ogniskowy elipsy. Ten parametr jest równy
p = a/ε - do = (a 2 - do 2)/c = b 2 /c
Elipsa ma inną ważną właściwość geometryczną: promienie ogniskowe F 1 M i F 2 M tworzą równe kąty ze styczną do elipsy w punkcie M (ryc. 7.6).
Ta nieruchomość ma jasne znaczenie fizyczne. Jeśli źródło światła zostanie umieszczone w ognisku F 1, wówczas promień wychodzący z tego ogniska po odbiciu od elipsy będzie przebiegał wzdłuż drugiego promienia ogniska, ponieważ po odbiciu będzie pod tym samym kątem do krzywizny, co przed odbiciem. Zatem wszystkie promienie wychodzące z ogniska F 1 zostaną skupione w drugim ognisku F 2 i odwrotnie. W oparciu o tę interpretację właściwość tę nazywa się właściwości optyczne elipsy.
Definicja. Elipsa to geometryczne miejsce punktów na płaszczyźnie, których suma odległości każdego z dwóch danych punktów tej płaszczyzny, zwanych ogniskami, jest wartością stałą (pod warunkiem, że wartość ta jest większa niż odległość między ogniskami) .
Oznaczmy ogniska poprzez odległość między nimi - przez i wartość stałą, równa kwocie odległości od każdego punktu elipsy do ognisk poprzez (zgodnie z warunkiem).
Konstruujmy kartezjański układ współrzędnych tak, aby ogniska znajdowały się na osi odciętej, a początek współrzędnych pokrywał się ze środkiem odcinka (ryc. 44). Wtedy ogniska będą miały następujące współrzędne: lewy fokus i prawy fokus. Wyprowadźmy równanie elipsy w wybranym przez nas układzie współrzędnych. W tym celu rozważmy dowolny punkt elipsy. Z definicji elipsy suma odległości od tego punktu do ognisk jest równa:
Korzystając ze wzoru na odległość między dwoma punktami, otrzymujemy zatem
Aby uprościć to równanie, zapisujemy je w postaci
Następnie podnosząc obie strony równania do kwadratu, otrzymujemy
lub po oczywistych uproszczeniach:
Teraz ponownie podnosimy obie strony równania, po czym mamy:
lub po identycznych przekształceniach:
Ponieważ zgodnie z warunkiem w definicji elipsy liczba jest dodatnia. Wprowadźmy notację
Wówczas równanie przyjmie następującą postać:
Z definicji elipsy współrzędne dowolnego z jej punktów spełniają równanie (26). Ale równanie (29) jest konsekwencją równania (26). W związku z tym spełniają go również współrzędne dowolnego punktu elipsy.
Można wykazać, że współrzędne punktów nie leżących na elipsie nie spełniają równania (29). Zatem równanie (29) jest równaniem elipsy. Nazywa się to równaniem kanonicznym elipsy.
Ustalmy kształt elipsy, korzystając z jej równania kanonicznego.
Przede wszystkim zwróćmy uwagę na fakt, że to równanie zawiera tylko nawet stopnie x i y. Oznacza to, że jeśli jakiś punkt należy do elipsy, to zawiera także punkt symetryczny do punktu względem osi odciętych oraz punkt symetryczny do punktu względem osi rzędnych. Zatem elipsa ma dwie wzajemnie prostopadłe osie symetrii, które w wybranym przez nas układzie współrzędnych pokrywają się z osiami współrzędnych. Osie symetrii elipsy będziemy odtąd nazywać osiami elipsy, a punkt ich przecięcia środkiem elipsy. Oś, na której znajdują się ogniska elipsy (w w tym przypadku oś x) nazywana jest osią ogniskową.
Najpierw określmy kształt elipsy w pierwszej ćwiartce. Aby to zrobić, rozwiążmy równanie (28) dla y:
Jest tu oczywiste, że , ponieważ y przyjmuje wartości urojone. W miarę zwiększania się od 0 do a y maleje od b do 0. Część elipsy leżąca w pierwszej ćwiartce będzie łukiem ograniczonym punktami B (0; b) i leżącym na osiach współrzędnych (ryc. 45). Korzystając teraz z symetrii elipsy, dochodzimy do wniosku, że elipsa ma kształt pokazany na ryc. 45.
Punkty przecięcia elipsy z osiami nazywane są wierzchołkami elipsy. Z symetrii elipsy wynika, że oprócz wierzchołków elipsa ma jeszcze dwa wierzchołki (patrz ryc. 45).
Odcinki i łączące przeciwne wierzchołki elipsy, a także ich długości, nazywane są odpowiednio dużą i małą osią elipsy. Liczby a i b nazywane są odpowiednio większą i mniejszą półosią elipsy.
Stosunek połowy odległości ognisk do półosi wielkiej elipsy nazywany jest mimośrodem elipsy i jest zwykle oznaczany literą:
Ponieważ , ekscentryczność elipsy jest mniejsza niż jedność: Ekscentryczność charakteryzuje kształt elipsy. Istotnie, ze wzoru (28) wynika, że im mniejszy mimośród elipsy, tym mniej jej półoś mała b różni się od półosi wielkiej a, czyli tym mniej wydłużona jest elipsa (wzdłuż osi ogniskowej).
W skrajnym przypadku wynikiem jest okrąg o promieniu a: , lub . Jednocześnie ogniska elipsy wydają się łączyć w jednym punkcie - w środku koła. Mimośród okręgu wynosi zero:
Połączenie elipsy z okręgiem można ustalić z innego punktu widzenia. Pokażmy, że elipsę z półosiami a i b można uważać za rzut koła o promieniu a.
Rozważmy dwie płaszczyzny P i Q, tworzące między sobą taki kąt a, dla którego (ryc. 46). Skonstruujmy układ współrzędnych w płaszczyźnie P, a w płaszczyźnie Q układ Oxy o wspólnym początku O i wspólnej osi odciętych pokrywającej się z linią przecięcia płaszczyzn. Rozważmy okrąg na płaszczyźnie P
ze środkiem w początku układu współrzędnych i promieniem równym a. Niech będzie dowolnie wybranym punktem na okręgu, będzie jego rzutem na płaszczyznę Q i niech będzie rzutem punktu M na oś Ox. Pokażmy, że punkt leży na elipsie z półosiami a i b.
Krzywe drugiego rzędu na płaszczyźnie znajdują się linie określone równaniami, w których zmienne współrzędne X I y zawarte są w drugim stopniu. Należą do nich elipsa, hiperbola i parabola.
Ogólna postać równania krzywej drugiego rzędu jest następująca:
Gdzie ALFABET- liczby i co najmniej jeden ze współczynników A, B, C nie równe zeru.
Przy rozwiązywaniu problemów z krzywymi drugiego rzędu najczęściej uwzględnia się równania kanoniczne elipsy, hiperboli i paraboli. Łatwo przejść do nich od równań ogólnych, temu poświęcony zostanie przykład 1 problemów z elipsami.
Elipsa określona równaniem kanonicznym
Definicja elipsy. Elipsa to zbiór wszystkich punktów płaszczyzny, dla których suma odległości do punktów zwanych ogniskami jest wartością stałą większą od odległości pomiędzy ogniskami.
Ogniska są zaznaczone jak na poniższym rysunku.
Równanie kanoniczne elipsy ma postać:
Gdzie A I B (A > B) - długości półosi, czyli połowy długości odcinków odciętych przez elipsę na osiach współrzędnych.
Linia prosta przechodząca przez ogniska elipsy jest jej osią symetrii. Inną osią symetrii elipsy jest linia prosta przechodząca przez środek odcinka prostopadłego do tego odcinka. Kropka O przecięcie tych linii służy jako środek symetrii elipsy lub po prostu środek elipsy.
Oś odciętych elipsy przecina się w punktach ( A, O) I (- A, O), a oś współrzędnych jest w punktach ( B, O) I (- B, O). Te cztery punkty nazywane są wierzchołkami elipsy. Odcinek pomiędzy wierzchołkami elipsy na osi x nazywany jest jej osią wielką, a na osi rzędnych osią mniejszą. Ich odcinki od góry do środka elipsy nazywane są półosiami.
Jeśli A = B, to równanie elipsy przyjmuje postać . To jest równanie okręgu o promieniu A, a okrąg jest szczególny przypadek elipsa. Elipsę można otrzymać z okręgu o promieniu A, jeśli skompresujesz go do A/B razy wzdłuż osi Oj .
Przykład 1. Sprawdź, czy prosta dana równaniem ogólnym jest 
, elipsa.
Rozwiązanie. Dokonujemy transformacji równanie ogólne. Korzystamy z przeniesienia wyrazu wolnego na prawą stronę, podziału równania wyraz po wyrazie przez tę samą liczbę i redukcji ułamków:
Odpowiedź. Równanie otrzymane w wyniku przekształceń jest równaniem kanonicznym elipsy. Dlatego ta linia jest elipsą.
Przykład 2. Utwórz równanie kanoniczne elipsy, jeśli jej półosie wynoszą odpowiednio 5 i 4.
Rozwiązanie. Patrzymy na wzór na równanie kanoniczne elipsy i zastępujemy: półoś wielka A= 5, oś półmała wynosi B= 4 . Otrzymujemy równanie kanoniczne elipsy:
Punkty i , zaznaczone na zielono na głównej osi, gdzie
są nazywane wydziwianie.
zwany ekscentryczność elipsa.
Postawa B/A charakteryzuje „płaskość” elipsy. Im mniejszy jest ten stosunek, tym bardziej elipsa jest wydłużona wzdłuż głównej osi. Jednakże stopień wydłużenia elipsy wyraża się częściej poprzez mimośrodowość, której wzór podano powyżej. W przypadku różnych elips mimośrodowość zmienia się od 0 do 1, zawsze pozostając mniejsza niż jedność.
Przykład 3. Utwórz równanie kanoniczne elipsy, jeśli odległość między ogniskami wynosi 8, a główna oś wynosi 10.
Rozwiązanie. Wyciągnijmy kilka prostych wniosków:
Jeżeli oś wielka jest równa 10, to jej połowa, czyli półoś A = 5 ,
Jeśli odległość między ogniskami wynosi 8, to liczba C współrzędnych ogniskowych jest równa 4.
Podstawiamy i obliczamy:
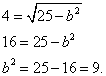
Wynikiem jest równanie kanoniczne elipsy:
Przykład 4. Utwórz równanie kanoniczne elipsy, jeśli jej główna oś wynosi 26, a mimośród wynosi .
Rozwiązanie. Jak wynika zarówno z rozmiaru głównej osi, jak i równania mimośrodu, półoś wielka elipsy A= 13. Z równania mimośrodu wyrażamy liczbę C, potrzebne do obliczenia długości mniejszej półosi:
.
Obliczamy kwadrat długości mniejszej półosi:
Tworzymy równanie kanoniczne elipsy:
Przykład 5. Wyznacz ogniska elipsy podane równaniem kanonicznym.
Rozwiązanie. Znajdź numer C, który wyznacza pierwsze współrzędne ognisk elipsy:
.
Otrzymujemy ogniska elipsy:
Przykład 6. Ogniska elipsy znajdują się na osi Wół symetrycznie względem początku. Ułóż równanie kanoniczne elipsy, jeśli:
1) odległość między ogniskami wynosi 30, a oś wielka 34
2) oś pomocnicza 24, a jedno z ognisk znajduje się w punkcie (-5; 0)
3) ekscentryczność, a jedno z ognisk znajduje się w punkcie (6; 0)
Kontynuujmy wspólne rozwiązywanie problemów z elipsami
Jeżeli jest to dowolny punkt elipsy (zaznaczony na zielono w prawej górnej części elipsy na rysunku) i jest odległością do tego punktu od ognisk, to wzory na odległości są następujące:
Dla każdego punktu należącego do elipsy suma odległości od ognisk jest stałą wartością równą 2 A.
Linie określone równaniami
są nazywane dyrektorki elipsa (na rysunku wzdłuż krawędzi znajdują się czerwone linie).
Z dwóch powyższych równań wynika, że dla dowolnego punktu elipsy
,
gdzie i są odległościami tego punktu do kierownic i .
Przykład 7. Biorąc pod uwagę elipsę. Napisz równanie na jego kierownice.
Rozwiązanie. Patrzymy na równanie kierownicy i stwierdzamy, że musimy znaleźć mimośród elipsy, tj. Mamy na to wszystkie dane. Obliczamy:
.
Otrzymujemy równanie kierownic elipsy:
Przykład 8. Utwórz równanie kanoniczne elipsy, jeśli jej ogniska są punktami, a kierownice liniami.
Wykłady z algebry i geometrii. 1 semestr.
Wykład 15. Elipsa.
Rozdział 15. Elipsa.
klauzula 1. Podstawowe definicje.
Definicja. Elipsa to GMT płaszczyzny, suma odległości do dwóch stałych punktów płaszczyzny, zwanych ogniskami, jest wartością stałą.
Definicja. Odległość od dowolnego punktu M płaszczyzny do ogniska elipsy nazywa się promieniem ogniskowym punktu M.
Oznaczenia: 
– ogniska elipsy, 
– promienie ogniskowe punktu M.
Z definicji elipsy punkt M jest punktem elipsy wtedy i tylko wtedy 
- stała wartość. Stała ta jest zwykle oznaczana jako 2a:
.
(1)
Zauważ, że 
.
Z definicji elipsy jej ogniska są punktami stałymi, więc odległość między nimi jest również wartością stałą dla danej elipsy.
Definicja. Odległość między ogniskami elipsy nazywa się ogniskową.
Przeznaczenie: 
.
Z trójkąta 
wynika z tego 
, tj.
.
Oznaczmy przez b liczbę równą 
, tj.
.
(2)
Definicja. Postawa
(3)
nazywa się mimośrodem elipsy.
Wprowadźmy na tej płaszczyźnie układ współrzędnych, który nazwiemy kanonicznym dla elipsy.
Definicja. Oś, na której leżą ogniska elipsy, nazywana jest osią ogniskową.
Skonstruujmy kanoniczny PDSC dla elipsy, patrz ryc. 2.
Wybieramy oś ogniskową jako oś odciętych i rysujemy oś rzędnych przez środek odcinka 
prostopadle do osi ogniskowej.
Wtedy ogniska mają współrzędne 
,
.
klauzula 2. Równanie kanoniczne elipsy.
Twierdzenie. W kanonicznym układzie współrzędnych elipsy równanie elipsy ma postać:
.
(4)
Dowód. Dowód przeprowadzamy w dwóch etapach. W pierwszym etapie udowodnimy, że współrzędne dowolnego punktu leżącego na elipsie spełniają równanie (4). W drugim etapie udowodnimy, że dowolne rozwiązanie równania (4) daje współrzędne punktu leżącego na elipsie. Z tego wynika, że równanie (4) spełniają te i tylko te punkty płaszczyzny współrzędnych, które leżą na elipsie. Z tego oraz z definicji równania krzywej wynika, że równanie (4) jest równaniem elipsy.
1) Niech punkt M(x, y) będzie punktem elipsy, tj. suma jego promieni ogniskowych wynosi 2a:
.
Skorzystajmy ze wzoru na odległość między dwoma punktami na płaszczyźnie współrzędnych i skorzystajmy z tego wzoru, aby znaleźć promienie ogniskowe danego punktu M:
,
, skąd otrzymujemy:
Przesuńmy jeden pierwiastek na prawą stronę równości i podnieśmy go do kwadratu:
Redukując otrzymujemy:
Przedstawiamy podobne, zmniejszamy o 4 i usuwamy pierwiastek:
.
Kwadrat
Otwórz nawiasy i skróć o 
:
gdzie otrzymujemy:
Korzystając z równości (2) otrzymujemy:
.
Dzielenie ostatniej równości przez 
, otrzymujemy równość (4) itd.
2) Niech teraz para liczb (x, y) spełnia równanie (4) i niech M(x, y) będzie odpowiednim punktem na płaszczyźnie współrzędnych Oxy.
Następnie z (4) wynika:
.
Podstawiamy tę równość do wyrażenia na promienie ogniskowe punktu M:
.
Tutaj użyliśmy równości (2) i (3).
Zatem, 
. Podobnie, 
.
Zauważmy teraz, że z równości (4) wynika to
Lub 
itp. 
, to nierówność jest następująca:
.
Stąd wynika z kolei, że
Lub 
I
,
.
(5)
Z równości (5) wynika, że 
, tj. punkt M(x, y) jest punktem elipsy itd.
Twierdzenie zostało udowodnione.
Definicja. Równanie (4) nazywa się równaniem kanonicznym elipsy.
Definicja. Kanoniczne osie współrzędnych elipsy nazywane są głównymi osiami elipsy.
Definicja. Początek kanonicznego układu współrzędnych elipsy nazywa się środkiem elipsy.
klauzula 3. Właściwości elipsy.
Twierdzenie. (Właściwości elipsy.)
1. W kanonicznym układzie współrzędnych elipsy wszystko
punkty elipsy leżą w prostokącie
,
.
2. Punkty leżą
3. Elipsa to krzywa symetryczna względem
ich główne osie.
4. Środek elipsy jest jej środkiem symetrii.
Dowód. 1, 2) Natychmiast wynika z kanonicznego równania elipsy.
3, 4) Niech M(x, y) będzie dowolnym punktem elipsy. Wtedy jego współrzędne spełniają równanie (4). Ale wtedy współrzędne punktów również spełniają równanie (4), a zatem są punktami elipsy, z której wynikają twierdzenia twierdzenia.
Twierdzenie zostało udowodnione.
Definicja. Wielkość 2a nazywana jest główną osią elipsy, wielkość a nazywa się półosią wielką elipsy.
Definicja. Wielkość 2b nazywa się małą osią elipsy, wielkość b nazywa się półmniejszą osią elipsy.
Definicja. Punkty przecięcia elipsy z jej głównymi osiami nazywane są wierzchołkami elipsy.
Komentarz. Elipsę można skonstruować w następujący sposób. W samolocie „wbijamy gwóźdź w punkty ogniskowe” i mocujemy do nich długość nici 
. Następnie bierzemy ołówek i za jego pomocą rozciągamy nić. Następnie przesuwamy grafit ołówkowy po płaszczyźnie, upewniając się, że nić jest napięta.
Z definicji ekscentryczności wynika, że
Ustalmy liczbę a i skierujmy liczbę c na zero. Następnie o godz 
,
I 
. W limicie, który otrzymujemy
Lub 
– równanie okręgu.
Pokierujmy teraz 
. Następnie 
,
i widzimy, że w granicy elipsa degeneruje się w odcinek prosty 
w zapisie rysunku 3.
klauzula 4. Równania parametryczne elipsy.
Twierdzenie. Pozwalać 
– dowolne liczby rzeczywiste. Następnie układ równań
,
(6)
są równaniami parametrycznymi elipsy w kanonicznym układzie współrzędnych elipsy.
Dowód. Wystarczy udowodnić, że układ równań (6) jest równoważny równaniu (4), czyli: mają ten sam zestaw rozwiązań.
1) Niech (x, y) będzie dowolnym rozwiązaniem układu (6). Podziel pierwsze równanie przez a, drugie przez b, podnieś oba równania do kwadratu i dodaj:
.
Te. każde rozwiązanie (x, y) układu (6) spełnia równanie (4).
2) I odwrotnie, niech para (x, y) będzie rozwiązaniem równania (4), tj.
.
Z tej równości wynika, że punkt o współrzędnych 
leży na okręgu o promieniu jednostkowym ze środkiem w początku, tj. jest punktem na okręgu trygonometrycznym, któremu odpowiada określony kąt 
:
Z definicji sinusa i cosinusa wynika to bezpośrednio
,
, Gdzie 
, z czego wynika, że para (x, y) jest rozwiązaniem układu (6) itd.
Twierdzenie zostało udowodnione.
Komentarz. Elipsę można otrzymać w wyniku równomiernego „ściśnięcia” okręgu o promieniu a w kierunku osi odciętej.
Pozwalać 
– równanie okręgu o środku w początku układu współrzędnych. „Ściśnięcie” okręgu do osi odciętych to nic innego jak przekształcenie płaszczyzny współrzędnych, przeprowadzone według następującej zasady. Dla każdego punktu M(x, y) kojarzymy punkt na tej samej płaszczyźnie 
, Gdzie 
,
- Stopień sprężania.
Dzięki tej transformacji każdy punkt na okręgu „przechodzi” do innego punktu na płaszczyźnie, który ma tę samą odciętą, ale mniejszą rzędną. Wyraźmy starą rzędną punktu poprzez nową:
i podstawiamy okręgi do równania:
.
Stąd otrzymujemy:
.
(7)
Wynika z tego, że jeżeli przed transformacją „zaciskania” punkt M(x, y) leżał na okręgu, tj. jego współrzędne spełniały równanie okręgu, to po przekształceniu „ściskania” punkt ten „przekształcił się” w punkt 
, którego współrzędne spełniają równanie elipsy (7). Jeśli chcemy otrzymać równanie elipsy z półosią b, musimy przyjąć współczynnik kompresji
.
klauzula 5. Styczna do elipsy.
Twierdzenie. Pozwalać 
– dowolny punkt elipsy
.
Następnie równanie stycznej do tej elipsy w punkcie 
ma postać:
.
(8)
Dowód. Wystarczy rozważyć przypadek, gdy punkt styczności leży w pierwszej lub drugiej ćwiartce płaszczyzny współrzędnych: 
. Równanie elipsy w górnej półpłaszczyźnie ma postać:
.
(9)
Użyjmy równania stycznego do wykresu funkcji 
w tym punkcie 
:
Gdzie 
– wartość pochodnej danej funkcji w punkcie 
. Elipsę w pierwszej ćwiartce można uznać za wykres funkcji (8). Znajdźmy jego pochodną i jej wartość w punkcie styczności:
,
. Tutaj skorzystaliśmy z faktu, że punkt styczny 
jest punktem elipsy i dlatego jego współrzędne spełniają równanie elipsy (9), tj.
.
Podstawiamy znalezioną wartość pochodnej do równania stycznego (10):
,
gdzie otrzymujemy:
Oznacza to:
Podzielmy tę równość przez 
:
.
Pozostaje to zauważyć 
, ponieważ kropka 
należy do elipsy i jej współrzędne spełniają jej równanie.
Równanie styczne (8) dowodzi się w podobny sposób w punkcie styczności leżącym w trzeciej lub czwartej ćwiartce płaszczyzny współrzędnych.
I wreszcie, możemy łatwo sprawdzić, że równanie (8) daje równanie styczne w punktach 
,
:
Lub 
, I 
Lub 
.
Twierdzenie zostało udowodnione.
klauzula 6. Właściwość lustrzana elipsy.
Twierdzenie. Styczna do elipsy ma kąty równe promieniom ogniskowym punktu styczności.
Pozwalać 
- punktem kontaktowym, 
,
– promienie ogniskowe punktu stycznego, P i Q – rzuty ognisk na styczną poprowadzoną do elipsy w tym punkcie 
.
Twierdzenie to stwierdza
.
(11)
Równość tę można interpretować jako równość kątów padania i odbicia promienia światła od elipsy uwolnionej z jej ogniska. Ta właściwość nazywana jest właściwością lustrzaną elipsy:
Promień światła uwolniony z ogniska elipsy, po odbiciu od zwierciadła elipsy, przechodzi przez kolejne ognisko elipsy.
Dowód twierdzenia. Aby udowodnić równość kątów (11), udowadniamy podobieństwo trójkątów 
I 
, w którym strony 
I 
będzie podobne. Ponieważ trójkąty są prostokątne, wystarczy udowodnić równość
Elipsa to miejsce geometryczne punktów na płaszczyźnie, suma odległości każdego z nich do dwóch danych punktów F_1, a F_2 to stała wartość (2a) większa od odległości (2c) pomiędzy nimi dane punkty(ryc. 3.36, a). Ta geometryczna definicja wyraża ogniskowa właściwość elipsy.
Ogniskowa właściwość elipsy
Punkty F_1 i F_2 nazywane są ogniskami elipsy, odległość między nimi 2c=F_1F_2 to ogniskowa, środek O odcinka F_1F_2 to środek elipsy, liczba 2a to długość głównej osi elipsy elipsa (odpowiednio liczba a jest półoś wielką elipsy). Odcinki F_1M i F_2M łączące dowolny punkt M elipsy z jej ogniskami nazywane są promieniami ogniskowymi punktu M. Odcinek łączący dwa punkty elipsy nazywa się cięciwą elipsy.
Stosunek e=\frac(c)(a) nazywany jest mimośrodem elipsy. Z definicji (2a>2c) wynika, że 0\leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр O совпадают, и эллипс является окружностью радиуса a (рис.3.36,6).
Geometryczna definicja elipsy, wyrażający jej właściwość ogniskową, jest równoznaczny z jej definicją analityczną - linią określoną przez równanie kanoniczne elipsy:
Rzeczywiście, wprowadźmy prostokątny układ współrzędnych (ryc. 3.36c). Za początek układu współrzędnych przyjmujemy środek O elipsy; za oś odciętych przyjmujemy linię prostą przechodzącą przez ogniska (oś ogniskową lub pierwszą oś elipsy) (kierunek dodatni biegnie od punktu F_1 do punktu F_2); przyjmijmy prostą prostopadłą do osi ogniskowej i przechodzącą przez środek elipsy (druga oś elipsy) jako oś rzędnych (kierunek na osi rzędnych dobieramy tak, aby prostokątny układ współrzędnych Oxy był prawidłowy) .
Utwórzmy równanie elipsy, korzystając z jej definicji geometrycznej, która wyraża właściwość ogniskową. W wybranym układzie współrzędnych wyznaczamy współrzędne ognisk F_1(-c,0),~F_2(c,0). Dla dowolnego punktu M(x,y) należącego do elipsy mamy:
\vline\,\overrightarrow(F_1M)\,\vline\,+\vline\,\overrightarrow(F_2M)\,\vline\,=2a.
Zapisując tę równość w postaci współrzędnych, otrzymujemy:
\sqrt((x+c)^2+y^2)+\sqrt((x-c)^2+y^2)=2a.
Przesuwamy drugi pierwiastek na prawą stronę, podnosimy obie strony równania i wprowadzamy podobne wyrazy:
(x+c)^2+y^2=4a^2-4a\sqrt((x-c)^2+y^2)+(x-c)^2+y^2~\Leftrightarrow ~4a\sqrt((x-c )^2+y^2)=4a^2-4cx.
Dzieląc przez 4, podnosimy obie strony równania:
a^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^ 2=a^2(a^2-c^2).
Mając wyznaczone b=\sqrt(a^2-c^2)>0, otrzymujemy b^2x^2+a^2y^2=a^2b^2. Dzieląc obie strony przez a^2b^2\ne0, otrzymujemy równanie kanoniczne elipsa:
\frac(x^2)(a^2)+\frac(y^2)(b^2)=1.
Dlatego wybrany układ współrzędnych jest kanoniczny.
Jeśli ogniska elipsy pokrywają się, wówczas elipsa jest okręgiem (ryc. 3.36,6), ponieważ a=b. W tym przypadku każdy prostokątny układ współrzędnych, którego początek znajduje się w tym punkcie, będzie kanoniczny O\równoważnik F_1\równoważnik F_2, a równanie x^2+y^2=a^2 jest równaniem okręgu o środku w punkcie O i promieniu równym a.
Rozumując Odwrotna kolejność, można wykazać, że wszystkie punkty, których współrzędne spełniają równanie (3.49), i tylko one, należą do geometrycznego miejsca punktów zwanego elipsą. Innymi słowy, analityczna definicja elipsy jest równoważna jej definicji geometrycznej, która wyraża ogniskową właściwość elipsy.
Właściwość reżyserska elipsy
Kierownice elipsy to dwie linie proste biegnące równolegle do osi rzędnych kanonicznego układu współrzędnych, w tej samej odległości od niej \frac(a^2)(c). W c=0, gdy elipsa jest okręgiem, nie ma kierownic (możemy założyć, że kierownice są w nieskończoności).
Elipsa z mimośrodem 0
Faktycznie, np. dla ogniska F_2 i kierownicy d_2 (ryc. 3.37,6) warunek \frac(r_2)(\rho_2)=e można zapisać w postaci współrzędnych:
\sqrt((x-c)^2+y^2)=e\cdot\!\left(\frac(a^2)(c)-x\right)
Pozbycie się irracjonalności i zastąpienie e=\frac(c)(a),~a^2-c^2=b^2, dochodzimy do kanonicznego równania elipsy (3.49). Podobne rozumowanie można przeprowadzić dla fokusu F_1 i reżysera d_1\dwukropek\frac(r_1)(\rho_1)=e.
Równanie elipsy w biegunowym układzie współrzędnych
Równanie elipsy w biegunowym układzie współrzędnych F_1r\varphi (rys. 3.37, c i 3.37 (2)) ma postać
r=\frac(p)(1-e\cdot\cos\varphi)
gdzie p=\frac(b^2)(a) jest parametrem ogniskowym elipsy.
W rzeczywistości wybierzmy lewe ognisko F_1 elipsy jako biegun biegunowego układu współrzędnych i promień F_1F_2 jako oś biegunową (ryc. 3.37, c). Wtedy dla dowolnego punktu M(r,\varphi), zgodnie z geometryczną definicją (właściwością ogniskową) elipsy, mamy r+MF_2=2a. Wyrażamy odległość pomiędzy punktami M(r,\varphi) i F_2(2c,0) (patrz):
\begin(aligned)F_2M&=\sqrt((2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0))=\\ &=\sqrt(r^2- 4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2).\end(wyrównane)
Zatem w postaci współrzędnych równanie elipsy F_1M+F_2M=2a ma postać
r+\sqrt(r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2)=2\cdot a.
Izolujemy pierwiastek, podnosimy obie strony równania, dzielimy przez 4 i przedstawiamy podobne wyrażenia:
r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac(c)(a)\cdot\cos \varphi\right)\!\cdot r=a^2-c^2.
Wyraź promień biegunowy r i dokonaj zamiany e=\frac(c)(a),~b^2=a^2-c^2,~p=\frac(b^2)(a):
r=\frac(a^2-c^2)(a\cdot(1-e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(b^2)(a\cdot(1 -e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(p)(1-e\cdot\cos\varphi),
co było do okazania
Znaczenie geometryczne współczynników w równaniu elipsy
Znajdźmy punkty przecięcia elipsy (patrz rys. 3.37a) z osiami współrzędnych (wierzchołkami elipsy). Podstawiając do równania y=0, znajdujemy punkty przecięcia elipsy z osią odciętych (z osią ogniskową): x=\pm a. Zatem długość odcinka osi ogniskowej zawartej wewnątrz elipsy wynosi 2a. Odcinek ten, jak zauważono powyżej, nazywany jest główną osią elipsy, a liczba a jest półosią wielką elipsy. Podstawiając x=0 otrzymujemy y=\pm b. Zatem długość odcinka drugiej osi elipsy zawartego wewnątrz elipsy jest równa 2b. Odcinek ten nazywany jest małą osią elipsy, a liczba b jest półmniejszą osią elipsy.
Naprawdę, b=\sqrt(a^2-c^2)\leqslant\sqrt(a^2)=a, a równość b=a uzyskujemy tylko w przypadku c=0, gdy elipsą jest okrąg. Postawa k=\frac(b)(a)\leqslant1 nazywa się współczynnikiem kompresji elipsy.
Uwagi 3.9
1. Proste x=\pm a,~y=\pm b ograniczają główny prostokąt na płaszczyźnie współrzędnych, wewnątrz którego znajduje się elipsa (patrz ryc. 3.37, a).
2. Elipsę można zdefiniować jako miejsce punktów uzyskane przez ściśnięcie koła do jego średnicy.
Rzeczywiście, niech równanie okręgu w prostokątnym układzie współrzędnych Oxy będzie wynosić x^2+y^2=a^2. Po skompresowaniu do osi x ze współczynnikiem 0 \begin(cases)x"=x,\\y"=k\cdot y.\end(cases) Podstawiając do równania okręgi x=x" i y=\frac(1)(k)y" otrzymujemy równanie na współrzędne obrazu M"(x",y") punktu M(x,y ) : (x")^2+(\left(\frac(1)(k)\cdot y"\right)\^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} ponieważ b=k\cdot a . To jest równanie kanoniczne elipsy. 3. Osie współrzędnych (kanonicznego układu współrzędnych) są osiami symetrii elipsy (zwanymi głównymi osiami elipsy), a jej środek jest środkiem symetrii. Rzeczywiście, jeśli punkt M(x,y) należy do elipsy. wówczas punkty M”(x,-y) i M””(-x,y), symetryczne do punktu M względem osi współrzędnych, również należą do tej samej elipsy. 4. Z równania elipsy w biegunowym układzie współrzędnych r=\frac(p)(1-e\cos\varphi)(patrz ryc. 3.37, c), wyjaśniono geometryczne znaczenie parametru ogniskowego - jest to połowa długości cięciwy elipsy przechodzącej przez jej ognisko prostopadle do osi ogniskowej (r=p przy \varphi=\frac(\pi)(2)). 5. Mimośród e charakteryzuje kształt elipsy, czyli różnicę między elipsą a okręgiem. Im większe e, tym bardziej wydłużona elipsa i im e jest bliższe zeru, tym elipsa jest bliżej okręgu (ryc. 3.38a). Rzeczywiście, biorąc pod uwagę, że e=\frac(c)(a) i c^2=a^2-b^2 , otrzymujemy e^2=\frac(c^2)(a^2)=\frac(a^2-b^2)(a^2)=1-(\left(\frac(a)(b)\right )\^2=1-k^2,
!} gdzie k jest współczynnikiem kompresji elipsy, 0 6. Równanie \frac(x^2)(a^2)+\frac(y^2)(b^2)=1 o godz 7. Równanie \frac((x-x_0)^2)(a^2)+\frac((y-y_0)^2)(b^2)=1,~a\geqslant b definiuje elipsę ze środkiem w punkcie O”(x_0,y_0), której osie są równoległe do osi współrzędnych (ryc. 3.38, c). Równanie to sprowadza się do równania kanonicznego za pomocą translacji równoległej (3.36). Gdy a=b=R równanie (x-x_0)^2+(y-y_0)^2=R^2 opisuje okrąg o promieniu R ze środkiem w punkcie O”(x_0,y_0) . Równanie parametryczne elipsy w kanonicznym układzie współrzędnych ma postać \begin(cases)x=a\cdot\cos(t),\\ y=b\cdot\sin(t),\end(cases)0\leqslant t<2\pi.
Rzeczywiście, podstawiając te wyrażenia do równania (3.49), dochodzimy do głównej tożsamości trygonometrycznej \cos^2t+\sin^2t=1. Przykład 3.20. Narysuj elipsę \frac(x^2)(2^2)+\frac(y^2)(1^2)=1 w kanonicznym układzie współrzędnych Oxy. Znajdź półosie, ogniskową, mimośrodowość, stopień kompresji, parametr ogniskowej, równania kierownicy. Rozwiązanie. Porównując podane równanie z równaniem kanonicznym wyznaczamy półosie: a=2 - półoś wielka, b=1 - półoś mała elipsy. Budujemy główny prostokąt o bokach 2a=4,~2b=2 ze środkiem w początku układu współrzędnych (ryc. 3.39). Biorąc pod uwagę symetrię elipsy, wpasowujemy ją w główny prostokąt. Jeśli to konieczne, określ współrzędne niektórych punktów elipsy. Na przykład, podstawiając x=1 do równania elipsy, otrzymujemy \frac(1^2)(2^2)+\frac(y^2)(1^2)=1 \quad \Leftrightarrow \quad y^2=\frac(3)(4) \quad \Leftrightarrow \ quad y=\pm\frac(\sqrt(3))(2). Dlatego punkty ze współrzędnymi \left(1;\,\frac(\sqrt(3))(2)\right)\!,~\left(1;\,-\frac(\sqrt(3))(2)\right)- należą do elipsy. Obliczanie stopnia sprężania k=\frac(b)(a)=\frac(1)(2); długość ogniskowa 2c=2\sqrt(a^2-b^2)=2\sqrt(2^2-1^2)=2\sqrt(3); ekscentryczność e=\frac(c)(a)=\frac(\sqrt(3))(2); parametr ogniskowy p=\frac(b^2)(a)=\frac(1^2)(2)=\frac(1)(2). Tworzymy równania kierownicy: x=\pm\frac(a^2)(c)~\Leftrightarrow~x=\pm\frac(4)(\sqrt(3)).Równanie parametryczne elipsy
