§ 4. MECHANICAL PROPERTIES
The ability of a metal to resist external forces is characterized by mechanical properties. Therefore, when choosing a material for the manufacture of machine parts, it is necessary first of all to take into account its mechanical properties: strength, elasticity, ductility, impact strength, hardness and endurance. These properties are determined by the results of mechanical tests, in which metals are exposed to external forces (loads). External forces can be static, dynamic or cyclic (repeatedly variable). Load causes stress and deformation in a solid.
Voltage- load value per unit cross-sectional area of the test sample. Deformation– change in the shape and size of a solid body under the influence of applied external forces. There are tensile (compressive), bending, torsion, and shear deformations (Fig. 8). In reality, a material can undergo one or more types of deformation at the same time.
Rice. 8. Types of deformations:
a - compression, b - tension, c - torsion, d - shear, e - bending

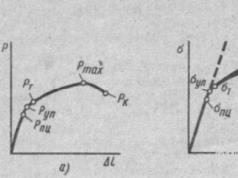
Rice. 9.Stretch Chart:
a - conditional diagram in P-∆l coordinates, b - conditional stress diagram and true stress diagram
To determine strength, elasticity and ductility, metals in the form of round or flat samples are tested for static tension (GOST 1497-73). Tests are carried out on tensile testing machines. As a result of the tests, a tensile diagram is obtained (Fig. 9). The abscissa axis of this diagram shows the deformation values, and the ordinate axis shows the loads applied to the sample.
Strength- the ability of a material to resist destruction under loads is assessed by its tensile strength and yield strength. An important indicator of the strength of a material is also the specific strength - the ratio of the tensile strength of the material to its density. Ultimate strength σ in (temporary resistance) is the conditional stress in Pa (N/m 2), corresponding to the greatest load preceding the destruction of the sample: σ in =P max /F 0, where P max is the greatest load, N; F 0 is the initial cross-sectional area of the working part of the sample, m 2 . True tensile strength Sk is the stress determined by the ratio of the load Pk at the moment of rupture to the area of the minimum cross-section of the sample after rupture Fk (Sk = Pk / Fk).
Yield strength (physical) σ t is the lowest stress (in MPa) at which the sample is deformed without a noticeable increase in load: σ t = P t / F 0, where P t is the load at which the yield plateau is observed, N.
Basically, only low-carbon steel and brass have a yield plateau. Other alloys do not have yield plateaus. For such materials, the yield strength (conditional) is determined, at which the permanent elongation reaches 0.2% of the design length of the sample: σ 0.2 = P 0.2 / F 0.
Elasticity- the ability of the material to restore its original shape and dimensions after the load P unit is removed is assessed by the proportionality limit σ pc and the elastic limit σ unit.
Proportionality limitσ pts - stress (MPa), above which the proportionality between the applied stress and the deformation of the sample σ pts = P pts / F 0 is violated.
Elastic limit(conditional) σ 0.05 is the conditional stress in MPa corresponding to the load at which the residual deformation first reaches 0.05% of the design length of the sample l0: σ 0.05 = P 0.05 / F 0, where P 0, 05 - elastic limit load, N.
Plastic, i.e., the ability of a material to take on a new shape and size under the influence of external forces without collapsing, is characterized by relative elongation and relative narrowing.
Relative extension(after rupture) δ is the ratio of the increment (l to -l 0) of the estimated length of the sample after rupture to its original estimated length l 0, expressed as a percentage: δ=[(l to -l 0)/l 0 ]100%.
Relative narrowing(after rupture) φ is the ratio of the difference between the initial and minimum areas (F 0 -F to) of the cross-section of the sample after rupture to the initial area F 0 of the cross-section, expressed as a percentage: φ=[(F 0 -F to)/F 0 ]100%.
The greater the relative elongation and contraction values for a material, the more ductile it is. For brittle materials these values are close to zero. The fragility of a structural material is a negative property.
Impact strength, i.e., the ability of a material to resist dynamic loads, is defined as the ratio of the work W (in MJ) spent on breaking a sample to its cross-sectional area F (in m 2) at the incision site KS = W/F.
For testing (GOST 9454-78), special standard samples are made in the form of square blocks with a notch. The sample is tested on pendulum pile drivers. The free-falling pendulum of the pile driver strikes the sample from the side opposite to the notch. At the same time, the work is recorded.
Determination of impact strength is especially important for some metals that operate at sub-zero temperatures and exhibit a tendency to cold brittleness. The lower the cold brittleness threshold, i.e. the temperature at which ductile fracture of a material turns into brittle, and the greater the reserve of viscosity of the material, the greater the impact strength of the material. Cold brittleness - a decrease in impact strength at low temperatures.
Cyclic viscosity- this is the ability of materials to absorb energy under repeatedly variable loads. Materials with high cyclic toughness quickly dampen vibrations, which are often the cause of premature failure. For example, cast iron, which has high cyclic viscosity, is in some cases (for frames and other body parts) a more valuable material than carbon steel.
Hardness call the ability of a material to resist the penetration of another, more solid body into it. Metal-cutting tools must have high hardness: cutters, drills, cutters, as well as surface-hardened parts. The hardness of the metal is determined by the Brinell, Rockwell and Vickers methods (Fig. 10).
Brinell method(GOST 9012-59) is based on the fact that a hardened steel ball is pressed into a flat metal surface under constant load. The diameter of the ball and the magnitude of the load are set depending on the hardness and thickness of the metal being tested. Brinell hardness is determined using a TSh hardness tester (ball hardness tester). The test is carried out as follows. On the surface of the sample whose hardness needs to be measured, an area of 3-5 cm 2 in size is cleaned with a file or an abrasive wheel. The sample is placed on the instrument table and raised until it comes into contact with a steel ball, which is mounted in the instrument spindle. The weight is lowered and presses the ball into the test sample. An imprint is formed on the surface of the metal. The larger the imprint, the softer the metal.
The measure of the hardness of the NV is taken as the ratio of the load to the surface area of the imprint with diameter d and depth t, which is formed when a ball of diameter D is pressed by force P (see Fig. 10, a).

Rice. 10. Determination of metal hardness by the Brinell (a), Rockwell (b) and Vickers (c) methods
The numerical value of hardness is determined as follows: measure the diameter of the print using an optical magnifying glass (with divisions) and using the obtained value, find the corresponding hardness number in the table attached to GOST.
The advantage of the Brinell method is the simplicity of testing and the accuracy of the results obtained. The Brinell method is not recommended for measuring the hardness of materials with HB>450, for example, hardened steel, since during measurement the ball is deformed and the readings are distorted.
Used for testing solid materials Rockwell method(GOST 9013-59). A diamond cone with an apex angle of 120° or a hardened steel ball with a diameter of 1.59 mm is pressed into the sample. Rockwell hardness is measured in arbitrary units. The conventional value of the hardness unit corresponds to the axial movement of the tip by 0.002 mm. The test is carried out on a TK device. The hardness value is determined by the depth of the indentation h and is counted using the indicator dial installed on the device. In all cases, the preload P0 is 100 N.
When testing metals with high hardness, a diamond cone is used and a total load P = P 0 + P 1 = 1500 N. Hardness is measured on the “C” scale and designated HRC.
If the test takes a steel ball and a total load of 1000 N, then the hardness is measured on the “B” scale and is designated HRB.
When testing very hard or thin products, use a diamond cone and a total load of 600 N. Hardness is measured on the “A” scale and is designated HRA. An example of Rockwell hardness designation: HRC 50 - hardness 50 on the “C” scale.
When determining hardness by the Vickers method (GOST 2999-75), a tetrahedral diamond pyramid with an apex angle of 136° is used as a tip pressed into the material. During testing, loads from 50 to 1000 N are used (smaller load values are used to determine the hardness of thin products and hard, hardened surface layers of metal). The numerical value of hardness is determined as follows: measure the lengths of both diagonals of the print after removing the load and using a microscope and using the resulting arithmetic average value of the diagonal length, find the corresponding hardness number in the table. An example of Vickers hardness designation is HV 500.
To assess the hardness of metals in small volumes, for example, on grains of metal or its structural components, a method is used to determine microhardness. The tip (indenter) of the device is a diamond tetrahedral pyramid (with an apex angle of 136°, the same as that of the pyramid during the Vickers test). The load on the indenter is small and amounts to 0.05-5 N, and the indent size is 5-30 microns. The test is carried out on a PMT-3 optical microscope equipped with a loading mechanism. Microhardness is assessed by the size of the indentation diagonal.
Fatigue is the process of gradual accumulation of damage to a material under the influence of repeated alternating stresses, leading to the formation of cracks and destruction. Metal fatigue is caused by the concentration of stress in its individual volumes, in which there are non-metallic inclusions, gas bubbles, various local defects, etc. A typical fatigue fracture is formed after the destruction of the sample as a result of repeated loading (Fig. 11) and consists of two different by the appearance of the parts. One part of the fracture 1 with a smooth (worn) surface is formed due to the friction of surfaces in the area of cracks arising from the action of repeatedly variable loads, the other part 2 with a granular fracture occurs at the moment of destruction of the sample. Fatigue tests are carried out on special machines. The most common machines are for repeated-alternating bending of a rotating sample, fixed at one or both ends, as well as machines for testing tensile-compression and repeated-alternating torsion. As a result of the tests, the endurance limit is determined, which characterizes fatigue resistance.
Mechanical properties characterize the resistance of a metal to deformation and destruction under the influence of mechanical forces (load).
The main mechanical properties include:
Strength
- plasticity
- impact strength
- hardness
Strength– this is the ability of a metal not to collapse under the influence of mechanical forces (load).
Plastic is the ability of a metal to change shape (deform) under the influence of mechanical forces (load) without destruction.
Determines the ability of a metal to withstand impact (dynamic) mechanical forces (shock loads).
Hardness is the ability of a metal to resist the penetration of other harder materials into it.
Types and conditions of mechanical testing of metals
To determine mechanical properties, the following types of tests are performed:
Tensile tests;
- static bending tests;
- impact bending tests;
- hardness measurement.
The conditions for testing samples include: temperature, type and nature of the application of load to the samples.
Test temperature:
Normal (+20°С);
- low (below +20°C, temperature 0...-60°C);
- high (above +20°C, temperature +100...+1200°C).
Type of loads:
| stretching | |
| compression | |
| bend |  |
| torsion |  |
| slice |  |
Character of load application:
The load increases slowly and smoothly or remains constant - static tests;
- the load is applied at high speeds; shock load - dynamic tests;
- multiple repeated variable load; load changes in magnitude or in magnitude and direction (tension and compression) - endurance tests.
Mechanical test samples
Mechanical tests are performed on standard samples. The shape and dimensions of the samples are established depending on the type of test.
For mechanical tensile tests, standard cylindrical (circular cross-section) and flat (rectangular cross-section) samples are used. For cylindrical samples, samples with a diameter dо=10 mm, short lо=5×do = 50 mm and long lо=10×do = 100 mm are taken as the main ones.


Flat samples have a thickness equal to the thickness of the sheet, and the width is set to 10, 15, 20 or 30 mm.

Flat sample without heads for tensile grips

Flat sample with heads
Mechanical properties determined by static tests
Static are tests in which the applied load to the sample increases slowly and smoothly.
In static tensile tests, the following basic mechanical characteristics of the metal are determined:
Yield strength (σ t);
- tensile strength or temporary resistance (σ in);
- relative elongation (δ);
- relative narrowing (ψ).
is the stress at which the sample deforms without a noticeable increase in tensile load.

is the stress at the maximum load preceding the failure of the sample.
is the ratio of the increment in the length of the sample after destruction to its initial length before testing.
is the ratio of the reduction in the cross-sectional area of the sample after destruction to its initial area before testing.
In static tensile testing, iron and other plastic metals have a yield plateau when the sample is elongated under a constant load Pm.

At maximum load Pmax, a narrowing of the cross section, the so-called “neck,” appears in one area of the sample. The destruction of the sample begins in the neck. Since the cross-section of the sample decreases, the destruction of the sample occurs at a load less than the maximum. During the test, the devices draw a tensile diagram from which the loads are determined. After testing, the destroyed samples are put together and the final length and diameter of the neck are measured. From these data, strength and ductility are calculated.

Mechanical impact testing
Dynamic tests are those in which the rate of deformation is significantly higher than in static tests.
Dynamic impact bending tests reveal the tendency of a metal to undergo brittle fracture. The method is based on the destruction of a sample with a notch (stress concentrator) with one blow of a pendulum pile driver.
The standard provides for samples with three types of notches:
U-shaped sample with radius R = 1 mm (KCU method);

V-shaped sample with radius R = 0.25 mm (KCV method);

sample I – shaped with a fatigue crack (KST method).

Impact strength is understood as the work of impact related to the initial cross-sectional area of the sample at the concentrator location.
After the test, the impact work required to destroy the sample is determined using the pendulum pile driver scale. The cross-sectional area of the sample is determined before failure.
DETERMINATION OF HARDNESS OF METALS
Hardness is the property of a metal to resist plastic deformation in the surface layer when a ball, cone or pyramid is indented. Hardness measurement is simple and quick to carry out and is performed without destroying the product. Three methods for determining hardness are widely used:
Brinell hardness (the unit of hardness is designated HB);
- Rockwell hardness (hardness unit is designated HR);
- Vickers hardness (hardness unit is designated HV).
Determination of Brinell hardness consists of pressing a steel ball with a diameter of D = 10 mm into the sample (product) under the influence of a load and measuring the indent diameter d after removing the load.

Brinell hardness is designated by numbers and letters HB, for example, 180 HB. The smaller the diameter of the print, the higher the hardness. The higher the hardness, the greater the strength of the metal and the less ductility. The softer the metal, the less the load on the device is set. So, when determining the hardness of steel and cast iron, the load is taken to be 3000 N, for nickel, copper and aluminum - 1000 N, for lead and tin - 250 N.
Determination of Rockwell hardness consists of pressing a tip with a diamond cone (scales A and C) or a steel ball with a diameter of 1.6 mm (scale B) into the test sample (product) under the action of successively applied preliminary (Po) and main (P) loads and in measurement tip penetration depth (h). Rockwell hardness is indicated by the numbers and letters HR indicating the scale. For example, 60 HRC (hardness 60 on the C scale).

Determination of Vickers hardness consists of pressing a diamond tip shaped like a regular tetrahedral pyramid into the sample (product) under the influence of a load and measuring the diagonal of the indentation d remaining after removing the load. The method is used to determine the hardness of thin parts and thin surface layers with high hardness. Vickers hardness is designated by numbers and letters HV, for example, 200 HV.

Static bending tests
Technological tests for static bending are used to determine the ability of a metal to accept a bend given in shape and size. Similar tests are carried out on welded joints.
Bend tests are carried out on samples made of sheet and shaped (rod, square, angle, channel, etc.) metal. For sheet metal, the sample width (b) is taken to be equal to double the thickness (2 t), but not less than 10 mm. The radius of the mandrel is indicated in the technical specifications.

There are three types of bending:
Bend to a certain angle;
- bend around the mandrel until the sides are parallel;
- bend close until the sides touch (flattening).
The absence of cracks, tears, delaminations or fractures in the sample is a sign that the sample has passed the test.
Methods for determining the mechanical properties of metals are divided into:
- static, when the load increases slowly and smoothly (tensile, compression, bending, torsion, hardness tests);
- dynamic, when the load grows at high speed (impact bending tests);
- cyclic, when the load changes repeatedly in magnitude and direction (fatigue tests).
Tensile test
When testing tensile strength, tensile strength (σ in), yield strength (σ t), relative elongation (δ) and relative contraction (ψ) are determined. Tests are carried out on tensile testing machines using standard samples with cross-sectional area Fo and working (calculated) length lo. As a result of the tests, a tensile diagram is obtained (Fig. 1). The abscissa axis indicates the value of the deformation, and the ordinate axis indicates the value of the load that is applied to the sample.
Ultimate strength (σ in) is the maximum load that the material can withstand without destruction, related to the initial cross-sectional area of the sample (Pmax/Fo).
Rice. 1. Tension diagram
It should be noted that when stretched, the sample elongates, and its cross-section continuously decreases. The true stress is determined by dividing the load acting at a certain moment by the area that the sample has at that moment. In everyday practice, true stresses are not determined, but conditional stresses are used, assuming that the cross section Fo of the sample remains unchanged.
The yield strength (σ t) is the load at which plastic deformation occurs, related to the initial cross-sectional area of the sample (Рт/Fo). However, during tensile tests, most alloys do not have yield plateaus on the diagrams. Therefore, the conditional yield strength (σ 0.2) is determined - the stress to which a plastic deformation of 0.2% corresponds. The selected value of 0.2% quite accurately characterizes the transition from elastic to plastic deformations.
The characteristics of the material also include the elastic limit (σ pr), which means the stress at which plastic deformation reaches a given value. Typically, residual strain values of 0.005 are used; 0.02; 0.05%. Thus, σ 0.05 = Ppr / Fo (Ppr is the load at which the residual elongation is 0.05%).
Limit of proportionality σ pc = Ppc / Fo (Ppc is the maximum load, under the action of which Hooke’s law is still satisfied).
Plasticity is characterized by relative elongation (δ) and relative contraction (ψ):
δ = [(lk - lo)/lo]∙100% ψ = [(Fo – Fk)/Fo]∙100%,
where lk is the final length of the sample; lo and Fo are the initial length and cross-sectional area of the sample; Fk is the cross-sectional area at the rupture site.
For low-plasticity materials, tensile tests are difficult, since minor distortions during installation of the sample introduce a significant error in determining the breaking load. Such materials are usually subjected to bending testing.
Hardness test
Regulations:
Hardness is the ability of a material to resist the penetration of another, harder body, an indenter. The hardness of the material is determined by the Brinell, Rockwell, Vickers, and Shore methods (Fig. 2).
 |
 |
 |
| A | b | V |
Rice. 2. Schemes for determining hardness according to Brinell (a), Rockwell (b) and Vickers (c)
The Brinell hardness of a metal is indicated by the letters HB and a number. To convert the hardness number to the SI system, use the coefficient K = 9.8 106, by which the Brinell hardness value is multiplied: HB = HB K, Pa.
The Brinell hardness method is not recommended for use for steels with a hardness of more than HB 450 and non-ferrous metals with a hardness of more than 200 HB.
For various materials, a correlation has been established between the ultimate strength (in MPa) and the hardness number HB: σ in ≈ 3.4 HB - for hot-rolled carbon steels; σ in ≈ 4.5 HB - for copper alloys, σ in ≈ 3.5 HB - for aluminum alloys.
Hardness determination by the Rockwell method is carried out by pressing a diamond cone or steel ball into the metal. The Rockwell device has three scales - A, B, C. The diamond cone is used to test hard materials (scales A and C), and the ball is used to test soft materials (scale B). Depending on the scale, hardness is designated by the letters HRB, HRC, HRA and is expressed in special units.
When measuring hardness using the Vickers method, a tetrahedral diamond pyramid is pressed into the metal surface (being ground or polished). This method is used to determine the hardness of thin parts and thin surface layers that have high hardness (for example, after nitriding). Vickers hardness is designated HV. The conversion of the hardness number HV to the SI system is carried out similarly to the conversion of the hardness number HB.
When measuring hardness using the Shore method, a ball with an indenter falls onto the sample, perpendicular to its surface, and the hardness is determined by the height of the ball’s rebound and is designated HS.
Kuznetsov-Herbert-Rehbinder method - hardness is determined by the damping time of the oscillations of a pendulum, the support of which is the metal under study.
Impact test
Impact strength characterizes the ability of a material to resist dynamic loads and the resulting tendency to brittle fracture. For impact testing, special samples with a notch are made, which are then destroyed on a pendulum impact driver (Fig. 3). Using the pendulum pile driver scale, the work K spent on destruction is determined, and the main characteristic obtained as a result of these tests is calculated - impact strength. It is determined by the ratio of the work of destruction of the sample to its cross-sectional area and is measured in MJ/m 2.
To designate impact strength, use the letters KS and add a third, which indicates the type of cut on the sample: U, V, T. The notation KCU means the impact strength of a sample with a U-like notch, KCV - with a V-like notch, and KCT - with a crack , created at the base of the cut. The work of destruction of a sample during impact tests contains two components: the work of crack initiation (Az) and the work of crack propagation (Ar).
Determining impact strength is especially important for metals that operate at low temperatures and exhibit a tendency to cold brittleness, that is, a decrease in impact strength as the operating temperature decreases.

Rice. 3. Scheme of a pendulum pile driver and impact sample
When performing impact tests on notched samples at low temperatures, the cold brittleness threshold is determined, which characterizes the effect of a decrease in temperature on the tendency of the material to brittle fracture. During the transition from ductile to brittle fracture, a sharp decrease in impact strength is observed in the temperature range, which is called the temperature threshold of cold brittleness. In this case, the structure of the fracture changes from fibrous matte (ductile fracture) to crystalline shiny (brittle fracture). The cold brittleness threshold is designated by a temperature range (tb. – txr.) or one temperature t50, at which 50% of the fibrous component is observed in the fracture of the sample or the value of impact strength is reduced by half.
The suitability of a material for operation at a given temperature is judged by the temperature margin of viscosity, which is determined by the difference between the operating temperature and the transition temperature of cold brittleness, and the larger it is, the more reliable the material.
Fatigue test
Fatigue is the process of gradual accumulation of damage to a material under the influence of repeated alternating stresses, which lead to the formation of cracks and destruction. Metal fatigue is caused by the concentration of stress in its individual volumes (in places of accumulation of non-metallic and gas inclusions, structural defects). The ability of a metal to resist fatigue is called endurance.
Fatigue tests are carried out on machines for repeated-alternating bending of a rotating sample, fixed at one or both ends, or on machines for testing tension-compression, or for repeated-alternating torsion. As a result of the tests, the endurance limit is determined, which characterizes the material’s resistance to fatigue.
Fatigue limit is the maximum stress under which fatigue failure does not occur after a basic number of loading cycles.
The endurance limit is denoted by σ R, where R is the cycle asymmetry coefficient.
To determine the endurance limit, at least ten samples are tested. Each specimen is tested at only one stress to failure or at a base number of cycles. The basic number of cycles must be at least 107 loads (for steel) and 108 (for non-ferrous metals).
An important characteristic of structural strength is survivability under cyclic loading, which is understood as the duration of operation of a part from the moment of initiation of the first macroscopic fatigue crack of 0.5...1 mm in size until final destruction. Survivability is of particular importance for the operational reliability of products, the trouble-free operation of which is maintained through early detection and prevention of further development of fatigue cracks.
Tensile testing of a metal consists of stretching a sample with plotting the dependence of the elongation of the sample (Δl) on the applied load (P), followed by rebuilding this diagram into a diagram of conditional stresses (σ - ε)
Tensile tests are carried out according to the same GOST, and the samples on which the tests are carried out are determined.
As mentioned above, during testing, a metal tensile diagram is constructed. It has several characteristic areas:

- Section OA is a section of proportionality between load P and elongation ∆l. This is the area where Hooke's law is preserved. This proportionality was discovered by Robert Hooke in 1670 and later became known as Hooke's law.
- The OB section is a section of elastic deformation. That is, if a load not exceeding Ru is applied to the sample and then unloaded, then during unloading the deformation of the sample will decrease according to the same law according to which they increased during loading
Above point B, the tension diagram deviates from a straight line - the deformation begins to grow faster than the load, and the diagram takes on a curvilinear appearance. At a load corresponding to Рт (point C), the diagram goes into a horizontal section. At this stage, the sample receives significant permanent elongation with virtually no increase in load. The formation of such a section on the stress-strain diagram is explained by the property of the material to deform under constant load. This property is called the fluidity of the material, and the section of the stress-strain diagram parallel to the abscissa axis is called the yield area.  Sometimes the yield plateau is wavy in nature. This more often concerns the stretching of plastic materials and is explained by the fact that first a local thinning of the section is formed, then this thinning spreads to the adjacent volume of the material and this process develops until, as a result of the propagation of such a wave, a general uniform elongation occurs, corresponding to the yield area. When there is a yield tooth, when determining the mechanical properties of a material, the concepts of upper and lower yield limits are introduced.
Sometimes the yield plateau is wavy in nature. This more often concerns the stretching of plastic materials and is explained by the fact that first a local thinning of the section is formed, then this thinning spreads to the adjacent volume of the material and this process develops until, as a result of the propagation of such a wave, a general uniform elongation occurs, corresponding to the yield area. When there is a yield tooth, when determining the mechanical properties of a material, the concepts of upper and lower yield limits are introduced.
After the yield plateau appears, the material again acquires the ability to resist stretching and the diagram rises. At point D the force reaches its maximum value Pmax. When the force Pmax is reached, a sharp local narrowing appears on the sample - a neck. A decrease in the cross-sectional area of the neck causes a drop in the load and at the moment corresponding to point K of the diagram, the sample ruptures.
The applied load to stretch a specimen depends on the geometry of that specimen. The larger the cross-sectional area, the higher the load required to stretch the sample. For this reason, the resulting machine diagram does not provide a qualitative assessment of the mechanical properties of the material. To eliminate the influence of sample geometry, the machine diagram is reconstructed in coordinates σ − ε by dividing the ordinate P by the original cross-sectional area of the sample A0 and the abscissa ∆l by lo. The diagram rearranged in this way is called a conditional stress diagram. Already from this new diagram, the mechanical characteristics of the material are determined.
The following mechanical characteristics are determined:
Proportionality limit σпз– the greatest stress after which the validity of Hooke’s law is violated σ = Eε, where E is the modulus of longitudinal elasticity, or the modulus of elasticity of the first kind. In this case, E =σ/ε = tanα, i.e. module E is the tangent of the angle of inclination of the rectilinear part of the diagram to the abscissa axis 
Elastic limit σу- conditional stress corresponding to the appearance of residual deformations of a certain specified value (0.05; 0.001; 0.003; 0.005%); the tolerance for residual deformation is indicated in the index at σу 
Yield strength σт– stress at which an increase in deformation occurs without a noticeable increase in tensile load
Also distinguished proof strength- this is the conditional stress at which the residual deformation reaches a certain value (usually 0.2% of the working length of the sample; then the conditional yield strength is denoted as σ0.2). The value of σ0.2 is determined, as a rule, for materials that do not have a plateau or yield tooth on the diagram
Metals are characterized by high ductility, thermal and electrical conductivity. They have a characteristic metallic luster.
About 80 elements of the periodic table of D.I. have properties of metals. Mendeleev. For metals, as well as for metal alloys, especially structural ones, mechanical properties are of great importance, the main ones being strength, ductility, hardness and impact strength.
Under the influence of an external load, stress and deformation arise in a solid body. related to the original cross-sectional area of the sample.
Deformation – this is a change in the shape and size of a solid body under the influence of external forces or as a result of physical processes that occur in the body during phase transformations, shrinkage, etc. Deformation may be elastic(disappears after the load is removed) and plastic(remains after the load is removed). With an ever-increasing load, elastic deformation, as a rule, turns into plastic, and then the sample collapses.
Depending on the method of applying the load, methods for testing the mechanical properties of metals, alloys and other materials are divided into static, dynamic and alternating.
Strength – the ability of metals to resist deformation or destruction under static, dynamic or alternating loads. The strength of metals under static loads is tested in tension, compression, bending and torsion. Tensile testing is mandatory. Strength under dynamic loads is assessed by specific impact strength, and under alternating loads - by fatigue strength.
To determine strength, elasticity and ductility, metals in the form of round or flat samples are tested for static tension. Tests are carried out on tensile testing machines. As a result of the tests, a tensile diagram is obtained (Fig. 3.1) . The abscissa axis of this diagram shows the strain values, and the ordinate axis shows the stress values applied to the sample.
The graph shows that no matter how small the applied stress, it causes deformation, and the initial deformations are always elastic and their magnitude is directly dependent on the stress. On the curve shown in the diagram (Fig. 3.1), elastic deformation is characterized by the line OA and its continuation.
Rice. 3.1. Strain curve
Above the point A the proportionality between stress and strain is violated. Stress causes not only elastic, but also residual, plastic deformation. Its value is equal to the horizontal segment from the dashed line to the solid curve.
During elastic deformation under the influence of an external force, the distance between atoms in the crystal lattice changes. Removing the load eliminates the cause that caused the change in the interatomic distance, the atoms return to their original places and the deformation disappears.
Plastic deformation is a completely different, much more complex process. During plastic deformation, one part of the crystal moves relative to another. If the load is removed, the displaced part of the crystal will not return to its original location; the deformation will persist. These shifts are revealed by microstructural examination. In addition, plastic deformation is accompanied by crushing of mosaic blocks inside the grains, and at significant degrees of deformation, a noticeable change in the shape of the grains and their location in space is also observed, and voids (pores) appear between the grains (sometimes inside the grains).
Represented dependency OAV(see Fig. 3.1) between externally applied voltage ( σ ) and the relative deformation caused by it ( ε ) characterizes the mechanical properties of metals.
· straight line slope OA shows metal hardness, or a characteristic of how a load applied from the outside changes interatomic distances, which, to a first approximation, characterizes the forces of interatomic attraction;
· tangent of the angle of inclination of the straight line OA proportional to elastic modulus (E), which is numerically equal to the quotient of stress divided by relative elastic deformation:
voltage, which is called the limit of proportionality ( σ pc), corresponds to the moment of appearance of plastic deformation. The more accurate the deformation measurement method, the lower the point lies A;
· in technical measurements a characteristic called yield strength (σ 0.2). This is a stress that causes a residual deformation equal to 0.2% of the length or other size of the sample or product;
maximum voltage ( σ c) corresponds to the maximum stress achieved during tension and is called temporary resistance or tensile strength .
Another characteristic of the material is the amount of plastic deformation that precedes fracture and is defined as a relative change in length (or cross-section) - the so-called relative extension (δ ) or relative narrowing (ψ ), they characterize the plasticity of the metal. Area under the curve OAV proportional to the work that must be expended to destroy the metal. This indicator, determined in various ways (mainly by striking a cut sample), characterizes viscosity metal
When a sample is stretched to the point of failure, the relationships between the applied force and the elongation of the sample are recorded graphically (Fig. 3.2), resulting in so-called deformation diagrams.

Rice. 3.2. Diagram "force (tension) - elongation"
The deformation of the sample when the alloy is loaded is first macroelastic, and then gradually and in different grains under unequal loads transforms into plastic, occurring through shear through the dislocation mechanism. The accumulation of dislocations as a result of deformation leads to strengthening of the metal, but when their density is significant, especially in individual areas, centers of destruction arise, ultimately leading to the complete destruction of the sample as a whole.
Tensile strength is assessed by the following characteristics:
1) tensile strength;
2) the limit of proportionality;
3) yield strength;
4) elastic limit;
5) elastic modulus;
6) yield strength;
7) relative elongation;
8) relative uniform elongation;
9) relative narrowing after rupture.
Tensile strength (tensile strength or tensile strength) σ in, is the voltage corresponding to the greatest load R V preceding the destruction of the sample:
σ in = P in /F 0,
This characteristic is mandatory for metals.
Proportionality limit (σ pc) – this is the conditional voltage R pc, at which the deviation from the proportional dependence of the bridge between deformation and load begins. It is equal to:
σ pc = P pc /F 0.
Values σ pc is measured in kgf/mm 2 or in MPa .
Yield strength (σ t) is the voltage ( R T) in which the sample deforms (flows) without a noticeable increase in load. Calculated by the formula:
σ t = R T / F 0 .
Elastic limit (σ 0.05) is the stress at which the residual elongation reaches 0.05% of the length of the section of the working part of the sample, equal to the base of the strain gauge. Elastic limit σ 0.05 is calculated using the formula:
σ 0,05 = P 0,05 /F 0 .
Elastic modulus (E) – the ratio of the increment in stress to the corresponding increment in elongation within the limits of elastic deformation. It is equal to:
E = Pl 0 /l avg F 0 ,
Where ∆Р– load increment; l 0– initial estimated length of the sample; l wed– average increment of elongation; F 0 – initial cross-sectional area.
Yield strength
(conditional)
– stress at which the residual elongation reaches 0.2% of the length of the sample section on its working part, the elongation of which is taken into account when determining the specified characteristic.
Calculated by the formula:
σ 0,2 = P 0,2 /F 0 .
The conditional yield strength is determined only if there is no yield plateau on the tensile diagram.
Relative extension (after the breakup) – one of the characteristics of the plasticity of materials, equal to the ratio of the increment in the estimated length of the sample after destruction ( l to) to the initial effective length ( l 0) in percentages:
Relative uniform elongation (δ р)– the ratio of the increment in the length of sections in the working part of the sample after rupture to the length before testing, expressed as a percentage.
Relative narrowing after rupture (ψ ), as well as relative elongation, is a characteristic of the plasticity of the material. Defined as the difference ratio F 0 and minimum ( F to) cross-sectional area of the sample after destruction to the initial cross-sectional area ( F 0), expressed as a percentage:
Elasticity – the property of metals to restore their previous shape after removal of external forces causing deformation. Elasticity is the opposite property of plasticity.
Very often, to determine strength, a simple, non-destructive, simplified method is used - measuring hardness.
Under hardness material is understood as resistance to penetration of a foreign body into it, i.e., in fact, hardness also characterizes resistance to deformation. There are many methods for determining hardness. The most common is Brinell method (Fig. 3.3, a), when the test body is subjected to force R a ball with a diameter of D. The Brinell hardness number (HH) is the load ( R), divided by the area of the spherical surface of the print (diameter d).

Rice. 3.3. Hardness test:
a – according to Brinell; b – according to Rockwell; c – according to Vickers
When measuring hardness Vickers method (Fig. 3.3, b) the diamond pyramid is pressed in. By measuring the diagonal of the print ( d), judge the hardness (HV) of the material.
When measuring hardness Rockwell method (Fig. 3.3, c) the indenter is a diamond cone (sometimes a small steel ball). The hardness number is the reciprocal of the indentation depth ( h). There are three scales: A, B, C (Table 3.1).
|
|
Brinell and Rockwell B scale methods are used for soft materials, Rockwell C scale method for hard materials, and Rockwell A scale method and Vickers method for thin layers (sheets). The described methods for measuring hardness characterize the average hardness of the alloy. In order to determine the hardness of individual structural components of the alloy, it is necessary to sharply localize the deformation, press the diamond pyramid into a certain place, found on a thin section at a magnification of 100 - 400 times under a very small load (from 1 to 100 gf), followed by measuring the diagonal of the indentation under a microscope . The resulting characteristic ( N) is called microhardness , and characterizes the hardness of a certain structural component.
Table 3.1 Test conditions when measuring hardness using the Rockwell method
|
Test conditions |
Designation t firmness |
|
|
R= 150 kgf |
||
|
When tested with diamond cone and load R= 60 kgf |
||
|
When pressing the steel ball and loading R= 100 kgf |
The NV value is measured in kgf/mm 2 (in this case, the units are often not indicated) or in SI - in MPa (1 kgf/mm 2 = 10 MPa).
Viscosity – the ability of metals to resist impact loads. Viscosity is the opposite property of brittleness. During operation, many parts experience not only static loads, but are also subject to shock (dynamic) loads. For example, such loads are experienced by the wheels of locomotives and cars at rail joints.
The main type of dynamic tests is impact loading of notched samples under bending conditions. Dynamic impact loading is carried out on pendulum impact drivers (Fig. 3.4), as well as with a falling load. In this case, the work expended on the deformation and destruction of the sample is determined.
Typically, in these tests, the specific work spent on deformation and destruction of the sample is determined. It is calculated using the formula:
KS =K/ S 0 ,
Where KS– specific work; TO– total work of deformation and destruction of the sample, J; S 0– cross-section of the sample at the incision site, m 2 or cm 2.

Rice. 3.4. Impact testing using a pendulum impact tester
The width of all types of specimens is measured before testing. The height of samples with a U- and V-shaped notch is measured before testing, and with a T-shaped notch after testing. Accordingly, the specific work of fracture deformation is denoted by KCU, KCV and KST.
Fragility metals at low temperatures are called cold brittleness . The value of impact strength is significantly lower than at room temperature.
Another characteristic of the mechanical properties of materials is fatigue strength. Some parts (shafts, connecting rods, springs, springs, rails, etc.) during operation experience loads that change in magnitude or simultaneously in magnitude and direction (sign). Under the influence of such alternating (vibration) loads, the metal seems to get tired, its strength decreases and the part collapses. This phenomenon is called tired metal, and the resulting fractures are fatigue. For such details you need to know endurance limit, those. the magnitude of the maximum stress that a metal can withstand without destruction for a given number of load changes (cycles) ( N).
Wear resistance – resistance of metals to wear due to friction processes. This is an important characteristic, for example, for contact materials and, in particular, for the contact wire and current-collecting elements of the current collector of electrified transport. Wear consists of the separation of individual particles from the rubbing surface and is determined by changes in the geometric dimensions or mass of the part.
Fatigue strength and wear resistance give the most complete picture of the durability of parts in structures, and toughness characterizes the reliability of these parts.