ಮ್ಯಾಟ್ರಿಕ್ಸ್ A ಯೊಂದಿಗೆ, AX = lX ನಂತಹ ಸಂಖ್ಯೆ l ಇದ್ದರೆ.

ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಸಂಖ್ಯೆ l ಅನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಸಮಾನ ಮೌಲ್ಯನಿರ್ವಾಹಕರು (ಮ್ಯಾಟ್ರಿಕ್ಸ್ A) ವೆಕ್ಟರ್ X ಗೆ ಅನುರೂಪವಾಗಿದೆ.

ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಐಜೆನ್ವೆಕ್ಟರ್ ಒಂದು ವೆಕ್ಟರ್ ಆಗಿದ್ದು, ಇದು ರೇಖೀಯ ಆಪರೇಟರ್ನ ಕ್ರಿಯೆಯ ಅಡಿಯಲ್ಲಿ, ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್ ಆಗಿ ರೂಪಾಂತರಗೊಳ್ಳುತ್ತದೆ, ಅಂದರೆ. ಕೇವಲ ಕೆಲವು ಸಂಖ್ಯೆಯಿಂದ ಗುಣಿಸಿ. ಇದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ, ಅಸಮರ್ಪಕ ವಾಹಕಗಳು ರೂಪಾಂತರಗೊಳ್ಳಲು ಹೆಚ್ಚು ಸಂಕೀರ್ಣವಾಗಿವೆ.

ಐಜೆನ್ವೆಕ್ಟರ್ನ ವ್ಯಾಖ್ಯಾನವನ್ನು ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯ ರೂಪದಲ್ಲಿ ಬರೆಯೋಣ:

ಎಲ್ಲಾ ನಿಯಮಗಳನ್ನು ಎಡಕ್ಕೆ ಸರಿಸೋಣ:

ನಂತರದ ವ್ಯವಸ್ಥೆಯನ್ನು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ರೂಪದಲ್ಲಿ ಈ ಕೆಳಗಿನಂತೆ ಬರೆಯಬಹುದು:

(A - lE)X = O

ಫಲಿತಾಂಶದ ವ್ಯವಸ್ಥೆಯು ಯಾವಾಗಲೂ ಶೂನ್ಯ ಪರಿಹಾರವನ್ನು ಹೊಂದಿರುತ್ತದೆ X = O. ಎಲ್ಲಾ ಉಚಿತ ಪದಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುವ ಅಂತಹ ವ್ಯವಸ್ಥೆಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಏಕರೂಪದ. ಅಂತಹ ಸಿಸ್ಟಮ್ನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಚೌಕವಾಗಿದ್ದರೆ ಮತ್ತು ಅದರ ನಿರ್ಣಾಯಕವು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿಲ್ಲದಿದ್ದರೆ, ಕ್ರಾಮರ್ನ ಸೂತ್ರಗಳನ್ನು ಬಳಸಿಕೊಂಡು ನಾವು ಯಾವಾಗಲೂ ಅನನ್ಯ ಪರಿಹಾರವನ್ನು ಪಡೆಯುತ್ತೇವೆ - ಶೂನ್ಯ. ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ನಿರ್ಣಾಯಕವು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿದ್ದರೆ ಮಾತ್ರ ವ್ಯವಸ್ಥೆಯು ಶೂನ್ಯವಲ್ಲದ ಪರಿಹಾರಗಳನ್ನು ಹೊಂದಿದೆ ಎಂದು ಸಾಬೀತುಪಡಿಸಬಹುದು, ಅಂದರೆ.

|ಎ - ಎಲ್‌ಇ| = = 0

ಅಜ್ಞಾತ l ನೊಂದಿಗೆ ಈ ಸಮೀಕರಣವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ (ವಿಶಿಷ್ಟ ಬಹುಪದೋಕ್ತಿ) ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ (ಲೀನಿಯರ್ ಆಪರೇಟರ್).

ರೇಖೀಯ ಆಪರೇಟರ್‌ನ ವಿಶಿಷ್ಟ ಬಹುಪದವು ಆಧಾರದ ಆಯ್ಕೆಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುವುದಿಲ್ಲ ಎಂದು ಸಾಬೀತುಪಡಿಸಬಹುದು.

ಉದಾಹರಣೆಗೆ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ A = ನಿಂದ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ರೇಖೀಯ ಆಪರೇಟರ್‌ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.

ಇದನ್ನು ಮಾಡಲು, ನಾವು ಸಂಯೋಜನೆ ಮಾಡೋಣ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ|ಎ - ಎಲ್‌ಇ| = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; ಐಜೆನ್ವಾಲ್ಯೂಸ್ l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.

ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನಾವು ಎರಡು ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಗಳನ್ನು ಪರಿಹರಿಸುತ್ತೇವೆ

(A + 5E) X = O

(A - 7E)X = O

ಅವುಗಳಲ್ಲಿ ಮೊದಲನೆಯದು, ವಿಸ್ತರಿತ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ರೂಪವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ

,

ಎಲ್ಲಿಂದ x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s, ಅಂದರೆ. X (1) = (-(2/3)s; s).

ಅವುಗಳಲ್ಲಿ ಎರಡನೆಯದು, ವಿಸ್ತರಿತ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ರೂಪವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ

,

ಎಲ್ಲಿಂದ x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, ಅಂದರೆ. X (2) = ((2/3)s 1; s 1).

ಹೀಗಾಗಿ, ಈ ರೇಖೀಯ ಆಪರೇಟರ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ರೂಪದ ಎಲ್ಲಾ ವೆಕ್ಟರ್‌ಗಳು (-(2/3) с; с) ಐಜೆನ್‌ವಾಲ್ಯೂ (-5) ಮತ್ತು ರೂಪದ ಎಲ್ಲಾ ವೆಕ್ಟರ್‌ಗಳು ((2/3) с 1 ; с 1) ಜೊತೆಗೆ ಐಜೆನ್ವಾಲ್ಯೂ 7.

ಅದರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಆಧಾರದ ಮೇಲೆ ಆಪರೇಟರ್ A ಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಕರ್ಣೀಯವಾಗಿದೆ ಮತ್ತು ರೂಪವನ್ನು ಹೊಂದಿದೆ ಎಂದು ಸಾಬೀತುಪಡಿಸಬಹುದು:

,

ಅಲ್ಲಿ ನಾನು ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು.

ಸಂಭಾಷಣೆಯು ಸಹ ನಿಜವಾಗಿದೆ: ಕೆಲವು ಆಧಾರದ ಮೇಲೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ A ಕರ್ಣೀಯವಾಗಿದ್ದರೆ, ಈ ಆಧಾರದ ಎಲ್ಲಾ ವಾಹಕಗಳು ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಆಗಿರುತ್ತವೆ.

ರೇಖೀಯ ಆಪರೇಟರ್ n ಜೋಡಿಯಾಗಿ ವಿಭಿನ್ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳನ್ನು ಹೊಂದಿದ್ದರೆ, ಅನುಗುಣವಾದ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ರೇಖೀಯವಾಗಿ ಸ್ವತಂತ್ರವಾಗಿರುತ್ತವೆ ಮತ್ತು ಅನುಗುಣವಾದ ಆಧಾರದ ಮೇಲೆ ಈ ಆಪರೇಟರ್‌ನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಕರ್ಣೀಯ ರೂಪವನ್ನು ಹೊಂದಿರುತ್ತದೆ ಎಂದು ಸಹ ಸಾಬೀತುಪಡಿಸಬಹುದು.

ಹಿಂದಿನ ಉದಾಹರಣೆಯೊಂದಿಗೆ ಇದನ್ನು ವಿವರಿಸೋಣ. ನಾವು ಅನಿಯಂತ್ರಿತ ಶೂನ್ಯವಲ್ಲದ ಮೌಲ್ಯಗಳನ್ನು c ಮತ್ತು c 1 ತೆಗೆದುಕೊಳ್ಳೋಣ, ಆದರೆ ವಾಹಕಗಳು X (1) ಮತ್ತು X (2) ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರವಾಗಿರುತ್ತವೆ, ಅಂದರೆ. ಆಧಾರವನ್ನು ರೂಪಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, c = c 1 = 3, ನಂತರ X (1) = (-2; 3), X (2) = (2; 3).

ಖಚಿತಪಡಿಸಿಕೊಳ್ಳೋಣ ರೇಖೀಯ ಸ್ವಾತಂತ್ರ್ಯಈ ವಾಹಕಗಳು:

12 ≠ 0. ಈ ಹೊಸ ಆಧಾರದಲ್ಲಿ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ A A * = ರೂಪವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ.

ಇದನ್ನು ಪರಿಶೀಲಿಸಲು, A * = C -1 AC ಸೂತ್ರವನ್ನು ಬಳಸೋಣ. ಮೊದಲಿಗೆ, ಸಿ -1 ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.

ಸಿ -1 = ;

ಕ್ವಾಡ್ರಾಟಿಕ್ ಆಕಾರಗಳು

ಕ್ವಾಡ್ರಾಟಿಕ್ ಆಕಾರ n ಅಸ್ಥಿರಗಳ f(x 1, x 2, x n) ಅನ್ನು ಮೊತ್ತ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಪ್ರತಿ ಪದವನ್ನು ಒಂದು ವೇರಿಯೇಬಲ್‌ಗಳ ವರ್ಗ ಅಥವಾ ಎರಡು ವಿಭಿನ್ನ ವೇರಿಯಬಲ್‌ಗಳ ಉತ್ಪನ್ನವನ್ನು ನಿರ್ದಿಷ್ಟ ಗುಣಾಂಕದೊಂದಿಗೆ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ: f(x 1 , x 2, x n) = (a ij = a ji).

ಈ ಗುಣಾಂಕಗಳಿಂದ ಕೂಡಿದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ A ಅನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ಚತುರ್ಭುಜ ರೂಪ. ಇದು ಯಾವಾಗಲೂ ಸಮ್ಮಿತೀಯಮ್ಯಾಟ್ರಿಕ್ಸ್ (ಅಂದರೆ ಮುಖ್ಯ ಕರ್ಣೀಯದ ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್, a ij = a ji).

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸಂಕೇತದಲ್ಲಿ, ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪವು f(X) = X T AX, ಅಲ್ಲಿ

ವಾಸ್ತವವಾಗಿ

ಉದಾಹರಣೆಗೆ, ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪವನ್ನು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ರೂಪದಲ್ಲಿ ಬರೆಯೋಣ.

ಇದನ್ನು ಮಾಡಲು, ನಾವು ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ. ಇದರ ಕರ್ಣೀಯ ಅಂಶಗಳು ಸ್ಕ್ವೇರ್ಡ್ ವೇರಿಯಬಲ್‌ಗಳ ಗುಣಾಂಕಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಉಳಿದ ಅಂಶಗಳು ಚತುರ್ಭುಜ ರೂಪದ ಅನುಗುಣವಾದ ಗುಣಾಂಕಗಳ ಅರ್ಧಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಅದಕ್ಕೇ

ಮ್ಯಾಟ್ರಿಕ್ಸ್-ಕಾಲಮ್ Y ನ ಕ್ಷೀಣಗೊಳ್ಳದ ರೇಖೀಯ ರೂಪಾಂತರದಿಂದ ವೇರಿಯೇಬಲ್‌ಗಳ ಮ್ಯಾಟ್ರಿಕ್ಸ್-ಕಾಲಮ್ ಅನ್ನು ಪಡೆಯೋಣ, ಅಂದರೆ. X = CY, ಇಲ್ಲಿ C ಎಂಬುದು n ನೇ ಕ್ರಮದ ಏಕವಚನವಲ್ಲದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ. ನಂತರ ಚತುರ್ಭುಜ ರೂಪ f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

ಹೀಗಾಗಿ, ಕ್ಷೀಣಗೊಳ್ಳದ ರೇಖೀಯ ರೂಪಾಂತರ C ಯೊಂದಿಗೆ, ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ರೂಪವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ: A * = C T AC.

ಉದಾಹರಣೆಗೆ, ರೇಖೀಯ ರೂಪಾಂತರದ ಮೂಲಕ f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದಿಂದ ಪಡೆದ ಚತುರ್ಭುಜ ರೂಪ f(y 1, y 2) ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.

ಚತುರ್ಭುಜ ರೂಪವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಅಂಗೀಕೃತ(ಇದು ಹೊಂದಿದೆ ಅಂಗೀಕೃತ ನೋಟ), i ≠ j ಗಾಗಿ ಅದರ ಎಲ್ಲಾ ಗುಣಾಂಕಗಳು a ij = 0 ಆಗಿದ್ದರೆ, ಅಂದರೆ.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = .

ಇದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಕರ್ಣೀಯವಾಗಿದೆ.

ಪ್ರಮೇಯ(ಇಲ್ಲಿ ಪುರಾವೆ ನೀಡಲಾಗಿಲ್ಲ). ಕ್ಷೀಣಗೊಳ್ಳದ ರೇಖೀಯ ರೂಪಾಂತರವನ್ನು ಬಳಸಿಕೊಂಡು ಯಾವುದೇ ಚತುರ್ಭುಜ ರೂಪವನ್ನು ಅಂಗೀಕೃತ ರೂಪಕ್ಕೆ ಇಳಿಸಬಹುದು.

ಉದಾಹರಣೆಗೆ, ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪವನ್ನು ಅಂಗೀಕೃತ ರೂಪಕ್ಕೆ ಇಳಿಸೋಣ
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

ಇದನ್ನು ಮಾಡಲು, ನಾವು ಮೊದಲು ಆಯ್ಕೆ ಮಾಡುತ್ತೇವೆ ಪರಿಪೂರ್ಣ ಚೌಕವೇರಿಯಬಲ್ x 1 ನೊಂದಿಗೆ:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

ಈಗ ನಾವು x 2 ವೇರಿಯೇಬಲ್‌ನೊಂದಿಗೆ ಸಂಪೂರ್ಣ ಚೌಕವನ್ನು ಆಯ್ಕೆ ಮಾಡುತ್ತೇವೆ:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10)x 3) 2 + (1/20)x 3 2.

ನಂತರ ಕ್ಷೀಣಗೊಳ್ಳದ ರೇಖಾತ್ಮಕ ರೂಪಾಂತರವು y 1 = x 1 + x 2, y 2 = x 2 + (1/10) x 3 ಮತ್ತು y 3 = x 3 ಈ ಚತುರ್ಭುಜ ರೂಪವನ್ನು ಅಂಗೀಕೃತ ರೂಪಕ್ಕೆ ತರುತ್ತದೆ f(y 1, y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ಅಂಗೀಕೃತ ರೂಪವನ್ನು ಅಸ್ಪಷ್ಟವಾಗಿ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ (ಅದೇ ಚತುರ್ಭುಜ ರೂಪವನ್ನು ಅಂಗೀಕೃತ ರೂಪಕ್ಕೆ ಕಡಿಮೆ ಮಾಡಬಹುದು ವಿವಿಧ ರೀತಿಯಲ್ಲಿ) ಆದಾಗ್ಯೂ, ಸ್ವೀಕರಿಸಲಾಗಿದೆ ವಿವಿಧ ರೀತಿಯಲ್ಲಿಅಂಗೀಕೃತ ರೂಪಗಳು ಹಲವಾರು ಸಾಮಾನ್ಯ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿವೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ ಹೇಳುವುದಾದರೆ, ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ಧನಾತ್ಮಕ (ಋಣಾತ್ಮಕ) ಗುಣಾಂಕಗಳೊಂದಿಗೆ ಪದಗಳ ಸಂಖ್ಯೆಯು ಈ ರೂಪಕ್ಕೆ ರೂಪವನ್ನು ಕಡಿಮೆ ಮಾಡುವ ವಿಧಾನವನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ (ಉದಾಹರಣೆಗೆ, ಪರಿಗಣಿಸಲಾದ ಉದಾಹರಣೆಯಲ್ಲಿ ಯಾವಾಗಲೂ ಎರಡು ಋಣಾತ್ಮಕ ಮತ್ತು ಒಂದು ಧನಾತ್ಮಕ ಗುಣಾಂಕ ಇರುತ್ತದೆ). ಈ ಆಸ್ತಿಯನ್ನು ಚತುರ್ಭುಜ ರೂಪಗಳ ಜಡತ್ವದ ನಿಯಮ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಅದೇ ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪವನ್ನು ಕ್ಯಾನೊನಿಕಲ್ ರೂಪಕ್ಕೆ ಬೇರೆ ರೀತಿಯಲ್ಲಿ ತರುವ ಮೂಲಕ ಇದನ್ನು ಪರಿಶೀಲಿಸೋಣ. ವೇರಿಯಬಲ್ x 2 ನೊಂದಿಗೆ ರೂಪಾಂತರವನ್ನು ಪ್ರಾರಂಭಿಸೋಣ:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2, ಅಲ್ಲಿ y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3) x 1 + (1/6) x 3 ಮತ್ತು y 3 = x 1. ಇಲ್ಲಿ y 1 ನಲ್ಲಿ ಋಣಾತ್ಮಕ ಗುಣಾಂಕ -3 ಮತ್ತು y 2 ಮತ್ತು y 3 ನಲ್ಲಿ ಎರಡು ಧನಾತ್ಮಕ ಗುಣಾಂಕಗಳು 3 ಮತ್ತು 2 (ಮತ್ತು ಇನ್ನೊಂದು ವಿಧಾನವನ್ನು ಬಳಸಿಕೊಂಡು ನಾವು y 2 ನಲ್ಲಿ ಋಣಾತ್ಮಕ ಗುಣಾಂಕ (-5) ಮತ್ತು ಎರಡು ಧನಾತ್ಮಕ ಗುಣಾಂಕಗಳನ್ನು ಪಡೆದುಕೊಂಡಿದ್ದೇವೆ: 2 ನಲ್ಲಿ y 1 ಮತ್ತು 1/20 y 3).

ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಶ್ರೇಣಿಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಎಂದು ಸಹ ಗಮನಿಸಬೇಕು ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ಶ್ರೇಣಿ, ಅಂಗೀಕೃತ ರೂಪದ ಶೂನ್ಯವಲ್ಲದ ಗುಣಾಂಕಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ರೇಖೀಯ ರೂಪಾಂತರಗಳ ಅಡಿಯಲ್ಲಿ ಬದಲಾಗುವುದಿಲ್ಲ.

ಚತುರ್ಭುಜ ರೂಪ f(X) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಧನಾತ್ಮಕವಾಗಿ (ಋಣಾತ್ಮಕ) ನಿಶ್ಚಿತ, ಶೂನ್ಯಕ್ಕೆ ಏಕಕಾಲದಲ್ಲಿ ಸಮಾನವಾಗಿರದ ವೇರಿಯೇಬಲ್‌ಗಳ ಎಲ್ಲಾ ಮೌಲ್ಯಗಳಿಗೆ, ಅದು ಧನಾತ್ಮಕವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. f(X) > 0 (ಋಣಾತ್ಮಕ, ಅಂದರೆ.
f(X)< 0).

ಉದಾಹರಣೆಗೆ, ಚತುರ್ಭುಜ ರೂಪ f 1 (X) = x 1 2 + x 2 2 ಧನಾತ್ಮಕ ಖಚಿತವಾಗಿದೆ, ಏಕೆಂದರೆ ಚೌಕಗಳ ಮೊತ್ತವಾಗಿದೆ, ಮತ್ತು ಚತುರ್ಭುಜ ರೂಪ f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 ಋಣಾತ್ಮಕ ನಿಶ್ಚಿತ, ಏಕೆಂದರೆ ಪ್ರತಿನಿಧಿಸುತ್ತದೆ ಇದನ್ನು f 2 (X) = -(x 1 - x 2) 2 ಎಂದು ಪ್ರತಿನಿಧಿಸಬಹುದು.

ಹೆಚ್ಚಿನ ಪ್ರಾಯೋಗಿಕ ಸಂದರ್ಭಗಳಲ್ಲಿ, ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ನಿರ್ದಿಷ್ಟ ಚಿಹ್ನೆಯನ್ನು ಸ್ಥಾಪಿಸುವುದು ಸ್ವಲ್ಪ ಹೆಚ್ಚು ಕಷ್ಟಕರವಾಗಿದೆ, ಆದ್ದರಿಂದ ಇದಕ್ಕಾಗಿ ನಾವು ಈ ಕೆಳಗಿನ ಪ್ರಮೇಯಗಳಲ್ಲಿ ಒಂದನ್ನು ಬಳಸುತ್ತೇವೆ (ನಾವು ಅವುಗಳನ್ನು ಪುರಾವೆಗಳಿಲ್ಲದೆ ರೂಪಿಸುತ್ತೇವೆ).

ಪ್ರಮೇಯ. ಒಂದು ಚತುರ್ಭುಜ ರೂಪವು ಧನಾತ್ಮಕ (ಋಣಾತ್ಮಕ) ನಿರ್ದಿಷ್ಟವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಎಲ್ಲಾ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಧನಾತ್ಮಕ (ಋಣಾತ್ಮಕ) ಆಗಿದ್ದರೆ ಮಾತ್ರ.

ಪ್ರಮೇಯ(ಸಿಲ್ವೆಸ್ಟರ್ ಮಾನದಂಡ). ಈ ರೂಪದ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಎಲ್ಲಾ ಪ್ರಮುಖ ಅಪ್ರಾಪ್ತ ವಯಸ್ಕರು ಧನಾತ್ಮಕವಾಗಿದ್ದರೆ ಮಾತ್ರ ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪವು ಧನಾತ್ಮಕವಾಗಿರುತ್ತದೆ.

ಮುಖ್ಯ (ಮೂಲೆಯಲ್ಲಿ) ಮೈನರ್ n ನೇ ಕ್ರಮಾಂಕದ kth ಆರ್ಡರ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ A ಅನ್ನು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಡಿಟರ್ಮಿನೆಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಇದು ಮ್ಯಾಟ್ರಿಕ್ಸ್ A () ನ ಮೊದಲ k ಸಾಲುಗಳು ಮತ್ತು ಕಾಲಮ್‌ಗಳಿಂದ ಕೂಡಿದೆ.

ಋಣಾತ್ಮಕ ನಿರ್ದಿಷ್ಟ ಚತುರ್ಭುಜ ರೂಪಗಳಿಗೆ ಪ್ರಧಾನ ಅಪ್ರಾಪ್ತ ವಯಸ್ಕರ ಚಿಹ್ನೆಗಳು ಪರ್ಯಾಯವಾಗಿರುತ್ತವೆ ಮತ್ತು ಮೊದಲ-ಕ್ರಮದ ಮೈನರ್ ಋಣಾತ್ಮಕವಾಗಿರಬೇಕು ಎಂಬುದನ್ನು ಗಮನಿಸಿ.

ಉದಾಹರಣೆಗೆ, ಚಿಹ್ನೆಯ ನಿಶ್ಚಿತತೆಗಾಗಿ ನಾವು f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪವನ್ನು ಪರಿಶೀಲಿಸೋಣ.

= (2 - l)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
. ಆದ್ದರಿಂದ, ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪವು ಧನಾತ್ಮಕ ನಿಶ್ಚಿತವಾಗಿದೆ.

ವಿಧಾನ 2. ಮ್ಯಾಟ್ರಿಕ್ಸ್ A D 1 = a 11 = 2 > 0 ರ ಮೊದಲ ಕ್ರಮಾಂಕದ ಪ್ರಿನ್ಸಿಪಲ್ ಮೈನರ್ D 2 = = 6 - 4 = 2 > 0. ಆದ್ದರಿಂದ, ಸಿಲ್ವೆಸ್ಟರ್ನ ಮಾನದಂಡದ ಪ್ರಕಾರ, ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪ ಧನಾತ್ಮಕ ಖಚಿತ.

ಚಿಹ್ನೆಯ ನಿಶ್ಚಿತತೆಗಾಗಿ ನಾವು ಇನ್ನೊಂದು ಚತುರ್ಭುಜ ರೂಪವನ್ನು ಪರಿಶೀಲಿಸುತ್ತೇವೆ, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

ವಿಧಾನ 1. A = ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ನಿರ್ಮಿಸೋಣ. ವಿಶಿಷ್ಟ ಸಮೀಕರಣವು ರೂಪವನ್ನು ಹೊಂದಿರುತ್ತದೆ = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. ಆದ್ದರಿಂದ, ಚತುರ್ಭುಜ ರೂಪವು ಋಣಾತ್ಮಕ ನಿಶ್ಚಿತವಾಗಿದೆ.

ವಿಧಾನ 2. ಮ್ಯಾಟ್ರಿಕ್ಸ್ A D 1 = a 11 = ನ ಮೊದಲ ಕ್ರಮದ ಪ್ರಮುಖ ಮೈನರ್
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. ಪರಿಣಾಮವಾಗಿ, ಸಿಲ್ವೆಸ್ಟರ್ನ ಮಾನದಂಡದ ಪ್ರಕಾರ, ಚತುರ್ಭುಜ ರೂಪವು ಋಣಾತ್ಮಕ ನಿಶ್ಚಿತವಾಗಿದೆ (ಮುಖ್ಯ ಅಪ್ರಾಪ್ತ ವಯಸ್ಕರ ಚಿಹ್ನೆಗಳು ಪರ್ಯಾಯವಾಗಿ, ಮೈನಸ್ನಿಂದ ಪ್ರಾರಂಭವಾಗುತ್ತದೆ).

ಮತ್ತು ಇನ್ನೊಂದು ಉದಾಹರಣೆಯಾಗಿ, ನಾವು ಚಿಹ್ನೆ-ನಿರ್ಧರಿತ ಚತುರ್ಭುಜ ರೂಪ f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 ಅನ್ನು ಪರಿಶೀಲಿಸುತ್ತೇವೆ.

ವಿಧಾನ 1. A = ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ನಿರ್ಮಿಸೋಣ. ವಿಶಿಷ್ಟ ಸಮೀಕರಣವು ರೂಪವನ್ನು ಹೊಂದಿರುತ್ತದೆ = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

ಈ ಸಂಖ್ಯೆಗಳಲ್ಲಿ ಒಂದು ಋಣಾತ್ಮಕ ಮತ್ತು ಇನ್ನೊಂದು ಧನಾತ್ಮಕವಾಗಿರುತ್ತದೆ. ಐಜೆನ್ವಾಲ್ಯೂಸ್ನ ಚಿಹ್ನೆಗಳು ವಿಭಿನ್ನವಾಗಿವೆ. ಪರಿಣಾಮವಾಗಿ, ಚತುರ್ಭುಜ ರೂಪವು ಋಣಾತ್ಮಕವಾಗಿ ಅಥವಾ ಧನಾತ್ಮಕವಾಗಿ ನಿರ್ದಿಷ್ಟವಾಗಿರುವುದಿಲ್ಲ, ಅಂದರೆ. ಈ ಚತುರ್ಭುಜ ರೂಪವು ಚಿಹ್ನೆ-ನಿರ್ದಿಷ್ಟವಾಗಿಲ್ಲ (ಇದು ಯಾವುದೇ ಚಿಹ್ನೆಯ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು).

ವಿಧಾನ 2. ಮ್ಯಾಟ್ರಿಕ್ಸ್ A D 1 = a 11 = 2 > 0 ರ ಮೊದಲ ಕ್ರಮದ ಪ್ರಿನ್ಸಿಪಲ್ ಮೈನರ್ D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

ಏಕರೂಪದ ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆ

ಏಕರೂಪದ ವ್ಯವಸ್ಥೆ ರೇಖೀಯ ಸಮೀಕರಣಗಳುರೂಪದ ವ್ಯವಸ್ಥೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ

ಈ ಸಂದರ್ಭದಲ್ಲಿ ಅದು ಸ್ಪಷ್ಟವಾಗಿದೆ , ಏಕೆಂದರೆ ಈ ನಿರ್ಣಾಯಕಗಳಲ್ಲಿನ ಒಂದು ಕಾಲಮ್‌ನ ಎಲ್ಲಾ ಅಂಶಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಅಪರಿಚಿತರು ಸೂತ್ರಗಳ ಪ್ರಕಾರ ಕಂಡುಬರುವುದರಿಂದ , ನಂತರ ಸಂದರ್ಭದಲ್ಲಿ Δ ≠ 0, ಸಿಸ್ಟಮ್ ಒಂದು ಅನನ್ಯ ಶೂನ್ಯ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ X = ವೈ = z= 0. ಆದಾಗ್ಯೂ, ಅನೇಕ ಸಮಸ್ಯೆಗಳಲ್ಲಿ ಆಸಕ್ತಿದಾಯಕ ಪ್ರಶ್ನೆಯೆಂದರೆ ಏಕರೂಪದ ವ್ಯವಸ್ಥೆಶೂನ್ಯವನ್ನು ಹೊರತುಪಡಿಸಿ ಪರಿಹಾರಗಳು.

ಪ್ರಮೇಯ.ರೇಖೀಯ ವ್ಯವಸ್ಥೆಗಾಗಿ ಏಕರೂಪದ ಸಮೀಕರಣಗಳುಶೂನ್ಯವಲ್ಲದ ಪರಿಹಾರವನ್ನು ಹೊಂದಿತ್ತು, ಇದು Δ ≠ 0 ಆಗಿರುವುದು ಅವಶ್ಯಕ ಮತ್ತು ಸಾಕಾಗುತ್ತದೆ.

ಆದ್ದರಿಂದ, ನಿರ್ಣಾಯಕ Δ ≠ 0 ಆಗಿದ್ದರೆ, ಸಿಸ್ಟಮ್ ವಿಶಿಷ್ಟ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ. Δ ≠ 0 ಆಗಿದ್ದರೆ, ರೇಖೀಯ ಏಕರೂಪದ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯು ಅನಂತ ಸಂಖ್ಯೆಯ ಪರಿಹಾರಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ.

ಉದಾಹರಣೆಗಳು.

ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ಮತ್ತು ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು

ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನೀಡಲಿ , X- ಕೆಲವು ಮ್ಯಾಟ್ರಿಕ್ಸ್-ಕಾಲಮ್, ಅದರ ಎತ್ತರವು ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಕ್ರಮದೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ ಎ. .

ಅನೇಕ ಸಮಸ್ಯೆಗಳಲ್ಲಿ ನಾವು ಸಮೀಕರಣವನ್ನು ಪರಿಗಣಿಸಬೇಕು X

ಅಲ್ಲಿ λ ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆ. ಯಾವುದೇ λ ಗೆ ಈ ಸಮೀಕರಣವು ಶೂನ್ಯ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ.

ಈ ಸಮೀಕರಣವು ಶೂನ್ಯವಲ್ಲದ ಪರಿಹಾರಗಳನ್ನು ಹೊಂದಿರುವ ಸಂಖ್ಯೆಯನ್ನು λ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಸಮಾನ ಮೌಲ್ಯಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ, ಎ Xಅಂತಹ λ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಐಜೆನ್ವೆಕ್ಟರ್ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ ಎ. ಏಕೆಂದರೆ ದಿ ಇ∙X = X, ನಂತರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸಮೀಕರಣವನ್ನು ಹೀಗೆ ಪುನಃ ಬರೆಯಬಹುದು ಅಥವಾ . ವಿಸ್ತೃತ ರೂಪದಲ್ಲಿ, ಈ ಸಮೀಕರಣವನ್ನು ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯಾಗಿ ಪುನಃ ಬರೆಯಬಹುದು. ನಿಜವಾಗಿಯೂ .

ಆದ್ದರಿಂದ

ಆದ್ದರಿಂದ, ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನಿರ್ಧರಿಸಲು ನಾವು ಏಕರೂಪದ ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆದುಕೊಂಡಿದ್ದೇವೆ x 1, x 2, x 3ವೆಕ್ಟರ್ X. ಒಂದು ವ್ಯವಸ್ಥೆಯು ಶೂನ್ಯವಲ್ಲದ ಪರಿಹಾರಗಳನ್ನು ಹೊಂದಲು ಸಿಸ್ಟಮ್ನ ನಿರ್ಣಾಯಕವು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರಬೇಕು ಮತ್ತು ಸಾಕಾಗುತ್ತದೆ, ಅಂದರೆ.

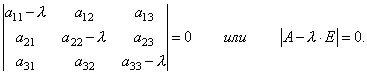
ಇದು λ ಗೆ 3ನೇ ಡಿಗ್ರಿ ಸಮೀಕರಣವಾಗಿದೆ. ಇದನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಮತ್ತು λ ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ.

ಪ್ರತಿ ಐಜೆನ್‌ವಾಲ್ಯೂ λ ಐಜೆನ್‌ವೆಕ್ಟರ್‌ಗೆ ಅನುರೂಪವಾಗಿದೆ X, ಇದರ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು λ ನ ಅನುಗುಣವಾದ ಮೌಲ್ಯದಲ್ಲಿ ಸಿಸ್ಟಮ್‌ನಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.

ಉದಾಹರಣೆಗಳು.

ವೆಕ್ಟರ್ ಬೀಜಗಣಿತ. ದಿ ಕಾನ್ಸೆಪ್ಟ್ ಆಫ್ ವೆಕ್ಟರ್

ಭೌತಶಾಸ್ತ್ರದ ವಿವಿಧ ಶಾಖೆಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡುವಾಗ, ಅವುಗಳ ಸಂಖ್ಯಾತ್ಮಕ ಮೌಲ್ಯಗಳನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸುವ ಮೂಲಕ ಸಂಪೂರ್ಣವಾಗಿ ನಿರ್ಧರಿಸುವ ಪ್ರಮಾಣಗಳಿವೆ, ಉದಾಹರಣೆಗೆ, ಉದ್ದ, ಪ್ರದೇಶ, ದ್ರವ್ಯರಾಶಿ, ತಾಪಮಾನ, ಇತ್ಯಾದಿ. ಅಂತಹ ಪ್ರಮಾಣಗಳನ್ನು ಸ್ಕೇಲಾರ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಅವುಗಳ ಜೊತೆಗೆ, ಪ್ರಮಾಣಗಳು ಸಹ ಇವೆ, ಸಂಖ್ಯಾತ್ಮಕ ಮೌಲ್ಯದ ಜೊತೆಗೆ, ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಅವುಗಳ ದಿಕ್ಕನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದು ಸಹ ಅಗತ್ಯವಾಗಿದೆ, ಉದಾಹರಣೆಗೆ, ದೇಹದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಶಕ್ತಿ, ವೇಗ ಮತ್ತು ವೇಗವರ್ಧನೆ ದೇಹವು ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಚಲಿಸುವಾಗ, ಉದ್ವೇಗ ಕಾಂತೀಯ ಕ್ಷೇತ್ರಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ, ಇತ್ಯಾದಿ. ಅಂತಹ ಪ್ರಮಾಣಗಳನ್ನು ವೆಕ್ಟರ್ ಪ್ರಮಾಣಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ನಾವು ಕಟ್ಟುನಿಟ್ಟಾದ ವ್ಯಾಖ್ಯಾನವನ್ನು ಪರಿಚಯಿಸೋಣ.

ನಿರ್ದೇಶಿಸಿದ ವಿಭಾಗಒಂದು ವಿಭಾಗವನ್ನು ಕರೆಯೋಣ, ಅದರ ತುದಿಗಳಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಅವುಗಳಲ್ಲಿ ಯಾವುದು ಮೊದಲನೆಯದು ಮತ್ತು ಎರಡನೆಯದು ಎಂದು ತಿಳಿಯುತ್ತದೆ.

ವೆಕ್ಟರ್ನಿರ್ದಿಷ್ಟ ಉದ್ದವನ್ನು ಹೊಂದಿರುವ ನಿರ್ದೇಶಿತ ವಿಭಾಗ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅಂದರೆ. ಇದು ಒಂದು ನಿರ್ದಿಷ್ಟ ಉದ್ದದ ವಿಭಾಗವಾಗಿದೆ, ಇದರಲ್ಲಿ ಅದನ್ನು ಸೀಮಿತಗೊಳಿಸುವ ಬಿಂದುಗಳಲ್ಲಿ ಒಂದನ್ನು ಪ್ರಾರಂಭವಾಗಿ ಮತ್ತು ಎರಡನೆಯದನ್ನು ಅಂತ್ಯವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಒಂದು ವೇಳೆ ಎ- ವೆಕ್ಟರ್ನ ಪ್ರಾರಂಭ, ಬಿಅದರ ಅಂತ್ಯ, ನಂತರ ವೆಕ್ಟರ್ ಅನ್ನು ಚಿಹ್ನೆಯಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ; ಜೊತೆಗೆ, ವೆಕ್ಟರ್ ಅನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಒಂದೇ ಅಕ್ಷರದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಚಿತ್ರದಲ್ಲಿ, ವೆಕ್ಟರ್ ಅನ್ನು ಒಂದು ವಿಭಾಗದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಅದರ ದಿಕ್ಕನ್ನು ಬಾಣದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.

ಘಟಕಅಥವಾ ಉದ್ದವೆಕ್ಟರ್ ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವ ನಿರ್ದೇಶಿತ ವಿಭಾಗದ ಉದ್ದ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಸೂಚಿಸಿದ || ಅಥವಾ ||.

ನಾವು ಶೂನ್ಯ ವೆಕ್ಟರ್ ಎಂದು ಕರೆಯಲ್ಪಡುವದನ್ನು ಸಹ ಸೇರಿಸುತ್ತೇವೆ, ಅದರ ಪ್ರಾರಂಭ ಮತ್ತು ಅಂತ್ಯವು ವೆಕ್ಟರ್‌ಗಳಾಗಿ ಸೇರಿಕೊಳ್ಳುತ್ತದೆ. ಇದನ್ನು ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ. ಶೂನ್ಯ ವೆಕ್ಟರ್ ನಿರ್ದಿಷ್ಟ ದಿಕ್ಕನ್ನು ಹೊಂದಿಲ್ಲ ಮತ್ತು ಅದರ ಮಾಡ್ಯುಲಸ್ ಶೂನ್ಯ ||=0.

ವಾಹಕಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಕೊಲಿನಿಯರ್, ಅವರು ಒಂದೇ ಸಾಲಿನಲ್ಲಿ ಅಥವಾ ಸಮಾನಾಂತರ ರೇಖೆಗಳಲ್ಲಿ ನೆಲೆಗೊಂಡಿದ್ದರೆ. ಇದಲ್ಲದೆ, ವಾಹಕಗಳು ಮತ್ತು ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿದ್ದರೆ, ನಾವು ಬರೆಯುತ್ತೇವೆ , ವಿರುದ್ಧ.

ಒಂದೇ ಸಮತಲಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿ ನೇರ ರೇಖೆಗಳ ಮೇಲೆ ಇರುವ ವೆಕ್ಟರ್ಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಕೋಪ್ಲಾನರ್.

ಎರಡು ವಾಹಕಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಸಮಾನ, ಅವು ಕಾಲಿನಿಯರ್ ಆಗಿದ್ದರೆ, ಒಂದೇ ದಿಕ್ಕನ್ನು ಹೊಂದಿರುತ್ತವೆ ಮತ್ತು ಉದ್ದದಲ್ಲಿ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ ಅವರು ಬರೆಯುತ್ತಾರೆ.

ವೆಕ್ಟರ್‌ಗಳ ಸಮಾನತೆಯ ವ್ಯಾಖ್ಯಾನದಿಂದ ವೆಕ್ಟರ್ ಅನ್ನು ಸಮಾನಾಂತರವಾಗಿ ಸಾಗಿಸಬಹುದು, ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಯಾವುದೇ ಹಂತದಲ್ಲಿ ಅದರ ಮೂಲವನ್ನು ಇರಿಸಬಹುದು.

ಉದಾಹರಣೆಗೆ.

ವೆಕ್ಟರ್‌ಗಳ ಮೇಲೆ ರೇಖೀಯ ಕಾರ್ಯಾಚರಣೆಗಳು

1. ವೆಕ್ಟರ್ ಅನ್ನು ಸಂಖ್ಯೆಯಿಂದ ಗುಣಿಸುವುದು.

   ವೆಕ್ಟರ್ ಮತ್ತು ಸಂಖ್ಯೆ λ ನ ಉತ್ಪನ್ನವು ಹೊಸ ವೆಕ್ಟರ್ ಆಗಿದೆ:

   ವೆಕ್ಟರ್ ಮತ್ತು ಸಂಖ್ಯೆಯ λ ನ ಉತ್ಪನ್ನವನ್ನು ಸೂಚಿಸಲಾಗಿದೆ.

   

   ಉದಾಹರಣೆಗೆ,ವೆಕ್ಟರ್‌ನಂತೆಯೇ ಅದೇ ದಿಕ್ಕಿನಲ್ಲಿ ನಿರ್ದೇಶಿಸಿದ ವೆಕ್ಟರ್ ಮತ್ತು ವೆಕ್ಟರ್‌ನ ಅರ್ಧದಷ್ಟು ಉದ್ದವನ್ನು ಹೊಂದಿದೆ.

   ಪರಿಚಯಿಸಲಾದ ಕಾರ್ಯಾಚರಣೆಯು ಈ ಕೆಳಗಿನವುಗಳನ್ನು ಹೊಂದಿದೆ ಗುಣಲಕ್ಷಣಗಳು:

2. ವೆಕ್ಟರ್ ಸೇರ್ಪಡೆ.

   ಲೆಟ್ ಮತ್ತು ಎರಡು ಅನಿಯಂತ್ರಿತ ವೆಕ್ಟರ್ ಆಗಿರಿ. ಅನಿಯಂತ್ರಿತ ಅಂಶವನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ ಓಮತ್ತು ವೆಕ್ಟರ್ ಅನ್ನು ನಿರ್ಮಿಸಿ. ಬಿಂದುವಿನಿಂದ ಅದರ ನಂತರ ಎವೆಕ್ಟರ್ ಅನ್ನು ಪಕ್ಕಕ್ಕೆ ಇಡೋಣ. ಮೊದಲ ವೆಕ್ಟರ್ನ ಆರಂಭವನ್ನು ಎರಡನೆಯ ಅಂತ್ಯದೊಂದಿಗೆ ಸಂಪರ್ಕಿಸುವ ವೆಕ್ಟರ್ ಅನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಮೊತ್ತಈ ವಾಹಕಗಳ ಮತ್ತು ಸೂಚಿಸಲಾಗುತ್ತದೆ .

   

   ವೆಕ್ಟರ್ ಸೇರ್ಪಡೆಯ ಸೂತ್ರೀಕರಿಸಿದ ವ್ಯಾಖ್ಯಾನವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜ ನಿಯಮ, ವಾಹಕಗಳ ಒಂದೇ ಮೊತ್ತವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಪಡೆಯಬಹುದು. ಹಂತದಿಂದ ಮುಂದೂಡೋಣ ಓವಾಹಕಗಳು ಮತ್ತು . ಈ ವೆಕ್ಟರ್‌ಗಳ ಮೇಲೆ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜವನ್ನು ನಿರ್ಮಿಸೋಣ OABC. ವೆಕ್ಟರ್‌ಗಳಿಂದ, ನಂತರ ವೆಕ್ಟರ್, ಇದು ಶೃಂಗದಿಂದ ಎಳೆಯಲಾದ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಕರ್ಣವಾಗಿದೆ ಓ, ನಿಸ್ಸಂಶಯವಾಗಿ ವೆಕ್ಟರ್‌ಗಳ ಮೊತ್ತವಾಗಿರುತ್ತದೆ.

   

   ಕೆಳಗಿನವುಗಳನ್ನು ಪರಿಶೀಲಿಸುವುದು ಸುಲಭ ವೆಕ್ಟರ್ ಸೇರ್ಪಡೆಯ ಗುಣಲಕ್ಷಣಗಳು.

3. ವೆಕ್ಟರ್ ವ್ಯತ್ಯಾಸ.

   ನೀಡಿರುವ ವೆಕ್ಟರ್‌ಗೆ ವೆಕ್ಟರ್ ಕೊಲಿನಿಯರ್, ಉದ್ದದಲ್ಲಿ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ವಿರುದ್ಧವಾಗಿ ನಿರ್ದೇಶಿಸಲ್ಪಡುತ್ತದೆ, ಇದನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ವಿರುದ್ದವೆಕ್ಟರ್ಗಾಗಿ ವೆಕ್ಟರ್ ಮತ್ತು ಇದನ್ನು ಸೂಚಿಸಲಾಗಿದೆ. λ = –1: ಸಂಖ್ಯೆಯಿಂದ ವೆಕ್ಟರ್ ಅನ್ನು ಗುಣಿಸಿದಾಗ ವಿರುದ್ಧ ವೆಕ್ಟರ್ ಅನ್ನು ಪರಿಗಣಿಸಬಹುದು.

ಐಜೆನ್ವಾಲ್ಯೂಸ್(ಸಂಖ್ಯೆಗಳು) ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು.
ಪರಿಹಾರಗಳ ಉದಾಹರಣೆಗಳು

ನೀನು ನೀನಾಗಿರು

ಎರಡೂ ಸಮೀಕರಣಗಳಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ.

ನಂತರ ಅದನ್ನು ಹಾಕೋಣ: .

ಪರಿಣಾಮವಾಗಿ: - ಎರಡನೇ ಐಜೆನ್ವೆಕ್ಟರ್.

ಪುನರಾವರ್ತಿಸೋಣ ಪ್ರಮುಖ ಅಂಶಗಳುಪರಿಹಾರಗಳು:

- ಪರಿಣಾಮವಾಗಿ ವ್ಯವಸ್ಥೆಯು ಖಂಡಿತವಾಗಿಯೂ ಹೊಂದಿದೆ ಸಾಮಾನ್ಯ ನಿರ್ಧಾರ(ಸಮೀಕರಣಗಳು ರೇಖಾತ್ಮಕವಾಗಿ ಅವಲಂಬಿತವಾಗಿವೆ);

- ನಾವು "y" ಅನ್ನು ಪೂರ್ಣಾಂಕದ ರೀತಿಯಲ್ಲಿ ಆಯ್ಕೆ ಮಾಡುತ್ತೇವೆ ಮತ್ತು ಮೊದಲ "x" ನಿರ್ದೇಶಾಂಕವು ಪೂರ್ಣಾಂಕ, ಧನಾತ್ಮಕ ಮತ್ತು ಸಾಧ್ಯವಾದಷ್ಟು ಚಿಕ್ಕದಾಗಿದೆ.

- ನಿರ್ದಿಷ್ಟ ಪರಿಹಾರವು ವ್ಯವಸ್ಥೆಯ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆಯೇ ಎಂದು ನಾವು ಪರಿಶೀಲಿಸುತ್ತೇವೆ.

ಉತ್ತರ .

ಮಧ್ಯಂತರ " ನಿಯಂತ್ರಣ ಬಿಂದುಗಳು"ಸಾಕಷ್ಟು ಸಾಕಾಗಿತ್ತು, ಆದ್ದರಿಂದ ಸಮಾನತೆಗಳನ್ನು ಪರಿಶೀಲಿಸುವುದು ತಾತ್ವಿಕವಾಗಿ ಅನಗತ್ಯವಾಗಿದೆ.

ಮಾಹಿತಿಯ ವಿವಿಧ ಮೂಲಗಳಲ್ಲಿ, ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಕಾಲಮ್‌ಗಳಲ್ಲಿ ಬರೆಯಲಾಗುವುದಿಲ್ಲ, ಆದರೆ ಸಾಲುಗಳಲ್ಲಿ ಬರೆಯಲಾಗುತ್ತದೆ, ಉದಾಹರಣೆಗೆ: (ಮತ್ತು, ಪ್ರಾಮಾಣಿಕವಾಗಿ ಹೇಳಬೇಕೆಂದರೆ, ನಾನು ಅವುಗಳನ್ನು ಸಾಲುಗಳಲ್ಲಿ ಬರೆಯಲು ಬಳಸಲಾಗುತ್ತದೆ). ಈ ಆಯ್ಕೆಯು ಸ್ವೀಕಾರಾರ್ಹವಾಗಿದೆ, ಆದರೆ ವಿಷಯದ ಬೆಳಕಿನಲ್ಲಿ ರೇಖೀಯ ರೂಪಾಂತರಗಳುತಾಂತ್ರಿಕವಾಗಿ ಬಳಸಲು ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ ಕಾಲಮ್ ವಾಹಕಗಳು.

ಬಹುಶಃ ಪರಿಹಾರವು ನಿಮಗೆ ಬಹಳ ಉದ್ದವಾಗಿದೆ ಎಂದು ತೋರುತ್ತದೆ, ಆದರೆ ಇದು ನಾನು ಮೊದಲ ಉದಾಹರಣೆಯನ್ನು ಹೆಚ್ಚು ವಿವರವಾಗಿ ಕಾಮೆಂಟ್ ಮಾಡಿದ್ದರಿಂದ ಮಾತ್ರ.

ಉದಾಹರಣೆ 2

ಮ್ಯಾಟ್ರಿಸಸ್

ಸ್ವಂತವಾಗಿ ತರಬೇತಿ ನೀಡೋಣ! ಪಾಠದ ಕೊನೆಯಲ್ಲಿ ಅಂತಿಮ ಕಾರ್ಯದ ಅಂದಾಜು ಉದಾಹರಣೆ.

ಕೆಲವೊಮ್ಮೆ ನೀವು ಮಾಡಬೇಕಾಗಿದೆ ಹೆಚ್ಚುವರಿ ಕಾರ್ಯ, ಅವುಗಳೆಂದರೆ:

ಅಂಗೀಕೃತ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವಿಭಜನೆಯನ್ನು ಬರೆಯಿರಿ

ಅದು ಏನು?

ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು ರೂಪುಗೊಂಡರೆ ಆಧಾರದ, ನಂತರ ಇದನ್ನು ಹೀಗೆ ಪ್ರತಿನಿಧಿಸಬಹುದು:

ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಕೂಡಿದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಲ್ಲಿದೆ, - ಕರ್ಣೀಯಅನುಗುಣವಾದ ಐಜೆನ್ವಾಲ್ಯೂಗಳೊಂದಿಗೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್.

ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ವಿಭಜನೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಅಂಗೀಕೃತಅಥವಾ ಕರ್ಣೀಯ.

ಮೊದಲ ಉದಾಹರಣೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ನೋಡೋಣ. ಇದರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು ರೇಖೀಯವಾಗಿ ಸ್ವತಂತ್ರ(ಕಾಲಿನಿಯರ್ ಅಲ್ಲದ) ಮತ್ತು ಆಧಾರವನ್ನು ರೂಪಿಸುತ್ತದೆ. ಅವರ ನಿರ್ದೇಶಾಂಕಗಳ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ರಚಿಸೋಣ:

ಆನ್ ಮುಖ್ಯ ಕರ್ಣೀಯಮ್ಯಾಟ್ರಿಕ್ಸ್ ಸೂಕ್ತ ಕ್ರಮದಲ್ಲಿಐಜೆನ್ವಾಲ್ಯೂಗಳು ನೆಲೆಗೊಂಡಿವೆ, ಮತ್ತು ಉಳಿದ ಅಂಶಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:
- ನಾನು ಮತ್ತೊಮ್ಮೆ ಆದೇಶದ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಒತ್ತಿಹೇಳುತ್ತೇನೆ: "ಎರಡು" 1 ನೇ ವೆಕ್ಟರ್ಗೆ ಅನುರೂಪವಾಗಿದೆ ಮತ್ತು ಆದ್ದರಿಂದ 1 ನೇ ಕಾಲಮ್ನಲ್ಲಿ "ಮೂರು" - 2 ನೇ ವೆಕ್ಟರ್ಗೆ ಇದೆ.

ಮೂಲಕ ಸಾಮಾನ್ಯ ಅಲ್ಗಾರಿದಮ್ಗೆಕಂಡುಹಿಡಿಯುವುದು ವಿಲೋಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್ಅಥವಾ ಗಾಸ್-ಜೋರ್ಡಾನ್ ವಿಧಾನನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ . ಇಲ್ಲ, ಅದು ಮುದ್ರಣದೋಷವಲ್ಲ! - ನಿಮ್ಮ ಮೊದಲು ಒಂದು ಅಪರೂಪದ ಘಟನೆಯಾಗಿದೆ, ಸೂರ್ಯಗ್ರಹಣದಂತೆ, ರಿವರ್ಸ್ ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾದಾಗ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಅಂಗೀಕೃತ ವಿಭಜನೆಯನ್ನು ಬರೆಯಲು ಇದು ಉಳಿದಿದೆ:

ಪ್ರಾಥಮಿಕ ರೂಪಾಂತರಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಸಿಸ್ಟಮ್ ಅನ್ನು ಪರಿಹರಿಸಬಹುದು ಮತ್ತು ಕೆಳಗಿನ ಉದಾಹರಣೆಗಳಲ್ಲಿ ನಾವು ಆಶ್ರಯಿಸುತ್ತೇವೆ ಈ ವಿಧಾನ. ಆದರೆ ಇಲ್ಲಿ "ಶಾಲೆ" ವಿಧಾನವು ಹೆಚ್ಚು ವೇಗವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ. 3 ನೇ ಸಮೀಕರಣದಿಂದ ನಾವು ವ್ಯಕ್ತಪಡಿಸುತ್ತೇವೆ: - ಎರಡನೇ ಸಮೀಕರಣಕ್ಕೆ ಬದಲಿಯಾಗಿ:

ಮೊದಲ ನಿರ್ದೇಶಾಂಕವು ಶೂನ್ಯವಾಗಿರುವುದರಿಂದ, ನಾವು ಒಂದು ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ, ಅದರ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣದಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ .

ಮತ್ತು ಮತ್ತೆ ರೇಖೀಯ ಸಂಬಂಧದ ಕಡ್ಡಾಯ ಉಪಸ್ಥಿತಿಗೆ ಗಮನ ಕೊಡಿ. ಕ್ಷುಲ್ಲಕ ಪರಿಹಾರ ಮಾತ್ರ ಸಿಕ್ಕಿದರೆ , ನಂತರ ಐಜೆನ್‌ವಾಲ್ಯೂ ತಪ್ಪಾಗಿ ಕಂಡುಬಂದಿದೆ, ಅಥವಾ ಸಿಸ್ಟಮ್ ಅನ್ನು ಕಂಪೈಲ್ ಮಾಡಲಾಗಿದೆ/ದೋಷದೊಂದಿಗೆ ಪರಿಹರಿಸಲಾಗಿದೆ.

ಕಾಂಪ್ಯಾಕ್ಟ್ ನಿರ್ದೇಶಾಂಕಗಳು ಮೌಲ್ಯವನ್ನು ನೀಡುತ್ತದೆ

ಐಜೆನ್ವೆಕ್ಟರ್:

ಮತ್ತು ಮತ್ತೊಮ್ಮೆ, ನಾವು ಪರಿಹಾರವನ್ನು ಕಂಡುಕೊಂಡಿದ್ದೇವೆ ಎಂದು ಪರಿಶೀಲಿಸುತ್ತೇವೆ ವ್ಯವಸ್ಥೆಯ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ. ನಂತರದ ಪ್ಯಾರಾಗಳಲ್ಲಿ ಮತ್ತು ನಂತರದ ಕಾರ್ಯಗಳಲ್ಲಿ, ಈ ಆಶಯವನ್ನು ಕಡ್ಡಾಯ ನಿಯಮವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಲು ನಾನು ಶಿಫಾರಸು ಮಾಡುತ್ತೇವೆ.

2) ಐಜೆನ್ವಾಲ್ಯೂಗಾಗಿ, ಅದೇ ತತ್ವವನ್ನು ಬಳಸಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ ಕೆಳಗಿನ ವ್ಯವಸ್ಥೆ:

ಸಿಸ್ಟಮ್ನ 2 ನೇ ಸಮೀಕರಣದಿಂದ ನಾವು ವ್ಯಕ್ತಪಡಿಸುತ್ತೇವೆ: - ಮೂರನೇ ಸಮೀಕರಣಕ್ಕೆ ಬದಲಿಯಾಗಿ:

"ಝೀಟಾ" ನಿರ್ದೇಶಾಂಕವು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುವುದರಿಂದ, ಅದು ಅನುಸರಿಸುವ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣದಿಂದ ನಾವು ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ ರೇಖೀಯ ಅವಲಂಬನೆ.

ಅವಕಾಶ

ಪರಿಹಾರವನ್ನು ಪರಿಶೀಲಿಸಲಾಗುತ್ತಿದೆ ವ್ಯವಸ್ಥೆಯ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ.

ಹೀಗಾಗಿ, ಐಜೆನ್ವೆಕ್ಟರ್: .

3) ಮತ್ತು ಅಂತಿಮವಾಗಿ, ಸಿಸ್ಟಮ್ ಐಜೆನ್ವಾಲ್ಯೂಗೆ ಅನುರೂಪವಾಗಿದೆ:

ಎರಡನೆಯ ಸಮೀಕರಣವು ಸರಳವಾಗಿ ಕಾಣುತ್ತದೆ, ಆದ್ದರಿಂದ ನಾವು ಅದನ್ನು ವ್ಯಕ್ತಪಡಿಸೋಣ ಮತ್ತು ಅದನ್ನು 1 ನೇ ಮತ್ತು 3 ನೇ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸೋಣ:

ಎಲ್ಲವೂ ಉತ್ತಮವಾಗಿದೆ - ರೇಖಾತ್ಮಕ ಸಂಬಂಧವು ಹೊರಹೊಮ್ಮಿದೆ, ಅದನ್ನು ನಾವು ಅಭಿವ್ಯಕ್ತಿಗೆ ಬದಲಿಸುತ್ತೇವೆ:

ಪರಿಣಾಮವಾಗಿ, "x" ಮತ್ತು "y" ಅನ್ನು "z" ಮೂಲಕ ವ್ಯಕ್ತಪಡಿಸಲಾಗಿದೆ: . ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಅಂತಹ ಸಂಬಂಧಗಳನ್ನು ನಿಖರವಾಗಿ ಸಾಧಿಸುವುದು ಅನಿವಾರ್ಯವಲ್ಲ; ಕೆಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ ಮೂಲಕ ಅಥವಾ ಮತ್ತು ಮೂಲಕ ವ್ಯಕ್ತಪಡಿಸಲು ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ. ಅಥವಾ "ರೈಲು" - ಉದಾಹರಣೆಗೆ, "X" ಮೂಲಕ "I", ಮತ್ತು "I" ಮೂಲಕ "Z"

ನಂತರ ಅದನ್ನು ಹಾಕೋಣ:

ಪರಿಹಾರ ಕಂಡುಬಂದಿದೆಯೇ ಎಂದು ನಾವು ಪರಿಶೀಲಿಸುತ್ತೇವೆ ವ್ಯವಸ್ಥೆಯ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ತೃಪ್ತಿಪಡಿಸುತ್ತದೆ ಮತ್ತು ಮೂರನೇ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಬರೆಯುತ್ತದೆ

ಉತ್ತರ: ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು:

ಜ್ಯಾಮಿತೀಯವಾಗಿ, ಈ ವಾಹಕಗಳು ಮೂರು ವಿಭಿನ್ನ ಪ್ರಾದೇಶಿಕ ದಿಕ್ಕುಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತವೆ ("ಅಲ್ಲಿ ಮತ್ತು ಮತ್ತೆ ಮತ್ತೆ"), ಅದರ ಪ್ರಕಾರ ರೇಖೀಯ ರೂಪಾಂತರಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್‌ಗಳನ್ನು (ಐಜೆನ್‌ವೆಕ್ಟರ್‌ಗಳು) ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳಾಗಿ ಪರಿವರ್ತಿಸುತ್ತದೆ.

ಸ್ಥಿತಿಯು ಅಂಗೀಕೃತ ವಿಭಜನೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವ ಅಗತ್ಯವಿದ್ದರೆ, ಇದು ಇಲ್ಲಿ ಸಾಧ್ಯ, ಏಕೆಂದರೆ ವಿಭಿನ್ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ವಿಭಿನ್ನ ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಸಂಬಂಧಿಸಿವೆ. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಮಾಡುವುದು ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ, ಕರ್ಣೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನಿಂದ ಸಂಬಂಧಿತಸಮಾನ ಮೌಲ್ಯಗಳು ಮತ್ತು ಕಂಡುಹಿಡಿಯಿರಿ ವಿಲೋಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್ .

ಷರತ್ತಿನ ಪ್ರಕಾರ, ನೀವು ಬರೆಯಬೇಕಾದರೆ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ಆಧಾರದ ಮೇಲೆ ರೇಖೀಯ ರೂಪಾಂತರ ಮ್ಯಾಟ್ರಿಕ್ಸ್, ನಂತರ ನಾವು ರೂಪದಲ್ಲಿ ಉತ್ತರವನ್ನು ನೀಡುತ್ತೇವೆ. ವ್ಯತ್ಯಾಸವಿದೆ, ಮತ್ತು ವ್ಯತ್ಯಾಸವು ಗಮನಾರ್ಹವಾಗಿದೆ!ಏಕೆಂದರೆ ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್ "ಡಿ" ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ.

ಇನ್ನಷ್ಟು ಸಮಸ್ಯೆ ಸರಳ ಲೆಕ್ಕಾಚಾರಗಳುಫಾರ್ ಸ್ವತಂತ್ರ ನಿರ್ಧಾರ:

ಉದಾಹರಣೆ 5

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನೀಡಿದ ರೇಖೀಯ ರೂಪಾಂತರದ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಹುಡುಕಿ

ನಿಮ್ಮ ಸ್ವಂತ ಸಂಖ್ಯೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವಾಗ, 3 ನೇ ಡಿಗ್ರಿ ಬಹುಪದಕ್ಕೆ ಹೋಗದಿರಲು ಪ್ರಯತ್ನಿಸಿ. ಹೆಚ್ಚುವರಿಯಾಗಿ, ನಿಮ್ಮ ಸಿಸ್ಟಮ್ ಪರಿಹಾರಗಳು ನನ್ನ ಪರಿಹಾರಗಳಿಂದ ಭಿನ್ನವಾಗಿರಬಹುದು - ಇಲ್ಲಿ ಯಾವುದೇ ಖಚಿತತೆ ಇಲ್ಲ; ಮತ್ತು ನೀವು ಕಂಡುಕೊಳ್ಳುವ ವೆಕ್ಟರ್‌ಗಳು ಮಾದರಿ ವೆಕ್ಟರ್‌ಗಳಿಂದ ಅವುಗಳ ಸಂಬಂಧಿತ ನಿರ್ದೇಶಾಂಕಗಳ ಅನುಪಾತದವರೆಗೆ ಭಿನ್ನವಾಗಿರಬಹುದು. ಉದಾಹರಣೆಗೆ, ಮತ್ತು. ಉತ್ತರವನ್ನು ರೂಪದಲ್ಲಿ ಪ್ರಸ್ತುತಪಡಿಸಲು ಇದು ಹೆಚ್ಚು ಕಲಾತ್ಮಕವಾಗಿ ಆಹ್ಲಾದಕರವಾಗಿರುತ್ತದೆ, ಆದರೆ ನೀವು ಎರಡನೇ ಆಯ್ಕೆಯಲ್ಲಿ ನಿಲ್ಲಿಸಿದರೆ ಪರವಾಗಿಲ್ಲ. ಆದಾಗ್ಯೂ, ಎಲ್ಲದಕ್ಕೂ ಸಮಂಜಸವಾದ ಮಿತಿಗಳಿವೆ; ಆವೃತ್ತಿಯು ಇನ್ನು ಮುಂದೆ ಉತ್ತಮವಾಗಿ ಕಾಣುವುದಿಲ್ಲ.

ಪಾಠದ ಕೊನೆಯಲ್ಲಿ ನಿಯೋಜನೆಯ ಅಂದಾಜು ಅಂತಿಮ ಮಾದರಿ.

ಬಹು ಐಜೆನ್‌ವಾಲ್ಯೂಗಳ ಸಂದರ್ಭದಲ್ಲಿ ಸಮಸ್ಯೆಯನ್ನು ಹೇಗೆ ಪರಿಹರಿಸುವುದು?

ಸಾಮಾನ್ಯ ಅಲ್ಗಾರಿದಮ್ಒಂದೇ ಆಗಿರುತ್ತದೆ, ಆದರೆ ಇದು ತನ್ನದೇ ಆದ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿದೆ, ಮತ್ತು ಪರಿಹಾರದ ಕೆಲವು ಭಾಗಗಳನ್ನು ಹೆಚ್ಚು ಕಟ್ಟುನಿಟ್ಟಾದ ಶೈಕ್ಷಣಿಕ ಶೈಲಿಯಲ್ಲಿ ಇರಿಸಿಕೊಳ್ಳಲು ಸಲಹೆ ನೀಡಲಾಗುತ್ತದೆ:

ಉದಾಹರಣೆ 6

ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹುಡುಕಿ

ಪರಿಹಾರ

ಸಹಜವಾಗಿ, ಅಸಾಧಾರಣವಾದ ಮೊದಲ ಕಾಲಮ್ ಅನ್ನು ದೊಡ್ಡದಾಗಿ ಮಾಡೋಣ:

ಮತ್ತು, ಕ್ವಾಡ್ರಾಟಿಕ್ ಟ್ರಿನೊಮಿಯಲ್ ಅನ್ನು ಅಪವರ್ತಿಸಿದ ನಂತರ:

ಪರಿಣಾಮವಾಗಿ, ಐಜೆನ್ವಾಲ್ಯೂಗಳನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ, ಅವುಗಳಲ್ಲಿ ಎರಡು ಗುಣಾಕಾರಗಳಾಗಿವೆ.

ಈಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

1) "ಸರಳೀಕೃತ" ಯೋಜನೆಯ ಪ್ರಕಾರ ಒಂಟಿ ಸೈನಿಕನೊಂದಿಗೆ ವ್ಯವಹರಿಸೋಣ:

ಕೊನೆಯ ಎರಡು ಸಮೀಕರಣಗಳಿಂದ, ಸಮಾನತೆಯು ಸ್ಪಷ್ಟವಾಗಿ ಗೋಚರಿಸುತ್ತದೆ, ಇದು ನಿಸ್ಸಂಶಯವಾಗಿ, ವ್ಯವಸ್ಥೆಯ 1 ನೇ ಸಮೀಕರಣಕ್ಕೆ ಬದಲಿಯಾಗಬೇಕು:

ನೀವು ಉತ್ತಮ ಸಂಯೋಜನೆಯನ್ನು ಕಾಣುವುದಿಲ್ಲ:
ಐಜೆನ್ವೆಕ್ಟರ್:

2-3) ಈಗ ನಾವು ಒಂದೆರಡು ಸೆಂಟ್ರಿಗಳನ್ನು ತೆಗೆದುಹಾಕುತ್ತೇವೆ. IN ಈ ವಿಷಯದಲ್ಲಿಇದು ಕೆಲಸ ಮಾಡಬಹುದು ಎರಡು ಅಥವಾ ಒಂದುಐಜೆನ್ವೆಕ್ಟರ್. ಬೇರುಗಳ ಬಹುಸಂಖ್ಯೆಯ ಹೊರತಾಗಿಯೂ, ನಾವು ಮೌಲ್ಯವನ್ನು ನಿರ್ಣಾಯಕಕ್ಕೆ ಬದಲಿಸುತ್ತೇವೆ ಅದು ನಮಗೆ ಮುಂದಿನದನ್ನು ತರುತ್ತದೆ ರೇಖೀಯ ಸಮೀಕರಣಗಳ ಏಕರೂಪದ ವ್ಯವಸ್ಥೆ:

ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು ನಿಖರವಾಗಿ ವೆಕ್ಟರ್ಗಳಾಗಿವೆ
ಪರಿಹಾರಗಳ ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆ

ವಾಸ್ತವವಾಗಿ, ಇಡೀ ಪಾಠದ ಉದ್ದಕ್ಕೂ ನಾವು ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆಯ ವಾಹಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದನ್ನು ಹೊರತುಪಡಿಸಿ ಏನನ್ನೂ ಮಾಡಲಿಲ್ಲ. ಸದ್ಯಕ್ಕೆ ಈ ಪದವು ವಿಶೇಷವಾಗಿ ಅಗತ್ಯವಿರಲಿಲ್ಲ. ಅಂದಹಾಗೆ, ಮರೆಮಾಚುವ ಸೂಟ್‌ಗಳಲ್ಲಿ ವಿಷಯವನ್ನು ತಪ್ಪಿಸಿಕೊಂಡ ಬುದ್ಧಿವಂತ ವಿದ್ಯಾರ್ಥಿಗಳು ಏಕರೂಪದ ಸಮೀಕರಣಗಳು, ಈಗ ಅದನ್ನು ಧೂಮಪಾನ ಮಾಡಲು ಒತ್ತಾಯಿಸಲಾಗುತ್ತದೆ.

ಹೆಚ್ಚುವರಿ ಸಾಲುಗಳನ್ನು ತೆಗೆದುಹಾಕುವುದು ಮಾತ್ರ ಕ್ರಮವಾಗಿದೆ. ಫಲಿತಾಂಶವು ಮಧ್ಯದಲ್ಲಿ ಔಪಚಾರಿಕ "ಹಂತ" ದೊಂದಿಗೆ ಒಂದು-ಮೂರು-ಮೂರು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ.
- ಮೂಲ ವೇರಿಯಬಲ್, - ಉಚಿತ ಅಸ್ಥಿರ. ಆದ್ದರಿಂದ ಎರಡು ಉಚಿತ ಅಸ್ಥಿರಗಳಿವೆ ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆಯ ಎರಡು ವಾಹಕಗಳು ಸಹ ಇವೆ.

ಉಚಿತ ಅಸ್ಥಿರಗಳ ವಿಷಯದಲ್ಲಿ ಮೂಲಭೂತ ವೇರಿಯಬಲ್ ಅನ್ನು ವ್ಯಕ್ತಪಡಿಸೋಣ: . "X" ನ ಮುಂದೆ ಶೂನ್ಯ ಗುಣಕವು ಸಂಪೂರ್ಣವಾಗಿ ಯಾವುದೇ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಲು ಅನುಮತಿಸುತ್ತದೆ (ಇದು ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯಿಂದ ಸ್ಪಷ್ಟವಾಗಿ ಗೋಚರಿಸುತ್ತದೆ).

ಈ ಸಮಸ್ಯೆಯ ಸಂದರ್ಭದಲ್ಲಿ, ಸಾಮಾನ್ಯ ಪರಿಹಾರವನ್ನು ಸತತವಾಗಿ ಬರೆಯಲು ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ, ಆದರೆ ಒಂದು ಕಾಲಮ್ನಲ್ಲಿ:

ಜೋಡಿಯು ಐಜೆನ್ವೆಕ್ಟರ್ಗೆ ಅನುರೂಪವಾಗಿದೆ:
ಜೋಡಿಯು ಐಜೆನ್ವೆಕ್ಟರ್ಗೆ ಅನುರೂಪವಾಗಿದೆ:

ಸೂಚನೆ : ಅತ್ಯಾಧುನಿಕ ಓದುಗರು ಈ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಮೌಖಿಕವಾಗಿ ಆಯ್ಕೆ ಮಾಡಬಹುದು - ಸರಳವಾಗಿ ಸಿಸ್ಟಮ್ ಅನ್ನು ವಿಶ್ಲೇಷಿಸುವ ಮೂಲಕ , ಆದರೆ ಇಲ್ಲಿ ಕೆಲವು ಜ್ಞಾನದ ಅಗತ್ಯವಿದೆ: ಮೂರು ಅಸ್ಥಿರಗಳಿವೆ, ಸಿಸ್ಟಮ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಶ್ರೇಣಿ- ಒಂದು, ಅಂದರೆ ಮೂಲಭೂತ ನಿರ್ಧಾರ ವ್ಯವಸ್ಥೆ 3 - 1 = 2 ವೆಕ್ಟರ್‌ಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ಆದಾಗ್ಯೂ, ಕಂಡುಬರುವ ವಾಹಕಗಳು ಈ ಜ್ಞಾನವಿಲ್ಲದೆ, ಸಂಪೂರ್ಣವಾಗಿ ಅರ್ಥಗರ್ಭಿತ ಮಟ್ಟದಲ್ಲಿ ಸ್ಪಷ್ಟವಾಗಿ ಗೋಚರಿಸುತ್ತವೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಮೂರನೇ ವೆಕ್ಟರ್ ಅನ್ನು ಇನ್ನಷ್ಟು "ಸುಂದರವಾಗಿ" ಬರೆಯಲಾಗುತ್ತದೆ: . ಆದಾಗ್ಯೂ, ಇನ್ನೊಂದು ಉದಾಹರಣೆಯಲ್ಲಿ, ಸರಳವಾದ ಆಯ್ಕೆಯು ಸಾಧ್ಯವಾಗದಿರಬಹುದು ಎಂದು ನಾನು ನಿಮಗೆ ಎಚ್ಚರಿಸುತ್ತೇನೆ, ಅದಕ್ಕಾಗಿಯೇ ಷರತ್ತು ಅನುಭವಿ ಜನರಿಗೆ ಉದ್ದೇಶಿಸಲಾಗಿದೆ. ಹೆಚ್ಚುವರಿಯಾಗಿ, ಮೂರನೇ ವೆಕ್ಟರ್ ಎಂದು ಏಕೆ ತೆಗೆದುಕೊಳ್ಳಬಾರದು? ಎಲ್ಲಾ ನಂತರ, ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು ಸಿಸ್ಟಮ್ನ ಪ್ರತಿಯೊಂದು ಸಮೀಕರಣವನ್ನು ಮತ್ತು ವೆಕ್ಟರ್ಗಳನ್ನು ಸಹ ಪೂರೈಸುತ್ತವೆ ರೇಖೀಯವಾಗಿ ಸ್ವತಂತ್ರ. ಈ ಆಯ್ಕೆಯು ತಾತ್ವಿಕವಾಗಿ ಸೂಕ್ತವಾಗಿದೆ, ಆದರೆ "ವಕ್ರ", ಏಕೆಂದರೆ "ಇತರ" ವೆಕ್ಟರ್ ಮೂಲಭೂತ ವ್ಯವಸ್ಥೆಯ ವಾಹಕಗಳ ರೇಖೀಯ ಸಂಯೋಜನೆಯಾಗಿದೆ.

ಉತ್ತರ: eigenvalues:, eigenvectors:

ಸ್ವತಂತ್ರ ಪರಿಹಾರಕ್ಕಾಗಿ ಇದೇ ಉದಾಹರಣೆ:

ಉದಾಹರಣೆ 7

ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹುಡುಕಿ

ಪಾಠದ ಕೊನೆಯಲ್ಲಿ ಅಂತಿಮ ವಿನ್ಯಾಸದ ಅಂದಾಜು ಮಾದರಿ.

6 ನೇ ಮತ್ತು 7 ನೇ ಉದಾಹರಣೆಗಳಲ್ಲಿ ರೇಖೀಯವಾಗಿ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳ ಟ್ರಿಪಲ್ ಅನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅಂಗೀಕೃತ ವಿಭಜನೆಯಲ್ಲಿ ಪ್ರತಿನಿಧಿಸುತ್ತದೆ ಎಂದು ಗಮನಿಸಬೇಕು. ಆದರೆ ಅಂತಹ ರಾಸ್್ಬೆರ್ರಿಸ್ ಎಲ್ಲಾ ಸಂದರ್ಭಗಳಲ್ಲಿ ಸಂಭವಿಸುವುದಿಲ್ಲ:

ಉದಾಹರಣೆ 8

ಪರಿಹಾರ: ವಿಶಿಷ್ಟ ಸಮೀಕರಣವನ್ನು ರಚಿಸೋಣ ಮತ್ತು ಪರಿಹರಿಸೋಣ:

ಮೊದಲ ಅಂಕಣದಲ್ಲಿ ನಿರ್ಣಾಯಕವನ್ನು ವಿಸ್ತರಿಸೋಣ:

ಪರಿಗಣಿಸಲಾದ ವಿಧಾನದ ಪ್ರಕಾರ ನಾವು ಮತ್ತಷ್ಟು ಸರಳೀಕರಣಗಳನ್ನು ಕೈಗೊಳ್ಳುತ್ತೇವೆ, ಮೂರನೇ ಹಂತದ ಬಹುಪದವನ್ನು ತಪ್ಪಿಸುತ್ತೇವೆ:

- ಸಮಾನ ಮೌಲ್ಯಗಳು.

ಈಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

1) ಮೂಲದಲ್ಲಿ ಯಾವುದೇ ತೊಂದರೆಗಳಿಲ್ಲ:

ಆಶ್ಚರ್ಯಪಡಬೇಡಿ, ಕಿಟ್ ಜೊತೆಗೆ, ಬಳಕೆಯಲ್ಲಿ ಅಸ್ಥಿರಗಳು ಸಹ ಇವೆ - ಇಲ್ಲಿ ಯಾವುದೇ ವ್ಯತ್ಯಾಸವಿಲ್ಲ.

3 ನೇ ಸಮೀಕರಣದಿಂದ ನಾವು ಅದನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತೇವೆ ಮತ್ತು ಅದನ್ನು 1 ನೇ ಮತ್ತು 2 ನೇ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸುತ್ತೇವೆ:

ಎರಡೂ ಸಮೀಕರಣಗಳಿಂದ ಇದು ಅನುಸರಿಸುತ್ತದೆ:

ನಂತರ ಅವಕಾಶ:

2-3) ಬಹು ಮೌಲ್ಯಗಳಿಗಾಗಿ ನಾವು ಸಿಸ್ಟಮ್ ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ .

ಸಿಸ್ಟಮ್ನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಬರೆಯೋಣ ಮತ್ತು ಪ್ರಾಥಮಿಕ ರೂಪಾಂತರಗಳನ್ನು ಬಳಸಿ, ಅದನ್ನು ಹಂತ ಹಂತವಾಗಿ ರೂಪಕ್ಕೆ ತರೋಣ:

ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್‌ವೆಕ್ಟರ್ ಒಂದು, ಕೊಟ್ಟಿರುವ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಿಂದ ಗುಣಿಸಿದಾಗ, ಕೊಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗೆ ಕಾರಣವಾಗುತ್ತದೆ. ಸರಳ ಪದಗಳಲ್ಲಿ, ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಐಜೆನ್ವೆಕ್ಟರ್ನಿಂದ ಗುಣಿಸಿದಾಗ, ಎರಡನೆಯದು ಒಂದೇ ಆಗಿರುತ್ತದೆ, ಆದರೆ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯಿಂದ ಗುಣಿಸಲ್ಪಡುತ್ತದೆ.

ವ್ಯಾಖ್ಯಾನ

ಐಜೆನ್ವೆಕ್ಟರ್ ಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್ V ಆಗಿದೆ, ಇದು ಒಂದು ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ M ನಿಂದ ಗುಣಿಸಿದಾಗ, ಕೆಲವು ಸಂಖ್ಯೆ λ ನಿಂದ ಸ್ವತಃ ಹೆಚ್ಚಾಗುತ್ತದೆ. ಬೀಜಗಣಿತದ ಸಂಕೇತದಲ್ಲಿ ಇದು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:

M × V = λ × V,

ಇಲ್ಲಿ λ ಎಂಬುದು ಮ್ಯಾಟ್ರಿಕ್ಸ್ M ನ ಐಜೆನ್‌ವಾಲ್ಯೂ ಆಗಿದೆ.

ಪರಿಗಣಿಸೋಣ ಸಂಖ್ಯಾತ್ಮಕ ಉದಾಹರಣೆ. ರೆಕಾರ್ಡಿಂಗ್ ಸುಲಭವಾಗುವಂತೆ, ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಲ್ಲಿರುವ ಸಂಖ್ಯೆಗಳನ್ನು ಅರ್ಧವಿರಾಮ ಚಿಹ್ನೆಯಿಂದ ಬೇರ್ಪಡಿಸಲಾಗುತ್ತದೆ. ನಾವು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಹೊಂದೋಣ:

• M = 0; 4;
• 6; 10.

ಅದನ್ನು ಕಾಲಮ್ ವೆಕ್ಟರ್ ಮೂಲಕ ಗುಣಿಸೋಣ:

• ವಿ = -2;

ನಾವು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಕಾಲಮ್ ವೆಕ್ಟರ್‌ನಿಂದ ಗುಣಿಸಿದಾಗ, ನಾವು ಕಾಲಮ್ ವೆಕ್ಟರ್ ಅನ್ನು ಸಹ ಪಡೆಯುತ್ತೇವೆ. ಕಟ್ಟುನಿಟ್ಟಾದ ಗಣಿತದ ಭಾಷೆಕಾಲಮ್ ವೆಕ್ಟರ್ ಮೂಲಕ 2 × 2 ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸುವ ಸೂತ್ರವು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 ಎಂದರೆ ಮೊದಲ ಸಾಲು ಮತ್ತು ಮೊದಲ ಕಾಲಮ್‌ನಲ್ಲಿರುವ ಮ್ಯಾಟ್ರಿಕ್ಸ್ M ನ ಅಂಶ, ಮತ್ತು M22 ಎಂದರೆ ಎರಡನೇ ಸಾಲು ಮತ್ತು ಎರಡನೇ ಕಾಲಮ್‌ನಲ್ಲಿರುವ ಅಂಶ. ನಮ್ಮ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ, ಈ ಅಂಶಗಳು M11 = 0, M12 = 4, M21 = 6, M22 10 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಕಾಲಮ್ ವೆಕ್ಟರ್‌ಗೆ, ಈ ಮೌಲ್ಯಗಳು V11 = –2, V21 = 1. ಈ ಸೂತ್ರದ ಪ್ರಕಾರ, ವೆಕ್ಟರ್‌ನಿಂದ ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಉತ್ಪನ್ನದ ಕೆಳಗಿನ ಫಲಿತಾಂಶವನ್ನು ನಾವು ಪಡೆಯುತ್ತೇವೆ:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

ಅನುಕೂಲಕ್ಕಾಗಿ, ಕಾಲಮ್ ವೆಕ್ಟರ್ ಅನ್ನು ಸಾಲಾಗಿ ಬರೆಯೋಣ. ಆದ್ದರಿಂದ, ನಾವು ಸ್ಕ್ವೇರ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ವೆಕ್ಟರ್ (-2; 1) ಮೂಲಕ ಗುಣಿಸಿದ್ದೇವೆ, ಇದರ ಪರಿಣಾಮವಾಗಿ ವೆಕ್ಟರ್ (4; -2). ನಿಸ್ಸಂಶಯವಾಗಿ, ಇದು λ = -2 ರಿಂದ ಗುಣಿಸಿದ ಅದೇ ವೆಕ್ಟರ್ ಆಗಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ ಲ್ಯಾಂಬ್ಡಾ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್‌ವಾಲ್ಯೂ ಅನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಒಂದು ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್ ಆಗಿದೆ, ಅಂದರೆ, ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಿಂದ ಗುಣಿಸಿದಾಗ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ತನ್ನ ಸ್ಥಾನವನ್ನು ಬದಲಾಯಿಸದ ವಸ್ತು. ವೆಕ್ಟರ್ ಬೀಜಗಣಿತದಲ್ಲಿ ಕೋಲಿನಿಯರಿಟಿಯ ಪರಿಕಲ್ಪನೆಯು ಜ್ಯಾಮಿತಿಯಲ್ಲಿ ಸಮಾನಾಂತರತೆಯ ಪದವನ್ನು ಹೋಲುತ್ತದೆ. ಜ್ಯಾಮಿತೀಯ ವ್ಯಾಖ್ಯಾನದಲ್ಲಿ, ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳು ವಿಭಿನ್ನ ಉದ್ದಗಳ ಸಮಾನಾಂತರ ನಿರ್ದೇಶಿತ ವಿಭಾಗಗಳಾಗಿವೆ. ಯೂಕ್ಲಿಡ್‌ನ ಕಾಲದಿಂದಲೂ, ಒಂದು ರೇಖೆಯು ಅನಂತ ಸಂಖ್ಯೆಯ ಸಾಲುಗಳನ್ನು ಸಮಾನಾಂತರವಾಗಿ ಹೊಂದಿದೆ ಎಂದು ನಮಗೆ ತಿಳಿದಿದೆ, ಆದ್ದರಿಂದ ಪ್ರತಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನಂತ ಸಂಖ್ಯೆಯ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹೊಂದಿದೆ ಎಂದು ಭಾವಿಸುವುದು ತಾರ್ಕಿಕವಾಗಿದೆ.

ಹಿಂದಿನ ಉದಾಹರಣೆಯಿಂದ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು (-8; 4), ಮತ್ತು (16; -8), ಮತ್ತು (32, -16) ಆಗಿರಬಹುದು ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ. ಇವೆಲ್ಲವೂ ಈಜೆನ್‌ವಾಲ್ಯೂ λ = -2 ಗೆ ಅನುಗುಣವಾದ ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳಾಗಿವೆ. ಈ ವೆಕ್ಟರ್‌ಗಳಿಂದ ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸಿದಾಗ, ನಾವು ಇನ್ನೂ 2 ಬಾರಿ ಮೂಲದಿಂದ ಭಿನ್ನವಾಗಿರುವ ವೆಕ್ಟರ್‌ನೊಂದಿಗೆ ಕೊನೆಗೊಳ್ಳುತ್ತೇವೆ. ಅದಕ್ಕಾಗಿಯೇ, ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸುವಾಗ, ರೇಖಾತ್ಮಕವಾಗಿ ಸ್ವತಂತ್ರ ವೆಕ್ಟರ್ ವಸ್ತುಗಳನ್ನು ಮಾತ್ರ ಕಂಡುಹಿಡಿಯುವುದು ಅವಶ್ಯಕ. ಹೆಚ್ಚಾಗಿ, n × n ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗೆ, n ಸಂಖ್ಯೆಯ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳಿರುತ್ತವೆ. ನಮ್ಮ ಕ್ಯಾಲ್ಕುಲೇಟರ್ ಅನ್ನು ಎರಡನೇ ಕ್ರಮಾಂಕದ ಚದರ ಮ್ಯಾಟ್ರಿಸಸ್‌ಗಳ ವಿಶ್ಲೇಷಣೆಗಾಗಿ ವಿನ್ಯಾಸಗೊಳಿಸಲಾಗಿದೆ, ಆದ್ದರಿಂದ ಫಲಿತಾಂಶವು ಯಾವಾಗಲೂ ಎರಡು ಐಜೆನ್‌ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತದೆ, ಅವುಗಳು ಹೊಂದಿಕೆಯಾಗುವ ಸಂದರ್ಭಗಳನ್ನು ಹೊರತುಪಡಿಸಿ.

ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ, ನಾವು ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಮುಂಚಿತವಾಗಿ ತಿಳಿದಿದ್ದೇವೆ ಮತ್ತು ಲ್ಯಾಂಬ್ಡಾ ಸಂಖ್ಯೆಯನ್ನು ಸ್ಪಷ್ಟವಾಗಿ ನಿರ್ಧರಿಸಿದ್ದೇವೆ. ಆದಾಗ್ಯೂ, ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಎಲ್ಲವೂ ಬೇರೆ ರೀತಿಯಲ್ಲಿ ನಡೆಯುತ್ತದೆ: ಐಜೆನ್ವಾಲ್ಯೂಗಳು ಮೊದಲು ಕಂಡುಬರುತ್ತವೆ ಮತ್ತು ನಂತರ ಮಾತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು.

ಪರಿಹಾರ ಅಲ್ಗಾರಿದಮ್

ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್ M ಅನ್ನು ಮತ್ತೊಮ್ಮೆ ನೋಡೋಣ ಮತ್ತು ಅದರ ಎರಡೂ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ಪ್ರಯತ್ನಿಸೋಣ. ಆದ್ದರಿಂದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:

• M = 0; 4;
• 6; 10.

ಮೊದಲು ನಾವು ಈಜೆನ್‌ವಾಲ್ಯೂ λ ಅನ್ನು ನಿರ್ಧರಿಸಬೇಕು, ಇದಕ್ಕೆ ಈ ಕೆಳಗಿನ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ನಿರ್ಣಾಯಕವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಅಗತ್ಯವಿದೆ:

• (0 - λ); 4;
• 6; (10 - λ).

ಮುಖ್ಯ ಕರ್ಣೀಯ ಅಂಶಗಳಿಂದ ಅಜ್ಞಾತ λ ಅನ್ನು ಕಳೆಯುವ ಮೂಲಕ ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ. ಪ್ರಮಾಣಿತ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ನಿರ್ಣಾಯಕವನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ:

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

ನಮ್ಮ ವೆಕ್ಟರ್ ಶೂನ್ಯವಲ್ಲದ ಕಾರಣ, ನಾವು ಫಲಿತಾಂಶದ ಸಮೀಕರಣವನ್ನು ರೇಖೀಯವಾಗಿ ಅವಲಂಬಿತವಾಗಿ ಸ್ವೀಕರಿಸುತ್ತೇವೆ ಮತ್ತು ನಮ್ಮ ನಿರ್ಣಾಯಕ detA ಅನ್ನು ಶೂನ್ಯಕ್ಕೆ ಸಮೀಕರಿಸುತ್ತೇವೆ.

(0 - λ) × (10 - λ) - 24 = 0

ಬ್ರಾಕೆಟ್‌ಗಳನ್ನು ತೆರೆಯೋಣ ಮತ್ತು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ವಿಶಿಷ್ಟ ಸಮೀಕರಣವನ್ನು ಪಡೆಯೋಣ:

λ 2 - 10λ - 24 = 0

ಇದು ಪ್ರಮಾಣಿತವಾಗಿದೆ ಚತುರ್ಭುಜ ಸಮೀಕರಣ, ಇದು ತಾರತಮ್ಯದ ಮೂಲಕ ಪರಿಹರಿಸಬೇಕಾಗಿದೆ.

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

ತಾರತಮ್ಯದ ಮೂಲವು sqrt(D) = 14, ಆದ್ದರಿಂದ λ1 = -2, λ2 = 12. ಈಗ ಪ್ರತಿ ಲ್ಯಾಂಬ್ಡಾ ಮೌಲ್ಯಕ್ಕೆ ನಾವು ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕು. ನಾವು λ = -2 ಗಾಗಿ ಸಿಸ್ಟಮ್ ಗುಣಾಂಕಗಳನ್ನು ವ್ಯಕ್ತಪಡಿಸೋಣ.

• M - λ × E = 2; 4;
• 6; 12.

ಈ ಸೂತ್ರದಲ್ಲಿ, E ಗುರುತಿನ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದೆ. ಫಲಿತಾಂಶದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಆಧರಿಸಿ, ನಾವು ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯನ್ನು ರಚಿಸುತ್ತೇವೆ:

2x + 4y = 6x + 12y,

ಇಲ್ಲಿ x ಮತ್ತು y ಐಜೆನ್ವೆಕ್ಟರ್ ಅಂಶಗಳಾಗಿವೆ.

ಎಡಭಾಗದಲ್ಲಿರುವ ಎಲ್ಲಾ X ಮತ್ತು ಬಲಭಾಗದಲ್ಲಿರುವ ಎಲ್ಲಾ Y ಗಳನ್ನು ಸಂಗ್ರಹಿಸೋಣ. ನಿಸ್ಸಂಶಯವಾಗಿ - 4x = 8y. ಅಭಿವ್ಯಕ್ತಿಯನ್ನು - 4 ರಿಂದ ಭಾಗಿಸಿ ಮತ್ತು x = –2y ಪಡೆಯಿರಿ. ಈಗ ನಾವು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಮೊದಲ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ನಿರ್ಧರಿಸಬಹುದು, ಅಪರಿಚಿತರ ಯಾವುದೇ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು (ರೇಖೀಯವಾಗಿ ಅವಲಂಬಿತ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳ ಅನಂತತೆಯನ್ನು ನೆನಪಿಡಿ). y = 1 ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ, ನಂತರ x = –2. ಆದ್ದರಿಂದ, ಮೊದಲ ಐಜೆನ್ವೆಕ್ಟರ್ V1 = (–2; 1) ನಂತೆ ಕಾಣುತ್ತದೆ. ಲೇಖನದ ಆರಂಭಕ್ಕೆ ಹಿಂತಿರುಗಿ. ಈ ವೆಕ್ಟರ್ ವಸ್ತುವೇ ನಾವು ಐಜೆನ್ವೆಕ್ಟರ್ ಪರಿಕಲ್ಪನೆಯನ್ನು ಪ್ರದರ್ಶಿಸಲು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸಿದ್ದೇವೆ.

ಈಗ λ = 12 ಗಾಗಿ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.

• M - λ × E = -12; 4
• 6; -2.

ರೇಖೀಯ ಸಮೀಕರಣಗಳ ಅದೇ ವ್ಯವಸ್ಥೆಯನ್ನು ರಚಿಸೋಣ;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x = ವೈ.

ಈಗ ನಾವು x = 1 ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತೇವೆ, ಆದ್ದರಿಂದ y = 3. ಹೀಗಾಗಿ, ಎರಡನೇ ಐಜೆನ್ವೆಕ್ಟರ್ V2 = (1; 3) ನಂತೆ ಕಾಣುತ್ತದೆ. ಕೊಟ್ಟಿರುವ ವೆಕ್ಟರ್‌ನಿಂದ ಮೂಲ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸಿದಾಗ, ಫಲಿತಾಂಶವು ಯಾವಾಗಲೂ ಅದೇ ವೆಕ್ಟರ್ ಅನ್ನು 12 ರಿಂದ ಗುಣಿಸಿದಾಗ ಇರುತ್ತದೆ. ಇಲ್ಲಿ ಪರಿಹಾರ ಅಲ್ಗಾರಿದಮ್ ಕೊನೆಗೊಳ್ಳುತ್ತದೆ. ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಹಸ್ತಚಾಲಿತವಾಗಿ ಹೇಗೆ ನಿರ್ಧರಿಸುವುದು ಎಂದು ಈಗ ನಿಮಗೆ ತಿಳಿದಿದೆ.

• ನಿರ್ಣಾಯಕ;
• ಜಾಡಿನ, ಅಂದರೆ, ಮುಖ್ಯ ಕರ್ಣೀಯ ಅಂಶಗಳ ಮೊತ್ತ;
• ಶ್ರೇಣಿ, ಅಂದರೆ ರೇಖೀಯ ಸ್ವತಂತ್ರ ಸಾಲುಗಳು/ಕಾಲಮ್‌ಗಳ ಗರಿಷ್ಠ ಸಂಖ್ಯೆ.

ಪ್ರೋಗ್ರಾಂ ಮೇಲಿನ ಅಲ್ಗಾರಿದಮ್ ಪ್ರಕಾರ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ, ಪರಿಹಾರ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸಾಧ್ಯವಾದಷ್ಟು ಕಡಿಮೆಗೊಳಿಸುತ್ತದೆ. ಪ್ರೋಗ್ರಾಂನಲ್ಲಿ ಲ್ಯಾಂಬ್ಡಾವನ್ನು "ಸಿ" ಅಕ್ಷರದಿಂದ ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ ಎಂದು ಗಮನಿಸುವುದು ಮುಖ್ಯ. ಸಂಖ್ಯಾತ್ಮಕ ಉದಾಹರಣೆಯನ್ನು ನೋಡೋಣ.

ಪ್ರೋಗ್ರಾಂ ಹೇಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ ಎಂಬುದರ ಉದಾಹರಣೆ

ಕೆಳಗಿನ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಾಗಿ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಪ್ರಯತ್ನಿಸೋಣ:

• M = 5; 13;
• 4; 14.

ಈ ಮೌಲ್ಯಗಳನ್ನು ಕ್ಯಾಲ್ಕುಲೇಟರ್‌ನ ಕೋಶಗಳಲ್ಲಿ ನಮೂದಿಸಿ ಮತ್ತು ಉತ್ತರವನ್ನು ಈ ಕೆಳಗಿನ ರೂಪದಲ್ಲಿ ಪಡೆಯೋಣ:

• ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಶ್ರೇಣಿ: 2;
• ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಡಿಟರ್ಮಿನೆಂಟ್: 18;
• ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಟ್ರೇಸ್: 19;
• ಐಜೆನ್ವೆಕ್ಟರ್ನ ಲೆಕ್ಕಾಚಾರ: c 2 - 19.00c + 18.00 (ವಿಶಿಷ್ಟ ಸಮೀಕರಣ);
• ಐಜೆನ್ವೆಕ್ಟರ್ ಲೆಕ್ಕಾಚಾರ: 18 (ಮೊದಲ ಲ್ಯಾಂಬ್ಡಾ ಮೌಲ್ಯ);
• ಐಜೆನ್ವೆಕ್ಟರ್ ಲೆಕ್ಕಾಚಾರ: 1 (ಎರಡನೇ ಲ್ಯಾಂಬ್ಡಾ ಮೌಲ್ಯ);
• ವೆಕ್ಟರ್ 1 ಗಾಗಿ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆ: -13x1 + 13y1 = 4x1 - 4y1;
• ವೆಕ್ಟರ್ 2 ಗಾಗಿ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆ: 4x1 + 13y1 = 4x1 + 13y1;
• ಐಜೆನ್ವೆಕ್ಟರ್ 1: (1; 1);
• ಐಜೆನ್ವೆಕ್ಟರ್ 2: (-3.25; 1).

ಹೀಗಾಗಿ, ನಾವು ಎರಡು ರೇಖೀಯ ಸ್ವತಂತ್ರ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳನ್ನು ಪಡೆದುಕೊಂಡಿದ್ದೇವೆ.

ತೀರ್ಮಾನ

ಲೀನಿಯರ್ ಬೀಜಗಣಿತ ಮತ್ತು ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರೇಖಾಗಣಿತವು ಯಾವುದೇ ಹೊಸಬರ ಎಂಜಿನಿಯರಿಂಗ್ ಮೇಜರ್‌ಗೆ ಪ್ರಮಾಣಿತ ವಿಷಯಗಳಾಗಿವೆ. ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ವಾಹಕಗಳು ಮತ್ತು ಮ್ಯಾಟ್ರಿಸಸ್ ಭಯಾನಕವಾಗಿದೆ, ಮತ್ತು ಅಂತಹ ತೊಡಕಿನ ಲೆಕ್ಕಾಚಾರಗಳಲ್ಲಿ ತಪ್ಪುಗಳನ್ನು ಮಾಡುವುದು ಸುಲಭ. ನಮ್ಮ ಪ್ರೋಗ್ರಾಂ ವಿದ್ಯಾರ್ಥಿಗಳು ತಮ್ಮ ಲೆಕ್ಕಾಚಾರಗಳನ್ನು ಪರಿಶೀಲಿಸಲು ಅಥವಾ ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಹುಡುಕುವ ಸಮಸ್ಯೆಯನ್ನು ಸ್ವಯಂಚಾಲಿತವಾಗಿ ಪರಿಹರಿಸಲು ಅನುಮತಿಸುತ್ತದೆ. ನಮ್ಮ ಕ್ಯಾಟಲಾಗ್‌ನಲ್ಲಿ ಇತರ ರೇಖೀಯ ಬೀಜಗಣಿತ ಕ್ಯಾಲ್ಕುಲೇಟರ್‌ಗಳಿವೆ; ಅವುಗಳನ್ನು ನಿಮ್ಮ ಅಧ್ಯಯನ ಅಥವಾ ಕೆಲಸದಲ್ಲಿ ಬಳಸಿ.

ವ್ಯಾಖ್ಯಾನ 9.3.ವೆಕ್ಟರ್ X ಎಂದು ಕರೆದರು ಐಜೆನ್ವೆಕ್ಟರ್ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ, ಅಂತಹ ಸಂಖ್ಯೆ ಇದ್ದರೆ λ, ಸಮಾನತೆ ಹೊಂದಿದೆ: ಎ X= λ X, ಅಂದರೆ, ಅನ್ವಯಿಸುವ ಫಲಿತಾಂಶ X ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನಿರ್ದಿಷ್ಟಪಡಿಸಿದ ರೇಖೀಯ ರೂಪಾಂತರ ಎ, ಸಂಖ್ಯೆಯಿಂದ ಈ ವೆಕ್ಟರ್ನ ಗುಣಾಕಾರವಾಗಿದೆ λ . ಸಂಖ್ಯೆಯೇ λ ಎಂದು ಕರೆದರು ಸಮಾನ ಮೌಲ್ಯಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ.

ಸೂತ್ರಗಳಿಗೆ ಪರ್ಯಾಯವಾಗಿ (9.3) x` j = λx j ,ಐಜೆನ್ವೆಕ್ಟರ್ನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನಿರ್ಧರಿಸಲು ನಾವು ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ:

. (9.5)

ಈ ರೇಖೀಯ ಏಕರೂಪದ ವ್ಯವಸ್ಥೆಯು ಅದರ ಮುಖ್ಯ ನಿರ್ಧಾರಕ 0 ಆಗಿದ್ದರೆ ಮಾತ್ರ ಕ್ಷುಲ್ಲಕ ಪರಿಹಾರವನ್ನು ಹೊಂದಿರುತ್ತದೆ (ಕ್ರಾಮರ್ ನಿಯಮ). ಈ ಸ್ಥಿತಿಯನ್ನು ರೂಪದಲ್ಲಿ ಬರೆಯುವ ಮೂಲಕ:

ಐಜೆನ್ವಾಲ್ಯೂಗಳನ್ನು ನಿರ್ಧರಿಸಲು ನಾವು ಸಮೀಕರಣವನ್ನು ಪಡೆಯುತ್ತೇವೆ λ , ಎಂದು ಕರೆಯುತ್ತಾರೆ ವಿಶಿಷ್ಟ ಸಮೀಕರಣ. ಸಂಕ್ಷಿಪ್ತವಾಗಿ ಇದನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಪ್ರತಿನಿಧಿಸಬಹುದು:

| A - λE | = 0, (9.6)

ಏಕೆಂದರೆ ಅದರ ಎಡಭಾಗವು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ನಿರ್ಣಾಯಕವನ್ನು ಹೊಂದಿರುತ್ತದೆ A-λE. ಬಹುಪದೋಕ್ತಿ ಸಂಬಂಧಿ λ | A - λE| ಎಂದು ಕರೆದರು ವಿಶಿಷ್ಟ ಬಹುಪದೋಕ್ತಿಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ.

ವಿಶಿಷ್ಟ ಬಹುಪದದ ಗುಣಲಕ್ಷಣಗಳು:

1) ರೇಖೀಯ ರೂಪಾಂತರದ ವಿಶಿಷ್ಟ ಬಹುಪದವು ಆಧಾರದ ಆಯ್ಕೆಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುವುದಿಲ್ಲ. ಪುರಾವೆ. (ನೋಡಿ (9.4)), ಆದರೆ ಆದ್ದರಿಂದ, . ಹೀಗಾಗಿ, ಇದು ಆಧಾರದ ಆಯ್ಕೆಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುವುದಿಲ್ಲ. ಇದರರ್ಥ | A-λE| ಹೊಸ ಆಧಾರದ ಮೇಲೆ ಚಲಿಸುವಾಗ ಬದಲಾಗುವುದಿಲ್ಲ.

2) ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆಗಿದ್ದರೆ ಎರೇಖೀಯ ರೂಪಾಂತರವಾಗಿದೆ ಸಮ್ಮಿತೀಯ(ಅವು. ಮತ್ತು ij = a ji), ನಂತರ ವಿಶಿಷ್ಟ ಸಮೀಕರಣದ ಎಲ್ಲಾ ಬೇರುಗಳು (9.6) ನೈಜ ಸಂಖ್ಯೆಗಳಾಗಿವೆ.

ಐಜೆನ್ವಾಲ್ಯೂಸ್ ಮತ್ತು ಐಜೆನ್ವೆಕ್ಟರ್ಗಳ ಗುಣಲಕ್ಷಣಗಳು:

1) ನೀವು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳಿಂದ ಆಧಾರವನ್ನು ಆರಿಸಿದರೆ x 1, x 2, x 3 , ಐಜೆನ್‌ವಾಲ್ಯೂಸ್‌ಗೆ ಅನುರೂಪವಾಗಿದೆ λ 1, λ 2, λ 3ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎ, ನಂತರ ಈ ಆಧಾರದ ಮೇಲೆ ರೇಖೀಯ ರೂಪಾಂತರ A ಕರ್ಣೀಯ ರೂಪದ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಹೊಂದಿದೆ:

(9.7) ಈ ಆಸ್ತಿಯ ಪುರಾವೆಯು ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ವ್ಯಾಖ್ಯಾನದಿಂದ ಅನುಸರಿಸುತ್ತದೆ.

2) ರೂಪಾಂತರದ ಸಮಾನ ಮೌಲ್ಯಗಳಾಗಿದ್ದರೆ ಎಭಿನ್ನವಾಗಿರುತ್ತವೆ, ನಂತರ ಅವುಗಳ ಅನುಗುಣವಾದ ಐಜೆನ್ವೆಕ್ಟರ್ಗಳು ರೇಖೀಯವಾಗಿ ಸ್ವತಂತ್ರವಾಗಿರುತ್ತವೆ.

3) ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ವಿಶಿಷ್ಟ ಬಹುಪದವಾಗಿದ್ದರೆ ಎಮೂರು ಹೊಂದಿದೆ ವಿವಿಧ ಬೇರುಗಳು, ನಂತರ ಕೆಲವು ಆಧಾರದಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಕರ್ಣೀಯ ನೋಟವನ್ನು ಹೊಂದಿದೆ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಈಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್‌ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ ನಾವು ಒಂದು ವಿಶಿಷ್ಟ ಸಮೀಕರಣವನ್ನು ರಚಿಸೋಣ: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

ಕಂಡುಬರುವ ಪ್ರತಿಯೊಂದು ಮೌಲ್ಯಕ್ಕೆ ಅನುಗುಣವಾದ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ λ. (9.5) ನಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ X (1) ={x 1, x 2, x 3) - ಐಜೆನ್ವೆಕ್ಟರ್ ಅನುಗುಣವಾದ λ 1 =-2, ನಂತರ

- ಸಹಕಾರಿ ಆದರೆ ಅನಿಶ್ಚಿತ ವ್ಯವಸ್ಥೆ. ಅದರ ಪರಿಹಾರವನ್ನು ರೂಪದಲ್ಲಿ ಬರೆಯಬಹುದು X (1) ={ಎ,0,-ಎ), ಇಲ್ಲಿ a ಯಾವುದೇ ಸಂಖ್ಯೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ, ನಮಗೆ ಅಗತ್ಯವಿದ್ದರೆ | X (1) |=1, X (1) =

ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಬದಲಿ (9.5) λ 2 =3, ನಾವು ಎರಡನೇ ಐಜೆನ್ವೆಕ್ಟರ್ನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನಿರ್ಧರಿಸಲು ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ - X (2) ={y 1,y 2,y 3}:

, ಎಲ್ಲಿ X (2) ={ಬಿ,-ಬಿ, ಬಿ) ಅಥವಾ, ಒದಗಿಸಿದ | X (2) |=1, X (2) =

ಫಾರ್ λ 3 = 6 ಐಜೆನ್ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ X (3) ={z 1, z 2, z 3}:

, X (3) ={ಸಿ,2c,c) ಅಥವಾ ಸಾಮಾನ್ಯ ಆವೃತ್ತಿಯಲ್ಲಿ

x (3) = ಎಂಬುದನ್ನು ಗಮನಿಸಬಹುದು X (1) X (2) = ab-ab= 0, X (1) X (3) = ac-ac= 0, X (2) X (3) = ಕ್ರಿ.ಪೂ- 2bc + bc= 0. ಹೀಗಾಗಿ, ಈ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳು ಜೋಡಿಯಾಗಿ ಆರ್ಥೋಗೋನಲ್ ಆಗಿರುತ್ತವೆ.

ಉಪನ್ಯಾಸ 10.

ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪಗಳು ಮತ್ತು ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಳೊಂದಿಗೆ ಅವುಗಳ ಸಂಪರ್ಕ. ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ಗುಣಲಕ್ಷಣಗಳು ಮತ್ತು ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು. ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪವನ್ನು ಅಂಗೀಕೃತ ರೂಪಕ್ಕೆ ಇಳಿಸುವುದು.

ವ್ಯಾಖ್ಯಾನ 10.1.ಕ್ವಾಡ್ರಾಟಿಕ್ ಆಕಾರನಿಜವಾದ ಅಸ್ಥಿರ x 1, x 2,..., x nಮೊದಲ ಪದವಿಯ ಉಚಿತ ಪದ ಮತ್ತು ನಿಯಮಗಳನ್ನು ಹೊಂದಿರದ ಈ ಅಸ್ಥಿರಗಳಲ್ಲಿ ಎರಡನೇ ಪದವಿಯ ಬಹುಪದೋಕ್ತಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಕ್ವಾಡ್ರಾಟಿಕ್ ರೂಪಗಳ ಉದಾಹರಣೆಗಳು:

(ಎನ್ = 2),

(ಎನ್ = 3). (10.1)

ಕೊನೆಯ ಉಪನ್ಯಾಸದಲ್ಲಿ ನೀಡಲಾದ ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ವ್ಯಾಖ್ಯಾನವನ್ನು ನಾವು ನೆನಪಿಸಿಕೊಳ್ಳೋಣ:

ವ್ಯಾಖ್ಯಾನ 10.2.ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಸಮ್ಮಿತೀಯ, ಒಂದು ವೇಳೆ, ಅಂದರೆ, ಮುಖ್ಯ ಕರ್ಣಕ್ಕೆ ಸಮ್ಮಿತೀಯವಾಗಿರುವ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅಂಶಗಳು ಸಮಾನವಾಗಿದ್ದರೆ.

ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ಮತ್ತು ಐಜೆನ್‌ವೆಕ್ಟರ್‌ಗಳ ಗುಣಲಕ್ಷಣಗಳು:

1) ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಎಲ್ಲಾ ಐಜೆನ್‌ವಾಲ್ಯೂಗಳು ನೈಜವಾಗಿವೆ.

ಪುರಾವೆ (ಇದಕ್ಕಾಗಿ ಎನ್ = 2).

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಬಿಡಿ ಎರೂಪವನ್ನು ಹೊಂದಿದೆ: . ವಿಶಿಷ್ಟ ಸಮೀಕರಣವನ್ನು ರಚಿಸೋಣ:

(10.2) ತಾರತಮ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

ಆದ್ದರಿಂದ, ಸಮೀಕರಣವು ನಿಜವಾದ ಬೇರುಗಳನ್ನು ಮಾತ್ರ ಹೊಂದಿದೆ.

2) ಐಜೆನ್ವೆಕ್ಟರ್ಸ್ಸಮ್ಮಿತೀಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಆರ್ಥೋಗೋನಲ್.

ಪುರಾವೆ (ಇದಕ್ಕಾಗಿ ಎನ್= 2).

ಐಜೆನ್ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳು ಮತ್ತು ಸಮೀಕರಣಗಳನ್ನು ಪೂರೈಸಬೇಕು.