Primārais tirgus ir Fišera kritērijs. Fišera kritērijs tiek izmantots, lai pārbaudītu hipotēzi, ka divu populāciju dispersijas ir vienādas - dokument

Fišera kritērijs

Fišera kritērijs tiek izmantots, lai pārbaudītu hipotēzi, ka divu dispersijas vispārējās populācijas, izplatīts saskaņā ar parasto likumu. Tas ir parametrisks kritērijs.

Fišera F testu sauc par dispersijas koeficientu, jo tas tiek veidots kā divu objektīvu salīdzināmo dispersiju novērtējumu attiecība.

Ļaujiet iegūt divus paraugus novērojumu rezultātā. No tiem dispersijas un kam Un brīvības pakāpes. Mēs pieņemsim, ka pirmais paraugs ir ņemts no populācijas ar dispersiju , bet otrais ir no vispārējās populācijas ar dispersiju . Par abu dispersiju vienādību tiek izvirzīta nulles hipotēze, t.i. H0:
vai . Lai šo hipotēzi noraidītu, ir jāpierāda atšķirības nozīmīgums noteiktā nozīmīguma līmenī
.

Kritērija vērtību aprēķina, izmantojot formulu:

Acīmredzot, ja novirzes ir vienādas, kritērija vērtība būs vienāda ar vienu. Citos gadījumos tas būs lielāks (mazāks) par vienu.

Testam ir Fišera sadalījums
. Fišera tests — divu virzienu tests un nulles hipotēze
noraidīts par labu alternatīvai
Ja . Lūk, kur
– attiecīgi pirmā un otrā parauga tilpums.

Sistēma STATISTICA realizē vienpusēju Fišera testu, t.i. maksimālā dispersija vienmēr tiek uzskatīta par kvalitāti. Šajā gadījumā nulles hipotēze tiek noraidīta par labu alternatīvai, ja.

Piemērs

Ļaujiet izvirzīt uzdevumu salīdzināt divu studentu grupu mācīšanas efektivitāti. Sasniegumu līmenis raksturo mācību procesa vadības līmeni, un izkliede ir mācību vadības kvalitāte, mācību procesa organizācijas pakāpe. Abi rādītāji ir neatkarīgi un vispārējs gadījums jāskata kopā. Katras studentu grupas mācību sasniegumu (matemātisko gaidu) līmeni raksturo vidējie aritmētiskie rādītāji un , un kvalitāti raksturo atbilstošās aplēšu izlases novirzes: un . Novērtējot pašreizējo snieguma līmeni, izrādījās, ka tas bija vienāds abiem skolēniem: = = 4,0. Izlases paraugi:
Un
. Brīvības pakāpju skaitļi, kas atbilst šiem aprēķiniem:
Un
. No šejienes, lai noteiktu atšķirības mācīšanās efektivitātē, mēs varam izmantot akadēmiskā snieguma stabilitāti, t.i. Pārbaudīsim hipotēzi.

Aprēķināsim
(skaitītājā jābūt lielai novirzei), . Saskaņā ar tabulām ( STATISTIKA – VarbūtībaIzplatīšanaKalkulators) mēs atrodam , kas ir mazāks nekā aprēķināts, tāpēc nulles hipotēze ir jānoraida par labu alternatīvai. Šis secinājums var neapmierināt pētnieku, jo viņu interesē attiecības patiesā vērtība
(mums vienmēr ir lielas atšķirības skaitītājā). Pārbaudot vienpusēju kritēriju, mēs iegūstam, ka tas ir mazāks par iepriekš aprēķināto vērtību. Tātad nulles hipotēze ir jānoraida par labu alternatīvai.

Fišera tests programmā STATISTICA Windows vidē

Hipotēzes (Fišera kritērija) pārbaudes piemērā mēs izmantojam (izveidojam) failu ar diviem mainīgajiem (fisher.sta):

Rīsi. 1. Tabula ar diviem neatkarīgiem mainīgajiem

Lai pārbaudītu hipotēzi, ir nepieciešams pamata statistikā ( PamataStatistikaunTabulas) atlasiet t-testu neatkarīgiem mainīgajiem. ( t-tests, neatkarīgs, pēc mainīgajiem).

Rīsi. 2. Parametrisko hipotēžu pārbaude

Pēc mainīgo atlases un taustiņa nospiešanas Kopsavilkums Tiek aprēķinātas standartnoviržu vērtības un Fišera kritērijs. Turklāt tiek noteikts nozīmīguma līmenis lpp, kurā atšķirība ir nenozīmīga.

Rīsi. 3. Hipotēžu pārbaudes rezultāti (F-tests)

Izmantojot VarbūtībaKalkulators un, iestatot parametru vērtības, varat izveidot Fišera sadalījuma grafiku ar atzīmēto aprēķināto vērtību.

Rīsi. 4. Hipotēzes pieņemšanas (noraidīšanas) joma (F-kritērijs)

Avoti.

Hipotēžu pārbaude par saistību starp divām dispersijām

URL: /tryfonov3/terms3/testdi.htm

6. lekcija. :8080/resources/math/mop/lections/lection_6.htm

F – Fišera kritērijs

URL: /home/portal/applications/Multivariatadvisor/F-Fisher/F-Fisheer.htm

Varbūtības statistikas pētījumu teorija un prakse.

URL: /active/referats/read/doc-3663-1.html

F – Fišera kritērijs

Fišera kritērijsļauj salīdzināt divu neatkarīgu paraugu izlases dispersijas. Lai aprēķinātu F emp, jāatrod divu paraugu dispersiju attiecība, lai lielākā dispersija būtu skaitītājā, bet mazākā – saucējā. Fišera kritērija aprēķināšanas formula ir šāda:

kur ir attiecīgi pirmā un otrā parauga dispersijas.

Tā kā saskaņā ar kritērija nosacījumu skaitītāja vērtībai ir jābūt lielākai vai vienādai ar saucēja vērtību, F emp vērtība vienmēr būs lielāka vai vienāda ar vienu.

Brīvības pakāpju skaitu nosaka arī vienkārši:

k 1 =n l - 1 pirmajai izlasei (t.i., izlasei, kuras dispersija ir lielāka) un k 2 = n 2 - 1 otrajam paraugam.

1. pielikumā Fišera kritērija kritiskās vērtības ir noteiktas ar vērtībām k 1 (tabulas augšējā līnija) un k 2 (tabulas kreisā kolonna).

Ja t em >t crit, tad tiek pieņemta nulles hipotēze, pretējā gadījumā tiek pieņemta alternatīva.

3. piemērs. Pārbaude tika veikta divās trešajās klasēs garīgo attīstību desmit studenti TURMSH testā. Iegūtās vidējās vērtības būtiski neatšķīrās, taču psihologu interesē jautājums, vai starp klasēm ir atšķirības garīgās attīstības rādītāju viendabīguma pakāpē.

Risinājums. Fišera testam ir jāsalīdzina testa rezultātu atšķirības abās klasēs. Pārbaudes rezultāti ir parādīti tabulā:

3. tabula.

Studentu nr.	Pirmā klase	Otrā klase

Aprēķinot mainīgo X un Y dispersijas, iegūstam:

s x 2 =572,83; s y 2 =174,04

Pēc tam, izmantojot formulu (8) aprēķinam, izmantojot Fišera F kritēriju, mēs atrodam:

Saskaņā ar tabulu no 1. pielikuma F kritērijam ar brīvības pakāpēm abos gadījumos, kas vienādas ar k = 10 - 1 = 9, mēs atrodam F crit = 3,18 (<3.29), следовательно, в терминах статистических гипотез можно утвер­ждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

6.2. Neparametriskie testi

Salīdzinot ar aci (procentos) rezultātus pirms un pēc jebkuras ietekmes, pētnieks nonāk pie secinājuma, ka, ja tiek novērotas atšķirības, tad ir atšķirības salīdzināmajos paraugos. Šī pieeja ir kategoriski nepieņemama, jo procentos nav iespējams noteikt atšķirību ticamības līmeni. Paši ņemtie procenti neļauj izdarīt statistiski ticamus secinājumus. Lai pierādītu jebkuras iejaukšanās efektivitāti, ir jāidentificē statistiski nozīmīga rādītāju novirzes (nobīdes) tendence. Lai atrisinātu šādas problēmas, pētnieks var izmantot vairākus diskriminācijas kritērijus. Tālāk mēs aplūkosim neparametriskos testus: zīmju testu un hī kvadrāta testu.

)

Kritērija φ* aprēķins

1. Nosakiet tās atribūta vērtības, kas būs kritērijs subjektu iedalīšanai tajos, kuriem ir “ietekme” un tajos, kuriem “nav ietekmes”. Ja raksturlielumu mēra kvantitatīvi, izmantojiet λ kritēriju, lai atrastu optimālo atdalīšanas punktu.

2. Uzzīmējiet četru šūnu (sinonīms: četru lauku) tabulu no divām kolonnām un divām rindām. Pirmā sleja ir “ir efekts”; otrā kolonna - “bez efekta”; pirmā rinda no augšas - 1 grupa (paraugs); otrā rinda - 2. grupa (paraugs).

4. Saskaitiet to subjektu skaitu pirmajā izlasē, kuriem nav ietekmes, un ievadiet šo skaitli tabulas augšējā labajā šūnā. Aprēķiniet divu augšējo šūnu summu. Tam jāsakrīt ar priekšmetu skaitu pirmajā grupā.

6. Saskaitiet to subjektu skaitu otrajā izlasē, kuriem nav “efekta”, un ievadiet šo skaitli tabulas apakšējā labajā šūnā. Aprēķiniet divu apakšējo šūnu summu. Tam jāsakrīt ar priekšmetu skaitu otrajā grupā (izlasē).

7. Nosakiet to subjektu procentuālo daļu, kuriem “ir ietekme”, attiecinot to skaitu ar kopējo subjektu skaitu noteiktā grupā (izlasē). Iegūtos procentus ierakstiet attiecīgi tabulas augšējā kreisajā un apakšējā kreisajā šūnā iekavās, lai nesajauktu tos ar absolūtajām vērtībām.

8. Pārbaudiet, vai kāds no salīdzināmajiem procentiem ir vienāds ar nulli. Ja tas tā ir, mēģiniet to mainīt, pārvietojot grupas atdalīšanas punktu vienā vai otrā virzienā. Ja tas nav iespējams vai nav vēlams, atsakieties no φ* kritērija un izmantojiet χ2 kritēriju.

9. Nosakiet saskaņā ar tabulu. XII 1. papildinājuma leņķi φ katram salīdzināmajam procentam.

kur: φ1 - leņķis, kas atbilst lielākajam procentam;

φ2 - leņķis, kas atbilst mazākajam procentam;

N1 - novērojumu skaits 1. paraugā;

N2 - novērojumu skaits 2. paraugā.

11. Salīdziniet iegūto vērtību φ* ar kritiskajām vērtībām: φ* ≤1,64 (p<0,05) и φ* ≤2,31 (р<0,01).

Ja φ*emp ≤φ*kr. H0 tiek noraidīts.

Ja nepieciešams, nosakiet precīzu iegūtā φ*emp nozīmīguma līmeni saskaņā ar tabulu. XIII 1. pielikums.

Šī metode ir aprakstīta daudzās rokasgrāmatās (Plokhinsky N.A., 1970; Gubler E.V., 1978; Ivanter E.V., Korosov A.V., 1992 utt.) Šis apraksts ir balstīts uz metodes versiju, kuru izstrādāja un prezentēja E.V. Gublers.

Kritērija mērķis φ*

Fišera kritērijs ir paredzēts divu paraugu salīdzināšanai pēc pētnieku interesējošās ietekmes (rādītāja) rašanās biežuma. Jo lielāks tas ir, jo ticamākas ir atšķirības.

Kritērija apraksts

Kritērijs novērtē atšķirību ticamību starp tiem procentiem no diviem paraugiem, kuros tika fiksēts mūs interesējošais efekts (rādītājs). Tēlaini izsakoties, mēs salīdzinām 2 labākos gabalus, kas sagriezti no 2 pīrāgiem, un izlemjam, kurš no tiem ir patiesi lielāks.

Fišera leņķiskās transformācijas būtība ir pārvērst procentus centrālā leņķa vērtībās, kuras mēra radiānos. Lielāks procents atbilst lielākam leņķim φ, un mazāks procents atbilst mazākam leņķim, taču attiecības šeit nav lineāras:

kur P ir procentuālais daudzums, kas izteikts vienības daļās (sk. 5.1. att.).

Pieaugot neatbilstībai starp leņķiem φ 1 un φ 2 un palielinot paraugu skaitu, kritērija vērtība pieaug. Jo lielāka ir φ* vērtība, jo lielāka iespēja, ka atšķirības ir būtiskas.

Hipotēzes

H 0 : Personu īpatsvars, kurā izpaužas pētītais efekts, 1. paraugā nav vairāk kā 2. paraugā.

H 1 : indivīdu īpatsvars, kuriem ir pētīts efekts, ir lielāks 1. paraugā nekā 2. paraugā.

Kritērija grafiskais attēlojums φ*

Leņķiskās transformācijas metode ir nedaudz abstraktāka nekā citi kritēriji.

Formulā, ko izmanto E.V. Gublers, aprēķinot φ vērtības, tiek pieņemts, ka 100% veido leņķi φ=3,142, tas ir, noapaļota vērtība π=3,14159... Tas ļauj mums parādīt salīdzinātos paraugus formā divi pusloki, no kuriem katrs simbolizē 100% no izlases populācijas. Objektu procentuālais daudzums ar “efektu” tiks attēlots kā sektori, ko veido centrālie leņķi φ. Attēlā 5.2. attēlā parādīti divi pusloki, kas ilustrē 1. piemēru. Pirmajā paraugā 60% subjektu atrisināja problēmu. Šis procents atbilst leņķim φ=1,772. Otrajā izlasē 40% subjektu atrisināja problēmu. Šis procents atbilst leņķim φ =1,369.

φ* kritērijs ļauj noteikt, vai viens no leņķiem patiešām ir statistiski nozīmīgi pārāks par otru konkrētajiem izlases lielumiem.

Kritērija ierobežojumi φ*

1. Neviena no salīdzināmajām proporcijām nedrīkst būt nulle. Formāli φ metodes piemērošanai nav šķēršļu gadījumos, kad novērojumu īpatsvars vienā no izlasēm ir vienāds ar 0. Taču šajos gadījumos rezultāts var izrādīties nepamatoti uzpūsts (Gubler E.V., 1978, p. 86).

2. Augšējais φ kritērijā nav ierobežojumu - paraugi var būt tik lieli, cik vēlaties.

Nolaist robeža - 2 novērojumi vienā no paraugiem. Tomēr divu paraugu skaitā ir jāievēro šādas attiecības:

a) ja vienā paraugā ir tikai 2 novērojumi, tad otrajā ir jābūt vismaz 30:

b) ja vienā no paraugiem ir tikai 3 novērojumi, tad otrajā ir jābūt vismaz 7:

c) ja vienā no paraugiem ir tikai 4 novērojumi, tad otrajā ir jābūt vismaz 5:

d) plkstn 1 , n 2 ≥ 5 Ir iespējami jebkādi salīdzinājumi.

Principā ir iespējams arī salīdzināt paraugus, kas neatbilst šim nosacījumam, piemēram, ar relācijun 1 =2, n 2 = 15, taču šajos gadījumos būtiskas atšķirības noteikt nebūs iespējams.

φ* kritērijam nav citu ierobežojumu.

Apskatīsim dažus piemērus, lai ilustrētu iespējaskritērijs φ*.

1. piemērs: paraugu salīdzināšana pēc kvalitatīvi noteikta rakstura.

2. piemērs: paraugu salīdzināšana saskaņā ar kvantitatīvi izmērītu raksturlielumu.

3. piemērs: paraugu salīdzinājums gan pēc raksturlieluma līmeņa, gan sadalījuma.

4. piemērs: φ* kritērija izmantošana kombinācijā ar kritērijuX Kolmogorovs-Smirnovs, lai sasniegtu visprecīzāko rezultātu.

1. piemērs - paraugu salīdzināšana pēc kvalitatīvi noteikta rakstura

Izmantojot šo kritēriju, mēs salīdzinām subjektu procentuālo daļu vienā izlasē, kam raksturīga kāda kvalitāte, ar to subjektu procentuālo daļu citā izlasē, kam raksturīga tāda pati kvalitāte.

Pieņemsim, ka mūs interesē, vai divas studentu grupas atšķiras ar panākumiem jaunas eksperimentālas problēmas risināšanā. Pirmajā 20 cilvēku grupā ar to tika galā 12 cilvēki, bet otrajā 25 cilvēku izlasē - 10. Pirmajā gadījumā problēmu atrisināju procentuālais daudzums būs 12/20·100%=60%. un otrajā 10/25·100%= 40%. Vai šie procenti būtiski atšķiras, ņemot vērā datus?n 1 Unn 2 ?

Šķiet, ka pat “ar aci” var noteikt, ka 60% ir ievērojami augstāks par 40%. Tomēr patiesībā šīs atšķirības, ņemot vērā datusn 1 , n 2 neuzticams.

Pārbaudīsim to. Tā kā mūs interesē problēmas risināšanas fakts, veiksmi eksperimentālas problēmas risināšanā uzskatīsim par “efektu”, bet neveiksmi tās risināšanā – par efekta neesamību.

Formulēsim hipotēzes.

H 0 : Personu īpatsvarsPirmajā grupā nebija vairāk cilvēku, kas izpildīja uzdevumu, nekā otrajā grupā.

H 1 : to cilvēku īpatsvars, kuri izpildīja uzdevumu pirmajā grupā, ir lielāks nekā otrajā grupā.

Tagad izveidosim tā saukto četru šūnu vai četru lauku tabulu, kas faktiski ir empīrisko frekvenču tabula divām atribūta vērtībām: “ir efekts” - “nav efekta”.

5.1. tabula

Četru šūnu tabula kritērija aprēķināšanai, salīdzinot divas priekšmetu grupas pēc problēmas atrisināju procentuālā daudzuma.

Grupas	“Ir efekts”: problēma atrisināta			"Bez efekta": problēma nav atrisināta			Summas
	Daudzums priekšmetiem	% dalīties		Daudzums priekšmetiem	% daļa
1 grupa		(60%)			(40%)
2. grupa		(40%)			(60%)
Summas

Četru šūnu tabulā parasti kolonnas “Ir efekts” un “Nav efekta” ir atzīmētas augšpusē, bet rindas “Grupa 1” un “Group 2” atrodas kreisajā pusē. Faktiski salīdzināšanā ir iesaistīti tikai lauki (šūnas) A un B, tas ir, procenti kolonnā “Ietekme ir”.

Saskaņā ar tabulu.XII1. pielikumā ir noteiktas φ vērtības, kas atbilst procentuālajai daļai katrā no grupām.

Tagad aprēķināsim φ* empīrisko vērtību, izmantojot formulu:

kur φ 1 - leņķis, kas atbilst lielākai % daļai;

φ 2 - leņķis, kas atbilst mazākajai % daļai;

n 1 - novērojumu skaits 1. paraugā;

n 2 - novērojumu skaits 2. paraugā.

Šajā gadījumā:

Saskaņā ar tabulu.XIII1. pielikumā mēs nosakām, kāds nozīmīguma līmenis atbilst φ* em=1,34:

p=0,09

Ir iespējams arī noteikt φ* kritiskās vērtības, kas atbilst psiholoģijā pieņemtajiem līmeņiem statistiskā nozīme:

Veidosim "nozīmības asi".

Iegūtā empīriskā vērtība φ* atrodas nesvarības zonā.

Atbilde: H 0 pieņemts. To cilvēku procentuālā daļa, kuri izpildīja uzdevumuVpirmā grupa ir ne vairāk kā otrajā grupā.

Var tikai just līdzi pētniekam, kurš 20% un pat 10% atšķirības uzskata par būtiskām, nepārbaudot to ticamību, izmantojot φ* kritēriju. Šajā gadījumā, piemēram, būtiskas būtu tikai vismaz 24,3% atšķirības.

Šķiet, ka, salīdzinot divus paraugus uz jebkura kvalitatīva pamata, φ kritērijs var mūs drīzāk apbēdināt, nevis iepriecināt. Tas, kas šķita nozīmīgs, var nebūt tāds no statistikas viedokļa.

Fišera kritērijam ir daudz vairāk iespēju iepriecināt pētnieku, ja salīdzinām divus paraugus pēc kvantitatīvi izmērītiem raksturlielumiem un var mainīt “efektu”.

2. piemērs - divu paraugu salīdzināšana pēc kvantitatīvi izmērīta raksturlieluma

Izmantojot šo kritēriju, mēs salīdzinām to subjektu procentuālo daļu vienā izlasē, kuri sasniedz noteiktu atribūta vērtības līmeni, ar to subjektu procentuālo daļu, kuri sasniedz šo līmeni citā izlasē.

G. A. Tļegenova (1990) pētījumā no 70 jauno arodskolu audzēkņiem vecumā no 14 līdz 16 gadiem, pamatojoties uz iegūtajiem rezultātiem, tika atlasīti 10 priekšmeti ar augstu punktu skaitu Agresijas skalā un 11 priekšmeti ar zemu punktu skaitu Agresijas skalā. aptauja, izmantojot Freiburgas personības anketu. Jānoskaidro, vai agresīvo un neagresīvo jauniešu grupas atšķiras pēc attāluma, ko viņi spontāni izvēlas sarunā ar kursa biedru. G. A. Tļegenova dati ir parādīti tabulā. 5.2. Var pamanīt, ka agresīvi jauni vīrieši biežāk izvēlas 50 distancicm vai pat mazāk, savukārt neagresīvi zēni biežāk izvēlas distanci, kas lielāka par 50 cm.

Tagad mēs varam uzskatīt 50 cm attālumu par kritisku un pieņemt, ka, ja objekta izvēlētais attālums ir mazāks vai vienāds ar 50 cm, tad “ietekme ir”, un, ja izvēlētais attālums ir lielāks par 50 cm, tad "nav efekta." Redzam, ka agresīvu jauniešu grupā efekts novērojams 7 no 10, t.i., 70% gadījumu, bet neagresīvo jauniešu grupā - 2 no 11, t.i., 18,2% gadījumu. . Šos procentus var salīdzināt, izmantojot φ* metodi, lai noteiktu to atšķirību nozīmīgumu.

5.2. tabula

Agresīvu un neagresīvu jauniešu izvēlētie attāluma rādītāji (cm) sarunā ar kursa biedru (pēc G.A. Tļegenova, 1990)

	1. grupa: zēni ar augstu punktu skaitu Agresijas skalāFPI- R (n 1 =10)		2. grupa: zēni ar zemām vērtībām agresijas skalāFPI- R (n 2 =11)
	d(c m )	% daļa	d(c M )	% daļa
"Ēd Efekts" d≤50 cm
				18,2%
"Nē efekts" d>50 cm
	80 QO			81,8%
Summas		100%		100%
Vidēji	5b:o		77.3

Formulēsim hipotēzes.

H 0 d ≤ 50 cm, agresīvo puišu grupā nav vairāk kā neagresīvo zēnu grupā.

H 1 : to cilvēku īpatsvars, kuri izvēlas attālumud≤ 50 cm, agresīvo jauniešu grupā vairāk nekā neagresīvo jauniešu grupā. Tagad izveidosim tā saukto četru šūnu tabulu.

53. tabula

Četru šūnu tabula φ* kritērija aprēķināšanai, salīdzinot agresīvo (nf=10) un neagresīviem jauniem vīriešiem (n2=11)

Grupas	"Ir efekts": d≤50			"Nav efekta." d>50			Summas
	Priekšmetu skaits	(% daļa)		Priekšmetu skaits	(% daļa)
1. grupa - agresīvi jaunieši		(70%)			(30%)
2. grupa - neagresīvi jaunieši		(180%)			(81,8%)
Summa

Saskaņā ar tabulu.XII1. pielikumā ir noteiktas φ vērtības, kas atbilst “efekta” procentuālajām daļām katrā no grupām.

Iegūtā empīriskā vērtība φ* atrodas nozīmīguma zonā.

Atbilde: H 0 noraidīts. PieņemtsH 1 . To cilvēku īpatsvars, kuri sarunā izvēlas attālumu, kas ir mazāks vai vienāds ar 50 cm, ir lielāks agresīvo jauniešu grupā nekā neagresīvo jauniešu grupā.

Pēc iegūtajiem rezultātiem varam secināt, ka agresīvāki jaunieši biežāk izvēlas distanci, kas mazāka par pusmetru, savukārt neagresīvie jaunieši biežāk izvēlas distanci, kas lielāka par pusmetru. Mēs redzam, ka agresīvi jauni vīrieši faktiski sazinās uz robežas starp intīmo (0-46 cm) un personīgo zonu (no 46 cm). Tomēr mēs atceramies, ka intīma distance starp partneriem ir ne tikai tuvu, labu attiecību, bet arīUnroku cīņa (HalleE. T., 1959).

3. piemērs - paraugu salīdzinājums gan pēc raksturlieluma līmeņa, gan sadalījuma.

Šajā lietošanas gadījumā mēs vispirms varam pārbaudīt, vai grupas atšķiras pēc kādas pazīmes līmeņiem, un pēc tam salīdzināt pazīmes sadalījumu abos paraugos. Šāds uzdevums var būt būtisks, analizējot atšķirības to vērtējumu diapazonos vai formā, kas iegūti, izmantojot jebkuru jaunu tehniku.

R. T. Čirkinas (1995) pētījumā pirmo reizi tika izmantota anketa, kuras mērķis bija identificēt tendenci no atmiņas apspiest faktus, nosaukumus, nodomus un darbības metodes personisko, ģimenes un profesionālo kompleksu dēļ. Anketa tika izveidota, piedaloties E.V.Sidorenko, pamatojoties uz materiāliem no grāmatas 3. Freids “Ikdienas dzīves psihopatoloģija”. Izmantojot šo anketu, kā arī Menestera-Korzini tehniku, tika pārbaudīta izlase, kurā bija 50 Pedagoģiskā institūta studenti, neprecēti, bez bērniem vecumā no 17 līdz 20 gadiem, lai identificētu personības nepietiekamības sajūtas intensitāti.vai"mazvērtības komplekss" (MeistarsG. Dž., KorsīniR. Dž., 1982).

Aptaujas rezultāti ir parādīti tabulā. 5.4.

Vai var teikt, ka pastāv kādas būtiskas sakarības starp represijas enerģijas rādītāju, kas diagnosticēts ar anketas palīdzību, un paša nepietiekamības sajūtas intensitātes rādītājiem?

5.4. tabula

Indikatori, kas liecina par personīgās nepietiekamības sajūtu intensitāti studentu grupās ar augstu (nj=18) un zema (n2=24) pārvietojuma enerģija

1. grupa: pārvietošanās enerģija no 19 līdz 31 punktam (n 1 =181		2. grupa: pārvietošanās enerģija no 7 līdz 13 punktiem (n 2 =24)
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30; 30 50; 50 60; 60		0; 0 5; 5; 5; 5 10; 10; 10; 10; 10; 10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30
Summas Vidēji	26,11	15,42

Neskatoties uz to, ka vidējā vērtība grupā ar enerģiskākām represijām ir augstāka, tajā tiek novērotas arī 5 nulles vērtības. Ja salīdzinām reitingu sadalījuma histogrammas abos paraugos, starp tiem atklājas pārsteidzošs kontrasts (5.3. att.).

Lai salīdzinātu divus sadalījumus, mēs varētu izmantot testuχ 2 vai kritērijsλ , bet šim mums būtu jāpaplašina rindas, turklāt abos izlasēsn <30.

φ* kritērijs ļaus pārbaudīt divu grafikā novēroto sadalījumu neatbilstības efektu, ja piekrītam pieņemt, ka “ietekme ir”, ja nepietiekamības sajūtas rādītājs ir ļoti zems (0) vai otrādi. , ļoti augstas vērtības (S30), un ka “nav efekta”, ja nepietiekamības sajūtas rādītājs ir vidēji no 5 līdz 25.

Formulēsim hipotēzes.

H 0 : Deficīta indeksa galējās vērtības (0 vai 30 vai vairāk) grupā ar enerģiskākām represijām nav biežākas kā grupā ar mazāk enerģiskām represijām.

H 1 : Deficīta indeksa galējās vērtības (0 vai 30 vai vairāk) grupā ar enerģiskākām represijām ir biežākas nekā grupā ar mazāk enerģiskām represijām.

Izveidosim četru šūnu tabulu, kas ir piemērota tālākai φ* kritērija aprēķināšanai.

5.5. tabula

Četru šūnu tabula φ* kritērija aprēķināšanai, salīdzinot grupas ar lielāku un zemāku represijas enerģiju, pamatojoties uz nepietiekamības rādītāju attiecību

Grupas	“Ietekme ir”: deficīta indikators ir 0 vai >30		“Bez efekta”: atteices indekss no 5 līdz 25		Summas
		(88,9%)		(11,1%)
		(33,3%)		(66,7%)
Summas

Saskaņā ar tabulu.XII1. pielikumā mēs nosakām φ vērtības, kas atbilst salīdzinātajiem procentiem:

Aprēķināsim φ* empīrisko vērtību:

φ* kritiskās vērtības jebkuramn 1 , n 2 , kā mēs atceramies no iepriekšējā piemēra, ir:

TabulaXIII1. pielikums ļauj precīzāk noteikt iegūtā rezultāta nozīmīguma līmeni: lpp<0,001.

Atbilde: H 0 noraidīts. PieņemtsH 1 . Deficīta indeksa galējās vērtības (0 vai 30 vai vairāk) grupā ar lielāku represijas enerģiju rodas biežāk nekā grupā ar mazāku represiju enerģiju.

Tātad subjektiem ar lielāku represiju enerģiju var būt gan ļoti augsti (30 vai vairāk), gan ļoti zemi (nulle) savas nepietiekamības sajūtas rādītāji. Var pieņemt, ka viņi apspiež gan savu neapmierinātību, gan nepieciešamību pēc panākumiem dzīvē. Šie pieņēmumi ir jāturpina pārbaudīt.

Iegūtais rezultāts neatkarīgi no tā interpretācijas apstiprina φ* kritērija iespējas, novērtējot pazīmes sadalījuma formas atšķirības divos paraugos.

Sākotnējā izlasē bija 50 cilvēki, bet 8 no tiem tika izslēgti no izskatīšanas, jo tiem bija vidējais represijas anerģijas indeksa rādītājs (14-15). Arī to nepietiekamības sajūtas intensitātes rādītāji ir vidēji: 6 vērtības pa 20 punktiem katra un 2 vērtības pa 25 punktiem.

φ* kritērija jaudīgās iespējas var pārbaudīt, apstiprinot pavisam citu hipotēzi, analizējot šī piemēra materiālus. Mēs varam pierādīt, piemēram, ka grupā ar lielāku represijas enerģiju nepietiekamības līmenis joprojām ir augstāks, neskatoties uz tās sadalījuma paradoksālo raksturu šajā grupā.

Formulēsim jaunas hipotēzes.

H 0 Augstākās deficīta indeksa vērtības (30 vai vairāk) grupā ar lielāku represijas enerģiju nav biežākas kā grupā ar mazāku represijas enerģiju.

H 1 : Augstākās deficīta indeksa vērtības (30 vai vairāk) grupā ar lielāku represijas enerģiju rodas biežāk nekā grupā ar mazāku represijas enerģiju. Izveidosim četru lauku tabulu, izmantojot tabulas datus. 5.4.

5.6. tabula

Četru šūnu tabula φ* kritērija aprēķināšanai, salīdzinot grupas ar lielāku un mazāku represijas enerģiju pēc nepietiekamības rādītāja līmeņa

Grupas	Kļūmes indikators “Ir efekts”* ir lielāks vai vienāds ar 30		“Bez efekta”: atteices līmenis ir mazāks 30		Summas
1. grupa - ar lielāku pārvietošanas enerģiju		(61,1%)		(38.9%)
2. grupa - ar mazāku pārvietošanas enerģiju		(25.0%)		(75.0%)
Summas

Saskaņā ar tabulu.XIII1. pielikumā mēs nosakām, ka šis rezultāts atbilst nozīmīguma līmenim p = 0,008.

Atbilde: Bet tas tiek noraidīts. PieņemtsHj: Augstākie deficīta rādītāji (30 un vairāk punkti) grupāArar lielāku pārvietošanās enerģiju rodas biežāk nekā grupā ar mazāku pārvietošanās enerģiju (p = 0,008).

Tātad, mēs varējām to pierādītVgrupaiArar enerģiskākām represijām dominē nepietiekamības indikatora galējās vērtības un tas, ka šis rādītājs pārsniedz tās vērtībassasniedztieši šajā grupā.

Tagad mēs varētu mēģināt pierādīt, ka grupā ar augstāku represijas enerģiju mazākas nepietiekamības indeksa vērtības ir biežāk sastopamas, neskatoties uz to, ka vidējā vērtībaV šai grupai ir vairāk (26,11 pret 15,42 grupāAr mazāka nobīde).

Formulēsim hipotēzes.

H 0 : Zemākie deficīta rādītāji (nulle) grupāAr represijas ar lielāku enerģiju nav biežākas kā grupāAr mazāk pārvietošanas enerģijas.

H 1 : Parādās zemākais deficīta līmenis (nulle).V grupa ar lielāku represijas enerģiju biežāk nekā grupāAr mazāk enerģiskas represijas. Sagrupēsim datus jaunā četru šūnu tabulā.

5.7. tabula

Četru šūnu tabula grupu salīdzināšanai ar dažādām represijas enerģijām, pamatojoties uz deficīta indikatora nulles vērtību biežumu

Grupas	"Ir efekts": atteices indikators ir 0		Nepietiekamības "nav efekta".	rādītājs nav vienāds ar 0	Summas
1. grupa - ar lielāku pārvietošanas enerģiju		(27,8%)		(72,2%)
1 grupa - ar mazāku pārvietošanas enerģiju		(8,3%)		(91,7%)
Summas

Mēs nosakām φ vērtības un aprēķinām φ* vērtību:

Atbilde: H 0 noraidīts. Zemākie nepietiekamības rādītāji (nulle) grupā ar lielāku represiju enerģiju ir biežāk nekā grupā ar mazāku represiju enerģiju (p<0,05).

Kopumā iegūtos rezultātus var uzskatīt par pierādījumu daļējai S. Freida un A. Adlera kompleksa jēdzienu sakritībai.

Zīmīgi, ka starp represijas enerģijas rādītāju un savas nepietiekamības sajūtas intensitātes rādītāju izlasē kopumā tika iegūta pozitīva lineāra korelācija (p = +0,491, p<0,01). Как мы можем убедиться, применение критерия φ* позволяет проникнуть в более тонкие и содержательно значимые соотношения между этими двумя показателями.

4. piemērs - φ* kritērija izmantošana kombinācijā ar kritēriju λ Kolmogorovs-Smirnovs, lai sasniegtu maksimumu precīzsrezultāts

Ja paraugus salīdzina pēc kādiem kvantitatīvi izmērītiem rādītājiem, rodas problēma noteikt sadalījuma punktu, ko var izmantot kā kritisko punktu, sadalot visus subjektus tajos, kuriem ir “ietekme” un tajos, kuriem “neiedarbojas”.

Principā punktu, kurā mēs sadalītu grupu apakšgrupās, kur ir efekts un kur efekta nav, var izvēlēties diezgan patvaļīgi. Mūs var interesēt jebkurš efekts, un tāpēc mēs varam sadalīt abus paraugus divās daļās jebkurā brīdī, ja vien tam ir kāda jēga.

Tomēr, lai maksimāli palielinātu φ* testa jaudu, ir jāizvēlas punkts, kurā atšķirības starp abām salīdzinātajām grupām ir vislielākās. Visprecīzāk to varam izdarīt, izmantojot kritērija aprēķināšanas algoritmuλ , kas ļauj noteikt divu paraugu maksimālās neatbilstības punktu.

Iespēja apvienot kritērijus φ* unλ aprakstījis E.V. Gubler (1978, 85.-88. lpp.). Mēģināsim izmantot šo metodi, lai atrisinātu šādu problēmu.

Kopīgā pētījumā M.A. Kuročkina, E.V. Sidorenko un Yu.A. Čurakovs (1992) Apvienotajā Karalistē veica divu kategoriju Anglijas ģimenes ārstu aptauju: a) ārsti, kuri atbalstīja medicīnas reformu un jau bija pārvērtuši savus uzņemšanas birojus par fondu turētājiem ar savu budžetu; b) ārsti, kuru kabinetiem joprojām nav pašu līdzekļu un tie tiek pilnībā nodrošināti no valsts budžeta. Anketas tika nosūtītas 200 ārstu izlasei, kas pārstāvēja Anglijas ārstu kopējo populāciju dažāda dzimuma, vecuma, darba stāža un darba vietas pārstāvju ziņā - lielajās pilsētās vai provincēs.

Uz anketu atbildēja 78 ārsti, no kuriem 50 strādāja uzgaidāmajās telpās ar līdzekļiem un 28 no uzgaidāmajām telpām bez līdzekļiem. Katram no ārstiem bija jāprognozē, kāda būs uzņemšanas daļa ar līdzekļiem nākamajā, 1993. gadā. Uz šo jautājumu atbildēja tikai 70 ārsti no 78, kas atsūtīja atbildes. To prognožu sadalījums ir parādīts tabulā. 5.8 atsevišķi ārstu grupai ar līdzekļiem un ārstu grupai bez līdzekļiem.

Vai ārstu ar līdzekļiem un ārstu bez līdzekļiem prognozes kaut kā atšķiras?

5.8. tabula

Ģimenes ārstu prognožu sadalījums par to, kāds būs neatliekamās palīdzības numuru īpatsvars ar līdzekļiem 1993.

Paredzamā daļa
uzņemšanas telpas ar līdzekļiem	ārsti ar fondu (n 1 =45)	ārsti bez fonda (n 2 =25)	Summas
1. no 0 līdz 20%	4	5	9
2. no 21 līdz 40%	15	UN	26
3. no 41 līdz 60%	18	5	23
4. no 61 līdz 80%	7	4	UN
5. no 81 līdz 100%	1	0	1
Summas	45	25	70

Noteiksim maksimālās neatbilstības punktu starp diviem atbilžu sadalījumiem, izmantojot 15. algoritmu no 4.3. punkta (sk. 5.9. tabulu).

5.9. tabula

Uzkrāto frekvenču maksimālās starpības aprēķins divu grupu ārstu prognožu sadalījumos

Prognozētā uzņemšanas daļa ar līdzekļiem (%)	Empīriskās izvēles biežums noteiktai atbilžu kategorijai		Empīriskās frekvences		Kumulatīvās empīriskās frekvences		Atšķirība (d)
	ārsti ar fondu(n 1 =45)	ārsti bez fonda (n 2 =25)	f* uh 1	f* a2	∑f* e1	∑f* a1
1. no 0 līdz 20% 2. no 21 līdz 40% 3. no 41 līdz 60% 4. no 61 līdz 80% 5. no 81 līdz 100%	4 15 18 7 1	5 11 5 4 0	0,089 0,333 0,400 0,156 0,022	0,200 0,440 0,200 0,160 0	0,089 0,422 0,822 0,978 1,000	0,200 0,640 0,840 1,000 1,000	0111 0,218 0,018 0,022 0

Maksimālā konstatētā atšķirība starp divām uzkrātajām empīriskajām frekvencēm ir0,218.

Šī starpība izrādās uzkrāta prognozes otrajā kategorijā. Mēģināsim izmantot šīs kategorijas augšējo robežu kā kritēriju, lai abus paraugus sadalītu apakšgrupā, kur “ir efekts”, un apakšgrupā, kur “efekta nav”. Mēs pieņemsim, ka ir “efekts”, ja konkrētais ārsts prognozē no 41 līdz 100% uzņemšanas ar līdzekļiem1993 gadā, un ka "nekāda efekta" nav, ja konkrētais ārsts prognozē no 0 līdz 40% uzņemšanas ar līdzekļiem1993 gadā. Mēs apvienojam prognožu kategoriju 1 un 2, no vienas puses, un prognožu kategoriju 3, 4 un 5, no otras puses. Iegūtais prognožu sadalījums ir parādīts tabulā. 5.10.

5.10. tabula

Prognožu sadale ārstiem ar līdzekļiem un ārstiem bez līdzekļiem

Prognozētā uzņemšanas daļa ar līdzekļiem (%1	Empīriskās frekvences noteiktas prognožu kategorijas izvēlei		Summas
	ārsti ar fondu(n 1 =45)	ārsti bez fonda(n 2 =25)
1. no 0 līdz 40%	19	16	35
2. no 41 līdz 100%	26	9	35
Summas	45	25	70

Mēs varam izmantot iegūto tabulu (5.10. tabula), lai pārbaudītu dažādas hipotēzes, salīdzinot jebkuras divas tās šūnas. Mēs atceramies, ka šī ir tā sauktā četru šūnu jeb četru lauku tabula.

Šeit mūs interesē, vai mediķi, kuriem jau ir līdzekļi, prognozē lielāku šīs kustības izaugsmi nākotnē nekā mediķi, kuriem līdzekļu nav. Tāpēc nosacīti uzskatām, ka “efekts ir”, kad prognoze ietilpst kategorijā no 41 līdz 100%. Lai vienkāršotu aprēķinus, mums tagad jāpagriež galds par 90°, pagriežot to pulksteņrādītāja virzienā. Jūs pat varat to izdarīt burtiski, pagriežot grāmatu kopā ar galdu. Tagad mēs varam pāriet uz darblapu φ* kritērija aprēķināšanai - Fišera leņķiskā transformācija.

Tabula 5.11

Četru šūnu tabula Fišera φ* testa aprēķināšanai, lai noteiktu atšķirības divu ģimenes ārstu grupu prognozēs

Grupa	Ir efekts - prognoze no 41 līdz 100%	Nav efekta - prognoze no 0 līdz 40%	Kopā
esgrupa - ārsti, kas paņēma fondu	26 (57.8%)	19 (42.2%)	45
IIgrupa - ārsti, kuri neņēma fondu	9 (36.0%)	16 (64.0%)	25
Kopā	35	35	70

Formulēsim hipotēzes.

H 0 : Personu īpatsvarsprognozējot līdzekļu izkliedi uz 41%-100% no visiem ārsta kabinetiem, ārstu grupā ar līdzekļiem nav vairāk kā ārstu grupā bez līdzekļiem.

H 1 : To cilvēku īpatsvars, kuri prognozē līdzekļu izkliedi līdz 41%-100% no visiem pieņemšanas līdzekļiem, ir lielāks ārstu grupā ar līdzekļiem nekā ārstu grupā bez līdzekļiem.

φ vērtību noteikšana 1 un φ 2 saskaņā ar tabuluXIIPielikums 1. Atcerieties, ka φ 1 vienmēr ir leņķis, kas atbilst lielākajam procentam.

Tagad noteiksim kritērija φ* empīrisko vērtību:

Saskaņā ar tabulu.XIII1. pielikumā mēs nosakām, kādam nozīmīguma līmenim atbilst šī vērtība: p = 0,039.

Izmantojot to pašu tabulu 1. pielikumā, varat noteikt kritērija φ* kritiskās vērtības:

Atbilde: Bet tas tiek noraidīts (p=0,039). To cilvēku īpatsvars, kuri prognozē līdzekļu izplatību uz41-100 % no visām pieņemšanām fondu pieņēmušo ārstu grupā pārsniedz šo īpatsvaru fondu nepieņēmušo ārstu grupā.

Proti, ārsti, kuri jau strādā savās uzgaidāmajās telpās par atsevišķu budžetu, šogad prognozē plašāku šīs prakses izplatību nekā ārsti, kuri vēl nav piekrituši pāriet uz neatkarīgu budžetu. Šim rezultātam ir vairākas interpretācijas. Piemēram, var pieņemt, ka ārsti katrā grupā zemapziņā savu uzvedību uzskata par tipiskāku. Tas var arī nozīmēt, ka ārsti, kuri jau ir pieņēmuši pašfinansējumu, mēdz pārspīlēt šīs kustības apjomu, jo viņiem ir jāpamato savs lēmums. Konstatētās atšķirības var nozīmēt arī kaut ko tādu, kas pilnībā neietilpst pētījumā uzdoto jautājumu lokā. Piemēram, ka ar neatkarīgu budžetu strādājošo ārstu aktivitāte veicina abu grupu pozīciju atšķirību saasināšanos. Viņi bija aktīvāki, kad piekrita ņemt līdzekļus, viņi bija aktīvāki, kad centās atbildēt uz anketu pa pastu; viņi ir aktīvāki, ja prognozē, ka līdzekļu saņemšanā aktīvāki būs citi mediķi.

Tā vai citādi mēs varam būt pārliecināti, ka atklātais statistisko atšķirību līmenis ir maksimālais iespējamais šiem reālajiem datiem. Mēs noteicām, izmantojot kritērijuλ abu sadalījumu maksimālās atšķirības punkts, un tieši šajā brīdī paraugi tika sadalīti divās daļās.

Jūsu zīme.

Funkcija FISCHER atgriež argumentu Fišera transformāciju uz X. Šī transformācija rada funkciju, kurai ir normāls, nevis šķībs sadalījums. Funkcija FISCHER tiek izmantota, lai pārbaudītu hipotēzi, izmantojot korelācijas koeficientu.

Funkcijas FISCHER apraksts programmā Excel

Strādājot ar šo funkciju, ir jāiestata mainīgā vērtība. Tūlīt ir vērts atzīmēt, ka ir dažas situācijas, kurās šī funkcija nedos rezultātus. Tas ir iespējams, ja mainīgais:

• nav skaitlis. Šādā situācijā funkcija FISCHER atgriezīs kļūdas vērtību #VALUE!;
• ir vērtība, kas ir mazāka par -1 vai lielāka par 1. Šajā gadījumā funkcija FISCHER atgriezīs kļūdas vērtību #NUM!.

Vienādojums, ko izmanto, lai matemātiski aprakstītu FISCHER funkciju, ir:

Z"=1/2*ln(1+x)/(1-x)

Apskatīsim šīs funkcijas izmantošanu, izmantojot 3 konkrētus piemērus.



Peļņas un izmaksu attiecības novērtējums, izmantojot FISHER funkciju

Piemērs 1. Izmantojot datus par komercorganizāciju darbību, nepieciešams novērtēt sakarību starp peļņu Y (miljonos rubļu) un produkta izstrādei izmantotajām izmaksām X (miljonos rubļu) (parādās 1. tabulā).

1. tabula. Sākotnējie dati:

№	X	Y
1	210 000 000,00 RUR	95 000 000,00 RUR
2	1 068 000 000,00 RUB	76 000 000,00 RUR
3	1 005 000 000,00 RUB	78 000 000,00 RUR
4	610 000 000,00 RUR	89 000 000,00 RUR
5	768 000 000,00 RUR	77 000 000,00 RUR
6	799 000 000,00 RUR	85 000 000,00 RUR

Šādu problēmu risināšanas shēma ir šāda:

1. Aprēķināts lineārais koeficients korelācijas r xy ;
2. Lineārās korelācijas koeficienta nozīmīgums tiek pārbaudīts, pamatojoties uz Stjudenta t-testu. Šajā gadījumā tiek izvirzīta un pārbaudīta hipotēze, ka korelācijas koeficients ir vienāds ar nulli. Lai pārbaudītu šo hipotēzi, tiek izmantota t-statistika. Ja hipotēze tiek apstiprināta, t-statistikai ir Stjudenta sadalījums. Ja aprēķinātā vērtība t p > t cr, tad tiek noraidīta hipotēze, kas norāda uz lineārās korelācijas koeficienta nozīmīgumu, tātad uz X un Y attiecības statistisko nozīmīgumu;
3. Statistiski nozīmīgam lineārās korelācijas koeficientam tiek noteikts intervāla novērtējums.
4. Lineārās korelācijas koeficienta intervāla aplēse tiek noteikta, pamatojoties uz apgriezto Fišera z-transformāciju;
5. Tiek aprēķināta lineārās korelācijas koeficienta standartkļūda.

Šīs problēmas risināšanas rezultāti ar programmā Excel izmantotajām funkcijām ir parādīti 1. attēlā.

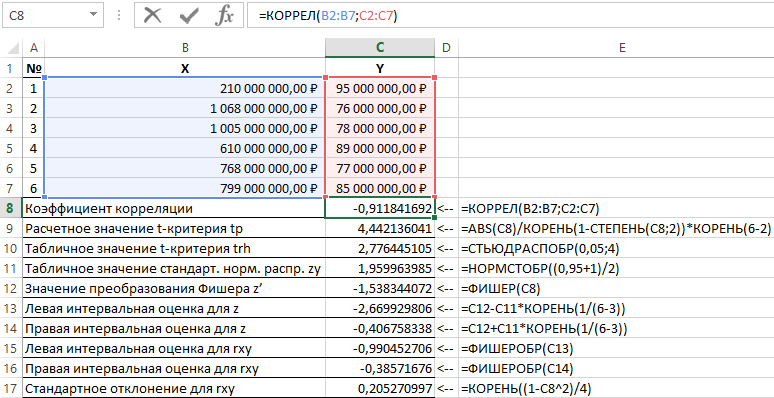
1. attēls – aprēķinu piemērs.

Nē.	Indikatora nosaukums	Aprēķina formula
1	Korelācijas koeficients	=KORREL(B2:B7,C2:C7)
2	Aprēķinātā t-testa vērtība tp	=ABS(C8)/SQRT(1-POWER(C8,2))*SQRT(6-2)
3	T-testa trh tabulas vērtība	=STUDITSATKLĀT(0,05,4)
4	Standarta tabulas vērtība normālais sadalījums zy	=NORMSINV((0,95+1)/2)
5	Fišera z’ transformācijas vērtība	=ZVEJS(C8)
6	Kreisā intervāla novērtējums z	=C12-C11*ROOT(1/(6-3))
7	Pareizais intervāla novērtējums z	=C12+C11*SAKNE(1/(6-3))
8	Kreisā intervāla aprēķins rxy	=FISHEROBR(C13)
9	Pareizais intervāla novērtējums rx	=FISHEROBR(C14)
10	Standarta novirze rxy	=SAKNE((1-C8^2)/4)

Tādējādi ar varbūtību 0,95 lineārās korelācijas koeficients atrodas diapazonā no (–0,386) līdz (–0,990) ar standarta kļūdu 0,205.

Regresijas statistiskā nozīmīguma pārbaude, izmantojot funkciju FASTER

2. piemērs: pārbaudiet vienādojuma statistisko nozīmīgumu daudzkārtēja regresija Izmantojot Fišera F testu, izdariet secinājumus.

Lai pārbaudītu vienādojuma nozīmīgumu kopumā, izvirzām hipotēzi H 0 par determinācijas koeficienta statistisko nenozīmību un pretējo hipotēzi H 1 par determinācijas koeficienta statistisko nozīmīgumu:

H 1: R2 ≠ 0.

Pārbaudīsim hipotēzes, izmantojot Fišera F testu. Rādītāji ir parādīti 2. tabulā.

2. tabula – Sākotnējie dati

Lai to izdarītu, programmā Excel mēs izmantojam funkciju:

ĀTRĀK (α;p;n-p-1)

• α ir ar doto sadalījumu saistītā varbūtība;
• p un n ir attiecīgi brīvības pakāpju skaitītājs un saucējs.

Zinot, ka α = 0,05, p = 2 un n = 53, mēs iegūstam šādu F crit vērtību (sk. 2. attēlu).

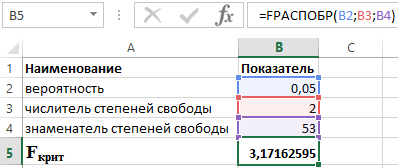
2. attēls – aprēķinu piemērs.

Tādējādi mēs varam teikt, ka F aprēķināts > F kritisks. Rezultātā tiek pieņemta hipotēze H 1 par determinācijas koeficienta statistisko nozīmīgumu.

Korelācijas indikatora vērtības aprēķināšana programmā Excel

3. piemērs. Izmantojot datus no 23 uzņēmumiem par: X ir produkta A cena, tūkstoši rubļu; Y ir tirdzniecības uzņēmuma peļņa, miljoni rubļu, tiek pētīta to atkarība. Novērtējums regresijas modelis deva šādu: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Kādu korelācijas rādītāju var noteikt pēc šiem datiem? Aprēķiniet korelācijas rādītāja vērtību un, izmantojot Fišera kritēriju, izdariet secinājumu par regresijas modeļa kvalitāti.

Noteiksim F crit no izteiksmes:

Aprēķinātais F = R2 /23*(1-R2)

kur R ir determinācijas koeficients, kas vienāds ar 0,67.

Tādējādi aprēķinātā vērtība F calc = 46.

Lai noteiktu F kritumu, mēs izmantojam Fišera sadalījumu (sk. 3. attēlu).

3. attēls – aprēķinu piemērs.

Tādējādi iegūtais regresijas vienādojuma novērtējums ir ticams.

Daudzkārtējās regresijas vienādojuma nozīmīgums kopumā, kā arī pāru regresijā tiek novērtēts, izmantojot Fišera kritēriju:

, (2.22)

Kur
– koeficientu kvadrātu summa uz vienu brīvības pakāpi;
– atlikušā kvadrātu summa uz vienu brīvības pakāpi;
– daudzkārtējās noteikšanas koeficients (indekss);
– mainīgo parametru skaits (V lineārā regresija sakrīt ar modelī iekļauto faktoru skaitu); – novērojumu skaits.

Tiek novērtēta ne tikai vienādojuma nozīme kopumā, bet arī regresijas modelī papildus iekļautā faktora nozīme. Šāda novērtējuma nepieciešamība ir saistīta ar to, ka ne katrs modelī iekļautais faktors var būtiski palielināt izskaidrotās variācijas īpatsvaru iegūtajā pazīmē. Turklāt, ja modelī ir vairāki faktori, tos modelī var ievadīt dažādās secībās. Faktoru savstarpējās korelācijas dēļ viena un tā paša faktora nozīmīgums var atšķirties atkarībā no tā ieviešanas secības modelī. Mērs, lai novērtētu faktora iekļaušanu modelī, ir privātais
-kritēriju, t.i. .

Privāts
-kritērijs ir balstīts uz papildus iekļauta faktora ietekmes radītā faktora dispersijas pieauguma salīdzināšanu ar atlikušo dispersiju uz vienu brīvības pakāpi regresijas modelim kopumā. IN vispārējs skats par faktoru Privāts
-kritērijs tiks noteikts kā

, (2.23)

Kur
– daudzkārtējas noteikšanas koeficients modelim ar pilnu faktoru kopumu,
– tas pats rādītājs, bet bez faktora iekļaušanas modelī ,- novērojumu skaits,
– parametru skaits modelī (bez brīvā termiņa).

Koeficienta faktiskā vērtība
- kritērijs tiek salīdzināts ar tabulu nozīmīguma līmenī
un brīvības pakāpju skaits: 1 un
. Ja faktiskā vērtība pārsniedz
, tad faktora papildu iekļaušana modelī ir statistiski pamatots un tīrais regresijas koeficients pie faktora statistiski nozīmīgi. Ja faktiskā vērtība ir mazāka par tabulas vērtību, tad faktora papildu iekļaušana modelī būtiski nepalielina pazīmes izskaidroto variāciju īpatsvaru , tāpēc nav lietderīgi to iekļaut modelī; Šā faktora regresijas koeficients šajā gadījumā ir statistiski nenozīmīgs.

Divfaktoru vienādojumam koeficienti
- kritērijiem ir šāda forma:

,
. (2.23a)

Izmantojot privātu
-kritēriju, var pārbaudīt visu regresijas koeficientu nozīmīgumu, pieņemot, ka katrs atbilstošais faktors daudzkārtējās regresijas vienādojumā ievadīts pēdējais.

-Skolēnu tests vairāku regresijas vienādojuma noteikšanai.

Privāts
-kritērijs novērtē tīro regresijas koeficientu nozīmīgumu. Zinot apjomu , ir iespējams noteikt -kritērijs regresijas koeficientam pie - m koeficients, , proti:

. (2.24)

Novērtējot tīro regresijas koeficientu nozīmīgumu ar -Studenta t-testu var veikt, nerēķinot daļējo
- kritēriji. Šajā gadījumā, tāpat kā pāru regresijā, katram faktoram tiek izmantota formula:

, (2.25)

Kur – tīrs regresijas koeficients pie faktora ,– regresijas koeficienta vidējā kvadrātiskā (standarta) kļūda .

Vairākkārtējai regresijas vienādojumam regresijas koeficienta vidējo kvadrātisko kļūdu var noteikt pēc šādas formulas:

, (2.26)

Kur ,– raksturlieluma standarta novirze ,
– daudzkārtējās regresijas vienādojuma determinācijas koeficients,
– faktora atkarības determinācijas koeficients ar visiem citiem faktoriem daudzkārtējās regresijas vienādojumā;
– brīvības pakāpju skaits noviržu kvadrātu atlikušajai summai.

Kā redzat, lai izmantotu šo formulu, ir nepieciešama starpfaktoru korelācijas matrica un atbilstošo determinācijas koeficientu aprēķins, izmantojot to
. Tātad par vienādojumu
regresijas koeficientu nozīmīguma novērtējums ,,ietver trīs starpfaktoru noteikšanas koeficientu aprēķinu:
,
,
.

Sakarība starp daļējās korelācijas koeficienta rādītājiem, daļējā
-kritēriji un -Studenta t-testu tīrajiem regresijas koeficientiem var izmantot faktoru izvēles procedūrā. Faktoru izslēgšanu, konstruējot regresijas vienādojumu ar eliminācijas metodi, praktiski var veikt ne tikai ar daļējās korelācijas koeficientiem, katrā solī izslēdzot faktoru ar mazāko nenozīmīgo daļējās korelācijas koeficienta vērtību, bet arī ar vērtībām. Un . Privāts
-kritēriju plaši izmanto, veidojot modeli, izmantojot mainīgo iekļaušanas metodi un pakāpeniskās regresijas metodi.