Pelajaran dan pembentangan tentang topik: "Fungsi kuasa. Sifat. Graf"
Bahan tambahan
Pengguna yang dihormati, jangan lupa tinggalkan komen, ulasan, hasrat anda! Semua bahan telah disemak oleh program anti-virus.
Alat bantu mengajar dan simulator di kedai dalam talian Integral untuk gred 11
Manual interaktif untuk gred 9–11 "Trigonometri"
Manual interaktif untuk gred 10–11 "Logaritma"
Fungsi kuasa, domain definisi.
Kawan-kawan, dalam pelajaran lepas kita belajar cara bekerja dengan nombor dengan eksponen rasional. Dalam pelajaran ini kita akan melihat fungsi kuasa dan menghadkan diri kita kepada kes di mana eksponen adalah rasional.Kami akan mempertimbangkan fungsi bentuk: $y=x^(\frac(m)(n))$.
Mari kita pertimbangkan dahulu fungsi yang eksponennya $\frac(m)(n)>1$.
Marilah kita diberikan fungsi tertentu $y=x^2*5$.
Mengikut takrifan yang kami berikan dalam pelajaran lepas: jika $x≥0$, maka domain takrifan fungsi kami ialah sinar $(x)$. Mari kita gambarkan secara skematik graf fungsi kita.

Sifat bagi fungsi $y=x^(\frac(m)(n))$, $0 2. Ia bukan genap mahupun ganjil.
3. Meningkat sebanyak $$,
b) $(2,10)$,
c) pada sinar $$.
Penyelesaian.
Kawan-kawan, adakah anda masih ingat bagaimana kami menemui nilai terbesar dan terkecil fungsi pada segmen dalam gred 10?
Betul, kami menggunakan derivatif. Mari selesaikan contoh kami dan ulangi algoritma untuk mencari yang terkecil dan nilai tertinggi.
1. Cari terbitan bagi fungsi yang diberi:
$y"=\frac(16)(5)*\frac(5)(2)x^(\frac(3)(2))-x^3=8x^(\frac(3)(2)) -x^3=8\sqrt(x^3)-x^3$.
2. Derivatif wujud di seluruh domain definisi fungsi asal, maka tiada titik kritikal. Mari cari titik pegun:
$y"=8\sqrt(x^3)-x^3=0$.
$8*\sqrt(x^3)=x^3$.
$64x^3=x^6$.
$x^6-64x^3=0$.
$x^3(x^3-64)=0$.
$x_1=0$ dan $x_2=\sqrt(64)=4$.
Segmen tertentu mengandungi hanya satu penyelesaian $x_2=4$.
Mari kita bina jadual nilai fungsi kita di hujung segmen dan pada titik ekstrem:
Jawapan: $y_(nama)=-862.65$ pada $x=9$; $y_(maks.)=38.4$ pada $x=4$.
Contoh. Selesaikan persamaan: $x^(\frac(4)(3))=24-x$.
Penyelesaian. Graf fungsi $y=x^(\frac(4)(3))$ meningkat, dan graf bagi fungsi $y=24-x$ berkurang. Lelaki, anda dan saya tahu: jika satu fungsi meningkat dan yang lain berkurangan, maka ia bersilang hanya pada satu titik, iaitu, kita hanya mempunyai satu penyelesaian.
Catatan:
$8^(\frac(4)(3))=\sqrt(8^4)=(\sqrt(8))^4=2^4=16$.
$24-8=16$.
Iaitu, dengan $x=8$ kami mendapat kesamaan yang betul $16=16$, ini adalah penyelesaian kepada persamaan kami.
Jawapan: $x=8$.
Contoh.
Graf fungsi: $y=(x-3)^\frac(3)(4)+2$.
Penyelesaian.
Graf fungsi kita diperolehi daripada graf fungsi $y=x^(\frac(3)(4))$, menganjaknya 3 unit ke kanan dan 2 unit ke atas. 
Contoh. Tulis persamaan untuk tangen kepada garis $y=x^(-\frac(4)(5))$ pada titik $x=1$.
Penyelesaian. Persamaan tangen ditentukan oleh formula yang kita ketahui:
$y=f(a)+f"(a)(x-a)$.
Dalam kes kami $a=1$.
$f(a)=f(1)=1^(-\frac(4)(5))=1$.
Mari cari derivatif:
$y"=-\frac(4)(5)x^(-\frac(9)(5))$.
Mari kita kira:
$f"(a)=-\frac(4)(5)*1^(-\frac(9)(5))=-\frac(4)(5)$.
Mari kita cari persamaan tangen:
$y=1-\frac(4)(5)(x-1)=-\frac(4)(5)x+1\frac(4)(5)$.
Jawapan: $y=-\frac(4)(5)x+1\frac(4)(5)$.
Masalah untuk diselesaikan secara bebas
1. Cari nilai terbesar dan terkecil bagi fungsi: $y=x^\frac(4)(3)$ pada segmen:a) $$.
b) $(4.50)$.
c) pada sinar $$.
3. Selesaikan persamaan: $x^(\frac(1)(4))=18-x$.
4. Bina graf bagi fungsi: $y=(x+1)^(\frac(3)(2))-1$.
5. Buat persamaan untuk tangen kepada garis lurus $y=x^(-\frac(3)(7))$ pada titik $x=1$.
Fungsi di mana X- kuantiti berubah-ubah, A– nombor yang diberi dipanggil Fungsi kuasa .
Jika kemudian ialah fungsi linear, grafnya ialah garis lurus (lihat perenggan 4.3, Rajah 4.7).
Jika kemudian - fungsi kuadratik, grafnya ialah parabola (lihat perenggan 4.3, Rajah 4.8).
Jika kemudian grafnya ialah parabola padu (lihat perenggan 4.3, Rajah 4.9).
Ini adalah fungsi songsang untuk
1. Domain: ![]()
2. Pelbagai makna:![]()
3. Genap dan ganjil: fungsinya ganjil.
4. Kekerapan fungsi: tidak berkala.
5. Sifar fungsi: X= 0 – satu-satunya sifar.
6. Fungsi ini tidak mempunyai nilai maksimum atau minimum.
7.
8. Graf fungsi Simetri kepada graf parabola padu berbanding garis lurus Y=X dan ditunjukkan dalam Rajah. 5.1.
 |
Fungsi kuasa
1. Domain: ![]()
2. Pelbagai makna:
3. Genap dan ganjil: fungsinya adalah sekata.
4. Kekerapan fungsi: tidak berkala.
5. Sifar fungsi: sifar tunggal X = 0.
6. Nilai terbesar dan terkecil fungsi: mengambil nilai terkecil untuk X= 0, ia sama dengan 0.
7. Menambah dan mengurangkan selang: fungsi itu berkurangan pada selang dan meningkat pada selang
8. Graf fungsi(untuk setiap N Î N) adalah “serupa” dengan graf parabola kuadratik (graf fungsi ditunjukkan dalam Rajah 5.2).

Fungsi kuasa
1. Domain: ![]()
2. Pelbagai makna: ![]()
3. Genap dan ganjil: fungsinya ganjil.
4. Kekerapan fungsi: tidak berkala.
5. Sifar fungsi: X= 0 – satu-satunya sifar.
6. Nilai tertinggi dan terendah:
7. Menambah dan mengurangkan selang: fungsi semakin meningkat ke atas keseluruhan domain definisi.
8. Graf fungsi(untuk setiap ) adalah "serupa" dengan graf parabola padu (graf fungsi ditunjukkan dalam Rajah 5.3).
 |
Fungsi kuasa![]()
1. Domain:
2. Pelbagai makna:
3. Genap dan ganjil: fungsinya ganjil.
4. Kekerapan fungsi: tidak berkala.
5. Sifar fungsi: tidak mempunyai sifar.
6. Nilai terbesar dan terkecil fungsi: fungsi tidak mempunyai nilai terbesar dan terkecil untuk mana-mana
7. Menambah dan mengurangkan selang: fungsi itu semakin berkurangan dalam domain definisinya.
8. Asimtot:(paksi OU) – asimtot menegak;
(paksi Oh) – asimtot mendatar.
9. Graf fungsi(untuk sesiapa N) adalah “serupa” dengan graf hiperbola (graf fungsi ditunjukkan dalam Rajah 5.4).
 |
Fungsi kuasa
1. Domain:
2. Pelbagai makna:
3. Genap dan ganjil: fungsinya adalah sekata.
4. Kekerapan fungsi: tidak berkala.
5. Nilai terbesar dan terkecil fungsi: fungsi tidak mempunyai nilai terbesar dan terkecil untuk mana-mana
6. Menambah dan mengurangkan selang: fungsi semakin meningkat dan menurun sebanyak
7. Asimtot: X= 0 (paksi OU) – asimtot menegak;
Y= 0 (paksi Oh) – asimtot mendatar.
8. Graf fungsi Ia adalah hiperbola kuadratik (Rajah 5.5).
 |
Fungsi kuasa
1. Domain:
2. Pelbagai makna:
3. Genap dan ganjil: fungsi tersebut tidak mempunyai sifat genap dan ganjil.
4. Kekerapan fungsi: tidak berkala.
5. Sifar fungsi: X= 0 – satu-satunya sifar.
6. Nilai terbesar dan terkecil fungsi: fungsi mengambil nilai terkecil bersamaan dengan 0 pada titik X= 0; paling tak penting.
7. Menambah dan mengurangkan selang: fungsi semakin meningkat ke atas keseluruhan domain definisi.
8. Setiap fungsi sedemikian untuk eksponen tertentu adalah songsang bagi fungsi yang disediakan
9. Graf fungsi"menyerupai" graf fungsi untuk sebarang N dan ditunjukkan dalam Rajah. 5.6.

Fungsi kuasa
1. Domain: ![]()
2. Pelbagai makna:![]()
3. Genap dan ganjil: fungsinya ganjil.
4. Kekerapan fungsi: tidak berkala.
5. Sifar fungsi: X= 0 – satu-satunya sifar.
6. Nilai terbesar dan terkecil fungsi: fungsi tidak mempunyai nilai terbesar dan terkecil untuk mana-mana
7. Menambah dan mengurangkan selang: fungsi semakin meningkat ke atas keseluruhan domain definisi.
8. Graf fungsi Ditunjukkan dalam Rajah. 5.7.
 |
Mari kita ingat sifat dan graf fungsi kuasa dengan integer penunjuk negatif.
Untuk n genap, :
Contoh fungsi:
Semua graf bagi fungsi tersebut melalui dua titik tetap: (1;1), (-1;1). Keanehan fungsi jenis ini ialah paritinya; graf adalah simetri berbanding paksi op-amp.

nasi. 1. Graf bagi suatu fungsi
Untuk n ganjil,:
Contoh fungsi:
Semua graf bagi fungsi tersebut melalui dua titik tetap: (1;1), (-1;-1). Keistimewaan fungsi jenis ini ialah ia ganjil; graf adalah simetri berkenaan dengan asalan.

nasi. 2. Graf bagi suatu fungsi
Mari kita ingat definisi asas.
Kuasa nombor bukan negatif a dengan eksponen positif rasional dipanggil nombor.
Kuasa nombor positif a dengan eksponen negatif rasional dipanggil nombor.
Untuk persamaan:
![]()
![]()
Sebagai contoh: ![]() ; - ungkapan tidak wujud, mengikut definisi, darjah dengan eksponen rasional negatif; wujud kerana eksponen ialah integer,
; - ungkapan tidak wujud, mengikut definisi, darjah dengan eksponen rasional negatif; wujud kerana eksponen ialah integer, ![]()
Mari kita beralih kepada mempertimbangkan fungsi kuasa dengan eksponen negatif yang rasional.
![]()
Sebagai contoh:
Untuk memplot graf fungsi ini, anda boleh membuat jadual. Kami akan melakukannya secara berbeza: pertama kami akan membina dan mengkaji graf penyebut - ia diketahui oleh kami (Rajah 3).

nasi. 3. Graf bagi suatu fungsi
Graf fungsi penyebut melalui titik tetap (1;1). Apabila memplot fungsi asal titik yang diberikan kekal, apabila punca juga cenderung kepada sifar, fungsinya cenderung kepada infiniti. Dan, sebaliknya, kerana x cenderung kepada infiniti, fungsi itu cenderung kepada sifar (Rajah 4).

nasi. 4. Graf fungsi
Mari kita pertimbangkan fungsi lain daripada keluarga fungsi yang sedang dikaji.
![]()
Adalah penting bahawa mengikut definisi
Mari kita pertimbangkan graf fungsi dalam penyebut: , graf fungsi ini diketahui oleh kita, ia meningkat dalam domain takrifnya dan melalui titik (1;1) (Rajah 5).

nasi. 5. Graf bagi suatu fungsi
Apabila memplot graf fungsi asal, titik (1;1) kekal, manakala punca juga cenderung kepada sifar, fungsi cenderung kepada infiniti. Dan, sebaliknya, kerana x cenderung kepada infiniti, fungsi itu cenderung kepada sifar (Rajah 6).

nasi. 6. Graf bagi suatu fungsi
Contoh yang dipertimbangkan membantu memahami cara graf mengalir dan apakah sifat fungsi yang sedang dikaji - fungsi dengan eksponen rasional negatif.
Graf fungsi keluarga ini melalui titik (1;1), fungsi berkurangan ke atas keseluruhan domain definisi.
Skop fungsi: ![]()
Fungsi tidak terhad dari atas, tetapi terhad dari bawah. Fungsi ini tidak mempunyai yang terbesar mahupun nilai terendah.
Fungsi ini berterusan dan mengambil semua nilai positif daripada sifar hingga tambah infiniti.
Fungsinya adalah cembung ke bawah (Rajah 15.7)
Titik A dan B diambil pada lengkung, segmen dilukis melaluinya, keseluruhan lengkung berada di bawah segmen, syarat ini berpuas hati untuk dua titik sewenang-wenangnya pada lengkung, oleh itu fungsinya adalah cembung ke bawah. nasi. 7.

nasi. 7. Kecembungan fungsi
Adalah penting untuk memahami bahawa fungsi keluarga ini dibatasi dari bawah dengan sifar, tetapi tidak mempunyai nilai terkecil.
Contoh 1 - cari maksimum dan minimum fungsi pada selang \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \]
Graf (Rajah 2).

Rajah 2. Graf fungsi $f\left(x\right)=x^(2n)$
Sifat fungsi kuasa dengan eksponen ganjil semula jadi
Domain definisi ialah semua nombor nyata.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- fungsinya ganjil.
$f(x)$ berterusan ke atas keseluruhan domain definisi.
Julat adalah semua nombor nyata.
$f"\kiri(x\kanan)=\kiri(x^(2n-1)\kanan)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Fungsi meningkat ke atas keseluruhan domain definisi.
$f\left(x\right)0$, untuk $x\in (0+\infty)$.
$f(""\kiri(x\kanan))=(\kiri(\kiri(2n-1\kanan)\cdot x^(2\kiri(n-1\kanan))\kanan))"=2 \kiri(2n-1\kanan)(n-1)\cdot x^(2n-3)$
\ \
Fungsinya ialah cekung untuk $x\in (-\infty ,0)$ dan cembung untuk $x\in (0+\infty)$.
Graf (Rajah 3).
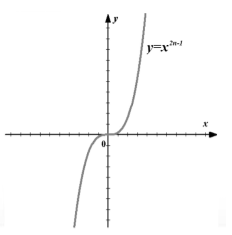
Rajah 3. Graf fungsi $f\left(x\right)=x^(2n-1)$
Fungsi kuasa dengan eksponen integer
Mula-mula, mari kita perkenalkan konsep ijazah dengan eksponen integer.
Definisi 3
Kuasa nombor nyata $a$ dengan eksponen integer $n$ ditentukan oleh formula:

Rajah 4.
Sekarang mari kita pertimbangkan fungsi kuasa dengan eksponen integer, sifat dan grafnya.
Definisi 4
$f\left(x\right)=x^n$ ($n\in Z)$ dipanggil fungsi kuasa dengan eksponen integer.
Jika darjah lebih besar daripada sifar, maka kita sampai kepada kes fungsi kuasa dengan eksponen semula jadi. Kami telah membincangkannya di atas. Untuk $n=0$ kita dapat fungsi linear$y=1$. Kami akan menyerahkan pertimbangannya kepada pembaca. Ia kekal untuk mempertimbangkan sifat fungsi kuasa dengan eksponen integer negatif
Sifat fungsi kuasa dengan eksponen integer negatif
Domain definisi ialah $\left(-\infty ,0\right)(0+\infty)$.
Jika eksponen adalah genap, maka fungsinya adalah genap, jika ia adalah ganjil, maka fungsinya adalah ganjil.
$f(x)$ berterusan ke atas keseluruhan domain definisi.
Skop:
Jika eksponen genap, maka $(0+\infty)$ jika ia ganjil, maka $\left(-\infty ,0\right)(0+\infty)$;
Untuk eksponen ganjil, fungsi berkurangan sebagai $x\in \left(-\infty ,0\right)(0+\infty)$. Jika eksponen genap, fungsi berkurangan sebagai $x\in (0+\infty)$. dan meningkat sebagai $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ ke atas keseluruhan domain definisi








