How to find out whether a system of equations has a solution. Online calculator

Solution of linear systems algebraic equations(SLAE) is undoubtedly the most important topic in the linear algebra course. Great amount problems from all branches of mathematics are reduced to solving systems linear equations. These factors explain the reason for this article. The material of the article is selected and structured so that with its help you can

• choose the optimal method for solving your system of linear algebraic equations,
• study the theory of the chosen method,
• solve your system of linear equations by considering detailed solutions to typical examples and problems.

Brief description of the article material.

First, we give all the necessary definitions, concepts and introduce notations.

Next, we will consider methods for solving systems of linear algebraic equations in which the number of equations is equal to the number of unknown variables and which have a unique solution. Firstly, we will focus on the Cramer method, secondly, we will show the matrix method for solving such systems of equations, thirdly, we will analyze the Gauss method (method sequential elimination unknown variables). To consolidate the theory, we will definitely solve several SLAEs in different ways.

After this, we will move on to solving systems of linear algebraic equations general view, in which the number of equations does not coincide with the number of unknown variables or the main matrix of the system is singular. Let us formulate the Kronecker-Capelli theorem, which allows us to establish the compatibility of SLAEs. Let us analyze the solution of systems (if they are compatible) using the concept of a basis minor of a matrix. We will also consider the Gauss method and describe in detail the solutions to the examples.

We will definitely dwell on the structure of the general solution of homogeneous and inhomogeneous systems of linear algebraic equations. Let us give the concept of a fundamental system of solutions and show how to write common decision SLAE using vectors of the fundamental solution system. For a better understanding, let's look at a few examples.

In conclusion, we will consider systems of equations that can be reduced to linear ones, as well as various tasks, in the solution of which SLAEs arise.

Page navigation.

Definitions, concepts, designations.

We will consider systems of p linear algebraic equations with n unknown variables (p can be equal to n) of the form

Unknown variables - coefficients (some real or complex numbers), - free terms (also real or complex numbers).

This form of recording SLAE is called coordinate.

IN matrix form writing this system of equations has the form,
Where - the main matrix of the system, - a column matrix of unknown variables, - a column matrix of free terms.

If we add a matrix-column of free terms to matrix A as the (n+1)th column, we get the so-called extended matrix systems of linear equations. Typically, an extended matrix is ​​denoted by the letter T, and the column of free terms is separated by a vertical line from the remaining columns, that is,

Solving a system of linear algebraic equations called a set of values ​​of unknown variables that turns all equations of the system into identities. Matrix equation for given values ​​of the unknown variables also becomes an identity.

If a system of equations has at least one solution, then it is called joint.

If a system of equations has no solutions, then it is called non-joint.

If a SLAE has a unique solution, then it is called certain; if there is more than one solution, then – uncertain.

If the free terms of all equations of the system are equal to zero , then the system is called homogeneous, otherwise - heterogeneous.

Solving elementary systems of linear algebraic equations.

If the number of equations of a system is equal to the number of unknown variables and the determinant of its main matrix is ​​not equal to zero, then such SLAEs will be called elementary. Such systems of equations have a unique solution, and in the case homogeneous system all unknown variables are zero.

We started studying such SLAEs in high school. When solving them, we took one equation, expressed one unknown variable in terms of others and substituted it into the remaining equations, then took the next equation, expressed the next unknown variable and substituted it into other equations, and so on. Or they used the addition method, that is, they added two or more equations to eliminate some unknown variables. We will not dwell on these methods in detail, since they are essentially modifications of the Gauss method.

The main methods for solving elementary systems of linear equations are the Cramer method, the matrix method and the Gauss method. Let's sort them out.

Solving systems of linear equations using Cramer's method.

Suppose we need to solve a system of linear algebraic equations

in which the number of equations is equal to the number of unknown variables and the determinant of the main matrix of the system is different from zero, that is, .

Let be the determinant of the main matrix of the system, and - determinants of matrices that are obtained from A by replacement 1st, 2nd, …, nth column respectively to the column of free members:

With this notation, unknown variables are calculated using the formulas of Cramer’s method as . This is how the solution to a system of linear algebraic equations is found using Cramer's method.

Example.

Cramer's method .

Solution.

The main matrix of the system has the form . Let's calculate its determinant (if necessary, see the article):

Since the determinant of the main matrix of the system is nonzero, the system has a unique solution that can be found by Cramer’s method.

Let's compose and calculate the necessary determinants (we obtain the determinant by replacing the first column in matrix A with a column of free terms, the determinant by replacing the second column with a column of free terms, and by replacing the third column of matrix A with a column of free terms):

Finding unknown variables using formulas :

Answer:

The main disadvantage of Cramer's method (if it can be called a disadvantage) is the complexity of calculating determinants when the number of equations in the system is more than three.

Solving systems of linear algebraic equations using the matrix method (using an inverse matrix).

Let a system of linear algebraic equations be given in matrix form, where the matrix A has dimension n by n and its determinant is nonzero.

Since , matrix A is invertible, that is, there is an inverse matrix. If we multiply both sides of the equality by the left, we get a formula for finding a matrix-column of unknown variables. This is how we obtained a solution to the system of linear algebraic equations matrix method.

Example.

Solve system of linear equations matrix method.

Solution.

Let's rewrite the system of equations in matrix form:

Because

then the SLAE can be solved using the matrix method. By using inverse matrix the solution to this system can be found as .

Let's construct the inverse matrix using the matrix from algebraic additions elements of matrix A (if necessary, see article):

It remains to calculate the matrix of unknown variables by multiplying the inverse matrix to a matrix-column of free members (if necessary, see the article):

Answer:

or in another notation x 1 = 4, x 2 = 0, x 3 = -1.

The main problem when finding solutions to systems of linear algebraic equations using the matrix method is the complexity of finding the inverse matrix, especially for square matrices of order higher than third.

Solving systems of linear equations using the Gauss method.

Suppose we need to find a solution to a system of n linear equations with n unknown variables
the determinant of the main matrix of which is different from zero.

The essence of the Gauss method consists of sequential exclusion of unknown variables: first, x 1 is excluded from all equations of the system, starting from the second, then x 2 is excluded from all equations, starting from the third, and so on, until only the unknown variable x n remains in the last equation. This process of transforming system equations to sequentially eliminate unknown variables is called direct Gaussian method. After finishing forward stroke using the Gauss method, x n is found from the last equation, using this value, x n-1 is calculated from the penultimate equation, and so on, x 1 is found from the first equation. The process of calculating unknown variables when moving from the last equation of the system to the first is called inverse of the Gaussian method.

Let us briefly describe the algorithm for eliminating unknown variables.

We will assume that , since we can always achieve this by rearranging the equations of the system. Let's eliminate the unknown variable x 1 from all equations of the system, starting with the second. To do this, to the second equation of the system we add the first, multiplied by , to the third equation we add the first, multiplied by , and so on, to the nth equation we add the first, multiplied by . The system of equations after such transformations will take the form

where and .

We would have arrived at the same result if we had expressed x 1 in terms of other unknown variables in the first equation of the system and substituted the resulting expression into all other equations. Thus, the variable x 1 is excluded from all equations, starting from the second.

Next, we proceed in a similar way, but only with part of the resulting system, which is marked in the figure

To do this, to the third equation of the system we add the second, multiplied by , to the fourth equation we add the second, multiplied by , and so on, to the nth equation we add the second, multiplied by . The system of equations after such transformations will take the form

where and . Thus, the variable x 2 is excluded from all equations, starting from the third.

Next, we proceed to eliminating the unknown x 3, while we act similarly with the part of the system marked in the figure

So we continue the direct progression of the Gaussian method until the system takes the form

From this moment we begin the reverse of the Gaussian method: we calculate x n from the last equation as , using the obtained value of x n we find x n-1 from the penultimate equation, and so on, we find x 1 from the first equation.

Example.

Solve system of linear equations Gauss method.

Solution.

Let us exclude the unknown variable x 1 from the second and third equations of the system. To do this, to both sides of the second and third equations we add the corresponding parts of the first equation, multiplied by and by, respectively:

Now we eliminate x 2 from the third equation by adding to its left and right sides the left and right sides of the second equation, multiplied by:

This completes the forward stroke of the Gauss method; we begin the reverse stroke.

From the last equation of the resulting system of equations we find x 3:

From the second equation we get .

From the first equation we find the remaining unknown variable and thereby complete the reverse of the Gauss method.

Answer:

X 1 = 4, x 2 = 0, x 3 = -1.

Solving systems of linear algebraic equations of general form.

IN general case the number of equations of the system p does not coincide with the number of unknown variables n:

Such SLAEs may have no solutions, have a single solution, or have infinitely many solutions. This statement also applies to systems of equations whose main matrix is ​​square and singular.

Kronecker–Capelli theorem.

Before finding a solution to a system of linear equations, it is necessary to establish its compatibility. The answer to the question when SLAE is compatible and when it is inconsistent is given by Kronecker–Capelli theorem:
In order for a system of p equations with n unknowns (p can be equal to n) to be consistent, it is necessary and sufficient that the rank of the main matrix of the system be equal to the rank of the extended matrix, that is, Rank(A)=Rank(T).

Let us consider, as an example, the application of the Kronecker–Capelli theorem to determine the compatibility of a system of linear equations.

Example.

Find out whether the system of linear equations has solutions.

Solution.

. Let's use the method of bordering minors. Minor of the second order different from zero. Let's look at the third-order minors bordering it:

Since all the bordering minors of the third order are equal to zero, the rank of the main matrix is ​​equal to two.

In turn, the rank of the extended matrix is equal to three, since the minor is of third order

different from zero.

Thus, Rang(A), therefore, using the Kronecker–Capelli theorem, we can conclude that the original system of linear equations is inconsistent.

Answer:

The system has no solutions.

So, we have learned to establish the inconsistency of a system using the Kronecker–Capelli theorem.

But how to find a solution to an SLAE if its compatibility is established?

To do this, we need the concept of a basis minor of a matrix and a theorem about the rank of a matrix.

Minor highest order matrix A, different from zero, is called basic.

From the definition of a basis minor it follows that its order is equal to the rank of the matrix. For a non-zero matrix A there can be several basis minors; there is always one basis minor.

For example, consider the matrix .

All third-order minors of this matrix are equal to zero, since the elements of the third row of this matrix are the sum of the corresponding elements of the first and second rows.

The following second-order minors are basic, since they are non-zero

Minors are not basic, since they are equal to zero.

Matrix rank theorem.

If the rank of a matrix of order p by n is equal to r, then all row (and column) elements of the matrix that do not form the chosen basis minor are linearly expressed in terms of the corresponding row (and column) elements forming the basis minor.

What does the matrix rank theorem tell us?

If, according to the Kronecker–Capelli theorem, we have established the compatibility of the system, then we choose any basis minor of the main matrix of the system (its order is equal to r), and exclude from the system all equations that do not form the selected basis minor. The SLAE obtained in this way will be equivalent to the original one, since the discarded equations are still redundant (according to the matrix rank theorem, they are a linear combination of the remaining equations).

As a result, after discarding unnecessary equations of the system, two cases are possible.

If the number of equations r in the resulting system is equal to the number of unknown variables, then it will be definite and the only solution can be found by the Cramer method, the matrix method or the Gauss method.

Example.

.

Solution.

Rank of the main matrix of the system is equal to two, since the minor is of second order different from zero. Extended Matrix Rank is also equal to two, since the only third order minor is zero

and the second-order minor considered above is different from zero. Based on the Kronecker–Capelli theorem, we can assert the compatibility of the original system of linear equations, since Rank(A)=Rank(T)=2.

As a basis minor we take . It is formed by the coefficients of the first and second equations:


The third equation of the system does not participate in the formation of the basis minor, so we exclude it from the system based on the theorem on the rank of the matrix:


This is how we obtained an elementary system of linear algebraic equations. Let's solve it using Cramer's method:


Answer:

x 1 = 1, x 2 = 2.

If the number of equations r in the resulting SLAE is less than the number of unknown variables n, then on the left sides of the equations we leave the terms that form the basis minor, and we transfer the remaining terms to the right sides of the equations of the system with the opposite sign.

The unknown variables (r of them) remaining on the left sides of the equations are called main.

Unknown variables (there are n - r pieces) that are on the right sides are called free.

Now we believe that free unknown variables can take arbitrary values, while the r main unknown variables will be expressed through free unknown variables in a unique way. Their expression can be found by solving the resulting SLAE using the Cramer method, the matrix method, or the Gauss method.

Let's look at it with an example.

Example.

Solve a system of linear algebraic equations .

Solution.

Let's find the rank of the main matrix of the system by the method of bordering minors. Let's take a 1 1 = 1 as a non-zero minor of the first order. Let's start searching for a non-zero minor of the second order bordering this minor:


This is how we found a non-zero minor of the second order. Let's start searching for a non-zero bordering minor of the third order:


Thus, the rank of the main matrix is ​​three. The rank of the extended matrix is ​​also equal to three, that is, the system is consistent.

We take the found non-zero minor of the third order as the basis one.

For clarity, we show the elements that form the basis minor:


We leave the terms involved in the basis minor on the left side of the equations of the system, and transfer the rest from opposite signs to the right sides:


Let's give the free unknown variables x 2 and x 5 arbitrary values, that is, we accept , where are arbitrary numbers. In this case, the SLAE will take the form


Let us solve the resulting elementary system of linear algebraic equations using Cramer’s method:


Hence, .

In your answer, do not forget to indicate free unknown variables.

Answer:

Where are arbitrary numbers.

Summarize.

To solve a system of general linear algebraic equations, we first determine its compatibility using the Kronecker–Capelli theorem. If the rank of the main matrix is ​​not equal to the rank of the extended matrix, then we conclude that the system is incompatible.

If the rank of the main matrix is ​​equal to the rank of the extended matrix, then we select a basis minor and discard the equations of the system that do not participate in the formation of the selected basis minor.

If the order of the basis minor is equal to the number of unknown variables, then the SLAE has a unique solution, which can be found by any method known to us.

If the order of the basis minor is less than the number of unknown variables, then on the left side of the system equations we leave the terms with the main unknown variables, transfer the remaining terms to the right sides and give arbitrary values ​​to the free unknown variables. From the resulting system of linear equations we find the main unknown variables using the Cramer method, the matrix method or the Gauss method.

Gauss method for solving systems of linear algebraic equations of general form.

The Gauss method can be used to solve systems of linear algebraic equations of any kind without first testing them for consistency. The process of sequential elimination of unknown variables makes it possible to draw a conclusion about both the compatibility and incompatibility of the SLAE, and if a solution exists, it makes it possible to find it.

From a computational point of view, the Gaussian method is preferable.

Watch it detailed description and analyzed examples in the article the Gauss method for solving systems of linear algebraic equations of general form.

Writing a general solution to homogeneous and inhomogeneous linear algebraic systems using vectors of the fundamental system of solutions.

In this section we'll talk on simultaneous homogeneous and inhomogeneous systems of linear algebraic equations with an infinite number of solutions.

Let us first deal with homogeneous systems.

Fundamental system of solutions homogeneous system of p linear algebraic equations with n unknown variables is a collection of (n – r) linearly independent solutions of this system, where r is the order of the basis minor of the main matrix of the system.

If we denote linearly independent solutions of a homogeneous SLAE as X (1) , X (2) , ..., X (n-r) (X (1) , X (2) , ..., X (n-r) are columnar matrices of dimension n by 1) , then the general solution of this homogeneous system is represented as a linear combination of vectors of the fundamental system of solutions with arbitrary constant coefficients C 1, C 2, ..., C (n-r), that is, .

What does the term general solution of a homogeneous system of linear algebraic equations (oroslau) mean?

The meaning is simple: the formula sets everything possible solutions the original SLAE, in other words, taking any set of values ​​of arbitrary constants C 1, C 2, ..., C (n-r), using the formula we will obtain one of the solutions to the original homogeneous SLAE.

Thus, if we find a fundamental system of solutions, then we can define all solutions of this homogeneous SLAE as .

Let us show the process of constructing a fundamental system of solutions to a homogeneous SLAE.

We select the basis minor of the original system of linear equations, exclude all other equations from the system and transfer all terms containing free unknown variables to the right-hand sides of the equations of the system with opposite signs. Let's give free unknowns variable values 1,0,0,…,0 and calculate the main unknowns by solving the resulting elementary system of linear equations in any way, for example, using the Cramer method. This will result in X (1) - the first solution of the fundamental system. If you give free unknown values 0,1,0,0,…,0 and calculate the main unknowns, we get X (2) . And so on. If we assign the values ​​0.0,…,0.1 to the free unknown variables and calculate the main unknowns, we obtain X (n-r) . In this way, a fundamental system of solutions to a homogeneous SLAE will be constructed and its general solution can be written in the form .

For inhomogeneous systems of linear algebraic equations, the general solution is represented in the form , where is the general solution of the corresponding homogeneous system, and is the particular solution of the original inhomogeneous SLAE, which we obtain by giving the free unknowns the values ​​0,0,...,0 and calculating the values ​​of the main unknowns.

Let's look at examples.

Example.

Find the fundamental system of solutions and the general solution of a homogeneous system of linear algebraic equations .

Solution.

The rank of the main matrix of homogeneous systems of linear equations is always equal to the rank of the extended matrix. Let's find the rank of the main matrix using the method of bordering minors. As a non-zero minor of the first order, we take element a 1 1 = 9 of the main matrix of the system. Let's find the bordering non-zero minor of the second order:

A minor of the second order, different from zero, has been found. Let's go through the third-order minors bordering it in search of a non-zero one:

All third-order bordering minors are equal to zero, therefore, the rank of the main and extended matrix is ​​equal to two. Let's take . For clarity, let us note the elements of the system that form it:

The third equation of the original SLAE does not participate in the formation of the basis minor, therefore, it can be excluded:

We leave the terms containing the main unknowns on the right sides of the equations, and transfer the terms with free unknowns to the right sides:

Let us construct a fundamental system of solutions to the original homogeneous system of linear equations. The fundamental system of solutions of this SLAE consists of two solutions, since the original SLAE contains four unknown variables, and the order of its basis minor is equal to two. To find X (1), we give the free unknown variables the values ​​x 2 = 1, x 4 = 0, then we find the main unknowns from the system of equations
.

§1. Systems of linear equations.

View system

called a system m linear equations with n unknown.

Here
- unknown, - coefficients for unknowns,
- free terms of the equations.

If all free terms of the equations are equal to zero, the system is called homogeneous.By decision system is called a collection of numbers
, when substituting them into the system instead of unknowns, all equations turn into identities. The system is called joint, if it has at least one solution. A compatible system that has a unique solution is called certain. The two systems are called equivalent, if the sets of their solutions coincide.

System (1) can be represented in matrix form using the equation

(2)

.

§2. Compatibility of systems of linear equations.

Let us call the extended matrix of system (1) the matrix

Kronecker-Capelli theorem. System (1) is consistent if and only if the rank of the system matrix is ​​equal to the rank of the extended matrix:

.

§3. Systems solutionn linear equations withn unknown.

Consider an inhomogeneous system n linear equations with n unknown:

(3)

Cramer's theorem.If the main determinant of the system (3)
, then the system has a unique solution, determined by the formulas:

those.
,

Where - determinant obtained from the determinant replacement th column to the column of free members.

If
, and at least one of ≠0, then the system has no solutions.

If
, then the system has infinitely many solutions.

System (3) can be solved using its matrix form (2). If the matrix rank A equals n, i.e.
, then the matrix A has an inverse
. Multiplying the matrix equation
to the matrix
on the left, we get:

.

The last equality expresses the method of solving systems of linear equations using an inverse matrix.

Example. Solve a system of equations using an inverse matrix.

Solution. Matrix
non-degenerate, since
, which means there is an inverse matrix. Let's calculate the inverse matrix:
.

,

Exercise. Solve the system using Cramer's method.

§4. Solving arbitrary systems of linear equations.

Let a non-homogeneous system of linear equations of the form (1) be given.

Let us assume that the system is consistent, i.e. the condition of the Kronecker-Capelli theorem is satisfied:
. If the matrix rank
(number of unknowns), then the system has a unique solution. If
, then the system has infinitely many solutions. Let me explain.

Let the rank of the matrix r(A)= r< n. Because the
, then there is some non-zero minor of order r. Let's call it the basic minor. The unknowns whose coefficients form a basis minor will be called basic variables. We call the remaining unknowns free variables. Let's rearrange the equations and renumber the variables so that this minor is located in the upper left corner of the system matrix:

.

First r lines are linearly independent, the rest are expressed through them. Therefore, these lines (equations) can be discarded. We get:

Let's give the free variables arbitrary numerical values: . Let us leave only the basic variables on the left side and move the free ones to the right side.

Got the system r linear equations with r unknown, whose determinant is different from 0. It has a unique solution.

This system is called the general solution of the system of linear equations (1). Otherwise: the expression of basic variables through free ones is called general decision systems. From it you can get an infinite number of private solutions, giving free variables arbitrary values. A particular solution obtained from a general one for zero values ​​of free variables is called basic solution. The number of different basic solutions does not exceed
. A basic solution with non-negative components is called supporting system solution.

Example.

,r=2.

Variables
- basic,
- free.

Let's add up the equations; let's express
through
:

- common decision.

- private solution for
.

- basic solution, reference.

§5. Gauss method.

The Gauss method is a universal method for studying and solving arbitrary systems of linear equations. It consists of reducing the system to a diagonal (or triangular) form by sequentially eliminating unknowns using elementary transformations that do not violate the equivalence of systems. A variable is considered excluded if it is contained in only one equation of the system with a coefficient of 1.

Elementary transformations systems are:

Multiplying an equation by a number other than zero;

Adding an equation multiplied by any number with another equation;

Rearranging equations;

Rejecting the equation 0 = 0.

Elementary transformations can be performed not on equations, but on extended matrices of the resulting equivalent systems.

Example.

Solution. Let us write down the extended matrix of the system:

.

Carrying out elementary transformations, we will reduce the left side of the matrix to unit form: we will create ones on the main diagonal, and zeros outside it.

Comment. If, when performing elementary transformations, an equation of the form 0 is obtained = k(Where To0), then the system is inconsistent.

The solution of systems of linear equations by the method of sequential elimination of unknowns can be written in the form tables.

The left column of the table contains information about excluded (basic) variables. The remaining columns contain the coefficients of the unknowns and the free terms of the equations.

The extended matrix of the system is recorded in the source table. Next, we begin to perform Jordan transformations:

1. Select a variable , which will become the basis. The corresponding column is called the key column. Choose an equation in which this variable will remain, being excluded from other equations. The corresponding table row is called a key row. Coefficient , standing at the intersection of a key row and a key column, is called a key.

2. The key string elements are divided into the key element.

3. The key column is filled with zeros.

4. The remaining elements are calculated using the rectangle rule. Make up a rectangle, at the opposite vertices of which there is a key element and a recalculated element; from the product of the elements located on the diagonal of the rectangle with the key element, the product of the elements of the other diagonal is subtracted, and the resulting difference is divided by the key element.

Example. Find the general solution and basic solution of the system of equations:

Solution.

General solution of the system:

Basic solution:
.

A single substitution transformation allows you to move from one basis of the system to another: instead of one of the main variables, one of the free variables is introduced into the basis. To do this, select a key element in the free variable column and perform transformations according to the above algorithm.

§6. Finding support solutions

The reference solution of a system of linear equations is a basic solution that does not contain negative components.

The reference solutions of the system are found by the Gaussian method when the following conditions are met.

1. In the original system, all free terms must be non-negative:
.

2. The key element is selected among the positive coefficients.

3. If a variable introduced into the basis has several positive coefficients, then the key line is the one in which the ratio of the free term to the positive coefficient is the smallest.

Note 1. If, in the process of eliminating unknowns, an equation appears in which all coefficients are non-positive and the free term
, then the system has no non-negative solutions.

Note 2. If there is not a single positive element in the columns of coefficients for free variables, then transition to another reference solution is impossible.

Example.

However, in practice two more cases are widespread:

– The system is inconsistent (has no solutions);
– The system is consistent and has infinitely many solutions.

Note : The term “consistency” implies that the system has at least some solution. In a number of problems, it is necessary to first examine the system for compatibility; how to do this, see the article on rank of matrices.

For these systems, the most universal of all solution methods is used - Gaussian method. In fact, the “school” method will also lead to the answer, but in higher mathematics it is customary to use the Gaussian method of sequential elimination of unknowns. Those who are not familiar with the Gaussian method algorithm, please study the lesson first Gaussian method for dummies.

The elementary matrix transformations themselves are exactly the same, the difference will be in the ending of the solution. First, let's look at a couple of examples when the system has no solutions (inconsistent).

Example 1

What immediately catches your eye about this system? The number of equations is less than the number of variables. If the number of equations is less than the number of variables, then we can immediately say that the system is either inconsistent or has infinitely many solutions. And all that remains is to find out.

The beginning of the solution is completely ordinary - we write down the extended matrix of the system and, using elementary transformations, bring it to a stepwise form:

(1) On the top left step we need to get +1 or –1. There are no such numbers in the first column, so rearranging the rows will not give anything. The unit will have to organize itself, and this can be done in several ways. I did this: To the first line we add the third line, multiplied by -1.

(2) Now we get two zeros in the first column. To the second line we add the first line multiplied by 3. To the third line we add the first line multiplied by 5.

(3) After the transformation has been completed, it is always advisable to see if it is possible to simplify the resulting strings? Can. We divide the second line by 2, at the same time getting the required –1 on the second step. Divide the third line by –3.

(4) Add the second line to the third line.

Probably everyone noticed the bad line that resulted from elementary transformations: . It is clear that this cannot be so. Indeed, let us rewrite the resulting matrix back to the system of linear equations:

If, as a result of elementary transformations, a string of the form is obtained, where is a number other than zero, then the system is inconsistent (has no solutions).

How to write down the ending of a task? Let’s draw with white chalk: “as a result of elementary transformations, a string of the form , where ” is obtained and give the answer: the system has no solutions (inconsistent).

If, according to the condition, it is required to RESEARCH the system for compatibility, then it is necessary to formalize the solution in a more solid style using the concept matrix rank and the Kronecker-Capelli theorem.

Please note that there is no reversal of the Gaussian algorithm here - there are no solutions and there is simply nothing to find.

Example 2

Solve a system of linear equations

This is an example for independent decision. Complete solution and the answer at the end of the lesson. I remind you again that your solution may differ from my solution; the Gaussian algorithm does not have strong “rigidity”.

Another technical feature of the solution: elementary transformations can be stopped At once, as soon as a line like , where . Let's consider conditional example: suppose that after the first transformation the matrix is ​​obtained . The matrix has not yet been reduced to echelon form, but there is no need for further elementary transformations, since a line of the form has appeared, where . The answer should be given immediately that the system is incompatible.

When a system of linear equations has no solutions, this is almost a gift, due to the fact that a short solution is obtained, sometimes literally in 2-3 steps.

But everything in this world is balanced, and a problem in which the system has infinitely many solutions is just longer.

Example 3

Solve a system of linear equations

There are 4 equations and 4 unknowns, so the system can either have a single solution, or have no solutions, or have infinitely many solutions. Be that as it may, the Gaussian method will in any case lead us to the answer. This is its versatility.

The beginning is again standard. Let us write down the extended matrix of the system and, using elementary transformations, bring it to a stepwise form:

That's all, and you were afraid.

(1) Please note that all numbers in the first column are divisible by 2, so 2 is fine on the top left step. To the second line we add the first line, multiplied by –4. To the third line we add the first line, multiplied by –2. To the fourth line we add the first line, multiplied by –1.

Attention! Many may be tempted by the fourth line subtract first line. This can be done, but it is not necessary; experience shows that the probability of an error in calculations increases several times. Just add: To the fourth line add the first line multiplied by –1 – exactly!

(2) The last three lines are proportional, two of them can be deleted.

Here again we need to show increased attention, but are the lines really proportional? To be on the safe side (especially for a teapot), it would be a good idea to multiply the second line by –1, and divide the fourth line by 2, resulting in three identical lines. And only after that remove two of them.

As a result of elementary transformations, the extended matrix of the system is reduced to a stepwise form:

When writing a task in a notebook, it is advisable to make the same notes in pencil for clarity.

Let us rewrite the corresponding system of equations:

There is no smell of a “ordinary” single solution to the system here. There is no bad line either. This means that this is the third remaining case - the system has infinitely many solutions. Sometimes, according to the condition, it is necessary to investigate the compatibility of the system (i.e. prove that a solution exists at all), you can read about this in the last paragraph of the article How to find the rank of a matrix? But for now let’s go over the basics:

An infinite set of solutions to a system is briefly written in the form of the so-called general solution of the system .

We find the general solution of the system using the inverse of the Gaussian method.

First we need to define what variables we have basic, and what variables free. You don’t have to bother yourself with the terms of linear algebra, just remember that there are such basic variables And free variables.

Basic variables always “sit” strictly on the steps of the matrix.
In this example, the basic variables are and

Free variables are everything remaining variables that did not receive a step. In our case there are two of them: – free variables.

Now you need All basic variables express only through free variables.

The reverse of the Gaussian algorithm traditionally works from the bottom up.
From the second equation of the system we express the basic variable:

Now look at the first equation: . First we substitute the found expression into it:

It remains to express the basic variable in terms of free variables:

In the end we got what we needed - All basic variables ( and ) are expressed only through free variables:

Actually, the general solution is ready:

How to write the general solution correctly?
Free variables are written into the general solution “by themselves” and strictly in their places. IN in this case free variables should be written in the second and fourth positions:
.

The resulting expressions for the basic variables and obviously needs to be written in the first and third positions:

Giving free variables arbitrary values, you can find infinitely many private solutions. The most popular values ​​are zeros, since the particular solution is the easiest to obtain. Let's substitute into the general solution:

– private solution.

Another sweet pair are ones, let’s substitute them into the general solution:

– another private solution.

It is easy to see that the system of equations has infinitely many solutions(since we can give free variables any values)

Each the particular solution must satisfy to each equation of the system. This is the basis for a “quick” check of the correctness of the solution. Take, for example, a particular solution and substitute it into the left side of each equation of the original system:

Everything must come together. And with any particular solution you receive, everything should also agree.

But, strictly speaking, checking a particular solution is sometimes deceiving, i.e. some particular solution may satisfy each equation of the system, but the general solution itself is actually found incorrectly.

Therefore, verification of the general solution is more thorough and reliable. How to check the resulting general solution ?

It's not difficult, but quite tedious. We need to take expressions basic variables, in this case and , and substitute them into the left side of each equation of the system.

To the left side of the first equation of the system:

To the left side of the second equation of the system:


The right side of the original equation is obtained.

Example 4

Solve the system using the Gaussian method. Find the general solution and two particular ones. Check the general solution.

This is an example for you to solve on your own. Here, by the way, again the number of equations is less than the number of unknowns, which means it is immediately clear that the system will either be inconsistent or have an infinite number of solutions. What is important in the decision process itself? Attention, and attention again. Full solution and answer at the end of the lesson.

And a couple more examples to reinforce the material

Example 5

Solve a system of linear equations. If the system has infinitely many solutions, find two particular solutions and check the general solution

Solution: Let's write down the extended matrix of the system and, using elementary transformations, bring it to a stepwise form:

(1) Add the first line to the second line. To the third line we add the first line multiplied by 2. To the fourth line we add the first line multiplied by 3.
(2) To the third line we add the second line, multiplied by –5. To the fourth line we add the second line, multiplied by –7.
(3) The third and fourth lines are the same, we delete one of them.

This is such a beauty:

Basic variables sit on the steps, therefore - basic variables.
There is only one free variable that did not get a step:

Reverse:
Let's express the basic variables through a free variable:
From the third equation:

Let's consider the second equation and substitute the found expression into it:

Let's consider the first equation and substitute the found expressions and into it:

Yes, a calculator that calculates ordinary fractions is still convenient.

So the general solution is:

Once again, how did it turn out? The free variable sits alone in its rightful fourth place. The resulting expressions for the basic variables also took their ordinal places.

Let us immediately check the general solution. The job is for blacks, but I have already done it, so catch it =)

We substitute three heroes , , into the left side of each equation of the system:

The corresponding right-hand sides of the equations are obtained, thus the general solution is found correctly.

Now from the found general solution we obtain two particular solutions. The only free variable here is the chef. No need to rack your brains.

Let it be then – private solution.
Let it be then – another private solution.

Answer: Common decision: , private solutions: , .

I shouldn’t have remembered about blacks... ...because all sorts of sadistic motives came into my head and I remembered the famous photoshop in which Ku Klux Klansmen in white robes are running across the field after a black football player. I sit and smile quietly. You know how distracting...

A lot of mathematics is harmful, so a similar final example for solving it yourself.

Example 6

Find the general solution to the system of linear equations.

I have already checked the general solution, the answer can be trusted. Your solution may differ from my solution, the main thing is that the general solutions coincide.

Many people probably noticed an unpleasant moment in the solutions: very often, when reversing the Gauss method, we had to tinker with ordinary fractions. In practice, this is indeed the case; cases where there are no fractions are much less common. Be prepared mentally and, most importantly, technically.

I will dwell on some features of the solution that were not found in the solved examples.

The general solution of the system may sometimes include a constant (or constants), for example: . Here one of the basic variables is equal to a constant number: . There is nothing exotic about this, it happens. Obviously, in this case, any particular solution will contain a five in the first position.

Rarely, but there are systems in which the number of equations is greater than the number of variables. The Gaussian method works in the most severe conditions; one should calmly reduce the extended matrix of the system to a stepwise form using a standard algorithm. Such a system may be inconsistent, may have infinitely many solutions, and, oddly enough, may have a single solution.

The Gaussian method, also called the method of sequential elimination of unknowns, is as follows. Using elementary transformations, a system of linear equations is brought to such a form that its matrix of coefficients turns out to be trapezoidal (the same as triangular or stepped) or close to trapezoidal (direct stroke of the Gaussian method, hereinafter simply straight stroke). An example of such a system and its solution is in the figure above.

In such a system, the last equation contains only one variable and its value can be unambiguously found. The value of this variable is then substituted into the previous equation ( inverse of the Gaussian method , then just the reverse), from which the previous variable is found, and so on.

In a trapezoidal (triangular) system, as we see, the third equation no longer contains variables y And x, and the second equation is the variable x .

After the matrix of the system has taken a trapezoidal shape, it is no longer difficult to understand the issue of compatibility of the system, determine the number of solutions and find the solutions themselves.

Advantages of the method:

1. when solving systems of linear equations with more than three equations and unknowns, the Gauss method is not as cumbersome as the Cramer method, since solving with the Gauss method requires fewer calculations;
2. the Gauss method can solve indeterminate systems of linear equations, that is, those that have a general solution (and we will analyze them in this lesson), and using the Cramer method, we can only state that the system is indeterminate;
3. you can solve systems of linear equations in which the number of unknowns is not equal to the number of equations (we will also analyze them in this lesson);
4. The method is based on elementary (school) methods - the method of substituting unknowns and the method of adding equations, which we touched on in the corresponding article.

In order for everyone to understand the simplicity with which trapezoidal (triangular, step) systems of linear equations are solved, we present a solution to such a system using reverse motion. Fast decision This system was shown in the picture at the beginning of the lesson.

Example 1. Solve a system of linear equations using inverse:

Solution. In this trapezoidal system the variable z can be uniquely found from the third equation. We substitute its value into the second equation and get the value of the variable y:

Now we know the values ​​of two variables - z And y. We substitute them into the first equation and get the value of the variable x:

From the previous steps we write out the solution to the system of equations:

To obtain such a trapezoidal system of linear equations, which we solved very simply, it is necessary to use a forward stroke associated with elementary transformations of the system of linear equations. It's also not very difficult.

Elementary transformations of a system of linear equations

Repeating the school method of algebraically adding the equations of a system, we found out that to one of the equations of the system we can add another equation of the system, and each of the equations can be multiplied by some numbers. As a result, we obtain a system of linear equations equivalent to this one. In it, one equation already contained only one variable, substituting the value of which into other equations, we come to a solution. Such addition is one of the types of elementary transformation of the system. When using the Gaussian method, we can use several types of transformations.

The animation above shows how the system of equations gradually turns into a trapezoidal one. That is, the one that you saw in the very first animation and convinced yourself that it is easy to find the values ​​of all unknowns from it. How to perform such a transformation and, of course, examples will be discussed further.

When solving systems of linear equations with any number of equations and unknowns in the system of equations and in the extended matrix of the system Can:

1. rearrange lines (this was mentioned at the very beginning of this article);
2. if other transformations result in equal or proportional rows, they can be deleted, except for one;
3. remove “zero” rows where all coefficients are equal to zero;
4. multiply or divide any string by a certain number;
5. to any line add another line, multiplied by a certain number.

As a result of the transformations, we obtain a system of linear equations equivalent to this one.

Algorithm and examples of solving a system of linear equations with a square matrix of the system using the Gauss method

Let us first consider solving systems of linear equations in which the number of unknowns is equal to the number of equations. The matrix of such a system is square, that is, the number of rows in it is equal to the number of columns.

Example 2. Solve a system of linear equations using the Gauss method

When solving systems of linear equations using school methods, we multiplied one of the equations term by term, so that the coefficients of the first variable in the two equations were opposite numbers. When adding equations, this variable is eliminated. The Gauss method works similarly.

To simplify appearance solutions let's create an extended matrix of the system:

In this matrix, the coefficients of the unknowns are located on the left before the vertical line, and the free terms are located on the right after the vertical line.

For the convenience of dividing coefficients for variables (to obtain division by unity) Let's swap the first and second rows of the system matrix. We obtain a system equivalent to this one, since in a system of linear equations the equations can be interchanged:

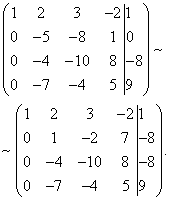
Using the new first equation eliminate the variable x from the second and all subsequent equations. To do this, to the second row of the matrix we add the first row multiplied by (in our case by ), to the third row - the first row multiplied by (in our case by ).

This is possible because

If our system of equations had more than three, then it would be necessary to add to all subsequent equations the first line, multiplied by the ratio of the corresponding coefficients, taken with a minus sign.

As a result, we obtain a matrix equivalent to this system new system equations in which all equations, starting from the second do not contain a variable x :

To simplify the second line of the resulting system, multiply it by and again obtain the matrix of a system of equations equivalent to this system:

Now, keeping the first equation of the resulting system unchanged, using the second equation we eliminate the variable y from all subsequent equations. To do this, to the third row of the system matrix we add the second row, multiplied by (in our case by ).

If there were more than three equations in our system, then we would have to add a second line to all subsequent equations, multiplied by the ratio of the corresponding coefficients taken with a minus sign.

As a result, we again obtain the matrix of a system equivalent to this system of linear equations:

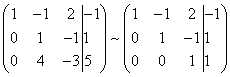
We have obtained an equivalent trapezoidal system of linear equations:

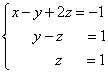
If the number of equations and variables is greater than in our example, then the process of sequentially eliminating variables continues until the system matrix becomes trapezoidal, as in our demo example.

We will find the solution “from the end” - the reverse move. For this from the last equation we determine z:
.
Substituting this value into the previous equation, we'll find y:

From the first equation we'll find x:

Answer: the solution to this system of equations is .

: in this case the same answer will be given if the system has a unique solution. If the system has an infinite number of solutions, then this will be the answer, and this is the subject of the fifth part of this lesson.

Solve a system of linear equations using the Gaussian method yourself, and then look at the solution

Here again we have an example of a consistent and definite system of linear equations, in which the number of equations is equal to the number of unknowns. The difference from our demo example from the algorithm is that there are already four equations and four unknowns.

Example 4. Solve a system of linear equations using the Gauss method:

Now you need to use the second equation to eliminate the variable from subsequent equations. Let's carry out preparatory work. To make it more convenient with the ratio of coefficients, you need to get one in the second column of the second row. To do this, subtract the third from the second line, and multiply the resulting second line by -1.

Let us now carry out the actual elimination of the variable from the third and fourth equations. To do this, add the second line, multiplied by , to the third line, and the second, multiplied by , to the fourth line.

Now, using the third equation, we eliminate the variable from the fourth equation. To do this, add the third line to the fourth line, multiplied by . We obtain an extended trapezoidal matrix.

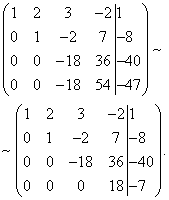
We obtained a system of equations to which the given system is equivalent:

Consequently, the resulting and given systems are compatible and definite. Final decision we find “from the end”. From the fourth equation we can directly express the value of the variable “x-four”:

We substitute this value into the third equation of the system and get

,

,

Finally, value substitution

The first equation gives

,

where do we find “x first”:

Answer: this system of equations has a unique solution .

You can also check the solution of the system on a calculator using Cramer's method: in this case, the same answer will be given if the system has a unique solution.

Solving applied problems using the Gauss method using the example of a problem on alloys

Systems of linear equations are used to model real objects in the physical world. Let's solve one of these problems - alloys. Similar problems - problems on mixtures, cost or specific gravity individual products in a product group and the like.

Example 5. Three pieces of alloy have a total mass of 150 kg. The first alloy contains 60% copper, the second - 30%, the third - 10%. Moreover, in the second and third alloys taken together there is 28.4 kg less copper than in the first alloy, and in the third alloy there is 6.2 kg less copper than in the second. Find the mass of each piece of the alloy.

Solution. We compose a system of linear equations:

We multiply the second and third equations by 10, we obtain an equivalent system of linear equations:

We create an extended matrix of the system:

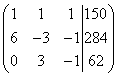
Attention, straight ahead. By adding (in our case, subtracting) one row multiplied by a number (we apply it twice), the following transformations occur with the extended matrix of the system:

The direct move is over. We obtained an expanded trapezoidal matrix.

We apply the reverse move. We find the solution from the end. We see that.

From the second equation we find

From the third equation -

You can also check the solution of the system on a calculator using Cramer's method: in this case, the same answer will be given if the system has a unique solution.

The simplicity of Gauss's method is evidenced by the fact that it took the German mathematician Carl Friedrich Gauss only 15 minutes to invent it. In addition to the method named after him, the saying “We should not confuse what seems incredible and unnatural to us with the absolutely impossible” is known from the works of Gauss - a kind of brief instructions to make discoveries.

In many applied problems there may not be a third constraint, that is, a third equation, then you have to solve a system of two equations with three unknowns using the Gaussian method, or, conversely, there are fewer unknowns than equations. We will now begin to solve such systems of equations.

Using the Gaussian method, you can determine whether any system is compatible or incompatible n linear equations with n variables.

The Gauss method and systems of linear equations with an infinite number of solutions

The next example is a consistent but indeterminate system of linear equations, that is, having an infinite number of solutions.

After performing transformations in the extended matrix of the system (rearranging rows, multiplying and dividing rows by a certain number, adding another to one row), rows of the form could appear

If in all equations having the form

Free terms are equal to zero, this means that the system is indefinite, that is, it has an infinite number of solutions, and equations of this type are “superfluous” and we exclude them from the system.

Example 6.

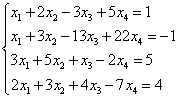
Solution. Let's create an extended matrix of the system. Then, using the first equation, we eliminate the variable from subsequent equations. To do this, add to the second, third and fourth lines the first, multiplied by :

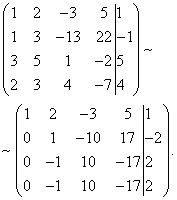
Now let's add the second line to the third and fourth.

As a result, we arrive at the system

The last two equations turned into equations of the form. These equations are satisfied for any value of the unknowns and can be discarded.

To satisfy the second equation, we can choose arbitrary values ​​for and , then the value for will be determined uniquely: . From the first equation the value for is also found uniquely: .

Both the given and the last systems are consistent, but uncertain, and the formulas

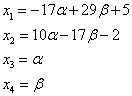
for arbitrary and give us all solutions of a given system.

Gauss method and systems of linear equations without solutions

The next example is an inconsistent system of linear equations, that is, one that has no solutions. The answer to such problems is formulated this way: the system has no solutions.

As already mentioned in connection with the first example, after performing transformations, rows of the form could appear in the extended matrix of the system

corresponding to an equation of the form

If among them there is at least one equation with a nonzero free term (i.e. ), then this system of equations is inconsistent, that is, it has no solutions and its solution is complete.

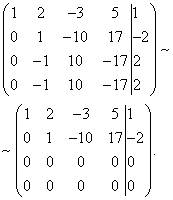
Example 7. Solve the system of linear equations using the Gauss method:

Solution. We compose an extended matrix of the system. Using the first equation, we exclude the variable from subsequent equations. To do this, add the first line multiplied by to the second line, the first line multiplied by the third line, and the first line multiplied by the fourth line.

Now you need to use the second equation to eliminate the variable from subsequent equations. To obtain integer ratios of coefficients, we swap the second and third rows of the extended matrix of the system.

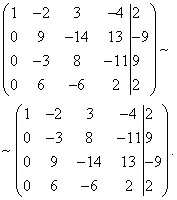
To exclude the third and fourth equations, add the second one multiplied by , to the third line, and the second multiplied by , to the fourth line.

Now, using the third equation, we eliminate the variable from the fourth equation. To do this, add the third line to the fourth line, multiplied by .

The given system is therefore equivalent to the following:

The resulting system is inconsistent, since its last equation cannot be satisfied by any values ​​of the unknowns. Therefore, this system has no solutions.

Lesson content

Linear equations in two variables

A schoolchild has 200 rubles to eat lunch at school. A cake costs 25 rubles, and a cup of coffee costs 10 rubles. How many cakes and cups of coffee can you buy for 200 rubles?

Let us denote the number of cakes by x, and the number of cups of coffee through y. Then the cost of the cakes will be denoted by the expression 25 x, and the cost of cups of coffee in 10 y .

25x— price x cakes
10y — price y cups of coffee

The total amount should be 200 rubles. Then we get an equation with two variables x And y

25x+ 10y= 200

How many roots does this equation have?

It all depends on the student’s appetite. If he buys 6 cakes and 5 cups of coffee, then the roots of the equation will be the numbers 6 and 5.

The pair of values ​​6 and 5 are said to be the roots of equation 25 x+ 10y= 200 . Written as (6; 5), with the first number being the value of the variable x, and the second - the value of the variable y .

6 and 5 are not the only roots that reverse equation 25 x+ 10y= 200 to identity. If desired, for the same 200 rubles a student can buy 4 cakes and 10 cups of coffee:

In this case, the roots of equation 25 x+ 10y= 200 is a pair of values ​​(4; 10).

Moreover, a schoolchild may not buy coffee at all, but buy cakes for the entire 200 rubles. Then the roots of equation 25 x+ 10y= 200 will be the values ​​8 and 0

Or vice versa, don’t buy cakes, but buy coffee for the entire 200 rubles. Then the roots of equation 25 x+ 10y= 200 the values ​​will be 0 and 20

Let's try to list all possible roots of equation 25 x+ 10y= 200 . Let us agree that the values x And y belong to the set of integers. And let these values ​​be greater than or equal to zero:

x∈Z, y∈ Z;
x ≥ 0, y ≥ 0

This will be convenient for the student himself. It is more convenient to buy whole cakes than, for example, several whole cakes and half a cake. It is also more convenient to take coffee in whole cups than, for example, several whole cups and half a cup.

Note that for odd x it is impossible to achieve equality under any circumstances y. Then the values x the following numbers will be 0, 2, 4, 6, 8. And knowing x can be easily determined y

Thus, we received the following pairs of values (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). These pairs are solutions or roots of Equation 25 x+ 10y= 200. They turn this equation into an identity.

Equation of the form ax + by = c called linear equation with two variables. The solution or roots of this equation are a pair of values ​​( x; y), which turns it into identity.

Note also that if a linear equation with two variables is written in the form ax + b y = c , then they say that it is written in canonical(normal) form.

Some linear equations in two variables can be reduced to canonical form.

For example, the equation 2(16x+ 3y − 4) = 2(12 + 8x − y) can be brought to mind ax + by = c. Let's open the brackets on both sides of this equation and get 32x + 6y − 8 = 24 + 16x − 2y . We group terms containing unknowns on the left side of the equation, and terms free of unknowns on the right. Then we get 32x− 16x+ 6y+ 2y = 24 + 8 . We present similar terms in both sides, we get equation 16 x+ 8y= 32. This equation is reduced to the form ax + by = c and is canonical.

Equation 25 discussed earlier x+ 10y= 200 is also a linear equation with two variables in canonical form. In this equation the parameters a , b And c are equal to the values ​​25, 10 and 200, respectively.

Actually the equation ax + by = c has countless solutions. Solving the equation 25x+ 10y= 200, we looked for its roots only on the set of integers. As a result, we obtained several pairs of values ​​that turned this equation into an identity. But on many rational numbers equation 25 x+ 10y= 200 will have infinitely many solutions.

To obtain new pairs of values, you need to take an arbitrary value for x, then express y. For example, let's take for the variable x value 7. Then we get an equation with one variable 25×7 + 10y= 200 in which one can express y

Let x= 15. Then the equation 25x+ 10y= 200 becomes 25 × 15 + 10y= 200. From here we find that y = −17,5

Let x= −3 . Then the equation 25x+ 10y= 200 becomes 25 × (−3) + 10y= 200. From here we find that y = −27,5

System of two linear equations with two variables

For the equation ax + by = c you can take arbitrary values ​​for as many times as you like x and find values ​​for y. Taken separately, such an equation will have countless solutions.

But it also happens that the variables x And y connected not by one, but by two equations. In this case they form the so-called system of linear equations in two variables. Such a system of equations can have one pair of values ​​(or in other words: “one solution”).

It may also happen that the system has no solutions at all. A system of linear equations can have countless solutions in rare and exceptional cases.

Two linear equations form a system when the values x And y enter into each of these equations.

Let's go back to the very first equation 25 x+ 10y= 200 . One of the pairs of values ​​for this equation was the pair (6; 5) . This is a case when for 200 rubles you could buy 6 cakes and 5 cups of coffee.

Let's formulate the problem so that the pair (6; 5) becomes the only solution for equation 25 x+ 10y= 200 . To do this, let’s create another equation that would connect the same x cakes and y cups of coffee.

Let us state the text of the problem as follows:

“The student bought several cakes and several cups of coffee for 200 rubles. A cake costs 25 rubles, and a cup of coffee costs 10 rubles. How many cakes and cups of coffee did the student buy if it is known that the number of cakes is one unit greater than the number of cups of coffee?

We already have the first equation. This is equation 25 x+ 10y= 200 . Now let's create an equation for the condition “the number of cakes is one unit greater than the number of cups of coffee” .

The number of cakes is x, and the number of cups of coffee is y. You can write this phrase using the equation x−y= 1. This equation will mean that the difference between cakes and coffee is 1.

x = y+ 1 . This equation means that the number of cakes is one more than the number of cups of coffee. Therefore, to obtain equality, one is added to the number of cups of coffee. This can be easily understood if we use the model of scales that we considered when studying the simplest problems:

We got two equations: 25 x+ 10y= 200 and x = y+ 1. Since the values x And y, namely 6 and 5 are included in each of these equations, then together they form a system. Let's write down this system. If the equations form a system, then they are framed by the system sign. The system symbol is a curly brace:

Let's decide this system. This will allow us to see how we arrive at the values ​​6 and 5. There are many methods for solving such systems. Let's look at the most popular of them.

Substitution method

The name of this method speaks for itself. Its essence is to substitute one equation into another, having previously expressed one of the variables.

In our system, nothing needs to be expressed. In the second equation x = y+ 1 variable x already expressed. This variable is equal to the expression y+ 1 . Then you can substitute this expression into the first equation instead of the variable x

After substituting the expression y+ 1 into the first equation instead x, we get the equation 25(y+ 1) + 10y= 200 . This is a linear equation with one variable. This equation is quite easy to solve:

We found the value of the variable y. Now let's substitute this value into one of the equations and find the value x. For this it is convenient to use the second equation x = y+ 1 . Let’s substitute the value into it y

This means that the pair (6; 5) is a solution to the system of equations, as we intended. We check and make sure that the pair (6; 5) satisfies the system:

Example 2

Let's substitute the first equation x= 2 + y into the second equation 3 x− 2y= 9. In the first equation the variable x equal to the expression 2 + y. Let’s substitute this expression into the second equation instead of x

Now let's find the value x. To do this, let's substitute the value y into the first equation x= 2 + y

This means that the solution to the system is the pair value (5; 3)

Example 3. Solve by substitution the following system equations:

Here, unlike previous examples, one of the variables is not expressed explicitly.

To substitute one equation into another, you first need .

It is advisable to express the variable that has a coefficient of one. The variable has a coefficient of one x, which is contained in the first equation x+ 2y= 11. Let's express this variable.

After variable expression x, our system will take the following form:

Now let's substitute the first equation into the second and find the value y

Let's substitute y x

This means that the solution to the system is a pair of values ​​(3; 4)

Of course, you can also express a variable y. This will not change the roots. But if you express y, The result is not a very simple equation, which will take more time to solve. It will look like this:

We see that in this example we express x much more convenient than expressing y .

Example 4. Solve the following system of equations using the substitution method:

Let us express in the first equation x. Then the system will take the form:

y

Let's substitute y into the first equation and find x. You can use the original equation 7 x+ 9y= 8, or use the equation in which the variable is expressed x. We will use this equation because it is convenient:

This means that the solution to the system is a pair of values ​​(5; −3)

Addition method

The addition method consists of adding the equations included in the system term by term. This addition results in a new equation with one variable. And solving such an equation is quite simple.

Let's solve the following system of equations:

Let's add the left side of the first equation with the left side of the second equation. And the right side of the first equation with the right side of the second equation. We get the following equality:

Let's look at similar terms:

As a result, we got the simplest equation 3 x= 27 whose root is 9. Knowing the value x you can find the value y. Let's substitute the value x into the second equation x−y= 3 . We get 9 − y= 3 . From here y= 6 .

This means that the solution to the system is a pair of values ​​(9; 6)

Example 2

Let's add the left side of the first equation with the left side of the second equation. And the right side of the first equation with the right side of the second equation. In the resulting equality we present similar terms:

As a result, we got the simplest equation 5 x= 20, whose root is 4. Knowing the value x you can find the value y. Let's substitute the value x into the first equation 2 x+y= 11. Let's get 8+ y= 11. From here y= 3 .

This means that the solution to the system is a pair of values ​​(4;3)

The addition process is not described in detail. It must be done mentally. When adding, both equations must be reduced to canonical form. That is, by the way ac + by = c .

From the examples considered, it is clear that the main purpose of adding equations is to get rid of one of the variables. But it is not always possible to immediately solve a system of equations using the addition method. Most often, the system is first brought to a form in which the equations included in this system can be added.

For example, the system can be solved immediately by addition. When adding both equations, the terms y And −y will disappear because their sum is zero. As a result, the simplest equation 11 is formed x= 22, whose root is 2. It will then be possible to determine y equal to 5.

And the system of equations The addition method cannot be solved immediately, since this will not lead to the disappearance of one of the variables. Addition will result in equation 8 x+ y= 28, which has an infinite number of solutions.

If both sides of the equation are multiplied or divided by the same number, not equal to zero, you get an equation equivalent to the given one. This rule is also true for a system of linear equations with two variables. One of the equations (or both equations) can be multiplied by any number. The result will be an equivalent system, the roots of which will coincide with the previous one.

Let's return to the very first system, which described how many cakes and cups of coffee a schoolchild bought. The solution to this system was a pair of values ​​(6; 5).

Let's multiply both equations included in this system by some numbers. Let's say we multiply the first equation by 2, and the second by 3

As a result, we got a system
The solution to this system is still the pair of values ​​(6; 5)

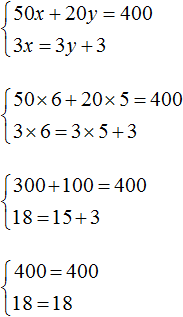
This means that the equations included in the system can be reduced to a form suitable for applying the addition method.

Let's return to the system , which we could not solve using the addition method.

Multiply the first equation by 6, and the second by −2

Then we get the following system:

Let's add up the equations included in this system. Adding components 12 x and −12 x will result in 0, addition 18 y and 4 y will give 22 y, and adding 108 and −20 gives 88. Then we get equation 22 y= 88, from here y = 4 .

If at first it’s hard to add equations in your head, then you can write down how it adds up left side of the first equation with the left side of the second equation, and the right side of the first equation with the right side of the second equation:

Knowing that the value of the variable y equals 4, you can find the value x. Let's substitute y into one of the equations, for example into the first equation 2 x+ 3y= 18. Then we get an equation with one variable 2 x+ 12 = 18. Let's move 12 to the right side, changing the sign, we get 2 x= 6, from here x = 3 .

Example 4. Solve the following system of equations using the addition method:

Let's multiply the second equation by −1. Then the system will take the following form:

Let's add both equations. Adding components x And −x will result in 0, addition 5 y and 3 y will give 8 y, and adding 7 and 1 gives 8. The result is equation 8 y= 8 whose root is 1. Knowing that the value y equals 1, you can find the value x .

Let's substitute y into the first equation, we get x+ 5 = 7, hence x= 2

Example 5. Solve the following system of equations using the addition method:

It is desirable that terms containing the same variables be located one below the other. Therefore, in the second equation the terms 5 y and −2 x Let's swap places. As a result, the system will take the form:

Let's multiply the second equation by 3. Then the system will take the form:

Now let's add both equations. As a result of addition we obtain equation 8 y= 16, whose root is 2.

Let's substitute y into the first equation, we get 6 x− 14 = 40. Let's move the term −14 to the right side, changing the sign, and get 6 x= 54 . From here x= 9.

Example 6. Solve the following system of equations using the addition method:

Let's get rid of fractions. Multiply the first equation by 36, and the second by 12

In the resulting system the first equation can be multiplied by −5, and the second by 8

Let's add up the equations in the resulting system. Then we get the simplest equation −13 y= −156 . From here y= 12. Let's substitute y into the first equation and find x

Example 7. Solve the following system of equations using the addition method:

Let us bring both equations to normal form. Here it is convenient to apply the rule of proportion in both equations. If in the first equation the right side is represented as , and the right side of the second equation as , then the system will take the form:

We have a proportion. Let's multiply its extreme and middle terms. Then the system will take the form:

Let's multiply the first equation by −3, and open the brackets in the second:

Now let's add both equations. As a result of adding these equations, we get an equality with zero on both sides:

It turns out that the system has countless solutions.

But we can’t just take arbitrary values ​​from the sky for x And y. We can specify one of the values, and the other will be determined depending on the value we specify. For example, let x= 2 . Let's substitute this value into the system:

As a result of solving one of the equations, the value for y, which will satisfy both equations:

The resulting pair of values ​​(2; −2) will satisfy the system:

Let's find another pair of values. Let x= 4. Let's substitute this value into the system:

You can tell by eye that the value y equals zero. Then we get a pair of values ​​(4; 0) that satisfies our system:

Example 8. Solve the following system of equations using the addition method:

Multiply the first equation by 6 and the second by 12

Let's rewrite what's left:

Let's multiply the first equation by −1. Then the system will take the form:

Now let's add both equations. As a result of addition, equation 6 is formed b= 48, whose root is 8. Substitute b into the first equation and find a

System of linear equations with three variables

A linear equation with three variables includes three variables with coefficients, as well as an intercept term. In canonical form it can be written as follows:

ax + by + cz = d

This equation has countless solutions. By giving two variables different values, a third value can be found. The solution in this case is a triple of values ​​( x; y; z) which turns the equation into an identity.

If the variables x, y, z are interconnected by three equations, then a system of three linear equations with three variables is formed. To solve such a system, you can use the same methods that apply to linear equations with two variables: the substitution method and the addition method.

Example 1. Solve the following system of equations using the substitution method:

Let us express in the third equation x. Then the system will take the form:

Now let's do the substitution. Variable x is equal to the expression 3 − 2y − 2z . Let's substitute this expression into the first and second equations:

Let's open the brackets in both equations and present similar terms:

We have arrived at a system of linear equations with two variables. In this case, it is convenient to use the addition method. As a result, the variable y will disappear and we can find the value of the variable z

Now let's find the value y. To do this, it is convenient to use the equation − y+ z= 4. Substitute the value into it z

Now let's find the value x. To do this, it is convenient to use the equation x= 3 − 2y − 2z . Let's substitute the values ​​into it y And z

Thus, the triple of values ​​(3; −2; 2) is a solution to our system. By checking we make sure that these values ​​satisfy the system:

Example 2. Solve the system using the addition method

Let's add the first equation with the second, multiplied by −2.

If the second equation is multiplied by −2, it takes the form −6x+ 6y − 4z = −4 . Now let's add it to the first equation:

We see that as a result of elementary transformations, the value of the variable was determined x. It is equal to one.

Let's return to the main system. Let's add the second equation with the third, multiplied by −1. If the third equation is multiplied by −1, it takes the form −4x + 5y − 2z = −1 . Now let's add it to the second equation:

We got the equation x− 2y= −1 . Let's substitute the value into it x which we found earlier. Then we can determine the value y

Now we know the meanings x And y. This allows you to determine the value z. Let's use one of the equations included in the system:

Thus, the triple of values ​​(1; 1; 1) is the solution to our system. By checking we make sure that these values ​​satisfy the system:

Problems on composing systems of linear equations

The task of composing systems of equations is solved by entering several variables. Next, equations are compiled based on the conditions of the problem. From the compiled equations they form a system and solve it. Having solved the system, it is necessary to check whether its solution satisfies the conditions of the problem.

Problem 1. A Volga car drove out of the city to the collective farm. She returned back along another road, which was 5 km shorter than the first. In total, the car traveled 35 km round trip. How many kilometers is the length of each road?

Solution

Let x— length of the first road, y- length of the second. If the car traveled 35 km round trip, then the first equation can be written as x+ y= 35. This equation describes the sum of the lengths of both roads.

It is said that the car returned along a road that was 5 km shorter than the first one. Then the second equation can be written as x− y= 5. This equation shows that the difference between the road lengths is 5 km.

Or the second equation can be written as x= y+ 5. We will use this equation.

Because the variables x And y in both equations denote the same number, then we can form a system from them:

Let's solve this system using some of the previously studied methods. In this case, it is convenient to use the substitution method, since in the second equation the variable x already expressed.

Substitute the second equation into the first and find y

Let's substitute the found value y in the second equation x= y+ 5 and we'll find x

The length of the first road was designated through the variable x. Now we have found its meaning. Variable x is equal to 20. This means that the length of the first road is 20 km.

And the length of the second road was indicated by y. The value of this variable is 15. This means the length of the second road is 15 km.

Let's check. First, let's make sure that the system is solved correctly:

Now let’s check whether the solution (20; 15) satisfies the conditions of the problem.

It was said that the car traveled a total of 35 km round trip. We add the lengths of both roads and make sure that the solution (20; 15) satisfies this condition: 20 km + 15 km = 35 km

The following condition: the car returned back along another road, which was 5 km shorter than the first . We see that solution (20; 15) also satisfies this condition, since 15 km is shorter than 20 km by 5 km: 20 km − 15 km = 5 km

When composing a system, it is important that the variables represent the same numbers in all equations included in this system.

So our system contains two equations. These equations in turn contain variables x And y, which represent the same numbers in both equations, namely road lengths of 20 km and 15 km.

Problem 2. Oak and pine sleepers were loaded onto the platform, 300 sleepers in total. It is known that all oak sleepers weighed 1 ton less than all pine sleepers. Determine how many oak and pine sleepers there were separately, if each oak sleeper weighed 46 kg, and each pine sleeper 28 kg.

Solution

Let x oak and y pine sleepers were loaded onto the platform. If there were 300 sleepers in total, then the first equation can be written as x+y = 300 .

All oak sleepers weighed 46 x kg, and the pine ones weighed 28 y kg. Since oak sleepers weighed 1 ton less than pine sleepers, the second equation can be written as 28y − 46x= 1000 . This equation shows that the difference in mass between oak and pine sleepers is 1000 kg.

Tons were converted to kilograms since the mass of oak and pine sleepers was measured in kilograms.

As a result, we obtain two equations that form the system

Let's solve this system. Let us express in the first equation x. Then the system will take the form:

Substitute the first equation into the second and find y

Let's substitute y into the equation x= 300 − y and find out what it is x

This means that 100 oak and 200 pine sleepers were loaded onto the platform.

Let's check whether the solution (100; 200) satisfies the conditions of the problem. First, let's make sure that the system is solved correctly:

It was said that there were 300 sleepers in total. We add up the number of oak and pine sleepers and make sure that the solution (100; 200) satisfies this condition: 100 + 200 = 300.

The following condition: all oak sleepers weighed 1 ton less than all pine sleepers . We see that the solution (100; 200) also satisfies this condition, since 46 × 100 kg of oak sleepers is lighter than 28 × 200 kg of pine sleepers: 5600 kg − 4600 kg = 1000 kg.

Problem 3. We took three pieces of copper-nickel alloy in ratios of 2: 1, 3: 1 and 5: 1 by weight. A piece weighing 12 kg was fused from them with a ratio of copper and nickel content of 4: 1. Find the mass of each original piece if the mass of the first is twice the mass of the second.