How to solve expressions with fractions. Dividing a common fraction by a fraction

The numerator, and that which is divided by is the denominator.

To write a fraction, first write the numerator, then draw a horizontal line under the number, and write the denominator below the line. The horizontal line that separates the numerator and denominator is called a fraction line. Sometimes it is depicted as an oblique "/" or "∕". In this case, the numerator is written to the left of the line, and the denominator to the right. So, for example, the fraction “two thirds” will be written as 2/3. For clarity, the numerator is usually written at the top of the line, and the denominator at the bottom, that is, instead of 2/3 you can find: ⅔.

To calculate the product of fractions, first multiply the numerator of one fractions to the numerator is different. Write the result in the numerator of the new fractions. After this, multiply the denominators. Enter the total value in the new fractions. For example, 1/3? 1/5 = 1/15 (1 × 1 = 1; 3 × 5 = 15).

To divide one fraction by another, first multiply the numerator of the first by the denominator of the second. Do the same with the second fraction (divisor). Or, before performing all the actions, first “flip” the divisor, if it is more convenient for you: the denominator should appear in place of the numerator. Then multiply the denominator of the dividend by the new denominator of the divisor and multiply the numerators. For example, 1/3: 1/5 = 5/3 = 1 2/3 (1 ? 5 = 5; 3 ? 1 = 3).

Sources:

• Basic fraction problems

Fractional numbers can be expressed in different ways exact value quantities. You can do the same math operations with fractions as you can with whole numbers: subtraction, addition, multiplication, and division. To learn to decide fractions, we must remember some of their features. They depend on the type fractions, the presence of an integer part, a common denominator. Some arithmetic operations after execution they require reduction of the fractional part of the result.

You will need

• - calculator

Instructions

Look closely at the numbers. If among the fractions there are decimals and irregular ones, sometimes it is more convenient to first perform operations with decimals, and then convert them to the irregular form. Can you translate fractions in this form initially, writing the value after the decimal point in the numerator and putting 10 in the denominator. If necessary, reduce the fraction by dividing the numbers above and below by one divisor. Fractions in which the whole part is isolated must be converted to the wrong form by multiplying it by the denominator and adding the numerator to the result. This value will become the new numerator fractions. To select a whole part from an initially incorrect one fractions, you need to divide the numerator by the denominator. Write the whole result from fractions. And the remainder of the division will become the new numerator, denominator fractions it does not change. For fractions with whole part it is possible to perform actions separately first for the integer and then for the fractional parts. For example, the sum of 1 2/3 and 2 ¾ can be calculated:
- Converting fractions to the wrong form:
- 1 2/3 + 2 ¾ = 5/3 + 11/4 = 20/12 + 33/12 = 53/12 = 4 5/12;
- Summing separately integers and fractional parts terms:
- 1 2/3 + 2 ¾ = (1+2) + (2/3 + ¾) = 3 +(8/12 + 9/12) = 3 + 12/17 = 3 + 1 5/12 = 4 5 /12.

Rewrite them using the “:” separator and continue with normal division.

To obtain the final result, reduce the resulting fraction by dividing the numerator and denominator by one whole number, the largest possible in in this case. In this case, there must be integers above and below the line.

note

Do not perform arithmetic with fractions whose denominators are different. Choose a number such that when you multiply the numerator and denominator of each fraction by it, the result is that the denominators of both fractions are equal.

Helpful advice

When writing fractional numbers, the dividend is written above the line. This quantity is designated as the numerator of the fraction. The divisor, or denominator, of the fraction is written below the line. For example, one and a half kilograms of rice as a fraction will be written as follows: 1 ½ kg of rice. If the denominator of a fraction is 10, the fraction is called a decimal. In this case, the numerator (dividend) is written to the right of the whole part, separated by a comma: 1.5 kg of rice. For ease of calculation, such a fraction can always be written in the wrong form: 1 2/10 kg of potatoes. To simplify, you can reduce the numerator and denominator values ​​by dividing them by one integer. In this example, you can divide by 2. The result will be 1 1/5 kg of potatoes. Make sure that the numbers you are going to perform arithmetic with are presented in the same form.

) and denominator by denominator (we get the denominator of the product).

Formula for multiplying fractions:

For example:

Before you begin multiplying numerators and denominators, you need to check whether the fraction can be reduced. If you can reduce the fraction, it will be easier for you to make further calculations.

Dividing a common fraction by a fraction.

Dividing fractions involving natural numbers.

It's not as scary as it seems. As in the case of addition, we convert the integer into a fraction with one in the denominator. For example:

Multiplying mixed fractions.

Rules for multiplying fractions (mixed):

• convert mixed fractions to improper fractions;
• multiplying the numerators and denominators of fractions;
• reduce the fraction;
• If you get an improper fraction, then we convert the improper fraction into a mixed fraction.

Note! To multiply mixed fraction to another mixed fraction, you must first convert them to the form of improper fractions, and then multiply them according to the rule for multiplying ordinary fractions.

The second way to multiply a fraction by a natural number.

It may be more convenient to use the second method of multiplication common fraction per number.

Note! To multiply a fraction by natural number It is necessary to divide the denominator of the fraction by this number, and leave the numerator unchanged.

From the example given above, it is clear that this option is more convenient to use when the denominator of a fraction is divided without a remainder by a natural number.

Multistory fractions.

In high school, three-story (or more) fractions are often encountered. Example:

To bring such a fraction to its usual form, use division through 2 points:

Note! When dividing fractions, the order of division is very important. Be careful, it's easy to get confused here.

Note, For example:

When dividing one by any fraction, the result will be the same fraction, only inverted:

Practical tips for multiplying and dividing fractions:

1. The most important thing when working with fractional expressions is accuracy and attentiveness. Do all calculations carefully and accurately, concentratedly and clearly. It's better to write a few extra lines in your draft than to get lost in mental calculations.

2. In tasks with different types fractions - go to the form of ordinary fractions.

3. We reduce all fractions until it is no longer possible to reduce.

4. We transform multi-level fractional expressions into ordinary ones using division through 2 points.

5. Divide a unit by a fraction in your head, simply turning the fraction over.

Lesson content

Adding fractions with like denominators

There are two types of addition of fractions:

1. Adding fractions with like denominators
2. Adding fractions with different denominators

First, let's learn the addition of fractions with like denominators. Everything is simple here. To add fractions with the same denominators, you need to add their numerators and leave the denominator unchanged. For example, let's add the fractions and . Add the numerators and leave the denominator unchanged:

This example can be easily understood if we remember the pizza, which is divided into four parts. If you add pizza to pizza, you get pizza:

Example 2. Add fractions and .

The answer turned out to be an improper fraction. When the end of the task comes, it is customary to get rid of improper fractions. To get rid of an improper fraction, you need to select the whole part of it. In our case, the whole part is easily isolated - two divided by two equals one:

This example can be easily understood if we remember about a pizza that is divided into two parts. If you add more pizza to the pizza, you get one whole pizza:

Example 3. Add fractions and .

Again, we add up the numerators and leave the denominator unchanged:

This example can be easily understood if we remember the pizza, which is divided into three parts. If you add more pizza to the pizza, you get pizza:

Example 4. Find the value of an expression

This example is solved in exactly the same way as the previous ones. The numerators must be added and the denominator left unchanged:

Let's try to depict our solution using a drawing. If you add pizzas to a pizza and add more pizzas, you get 1 whole pizza and more pizzas.

As you can see, there is nothing complicated about adding fractions with the same denominators. It is enough to understand the following rules:

1. To add fractions with the same denominator, you need to add their numerators and leave the denominator unchanged;

Adding fractions with different denominators

Now let's learn how to add fractions with different denominators. When adding fractions, the denominators of the fractions must be the same. But they are not always the same.

For example, fractions can be added because they have same denominators.

But fractions cannot be added right away, since these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

There are several ways to reduce fractions to the same denominator. Today we will look at only one of them, since the other methods may seem complicated for a beginner.

The essence of this method is that first the LCM of the denominators of both fractions is searched. The LCM is then divided by the denominator of the first fraction to obtain the first additional factor. They do the same with the second fraction - the LCM is divided by the denominator of the second fraction and a second additional factor is obtained.

The numerators and denominators of the fractions are then multiplied by their additional factors. As a result of these actions, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to add such fractions.

Example 1. Let's add the fractions and

First of all, we find the least common multiple of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 2. The least common multiple of these numbers is 6

LCM (2 and 3) = 6

Now let's return to fractions and . First, divide the LCM by the denominator of the first fraction and get the first additional factor. LCM is the number 6, and the denominator of the first fraction is the number 3. Divide 6 by 3, we get 2.

The resulting number 2 is the first additional multiplier. We write it down to the first fraction. To do this, make a small oblique line over the fraction and write down the additional factor found above it:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction and get the second additional factor. LCM is the number 6, and the denominator of the second fraction is the number 2. Divide 6 by 2, we get 3.

The resulting number 3 is the second additional multiplier. We write it down to the second fraction. Again, we make a small oblique line over the second fraction and write down the additional factor found above it:

Now we have everything ready for addition. It remains to multiply the numerators and denominators of the fractions by their additional factors:

Look carefully at what we have come to. We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to add such fractions. Let's take this example to the end:

This completes the example. It turns out to add .

Let's try to depict our solution using a drawing. If you add pizza to a pizza, you get one whole pizza and another sixth of a pizza:

Reducing fractions to the same (common) denominator can also be depicted using a picture. Reducing the fractions and to a common denominator, we got the fractions and . These two fractions will be represented by the same pieces of pizza. The only difference will be that this time they will be divided into equal shares (reduced to the same denominator).

The first drawing represents a fraction (four pieces out of six), and the second drawing represents a fraction (three pieces out of six). Adding these pieces we get (seven pieces out of six). This fraction is improper, so we highlighted the whole part of it. As a result, we got (one whole pizza and another sixth pizza).

Please note that we have described this example in too much detail. IN educational institutions It’s not customary to write in such detail. You need to be able to quickly find the LCM of both denominators and additional factors to them, as well as quickly multiply the found additional factors by your numerators and denominators. If we were at school, we would have to write this example as follows:

But there is also back side medals. If you do not take detailed notes in the first stages of studying mathematics, then questions of the sort begin to appear. “Where does that number come from?”, “Why do fractions suddenly turn into completely different fractions? «.

To make it easier to add fractions with different denominators, you can use the following step-by-step instructions:

1. Find the LCM of the denominators of fractions;
2. Divide the LCM by the denominator of each fraction and obtain an additional factor for each fraction;
3. Multiply the numerators and denominators of fractions by their additional factors;
4. Add fractions that have the same denominators;
5. If the answer turns out to be an improper fraction, then select its whole part;

Example 2. Find the value of an expression .

Let's use the instructions given above.

Step 1. Find the LCM of the denominators of the fractions

Find the LCM of the denominators of both fractions. The denominators of fractions are the numbers 2, 3 and 4

Step 2. Divide the LCM by the denominator of each fraction and get an additional factor for each fraction

Divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 2. Divide 12 by 2, we get 6. We got the first additional factor 6. We write it above the first fraction:

Now we divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 3. Divide 12 by 3, we get 4. We get the second additional factor 4. We write it above the second fraction:

Now we divide the LCM by the denominator of the third fraction. LCM is the number 12, and the denominator of the third fraction is the number 4. Divide 12 by 4, we get 3. We get the third additional factor 3. We write it above the third fraction:

Step 3. Multiply the numerators and denominators of the fractions by their additional factors

We multiply the numerators and denominators by their additional factors:

Step 4. Add fractions with the same denominators

We came to the conclusion that fractions that had different denominators turned into fractions that had the same (common) denominators. All that remains is to add these fractions. Add it up:

The addition didn't fit on one line, so we moved the remaining expression to the next line. This is allowed in mathematics. When an expression does not fit on one line, it is moved to the next line, and it is necessary to put an equal sign (=) at the end of the first line and at the beginning of the new line. The equal sign on the second line indicates that this is a continuation of the expression that was on the first line.

Step 5. If the answer turns out to be an improper fraction, then select the whole part of it

Our answer turned out to be an improper fraction. We have to highlight a whole part of it. We highlight:

We received an answer

Subtracting fractions with like denominators

There are two types of subtraction of fractions:

1. Subtracting fractions with like denominators
2. Subtracting fractions with different denominators

First, let's learn how to subtract fractions with like denominators. Everything is simple here. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, but leave the denominator the same.

For example, let's find the value of the expression . To solve this example, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged. Let's do this:

This example can be easily understood if we remember the pizza, which is divided into four parts. If you cut pizzas from a pizza, you get pizzas:

Example 2. Find the value of the expression.

Again, from the numerator of the first fraction, subtract the numerator of the second fraction, and leave the denominator unchanged:

This example can be easily understood if we remember the pizza, which is divided into three parts. If you cut pizzas from a pizza, you get pizzas:

Example 3. Find the value of an expression

This example is solved in exactly the same way as the previous ones. From the numerator of the first fraction you need to subtract the numerators of the remaining fractions:

As you can see, there is nothing complicated about subtracting fractions with the same denominators. It is enough to understand the following rules:

1. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged;
2. If the answer turns out to be an improper fraction, then you need to highlight the whole part of it.

Subtracting fractions with different denominators

For example, you can subtract a fraction from a fraction because the fractions have the same denominators. But you cannot subtract a fraction from a fraction, since these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

The common denominator is found using the same principle that we used when adding fractions with different denominators. First of all, find the LCM of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained, which is written above the first fraction. Similarly, the LCM is divided by the denominator of the second fraction and a second additional factor is obtained, which is written above the second fraction.

The fractions are then multiplied by their additional factors. As a result of these operations, fractions that had different denominators are converted into fractions that have the same denominators. And we already know how to subtract such fractions.

Example 1. Find the meaning of the expression:

These fractions have different denominators, so you need to reduce them to the same (common) denominator.

First we find the LCM of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 4. The least common multiple of these numbers is 12

LCM (3 and 4) = 12

Now let's return to fractions and

Let's find an additional factor for the first fraction. To do this, divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 3. Divide 12 by 3, we get 4. Write a four above the first fraction:

We do the same with the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 4. Divide 12 by 4, we get 3. Write a three over the second fraction:

Now we are ready for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to subtract such fractions. Let's take this example to the end:

We received an answer

Let's try to depict our solution using a drawing. If you cut pizza from a pizza, you get pizza

This is the detailed version of the solution. If we were at school, we would have to solve this example shorter. Such a solution would look like this:

Reducing fractions to a common denominator can also be depicted using a picture. Reducing these fractions to a common denominator, we got the fractions and . These fractions will be represented by the same pizza slices, but this time they will be divided into equal shares (reduced to the same denominator):

The first picture shows a fraction (eight pieces out of twelve), and the second picture shows a fraction (three pieces out of twelve). By cutting three pieces from eight pieces, we get five pieces out of twelve. The fraction describes these five pieces.

Example 2. Find the value of an expression

These fractions have different denominators, so first you need to reduce them to the same (common) denominator.

Let's find the LCM of the denominators of these fractions.

The denominators of the fractions are the numbers 10, 3 and 5. The least common multiple of these numbers is 30

LCM(10, 3, 5) = 30

Now we find additional factors for each fraction. To do this, divide the LCM by the denominator of each fraction.

Let's find an additional factor for the first fraction. LCM is the number 30, and the denominator of the first fraction is the number 10. Divide 30 by 10, we get the first additional factor 3. We write it above the first fraction:

Now we find an additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 30, and the denominator of the second fraction is the number 3. Divide 30 by 3, we get the second additional factor 10. We write it above the second fraction:

Now we find an additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is the number 30, and the denominator of the third fraction is the number 5. Divide 30 by 5, we get the third additional factor 6. We write it above the third fraction:

Now everything is ready for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that had the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.

The continuation of the example will not fit on one line, so we move the continuation to the next line. Don't forget about the equal sign (=) on the new line:

The answer turned out to be a regular fraction, and everything seems to suit us, but it is too cumbersome and ugly. We should make it simpler. What can be done? You can shorten this fraction.

To reduce a fraction, you need to divide its numerator and denominator by (GCD) of the numbers 20 and 30.

So, we find the gcd of numbers 20 and 30:

Now we return to our example and divide the numerator and denominator of the fraction by the found gcd, that is, by 10

We received an answer

Multiplying a fraction by a number

To multiply a fraction by a number, you need to multiply the numerator of the given fraction by that number and leave the denominator the same.

Example 1. Multiply a fraction by the number 1.

Multiply the numerator of the fraction by the number 1

The recording can be understood as taking half 1 time. For example, if you take pizza once, you get pizza

From the laws of multiplication we know that if the multiplicand and the factor are swapped, the product will not change. If the expression is written as , then the product will still be equal to . Again, the rule for multiplying a whole number and a fraction works:

This notation can be understood as taking half of one. For example, if there is 1 whole pizza and we take half of it, then we will have pizza:

Example 2. Find the value of an expression

Multiply the numerator of the fraction by 4

The answer was an improper fraction. Let's highlight the whole part of it:

The expression can be understood as taking two quarters 4 times. For example, if you take 4 pizzas, you will get two whole pizzas

And if we swap the multiplicand and the multiplier, we get the expression . It will also be equal to 2. This expression can be understood as taking two pizzas from four whole pizzas:

Multiplying fractions

To multiply fractions, you need to multiply their numerators and denominators. If the answer turns out to be an improper fraction, you need to highlight the whole part of it.

Example 1. Find the value of the expression.

We received an answer. It is advisable to reduce this fraction. The fraction can be reduced by 2. Then final decision will take the following form:

The expression can be understood as taking a pizza from half a pizza. Let's say we have half a pizza:

How to take two thirds from this half? First you need to divide this half into three equal parts:

And take two from these three pieces:

We'll make pizza. Remember what pizza looks like when divided into three parts:

One piece of this pizza and the two pieces we took will have the same dimensions:

In other words, we are talking about the same size pizza. Therefore the value of the expression is

Example 2. Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer was an improper fraction. Let's highlight the whole part of it:

Example 3. Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer turned out to be a regular fraction, but it would be good if it was shortened. To reduce this fraction, you need to divide the numerator and denominator of this fraction by the greatest common divisor (GCD) of the numbers 105 and 450.

So, let’s find the gcd of numbers 105 and 450:

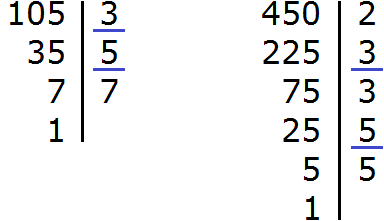
Now we divide the numerator and denominator of our answer by the gcd that we have now found, that is, by 15

Representing a whole number as a fraction

Any whole number can be represented as a fraction. For example, the number 5 can be represented as . This will not change the meaning of five, since the expression means “the number five divided by one,” and this, as we know, is equal to five:

Reciprocal numbers

Now we will get acquainted with very interesting topic in mathematics. It's called "reverse numbers".

Definition. Reverse to numbera is a number that, when multiplied bya gives one.

Let's substitute in this definition instead of the variable a number 5 and try to read the definition:

Reverse to number 5 is a number that, when multiplied by 5 gives one.

Is it possible to find a number that, when multiplied by 5, gives one? It turns out it is possible. Let's imagine five as a fraction:

Then multiply this fraction by itself, just swap the numerator and denominator. In other words, let’s multiply the fraction by itself, only upside down:

What will happen as a result of this? If we continue to solve this example, we get one:

This means that the inverse of the number 5 is the number , since when you multiply 5 by you get one.

The reciprocal of a number can also be found for any other integer.

You can also find the reciprocal of any other fraction. To do this, just turn it over.

Dividing a fraction by a number

Let's say we have half a pizza:

Let's divide it equally between two. How much pizza will each person get?

It can be seen that after dividing half the pizza, two equal pieces were obtained, each of which constitutes a pizza. So everyone gets a pizza.

Division of fractions is done using reciprocals. Reciprocal numbers allow you to replace division with multiplication.

To divide a fraction by a number, you need to multiply the fraction by the inverse of the divisor.

Using this rule, we will write down the division of our half of the pizza into two parts.

So, you need to divide the fraction by the number 2. Here the dividend is the fraction and the divisor is the number 2.

To divide a fraction by the number 2, you need to multiply this fraction by the reciprocal of the divisor 2. The reciprocal of the divisor 2 is the fraction. So you need to multiply by

Now that we have learned how to add and multiply individual fractions, we can look at more complex designs. For example, what if the same problem involves adding, subtracting, and multiplying fractions?

First of all, you need to convert all fractions to improper ones. Then we perform the required actions sequentially - in the same order as for ordinary numbers. Namely:

1. Exponentiation is done first - get rid of all expressions containing exponents;
2. Then - division and multiplication;
3. The last step is addition and subtraction.

Of course, if there are parentheses in the expression, the order of operations changes - everything that is inside the parentheses must be counted first. And remember about improper fractions: you need to highlight the whole part only when all other actions have already been completed.

Let's convert all the fractions from the first expression to improper ones, and then perform the following steps:

Now let's find the value of the second expression. There are no fractions with an integer part, but there are parentheses, so first we perform addition, and only then division. Note that 14 = 7 · 2. Then:

Finally, consider the third example. There are brackets and a degree here - it is better to count them separately. Considering that 9 = 3 3, we have:

Pay attention to the last example. To raise a fraction to a power, you must separately raise the numerator to this power, and separately, the denominator.

You can decide differently. If we recall the definition of a degree, the problem will be reduced to the usual multiplication of fractions:

Multistory fractions

Until now, we have considered only “pure” fractions, when the numerator and denominator are ordinary numbers. This is quite consistent with the definition of a number fraction given in the very first lesson.

But what if you put a more complex object in the numerator or denominator? For example, another numerical fraction? Such constructions arise quite often, especially when working with long expressions. Here are a couple of examples:

There is only one rule for working with multi-story fractions: you must get rid of them immediately. Removing “extra” floors is quite simple, if you remember that the slash means the standard division operation. Therefore, any fraction can be rewritten as follows:

Using this fact and following the procedure, we can easily reduce any multi-story fraction to an ordinary one. Take a look at the examples:

Task. Convert multistory fractions to ordinary ones:

In each case, we rewrite the main fraction, replacing the dividing line with a division sign. Also remember that any integer can be represented as a fraction with a denominator of 1. That is 12 = 12/1; 3 = 3/1. We get:

In the last example, the fractions were canceled before the final multiplication.

Specifics of working with multi-level fractions

There is one subtlety in multi-level fractions that must always be remembered, otherwise you can get the wrong answer, even if all the calculations were correct. Take a look:

1. The numerator contains the single number 7, and the denominator contains the fraction 12/5;
2. The numerator contains the fraction 7/12, and the denominator contains the separate number 5.

So, for one recording we got two completely different interpretations. If you count, the answers will also be different:

To ensure that the record is always read unambiguously, use a simple rule: the dividing line of the main fraction must be longer than the line of the nested fraction. Preferably several times.

If you follow this rule, then the above fractions should be written as follows:

Yes, it's probably unsightly and takes up too much space. But you will count correctly. Finally, a couple of examples where multi-story fractions actually arise:

Task. Find the meanings of the expressions:

So, let's work with the first example. Let's convert all fractions to improper ones, and then perform addition and division operations:

Let's do the same with the second example. Let's convert all fractions to improper ones and perform the required operations. In order not to bore the reader, I will omit some obvious calculations. We have:

Due to the fact that the numerator and denominator of the basic fractions contain sums, the rule for writing multi-story fractions is observed automatically. Also, in the last example, we intentionally left 46/1 in fraction form to perform division.

I will also note that in both examples the fraction bar actually replaces the parentheses: first of all, we found the sum, and only then the quotient.

Some will say that the transition to improper fractions in the second example was clearly redundant. Perhaps this is true. But by doing this we insure ourselves against mistakes, because next time the example may turn out to be much more complicated. Choose for yourself what is more important: speed or reliability.

Fraction- a form of representing a number in mathematics. The fraction bar denotes the division operation. Numerator fraction is called the dividend, and denominator- divider. For example, in a fraction the numerator is 5 and the denominator is 7.

Correct A fraction is called in which the modulus of the numerator is greater than the modulus of the denominator. If a fraction is proper, then the modulus of its value is always less than 1. All other fractions are wrong.

The fraction is called mixed, if it is written as an integer and a fraction. This is the same as the sum of this number and the fraction:

The main property of a fraction

If the numerator and denominator of a fraction are multiplied by the same number, then the value of the fraction will not change, that is, for example,

Reducing fractions to a common denominator

To bring two fractions to a common denominator, you need:

1. Multiply the numerator of the first fraction by the denominator of the second
2. Multiply the numerator of the second fraction by the denominator of the first
3. Replace the denominators of both fractions with their product

Operations with fractions

Addition. To add two fractions you need

1. Add the new numerators of both fractions and leave the denominator unchanged

Example:

Subtraction. To subtract one fraction from another, you need

1. Reduce fractions to a common denominator
2. Subtract the numerator of the second from the numerator of the first fraction, and leave the denominator unchanged

Example:

Multiplication. To multiply one fraction by another, multiply their numerators and denominators:

Division. To divide one fraction by another, multiply the numerator of the first fraction by the denominator of the second, and multiply the denominator of the first fraction by the numerator of the second: