Урок та презентація на тему: "Ступіньні функції. Властивості. Графіки"
Додаткові матеріали
Шановні користувачі, не забувайте залишати свої коментарі, відгуки, побажання! Усі матеріали перевірені антивірусною програмою.
Навчальні посібники та тренажери в інтернет-магазині "Інтеграл" для 11 класу
Інтерактивний посібник для 9–11 класів "Тригонометрія"
Інтерактивний посібник для 10–11 класів "Логарифми"
Ступінні функції, область визначення.
Діти, на минулому уроці ми дізналися, як працювати з числами з раціональним показником ступеня. На цьому уроці ми розглянемо статечні функції та обмежимося нагодою, коли показник ступеня раціональний.Ми розглядатимемо функції виду: $y=x^(\frac(m)(n))$.
Розглянемо спочатку функції, які мають показник ступеня $\frac(m)(n)>1$.
Нехай нам дано конкретну функцію $y=x^2*5$.
Відповідно до визначення, яке ми дали минулого уроці: якщо $x≥0$, тобто область визначення нашої функції - це промінь $(x)$. Давайте схематично зобразимо наш графік функції.

Властивості функції $y=x^(\frac(m)(n))$, $0 2. Не є ні парною, ні непарною.
3. Зростає на $$,
б) $ (2,10) $,
в) на промені $$.
Рішення.
Хлопці, ви пам'ятаєте, як ми знаходили найбільше та найменше значення функції на відрізку в 10 класі?
Правильно, ми використали похідну. Давайте розв'яжемо наш приклад і повторимо алгоритм пошуку найменшого і найбільшого значення.
1. Знайдемо похідну заданої функції:
$y"=\frac(16)(5)*\frac(5)(2)x^(\frac(3)(2))-x^3=8x^(\frac(3)(2)) -x^3=8sqrt(x^3)-x^3$.
2. Похідна існує по всій області визначення вихідної функції, тоді критичних точок немає. Знайдемо стаціонарні точки:
$y"=8\sqrt(x^3)-x^3=0$.
$8*\sqrt(x^3)=x^3$.
$64x^3=x^6$.
$x^6-64x^3=0$.
$ x ^ 3 (x ^ 3-64) = 0 $.
$x_1=0$ і $x_2=\sqrt(64)=4$.
Заданому відрізку належить лише одне рішення $x_2=4$.
Побудуємо таблицю значень нашої функції на кінцях відрізка та у точці екстремуму:
Відповідь: $ y_ (найм.) = -862,65 $ при $ x = 9 $; $ y_ (Наиб.) = 38,4 $ при $ x = 4 $.
приклад. Розв'язати рівняння: $x^(\frac(4)(3))=24-x$.
Рішення. Графік функції $y=x^(\frac(4)(3))$ зростає, а графік функції $у=24-х$ зменшується. Діти, ми з вами знаємо: якщо одна функція зростає, а інша зменшується, то вони перетинаються лише в одній точці, тобто у нас лише одне рішення.
Зауважимо:
$8^(\frac(4)(3))=\sqrt(8^4)=(\sqrt(8))^4=2^4=16$.
$24-8=16$.
Тобто при $х=8$ ми здобули правильну рівність $16=16$, це і є рішення нашого рівняння.
Відповідь: $ х = 8 $.
приклад.
Побудувати графік функції: $ y = (x-3) ^ \ frac (3) (4) + 2 $.
Рішення.
Графік нашої функції виходить із графіка функції $y=x^(\frac(3)(4))$, усуненням його на 3 одиниці вправо і 2 одиниці вгору. 
приклад. Скласти рівняння дотичної до прямої $y=x^(-\frac(4)(5))$ у точці $х=1$.
Рішення. Рівняння дотичної визначається відомою нам формулою:
$y=f(a)+f"(a)(x-a)$.
У нашому випадку $a = 1 $.
$f(a)=f(1)=1^(-\frac(4)(5))=1$.
Знайдемо похідну:
$y"=-\frac(4)(5)x^(-\frac(9)(5))$.
Обчислимо:
$f"(a)=-\frac(4)(5)*1^(-\frac(9)(5))=-\frac(4)(5)$.
Знайдемо рівняння дотичної:
$y=1-\frac(4)(5)(x-1)=-\frac(4)(5)x+1\frac(4)(5)$.
Відповідь: $y=-\frac(4)(5)x+1\frac(4)(5)$.
Завдання для самостійного вирішення
1. Знайти найбільше та найменше значення функції: $y=x^\frac(4)(3)$ на відрізку:а) $$.
б) $ (4,50) $.
в) на промені $$.
3. Розв'язати рівняння: $x^(\frac(1)(4))=18-x$.
4. Побудувати графік функції: $y=(x+1)^(\frac(3)(2))-1$.
5. Скласти рівняння дотичної до прямої $y=x^(-\frac(3)(7))$ у точці $х=1$.
Функція де Х- Змінна величина, A- Задане число, називається Ступіньною функцією .
Якщо це – лінійна функція, її графік – пряма лінія (див. параграф 4.3, рис. 4.7).
Якщо то - квадратична функція, її графік парабола (див. параграф 4.3, рис. 4.8).
Якщо її графік – кубічна парабола (див. параграф 4.3, рис. 4.9).
Це зворотна функція для
1. Область визначення: ![]()
2. Безліч значень:![]()
3. Парність та непарність:функція непарна.
4. Періодичність функції:неперіодична.
5. Нулі функції: X= 0 – єдиний нуль.
6. найбільшого та найменшого значень функція не має.
7.
8. Графік функціїСиметричний графіку кубічної параболи щодо прямої Y =Xта зображений на рис. 5.1.
 |
Ступінна функція
1. Область визначення: ![]()
2. Безліч значень:
3. Парність та непарність:функція парна.
4. Періодичність функції:неперіодична.
5. Нулі функції:єдиний нуль X = 0.
6. Найбільше та найменше значення функції:приймає найменше значення для X= 0, воно дорівнює 0.
7. Проміжки зростання та спадання:функція є спадною на проміжку і зростаючою на проміжку
8. Графік функції(для кожного N Î N) «схожий» на графік квадратичної параболи (графіки функцій зображені на рис. 5.2).

Ступінна функція
1. Область визначення: ![]()
2. Безліч значень: ![]()
3. Парність та непарність:функція непарна.
4. Періодичність функції:неперіодична.
5. Нулі функції: X= 0 – єдиний нуль.
6. Найбільше та найменше значення:
7. Проміжки зростання та спадання:функція є зростаючою по всій області визначення.
8. Графік функції(Для кожного) «схожий» на графік кубічної параболи (графіки функцій зображені на рис. 5.3).
 |
Ступінна функція![]()
1. Область визначення:
2. Безліч значень:
3. Парність та непарність:функція непарна.
4. Періодичність функції:неперіодична.
5. Нулі функції:нулів немає.
6. Найбільше та найменше значення функції:найбільшого та найменшого значень функція не має за будь-якого
7. Проміжки зростання та спадання:функція є спадною в області визначення.
8. Асимптоти:(вісь Оу) - вертикальна асимптота;
(вісь Ох) – горизонтальна асимптота.
9. Графік функції(для будь-якого N) «схожий» на графік гіперболи (графіки функцій зображені на рис. 5.4).
 |
Ступінна функція
1. Область визначення:
2. Безліч значень:
3. Парність та непарність:функція парна.
4. Періодичність функції:неперіодична.
5. Найбільше та найменше значення функції:найбільшого та найменшого значень функція не має за будь-якого
6. Проміжки зростання та спадання:функція є зростаючою на і спадаючою на
7. Асимптоти: X= 0 (вісь Оу) - вертикальна асимптота;
Y= 0 (вісь Ох) – горизонтальна асимптота.
8. Графіками функційЄ квадратичні гіперболи (рис. 5.5).
 |
Ступінна функція
1. Область визначення:
2. Безліч значень:
3. Парність та непарність:функція не має властивості парності та непарності.
4. Періодичність функції:неперіодична.
5. Нулі функції: X= 0 – єдиний нуль.
6. Найбільше та найменше значення функції:найменше значення, що дорівнює 0, функція приймає в точці X= 0; найбільшого значення немає.
7. Проміжки зростання та спадання:функція є зростаючою по всій області визначення.
8. Кожна така функція за певного показника є зворотною для функції за умови
9. Графік функції«схожий» на графік функції за будь-якого Nта зображений на рис. 5.6.

Ступінна функція
1. Область визначення: ![]()
2. Безліч значень:![]()
3. Парність та непарність:функція непарна.
4. Періодичність функції:неперіодична.
5. Нулі функції: X= 0 – єдиний нуль.
6. Найбільше та найменше значення функції:найбільшого та найменшого значень функція не має за будь-якого
7. Проміжки зростання та спадання:функція є зростаючою по всій області визначення.
8. Графік функціїЗображено на рис. 5.7.
 |
Нагадаємо властивості та графіки статечних функцій з цілим негативним показником.
При парних n, :
Приклад функції:
Усі графіки таких функцій проходять через дві фіксовані точки: (1; 1), (-1; 1). Особливість функцій цього виду - їх парність, графіки симетричні щодо осі ОУ.

Мал. 1. Графік функції
При непарних n, :
Приклад функції:
Усі графіки таких функцій проходять через дві фіксовані точки: (1; 1), (-1; -1). Особливість функцій цього виду - їх непарність, графіки симетричні щодо початку координат.

Мал. 2. Графік функції
Нагадаємо основне визначення.
Ступенем невід'ємного числа з раціональним позитивним показником називається число .
Ступенем позитивного числа з раціональним негативним показником називається число .
Для виконується рівність:
![]()
![]()
Наприклад: ![]() ; - Вираз не існує за визначенням ступеня з негативним раціональним показником; існує, тому що показник ступеня цілий,
; - Вираз не існує за визначенням ступеня з негативним раціональним показником; існує, тому що показник ступеня цілий, ![]()
Перейдемо до розгляду статечних функцій із раціональним негативним показником.
![]()
Наприклад:
Для побудови графіка цієї функції можна скласти таблицю. Ми зробимо інакше: спочатку побудуємо та вивчимо графік знаменника – він нам відомий (рисунок 3).

Мал. 3. Графік функції
Графік функції знаменника проходить через фіксовану точку (1; 1). При побудові графіка вихідної функції дана точказалишається, при корінь також прагне нуля, функція прагне нескінченності. І, навпаки, при прагненні х до нескінченності функція прагне нуля (рисунок 4).

Мал. 4. Графік функції
Розглянемо ще одну функцію із сімейства досліджуваних функцій.
![]()
Важливо, що за визначенням
Розглянемо графік функції, що стоїть у знаменнику: , графік цієї функції нам відомий, вона зростає у своїй області визначення і проходить через точку (1;1) (рисунок 5).

Мал. 5. Графік функції
При побудові графіка вихідної функції точка (1;1) залишається, при корінь також прагне нулю, функція прагне нескінченності. І, навпаки, при прагненні х до нескінченності функція прагне нуля (рисунок 6).

Мал. 6. Графік функції
Розглянуті приклади допомагають зрозуміти, яким чином проходить графік і які властивості функції, що вивчається - функції з негативним раціональним показником.
Графіки функцій даного сімейства проходять через точку (1;1), функція зменшується по всій області визначення.
Область визначення функції: ![]()
Функція не обмежена згори, але знизу. Функція не має ні найбільшого, ні найменшого значення.
Функція безперервна, набуває всіх позитивних значень від нуля до плюс нескінченності.
Функція опукла вниз (рисунок 15.7)
На кривій взяті точки А і В, через них проведений відрізок, вся крива знаходиться нижче відрізка, ця умовавиконується для довільних двох точок на кривій, отже функція випукла вниз. Мал. 7.

Мал. 7. Випуклість функції
Важливо зрозуміти, що функції даного сімейства обмежені знизу банкрутом, але найменшого значення немає.
Приклад 1 - знайти максимум і мінімум функції на інтервалі \[(\mathop(lim)_(x\to +\infty) x^(2n)\)=+\infty \]
Графік (рис. 2).

Малюнок 2. Графік функції $f\left(x\right)=x^(2n)$
Властивості статечної функції з натуральним непарним показником
Область визначення - всі дійсні числа.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- функція непарна.
$f(x)$ - безперервна по всій області визначення.
Область значення - всі дійсні числа.
$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Функція зростає по всій області визначення.
$f\left(x\right)0$, при $x\in (0,+\infty)$.
$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$
\ \
Функція увігнута, за $x\in (-\infty ,0)$ і опукла, за $x\in (0,+\infty)$.
Графік (рис. 3).
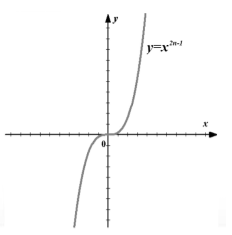
Малюнок 3. Графік функції $f\left(x\right)=x^(2n-1)$
Ступенева функція з цілим показником
Спочатку введемо поняття ступеня з цілим показником.
Визначення 3
Ступінь дійсного числа $a$ з цілим показником $n$ визначається формулою:

Малюнок 4.
Розглянемо тепер статечну функцію з цілим показником, її властивості та графік.
Визначення 4
$f\left(x\right)=x^n$ ($n\in Z)$ називається статечною функцією з цілим показником.
Якщо ступінь більший за нуль, то ми приходимо до випадку статечної функції з натуральним показником. Його ми вже розглянули вище. При $n=0$ ми отримаємо лінійну функцію$ y = 1 $. Її розгляд залишимо читачеві. Залишилося розглянути властивості статечної функції з негативним показником
Властивості статечної функції із негативним цілим показником
Область визначення - $ \ left (- \ infty, 0 \ right) (0, + \ infty) $.
Якщо показник парний, то функція парна, якщо непарна, то функція непарна.
$f(x)$ - безперервна по всій області визначення.
Область значення:
Якщо показник парний, то $(0,+\infty)$, якщо непарний, то $\left(-\infty ,0\right)(0,+\infty)$.
При непарному показнику функція зменшується, за $x\in \left(-\infty ,0\right)(0,+\infty)$. При парному показнику функція зменшується за $x\in (0,+\infty)$. і зростає, за $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ на всій області визначення








