Here you can solve the system for free linear equations Gauss method online large sizes in complex numbers with a very detailed solution. Our calculator can solve online both the usual definite and indefinite systems of linear equations using the Gaussian method, which has an infinite number of solutions. In this case, in the answer you will receive the dependence of some variables through other, free ones. You can also check the system of equations for consistency online using the Gaussian solution.
About the method
When solving a system of linear equations online method Gauss the following steps are performed.
- We write the extended matrix.
- In fact, the solution is divided into forward and backward steps of the Gaussian method. The direct step of the Gaussian method is the reduction of a matrix to a stepwise form. The reverse of the Gaussian method is the reduction of a matrix to a special stepwise form. But in practice, it is more convenient to immediately zero out what is located both above and below the element in question. Our calculator uses exactly this approach.
- It is important to note that when solving using the Gaussian method, the presence in the matrix of at least one zero row with a NOT zero right side(column of free members) indicates the incompatibility of the system. Solution linear system in this case it does not exist.
To best understand how the Gaussian algorithm works online, enter any example, select “very detailed solution” and view its solution online.
Gauss method, also called method sequential elimination unknowns is as follows. Using elementary transformations, a system of linear equations is brought to such a form that its matrix of coefficients turns out to be trapezoidal (the same as triangular or stepped) or close to trapezoidal (direct stroke of the Gaussian method, hereinafter simply straight stroke). An example of such a system and its solution is in the figure above.
In such a system, the last equation contains only one variable and its value can be unambiguously found. The value of this variable is then substituted into the previous equation ( inverse of the Gaussian method , then just the reverse), from which the previous variable is found, and so on.
In a trapezoidal (triangular) system, as we see, the third equation no longer contains variables y And x, and the second equation is the variable x .
After the matrix of the system has taken a trapezoidal shape, it is no longer difficult to understand the issue of compatibility of the system, determine the number of solutions and find the solutions themselves.
Advantages of the method:
- when solving systems of linear equations with more than three equations and unknowns, the Gauss method is not as cumbersome as the Cramer method, since solving with the Gauss method requires fewer calculations;
- Using the Gauss method, you can solve indefinite systems of linear equations, that is, having common decision(and we will look at them in this lesson), but using Cramer’s method, we can only state that the system is uncertain;
- you can solve systems of linear equations in which the number of unknowns is not equal to the number of equations (we will also analyze them in this lesson);
- The method is based on elementary (school) methods - the method of substituting unknowns and the method of adding equations, which we touched on in the corresponding article.
In order for everyone to understand the simplicity with which trapezoidal (triangular, step) systems of linear equations are solved, we present a solution to such a system using reverse motion. Fast decision This system was shown in the picture at the beginning of the lesson.
Example 1. Solve a system of linear equations using inverse:
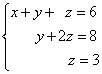
Solution. In this trapezoidal system the variable z can be uniquely found from the third equation. We substitute its value into the second equation and get the value of the variable y:
Now we know the values of two variables - z And y. We substitute them into the first equation and get the value of the variable x:
From the previous steps we write out the solution to the system of equations:
To obtain such a trapezoidal system of linear equations, which we solved very simply, it is necessary to use a forward stroke associated with elementary transformations of the system of linear equations. It's also not very difficult.
Elementary transformations of a system of linear equations
Repeating the school method of algebraically adding the equations of a system, we found out that to one of the equations of the system we can add another equation of the system, and each of the equations can be multiplied by some numbers. As a result, we obtain a system of linear equations equivalent to this one. In it, one equation already contained only one variable, substituting the value of which into other equations, we come to a solution. Such addition is one of the types of elementary transformation of the system. When using the Gaussian method, we can use several types of transformations.
The animation above shows how the system of equations gradually turns into a trapezoidal one. That is, the one that you saw in the very first animation and convinced yourself that it is easy to find the values of all unknowns from it. How to perform such a transformation and, of course, examples will be discussed further.
When solving systems of linear equations with any number of equations and unknowns in the system of equations and in the extended matrix of the system Can:
- rearrange lines (this was mentioned at the very beginning of this article);
- if other transformations result in equal or proportional rows, they can be deleted, except for one;
- remove “zero” rows where all coefficients are equal to zero;
- multiply or divide any string by a certain number;
- to any line add another line, multiplied by a certain number.
As a result of the transformations, we obtain a system of linear equations equivalent to this one.
Algorithm and examples of solving a system of linear equations with a square matrix of the system using the Gauss method
Let us first consider solving systems of linear equations in which the number of unknowns is equal to the number of equations. The matrix of such a system is square, that is, the number of rows in it is equal to the number of columns.
Example 2. Solve a system of linear equations using the Gauss method
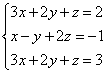
When solving systems of linear equations using school methods, we multiplied one of the equations term by term by a certain number, so that the coefficients of the first variable in the two equations were opposite numbers. When adding equations, this variable is eliminated. The Gauss method works similarly.
To simplify appearance solutions let's create an extended matrix of the system:
In this matrix, the coefficients of the unknowns are located on the left before the vertical line, and the free terms are located on the right after the vertical line.
For the convenience of dividing coefficients for variables (to obtain division by unity) Let's swap the first and second rows of the system matrix. We obtain a system equivalent to this one, since in a system of linear equations the equations can be interchanged:
Using the new first equation eliminate the variable x from the second and all subsequent equations. To do this, to the second row of the matrix we add the first row multiplied by (in our case by ), to the third row - the first row multiplied by (in our case by ).
This is possible because
If our system of equations had more than three, then it would be necessary to add to all subsequent equations the first line, multiplied by the ratio of the corresponding coefficients, taken with a minus sign.
As a result, we obtain a matrix equivalent to this system of a new system of equations, in which all equations, starting from the second do not contain a variable x :
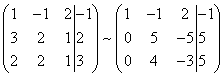
To simplify the second line of the resulting system, multiply it by and again obtain the matrix of a system of equations equivalent to this system:
Now, keeping the first equation of the resulting system unchanged, using the second equation we eliminate the variable y from all subsequent equations. To do this, to the third row of the system matrix we add the second row, multiplied by (in our case by ).
If there were more than three equations in our system, then we would have to add a second line to all subsequent equations, multiplied by the ratio of the corresponding coefficients taken with a minus sign.
As a result, we again obtain the matrix of a system equivalent to this system of linear equations:
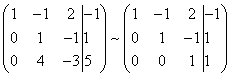
We have obtained an equivalent trapezoidal system of linear equations:
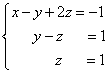
If the number of equations and variables is greater than in our example, then the process of sequentially eliminating variables continues until the system matrix becomes trapezoidal, as in our demo example.
We will find the solution “from the end” - the reverse move. For this from the last equation we determine z:
.
Substituting this value into the previous equation, we'll find y:
From the first equation we'll find x:
Answer: the solution to this system of equations is 
.
: in this case the same answer will be given if the system has a unique solution. If the system has an infinite number of solutions, then this will be the answer, and this is the subject of the fifth part of this lesson.
Solve a system of linear equations using the Gaussian method yourself, and then look at the solution
Here again we have an example of a consistent and definite system of linear equations, in which the number of equations is equal to the number of unknowns. The difference from our demo example from the algorithm is that there are already four equations and four unknowns.
Example 4. Solve a system of linear equations using the Gauss method:
Now you need to use the second equation to eliminate the variable from subsequent equations. Let's carry out preparatory work. To make it more convenient with the ratio of coefficients, you need to get one in the second column of the second row. To do this, subtract the third from the second line, and multiply the resulting second line by -1.
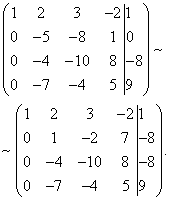
Let us now carry out the actual elimination of the variable from the third and fourth equations. To do this, add the second line, multiplied by , to the third line, and the second, multiplied by , to the fourth line.
Now, using the third equation, we eliminate the variable from the fourth equation. To do this, add the third line to the fourth line, multiplied by . We obtain an extended trapezoidal matrix.
We have obtained a system of equations that is equivalent to this system:
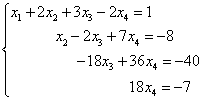
Consequently, the resulting and given systems are compatible and definite. Final decision we find “from the end”. From the fourth equation we can directly express the value of the variable “x-four”:
We substitute this value into the third equation of the system and get
,
,
Finally, value substitution
The first equation gives
,
where do we find “x first”:
Answer: this system of equations has a unique solution 
.
You can also check the solution of the system on a calculator using Cramer's method: in this case, the same answer will be given if the system has a unique solution.
Solving applied problems using the Gauss method using the example of a problem on alloys
Systems of linear equations are used to model real objects in the physical world. Let's solve one of these problems - alloys. Similar problems - problems on mixtures, cost or specific gravity individual products in a product group and the like.
Example 5. Three pieces of alloy have a total mass of 150 kg. The first alloy contains 60% copper, the second - 30%, the third - 10%. Moreover, in the second and third alloys taken together there is 28.4 kg less copper than in the first alloy, and in the third alloy there is 6.2 kg less copper than in the second. Find the mass of each piece of the alloy.
Solution. We compose a system of linear equations:
We multiply the second and third equations by 10, we obtain an equivalent system of linear equations:
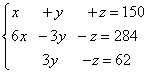
We create an extended matrix of the system:
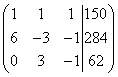
Attention, straight ahead. By adding (in our case, subtracting) one row multiplied by a number (we apply it twice), the following transformations occur with the extended matrix of the system:
The direct move is over. We obtained an expanded trapezoidal matrix.
We apply the reverse move. We find the solution from the end. We see that.
From the second equation we find
From the third equation -
You can also check the solution of the system on a calculator using Cramer's method: in this case, the same answer will be given if the system has a unique solution.
The simplicity of Gauss's method is evidenced by the fact that it took the German mathematician Carl Friedrich Gauss only 15 minutes to invent it. In addition to the method named after him, the saying “We should not confuse what seems incredible and unnatural to us with the absolutely impossible” is known from the works of Gauss - a kind of brief instructions to make discoveries.
In many applied problems there may not be a third constraint, that is, a third equation, then you have to solve a system of two equations with three unknowns using the Gaussian method, or, conversely, there are fewer unknowns than equations. We will now begin to solve such systems of equations.
Using the Gaussian method, you can determine whether any system is compatible or incompatible n linear equations with n variables.
The Gauss method and systems of linear equations with an infinite number of solutions
The next example is a consistent but indeterminate system of linear equations, that is, having an infinite number of solutions.
After performing transformations in the extended matrix of the system (rearranging rows, multiplying and dividing rows by a certain number, adding another to one row), rows of the form could appear
If in all equations having the form
Free terms are equal to zero, this means that the system is indefinite, that is, it has an infinite number of solutions, and equations of this type are “superfluous” and we exclude them from the system.
Example 6.
Solution. Let's create an extended matrix of the system. Then, using the first equation, we eliminate the variable from subsequent equations. To do this, add to the second, third and fourth lines the first, multiplied by :
Now let's add the second line to the third and fourth.
As a result, we arrive at the system
The last two equations turned into equations of the form. These equations are satisfied for any value of the unknowns and can be discarded.
To satisfy the second equation, we can choose arbitrary values for and , then the value for will be determined uniquely: 
. From the first equation the value for is also found uniquely: 
.
Both the given and the last systems are consistent, but uncertain, and the formulas
for arbitrary and give us all solutions of a given system.
Gauss method and systems of linear equations without solutions
The next example is an inconsistent system of linear equations, that is, one that has no solutions. The answer to such problems is formulated this way: the system has no solutions.
As already mentioned in connection with the first example, after performing transformations, rows of the form could appear in the extended matrix of the system
corresponding to an equation of the form
If among them there is at least one equation with a nonzero free term (i.e. ), then this system of equations is inconsistent, that is, it has no solutions and its solution is complete.
Example 7. Solve the system of linear equations using the Gauss method:
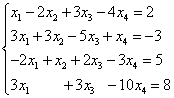
Solution. We compose an extended matrix of the system. Using the first equation, we exclude the variable from subsequent equations. To do this, add the first line multiplied by to the second line, the first line multiplied by the third line, and the first line multiplied by the fourth line.
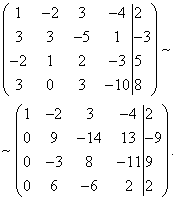
Now you need to use the second equation to eliminate the variable from subsequent equations. To obtain integer ratios of coefficients, we swap the second and third rows of the extended matrix of the system.
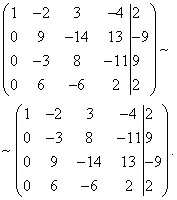
To exclude the third and fourth equations, add the second one multiplied by , to the third line, and the second multiplied by , to the fourth line.
Now, using the third equation, we eliminate the variable from the fourth equation. To do this, add the third line to the fourth line, multiplied by .
The given system is therefore equivalent to the following:
The resulting system is inconsistent, since its last equation cannot be satisfied by any values of the unknowns. Therefore, this system has no solutions.
Gauss method perfect for solving systems of linear algebraic equations (SLAEs). It has a number of advantages compared to other methods:
- firstly, there is no need to first examine the system of equations for consistency;
- secondly, the Gauss method can solve not only SLAEs in which the number of equations coincides with the number of unknown variables and the main matrix of the system is non-singular, but also systems of equations in which the number of equations does not coincide with the number of unknown variables or the determinant of the main matrix is equal to zero;
- thirdly, the Gaussian method leads to results with a relatively small number of computational operations.
Brief overview of the article.
First, we give the necessary definitions and introduce notations.
Next, we will describe the algorithm of the Gauss method for the simplest case, that is, for systems of linear algebraic equations, the number of equations in which coincides with the number of unknown variables and the determinant of the main matrix of the system is not equal to zero. When solving such systems of equations, the essence of the Gauss method is most clearly visible, which is the sequential elimination of unknown variables. Therefore, the Gaussian method is also called the method of sequential elimination of unknowns. We will show detailed solutions of several examples.
In conclusion, we will consider the solution by the Gauss method of systems of linear algebraic equations, the main matrix of which is either rectangular or singular. The solution to such systems has some features, which we will examine in detail using examples.
Page navigation.
Basic definitions and notations.
Consider a system of p linear equations with n unknowns (p can be equal to n):
Where are unknown variables, are numbers (real or complex), and are free terms.
If 
, then the system of linear algebraic equations is called homogeneous, otherwise - heterogeneous.
The set of values of unknown variables for which all equations of the system become identities is called decision of the SLAU.
If there is at least one solution to a system of linear algebraic equations, then it is called joint, otherwise - non-joint.
If a SLAE has a unique solution, then it is called certain. If there is more than one solution, then the system is called uncertain.
They say that the system is written in coordinate form, if it has the form
.
This system in matrix form records has the form , where 
- the main matrix of the SLAE, - the matrix of the column of unknown variables, - the matrix of free terms.
If we add a matrix-column of free terms to matrix A as the (n+1)th column, we get the so-called extended matrix systems of linear equations. Typically, an extended matrix is denoted by the letter T, and the column of free terms is separated by a vertical line from the remaining columns, that is, 
The square matrix A is called degenerate, if its determinant is zero. If , then matrix A is called non-degenerate.
The following point should be noted.
If we perform with a system of linear algebraic equations the following actions
- swap two equations,
- multiply both sides of any equation by an arbitrary and non-zero real (or complex) number k,
- to both sides of any equation add the corresponding parts of another equation, multiplied by an arbitrary number k,
then you get an equivalent system that has the same solutions (or, just like the original one, has no solutions).
For an extended matrix of a system of linear algebraic equations, these actions will mean carrying out elementary transformations with the rows:
- swapping two lines,
- multiplying all elements of any row of matrix T by a nonzero number k,
- adding to the elements of any row of a matrix the corresponding elements of another row, multiplied by an arbitrary number k.
Now we can proceed to the description of the Gauss method.
Solving systems of linear algebraic equations, in which the number of equations is equal to the number of unknowns and the main matrix of the system is non-singular, using the Gauss method.
What would we do at school if we were given the task of finding a solution to a system of equations? 
.
Some would do that.
Note that adding to the left side of the second equation left side first, and to the right side - the right one, you can get rid of the unknown variables x 2 and x 3 and immediately find x 1: 
We substitute the found value x 1 =1 into the first and third equations of the system: 
If we multiply both sides of the third equation of the system by -1 and add them to the corresponding parts of the first equation, we get rid of the unknown variable x 3 and can find x 2: 
We substitute the resulting value x 2 = 2 into the third equation and find the remaining unknown variable x 3: 
Others would have done differently.
Let us resolve the first equation of the system with respect to the unknown variable x 1 and substitute the resulting expression into the second and third equations of the system in order to exclude this variable from them: 
Now let’s solve the second equation of the system for x 2 and substitute the resulting result into the third equation to eliminate the unknown variable x 2 from it: 
From the third equation of the system it is clear that x 3 =3. From the second equation we find 
, and from the first equation we get .
Familiar solutions, right?
The most interesting thing here is that the second solution method is essentially the method of sequential elimination of unknowns, that is, the Gaussian method. When we expressed the unknown variables (first x 1, at the next stage x 2) and substituted them into the remaining equations of the system, we thereby excluded them. We carried out elimination until there was only one unknown variable left in the last equation. The process of sequentially eliminating unknowns is called direct Gaussian method. After finishing forward stroke we now have the opportunity to calculate the unknown variable in the last equation. With its help, we find the next unknown variable from the penultimate equation, and so on. The process of sequentially finding unknown variables while moving from the last equation to the first is called inverse of the Gaussian method.
It should be noted that when we express x 1 in terms of x 2 and x 3 in the first equation, and then substitute the resulting expression into the second and third equations, the following actions lead to the same result:
Indeed, such a procedure also makes it possible to eliminate the unknown variable x 1 from the second and third equations of the system: 
Nuances with the elimination of unknown variables using the Gaussian method arise when the equations of the system do not contain some variables.
For example, in SLAU 
in the first equation there is no unknown variable x 1 (in other words, the coefficient in front of it is zero). Therefore, we cannot solve the first equation of the system for x 1 in order to eliminate this unknown variable from the remaining equations. The way out of this situation is to swap the equations of the system. Since we are considering systems of linear equations whose determinants of the main matrices are different from zero, there is always an equation in which the variable we need is present, and we can rearrange this equation to the position we need. For our example, it is enough to swap the first and second equations of the system 
, then you can resolve the first equation for x 1 and exclude it from the remaining equations of the system (although x 1 is no longer present in the second equation).
We hope you get the gist.
Let's describe Gaussian method algorithm.
Suppose we need to solve a system of n linear algebraic equations with n unknowns variables of the form 
, and let the determinant of its main matrix be different from zero.
We will assume that , since we can always achieve this by rearranging the equations of the system. Let's eliminate the unknown variable x 1 from all equations of the system, starting with the second. To do this, to the second equation of the system we add the first, multiplied by , to the third equation we add the first, multiplied by , and so on, to the nth equation we add the first, multiplied by . The system of equations after such transformations will take the form 
where and 
.
We would have arrived at the same result if we had expressed x 1 in terms of other unknown variables in the first equation of the system and substituted the resulting expression into all other equations. Thus, the variable x 1 is excluded from all equations, starting from the second.
Next, we proceed in a similar way, but only with part of the resulting system, which is marked in the figure 
To do this, to the third equation of the system we add the second, multiplied by , to the fourth equation we add the second, multiplied by , and so on, to the nth equation we add the second, multiplied by . The system of equations after such transformations will take the form 
where and 
. Thus, the variable x 2 is excluded from all equations, starting from the third.
Next, we proceed to eliminating the unknown x 3, while we act similarly with the part of the system marked in the figure 
So we continue the direct progression of the Gaussian method until the system takes the form 
From this moment we begin the reverse of the Gaussian method: we calculate x n from the last equation as , using the obtained value of x n we find x n-1 from the penultimate equation, and so on, we find x 1 from the first equation.
Let's look at the algorithm using an example.
Example.
Gauss method.
Solution.
The coefficient a 11 is different from zero, so let’s proceed to the direct progression of the Gaussian method, that is, to the exclusion of the unknown variable x 1 from all equations of the system except the first. To do this, to the left and right sides of the second, third and fourth equations, add the left and right sides of the first equation, multiplied by , respectively. 
And : 
The unknown variable x 1 has been eliminated, let's move on to eliminating x 2 . To the left and right sides of the third and fourth equations of the system we add the left and right sides of the second equation, multiplied by respectively 
And 
:
To complete the forward progression of the Gaussian method, we need to eliminate the unknown variable x 3 from the last equation of the system. Let us add to the left and right sides of the fourth equation, respectively, the left and right sides of the third equation, multiplied by 
:
You can begin the reverse of the Gaussian method.
From the last equation we have 
,
from the third equation we get,
from the second,
from the first one.
To check, you can substitute the obtained values of the unknown variables into the original system of equations. All equations turn into identities, which indicates that the solution using the Gauss method was found correctly.
Answer:
Now let’s give a solution to the same example using the Gaussian method in matrix notation.
Example.
Find the solution to the system of equations Gauss method.
Solution.
The extended matrix of the system has the form 
. At the top of each column are the unknown variables that correspond to the elements of the matrix.
The direct approach of the Gaussian method here involves reducing the extended matrix of the system to a trapezoidal form using elementary transformations. This process is similar to the elimination of unknown variables that we did with the system in coordinate form. Now you will see this.
Let's transform the matrix so that all elements in the first column, starting from the second, become zero. To do this, to the elements of the second, third and fourth lines we add the corresponding elements of the first line multiplied by , and accordingly: 
Next, we transform the resulting matrix so that in the second column all elements, starting from the third, become zero. This would correspond to eliminating the unknown variable x 2 . To do this, to the elements of the third and fourth rows we add the corresponding elements of the first row of the matrix, multiplied by respectively And :
It remains to exclude the unknown variable x 3 from the last equation of the system. To do this, to the elements of the last row of the resulting matrix we add the corresponding elements of the penultimate row, multiplied by :
It should be noted that this matrix corresponds to a system of linear equations 
which was obtained earlier after a forward move.
It's time to turn back. In matrix notation, the inverse of the Gaussian method involves transforming the resulting matrix such that the matrix marked in the figure 
became diagonal, that is, took the form 
where are some numbers.
These transformations are similar to the forward transformations of the Gaussian method, but are performed not from the first line to the last, but from the last to the first.
Add to the elements of the third, second and first lines the corresponding elements of the last line, multiplied by 
, on and on 
respectively: 
Now add to the elements of the second and first lines the corresponding elements of the third line, multiplied by and by, respectively: 
At the last step of the reverse Gaussian method, to the elements of the first row we add the corresponding elements of the second row, multiplied by: 
The resulting matrix corresponds to the system of equations 
, from where we find the unknown variables.
Answer:
NOTE.
When using the Gauss method to solve systems of linear algebraic equations, approximate calculations should be avoided, as this can lead to completely incorrect results. We recommend not rounding decimals. Better from decimals go to ordinary fractions.
Example.
Solve a system of three equations using the Gauss method 
.
Solution.
Note that in this example the unknown variables have a different designation (not x 1, x 2, x 3, but x, y, z). Let's move on to ordinary fractions: 
Let us exclude the unknown x from the second and third equations of the system: 
In the resulting system, the unknown variable y is absent in the second equation, but y is present in the third equation, therefore, let’s swap the second and third equations: 
This completes the direct progression of the Gauss method (there is no need to exclude y from the third equation, since this unknown variable no longer exists).
Let's start the reverse move.
From the last equation we find 
,
from the penultimate 
from the first equation we have 
Answer:
X = 10, y = 5, z = -20.
Solving systems of linear algebraic equations in which the number of equations does not coincide with the number of unknowns or the main matrix of the system is singular, using the Gauss method.
Systems of equations, the main matrix of which is rectangular or square singular, may have no solutions, may have a single solution, or may have an infinite number of solutions.
Now we will understand how the Gauss method allows us to establish the compatibility or inconsistency of a system of linear equations, and in the case of its compatibility, determine all solutions (or one single solution).
In principle, the process of eliminating unknown variables in the case of such SLAEs remains the same. However, it is worth going into detail about some situations that may arise.
Let's move on to the most important stage.
So, let us assume that the system of linear algebraic equations, after completing the forward progression of the Gauss method, takes the form 
and not a single equation was reduced to (in this case we would conclude that the system is incompatible). A logical question arises: “What to do next”?
Let us write down the unknown variables that come first in all equations of the resulting system: 
In our example these are x 1, x 4 and x 5. On the left sides of the equations of the system we leave only those terms that contain the written unknown variables x 1, x 4 and x 5, the remaining terms are transferred to the right side of the equations with the opposite sign: 
Let's give the unknown variables that are on the right sides of the equations arbitrary values, where 
- arbitrary numbers: 
After this, the right-hand sides of all equations of our SLAE contain numbers and we can proceed to the reverse of the Gaussian method.
From the last equation of the system we have, from the penultimate equation we find, from the first equation we get 
The solution to a system of equations is a set of values of unknown variables 
Giving Numbers different values, we will obtain different solutions to the system of equations. That is, our system of equations has infinitely many solutions.
Answer:
Where - arbitrary numbers.
To consolidate the material, we will analyze in detail the solutions of several more examples.
Example.
Decide homogeneous system linear algebraic equations 
Gauss method.
Solution.
Let us exclude the unknown variable x from the second and third equations of the system. To do this, to the left and right sides of the second equation, we add, respectively, the left and right sides of the first equation, multiplied by , and to the left and right sides of the third equation, we add the left and right sides of the first equation, multiplied by: 
Now let’s exclude y from the third equation of the resulting system of equations: 
The resulting SLAE is equivalent to the system 
.
We leave on the left side of the system equations only the terms containing the unknown variables x and y, and move the terms with the unknown variable z to the right side: 
Two systems of linear equations are called equivalent if the set of all their solutions coincides.
Elementary transformations of a system of equations are:
- Deleting trivial equations from the system, i.e. those for which all coefficients are equal to zero;
- Multiplying any equation by a number other than zero;
- Adding to any i-th equation any j-th equation multiplied by any number.
A variable x i is called free if this variable is not allowed, but the entire system of equations is allowed.
Theorem. Elementary transformations transform a system of equations into an equivalent one.
The meaning of the Gaussian method is to transform the original system of equations and obtain an equivalent resolved or equivalent inconsistent system.
So, the Gaussian method consists of the following steps:
- Let's look at the first equation. Let's choose the first non-zero coefficient and divide the entire equation by it. We obtain an equation in which some variable x i enters with a coefficient of 1;
- Let's subtract this equation from all the others, multiplying it by such numbers that the coefficients of the variable x i in the remaining equations are zeroed. We obtain a system resolved with respect to the variable x i and equivalent to the original one;
- If trivial equations arise (rarely, but it happens; for example, 0 = 0), we cross them out of the system. As a result, there are one fewer equations;
- We repeat the previous steps no more than n times, where n is the number of equations in the system. Each time we select a new variable for “processing”. If inconsistent equations arise (for example, 0 = 8), the system is inconsistent.
As a result, after a few steps we will obtain either a resolved system (possibly with free variables) or an inconsistent one. Allowed systems fall into two cases:
- The number of variables is equal to the number of equations. This means that the system is defined;
- Number of variables more number equations. We collect all the free variables on the right - we get formulas for the allowed variables. These formulas are written in the answer.
That's all! System of linear equations solved! This is a fairly simple algorithm, and to master it you do not have to contact a higher mathematics tutor. Let's look at an example:
Task. Solve the system of equations:
Description of steps:
- Subtract the first equation from the second and third - we get the allowed variable x 1;
- We multiply the second equation by (−1), and divide the third equation by (−3) - we get two equations in which the variable x 2 enters with a coefficient of 1;
- We add the second equation to the first, and subtract from the third. We get the allowed variable x 2 ;
- Finally, we subtract the third equation from the first - we get the allowed variable x 3;
- We have received an approved system, write down the response.
The general solution to a simultaneous system of linear equations is new system, equivalent to the original one, in which all allowed variables are expressed in terms of free ones.
When might a general solution be needed? If you have to do fewer steps than k (k is how many equations there are). However, the reasons why the process ends at some step l< k , может быть две:
- After the lth step, we obtained a system that does not contain an equation with number (l + 1). In fact, this is good, because... the authorized system is still obtained - even a few steps earlier.
- After the lth step, we obtained an equation in which all coefficients of the variables are equal to zero, and the free coefficient is different from zero. This is a contradictory equation, and, therefore, the system is inconsistent.
It is important to understand that the emergence of an inconsistent equation using the Gaussian method is a sufficient basis for inconsistency. At the same time, we note that as a result of the lth step, no trivial equations can remain - all of them are crossed out right in the process.
Description of steps:
- Subtract the first equation, multiplied by 4, from the second. We also add the first equation to the third - we get the allowed variable x 1;
- Subtract the third equation, multiplied by 2, from the second - we get the contradictory equation 0 = −5.
So, the system is inconsistent because an inconsistent equation has been discovered.
Task. Explore compatibility and find a general solution to the system:
Description of steps:
- We subtract the first equation from the second (after multiplying by two) and the third - we get the allowed variable x 1;
- Subtract the second equation from the third. Since all the coefficients in these equations are the same, the third equation will become trivial. At the same time, multiply the second equation by (−1);
- Subtract the second from the first equation - we get the allowed variable x 2. The entire system of equations is now also resolved;
- Since the variables x 3 and x 4 are free, we move them to the right to express the allowed variables. This is the answer.
So, the system is consistent and indeterminate, since there are two allowed variables (x 1 and x 2) and two free ones (x 3 and x 4).
