Encontrar derivada de una función trigonométrica necesitará usar tabla de derivados, a saber, las derivadas 6-13.
cuando encuentres derivadas primas funciones trigonométricas Para evitar errores comunes, debes prestar atención a los siguientes puntos:
- en una expresión de función, uno de los términos suele ser seno, coseno u otra función trigonométrica no del argumento de la función, sino del número (constante), por lo tanto la derivada de este término es igual a cero;
- casi siempre es necesario simplificar la expresión obtenida como resultado de la derivación, y para ello es necesario utilizar con confianza el conocimiento de operaciones con fracciones;
- Para simplificar una expresión, casi siempre es necesario conocer las identidades trigonométricas, por ejemplo, la fórmula doble angulo y la fórmula de la unidad como la suma de los cuadrados del seno y el coseno.
Ejemplo 1. Encuentra la derivada de una función.
Solución. digamos con derivada del coseno Todo está claro, dirán muchos de los que empiezan a estudiar derivados. Qué pasa derivada del seno doce dividido por pi? Respuesta: ¡considéralo igual a cero! Aquí el seno (¡después de todo, una función!) es una trampa, porque el argumento no es la variable X ni ninguna otra variable, sino simplemente un número. Es decir, el seno de este número también es un número. Y la derivada de un número (constante), como sabemos por la tabla de derivadas, es igual a cero. Entonces, dejamos solo el seno negativo de X y encontramos su derivada, sin olvidarnos del signo:
![]() .
.
Ejemplo 2. Encuentra la derivada de una función.
![]() .
.
Solución. El segundo término es el mismo caso que el primer término en el ejemplo anterior. Es decir, es un número y la derivada del número es cero. Encontramos la derivada del segundo término como derivada del cociente:
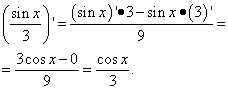
Ejemplo 3. Encuentra la derivada de una función.
Solución. Este es otro problema: aquí en el primer término no hay arcoseno ni ninguna otra función trigonométrica, pero sí hay x, lo que significa que es una función de x. Por tanto, lo diferenciamos como un término en la suma de funciones:

Aquí se requirieron habilidades en operaciones con fracciones, es decir, en la eliminación de la estructura de tres pisos de una fracción.
Ejemplo 4. Encuentra la derivada de una función.
![]() .
.
Solución. Aquí la letra "phi" juega el mismo papel que "x" en los casos anteriores (y en la mayoría de los demás, pero no en todos): la variable independiente. Por tanto, cuando buscamos la derivada de un producto de funciones, no nos apresuraremos a declarar la derivada de la raíz de “phi” igual a cero. Entonces:
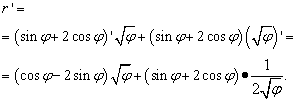
Pero la solución no termina ahí. Dado que los términos similares se recogen entre dos corchetes, todavía debemos transformar (simplificar) la expresión. Por lo tanto, multiplicamos los paréntesis por los factores detrás de ellos, luego llevamos los términos a un denominador común y realizamos otras transformaciones elementales:

Ejemplo 5. Encuentra la derivada de una función.
Solución. En este ejemplo, necesitaremos saber qué existe tal función trigonométrica, la secante, y sus fórmulas hasta el coseno. Diferenciamos:

Ejemplo 6. Encuentra la derivada de una función.
![]() .
.
Solución. En este ejemplo, se nos pedirá que recordemos la fórmula del doble ángulo de la escuela. Pero primero diferenciemos:

![]() ,
,
(esta es la fórmula del doble ángulo)
Se presentan las derivadas de funciones trigonométricas inversas y la derivación de sus fórmulas. También se dan expresiones para derivadas de orden superior. Enlaces a páginas con una descripción más detallada de la derivación de fórmulas.
Primero, derivamos la fórmula para la derivada del arcoseno. Dejar
y = arcosen x.
Dado que el arcoseno es la función inversa del seno, entonces
.
Aquí y es una función de x. Derivar con respecto a la variable x:
.
Aplicamos:
.
Entonces encontramos:
.
Porque entonces . Entonces
.
Y la fórmula anterior toma la forma:
. De aquí
.
Exactamente de esta manera puedes obtener la fórmula para la derivada del arco coseno. Sin embargo, es más fácil utilizar una fórmula que relacione funciones trigonométricas inversas:
.
Entonces
.
Se presenta una descripción más detallada en la página “Derivación de las derivadas de arcoseno y arcocoseno”. ahí se da derivación de derivadas de dos maneras- discutido anteriormente y según la fórmula para la derivada de la función inversa.
Derivación de derivadas de arcotangente y arcocotangente.
De la misma forma encontraremos las derivadas de arcotangente y arcocotangente.
Dejar
y = arctán x.
Arctangente es la función inversa de la tangente:
.
Derivar con respecto a la variable x:
.
Aplicamos la fórmula para la derivada de una función compleja:
.
Entonces encontramos:
.
Derivada del arco cotangente:
.
Derivados arcoseno
Dejar
.
Ya hemos encontrado la derivada de primer orden del arcoseno:
.
Al derivar, encontramos la derivada de segundo orden:
;
.
También se puede escribir de la siguiente forma:
.
De aquí obtenemos ecuación diferencial, que se satisface con las derivadas arcoseno de primer y segundo orden:
.
Al diferenciar esta ecuación, podemos encontrar derivadas de orden superior.
Derivada de arcoseno de enésimo orden
La derivada del arcoseno de enésimo orden tiene la siguiente forma:
,
donde es un polinomio de grado. Está determinado por las fórmulas:
;
.
Aquí .
El polinomio satisface la ecuación diferencial:
.
Derivada de arcocoseno de enésimo orden
Las derivadas del arco coseno se obtienen a partir de las derivadas del arco seno utilizando la fórmula trigonométrica:
.
Por tanto, las derivadas de estas funciones difieren sólo en el signo:
.
Derivadas de arcotangente
Dejar . Encontramos la derivada del arco cotangente de primer orden:
.
Dividamos la fracción en su forma más simple:
.
Aquí está la unidad imaginaria, .
Diferenciamos una vez y llevamos la fracción a un denominador común:
.
Sustituyendo obtenemos:
.
Derivada de arcotangente de enésimo orden
Así, la derivada del arcotangente de enésimo orden se puede representar de varias formas:
;
.
Derivadas del arco cotangente
Déjalo ser ahora. Apliquemos la fórmula que conecta funciones trigonométricas inversas:
.
Entonces, la derivada de enésimo orden del arco tangente difiere solo en signo de la derivada del arco tangente:
.
Sustituyendo , encontramos:
.
Referencias:
NUEVO MÉJICO. Gunter, R.O. Kuzmin, Colección de problemas de matemáticas superiores, “Lan”, 2003.
Al derivar la primera fórmula de la tabla, partiremos de la definición de la función derivada en un punto. vamos a donde X– cualquier número real, es decir, X– cualquier número del dominio de definición de la función. Anotemos el límite de la relación entre el incremento de la función y el incremento del argumento en: ![]()
Cabe señalar que bajo el signo de límite se obtiene la expresión, que no es la incertidumbre del cero dividida por cero, ya que el numerador no contiene un valor infinitesimal, sino precisamente cero. En otras palabras, el incremento de una función constante es siempre cero.
De este modo, derivada de una función constantees igual a cero en todo el dominio de definición.
Derivada de una función de potencia.
Fórmula derivada función de potencia parece ![]() , donde el exponente pag– cualquier número real.
, donde el exponente pag– cualquier número real.
Primero demostremos la fórmula del exponente natural, es decir, de pag = 1, 2, 3,…
Usaremos la definición de derivada. Anotemos el límite de la relación entre el incremento de una función de potencia y el incremento del argumento: 
Para simplificar la expresión en el numerador, recurrimos a la fórmula binomial de Newton: 
Por eso, 
Esto prueba la fórmula para la derivada de una función potencia para un exponente natural.
Derivada de una función exponencial.
Presentamos la derivación de la fórmula derivada basada en la definición:
Hemos llegado a la incertidumbre. Para expandirlo, introducimos una nueva variable y en . Entonces . En la última transición, utilizamos la fórmula para pasar a una nueva base logarítmica.
Sustituyamos en el límite original: 
Si recordamos el segundo límite notable, llegamos a la fórmula para la derivada de la función exponencial: 
Derivada de una función logarítmica.
Demostremos la fórmula para la derivada de una función logarítmica para todos X del dominio de definición y todos los valores válidos de la base a logaritmo Por definición de derivada tenemos: 
Como habrás notado, durante la demostración las transformaciones se realizaron utilizando las propiedades del logaritmo. Igualdad  es cierto debido al segundo límite notable.
es cierto debido al segundo límite notable.
Derivadas de funciones trigonométricas.
Para derivar fórmulas para derivadas de funciones trigonométricas, tendremos que recordar algunas fórmulas trigonométricas, así como el primer límite destacable.
Por definición de la derivada de la función seno tenemos ![]() .
.
Usemos la fórmula de diferencia de senos: 
Queda por abordar el primer límite destacable: 
Por tanto, la derivada de la función pecado x Hay porque x.
La fórmula de la derivada del coseno se demuestra exactamente de la misma manera. 
Por tanto, la derivada de la función porque x Hay –pecado x.
Deduciremos fórmulas para la tabla de derivadas de tangente y cotangente utilizando reglas de diferenciación probadas (derivada de una fracción). 
Derivadas de funciones hiperbólicas.
Las reglas de diferenciación y la fórmula para la derivada de la función exponencial de la tabla de derivadas nos permiten derivar fórmulas para las derivadas del seno, coseno, tangente y cotangente hiperbólicos. 
Derivada de la función inversa.
Para evitar confusiones durante la presentación, denotamos en subíndice el argumento de la función mediante el cual se realiza la diferenciación, es decir, es la derivada de la función. f(x) Por X.
Ahora formulemos Regla para encontrar la derivada de una función inversa.
Deja que las funciones y = f(x) Y x = g(y) mutuamente inversos, definidos en los intervalos y respectivamente. Si en un punto existe una derivada finita distinta de cero de la función f(x), entonces en el punto hay una derivada finita de la función inversa g(y), y ![]() . en otra publicación
. en otra publicación ![]() .
.
Esta regla puede reformularse para cualquier X del intervalo, entonces obtenemos  .
.
Comprobemos la validez de estas fórmulas.
Encontremos la función inversa del logaritmo natural. ![]() (Aquí y es una función y X- argumento). Habiendo resuelto esta ecuación para X, obtenemos (aquí X es una función y y– su argumento). Eso es,
(Aquí y es una función y X- argumento). Habiendo resuelto esta ecuación para X, obtenemos (aquí X es una función y y– su argumento). Eso es, ![]() y funciones mutuamente inversas.
y funciones mutuamente inversas.
De la tabla de derivadas vemos que ![]() Y
Y ![]() .
.
Asegurémonos de que las fórmulas para encontrar las derivadas de la función inversa nos lleven a los mismos resultados: 
Desde el curso de geometría y matemáticas, los escolares están acostumbrados a que el concepto de derivada se les transmite a través del área de una figura, diferenciales, límites de funciones, así como límites. Intentemos ver el concepto de derivada desde un ángulo diferente y determinemos cómo se pueden vincular las funciones derivada y trigonométrica.
Entonces, consideremos una curva arbitraria descrita por la función abstracta y = f(x).
Imaginemos que el horario es un mapa de una ruta turística. El incremento ∆x (delta x) en la figura es una cierta distancia del camino, y ∆y es el cambio en la altura del camino sobre el nivel del mar.
Entonces resulta que la relación ∆x/∆y caracterizará la complejidad de la ruta en cada segmento de la ruta. Habiendo aprendido este valor, puedes decir con confianza si el ascenso/descenso es empinado, si necesitarás equipo de escalada y si los turistas necesitan un cierto entrenamiento físico. Pero este indicador será válido sólo para un pequeño intervalo ∆x.
Si el organizador del viaje toma los valores de los puntos de inicio y fin del sendero, es decir, ∆x es igual a la longitud del recorrido, entonces no podrá obtener datos objetivos sobre el grado de dificultad. del viaje. Por lo tanto, es necesario construir otra gráfica que caracterice la velocidad y “calidad” de los cambios de ruta, es decir, determinar la relación ∆x/∆y para cada “metro” de ruta.
Este gráfico será una derivada visual para una ruta específica y describirá objetivamente sus cambios en cada intervalo de interés. Es muy sencillo verificar esto; el valor ∆x/∆y no es más que un diferencial tomado para un valor específico de x e y. Apliquemos la diferenciación no a coordenadas específicas, sino a la función en su conjunto:

Funciones derivadas y trigonométricas
Las funciones trigonométricas están indisolublemente ligadas a las derivadas. Esto se puede entender en el siguiente dibujo. La figura del eje de coordenadas muestra la función Y = f (x): la curva azul.
K (x0; f (x0)) es un punto arbitrario, x0 + ∆x es el incremento a lo largo del eje OX y f (x0 + ∆x) es el incremento a lo largo del eje OY en un cierto punto L.

Dibujemos una línea recta que pase por los puntos K y L y construyamos triángulo rectángulo KLN. Si mueve mentalmente el segmento LN a lo largo del gráfico Y = f (x), entonces los puntos L y N tenderán a los valores K (x0; f (x0)). Llamemos a este punto el comienzo condicional de la gráfica: el límite; si la función es infinita, al menos en uno de los intervalos, esta tendencia también será infinita y su valor límite será cercano a 0.
La naturaleza de esta tendencia se puede describir mediante una tangente al punto seleccionado y = kx + b o mediante una gráfica de la derivada de la función original dy, la línea recta verde.
¿Pero dónde está la trigonometría aquí? Todo es muy simple, considera el triángulo rectángulo KLN. El valor diferencial para un punto específico K es la tangente del ángulo α o ∠K:

De esta forma, podemos describir el significado geométrico de la derivada y su relación con las funciones trigonométricas.
Fórmulas derivadas para funciones trigonométricas.
Se deben memorizar las transformaciones de seno, coseno, tangente y cotangente a la hora de determinar la derivada.

Las dos últimas fórmulas no son un error, la cuestión es que existe una diferencia entre definir la derivada de un argumento simple y una función en la misma capacidad.
Veamos una tabla comparativa con fórmulas para las derivadas de seno, coseno, tangente y cotangente:

También se han derivado fórmulas para las derivadas de arcoseno, arcocoseno, arcotangente y arcocotangente, aunque se utilizan muy raramente:

Vale la pena señalar que las fórmulas anteriores claramente no son suficientes para resolver con éxito tareas USE típicas, lo que se demostrará al resolver un ejemplo específico de cómo encontrar la derivada de una expresión trigonométrica.
Ejercicio: Es necesario encontrar la derivada de la función y encontrar su valor para π/4:

Solución: Para encontrar y’ es necesario recordar las fórmulas básicas para convertir la función original en una derivada, es decir.
Sujeto:"Derivada de funciones trigonométricas".
tipo de lección– una lección de consolidación de conocimientos.
Formulario de lección– lección integrada.
Lugar de la lección en el sistema de lecciones de esta sección- lección general.
Los objetivos se establecen de forma integral:
- educativo: conocer las reglas de diferenciación, poder aplicar las reglas para calcular derivadas al resolver ecuaciones y desigualdades; mejorar la materia, incluidas las habilidades y destrezas computacionales; Habilidades computacionales;
- desarrollando: desarrollo de habilidades intelectuales y lógicas e intereses cognitivos;
- educativo: cultivar la adaptabilidad a condiciones modernas capacitación.
Métodos:
- reproductiva y productiva;
- práctico y verbal;
- Trabajo independiente;
- aprendizaje programado, T.S.O.;
- combinación de frontal, grupo y trabajo individual;
- aprendizaje diferenciado;
- deductivo inductivo.
Formas de control:
- encuesta oral,
- control programado,
- Trabajo independiente,
- tareas individuales en la computadora,
- revisión por pares utilizando la tarjeta de diagnóstico del estudiante.
DURANTE LAS CLASES
I. Momento organizacional
II. Actualización de conocimientos de referencia.
a) Comunicar metas y objetivos:
- conocer las reglas de diferenciación, poder aplicar las reglas para calcular derivadas al resolver problemas, ecuaciones y desigualdades;
- mejorar la materia, incluidas las habilidades y destrezas computacionales; Habilidades computacionales;
- desarrollar habilidades intelectuales y lógicas e intereses cognitivos;
- cultivar la adaptabilidad a las condiciones modernas de aprendizaje.
b) Repetición de material educativo
Reglas para calcular derivadas (repetición de fórmulas en una computadora con sonido). doc.7.
- ¿Cuál es la derivada del seno?
- ¿Cuál es la derivada del coseno?
- ¿Cuál es la derivada de la tangente?
- ¿Cuál es la derivada de la cotangente?
III. trabajo oral
Encuentra la derivada. |
|||
Opción 1. |
Opcion 2. |
||
en = 2X + 5. |
en = 2X – 5. |
||
en= 4cos X. |
en= 3pecado X. |
||
en= tg X+ctg X. |
en= tg X-ctg X. |
||
en= pecado 3 X. |
en= porque 4 X. |
||
Opciones de respuesta. |
|||
– 4pecado X |
– 3cos X |
||
1/cos 2 X+ 1/pecado 2 X |
1/cos 2 X–1/pecado 2 X |
1/pecado 2 X–1/cos 2 X |
|
– 4sin4 X |
– 3cos3 X |
||
Intercambio de cuadernos. En las tarjetas de diagnóstico, marque las tareas completadas correctamente con un signo + y las tareas completadas incorrectamente con un signo –.
IV. Resolver ecuaciones usando derivada
– ¿Cómo encontrar los puntos en los que la derivada es cero?
Encontrar los puntos en los que la derivada esta función es igual a cero, necesitas:
– determinar la naturaleza de la función,
– encontrar área definiciones de funciones,
– encontrar la derivada de esta función,
- resuelve la ecuación F "(X) = 0,
– elige la respuesta correcta.
Tarea 1.
Dado: en
= X-pecado X.
Encontrar: puntos en los que la derivada es cero.
Solución. La función está definida y diferenciable en el conjunto de todos los números reales, ya que las funciones están definidas y diferenciables en el conjunto de todos los números reales gramo(X) = X Y t(X) = – pecado X.
Usando las reglas de diferenciación, obtenemos F
"(X) = (X-pecado X)" = (X)" - (pecado X)" = 1 – porque X.
Si F "(X) = 0, entonces 1 – cos X = 0.
porque X= 1/; eliminemos la irracionalidad en el denominador, obtenemos cos X
= /2.
Según la fórmula t= ± arcocos a+ 2n, n Z, obtenemos: X= ± arccos /2 + 2n, nZ.
Respuesta: x = ± /4 + 2n, nZ.
V. Resolver ecuaciones usando un algoritmo.
Encuentre en qué puntos la derivada desaparece.
F(X) = pecado X+porque X |
F(X) = pecado 2 X – X |
F(X) = 2X+cos(4 X – ) |
El estudiante puede elegir cualquiera de los tres ejemplos. El primer ejemplo está calificado como " 3 ", segundo - " 4 ", tercero - " 5 " Solución en cuadernos seguida de comprobación mutua. Un estudiante decide en la pizarra. Si la solución resulta ser incorrecta, entonces el estudiante debe volver al algoritmo e intentar resolverlo nuevamente.
Control programado.
Opción 1 |
opcion 2 |
|||
y = 2X 3 |
y = 3X 2 |
|||
y = 1/4 X 4 + 2X 2 – 7 |
y = 1/2 X 4 + 4X + 5 |
|||
y = X 3 + 4X 2
– 3X. |
y = 2X 3 – 9X 2
+ 12X + 7. |
|||
y= pecado 2 X– porque 3 X. |
y= porque 2 X– pecado 3 X. |
|||
y= tg X–ctg( X + /4). |
y=ctg X+tg( X – /4). |
|||
y= pecado 2 X. |
y= porque 2 X. |
|||
Opciones de respuesta. |
||||
|
| ||||