Resolver problemas en 8. I

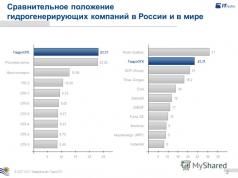
Objetivos:

• Educativo: repetir las fórmulas básicas y reglas de diferenciación, el significado geométrico de la derivada; formar la habilidad aplicación compleja conocimientos, destrezas, habilidades y su transferencia a nuevas condiciones; evaluar los conocimientos, habilidades y habilidades de los estudiantes sobre este tema en preparación para el Examen Estatal Unificado.
• De desarrollo: promover el desarrollo de operaciones mentales: análisis, síntesis, generalización; formación de habilidades de autoestima.
• Educativo: promover el deseo de mejora continua del conocimiento

Equipo:

• Proyector multimedia.

Tipo de lección: sistematización y generalizaciones.
Alcance del conocimiento: dos lecciones (90 min.)
Resultado Esperado: Los profesores utilizan los conocimientos adquiridos en aplicaciones prácticas, al tiempo que desarrollan habilidades comunicativas, creativas y de búsqueda, y la capacidad de analizar la tarea recibida.

Estructura de la lección:

1. Org. Momento, actualización de los conocimientos necesarios para la solución. tareas practicas de los materiales del Examen Estatal Unificado.
2. Parte práctica (probar los conocimientos de los estudiantes).
3. Reflexión, tarea creativa.

Avance de la consulta

I. Momento organizativo.

Mensaje del tema de la lección, objetivos de la lección, motivación. actividades educacionales(mediante la creación de una base de conocimientos teóricos problemáticos).

II. Actualización de la experiencia subjetiva de los estudiantes y sus conocimientos.

Revise las reglas y definiciones.

1) si en un punto la función es continua y en él la derivada cambia de signo de más a menos, entonces es un punto máximo;

2) si en un punto la función es continua y en él la derivada cambia de signo de menos a más, entonces es un punto mínimo.

• Puntos críticos – estos son puntos internos del dominio de definición de una función en los que la derivada no existe o es igual a cero.
• Una señal suficiente de aumento, descendiendo funciones .
• Si f "(x)>0 para todo x del intervalo (a; b), entonces la función aumenta en el intervalo (a; b).
• Si f "(x)<0 для всех х из промежутка (а; в), то функция убывает на промежутке (а; в).

• Algoritmo para encontrar el mayor y los valores más pequeños de una función en el segmento [a;b], si se da una gráfica de la derivada de la función:

Si la derivada de un segmento es positiva, entonces a es el valor más pequeño y b es el valor más grande.

Si la derivada de un segmento es negativa, entonces a es el valor más grande y b es el valor más pequeño.

Significado geométrico la derivada es la siguiente. Si es posible trazar una tangente a la gráfica de la función y = f(x) en el punto con la abscisa x0 que no es paralela al eje y, entonces f "(x0) expresa la pendiente de la tangente: κ = f "(x0). Dado que κ = tanα, la igualdad f "(x0) = tanα es verdadera

Consideremos tres casos:

1. La tangente trazada a la gráfica de la función formaba un ángulo agudo con el eje OX, es decir α< 90º. Производная положительная.
2. La tangente formaba un ángulo obtuso con el eje OX, es decir α > 90º. La derivada es negativa.
3. La tangente es paralela al eje OX. La derivada es cero.

Ejercicio 1. La figura muestra un gráfico. funciones y = f(x) y la tangente a esta gráfica dibujada en el punto con abscisa -1. Encuentre el valor de la derivada de la función f(x) en el punto x0 = -1

Solución: a) La tangente trazada a la gráfica de la función forma un ángulo obtuso con el eje OX. Usando la fórmula de reducción encontramos la tangente de este ángulo tg(180º - α) = - tanα. Esto significa f "(x) = - tanα. Por lo que estudiamos anteriormente, sabemos que la tangente es igual a la relación entre el lado opuesto y el lado adyacente.

Para ello, construimos un triángulo rectángulo de modo que los vértices del triángulo queden en los vértices de las celdas. Contamos las celdas del lado opuesto y del adyacente. Divida el lado opuesto por el lado adyacente (Diapositiva 44).

b) La tangente trazada a la gráfica de la función forma un ángulo agudo con el eje OX.

f "(x)= tgα. La respuesta será positiva. (Diapositiva 30)

Ejercicio 2. La figura muestra un gráfico. derivado función f(x), definida en el intervalo (-4; 13). Encuentra los intervalos en los que la función disminuye. En tu respuesta indica la longitud del mayor de ellos.

Solución: f "(x)< 0 функция убывает. Находим длину,который имеет наибольший участок.(Слайд 34)

Parte práctica.
35 min. Las diapositivas preparadas requieren conocimientos teóricos sobre el tema de la lección. El propósito de las diapositivas es permitir a los estudiantes mejorar y aplicar de manera práctica sus conocimientos.
Usando diapositivas puedes:
- encuesta frontal (se tienen en cuenta las características individuales de los estudiantes);
- se aclara la formulación informativa de los principales conceptos, propiedades y definiciones;
- algoritmo para la resolución de problemas. Los estudiantes deben responder las diapositivas.

IV. Trabajo individual. Resolver problemas mediante diapositivas.

V. Resumiendo la lección, reflexión.

Solución. Los puntos máximos corresponden a los puntos donde el signo de la derivada cambia de más a menos. En el segmento, la función tiene dos puntos máximos x = 4 y x = 4. Respuesta: 2. La figura muestra una gráfica de la derivada de la función f(x), definida en el intervalo (10; 8). Encuentra el número de puntos máximos de la función f(x) en el segmento.

Solución. La figura muestra una gráfica de la función y=f(x), definida en el intervalo (1; 12). Determina el número de puntos enteros en los que la derivada de la función es negativa. La derivada de la función es negativa en aquellos intervalos en los que la función disminuye, es decir, en los intervalos (0,5; 3), (6; 10) y (11; 12). Contienen puntos enteros 1, 2, 7, 8 y 9. Hay 5 puntos en total. Respuesta: 5.

La figura muestra una gráfica de la derivada de la función f(x), definida en el intervalo (10; 4). Encuentra los intervalos de disminución de la función f(x). En tu respuesta indica la longitud del mayor de ellos. Solución. Los intervalos decrecientes de la función f(x) corresponden a los intervalos en los que la derivada de la función es negativa, es decir, el intervalo (9; 6) de longitud 3 y el intervalo (2; 3) de longitud 5. La longitud del mayor de ellos es 5. Respuesta: 5.

La figura muestra una gráfica de la derivada de la función f(x), definida en el intervalo (7; 14). Encuentra el número de puntos máximos de la función f(x) en el segmento. Solución. Los puntos máximos corresponden a los puntos donde el signo de la derivada cambia de positivo a negativo. En el segmento la función tiene un punto máximo x = 7. Respuesta: 1.

La figura muestra una gráfica de la derivada de la función f(x), definida en el intervalo (8; 6). Encuentra los intervalos de aumento de la función f(x). En tu respuesta indica la longitud del mayor de ellos. Solución. Los intervalos de aumento de la función f(x) corresponden a los intervalos en los que la derivada de la función es positiva, es decir, los intervalos (7; 5), (2; 5). El mayor de ellos es el intervalo (2; 5), cuya longitud es 3.

La figura muestra una gráfica de la derivada de la función f(x), definida en el intervalo (7; 10). Encuentra el número de puntos mínimos de la función f(x) en el segmento. Solución. Los puntos mínimos corresponden a los puntos donde el signo de la derivada cambia de menos a más. En el segmento la función tiene un punto mínimo x = 4. Respuesta: 1.

La figura muestra una gráfica de la derivada de la función f(x), definida en el intervalo (16; 4). Encuentra el número de puntos extremos de la función f(x) en el segmento. Solución. Los puntos extremos corresponden a los puntos donde cambia el signo de la derivada y los ceros de la derivada que se muestran en el gráfico. La derivada desaparece en los puntos 13, 11, 9, 7. La función tiene 4 puntos extremos en el segmento. Respuesta: 4.

La figura muestra una gráfica de la función y=f(x), definida en el intervalo (2; 12). Encuentra la suma de los puntos extremos de la función f(x). Solución. La función dada tiene máximos en los puntos 1, 4, 9, 11 y mínimos en los puntos 2, 7, 10. Por lo tanto, la suma de los puntos extremos es = 44. Respuesta: 44.

La figura muestra una gráfica de la función y=f(x) y una tangente a ella en el punto con la abscisa x 0. Encuentra el valor de la derivada de la función f(x) en el punto x 0. Solución. El valor de la derivada en el punto de tangencia es igual a la pendiente de la tangente, que a su vez es igual a la tangente del ángulo de inclinación de esta tangente al eje de abscisas. Construyamos un triángulo con vértices en los puntos A (2; 2), B (2; 0), C (6; 0). El ángulo de inclinación de la tangente al eje x será igual al ángulo adyacente al ángulo ACB.

La figura muestra una gráfica de la función y = f(x) y una tangente a esta gráfica en el punto de abscisa igual a 3. Encuentra el valor de la derivada de esta función en el punto x = 3. Para resolver, usamos la significado geométrico de la derivada: el valor de la derivada de la función en el punto es igual a la pendiente de la tangente a la gráfica de esta función trazada en este punto. El ángulo tangente es igual a la tangente del ángulo entre la tangente y la dirección positiva del eje x (tg α). Ángulo α = β, como ángulos transversales con rectas paralelas y=0, y=1 y una secante-tangente. Para el triángulo ABC

La figura muestra la gráfica de la función y=f(x) y su tangente en el punto con la abscisa x 0. Encuentra el valor de la derivada de la función f(x) en el punto x 0. Basado en la propiedades de la tangente, la fórmula para la tangente a la función f(x) en el punto x 0 es igual a y=f (x 0) x+b, b=const La figura muestra que la tangente a la función f( x) en el punto x 0 pasa por los puntos (-3;2), (5,4). Por lo tanto, podemos crear un sistema de ecuaciones.

Fuentes

Clases individuales vía SKYPE sobre una formación online eficaz para el Examen Estatal Unificado de Matemáticas.

Los problemas del tipo B8 son problemas sobre la aplicación de funciones derivadas. Objetivos en tareas:

• encontrar la derivada en un punto determinado
• determinar los extremos de la función, puntos máximos y mínimos.
• intervalos de aumento y decrecimiento

Veamos algunos ejemplos. Tarea v8.1: la figura muestra la gráfica de la función y=f (x) y su tangente en el punto con la abscisa x0. Encuentra el valor de la derivada de la función y=f (x) en el punto x0.

Un poco de teoría. Si la tangente es creciente, entonces la derivada será positiva, y si la tangente es decreciente, entonces la derivada será negativa. Derivada de la función y’= tgА, donde A es el ángulo de inclinación de la tangente al eje X

Solución: en nuestro ejemplo, la tangente es creciente, lo que significa que la derivada será positiva. Considere el triángulo rectángulo ABC y encuentre a partir de él tan A = BC/AB, donde BC es la distancia entre los puntos característicos a lo largo del eje y, AB es la distancia entre los puntos a lo largo del eje x. Los puntos característicos del gráfico están resaltados con puntos en negrita y designados con las letras A y C. Los puntos característicos deben ser claros y completos. Del gráfico se desprende claramente que AB = 5+3 = 8, y sol = 3-1 = 2,

tgα= BC/AB=2/8=1/4=0,25, de ahí la derivada y’=0,25

Respuesta: 0,25

Tarea B8.2 La figura muestra una gráfica de la función y=f(x), definida en el intervalo (-9;4). Encuentra la suma de las abscisas de los puntos extremos de las funciones f(x)

Solución: Primero, definamos ¿qué son los puntos extremos? Estos son los puntos en los que la derivada cambia de signo al contrario, es decir, todas las “colinas” y “valles”. En nuestro ejemplo, tenemos 4 "deslizamientos" y 4 "depresiones". Movamos todos los puntos del "paisaje" al eje X y encontramos el valor de la abscisa, ahora sumamos el valor completo de estos puntos a lo largo del eje X.

obtenemos -8-7-5-3-2+0+1+3=-21

Respuesta: -21

mira un video tutorial sobre cómo resolver esta tarea

Resolver tareas B8 usando materiales. banco abierto Problemas del Examen Estatal Unificado de Matemáticas 2012 La recta y = 4x + 11 es paralela a la tangente a la gráfica de la función y = x2 + 8x + 6. Encuentra la abscisa del punto de tangencia No. 1 Solución: Si la recta es paralela a la tangente a la gráfica de la función en algún punto (llamémosla xo), entonces su pendiente (en nuestro caso k = 4 de la ecuación y = 4x +11) es igual al valor de la derivada de la función en el punto xo: k = f ′(xo) = 4Derivada de la función f′(x) = (x2+8x + 6) ′= 2x +8. Esto significa que para encontrar el punto de tangencia deseado es necesario que 2xo + 8 = 4, de donde xo = – 2. Respuesta: – 2. La recta y = 3x + 11 es tangente a la gráfica

funciones y = x3−3x2− 6x + 6.

Encuentra la abscisa del punto tangente.

Solución No. 2: Tenga en cuenta que si la recta es tangente a la gráfica, entonces su pendiente (k = 3) debe ser igual a la derivada de la función en el punto de tangencia, de donde tenemos Zx2 − 6x − 6 = 3 , es decir, Zx2 − 6x − 9 = 0 o x2 − 2x − 3 = 0. Esta ecuación cuadrática tiene dos raíces: −1 y 3. Por tanto, hay dos puntos en los que la tangente a la gráfica de la función y = x3 − 3x2 − 6x + 6 tiene una pendiente igual a 3. Para determinar cuál de estos dos puntos la recta y = 3x + 11 toca la gráfica de la función, calculamos los valores de la función en estos puntos y comprobar si satisfacen la ecuación tangente. El valor de la función en el punto −1 es y(−1) = −1 − 3 + 6 + 6 = 8, y el valor en el punto 3 es y(3) = 27 − 27 − 18 + 6 = −12. Tenga en cuenta que el punto con coordenadas (−1; 8) satisface la ecuación tangente, ya que 8 = −3 + 11. Pero el punto (3; −12) no satisface la ecuación tangente, ya que −12 ≠ 9 + 11. Esto significa que la abscisa requerida del punto de tangencia es −1. Respuesta: −1. La figura muestra una gráfica de y = f ′(x), la derivada de la función f(x), definida en el intervalo (–10; 8). ¿En qué punto del segmento [–8; –4] la función f(x) toma el valor más pequeño No. 3 Solución: Tenga en cuenta que en el segmento [–8; –4] la derivada de la función es negativa, lo que significa que la función en sí es decreciente, lo que significa que toma el valor más pequeño en este segmento en el extremo derecho del segmento, es decir, en el punto –4.у = f ′(x) f(x) –Respuesta: –4 .La figura muestra una gráfica de y = f ′(x) – la derivada de la función f(x), definida en el intervalo (–8; 8). Encuentre el número de puntos extremos de la función f(x) pertenecientes al segmento [– 6; 6].No.4Solución: En el punto extremo, la derivada de la función es igual a 0 o no existe. Se puede ver que existen puntos que pertenecen al segmento [–6; 6] tres. En este caso, en cada punto la derivada cambia de signo de “+” a “–”, o de “–” a “+”.у = f ′(x) ++––Respuesta: 3. La figura muestra la gráfica de у = f ′(x) – derivada de la función f(x), definida en el intervalo (–8; 10). Encuentre el punto extremo de la función f(x) en el intervalo (– 4; 8) No. 5. Solución: Tenga en cuenta que en el intervalo (–4; 8) la derivada en el punto xo = 4 se vuelve 0 y al pasar por este punto la derivada de signo cambia de “-” a “+”, el punto 4 es el punto extremo deseado de la función en un intervalo dado. y = f ′(x) +–Respuesta: 4. La figura muestra una gráfica de y = f ′(x) – la derivada de la función f(x), definida en el intervalo (–8; 8). Encuentra el número de puntos en los que la tangente a la gráfica de la función f(x) es paralela a la recta y = –2x + 2 o coincide con ella No. 6 Solución: Si la tangente a la gráfica de la función f (x) es paralela a la recta y = –2x+ 2 o coincide con ella, entonces su pendiente k = –2, lo que significa que necesitamos encontrar el número de puntos en los que la derivada de la función f ′(x) = – 2. Para hacer esto, dibuje una línea y = –2 en la gráfica derivada y cuente el número de puntos en la gráfica derivada que se encuentran en esta línea. Hay 4 de estos puntos: y = f ′(x) y = –2Respuesta: 4. La figura muestra una gráfica de la función y = f(x), definida en el intervalo (–6; 5). Determine el número de puntos enteros en los cuales la derivada de la función es negativa No. 7y Solución: Tenga en cuenta que la derivada de una función es negativa si la función f(x) en sí es decreciente, lo que significa que es necesario encontrar el número de puntos enteros incluidos en los intervalos de la función decreciente. Hay 6 de estos puntos: x = −4, x = −3, x = −2, x = −1, x = 0, x = 3.y = f(x ) x–6–45–1–20–33Respuesta: 6. La figura muestra la gráfica de la función y = f(x), definida en el intervalo (–6; 6). Encuentra el número de puntos en los que la tangente a la gráfica de la función es paralela a la recta y = –5. No. 8ySolución: La recta y = −5 es horizontal, lo que significa que si la tangente a la gráfica de la función es paralela a ella, entonces también es horizontal. En consecuencia, la pendiente en los puntos requeridos k = f′(x)= 0. En nuestro caso, estos son puntos extremos. Hay 6 de estos puntos, él en el punto de abscisa xo. Encuentra el valor de la derivada de la función f(x) en el punto xo. No. 9 Solución: El valor de la derivada de la función f′(хo) = tanα = k al coeficiente equiangular de la tangente trazada a la gráfica de esta función en un punto dado. En nuestro caso, k > 0, ya que α es un ángulo agudo (tgα > 0), para encontrar el coeficiente angular elegimos dos puntos A y B situados en la tangente, cuyas abscisas y ordenadas son números enteros. Ahora determinemos el módulo del coeficiente angular. Para ello construiremos el triángulo ABC. tgα =ВС: AC = 5: 4 = 1,25 у = f(x) Вα5хоαС4АRespuesta: 1,25 La figura muestra una gráfica de la función у = f(x), definida en el intervalo (–10; 2) y la tangente a en el punto con abscisa xo Encuentra el valor de la derivada de la función f(x) en el punto xo. No. 10Solución: El valor de la derivada de la función f′(хo) = tanα = k al coeficiente equiangular de la tangente trazada a la gráfica de esta función en un punto dado. En nuestro caso k< 0, так как α– тупой угол (tgα < 0).Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа. Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC. tg(180°−α) = ВС: АС = 6: 8 = 0,75 tgα = − tg (180°−α) = −0,75Ву = f(x) α6хо180°− αСА8Ответ: −0,75.На рисунке изображен график производной у = f ′(x) –функции f(x), определенной на интервале (–11; 11). Найдите количество точек максимума функции f(x) на отрезке [−10; 10]. №11.Решение: В точке экстремума производная функции равна 0 либо не существует. Видно, что таких точек принадлежащих отрезку [−10; 10] пять. В точках х2и х4 производная меняет знак с «+» на «−» – это точки максимума.уу = f ′(x) +++–100–––х10f(x) х3х5х2х4х1maxmaxОтвет: 2.Прямая у = 4х – 4является касательной к графику функции ах2+ 34х + 11. Найдите а.№12Решение:Производная функции в точке касания должна совпадать с угловым коэффициентом прямой. Откуда, если за хo принять абсциссу точки касания, имеем: 2ахo+ 34 = 4. То есть ахo =–15. Найдем значение исходной функции в точке касания:ахo2 + 34хo + 11 = –15xo+ 34хo + 11 = 19хo + 11.Так как прямая у = 4х – 4– касательная, имеем: 19хo + 11 =4хo–4, откуда хo = –1. А значитa = 15. Ответ: 15.Прямая у = –4х – 5 является касательной к графику функции 9х2+bх + 20. Найдите b,учитывая, что абсцисса точки касания больше 0.№13Решение. Если хо– абсцисса точки касания, то 18xo+ b = –4, откуда b = –4 –18хо. Аналогично задаче№12 найдем хо:9xo2+ (–4 –18хо)xo+20 = – 4хo – 5, 9xo2–4xo –18хо2+20 + 4хo + 5 = 0,–9xo2+25 = 0,хо2 = 25/9. Откуда xo = 5/3или xo = –5/3. Условию задачи соответствует только положительный корень, значит xo = 5/3, следовательно b = –4 –18∙ 5/3, имеем b = –34. Ответ: –34.Прямая у = 2х – 6является касательной к графику функции х2+ 12х + с. Найдите с.№14Решение. Аналогично предыдущим задачам обозначим абсциссу точки касания хо и приравняем значение производной функции в точке хо угловому коэффициенту касательной. 2хо + 12 = 2, откуда xo= –5. Значение исходной функции в точке –5 равно: 25 – 60 + с = с – 35, значит с – 35 = 2∙(–5) – 6, откуда с = 19. Ответ: 19.Материальная точка движется прямолинейно по закону x(t) = 0,5t2 – 2t – 6, где x – расстояние от точки отсчета в метрах, t– время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6с.№15Решение. Так как мгновенная скорость точки в момент времени to, movimiento rectilíneo realizada según la ley x = x(t), es igual al valor de la derivada de la función xnput = to, la velocidad deseada será x ′(t) = 0,5 ∙ 2t – 2 = t – 2.x ′ (6) = 6 – 2 = 4 m/s Respuesta: 4. Un punto material se mueve rectilíneamente según la ley x(t) = 0.5t2 – 2t – 22, donde x es la distancia desde el punto de referencia en metros, t es el tiempo en segundos, medido desde el inicio del movimiento. ¿En qué momento (en segundos) su velocidad fue igual a 4 m/s? Solución No. 16. Dado que la velocidad instantánea de un punto en el tiempo a, movimiento rectilíneo realizado según la ley x = x(t), es igual al valor de la derivada de la función xnput = a, la velocidad deseada será x ′(a) = 0.5 ∙ 2a – 2 = a – 2, Porque por condición, x ′(to) = 4, luego to – 2 = 4, de donde to = 4 + 2 = 6 m/s Respuesta: 6. La figura muestra una gráfica de la función y = f(x), definida en el intervalo (– 8; 6).Encuentra la suma de los puntos extremos de la función f(x).No.17Solución: Los puntos extremos son puntos mínimo y máximo. Se puede ver que hay cinco puntos que pertenecen al intervalo (–8; 6). Encontremos la suma de sus abscisas: -6 + (-4) + (-2) + 2 + 4 = 6.у = f ′(x) Respuesta: 6. La figura muestra una gráfica de la derivada y = f ′ (x) – función f (x), definida en el intervalo (–10; 8). Encuentre los intervalos de la función creciente f(x). En tu respuesta, indica la suma de puntos enteros incluidos en estos intervalos. Solución: Tenga en cuenta que la función f(x) aumenta si la derivada de la función es positiva; lo que significa que es necesario encontrar la suma de los puntos enteros incluidos en los intervalos de la función creciente. Hay 7 puntos: x = −3, x = −2, x = 3, x = 4, x = 5, x = 6, x = 7. Su suma: −3+(−2)+3+4+5+6+7 = 20у = f ′(x) ++3-357Respuesta: 20. Materiales utilizados

Examen del Estado Unificado 2012. Matemáticas. Problema B8. Significado geométrico de derivada. Libro de trabajo/ Ed. ALABAMA. Semenov e I.V. Yáshchenko. 3ª edición. estereotipo. − M.: MTsNMO, 2012. − 88 p.

http://mathege.ru/or/ege/Main− Materiales del banco abierto de tareas de matemáticas 2012