ઇજેનવેલ્યુ અને ઇજેનવેક્ટર. મેટ્રિક્સના ઇજેનવેલ્યુ અને ઇજેનવેક્ટર

સજાતીય રેખીય સમીકરણોની સિસ્ટમ

સજાતીય સિસ્ટમ રેખીય સમીકરણોફોર્મની સિસ્ટમ કહેવાય છે

તે સ્પષ્ટ છે કે આ કિસ્સામાં , કારણ કે આ નિર્ધારકોમાંના એક કૉલમના તમામ ઘટકો શૂન્ય સમાન છે.

કારણ કે અજ્ઞાત સૂત્રો મુજબ મળી આવે છે , પછી કિસ્સામાં જ્યારે Δ ≠ 0, સિસ્ટમ પાસે અનન્ય શૂન્ય ઉકેલ છે x = y = z= 0. જો કે, ઘણી સમસ્યાઓમાં રસપ્રદ પ્રશ્ન એ છે કે શું સજાતીય સિસ્ટમશૂન્ય સિવાયના ઉકેલો.

પ્રમેય.રેખીય સિસ્ટમ માટે ક્રમમાં સજાતીય સમીકરણોબિન-શૂન્ય ઉકેલ હતો, તે જરૂરી અને પૂરતું છે કે Δ ≠ 0.

તેથી, જો નિર્ણાયક Δ ≠ 0 હોય, તો સિસ્ટમ પાસે અનન્ય ઉકેલ છે. જો Δ ≠ 0 હોય, તો રેખીય સજાતીય સમીકરણોની સિસ્ટમમાં અસંખ્ય ઉકેલો હોય છે.

ઉદાહરણો.

મેટ્રિક્સના ઇજેનવેક્ટર અને ઇજેનવેલ્યુ

એક ચોરસ મેટ્રિક્સ આપવા દો , એક્સ- કેટલાક મેટ્રિક્સ-કૉલમ, જેની ઊંચાઈ મેટ્રિક્સના ક્રમ સાથે સુસંગત છે એ. .

ઘણી સમસ્યાઓમાં આપણે માટેના સમીકરણને ધ્યાનમાં લેવું પડશે એક્સ

જ્યાં λ એ ચોક્કસ સંખ્યા છે. તે સ્પષ્ટ છે કે કોઈપણ λ માટે આ સમીકરણ શૂન્ય ઉકેલ ધરાવે છે.

સંખ્યા λ જેના માટે આ સમીકરણ બિન-શૂન્ય ઉકેલો ધરાવે છે તેને કહેવામાં આવે છે eigenvalueમેટ્રિસિસ એ, એ એક્સઆવા માટે λ કહેવાય છે eigenvectorમેટ્રિસિસ એ.

ચાલો મેટ્રિક્સનું ઇજેનવેક્ટર શોધીએ એ. કારણ કે ઇ∙X = X, પછી મેટ્રિક્સ સમીકરણ તરીકે ફરીથી લખી શકાય છે અથવા . વિસ્તૃત સ્વરૂપમાં, આ સમીકરણ રેખીય સમીકરણોની સિસ્ટમ તરીકે ફરીથી લખી શકાય છે. ખરેખર .

અને તેથી

તેથી, અમે કોઓર્ડિનેટ્સ નક્કી કરવા માટે સજાતીય રેખીય સમીકરણોની સિસ્ટમ મેળવી છે. x 1, x 2, x 3વેક્ટર એક્સ. સિસ્ટમમાં બિન-શૂન્ય ઉકેલો હોય તે માટે તે જરૂરી અને પૂરતું છે કે સિસ્ટમનો નિર્ણાયક શૂન્ય સમાન હોય, એટલે કે.

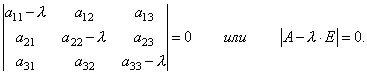
આ λ માટે 3જી ડિગ્રીનું સમીકરણ છે. તે કહેવાય છે લાક્ષણિક સમીકરણમેટ્રિસિસ એઅને λ ના ઇજનવેલ્યુ નક્કી કરવા માટે સેવા આપે છે.

દરેક eigenvalue λ એ eigenvector ને અનુલક્ષે છે એક્સ, જેના કોઓર્ડિનેટ્સ સિસ્ટમમાંથી λ ના અનુરૂપ મૂલ્ય પર નક્કી કરવામાં આવે છે.

ઉદાહરણો.

વેક્ટર બીજગણિત. વેક્ટરનો ખ્યાલ

ભૌતિકશાસ્ત્રની વિવિધ શાખાઓનો અભ્યાસ કરતી વખતે, એવા જથ્થાઓ છે જે તેમના આંકડાકીય મૂલ્યોને સ્પષ્ટ કરીને સંપૂર્ણપણે નક્કી કરવામાં આવે છે, ઉદાહરણ તરીકે, લંબાઈ, ક્ષેત્રફળ, સમૂહ, તાપમાન વગેરે. આવા જથ્થાઓને સ્કેલર કહેવામાં આવે છે. જો કે, તેમના ઉપરાંત, ત્યાં પણ માત્રા છે, જે નક્કી કરવા માટે, સંખ્યાત્મક મૂલ્ય ઉપરાંત, અવકાશમાં તેમની દિશા જાણવી પણ જરૂરી છે, ઉદાહરણ તરીકે, શરીર પર કાર્ય કરતું બળ, ગતિ અને પ્રવેગક. શરીર જ્યારે અવકાશમાં ફરે છે, તણાવ ચુંબકીય ક્ષેત્રઅવકાશમાં આપેલ બિંદુ પર, વગેરે. આવા જથ્થાઓને વેક્ટર જથ્થા કહેવામાં આવે છે.

ચાલો કડક વ્યાખ્યા રજૂ કરીએ.

નિર્દેશિત સેગમેન્ટચાલો એક સેગમેન્ટને કૉલ કરીએ, જેના છેડાને સંબંધિત છે તે જાણીતું છે કે તેમાંથી કયો પહેલો છે અને કયો બીજો છે.

વેક્ટરચોક્કસ લંબાઈ ધરાવતો નિર્દેશિત સેગમેન્ટ કહેવાય છે, એટલે કે. આ ચોક્કસ લંબાઈનો એક સેગમેન્ટ છે, જેમાં તેને મર્યાદિત કરતા બિંદુઓમાંથી એક શરૂઆત તરીકે અને બીજાને અંત તરીકે લેવામાં આવે છે. જો એ- વેક્ટરની શરૂઆત, બીતેનો અંત છે, પછી વેક્ટરને પ્રતીક દ્વારા સૂચવવામાં આવે છે વધુમાં, વેક્ટરને ઘણીવાર એક અક્ષર દ્વારા સૂચવવામાં આવે છે. આકૃતિમાં, વેક્ટર એક સેગમેન્ટ દ્વારા અને તેની દિશા તીર દ્વારા દર્શાવવામાં આવી છે.

મોડ્યુલઅથવા લંબાઈવેક્ટરને નિર્દેશિત સેગમેન્ટની લંબાઈ કહેવામાં આવે છે જે તેને વ્યાખ્યાયિત કરે છે. દ્વારા સૂચિત || અથવા ||.

અમે કહેવાતા શૂન્ય વેક્ટરનો પણ સમાવેશ કરીશું, જેની શરૂઆત અને અંત એકસરખા છે, વેક્ટર તરીકે. તે નિયુક્ત થયેલ છે. શૂન્ય વેક્ટરને કોઈ ચોક્કસ દિશા હોતી નથી અને તેનું મોડ્યુલસ શૂન્ય છે ||=0.

વેક્ટર કહેવામાં આવે છે સમરેખા, જો તેઓ સમાન રેખા પર અથવા સમાંતર રેખાઓ પર સ્થિત હોય. તદુપરાંત, જો વેક્ટર અને એક જ દિશામાં હોય, તો આપણે વિરુદ્ધ લખીશું.

સમાન વિમાનની સમાંતર સીધી રેખાઓ પર સ્થિત વેક્ટર કહેવામાં આવે છે કોપ્લાનર.

બે વેક્ટર કહેવાય છે સમાન, જો તેઓ સમરેખા હોય, તો દિશા સમાન હોય અને લંબાઈમાં સમાન હોય. આ કિસ્સામાં તેઓ લખે છે.

વેક્ટર્સની સમાનતાની વ્યાખ્યા પરથી તે અનુસરે છે કે વેક્ટરને અવકાશમાં કોઈપણ બિંદુએ તેના મૂળને મૂકીને, પોતાની સાથે સમાંતર પરિવહન કરી શકાય છે.

દાખ્લા તરીકે.

વેક્ટર પર રેખીય કામગીરી

1. સંખ્યા વડે વેક્ટરનો ગુણાકાર.

   વેક્ટરનું ઉત્પાદન અને સંખ્યા λ એ એક નવો વેક્ટર છે જેમ કે:

   વેક્ટર અને સંખ્યા λ નું ઉત્પાદન λ દ્વારા સૂચવવામાં આવે છે.

   

   દાખ્લા તરીકે,વેક્ટરની સમાન દિશામાં નિર્દેશિત વેક્ટર છે અને તેની લંબાઈ વેક્ટર કરતા અડધી છે.

   રજૂ કરાયેલ કામગીરીમાં નીચે મુજબ છે ગુણધર્મો:

2. વેક્ટર ઉમેરો.

   ચાલો અને બે મનસ્વી વેક્ટર બનો. ચાલો એક મનસ્વી મુદ્દો લઈએ ઓઅને વેક્ટર બનાવો. તે પછી બિંદુ પરથી એચાલો વેક્ટરને બાજુએ મૂકીએ. પ્રથમ વેક્ટરની શરૂઆતને બીજાના અંત સાથે જોડતો વેક્ટર કહેવાય છે રકમઆ વેક્ટર્સમાંથી અને સૂચવવામાં આવે છે .

   

   વેક્ટર ઉમેરણની ઘડાયેલી વ્યાખ્યા કહેવામાં આવે છે સમાંતરગ્રામ નિયમ, કારણ કે વેક્ટરનો સમાન સરવાળો નીચે પ્રમાણે મેળવી શકાય છે. ચાલો મુદ્દા પરથી મુલતવી રાખીએ ઓવેક્ટર અને . ચાલો આ વેક્ટર પર સમાંતર ચતુષ્કોણ બનાવીએ OABC. વેક્ટર હોવાથી, પછી વેક્ટર, જે શિરોબિંદુમાંથી દોરેલા સમાંતરગ્રામનો કર્ણ છે ઓ, દેખીતી રીતે વેક્ટરનો સરવાળો હશે.

   

   નીચેની તપાસ કરવી સરળ છે વેક્ટર ઉમેરણના ગુણધર્મો.

3. વેક્ટર તફાવત.

   આપેલ વેક્ટરને સમકક્ષ વેક્ટર, લંબાઈમાં સમાન અને વિરુદ્ધ દિશામાન કહેવાય છે વિરુદ્ધવેક્ટર માટે વેક્ટર અને દ્વારા સૂચવવામાં આવે છે. વિરુદ્ધ વેક્ટરને વેક્ટરને સંખ્યા λ = –1 દ્વારા ગુણાકાર કરવાના પરિણામ તરીકે ગણી શકાય: .

વ્યાખ્યા 9.3.વેક્ટર એક્સ કહેવાય છે eigenvectorમેટ્રિસિસ એ, જો આવી સંખ્યા હોય λ, કે સમાનતા ધરાવે છે: એ એક્સ= λ એક્સ, એટલે કે, માટે અરજી કરવાનું પરિણામ એક્સ મેટ્રિક્સ દ્વારા ઉલ્લેખિત રેખીય પરિવર્તન એ, એ સંખ્યા દ્વારા આ વેક્ટરનો ગુણાકાર છે λ . નંબર પોતે λ કહેવાય છે eigenvalueમેટ્રિસિસ એ.

સૂત્રોમાં અવેજીમાં (9.3) x` j = λx j ,અમે eigenvector ના કોઓર્ડિનેટ્સ નક્કી કરવા માટે સમીકરણોની સિસ્ટમ મેળવીએ છીએ:

. (9.5)

આ રેખીય સજાતીય પ્રણાલીમાં બિન-તુચ્છ ઉકેલ માત્ર ત્યારે જ હશે જો તેનો મુખ્ય નિર્ણાયક 0 (ક્રેમરનો નિયમ) હોય. ફોર્મમાં આ શરત લખીને:

અમે eigenvalues ​​નક્કી કરવા માટે એક સમીકરણ મેળવીએ છીએ λ , કહેવાય છે લાક્ષણિક સમીકરણ. સંક્ષિપ્તમાં તે નીચે મુજબ રજૂ કરી શકાય છે:

| A - λE | = 0, (9.6)

કારણ કે તેની ડાબી બાજુ મેટ્રિક્સનો નિર્ણાયક ધરાવે છે A-λE. બહુપદી સંબંધી λ | A - λE| કહેવાય છે લાક્ષણિક બહુપદીમેટ્રિસ એ.

લાક્ષણિક બહુપદીના ગુણધર્મો:

1) રેખીય પરિવર્તનની લાક્ષણિકતા બહુપદી આધારની પસંદગી પર આધારિત નથી. પુરાવો. (જુઓ (9.4 ટકા), પરંતુ તેથી, . આમ, તે આધારની પસંદગી પર આધારિત નથી. મતલબ કે | A-λE| જ્યારે નવા આધાર પર જતા હોય ત્યારે બદલાતું નથી.

2) જો મેટ્રિક્સ એરેખીય પરિવર્તન છે સપ્રમાણ(તે. અને ij =a જી), તો પછી લાક્ષણિક સમીકરણ (9.6) ના તમામ મૂળ વાસ્તવિક સંખ્યાઓ છે.

ઇજેનવેલ્યુ અને ઇજેનવેક્ટરના ગુણધર્મો:

1) જો તમે eigenvectors માંથી આધાર પસંદ કરો છો x 1, x 2, x 3 , eigenvalues ​​ને અનુરૂપ λ 1, λ 2, λ 3મેટ્રિસિસ એ, તો પછી આ આધાર પર રેખીય રૂપાંતરણ A પાસે ત્રાંસા સ્વરૂપનું મેટ્રિક્સ છે:

(9.7) આ ગુણધર્મનો પુરાવો eigenvectors ની વ્યાખ્યામાંથી અનુસરે છે.

2) જો રૂપાંતરણના મૂલ્યો એઅલગ હોય છે, તો પછી તેમના અનુરૂપ એઇજેનવેક્ટર રેખીય રીતે સ્વતંત્ર હોય છે.

3) જો મેટ્રિક્સની લાક્ષણિક બહુપદી હોય એત્રણ ધરાવે છે વિવિધ મૂળ, પછી અમુક આધારે મેટ્રિક્સ એકર્ણ દેખાવ ધરાવે છે.

ચાલો મેટ્રિક્સના eigenvalues ​​અને eigenvectors શોધીએ ચાલો કંપોઝ કરીએ લાક્ષણિક સમીકરણ: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

ચાલો દરેક મળેલ મૂલ્યને અનુરૂપ eigenvectors ના કોઓર્ડિનેટ્સ શોધીએ λ. (9.5) થી તે અનુસરે છે કે જો એક્સ (1) ={x 1, x 2, x 3) – અનુરૂપ eigenvector λ 1 =-2, પછી

- સહકારી પરંતુ અનિશ્ચિત સિસ્ટમ. તેનું સોલ્યુશન ફોર્મમાં લખી શકાય છે એક્સ (1) ={a,0,-a), જ્યાં a કોઈપણ સંખ્યા છે. ખાસ કરીને, જો આપણને તેની જરૂર હોય તો | x (1) |=1, એક્સ (1) =

સિસ્ટમમાં અવેજી (9.5) λ 2 =3, અમે બીજા ઇજનવેક્ટરના કોઓર્ડિનેટ્સ નક્કી કરવા માટે સિસ્ટમ મેળવીએ છીએ - x (2) ={y 1, y 2, y 3}:

, ક્યાં એક્સ (2) ={b,-b,b) અથવા, પ્રદાન કરેલ | x (2) |=1, x (2) =

માટે λ 3 = 6 eigenvector શોધો x (3) ={z 1 , z 2 , z 3}:

, x (3) ={c,2c,c) અથવા સામાન્યકૃત સંસ્કરણમાં

x (3) = તે નોંધી શકાય છે એક્સ (1) એક્સ (2) = ab–ab= 0, x (1) x (3) = એસી-એસી= 0, x (2) x (3) = પૂર્વે- 2bc + bc= 0. આમ, આ મેટ્રિક્સના eigenvectors જોડી પ્રમાણે ઓર્થોગોનલ છે.

વ્યાખ્યાન 10.

ચતુર્ભુજ સ્વરૂપો અને સપ્રમાણ મેટ્રિસિસ સાથે તેમનું જોડાણ. સપ્રમાણ મેટ્રિક્સના ઇજેનવેક્ટર અને ઇજેનવેલ્યુના ગુણધર્મો. ચતુર્ભુજ સ્વરૂપને પ્રમાણભૂત સ્વરૂપમાં ઘટાડવું.

વ્યાખ્યા 10.1.ચતુર્ભુજ આકારવાસ્તવિક ચલો x 1, x 2, …, x nઆ ચલોમાં દ્વિતીય ડિગ્રીનો બહુપદી કહેવાય છે જેમાં પ્રથમ ડિગ્રીની મુક્ત પદ અને શરતો હોતી નથી.

ચતુર્ભુજ સ્વરૂપોના ઉદાહરણો:

(n = 2),

(n = 3). (10.1)

ચાલો છેલ્લા લેક્ચરમાં આપેલ સપ્રમાણ મેટ્રિક્સની વ્યાખ્યા યાદ કરીએ:

વ્યાખ્યા 10.2.ચોરસ મેટ્રિક્સ કહેવાય છે સપ્રમાણ, જો , એટલે કે, જો મેટ્રિક્સ તત્વો જે મુખ્ય કર્ણ વિશે સપ્રમાણ હોય તે સમાન હોય.

સપ્રમાણ મેટ્રિક્સના ઇજેનવેલ્યુ અને ઇજેનવેક્ટરના ગુણધર્મો:

1) સપ્રમાણ મેટ્રિક્સના તમામ ઇજેન મૂલ્યો વાસ્તવિક છે.

પુરાવો (માટે n = 2).

મેટ્રિક્સ દો એફોર્મ ધરાવે છે: . ચાલો એક લાક્ષણિક સમીકરણ બનાવીએ:

(10.2) ચાલો ભેદભાવ શોધીએ:

તેથી, સમીકરણ માત્ર વાસ્તવિક મૂળ ધરાવે છે.

2) ઇજેનવેક્ટરસપ્રમાણ મેટ્રિક્સ ઓર્થોગોનલ છે.

પુરાવો (માટે n= 2).

eigenvectors ના કોઓર્ડિનેટ્સ અને સમીકરણોને સંતોષવા જ જોઈએ.

www.siteતમને શોધવા માટે પરવાનગી આપે છે. સાઇટ ગણતરી કરે છે. થોડીક સેકન્ડોમાં સર્વર યોગ્ય ઉકેલ આપશે. મેટ્રિક્સ માટે લાક્ષણિક સમીકરણહશે બીજગણિતીય અભિવ્યક્તિ, નિર્ણાયકની ગણતરી માટેના નિયમ દ્વારા જોવા મળે છે મેટ્રિસિસ મેટ્રિસિસ, જ્યારે મુખ્ય કર્ણની સાથે કર્ણ તત્વો અને ચલના મૂલ્યોમાં તફાવત હશે. ગણતરી કરતી વખતે મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણ, દરેક તત્વ મેટ્રિસિસઅનુરૂપ અન્ય ઘટકો સાથે ગુણાકાર કરવામાં આવશે મેટ્રિસિસ. મોડમાં શોધો ઓનલાઇનમાત્ર ચોરસ માટે જ શક્ય છે મેટ્રિસિસ. શોધ કામગીરી મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણતત્વોના ઉત્પાદનના બીજગણિત સરવાળાની ગણતરી કરવા માટે ઘટાડે છે મેટ્રિસિસનિર્ણાયક શોધવાના પરિણામે મેટ્રિસિસ, માત્ર નક્કી કરવાના હેતુ માટે મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણ. આ ઓપરેશનસિદ્ધાંતમાં વિશેષ સ્થાન ધરાવે છે મેટ્રિસિસ, તમને મૂળનો ઉપયોગ કરીને eigenvalues ​​અને વેક્ટર્સ શોધવાની મંજૂરી આપે છે. શોધવાનું કાર્ય મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણગુણાકાર તત્વો સમાવે છે મેટ્રિસિસચોક્કસ નિયમ અનુસાર આ ઉત્પાદનોનો સારાંશ દ્વારા અનુસરવામાં આવે છે. www.siteશોધે છે મેટ્રિક્સ માટે લાક્ષણિક સમીકરણમોડમાં આપેલ પરિમાણ ઓનલાઇન. ગણતરી મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણતેના પરિમાણને જોતાં, આ સંખ્યાત્મક અથવા સાંકેતિક ગુણાંક સાથે બહુપદી શોધી રહ્યું છે, જે નિર્ણાયકની ગણતરી માટેના નિયમ અનુસાર જોવા મળે છે. મેટ્રિસિસ- અનુરૂપ તત્વોના ઉત્પાદનોના સરવાળા તરીકે મેટ્રિસિસ, માત્ર નક્કી કરવાના હેતુ માટે મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણ. ચતુર્ભુજ માટે ચલના સંદર્ભમાં બહુપદી શોધવી મેટ્રિસિસ, વ્યાખ્યા તરીકે મેટ્રિક્સ માટે લાક્ષણિક સમીકરણ, સિદ્ધાંતમાં સામાન્ય મેટ્રિસિસ. બહુપદીના મૂળનો અર્થ મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણમાટે eigenvectors અને eigenvalues ​​નક્કી કરવા માટે વપરાય છે મેટ્રિસિસ. વધુમાં, જો નિર્ણાયક મેટ્રિસિસપછી શૂન્ય બરાબર હશે મેટ્રિક્સનું લાક્ષણિક સમીકરણહજુ પણ અસ્તિત્વમાં રહેશે, વિપરીત વિપરીત મેટ્રિસિસ. ગણતરી કરવા માટે મેટ્રિક્સ માટે લાક્ષણિક સમીકરણઅથવા એક સાથે અનેક શોધો મેટ્રિસીસ લાક્ષણિક સમીકરણો, તમારે ઘણો સમય અને પ્રયત્નો ખર્ચવાની જરૂર છે, જ્યારે અમારું સર્વર થોડીક સેકંડમાં શોધી લેશે મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણ. આ કિસ્સામાં, શોધવાનો જવાબ મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણસાચા અને પર્યાપ્ત ચોકસાઈ સાથે હશે, પછી ભલે નંબરો શોધવામાં આવે મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણઅતાર્કિક હશે. સાઇટ પર www.siteતત્વોમાં અક્ષર પ્રવેશો માન્ય છે મેટ્રિસિસ, તે જ મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણગણતરી કરતી વખતે સામાન્ય પ્રતીકાત્મક સ્વરૂપમાં રજૂ કરી શકાય છે ઓનલાઇન મેટ્રિક્સનું લાક્ષણિક સમીકરણ. શોધવાની સમસ્યાને ઉકેલતી વખતે મેળવેલા જવાબને તપાસવું ઉપયોગી છે મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણસાઇટનો ઉપયોગ કરીને www.site. બહુપદીની ગણતરીની કામગીરી કરતી વખતે - મેટ્રિક્સનું લાક્ષણિક સમીકરણ, આ સમસ્યા હલ કરતી વખતે તમારે સાવચેત અને અત્યંત ધ્યાન કેન્દ્રિત કરવાની જરૂર છે. બદલામાં, અમારી સાઇટ તમને વિષય પરના તમારા નિર્ણયને તપાસવામાં મદદ કરશે ઑનલાઇન મેટ્રિક્સનું લાક્ષણિક સમીકરણ. જો તમારી પાસે ઉકેલાયેલી સમસ્યાઓની લાંબી તપાસ માટે સમય નથી, તો પછી www.siteશોધવા અને ગણતરી કરતી વખતે ચેક કરવા માટે ચોક્કસપણે એક અનુકૂળ સાધન હશે મેટ્રિક્સ ઓનલાઇન માટે લાક્ષણિક સમીકરણ.

સ્ક્વેર મેટ્રિક્સનો ઇજેનવેક્ટર એ છે કે જ્યારે આપેલ મેટ્રિક્સ દ્વારા ગુણાકાર કરવામાં આવે છે, ત્યારે તે કોલિનિયર વેક્ટરમાં પરિણમે છે. સાદા શબ્દોમાં, જ્યારે મેટ્રિક્સને eigenvector દ્વારા ગુણાકાર કરવામાં આવે છે, ત્યારે બાદમાં સમાન રહે છે, પરંતુ ચોક્કસ સંખ્યા દ્વારા ગુણાકાર કરવામાં આવે છે.

વ્યાખ્યા

eigenvector એ બિન-શૂન્ય વેક્ટર V છે, જેને જ્યારે ચોરસ મેટ્રિક્સ M વડે ગુણાકાર કરવામાં આવે છે, ત્યારે તે પોતે અમુક સંખ્યા λ દ્વારા વધે છે. બીજગણિત સંકેતોમાં તે આના જેવું દેખાય છે:

M × V = λ × V,

જ્યાં λ એ મેટ્રિક્સ M નું eigenvalue છે.

ચાલો વિચાર કરીએ સંખ્યાત્મક ઉદાહરણ. રેકોર્ડિંગની સરળતા માટે, મેટ્રિક્સમાં સંખ્યાઓને અર્ધવિરામ દ્વારા અલગ કરવામાં આવશે. ચાલો મેટ્રિક્સ લઈએ:

• એમ = 0; 4;
• 6; 10.

ચાલો તેને કૉલમ વેક્ટર દ્વારા ગુણાકાર કરીએ:

• V = -2;

જ્યારે આપણે મેટ્રિક્સને કૉલમ વેક્ટર વડે ગુણાકાર કરીએ છીએ, ત્યારે અમને કૉલમ વેક્ટર પણ મળે છે. કડક ગાણિતિક ભાષાકૉલમ વેક્ટર દ્વારા 2 × 2 મેટ્રિક્સનો ગુણાકાર કરવા માટેનું સૂત્ર આના જેવું દેખાશે:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 એટલે પ્રથમ પંક્તિ અને પ્રથમ કૉલમમાં સ્થિત મેટ્રિક્સ Mનું તત્વ અને M22 એટલે બીજી પંક્તિ અને બીજી કૉલમમાં સ્થિત તત્વ. અમારા મેટ્રિક્સ માટે, આ તત્વો M11 = 0, M12 = 4, M21 = 6, M22 10 સમાન છે. કૉલમ વેક્ટર માટે, આ મૂલ્યો V11 = –2, V21 = 1 સમાન છે. આ સૂત્ર મુજબ, આપણને વેક્ટર દ્વારા ચોરસ મેટ્રિક્સના ગુણાંકનું નીચેનું પરિણામ મળે છે:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

સગવડ માટે, ચાલો કૉલમ વેક્ટરને એક પંક્તિમાં લખીએ. તેથી, અમે વેક્ટર (-2; 1) વડે ચોરસ મેટ્રિક્સનો ગુણાકાર કર્યો, પરિણામે વેક્ટર (4; -2). દેખીતી રીતે, આ તે જ વેક્ટર છે જેનો λ = -2 દ્વારા ગુણાકાર કરવામાં આવે છે. લેમ્બડા માં આ બાબતેમેટ્રિક્સનું eigenvalue સૂચવે છે.

મેટ્રિક્સનો ઇજેનવેક્ટર એ સમસ્તર વેક્ટર છે, એટલે કે, એક પદાર્થ કે જે મેટ્રિક્સ દ્વારા ગુણાકાર કરવામાં આવે ત્યારે અવકાશમાં તેની સ્થિતિ બદલાતી નથી. વેક્ટર બીજગણિતમાં સમન્વયની વિભાવના ભૂમિતિમાં સમાનતાની પરિભાષા જેવી જ છે. ભૌમિતિક અર્થઘટનમાં, કોલિનિયર વેક્ટર વિવિધ લંબાઈના સમાંતર નિર્દેશિત સેગમેન્ટ્સ છે. યુક્લિડના સમયથી, આપણે જાણીએ છીએ કે એક રેખા તેની સમાંતર અનંત સંખ્યામાં રેખાઓ ધરાવે છે, તેથી તે ધારવું તાર્કિક છે કે દરેક મેટ્રિક્સમાં અનંત સંખ્યામાં ઇજનવેક્ટર છે.

અગાઉના ઉદાહરણ પરથી તે સ્પષ્ટ છે કે ઇજનવેક્ટર (-8; 4), અને (16; -8), અને (32, -16) હોઈ શકે છે. આ બધા કોલિનિયર વેક્ટર છે જે eigenvalue λ = -2 ને અનુરૂપ છે. આ વેક્ટર દ્વારા મૂળ મેટ્રિક્સનો ગુણાકાર કરતી વખતે, આપણે હજી પણ એવા વેક્ટર સાથે સમાપ્ત થઈશું જે મૂળથી 2 વખતથી અલગ હશે. તેથી જ, જ્યારે eigenvector શોધવાની સમસ્યાઓનું નિરાકરણ કરતી વખતે, માત્ર રેખીય રીતે સ્વતંત્ર વેક્ટર ઑબ્જેક્ટ્સ શોધવા જરૂરી છે. મોટાભાગે, n × n મેટ્રિક્સ માટે, ત્યાં n નંબર eigenvectors હોય છે. અમારું કેલ્ક્યુલેટર બીજા-ક્રમના ચોરસ મેટ્રિસિસના વિશ્લેષણ માટે રચાયેલ છે, તેથી લગભગ હંમેશા પરિણામ બે ઇજેનવેક્ટર શોધશે, સિવાય કે જ્યારે તેઓ એકરૂપ થાય.

ઉપરના ઉદાહરણમાં, અમે મૂળ મેટ્રિક્સના ઇજેનવેક્ટરને અગાઉથી જાણતા હતા અને સ્પષ્ટપણે લેમ્બડા નંબર નક્કી કર્યો હતો. જો કે, વ્યવહારમાં, બધું બીજી રીતે થાય છે: ઇજેનવેલ્યુઝ પ્રથમ જોવા મળે છે અને પછી જ ઇજેનવેક્ટર.

ઉકેલ અલ્ગોરિધમનો

ચાલો મૂળ મેટ્રિક્સ M પર ફરી નજર કરીએ અને તેના બંને ઇજેનવેક્ટર શોધવાનો પ્રયાસ કરીએ. તેથી મેટ્રિક્સ આના જેવો દેખાય છે:

• એમ = 0; 4;
• 6; 10.

પ્રથમ આપણે એઇજેનવેલ્યુ λ નક્કી કરવાની જરૂર છે, જેના માટે નીચેના મેટ્રિક્સના નિર્ણાયકની ગણતરી કરવાની જરૂર છે:

• (0 − λ); 4;
• 6; (10 − λ).

આ મેટ્રિક્સ મુખ્ય કર્ણ પરના તત્વોમાંથી અજાણ્યા λ બાદ કરીને મેળવવામાં આવે છે. નિર્ણાયક પ્રમાણભૂત સૂત્રનો ઉપયોગ કરીને નક્કી કરવામાં આવે છે:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

આપણું વેક્ટર બિન-શૂન્ય હોવું આવશ્યક હોવાથી, અમે પરિણામી સમીકરણને રેખીય રીતે આધારિત તરીકે સ્વીકારીએ છીએ અને અમારા નિર્ણાયક detA ને શૂન્ય સાથે સરખાવીએ છીએ.

(0 − λ) × (10 − λ) − 24 = 0

ચાલો કૌંસ ખોલીએ અને મેટ્રિક્સનું લાક્ષણિક સમીકરણ મેળવીએ:

λ 2 − 10λ − 24 = 0

આ પ્રમાણભૂત છે ચતુર્ભુજ સમીકરણ, જેને ભેદભાવના માધ્યમથી ઉકેલવાની જરૂર છે.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

ભેદભાવનું મૂળ sqrt(D) = 14 છે, તેથી λ1 = -2, λ2 = 12. હવે દરેક લેમ્બડા મૂલ્ય માટે આપણે eigenvector શોધવાની જરૂર છે. ચાલો λ = -2 માટે સિસ્ટમ ગુણાંક વ્યક્ત કરીએ.

• M − λ × E = 2; 4;
• 6; 12.

આ સૂત્રમાં, E એ ઓળખ મેટ્રિક્સ છે. પરિણામી મેટ્રિક્સના આધારે, અમે રેખીય સમીકરણોની સિસ્ટમ બનાવીએ છીએ:

2x + 4y = 6x + 12y,

જ્યાં x અને y એ eigenvector તત્વો છે.

ચાલો બધા X ડાબી બાજુએ અને બધા Y ને જમણી બાજુએ એકત્રિત કરીએ. દેખીતી રીતે - 4x = 8y. અભિવ્યક્તિને - 4 વડે વિભાજીત કરો અને x = –2y મેળવો. હવે આપણે અજ્ઞાતના કોઈપણ મૂલ્યો લઈને (રેખીય રીતે આશ્રિત આઈજેનવેક્ટરની અનંતતાને યાદ રાખો) લઈને મેટ્રિક્સનો પ્રથમ ઈજનવેક્ટર નક્કી કરી શકીએ છીએ. ચાલો y = 1 લઈએ, પછી x = –2. તેથી, પ્રથમ eigenvector V1 = (–2; 1) જેવો દેખાય છે. લેખની શરૂઆતમાં પાછા ફરો. આ વેક્ટર ઑબ્જેક્ટ હતું કે અમે ઇજનવેક્ટરની વિભાવનાને દર્શાવવા માટે મેટ્રિક્સનો ગુણાકાર કર્યો.

હવે ચાલો λ = 12 માટે eigenvector શોધીએ.

• M - λ × E = -12; 4
• 6; -2.

ચાલો રેખીય સમીકરણોની સમાન સિસ્ટમ બનાવીએ;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x = y.

હવે આપણે x = 1 લઈએ છીએ, તેથી y = 3. આમ, બીજો eigenvector V2 = (1; 3) જેવો દેખાય છે. આપેલ વેક્ટર દ્વારા મૂળ મેટ્રિક્સનો ગુણાકાર કરતી વખતે, પરિણામ હંમેશા સમાન વેક્ટરને 12 વડે ગુણાકાર કરવામાં આવશે. આ તે છે જ્યાં સોલ્યુશન અલ્ગોરિધમ સમાપ્ત થાય છે. હવે તમે જાણો છો કે મેટ્રિક્સના eigenvector ને મેન્યુઅલી કેવી રીતે નક્કી કરવું.

• નિર્ણાયક
• ટ્રેસ, એટલે કે, મુખ્ય કર્ણ પરના તત્વોનો સરવાળો;
• રેન્ક, એટલે કે, રેખીય રીતે સ્વતંત્ર પંક્તિઓ/સ્તંભોની મહત્તમ સંખ્યા.

પ્રોગ્રામ ઉપરોક્ત અલ્ગોરિધમ અનુસાર કાર્ય કરે છે, શક્ય તેટલું સોલ્યુશન પ્રક્રિયાને ટૂંકી કરે છે. તે નિર્દેશ કરવો મહત્વપૂર્ણ છે કે પ્રોગ્રામમાં લેમ્બડાને "c" અક્ષર દ્વારા નિયુક્ત કરવામાં આવે છે. ચાલો સંખ્યાત્મક ઉદાહરણ જોઈએ.

પ્રોગ્રામ કેવી રીતે કાર્ય કરે છે તેનું ઉદાહરણ

ચાલો નીચેના મેટ્રિક્સ માટે ઇજેનવેક્ટર નક્કી કરવાનો પ્રયાસ કરીએ:

• એમ = 5; 13;
• 4; 14.

ચાલો કેલ્ક્યુલેટરના કોષોમાં આ મૂલ્યો દાખલ કરીએ અને નીચેના સ્વરૂપમાં જવાબ મેળવીએ:

• મેટ્રિક્સ રેન્ક: 2;
• મેટ્રિક્સ નિર્ણાયક: 18;
• મેટ્રિક્સ ટ્રેસ: 19;
• eigenvector ની ગણતરી: c 2 − 19.00c + 18.00 (લાક્ષણિક સમીકરણ);
• ઇજેનવેક્ટર ગણતરી: 18 (પ્રથમ લેમ્બડા મૂલ્ય);
• Eigenvector ગણતરી: 1 (સેકન્ડ લેમ્બડા મૂલ્ય);
• વેક્ટર 1 માટે સમીકરણોની સિસ્ટમ: -13x1 + 13y1 = 4x1 − 4y1;
• વેક્ટર 2 માટે સમીકરણોની સિસ્ટમ: 4x1 + 13y1 = 4x1 + 13y1;
• ઇજેનવેક્ટર 1: (1; 1);
• Eigenvector 2: (-3.25; 1).

આમ, અમે બે રેખીય રીતે સ્વતંત્ર eigenvectors મેળવ્યા.

નિષ્કર્ષ

રેખીય બીજગણિત અને વિશ્લેષણાત્મક ભૂમિતિ એ કોઈપણ નવા એન્જિનિયરિંગ વિદ્યાર્થી માટે પ્રમાણભૂત વિષયો છે. વેક્ટર અને મેટ્રિસિસની મોટી સંખ્યા ભયાનક છે, અને આવી બોજારૂપ ગણતરીઓમાં ભૂલો કરવી સરળ છે. અમારો પ્રોગ્રામ વિદ્યાર્થીઓને તેમની ગણતરીઓ તપાસવા અથવા eigenvector શોધવાની સમસ્યાને આપમેળે ઉકેલવા દેશે. અમારી સૂચિમાં અન્ય રેખીય બીજગણિત કેલ્ક્યુલેટર છે તેનો તમારા અભ્યાસ અથવા કાર્યમાં ઉપયોગ કરો.