A matrisi ilə, AX = lX olan l ədədi varsa.

Bu halda l rəqəmi çağırılır xüsusi dəyər X vektoruna uyğun olan operator (A matrisi).

Başqa sözlə, xüsusi vektor xətti operatorun təsiri altında kollinear vektora çevrilən vektordur, yəni. sadəcə bir ədədə çarpın. Bunun əksinə olaraq, düzgün olmayan vektorların çevrilməsi daha mürəkkəbdir.

Xüsusi vektorun tərifini tənliklər sistemi şəklində yazaq:

Bütün şərtləri sol tərəfə keçirək:

Sonuncu sistem matris şəklində aşağıdakı kimi yazıla bilər:

(A - lE)X = O

Alınan sistemin həmişə sıfır həlli X = O olur. Bütün sərbəst şərtlərin sıfıra bərabər olduğu belə sistemlər adlanır. homojen. Belə bir sistemin matrisi kvadratdırsa və onun təyinedicisi sıfıra bərabər deyilsə, Kramer düsturlarından istifadə edərək həmişə unikal bir həll əldə edəcəyik - sıfır. Sübut edilə bilər ki, sistemin sıfırdan fərqli həlləri yalnız və yalnız bu matrisin determinantı sıfıra bərabər olduqda, yəni.

|A - lE| = = 0

Naməlum l olan bu tənliyə deyilir xarakterik tənlik (xarakterik polinom) matrisi A (xətti operator).

Sübut etmək olar ki, xətti operatorun xarakterik çoxhədli bazisin seçilməsindən asılı deyil.

Məsələn, A = matrisi ilə müəyyən edilmiş xətti operatorun xüsusi qiymətlərini və xüsusi vektorlarını tapaq.

Bunun üçün bəstələyək xarakterik tənlik|A - lE| = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; xüsusi dəyərlər l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.

Xüsusi vektorları tapmaq üçün iki tənlik sistemini həll edirik

(A + 5E)X = O

(A - 7E)X = O

Bunlardan birincisi üçün genişləndirilmiş matris formasını alır

,

buradan x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s, yəni. X (1) = (-(2/3)s; s).

Onlardan ikincisi üçün genişləndirilmiş matris formasını alır

,

buradan x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, yəni. X (2) = ((2/3)s 1; s 1).

Beləliklə, bu xətti operatorun xüsusi vektorları xüsusi dəyəri (-5) olan (-(2/3)с; с) formasının bütün vektorları və ((2/3)с 1 ; с 1) formasının bütün vektorlarıdır. xüsusi dəyər 7.

Sübut edilə bilər ki, A operatorunun öz vektorlarından ibarət bazada matrisi diaqonaldır və formaya malikdir:

,

burada l i bu matrisin xüsusi qiymətləridir.

Əksi də doğrudur: əgər hansısa əsasda A matrisi diaqonaldırsa, bu bazisin bütün vektorları bu matrisin xüsusi vektorları olacaqdır.

Onu da sübut etmək olar ki, əgər xətti operatorun n qoşa ayrı-ayrı xas qiymətləri varsa, onda müvafiq məxsusi vektorlar xətti müstəqildir və bu operatorun müvafiq bazisdəki matrisi diaqonal formaya malikdir.

Bunu əvvəlki nümunə ilə izah edək. Gəlin ixtiyari sıfırdan fərqli c və c 1 dəyərlərini götürək, lakin X (1) və X (2) vektorları xətti müstəqil olsun, yəni. əsas təşkil edərdi. Məsələn, c = c 1 = 3 olsun, sonra X (1) = (-2; 3), X (2) = (2; 3).

Gəlin əmin olaq xətti müstəqillik bu vektorlar:

12 ≠ 0. Bu yeni əsasda A matrisi A * = formasını alacaq.

Bunu yoxlamaq üçün A * = C -1 AC düsturundan istifadə edək. Əvvəlcə C -1 tapaq.

C -1 = ;

Kvadrat formalar

Kvadrat forma n dəyişənin f(x 1, x 2, x n) hər həddi ya dəyişənlərdən birinin kvadratı, ya da müəyyən əmsalla alınan iki müxtəlif dəyişənin hasili olan cəm adlanır: f(x 1) , x 2, x n) = (a ij = a ji).

Bu əmsallardan ibarət olan A matrisi adlanır matris kvadrat forma. Həmişə belədir simmetrik matris (yəni əsas diaqonala görə simmetrik olan matris, a ij = a ji).

Matris qeydində kvadrat forma f(X) = X T AX, burada

Həqiqətən

Məsələn, kvadrat formanı matris formasında yazaq.

Bunun üçün kvadrat formalı matrisa tapırıq. Onun diaqonal elementləri kvadrat dəyişənlərin əmsallarına, qalan elementləri isə kvadrat formanın müvafiq əmsallarının yarısına bərabərdir. Buna görə də

Dəyişənlərin X matris-sütununu Y matrisa-sütununun degenerasiya olunmayan xətti çevrilməsi ilə alınsın, yəni. X = CY, burada C n-ci dərəcəli qeyri-sinqulyar matrisdir. Onda f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y kvadrat forması.

Beləliklə, qeyri-degenerativ C xətti çevrilməsi ilə kvadrat formanın matrisi aşağıdakı formanı alır: A * = C T AC.

Məsələn, f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 kvadrat formasından xətti çevirmə yolu ilə alınan f(y 1, y 2) kvadrat formasını tapaq.

Kvadrat forma deyilir kanonik(O var kanonik görünüş), onun bütün əmsalları i ≠ j üçün a ij = 0 olarsa, yəni.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = .

Onun matrisi diaqonaldır.

Teorem(sübut burada verilmir). İstənilən kvadrat forma qeyri-degenerativ xətti transformasiyadan istifadə edərək kanonik formaya endirilə bilər.

Məsələn, kvadrat formanı kanonik formaya endirək
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Bunu etmək üçün əvvəlcə seçirik mükəmməl kvadrat x 1 dəyişəni ilə:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

İndi x 2 dəyişəni ilə tam kvadrat seçirik:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10)x 3) 2 + (1/20)x 3 2.

Onda degenerasiyaya uğramayan y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 və y 3 = x 3 xətti transformasiyası bu kvadrat formanı f(y 1, y 2) kanonik formasına gətirir. , y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Qeyd edək ki, kvadrat formanın kanonik forması birmənalı şəkildə müəyyən edilir (eyni kvadrat forma kanonik formaya endirilə bilər) fərqli yollar). Bununla belə, alınan fərqli yollar kanonik formalar bir sıra ümumi xüsusiyyətlərə malikdir. Xüsusilə, kvadrat formanın müsbət (mənfi) əmsallı hədlərinin sayı formanı bu formaya endirmə üsulundan asılı deyildir (məsələn, nəzərdən keçirilən nümunədə həmişə iki mənfi və bir müsbət əmsal olacaqdır). Bu xassə kvadrat formaların ətalət qanunu adlanır.

Gəlin, eyni kvadrat formanı başqa bir şəkildə kanonik formaya gətirməklə bunu təsdiq edək. Transformasiyaya x 2 dəyişəni ilə başlayaq:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2, burada y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 və y 3 = x 1. Burada y 1-də mənfi -3 əmsalı və y 2 və y 3-də iki müsbət 3 və 2 əmsalları var (və başqa bir üsuldan istifadə edərək y 2-də mənfi (-5) və iki müsbət əmsal əldə etdik: y 1-də 2. və y 3-də 1/20).

Onu da qeyd etmək lazımdır ki, kvadrat formalı matrisin rütbəsi adlanır kvadrat formanın dərəcəsi, kanonik formanın sıfırdan fərqli əmsallarının sayına bərabərdir və xətti çevrilmələr zamanı dəyişmir.

f(X) kvadrat forması adlanır müsbət (mənfi) müəyyən, dəyişənlərin eyni vaxtda sıfıra bərabər olmayan bütün dəyərləri üçün müsbətdirsə, yəni. f(X) > 0 (mənfi, yəni.
f(X)< 0).

Məsələn, f 1 (X) = x 1 2 + x 2 2 kvadrat forması müsbət müəyyəndir, çünki kvadratların cəmidir və f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 kvadrat forması mənfi müəyyəndir, çünki təmsil edir f 2 (X) = -(x 1 - x 2) 2 kimi göstərilə bilər.

Əksər praktik situasiyalarda kvadrat formanın müəyyən işarəsini təyin etmək bir qədər çətindir, buna görə də bunun üçün aşağıdakı teoremlərdən birini istifadə edirik (onları sübut etmədən tərtib edəcəyik).

Teorem. Kvadrat forma müsbət (mənfi) müəyyəndir, o zaman və yalnız onun matrisinin bütün xüsusi dəyərləri müsbət (mənfi) olarsa.

Teorem(Silvester meyarı). Kvadrat forma yalnız və yalnız bu formanın matrisinin bütün aparıcı kiçikləri müsbət olduqda müsbət müəyyəndir.

Əsas (künc) kiçik A () matrisinin birinci k sətir və sütunlarından ibarət n-ci dərəcəli k-ci dərəcəli A matrisi matrisin determinantı adlanır.

Qeyd edək ki, mənfi müəyyən kvadrat formalar üçün əsas kiçiklərin işarələri bir-birini əvəz edir və birinci dərəcəli kiçik mənfi olmalıdır.

Məsələn, işarənin müəyyənliyi üçün f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 kvadrat formasını araşdıraq.

= (2 - l)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
. Buna görə də kvadrat forma müsbət müəyyəndir.

Metod 2. A D 1 = a 11 = 2 > 0 birinci dərəcəli matrisin baş minoru. İkinci dərəcəli D 2 = = 6 - 4 = 2 > 0. Buna görə də Silvestr kriteriyasına görə kvadrat forma müsbət müəyyən.

İşarənin müəyyənliyi üçün başqa kvadrat formanı araşdırırıq, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metod 1. A = kvadratik formalı matrisa quraq. Xarakterik tənlik formaya malik olacaq = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Buna görə də kvadrat forma mənfi müəyyəndir.

Metod 2. A D 1 = a 11 = birinci dərəcəli matrisin əsas minoru
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Deməli, Silvestr meyarına görə kvadrat forma mənfi müəyyəndir (əsas azyaşlıların işarələri mənfidən başlayaraq növbələşir).

Başqa bir misal olaraq, işarə ilə təyin olunan f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 kvadrat formasını araşdırırıq.

Metod 1. A = kvadratik formalı matrisa quraq. Xarakterik tənlik formaya malik olacaq = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Bu rəqəmlərdən biri mənfi, digəri isə müsbətdir. Şəxsi dəyərlərin əlamətləri fərqlidir. Deməli, kvadrat forma nə mənfi, nə də müsbət müəyyən ola bilər, yəni. bu kvadrat forma işarə-müəyyən deyil (hər hansı işarənin qiymətini qəbul edə bilər).

Metod 2. Birinci dərəcəli matrisin əsas minoru A D 1 = a 11 = 2 > 0. İkinci dərəcəli D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

HOMogen Xətti TƏNLƏR SİSTEMİ

Homojen sistem xətti tənliklər forma sistemi adlanır

Aydındır ki, bu halda , çünki bu təyinedicilərdəki sütunlardan birinin bütün elementləri sıfıra bərabərdir.

Çünki naməlumlar düsturlara uyğun tapılır , onda Δ ≠ 0 olduqda, sistemin unikal sıfır həlli var x = y = z= 0. Lakin bir çox məsələlərdə maraqlı sual olub-olmamasıdır homojen sistem sıfırdan başqa həllər.

Teorem. Xətti sistem üçün homojen tənliklər sıfırdan fərqli həlli var idi, Δ ≠ 0 olması zəruri və kifayətdir.

Deməli, müəyyənedici Δ ≠ 0 olarsa, sistemin unikal həlli var. Əgər Δ ≠ 0 olarsa, onda xətti bircins tənliklər sisteminin sonsuz sayda həlli var.

Nümunələr.

Bir matrisin xüsusi vektorları və xüsusi qiymətləri

Kvadrat matris verilsin , X– hündürlüyü matrisin sırası ilə üst-üstə düşən bəzi matris-sütun A. .

Bir çox məsələlərdə tənliyi nəzərə almalıyıq X

burada λ müəyyən bir ədəddir. Aydındır ki, istənilən λ üçün bu tənliyin sıfır həlli var.

Bu tənliyin sıfırdan fərqli həlli olduğu λ ədədi adlanır xüsusi dəyər matrislər A, A X belə λ adlanır məxsus vektor matrislər A.

Matrisin xüsusi vektorunu tapaq A. Çünki E∙X = X, onda matris tənliyi kimi yenidən yazıla bilər və ya . Genişləndirilmiş formada bu tənlik xətti tənliklər sistemi kimi yenidən yazıla bilər. Həqiqətən .

Və buna görə də

Beləliklə, koordinatları təyin etmək üçün homojen xətti tənliklər sistemi əldə etdik x 1, x 2, x 3 vektor X. Bir sistemin sıfırdan fərqli həlləri olması üçün sistemin determinantının sıfıra bərabər olması zəruri və kifayətdir, yəni.

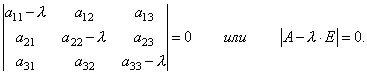
Bu λ üçün 3-cü dərəcəli tənlikdir. Bu adlanır xarakterik tənlik matrislər A və λ-nin xüsusi qiymətlərini təyin etməyə xidmət edir.

Hər bir xüsusi dəyər λ xüsusi vektora uyğundur X, onun koordinatları sistemdən müvafiq λ qiymətində müəyyən edilir.

Nümunələr.

VEKTOR CƏBRİ. VEKTOR KONSEPSİYASI

Fizikanın müxtəlif sahələrini öyrənərkən onların ədədi qiymətləri göstərilməklə tam müəyyən edilən kəmiyyətlər, məsələn, uzunluq, sahə, kütlə, temperatur və s. Belə kəmiyyətlərə skalyar deyilir. Bununla belə, bunlara əlavə olaraq, kəmiyyətlər də var ki, onları müəyyən etmək üçün ədədi qiymətdən əlavə, onların kosmosda istiqamətini də bilmək lazımdır, məsələn, bədənə təsir edən qüvvə, sürət və sürətlənmə. kosmosda hərəkət edərkən bədən, gərginlik maqnit sahəsi fəzanın müəyyən nöqtəsində və s. Belə kəmiyyətlərə vektor kəmiyyətlər deyilir.

Gəlin ciddi bir tərif təqdim edək.

İstiqamətləndirilmiş seqment Onlardan hansının birinci, hansının ikinci olduğu uclarına nisbətən məlum olan seqmenti adlandıraq.

Vektor müəyyən uzunluğa malik yönəldilmiş seqment adlanır, yəni. Bu, müəyyən bir uzunluqda bir seqmentdir, burada onu məhdudlaşdıran nöqtələrdən biri başlanğıc, ikincisi isə son kimi qəbul edilir. Əgər A- vektorun başlanğıcı, B onun sonu, onda vektor simvolla işarələnir, əlavə olaraq vektor çox vaxt tək hərflə işarələnir. Şəkildə vektor seqmentlə, istiqaməti isə oxla göstərilir.

Modul və ya uzunluq Bir vektor onu təyin edən istiqamətlənmiş seqmentin uzunluğu adlanır. || ilə işarələnir və ya ||.

Biz həmçinin vektor kimi başlanğıcı və sonu üst-üstə düşən sıfır vektorunu da daxil edəcəyik. Təyin olunub. Sıfır vektorunun xüsusi istiqaməti yoxdur və onun modulu sıfırdır ||=0.

Vektorlar deyilir kollinear, əgər onlar eyni xətt üzərində və ya paralel xətlər üzərində yerləşirlərsə. Üstəlik və vektorları eyni istiqamətdədirsə, əksini yazacağıq.

Eyni müstəviyə paralel düz xətlər üzərində yerləşən vektorlara deyilir düzbucaqlı.

İki vektor deyilir bərabərdir, əgər onlar kollineardırsa, eyni istiqamətə malikdirlər və uzunluğu bərabərdirlər. Bu halda yazırlar.

Vektorların bərabərliyinin tərifindən belə çıxır ki, vektor mənşəyini fəzanın istənilən nöqtəsində yerləşdirərək özünə paralel daşına bilər.

Misal üçün.

VEKTORLAR ÜZRƏ XƏTİ ƏMƏLƏLƏR

1. Bir vektorun ədədə vurulması.

   Vektor və λ ədədinin hasili yeni vektordur, belə ki:

   Vektor və λ ədədinin hasili ilə işarələnir.

   

   Misal üçün, vektorla eyni istiqamətə yönəlmiş və vektorun uzunluğunun yarısına bərabər olan vektor var.

   Təqdim olunan əməliyyat aşağıdakılara malikdir xassələri:

2. Vektor əlavəsi.

   Qoy və iki ixtiyari vektor olsun. Gəlin ixtiyari bir məqamı götürək O və vektor qurun. Bundan sonra nöqtədən A vektoru bir kənara qoyaq. Birinci vektorun əvvəlini ikincinin sonu ilə birləşdirən vektor deyilir məbləğ bu vektorların və işarələnir .

   

   Vektor əlavəsinin tərtib edilmiş tərifi adlanır paraleloqram qaydası, çünki vektorların eyni cəmini aşağıdakı kimi almaq olar. Nöqtədən təxirə salaq O vektorlar və . Bu vektorlar üzərində paraleloqram quraq OABC. Vektorlar olduğundan, təpədən çəkilmiş paraleloqramın diaqonalı olan vektor O, açıq-aydın vektorların cəmi olacaq.

   

   Aşağıdakıları yoxlamaq asandır vektor əlavəsinin xassələri.

3. Vektor fərqi.

   Verilmiş vektora kollinear, uzunluğu bərabər və əks istiqamətdə olan vektor deyilir əks vektor üçün vektor və ilə işarələnir. Əks vektor vektorun λ = –1 ədədinə vurulmasının nəticəsi hesab edilə bilər: .

Xüsusi dəyərlər(ədədlər) və xüsusi vektorlar.
Həll nümunələri

Özün ol

Hər iki tənlikdən belə nəticə çıxır.

O zaman qoyaq: .

Nəticə olaraq: – ikinci xüsusi vektor.

təkrar edək mühüm məqamlar həllər:

– ortaya çıxan sistem, şübhəsiz ki, var ümumi qərar(tənliklər xətti asılıdır);

– biz “y”-ni elə seçirik ki, tam ədəd olsun və birinci “x” koordinatı tam, müsbət və mümkün qədər kiçik olsun.

– xüsusi həllin sistemin hər bir tənliyini təmin etdiyini yoxlayırıq.

Cavab verin .

Aralıq " nəzarət nöqtələri" kifayət qədər kifayət idi, buna görə də bərabərlikləri yoxlamaq, prinsipcə, lazımsızdır.

Müxtəlif məlumat mənbələrində xüsusi vektorların koordinatları çox vaxt sütunlarda deyil, sətirlərdə yazılır, məsələn: (və düzünü desəm, mən özüm onları sətirlərlə yazmağa öyrəşmişəm). Bu seçim məqbuldur, lakin mövzunun işığında xətti çevrilmələr texniki cəhətdən istifadə etmək daha rahatdır sütun vektorları.

Ola bilsin ki, həll yolu sizə çox uzun göründü, amma bu, ilk nümunəni çox ətraflı şərh etdiyim üçün.

Misal 2

Matrislər

Gəlin özümüz məşq edək! Dərsin sonunda yekun tapşırığın təxmini nümunəsi.

Bəzən etmək lazımdır əlavə tapşırıq, yəni:

kanonik matrisin parçalanmasını yazın

Bu nədir?

Əgər matrisin xüsusi vektorları əmələ gəlirsə əsas, onda aşağıdakı kimi təmsil oluna bilər:

Xüsusi vektorların koordinatlarından ibarət matris haradadır, - diaqonal müvafiq xüsusi qiymətləri olan matris.

Bu matrisin parçalanması adlanır kanonik və ya diaqonal.

Birinci nümunənin matrisinə baxaq. Onun xüsusi vektorları xətti müstəqil(qeyri-kollinear) və əsas təşkil edir. Onların koordinatlarının matrisini yaradaq:

Aktiv əsas diaqonal matrislər müvafiq qaydada yerləşirlər özəl dəyərlər, və qalan elementlər sıfıra bərabərdir:
– Mən bir daha nizamın vacibliyini vurğulayıram: “iki” 1-ci vektora uyğundur və buna görə də 1-ci sütunda, “üç” – 2-ci vektorda yerləşir.

By adi alqoritmə tapmaq tərs matris və ya Gauss-Jordan metodu Biz tapdıq . Xeyr, bu, hərf səhvi deyil! - sizdən əvvəl günəş tutulması kimi nadir bir hadisədir, əksi orijinal matrislə üst-üstə düşür.

Matrisin kanonik parçalanmasını yazmaq qalır:

Sistem elementar çevrilmələrdən istifadə etməklə həll edilə bilər və aşağıdakı nümunələrdə müraciət edəcəyik bu üsul. Ancaq burada "məktəb" üsulu daha sürətli işləyir. 3-cü tənlikdən ifadə edirik: – ikinci tənliyə əvəz edirik:

Birinci koordinat sıfır olduğundan, hər bir tənlikdən belə bir sistem əldə edirik.

Və yenidən xətti əlaqənin məcburi mövcudluğuna diqqət yetirin. Yalnız əhəmiyyətsiz bir həll əldə edilsə , sonra ya özəl dəyər səhv tapılıb, ya da sistem xəta ilə tərtib edilib/həll edilib.

Kompakt koordinatlar dəyəri verir

Xüsusi vektor:

Və bir daha həllin tapıldığını yoxlayırıq sistemin hər bir tənliyini təmin edir. Sonrakı bəndlərdə və sonrakı tapşırıqlarda bu istəyi məcburi qayda kimi qəbul etməyi məsləhət görürəm.

2) Şəxsi dəyər üçün eyni prinsipdən istifadə edərək əldə edirik aşağıdakı sistem:

Sistemin 2-ci tənliyindən ifadə edirik: – üçüncü tənliyi əvəz edirik:

"Zeta" koordinatı sıfıra bərabər olduğundan, onun əməl etdiyi hər bir tənlikdən bir sistem alırıq. xətti asılılıq.

Qoy

Həll olduğunu yoxlamaq sistemin hər bir tənliyini təmin edir.

Beləliklə, xüsusi vektor: .

3) Və nəhayət, sistem öz dəyərinə uyğundur:

İkinci tənlik ən sadə görünür, ona görə də onu ifadə edək və 1-ci və 3-cü tənliklərlə əvəz edək:

Hər şey qaydasındadır - xətti əlaqə yaranıb, onu ifadə ilə əvəz edirik:

Nəticədə “x” və “y” “z” vasitəsilə ifadə olundu: . Praktikada bu cür əlaqələrə dəqiq nail olmaq lazım deyil, bəzi hallarda həm vasitəsilə, həm də vasitəsilə ifadə etmək daha rahatdır. Və ya hətta "qatar" - məsələn, "X" "I" və "I" "Z" vasitəsilə

O zaman qoyaq:

Həllin tapıldığını yoxlayırıq sistemin hər bir tənliyini ödəyir və üçüncü xüsusi vektoru yazır

Cavab verin: özəl vektorlar:

Həndəsi olaraq bu vektorlar üç müxtəlif fəza istiqamətini müəyyən edir ("Orada və yenidən geri"), hansına görə xətti transformasiya sıfırdan fərqli vektorları (xüsusi vektorları) kollinear vektorlara çevirir.

Əgər şərt kanonik parçalanmanın tapılmasını tələb edirdisə, bu, burada mümkündür, çünki müxtəlif xüsusi qiymətlər müxtəlif xətti müstəqil xüsusi vektorlara uyğundur. Matris yaratmaq onların koordinatlarından diaqonal matris -dan müvafiq xüsusi qiymətlər və tapın tərs matris .

Əgər şərtlə yazmaq lazımdırsa xüsusi vektorlar əsasında xətti çevrilmə matrisi, sonra cavabı formada veririk. Fərq var və fərq əhəmiyyətlidir!Çünki bu matris “de” matrisidir.

Daha çox problem sadə hesablamalarüçün müstəqil qərar:

Misal 5

Matrislə verilmiş xətti çevrilmənin xüsusi vektorlarını tapın

Öz nömrələrinizi taparkən, 3-cü dərəcəli çoxhədliyə qədər getməməyə çalışın. Bundan əlavə, sizin sistem həlləriniz mənim həllərimdən fərqli ola bilər - burada heç bir əminlik yoxdur; və tapdığınız vektorlar nümunə vektorlarından müvafiq koordinatlarının mütənasibliyinə qədər fərqli ola bilər. Məsələn, və. Cavabı formada təqdim etmək daha estetik baxımdan xoşdur, amma ikinci variantda dayansanız, yaxşı olar. Bununla belə, hər şey üçün ağlabatan məhdudiyyətlər var; versiya artıq çox yaxşı görünmür.

Dərsin sonunda tapşırığın təxmini yekun nümunəsi.

Çoxsaylı xüsusi qiymətlər halında problemi necə həll etmək olar?

Ümumi alqoritm eyni qalır, lakin onun öz xüsusiyyətləri var və həllin bəzi hissələrini daha sərt akademik üslubda saxlamaq məsləhətdir:

Misal 6

Şəxsi dəyərləri və xüsusi vektorları tapın

Həll

Əlbəttə ki, inanılmaz birinci sütunu böyük hərflə yazaq:

Kvadrat üçhəmi faktorlara ayırdıqdan sonra:

Nəticədə ikisi çoxluq təşkil edən xüsusi qiymətlər əldə edilir.

Xüsusi vektorları tapaq:

1) Gəlin "sadələşdirilmiş" sxemə görə tək əsgərlə məşğul olaq:

Son iki tənlikdən bərabərlik aydın görünür, bu, açıq şəkildə sistemin 1-ci tənliyinə əvəz edilməlidir:

Daha yaxşı birləşmə tapa bilməyəcəksiniz:
Xüsusi vektor:

2-3) İndi bir neçə gözətçini çıxarırıq. IN bu halda nəticə verə bilər ya iki, ya bir məxsus vektor. Köklərin çoxluğundan asılı olmayaraq, dəyəri determinantda əvəz edirik bizə növbəti gətirir xətti tənliklərin homojen sistemi:

Xüsusi vektorlar tam vektorlardır
əsas həllər sistemi

Əslində, bütün dərs boyu biz fundamental sistemin vektorlarını tapmaqdan başqa heç nə etmədik. Sadəcə olaraq, hələlik bu müddət xüsusi tələb olunmur. Yeri gəlmişkən, kamuflyaj kostyumlarında mövzunu qaçıran o ağıllı tələbələr homojen tənliklər, indi siqaret çəkməyə məcbur olacaq.

Yeganə tədbir əlavə xətləri silmək idi. Nəticə ortada rəsmi "addım" olan bir-üç matrisdir.
– əsas dəyişən, – sərbəst dəyişənlər. Beləliklə, iki sərbəst dəyişən var fundamental sistemin iki vektoru da var.

Baza dəyişənini sərbəst dəyişənlərlə ifadə edək: . "X" qarşısındakı sıfır çarpan ona tamamilə hər hansı bir dəyəri almağa imkan verir (tənliklər sistemindən aydın görünür).

Bu problemin kontekstində ümumi həlli sətirdə deyil, sütunda yazmaq daha rahatdır:

Cütlük xüsusi vektora uyğundur:
Cütlük xüsusi vektora uyğundur:

Qeyd : mürəkkəb oxucular bu vektorları şifahi olaraq seçə bilərlər - sadəcə sistemi təhlil etməklə , lakin burada bəzi biliklərə ehtiyac var: üç dəyişən var, sistem matrisinin dərəcəsi- bir, yəni əsas qərar sistemi 3 – 1 = 2 vektordan ibarətdir. Bununla belə, aşkar edilmiş vektorlar hətta bu məlumat olmadan, sırf intuitiv səviyyədə aydın görünür. Bu halda üçüncü vektor daha da “gözəl” yazılacaq: . Bununla belə, xəbərdarlıq edirəm ki, başqa bir misalda sadə seçim mümkün olmaya bilər, ona görə də bənd təcrübəli insanlar üçün nəzərdə tutulub. Bundan əlavə, niyə üçüncü vektor kimi qəbul etməyək? Axı onun koordinatları da sistemin hər bir tənliyini və vektorlarını ödəyir xətti müstəqil. Bu seçim, prinsipcə, uyğundur, lakin "əyri", çünki "digər" vektor əsas sistemin vektorlarının xətti birləşməsidir.

Cavab verin: xüsusi dəyərlər: , xüsusi vektorlar:

Müstəqil bir həll üçün oxşar bir nümunə:

Misal 7

Şəxsi dəyərləri və xüsusi vektorları tapın

Dərsin sonunda yekun dizaynın təxmini nümunəsi.

Qeyd etmək lazımdır ki, həm 6-cı, həm də 7-ci misallarda üçlü xətti müstəqil xüsusi vektorlar alınır və buna görə də orijinal matris kanonik parçalanmada təmsil olunur. Ancaq belə moruq bütün hallarda olmur:

Misal 8

Həll: Xarakterik tənliyi yaradaq və həll edək:

Birinci sütundakı determinantı genişləndirək:

Üçüncü dərəcəli polinomdan qaçaraq, nəzərdən keçirilən üsula uyğun olaraq əlavə sadələşdirmələr aparırıq:

- xüsusi dəyərlər.

Xüsusi vektorları tapaq:

1) Köklə bağlı heç bir çətinlik yoxdur:

Təəccüblənməyin, dəstdən əlavə istifadədə dəyişənlər də var - burada heç bir fərq yoxdur.

3-cü tənlikdən onu ifadə edirik və 1-ci və 2-ci tənliklərə əvəz edirik:

Hər iki tənlikdən belə çıxır:

Qoy o zaman:

2-3) Çoxsaylı dəyərlər üçün sistemi alırıq .

Sistemin matrisini yazaq və elementar çevrilmələrdən istifadə edərək onu mərhələli formaya gətirək:

Kvadrat matrisin öz vektoru odur ki, verilmiş matrislə vurulduqda kollinear vektor yaranır. Sadə sözlərlə, bir matrisi öz vektorla çarparkən, sonuncu eyni qalır, lakin müəyyən bir ədədə vurulur.

Tərif

Öz vektor sıfırdan fərqli V vektordur, M kvadrat matrisə vurulduqda özü müəyyən λ ədədi ilə artır. Cəbri qeydlərdə belə görünür:

M × V = λ × V,

burada λ M matrisinin xüsusi dəyəridir.

Gəlin nəzərdən keçirək ədədi nümunə. Qeydiyyatın asanlığı üçün matrisdəki nömrələr nöqtəli vergüllə ayrılacaq. Gəlin bir matris əldə edək:

• M = 0; 4;
• 6; 10.

Onu sütun vektoruna vuraq:

• V = -2;

Bir matrisi sütun vektoruna vurduqda, bir sütun vektoru da alırıq. sərt riyazi dil 2 × 2 matrisi sütun vektoruna vurmaq üçün düstur belə görünür:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 birinci sətirdə və birinci sütunda yerləşən M matrisinin elementini, M22 isə ikinci sətirdə və ikinci sütunda yerləşən elementi bildirir. Matrisimiz üçün bu elementlər M11 = 0, M12 = 4, M21 = 6, M22 10-a bərabərdir. Sütun vektoru üçün bu dəyərlər V11 = –2, V21 = 1-ə bərabərdir. Bu düstura görə, kvadrat matrisin vektorla hasilinin aşağıdakı nəticəsini alırıq:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Rahatlıq üçün sütun vektorunu bir sıraya yazaq. Beləliklə, kvadrat matrisi vektora (-2; 1) vurduq, nəticədə vektor (4; -2) oldu. Aydındır ki, bu λ = -2 ilə vurulan eyni vektordur. Lambda bu halda matrisin öz dəyərini bildirir.

Bir matrisin özünəməxsus vektoru kollinear vektordur, yəni bir matrislə vurulduqda məkanda mövqeyini dəyişməyən bir cisimdir. Vektor cəbrində kollinearlıq anlayışı həndəsədəki paralellik termininə bənzəyir. Həndəsi şərhdə kollinear vektorlar müxtəlif uzunluqlu paralel istiqamətlənmiş seqmentlərdir. Evklid dövründən biz bilirik ki, bir xəttin ona paralel sonsuz sayda xətləri var, ona görə də hər bir matrisin sonsuz sayda öz vektoru olduğunu düşünmək məntiqlidir.

Əvvəlki nümunədən aydın olur ki, xüsusi vektorlar (-8; 4) və (16; -8) və (32, -16) ola bilər. Bunların hamısı λ = -2 xüsusi dəyərə uyğun gələn kollinear vektorlardır. Orijinal matrisi bu vektorlara vurduqda, yenə də orijinaldan 2 dəfə fərqlənən vektorla nəticələnəcəyik. Məhz buna görə də xüsusi vektorun tapılması məsələlərini həll edərkən yalnız xətti müstəqil vektor obyektlərini tapmaq lazımdır. Çox vaxt n × n matris üçün n sayda xüsusi vektor olur. Kalkulyatorumuz ikinci dərəcəli kvadrat matrislərin təhlili üçün nəzərdə tutulmuşdur, ona görə də demək olar ki, həmişə nəticə üst-üstə düşdüyü hallar istisna olmaqla, iki xüsusi vektor tapacaqdır.

Yuxarıdakı misalda biz ilkin matrisin xüsusi vektorunu əvvəlcədən bilirdik və lambda sayını aydın şəkildə təyin etdik. Bununla belə, praktikada hər şey tərsinə baş verir: əvvəlcə öz dəyərləri, sonra isə öz vektorları tapılır.

Həll alqoritmi

Orijinal M matrisinə yenidən baxaq və onun hər iki xüsusi vektorunu tapmağa çalışaq. Beləliklə, matris belə görünür:

• M = 0; 4;
• 6; 10.

Əvvəlcə aşağıdakı matrisin determinantının hesablanmasını tələb edən λ xüsusi dəyərini təyin etməliyik:

• (0 − λ); 4;
• 6; (10 − λ).

Bu matris əsas diaqonaldakı elementlərdən naməlum λ çıxılmaqla əldə edilir. Determinant standart düsturla müəyyən edilir:

• detA = M11 × M21 - M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Bizim vektorumuz sıfırdan fərqli olmalı olduğundan, nəticədə yaranan tənliyi xətti asılı olaraq qəbul edirik və determinantımızı detA-nı sıfıra bərabərləşdiririk.

(0 − λ) × (10 − λ) − 24 = 0

Mötərizələri açaq və matrisin xarakterik tənliyini əldə edək:

λ 2 − 10λ − 24 = 0

Bu standartdır kvadrat tənlik diskriminant vasitəsilə həll edilməli olan.

D = b 2 − 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

Diskriminantın kökü sqrt(D) = 14, buna görə də λ1 = -2, λ2 = 12. İndi hər lambda dəyəri üçün biz xüsusi vektoru tapmalıyıq. λ = -2 üçün sistem əmsallarını ifadə edək.

• M − λ × E = 2; 4;
• 6; 12.

Bu düsturda E eynilik matrisidir. Yaranan matrisə əsaslanaraq xətti tənliklər sistemi yaradırıq:

2x + 4y = 6x + 12y,

burada x və y xüsusi vektor elementləridir.

Soldakı bütün X-ləri və sağdakı bütün Y-ləri toplayaq. Aydındır ki, - 4x = 8y. İfadəni - 4-ə bölün və x = –2y alın. İndi naməlumların istənilən qiymətini götürərək matrisin birinci xüsusi vektorunu təyin edə bilərik (xətti asılı olan xüsusi vektorların sonsuzluğunu xatırlayın). y = 1 götürək, sonra x = –2. Buna görə də birinci xüsusi vektor V1 = (–2; 1) kimi görünür. Məqalənin əvvəlinə qayıdın. Məhz bu vektor obyekti idi ki, biz xüsusi vektor anlayışını nümayiş etdirmək üçün matrisi vurduq.

İndi λ = 12 üçün məxsusi vektoru tapaq.

• M - λ × E = -12; 4
• 6; -2.

Eyni xətti tənliklər sistemini yaradaq;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x = y.

İndi x = 1 götürürük, buna görə də y = 3. Beləliklə, ikinci xüsusi vektor V2 = (1; 3) kimi görünür. Orijinal matrisi verilmiş vektora vurduqda nəticə həmişə eyni vektorun 12-yə vurulması olacaq. Həll alqoritmi burada bitir. İndi matrisin öz vektorunu əl ilə necə təyin edəcəyinizi bilirsiniz.

• təyinedici;
• iz, yəni əsas diaqonaldakı elementlərin cəmi;
• rütbə, yəni xətti müstəqil sətirlərin/sütunların maksimum sayı.

Proqram yuxarıdakı alqoritmə uyğun işləyir, həll prosesini mümkün qədər qısaldır. Proqramda lambdanın "c" hərfi ilə təyin olunduğunu qeyd etmək vacibdir. Rəqəmsal bir nümunəyə baxaq.

Proqramın necə işlədiyinə dair nümunə

Aşağıdakı matrisin öz vektorlarını təyin etməyə çalışaq:

• M = 5; 13;
• 4; 14.

Gəlin bu dəyərləri kalkulyatorun xanalarına daxil edək və cavabı aşağıdakı formada alaq:

• Matris dərəcəsi: 2;
• Matris təyinedicisi: 18;
• Matris izi: 19;
• Xüsusi vektorun hesablanması: c 2 − 19.00c + 18.00 (xarakteristik tənlik);
• Özvektorun hesablanması: 18 (birinci lambda dəyəri);
• Özvektorun hesablanması: 1 (ikinci lambda dəyəri);
• 1-ci vektor üçün tənliklər sistemi: -13x1 + 13y1 = 4x1 − 4y1;
• 2-ci vektor üçün tənliklər sistemi: 4x1 + 13y1 = 4x1 + 13y1;
• Xüsusi vektor 1: (1; 1);
• Xüsusi vektor 2: (-3,25; 1).

Beləliklə, iki xətti müstəqil xüsusi vektor əldə etdik.

Nəticə

Xətti cəbr və analitik həndəsə hər bir birinci kurs tələbəsi üçün standart fənlərdir. Vektorların və matrislərin çoxluğu qorxuncdur və belə ağır hesablamalarda səhv etmək asandır. Proqramımız tələbələrə öz hesablamalarını yoxlamağa və ya öz vektoru tapmaq məsələsini avtomatik həll etməyə imkan verəcək. Kataloqumuzda başqa xətti cəbr kalkulyatorları var, onlardan dərsinizdə və ya işinizdə istifadə edin.

Tərif 9.3. Vektor X çağırdı məxsus vektor matrislər A, əgər belə bir nömrə varsa λ, bərabərliyi təmin edir: A X= λ X, yəni müraciətin nəticəsidir X matris tərəfindən təyin olunan xətti transformasiya A, bu vektorun ədədə vurulmasıdır λ . Nömrənin özü λ çağırdı xüsusi dəyər matrislər A.

Düsturlara əvəz edilməsi (9.3) x` j = λx j , xüsusi vektorun koordinatlarını təyin etmək üçün tənliklər sistemini alırıq:

. (9.5)

Bu xətti homojen sistemin qeyri-trivial həlli yalnız onun əsas determinantı 0 olarsa (Kramer qaydası) olacaqdır. Bu şərti formada yazmaqla:

xüsusi qiymətləri təyin etmək üçün tənlik alırıq λ , çağırdı xarakterik tənlik. Qısaca onu aşağıdakı kimi təqdim etmək olar:

| A - λE | = 0, (9.6)

çünki onun sol tərəfi matrisin determinantını ehtiva edir A-λE. Polinom nisbi λ | A - λE| çağırdı xarakterik polinom matrislər A.

Xarakterik polinomun xassələri:

1) Xətti çevrilmənin xarakterik polinomu bazisin seçilməsindən asılı deyil. Sübut. (bax (9.4)), lakin deməli, . Beləliklə, əsas seçimindən asılı deyil. Bu o deməkdir ki, | A-λE| yeni bazaya keçərkən dəyişmir.

2) Əgər matris A xətti çevrilmədir simmetrik(bunlar. və ij =a ji), onda (9.6) xarakterik tənliyin bütün kökləri həqiqi ədədlərdir.

Xüsusi qiymətlərin və xüsusi vektorların xüsusiyyətləri:

1) Şəxsi vektorlardan əsas seçsəniz x 1, x 2, x 3 , xüsusi qiymətlərə uyğundur λ 1, λ 2, λ 3 matrislər A, onda bu əsasda xətti çevrilmə A diaqonal formalı matrisa malikdir:

(9.7) Bu xassənin sübutu xüsusi vektorların tərifindən irəli gəlir.

2) Çevrilmənin xüsusi qiymətləri olarsa A fərqlidirlər, onda onların müvafiq məxsusi vektorları xətti müstəqildir.

3) Əgər matrisin xarakterik polinomu Aüçü var müxtəlif köklər, sonra hansısa əsasda matris A diaqonal görünüşə malikdir.

Matrisin xüsusi qiymətlərini və xüsusi vektorlarını tapaq Xarakterik tənlik yaradaq: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Tapılan hər bir qiymətə uyğun olan xüsusi vektorların koordinatlarını tapaq λ. (9.5)-dən belə çıxır ki, əgər X (1) ={x 1 , x 2 , x 3) – uyğun olan xüsusi vektor λ 1 =-2, onda

- kooperativ, lakin qeyri-müəyyən sistem. Onun həlli formada yazıla bilər X (1) ={a,0,-a), burada a istənilən ədəddir. Xüsusilə, biz bunu tələb etsək | x (1) |=1, X (1) =

Sistemə dəyişdirmə (9.5) λ 2 =3, ikinci xüsusi vektorun koordinatlarını təyin etmək üçün bir sistem əldə edirik - x (2) ={y 1 ,y 2 ,y 3}:

, harada X (2) ={b,-b,b) və ya, təmin | x (2) |=1, x (2) =

üçün λ 3 = 6 xüsusi vektoru tapın x (3) ={z 1 , z 2 , z 3}:

, x (3) ={c,2c,c) və ya normallaşdırılmış versiyada

x (3) = Bunu qeyd etmək olar X (1) X (2) = ab–ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = e.ə- 2bc + e.ə= 0. Beləliklə, bu matrisin məxsusi vektorları qoşa ortoqonaldır.

Mühazirə 10.

Kvadrat formalar və onların simmetrik matrislərlə əlaqəsi. Simmetrik matrisin xüsusi vektorlarının və xüsusi qiymətlərinin xassələri. Kvadrat formanın kanonik formaya endirilməsi.

Tərif 10.1.Kvadrat forma real dəyişənlər x 1, x 2,…, x n bu dəyişənlərdə birinci dərəcənin sərbəst termini və həddi olmayan ikinci dərəcəli çoxhəd adlanır.

Kvadrat formaların nümunələri:

(n = 2),

(n = 3). (10.1)

Son mühazirədə verilmiş simmetrik matrisin tərifini xatırlayaq:

Tərif 10.2. Kvadrat matrisa deyilir simmetrik, əgər , yəni əsas diaqonal üzrə simmetrik olan matrisin elementləri bərabərdirsə.

Simmetrik matrisin xüsusi qiymətlərinin və xüsusi vektorlarının xassələri:

1) Simmetrik matrisin bütün xüsusi qiymətləri həqiqidir.

Sübut (üçün n = 2).

Matris olsun A formaya malikdir: . Xarakterik tənlik yaradaq:

(10.2) Diskriminantı tapaq:

Buna görə də tənliyin yalnız həqiqi kökləri var.

2) Simmetrik matrisin məxsusi vektorları ortoqonaldır.

Sübut (üçün n= 2).

Xüsusi vektorların koordinatları və tənlikləri təmin etməlidir.