„Matematik, stejně jako umělec nebo básník, vytváří vzory. A pokud jsou jeho vzory stabilnější, je to jen proto, že jsou složeny z představ... Vzory matematika, stejně jako vzory umělce nebo básníka, musí být krásné; Nápady, stejně jako barvy nebo slova, spolu musí korespondovat. Krása je první požadavek: na světě není místo pro ošklivou matematiku».
G.H.Hardy
V první kapitole bylo poznamenáno, že existují primitivové docela jednoduché funkce, které již nelze vyjádřit prostřednictvím elementární funkce. V tomto ohledu nabývají na praktickém významu ty třídy funkcí, o kterých můžeme přesně říci, že jejich primitivními funkcemi jsou elementární funkce. Tato třída funkcí zahrnuje racionální funkce, představující poměr dvou algebraických polynomů. Mnoho problémů vede k integraci racionálních zlomků. Proto je velmi důležité umět takové funkce integrovat.
2.1.1. Zlomkové racionální funkce
Racionální zlomek(nebo zlomková racionální funkce) je vztah dvou algebraických polynomů:
kde a jsou polynomy.
Připomeňme vám to polynom (polynom, celou racionální funkci) nstupně nazývá funkce formuláře
Kde 
– reálná čísla. Například,
– polynom prvního stupně;
– polynom čtvrtého stupně atd.
Zavolá se racionální zlomek (2.1.1). opravit, pokud je stupeň nižší než stupeň , tzn. n<m, jinak se nazývá zlomek špatně.
Jakýkoli nevlastní zlomek může být reprezentován jako součet polynomu (celá část) a vlastního zlomku (zlomková část). Oddělení celé a zlomkové části nevlastního zlomku lze provést podle pravidla pro dělení polynomů „rohem“.
Příklad 2.1.1. Identifikujte celé a zlomkové části následujících nesprávných racionálních zlomků:
A) 
, b) 
.
Řešení . a) Pomocí algoritmu „rohového“ dělení dostaneme
Tak dostáváme
.
b) Zde také používáme algoritmus „rohového“ dělení:
V důsledku toho dostáváme
.
Pojďme si to shrnout. V obecném případě lze neurčitý integrál racionálního zlomku reprezentovat jako součet integrálů polynomu a vlastního racionálního zlomku. Hledání primitivních derivátů polynomů není obtížné. Proto v následujícím budeme uvažovat hlavně o správných racionálních zlomcích.
2.1.2. Nejjednodušší racionální zlomky a jejich integrace
Mezi vlastními racionálními zlomky existují čtyři typy, které jsou klasifikovány jako nejjednodušší (elementární) racionální zlomky:
|
3) |
4) |
,
,kde je celé číslo, 
, tj. kvadratický trinom 
nemá skutečné kořeny.
Integrace jednoduchých zlomků typu 1 a typu 2 nepředstavuje velké potíže:
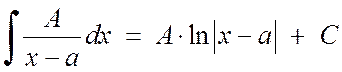, (2.1.3)
. (2.1.4)
Uvažujme nyní integraci jednoduchých zlomků 3. typu, ale nebudeme uvažovat zlomky 4. typu.
Začněme s integrály formuláře
.
Tento integrál se obvykle vypočítá izolací plné náměstí ve jmenovateli. Výsledkem je tabulkový integrál následujícího tvaru
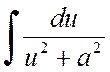nebo 
.
Příklad 2.1.2. Najděte integrály:
A)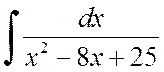 
, b) 
.
Řešení . a) Vyberte celý čtverec z kvadratického trinomu:
Odtud najdeme
b) Izolováním úplného čtverce z kvadratického trinomu získáme:
Tedy,
.
Chcete-li najít integrál
můžete izolovat derivaci jmenovatele v čitateli a rozšířit integrál na součet dvou integrálů: první z nich substitucí 
přijde na vzhled
,
a druhý - k výše uvedenému.
Příklad 2.1.3. Najděte integrály:
.
Řešení
. Všimněte si toho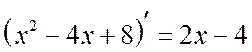 
. Izolujme derivaci jmenovatele v čitateli:
První integrál se vypočítá pomocí substituce 
:
Ve druhém integrálu vybereme ve jmenovateli dokonalý čtverec
Konečně se dostáváme
2.1.3. Správná racionální expanze zlomku
pro součet jednoduchých zlomků
Jakýkoli správný racionální zlomek 
může být reprezentován jedinečným způsobem jako součet jednoduchých zlomků. K tomu musí být jmenovatel faktorizován. Z vyšší algebry je známo, že každý polynom s reálnými koeficienty
Racionální funkce je zlomek tvaru , jehož čitatelem a jmenovatelem jsou polynomy nebo součiny polynomů.
Příklad 1 Krok 2
.
Neurčené koeficienty vynásobíme polynomy, které nejsou v tomto jednotlivém zlomku, ale jsou v jiných výsledných zlomcích:
Otevřeme závorky a přirovnáme čitatele původního integrandu k výslednému výrazu:
Na obou stranách rovnosti hledáme členy se stejnými mocninami x a skládáme z nich soustavu rovnic:
.
Zrušíme všechna x a získáme ekvivalentní systém rovnic:
.
Konečná expanze integrandu na součet jednoduchých zlomků je tedy:
.
Příklad 2 Krok 2 V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Nyní začneme hledat nejisté koeficienty. Abychom to udělali, přirovnáme čitatele původního zlomku ve funkčním výrazu k čitateli výrazu získaného po zmenšení součtu zlomků na společného jmenovatele:
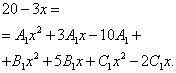
Nyní je potřeba vytvořit a vyřešit soustavu rovnic. K tomu srovnáme koeficienty proměnné na odpovídající stupeň v čitateli původního výrazu funkce a podobné koeficienty ve výrazu získaném v předchozím kroku:
Vyřešíme výsledný systém:
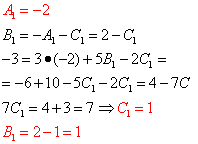
Takže odtud
.
Příklad 3 Krok 2 V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
Začneme hledat nejisté koeficienty. Abychom to udělali, přirovnáme čitatele původního zlomku ve funkčním výrazu k čitateli výrazu získaného po zmenšení součtu zlomků na společného jmenovatele:
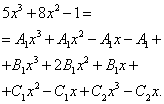
Stejně jako v předchozích příkladech sestavíme soustavu rovnic:
Zmenšíme x a dostaneme ekvivalentní systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
.
Příklad 4. Krok 2 V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Z předchozích příkladů již víme, jak dát čitatel původního zlomku na roveň výrazu v čitateli získaném po rozložení zlomku na součet jednoduchých zlomků a přivedení tohoto součtu na společného jmenovatele. Proto pouze pro účely kontroly uvádíme výsledný systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
Příklad 5. Krok 2 V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Tento součet nezávisle zredukujeme na společného jmenovatele, čímž přirovnáme čitatele tohoto výrazu k čitateli původního zlomku. Výsledkem by měl být následující systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
.
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
.
Příklad 6. Krok 2 V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
S tímto množstvím provedeme stejné akce jako v předchozích příkladech. Výsledkem by měl být následující systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
.
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
.
Příklad 7. Krok 2 V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Po určitých akcích s výsledným množstvím by měl být získán následující systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
.
Příklad 8. Krok 2 V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Udělejme nějaké změny v akcích, které již byly převedeny do automatizace, abychom získali systém rovnic. Existuje umělá technika, která v některých případech pomáhá vyhnout se zbytečným výpočtům. Přivedením součtu zlomků na společného jmenovatele získáme a přirovnáním čitatele tohoto výrazu k čitateli původního zlomku získáme.
TÉMA: Integrace racionálních zlomků.
Pozor! Při studiu jedné ze základních metod integrace: integrace racionálních zlomků je nutné vzít v úvahu polynomy v komplexní doméně, aby bylo možné provést rigorózní důkazy. Proto je to nutné studovat předem některé vlastnosti komplexních čísel a operace s nimi.
Integrace jednoduchých racionálních zlomků.
Li P(z) A Q(z) jsou polynomy v komplexní oblasti, pak jsou to racionální zlomky. Jmenuje se opravit, pokud stupeň P(z) menší stupeň Q(z) , A špatně, pokud stupeň R ne méně než titul Q.
Jakýkoli nesprávný zlomek může být reprezentován jako: 
,
P(z) = Q(z) S(z) + R(z),
A R(z) – polynom, jehož stupeň je menší než stupeň Q(z).
Integrace racionálních zlomků tedy sestává z integrace polynomů, tedy mocninných funkcí a vlastních zlomků, protože jde o vlastní zlomek.
Definice 5. Nejjednodušší (neboli elementární) zlomky jsou následující typy zlomků:
1) , 2) , 3) , 4) 
.
Pojďme zjistit, jak se integrují.
3) 
(studoval dříve).
Věta 5. Každý vlastní zlomek lze vyjádřit jako součet jednoduchých zlomků (bez důkazu).
Důsledek 1. Je-li správný racionální zlomek a jsou-li mezi kořeny polynomu pouze jednoduché reálné kořeny, pak při rozkladu zlomku na součet jednoduchých zlomků budou pouze jednoduché zlomky 1. typu:
Příklad 1
Důsledek 2. Je-li správný racionální zlomek a je-li mezi kořeny polynomu pouze více reálných kořenů, pak při rozkladu zlomku na součet jednoduchých zlomků budou pouze jednoduché zlomky 1. a 2. typu :
Příklad 2
Důsledek 3. Je-li správný racionální zlomek a jsou-li mezi kořeny polynomu pouze jednoduché složené sdružené kořeny, pak při rozkladu zlomku na součet jednoduchých zlomků budou pouze jednoduché zlomky 3. typu:
Příklad 3
Důsledek 4. Je-li správný racionální zlomek a je-li mezi kořeny polynomu pouze více komplexních sdružených kořenů, pak při rozkladu zlomku na součet jednoduchých zlomků budou pouze jednoduché zlomky 3. a 4. typy:
Pro určení neznámých koeficientů v daných expanzích postupujte následovně. Levá a pravá strana rozšíření obsahující neznámé koeficienty se vynásobí. Získá se rovnost dvou polynomů. Z něj se získají rovnice pro požadované koeficienty pomocí:
1. rovnost platí pro všechny hodnoty X (metoda částečné hodnoty). V tomto případě se získá libovolný počet rovnic, z nichž libovolné m umožňuje najít neznámé koeficienty.
2. koeficienty se shodují pro stejné stupně X (metoda nejisté koeficienty). V tomto případě je získána soustava m - rovnic s m - neznámými, ze kterých jsou nalezeny neznámé koeficienty.
3. kombinovaná metoda.
Příklad 5. Rozbalte zlomek 
k těm nejjednodušším.
Řešení:
Pojďme najít koeficienty A a B.
Metoda 1 – metoda soukromé hodnoty:
Metoda 2 – metoda neurčených koeficientů:
Odpověď: 
Integrování racionálních zlomků.
Věta 6. Neurčitý integrál jakéhokoli racionálního zlomku na jakémkoli intervalu, na kterém se jeho jmenovatel nerovná nule, existuje a je vyjádřen pomocí elementárních funkcí, jmenovitě racionálních zlomků, logaritmů a arkustangens.
Důkaz.
Představme si racionální zlomek ve tvaru: 
. V tomto případě je posledním členem vlastní zlomek a podle věty 5 může být reprezentován jako lineární kombinace jednoduchých zlomků. Integrace racionálního zlomku se tedy redukuje na integraci polynomu S(x)
a jednoduché zlomky, jejichž primitivní prvky, jak bylo ukázáno, mají tvar naznačený ve větě.
Komentář. Hlavním problémem je v tomto případě faktorizace jmenovatele, tedy hledání všech jeho kořenů.
Příklad 1. Najděte integrál
Vše výše uvedené v předchozích odstavcích nám umožňuje formulovat základní pravidla pro integraci racionálních zlomků.
1. Je-li racionální zlomek nevlastní, pak je reprezentován jako součet polynomu a vlastního racionálního zlomku (viz odstavec 2).
To redukuje integraci nevlastního racionálního zlomku na integraci polynomu a správného racionálního zlomku.
2. Faktor jmenovatele vlastního zlomku.
3. Vlastní racionální zlomek se rozloží na součet jednoduchých zlomků. To redukuje integraci správného racionálního zlomku na integraci jednoduchých zlomků.
Podívejme se na příklady.
Příklad 1. Najděte .
Řešení. Pod integrálem je nevlastní racionální zlomek. Výběrem celé části dostaneme
Proto,
Všimněte si, že rozšiřme správný racionální zlomek
na jednoduché zlomky:
(viz vzorec (18)). Proto
Tak konečně máme
Příklad 2. Najděte
Řešení. Pod integrálem je správný racionální zlomek.
Rozložením na jednodušší zlomky (viz vzorec (16)) získáme
Materiál uvedený v tomto tématu vychází z informací uvedených v tématu "Racionální zlomky. Rozklad racionálních zlomků na elementární (jednoduché) zlomky". Vřele doporučuji, abyste si toto téma alespoň prolétli, než přejdete k přečtení tohoto materiálu. Navíc budeme potřebovat tabulku neurčitých integrálů.
Dovolte mi, abych vám připomněl několik termínů. Byly probrány v odpovídajícím tématu, proto se zde omezím na stručnou formulaci.
Poměr dvou polynomů $\frac(P_n(x))(Q_m(x))$ se nazývá racionální funkce nebo racionální zlomek. Racionální zlomek se nazývá opravit, pokud $n< m$, т.е. если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе. В противном случае (если $n ≥ m$) дробь называется špatně.
Elementární (jednoduché) racionální zlomky jsou racionální zlomky čtyř typů:
- $\frac(A)(x-a)$;
- $\frac(A)((x-a)^n)$ ($n=2,3,4, \ldots$);
- $\frac(Mx+N)(x^2+px+q)$ ($p^2-4q< 0$);
- $\frac(Mx+N)((x^2+px+q)^n)$ ($p^2-4q< 0$; $n=2,3,4,\ldots$).
Poznámka (žádoucí pro úplnější porozumění textu): show\hide
Proč je potřeba podmínka $p^2-4q?< 0$ в дробях третьего и четвертого типов? Рассмотрим квадратное уравнение $x^2+px+q=0$. Дискриминант этого уравнения $D=p^2-4q$. По сути, условие $p^2-4q < 0$ означает, что $D < 0$. Если $D < 0$, то уравнение $x^2+px+q=0$ не имеет действительных корней. Т.е. выражение $x^2+px+q$ неразложимо на множители. Именно эта неразложимость нас и интересует.
Například pro výraz $x^2+5x+10$ dostaneme: $p^2-4q=5^2-4\cdot 10=-15$. Protože $p^2-4q=-15< 0$, то выражение $x^2+5x+10$ нельзя разложить на множители.
Mimochodem, pro tuto kontrolu není vůbec nutné, aby koeficient před $x^2$ byl roven 1. Například pro $5x^2+7x-3=0$ dostaneme: $D=7^ 2-4\cdot 5 \cdot (-3)=$109. Protože $D > 0$, výraz $5x^2+7x-3$ je faktorizovatelný.
Lze nalézt příklady racionálních zlomků (vlastních i nevlastních), stejně jako příklady rozkladu racionálního zlomku na elementární. Zde nás budou zajímat pouze otázky jejich integrace. Začněme integrací elementárních zlomků. Takže každý ze čtyř výše uvedených typů elementárních zlomků lze snadno integrovat pomocí níže uvedených vzorců. Dovolte mi připomenout, že při integraci zlomků typů (2) a (4) se předpokládá $n=2,3,4,\ldots$. Vzorce (3) a (4) vyžadují splnění podmínky $p^2-4q< 0$.
\begin(rovnice) \int \frac(A)(x-a) dx=A\cdot \ln |x-a|+C \end(rovnice) \begin(rovnice) \int\frac(A)((x-a)^n )dx=-\frac(A)((n-1)(x-a)^(n-1))+C \end(rovnice) \begin(rovnice) \int \frac(Mx+N)(x^2 +px+q) dx= \frac(M)(2)\cdot \ln (x^2+px+q)+\frac(2N-Mp)(\sqrt(4q-p^2))\arctg\ frac(2x+p)(\sqrt(4q-p^2))+C \end(rovnice)
Pro $\int\frac(Mx+N)((x^2+px+q)^n)dx$ se provede substituce $t=x+\frac(p)(2)$, po které je výsledný interval rozdělena na dvě. První se vypočítá zadáním pod znaménkem rozdílu a druhý bude mít tvar $I_n=\int\frac(dt)((t^2+a^2)^n)$. Tento integrál se bere pomocí rekurentního vztahu
\begin(rovnice) I_(n+1)=\frac(1)(2na^2)\frac(t)((t^2+a^2)^n)+\frac(2n-1)(2na ^2)I_n,\; n\in N\end (rovnice)
Výpočet takového integrálu je probrán v příkladu č. 7 (viz třetí část).
Schéma pro výpočet integrálů racionálních funkcí (racionálních zlomků):
- Pokud je integrand elementární, použijte vzorce (1)-(4).
- Pokud integrand není elementární, reprezentujte jej jako součet elementárních zlomků a poté integrujte pomocí vzorců (1)-(4).
Výše uvedený algoritmus pro integraci racionálních zlomků má nespornou výhodu - je univerzální. Tito. pomocí tohoto algoritmu můžete integrovat žádný racionální zlomek. Proto jsou téměř všechny změny proměnných v neurčitém integrálu (Euler, Čebyšev, univerzální goniometrická substituce) provedeny tak, že po této změně dostaneme racionální zlomek pod intervalem. A pak na něj aplikujte algoritmus. Po krátké poznámce analyzujeme přímou aplikaci tohoto algoritmu na příkladech.
$$ \int\frac(7dx)(x+9)=7\ln|x+9|+C. $$
V zásadě lze tento integrál snadno získat bez mechanické aplikace vzorce. Pokud odebereme konstantu $7$ ze znaménka integrálu a vezmeme v úvahu, že $dx=d(x+9)$, dostaneme:
$$ \int\frac(7dx)(x+9)=7\cdot \int\frac(dx)(x+9)=7\cdot \int\frac(d(x+9))(x+9 )=|u=x+9|=7\cdot\int\frac(du)(u)=7\ln|u|+C=7\ln|x+9|+C. $$
Pro podrobné informace doporučuji podívat se do tématu. Podrobně vysvětluje, jak se takové integrály řeší. Mimochodem, vzorec je dokázán stejnými transformacemi, které byly použity v tomto odstavci při jeho „ručním řešení“.
2) Opět existují dva způsoby: použijte hotový vzorec nebo se bez něj obejděte. Pokud použijete vzorec, měli byste vzít v úvahu, že koeficient před $x$ (číslo 4) bude muset být odstraněn. Chcete-li to provést, jednoduše vyjměte tyto čtyři ze závorek:
$$ \int\frac(11dx)((4x+19)^8)=\int\frac(11dx)(\left(4\left(x+\frac(19)(4)\vpravo)\vpravo)^ 8)= \int\frac(11dx)(4^8\left(x+\frac(19)(4)\vpravo)^8)=\int\frac(\frac(11)(4^8)dx) (\left(x+\frac(19)(4)\right)^8). $$
Nyní je čas použít vzorec:
$$ \int\frac(\frac(11)(4^8)dx)(\left(x+\frac(19)(4)\right)^8)=-\frac(\frac(11)(4 ^8))((8-1)\left(x+\frac(19)(4) \right)^(8-1))+C= -\frac(\frac(11)(4^8)) (7\left(x+\frac(19)(4) \right)^7)+C=-\frac(11)(7\cdot 4^8 \left(x+\frac(19)(4) \right )^7)+C. $$
Můžete se obejít bez použití vzorce. A to i bez vyjmutí konstantních 4 $ z hranatých závorek. Pokud vezmeme v úvahu, že $dx=\frac(1)(4)d(4x+19)$, dostaneme:
$$ \int\frac(11dx)((4x+19)^8)=11\int\frac(dx)((4x+19)^8)=\frac(11)(4)\int\frac( d(4x+19))((4x+19)^8)=|u=4x+19|=\\ =\frac(11)(4)\int\frac(du)(u^8)=\ frac(11)(4)\int u^(-8)\;du=\frac(11)(4)\cdot\frac(u^(-8+1))(-8+1)+C= \\ =\frac(11)(4)\cdot\frac(u^(-7))(-7)+C=-\frac(11)(28)\cdot\frac(1)(u^7 )+C=-\frac(11)(28(4x+19)^7)+C. $$
Podrobné vysvětlení hledání takových integrálů je uvedeno v tématu „Integrace substitucí (substituce pod diferenciálním znaménkem)“.
3) Potřebujeme integrovat zlomek $\frac(4x+7)(x^2+10x+34)$. Tento zlomek má strukturu $\frac(Mx+N)(x^2+px+q)$, kde $M=4$, $N=7$, $p=10$, $q=34$. Abyste se však ujistili, že se skutečně jedná o elementární zlomek třetího typu, musíte zkontrolovat, zda je splněna podmínka $p^2-4q< 0$. Так как $p^2-4q=10^2-4\cdot 34=-16 < 0$, то мы действительно имеем дело с интегрированием элементарной дроби третьего типа. Как и в предыдущих пунктах есть два пути для нахождения $\int\frac{4x+7}{x^2+10x+34}dx$. Первый путь - банально использовать формулу . Подставив в неё $M=4$, $N=7$, $p=10$, $q=34$ получим:
$$ \int\frac(4x+7)(x^2+10x+34)dx = \frac(4)(2)\cdot \ln (x^2+10x+34)+\frac(2\cdot 7-4\cdot 10)(\sqrt(4\cdot 34-10^2)) \arctg\frac(2x+10)(\sqrt(4\cdot 34-10^2))+C=\\ = 2\cdot \ln (x^2+10x+34)+\frac(-26)(\sqrt(36)) \arctg\frac(2x+10)(\sqrt(36))+C =2\cdot \ln (x^2+10x+34)+\frac(-26)(6) \arctg\frac(2x+10)(6)+C=\\ =2\cdot \ln (x^2+10x +34)-\frac(13)(3) \arctg\frac(x+5)(3)+C. $$
Řešíme stejný příklad, ale bez použití hotového vzorce. Zkusme izolovat derivaci jmenovatele v čitateli. Co to znamená? Víme, že $(x^2+10x+34)"=2x+10$. Je to výraz $2x+10$, který musíme v čitateli izolovat. Čitatel zatím obsahuje pouze $4x+7$, ale to nebude trvat dlouho, aplikujme na čitatel následující transformaci:
$$ 4x+7=2\cdot 2x+7=2\cdot (2x+10-10)+7=2\cdot(2x+10)-2\cdot 10+7=2\cdot(2x+10) -13. $$
Nyní se v čitateli objeví požadovaný výraz $2x+10$. A náš integrál lze přepsat takto:
$$ \int\frac(4x+7)(x^2+10x+34) dx= \int\frac(2\cdot(2x+10)-13)(x^2+10x+34)dx. $$
Rozdělme integrand na dva. No, a proto je samotný integrál také „rozdvojený“:
$$ \int\frac(2\cdot(2x+10)-13)(x^2+10x+34)dx=\int \left(\frac(2\cdot(2x+10))(x^2 +10x+34)-\frac(13)(x^2+10x+34) \vpravo)\; dx=\\ =\int \frac(2\cdot(2x+10))(x^2+10x+34)dx-\int\frac(13dx)(x^2+10x+34)=2\cdot \int \frac((2x+10)dx)(x^2+10x+34)-13\cdot\int\frac(dx)(x^2+10x+34). $$
Promluvme si nejprve o prvním integrálu, tzn. asi $\int \frac((2x+10)dx)(x^2+10x+34)$. Protože $d(x^2+10x+34)=(x^2+10x+34)"dx=(2x+10)dx$, pak čitatel integrandu obsahuje diferenciál jmenovatele. Stručně řečeno, místo toho výrazu $( 2x+10)dx$ napíšeme $d(x^2+10x+34)$.
Nyní si řekněme pár slov o druhém integrálu. Vyberme celý čtverec ve jmenovateli: $x^2+10x+34=(x+5)^2+9$. Navíc bereme v úvahu $dx=d(x+5)$. Nyní lze součet integrálů, které jsme získali dříve, přepsat do trochu jiné formy:
$$ 2\cdot\int \frac((2x+10)dx)(x^2+10x+34)-13\cdot\int\frac(dx)(x^2+10x+34) =2\cdot \int \frac(d(x^2+10x+34))(x^2+10x+34)-13\cdot\int\frac(d(x+5))((x+5)^2+ 9). $$
Pokud provedeme substituci $u=x^2+10x+34$ v prvním integrálu, bude mít tvar $\int\frac(du)(u)$ a bude mít snadné použití druhý vzorec od . Pokud jde o druhý integrál, je pro něj možná změna $u=x+5$, po které bude mít tvar $\int\frac(du)(u^2+9)$. Tento čistá voda jedenáctý vzorec z tabulky neurčitých integrálů. Takže, když se vrátíme k součtu integrálů, máme:
$$ 2\cdot\int \frac(d(x^2+10x+34))(x^2+10x+34)-13\cdot\int\frac(d(x+5))((x+ 5) )^2+9) =2\cdot\ln(x^2+10x+34)-\frac(13)(3)\arctg\frac(x+5)(3)+C. $$
Dostali jsme stejnou odpověď jako při aplikaci vzorce, což, přísně vzato, není překvapivé. Obecně platí, že vzorec se dokazuje stejnými metodami, které jsme použili k nalezení tohoto integrálu. Věřím, že pozornému čtenáři zde možná napadne jedna otázka, proto ji zformuluji:
Otázka č. 1
Pokud použijeme druhý vzorec z tabulky neurčitých integrálů na integrál $\int \frac(d(x^2+10x+34))(x^2+10x+34)$, dostaneme následující:
$$ \int \frac(d(x^2+10x+34))(x^2+10x+34)=|u=x^2+10x+34|=\int\frac(du)(u) =\ln|u|+C=\ln|x^2+10x+34|+C. $$
Proč v řešení nebyl žádný modul?
Odpověď na otázku č. 1
Otázka je zcela přirozená. Modul chyběl pouze proto, že výraz $x^2+10x+34$ pro libovolné $x\in R$ je větší než nula. To je docela snadné ukázat několika způsoby. Například, protože $x^2+10x+34=(x+5)^2+9$ a $(x+5)^2 ≥ 0$, pak $(x+5)^2+9 > 0$ . Můžete přemýšlet jinak, aniž byste použili výběr úplného čtverce. Od $10^2-4\cdot 34=-16< 0$, то $x^2+10x+34 >0$ za jakékoli $x\in R$ (pokud toto logický řetězec Je to úžasné, doporučuji shlédnout grafická metodařešení kvadratických nerovností). V každém případě, protože $x^2+10x+34 > 0$, pak $|x^2+10x+34|=x^2+10x+34$, tzn. Místo modulu můžete použít běžné závorky.
Všechny body příkladu č. 1 jsou vyřešeny, zbývá jen zapsat odpověď.
Odpověď:
- $\int\frac(7dx)(x+9)=7\ln|x+9|+C$;
- $\int\frac(11dx)((4x+19)^8)=-\frac(11)(28(4x+19)^7)+C$;
- $\int\frac(4x+7)(x^2+10x+34)dx=2\cdot\ln(x^2+10x+34)-\frac(13)(3)\arctg\frac(x +5)(3)+C$.
Příklad č. 2
Najděte integrál $\int\frac(7x+12)(3x^2-5x-2)dx$.
Na první pohled je integrandový zlomek $\frac(7x+12)(3x^2-5x-2)$ velmi podobný elementárnímu zlomku třetího typu, tzn. podle $\frac(Mx+N)(x^2+px+q)$. Zdá se, že jediným rozdílem je koeficient $3$ před $x^2$, ale odstranění koeficientu netrvá dlouho (vyjměte jej z hranatých závorek). Tato podobnost je však zřejmá. Pro zlomek $\frac(Mx+N)(x^2+px+q)$ je podmínka $p^2-4q povinná< 0$, которое гарантирует, что знаменатель $x^2+px+q$ нельзя разложить на множители. Проверим, как обстоит дело с разложением на множители у знаменателя нашей дроби, т.е. у многочлена $3x^2-5x-2$.
Náš koeficient před $x^2$ není roven jedné, proto zkontrolujte podmínku $p^2-4q< 0$ напрямую мы не можем. Однако тут нужно вспомнить, откуда взялось выражение $p^2-4q$. Это всего лишь дискриминант kvadratická rovnice$x^2+px+q=0$. Pokud je diskriminant menší než nula, pak výraz $x^2+px+q$ nelze faktorizovat. Vypočítejme diskriminant polynomu $3x^2-5x-2$ umístěný ve jmenovateli našeho zlomku: $D=(-5)^2-4\cdot 3\cdot(-2)=49$. Takže $D > 0$, proto výraz $3x^2-5x-2$ lze faktorizovat. To znamená, že zlomek $\frac(7x+12)(3x^2-5x-2)$ není elementární zlomek třetího typu a použijte $\int\frac(7x+12)(3x^2- ) k integrálnímu vzorci 5x-2)dx$ není možné.
Pokud daný racionální zlomek není elementární zlomek, pak je třeba jej reprezentovat jako součet elementárních zlomků a poté integrovat. Zkrátka využijte stezku. Podrobně je napsáno, jak rozložit racionální zlomek na elementární. Začněme faktorováním jmenovatele:
$$ 3x^2-5x-2=0;\\ \begin(zarovnáno) & D=(-5)^2-4\cdot 3\cdot(-2)=49;\\ & x_1=\frac( -(-5)-\sqrt(49))(2\cdot 3)=\frac(5-7)(6)=\frac(-2)(6)=-\frac(1)(3); \\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot 3)=\frac(5+7)(6)=\frac(12)(6)=2.\ \\konec (zarovnáno)\\ 3x^2-5x-2=3\cdot\left(x-\left(-\frac(1)(3)\right)\right)\cdot (x-2)= 3\cdot\left(x+\frac(1)(3)\right)(x-2). $$
Subinterkální zlomek uvádíme v této podobě:
$$ \frac(7x+12)(3x^2-5x-2)=\frac(7x+12)(3\cdot\left(x+\frac(1)(3)\vpravo)(x-2) )=\frac(\frac(7)(3)x+4)(\levá(x+\frac(1)(3)\vpravo)(x-2)). $$
Nyní rozložme zlomek $\frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))$ na elementární:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2)) =\frac(A)(x+\frac( 1)(3))+\frac(B)(x-2)=\frac(A(x-2)+B\levý(x+\frac(1)(3)\vpravo))(\levý(x+ \frac(1)(3)\right)(x-2));\\ \frac(7)(3)x+4=A(x-2)+B\left(x+\frac(1)( 3)\vpravo). $$
Koeficienty $A$ a $B$ lze nalézt dvěma standardními způsoby: metodou neurčitých koeficientů a metodou substituce dílčích hodnot. Použijme metodu substituce částečné hodnoty, dosazením $x=2$ a poté $x=-\frac(1)(3)$:
$$ \frac(7)(3)x+4=A(x-2)+B\levý(x+\frac(1)(3)\vpravo).\\ x=2;\; \frac(7)(3)\cdot 2+4=A(2-2)+B\left(2+\frac(1)(3)\vpravo); \; \frac(26)(3)=\frac(7)(3)B;\; B=\frac(26)(7).\\ x=-\frac(1)(3);\; \frac(7)(3)\cdot \left(-\frac(1)(3) \right)+4=A\left(-\frac(1)(3)-2\right)+B\left (-\frac(1)(3)+\frac(1)(3)\right); \; \frac(29)(9)=-\frac(7)(3)A;\; A=-\frac(29\cdot 3)(9\cdot 7)=-\frac(29)(21).\\ $$
Vzhledem k tomu, že koeficienty byly nalezeny, zbývá pouze zapsat hotové rozšíření:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))=\frac(-\frac(29)( 21))(x+\frac(1)(3))+\frac(\frac(26)(7))(x-2). $$
V zásadě můžete tento záznam nechat, ale líbí se mi přesnější možnost:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))=-\frac(29)(21)\ cdot\frac(1)(x+\frac(1)(3))+\frac(26)(7)\cdot\frac(1)(x-2). $$
Vrátíme-li se k původnímu integrálu, dosadíme do něj výsledné rozšíření. Potom rozdělíme integrál na dva a na každý použijeme vzorec. Dávám přednost okamžitému umístění konstant mimo znaménko integrálu:
$$ \int\frac(7x+12)(3x^2-5x-2)dx =\int\left(-\frac(29)(21)\cdot\frac(1)(x+\frac(1) (3))+\frac(26)(7)\cdot\frac(1)(x-2)\vpravo)dx=\\ =\int\left(-\frac(29)(21)\cdot\ frac(1)(x+\frac(1)(3))\right)dx+\int\left(\frac(26)(7)\cdot\frac(1)(x-2)\right)dx =- \frac(29)(21)\cdot\int\frac(dx)(x+\frac(1)(3))+\frac(26)(7)\cdot\int\frac(dx)(x-2 )dx=\\ =-\frac(29)(21)\cdot\ln\left|x+\frac(1)(3)\right|+\frac(26)(7)\cdot\ln|x- 2|+C. $$
Odpověď: $\int\frac(7x+12)(3x^2-5x-2)dx=-\frac(29)(21)\cdot\ln\left|x+\frac(1)(3)\vpravo| +\frac(26)(7)\cdot\ln|x-2|+C$.
Příklad č. 3
Najděte integrál $\int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx$.
Potřebujeme integrovat zlomek $\frac(x^2-38x+157)((x-1)(x+4)(x-9))$. Čitatel obsahuje polynom druhého stupně a jmenovatel obsahuje polynom třetího stupně. Protože stupeň polynomu v čitateli je menší než stupeň polynomu ve jmenovateli, tzn. 2 $< 3$, то подынтегральная дробь является правильной. Разложение этой дроби на элементарные (простейшие) было получено в примере №3 на странице, посвящённой разложению рациональных дробей на элементарные. Полученное разложение таково:
$$ \frac(x^2-38x+157)((x-1)(x+4)(x-9))=-\frac(3)(x-1)+\frac(5)(x +4)-\frac(1)(x-9). $$
Stačí rozdělit daný integrál na tři a na každý aplikovat vzorec. Dávám přednost okamžitému umístění konstant mimo znaménko integrálu:
$$ \int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx=\int\left(-\frac(3)(x-1) +\frac(5)(x+4)-\frac(1)(x-9) \right)dx=\\=-3\cdot\int\frac(dx)(x-1)+ 5\cdot \int\frac(dx)(x+4)-\int\frac(dx)(x-9)=-3\ln|x-1|+5\ln|x+4|-\ln|x- 9|+C. $$
Odpověď: $\int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx=-3\ln|x-1|+5\ln|x+ 4 |-\ln|x-9|+C$.
Pokračování rozboru příkladů tohoto tématu se nachází v druhé části.
