Najít derivace goniometrické funkce potřeba použít tabulka derivátů, a to deriváty 6-13.
Když najdete prvotřídní deriváty goniometrické funkce Abyste se vyhnuli běžným chybám, měli byste věnovat pozornost následujícím bodům:
- ve výrazu funkce je často jeden z termínů sinus, kosinus nebo jiná goniometrická funkce ne z argumentu funkce, ale z čísla (konstanty), proto je derivace tohoto členu rovna nule;
- téměř vždy musíte zjednodušit výraz získaný v důsledku diferenciace, a proto musíte s jistotou používat znalosti operací se zlomky;
- Pro zjednodušení výrazu téměř vždy potřebujete znát goniometrické identity, například vzorec dvojitý úhel a vzorec pro jednotu jako součet druhých mocnin sinus a kosinus.
Příklad 1. Najděte derivaci funkce
Řešení. Řekněme s derivát kosinu vše je jasné, řekne si mnozí, kteří začínají studovat deriváty. Co takhle derivace sinus dvanáct děleno pí? Odpověď: považujte to za rovné nule! Zde je sinus (koneckonců funkce!) pastí, protože argumentem není proměnná X ani jiná proměnná, ale pouze číslo. To znamená, že sinus tohoto čísla je také číslo. A derivace čísla (konstanty), jak víme z tabulky derivací, je rovna nule. Takže ponecháme pouze mínus sinus X a najdeme jeho derivaci, nezapomeneme na znaménko:
![]() .
.
Příklad 2 Najděte derivaci funkce
![]() .
.
Řešení. Druhý termín je stejný případ jako první termín v předchozím příkladu. To znamená, že je to číslo a derivace čísla je nula. Najdeme derivaci druhého členu jako derivaci kvocientu:
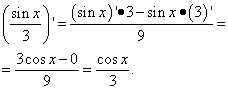
Příklad 3 Najděte derivaci funkce
Řešení. To je další problém: zde v prvním členu není žádný arkussinus nebo jiná trigonometická funkce, ale existuje x, což znamená, že je funkcí x. Proto jej rozlišujeme jako termín v součtu funkcí:

Zde byly vyžadovány dovednosti v operacích se zlomky, konkrétně v odstranění třípatrové struktury zlomku.
Příklad 4. Najděte derivaci funkce
![]() .
.
Řešení. Písmeno "phi" zde hraje stejnou roli jako "x" v předchozích případech (a ve většině ostatních, ale ne ve všech) - nezávislá proměnná. Když tedy hledáme derivaci součinu funkcí, nebudeme spěchat, abychom prohlašovali derivaci odmocniny „phi“ za rovnou nule. Tak:
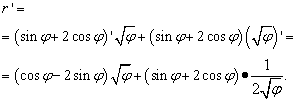
Tím ale řešení nekončí. Vzhledem k tomu, že podobné výrazy jsou shromážděny ve dvou závorkách, musíme výraz transformovat (zjednodušit). Závorky tedy vynásobíme faktory, které za nimi stojí, a poté přivedeme členy ke společnému jmenovateli a provedeme další elementární transformace:

Příklad 5. Najděte derivaci funkce
Řešení. V tomto příkladu budeme potřebovat znát skutečnost, že existuje taková goniometrická funkce - sečna - a její vzorce přes kosinus. Pojďme rozlišovat:

Příklad 6. Najděte derivaci funkce
![]() .
.
Řešení. V tomto příkladu si budeme muset pamatovat vzorec dvojitého úhlu ze školy. Nejprve ale rozlišujme:

![]() ,
,
(toto je vzorec dvojitého úhlu)
Jsou uvedeny derivace inverzních goniometrických funkcí a odvození jejich vzorců. Jsou také uvedeny výrazy pro deriváty vyššího řádu. Odkazy na stránky s podrobnějším popisem odvození vzorců.
Nejprve odvodíme vzorec pro derivaci arkussinus. Nechat
y = arcsin x.
Protože arcsinus je inverzní funkcí sinus
.
Zde je y funkcí x. Diferencujte s ohledem na proměnnou x:
.
Aplikujeme:
.
Tak jsme našli:
.
Protože pak . Pak
.
A předchozí vzorec má tvar:
. Odtud
.
Přesně tímto způsobem můžete získat vzorec pro derivaci arc cosinus. Je však jednodušší použít vzorec týkající se inverzních goniometrických funkcí:
.
Pak
.
Podrobnější popis je uveden na stránce „Odvození derivátů arcsinu a arckosinu“. Tam je to dáno odvození derivátů dvěma způsoby- diskutované výše a podle vzorce pro derivaci inverzní funkce.
Odvození derivací arkustangens a arkotangens
Stejným způsobem najdeme deriváty arkustangens a arkotangens.
Nechat
y = arctan x.
Arktangens je inverzní funkce tečny:
.
Diferencujte s ohledem na proměnnou x:
.
Aplikujeme vzorec pro derivaci komplexní funkce:
.
Tak jsme našli:
.
Derivát obloukového kotangens:
.
Deriváty arcsinu
Nechat
.
Již jsme našli derivaci prvního řádu arcsinus:
.
Odlišením najdeme derivaci druhého řádu:
;
.
Může být také zapsán v následujícím tvaru:
.
Odtud se dostáváme diferenciální rovnice, který je splněn arcsinusovými derivacemi prvního a druhého řádu:
.
Derivováním této rovnice můžeme najít derivace vyšších řádů.
Derivace arcsinusu n-tého řádu
Derivace arkussinus n-tého řádu má následující tvar:
,
kde je polynom stupně . Určuje se podle vzorců:
;
.
Tady .
Polynom splňuje diferenciální rovnici:
.
Derivace arkkosinu n-tého řádu
Derivace pro arc cosinus se získají z derivací pro arc sinus pomocí trigonometrického vzorce:
.
Proto se derivace těchto funkcí liší pouze znaménkem:
.
Deriváty arkustangens
Nechte Našli jsme derivaci obloukového kotangens prvního řádu:
.
Rozdělme zlomek do jeho nejjednodušší podoby:
.
Zde je pomyslná jednotka, .
Jednou derivujeme a zlomek přivedeme ke společnému jmenovateli:
.
Nahrazením získáme:
.
Derivace arkustangens n-tého řádu
Derivace arkustangens n-tého řádu tedy může být reprezentována několika způsoby:
;
.
Deriváty obloukového kotangens
Nech to být teď. Použijme vzorec spojující inverzní goniometrické funkce:
.
Potom se derivace arkus tangens n-tého řádu liší od derivace arkus tangens pouze znaménkem:
.
Nahrazením najdeme:
.
Reference:
N.M. Gunter, R.O. Kuzmin, Sbírka úloh z vyšší matematiky, „Lan“, 2003.
Při odvození úplně prvního vzorce tabulky budeme vycházet z definice derivační funkce v bodě. Vezměme kam X– jakékoli reálné číslo, tj. X– libovolné číslo z definičního oboru funkce. Zapišme limitu poměru přírůstku funkce k přírůstku argumentu na : ![]()
Je třeba poznamenat, že pod mezním znaménkem se získá výraz, kterým není nejistota nuly dělená nulou, protože čitatel neobsahuje nekonečně malou hodnotu, ale právě nulu. Jinými slovy, přírůstek konstantní funkce je vždy nulový.
Tím pádem, derivace konstantní funkcese rovná nule v celé oblasti definice.
Derivace mocninné funkce.
Odvozovací vzorec výkonová funkce vypadá jako ![]() , kde exponent p– libovolné reálné číslo.
, kde exponent p– libovolné reálné číslo.
Dokažme nejprve vzorec pro přirozený exponent, tedy pro p = 1, 2, 3, …
Použijeme definici derivace. Zapišme si limitu poměru přírůstku mocninné funkce k přírůstku argumentu: 
Pro zjednodušení výrazu v čitateli se obrátíme na Newtonův binomický vzorec: 
Proto, 
To dokazuje vzorec pro derivaci mocninné funkce pro přirozený exponent.
Derivace exponenciální funkce.
Uvádíme odvození derivačního vzorce na základě definice:
Dospěli jsme k nejistotě. Abychom ji rozšířili, zavedeme novou proměnnou a na adrese . Pak . V posledním přechodu jsme použili vzorec pro přechod na nový logaritmický základ.
Dosadíme do původního limitu: 
Vzpomeneme-li si na druhou pozoruhodnou limitu, dostaneme se ke vzorci pro derivaci exponenciální funkce: 
Derivace logaritmické funkce.
Dokažme vzorec pro derivaci logaritmické funkce pro všechny X z domény definice a všech platných hodnot báze A logaritmus Podle definice derivátu máme: 
Jak jste si všimli, během důkazu byly transformace prováděny pomocí vlastností logaritmu. Rovnost  je pravdivý kvůli druhému pozoruhodnému limitu.
je pravdivý kvůli druhému pozoruhodnému limitu.
Derivace goniometrických funkcí.
Abychom odvodili vzorce pro derivace goniometrických funkcí, budeme si muset připomenout některé trigonometrické vzorce a také první pozoruhodnou limitu.
Definicí derivace pro funkci sinus, kterou máme ![]() .
.
Použijme rozdíl sinusového vzorce: 
Zbývá se obrátit k prvnímu pozoruhodnému limitu: 
Tedy derivace funkce hřích x Tady je cos x.
Vzorec pro derivaci kosinusu se dokazuje úplně stejným způsobem. 
Tedy derivace funkce cos x Tady je – hřích x.
Vzorce pro tabulku derivací pro tečnu a kotangens odvodíme pomocí osvědčených pravidel derivování (derivace zlomku). 
Deriváty hyperbolických funkcí.
Pravidla derivace a vzorec pro derivaci exponenciální funkce z tabulky derivací nám umožňují odvodit vzorce pro derivace hyperbolického sinu, kosinu, tangens a kotangens. 
Derivace inverzní funkce.
Abychom předešli zmatkům při prezentaci, označme dolním indexem argument funkce, pomocí které se derivace provádí, to znamená, že je to derivace funkce f(x) Podle X.
Nyní formulujme pravidlo pro nalezení derivace inverzní funkce.
Nechte funkce y = f(x) A x = g(y) vzájemně inverzní, definované na intervalech resp. Pokud v bodě existuje konečná nenulová derivace funkce f(x), pak v bodě existuje konečná derivace inverzní funkce g(y), a ![]() . V jiném příspěvku
. V jiném příspěvku ![]() .
.
Toto pravidlo lze přeformulovat pro všechny X z intervalu , pak dostaneme  .
.
Pojďme zkontrolovat platnost těchto vzorců.
Pojďme najít inverzní funkci pro přirozený logaritmus ![]() (Tady y je funkce a X- argument). Po vyřešení této rovnice pro X, dostaneme (zde X je funkce a y– její argument). to znamená,
(Tady y je funkce a X- argument). Po vyřešení této rovnice pro X, dostaneme (zde X je funkce a y– její argument). to znamená, ![]() a vzájemně inverzní funkce.
a vzájemně inverzní funkce.
Z tabulky derivátů to vidíme ![]() A
A ![]() .
.
Ujistěte se, že vzorce pro hledání derivací inverzní funkce nás vedou ke stejným výsledkům: 
Z kurzu geometrie a matematiky jsou školáci zvyklí na to, že pojem derivace je jim zprostředkován prostřednictvím oblasti figury, diferenciálů, limitů funkcí a také limit. Zkusme se podívat na pojem derivace z jiného úhlu a určit, jak lze derivační a goniometrické funkce propojit.
Uvažujme tedy nějakou libovolnou křivku, která je popsána abstraktní funkcí y = f(x).
Představme si, že jízdní řád je mapa turistické trasy. Přírůstek ∆x (delta x) na obrázku je určitá vzdálenost dráhy a ∆y je změna výšky dráhy nad hladinou moře.
Pak se ukáže, že poměr ∆x/∆y bude charakterizovat složitost trasy na každém úseku trasy. Když se tuto hodnotu naučíte, můžete s jistotou říci, zda je výstup/sestup strmý, zda budete potřebovat horolezecké vybavení a zda turisté potřebují určité fyzický trénink. Tento indikátor však bude platný pouze pro jeden malý interval ∆x.
Pokud organizátor výletu vezme hodnoty pro počáteční a koncový bod stezky, to znamená, že ∆x se rovná délce trasy, nebude schopen získat objektivní údaje o stupni obtížnosti. výletu. Proto je nutné sestrojit další graf, který bude charakterizovat rychlost a „kvalitu“ změn v cestě, jinými slovy určit poměr ∆x/∆y pro každý „metr“ trasy.
Tento graf bude vizuální derivací pro konkrétní cestu a bude objektivně popisovat její změny v každém intervalu zájmu. Ověřit si to je velmi jednoduché, hodnota ∆x/∆y není nic jiného než rozdíl uvažovaný pro konkrétní hodnotu x a y. Aplikujme derivaci nikoli na konkrétní souřadnice, ale na funkci jako celek:

Derivační a goniometrické funkce
Goniometrické funkce jsou neoddělitelně spojeny s derivacemi. To lze pochopit z následujícího výkresu. Na obrázku souřadné osy je znázorněna funkce Y = f (x) - modrá křivka.
K (x0; f (x0)) je libovolný bod, x0 + ∆x je přírůstek podél osy OX a f (x0 + ∆x) je přírůstek podél osy OY v určitém bodě L.

Narýsujme přímku body K a L a sestrojme pravoúhlý trojuhelník KLN. Pokud mentálně posunete segment LN podél grafu Y = f (x), body L a N budou mít tendenci k hodnotám K (x0; f (x0)). Nazvěme tento bod podmíněný začátek grafu – limita, pokud je funkce nekonečná, alespoň na jednom z intervalů, bude i tato tendence nekonečná a její mezní hodnota se bude blížit 0.
Charakter této tendence lze popsat tečnou ke zvolenému bodu y = kx + b nebo grafem derivace původní funkce dy - zelené přímky.
Ale kde je tady trigonometrie?! Vše je velmi jednoduché, zvažte pravoúhlý trojúhelník KLN. Rozdílová hodnota pro určitý bod K je tangens úhlu α nebo ∠K:

Tímto způsobem můžeme popsat geometrický význam derivace a její vztah k goniometrickým funkcím.
Derivační vzorce pro goniometrické funkce
Transformace sinus, kosinus, tangens a kotangens při určování derivace je třeba si zapamatovat.

Poslední dva vzorce nejsou chybou, jde o to, že je rozdíl mezi definováním derivace jednoduchého argumentu a funkce ve stejné kapacitě.
Podívejme se na srovnávací tabulku se vzorci pro derivace sinus, kosinus, tangens a kotangens:

Vzorce byly také odvozeny pro deriváty arcsinus, arckosinu, arctangens a arckotangens, i když se používají extrémně zřídka:

Stojí za zmínku, že výše uvedené vzorce zjevně nestačí k úspěšnému řešení typických úloh USE, což se ukáže při řešení konkrétního příkladu hledání derivace goniometrického výrazu.
Cvičení: Je nutné najít derivaci funkce a najít její hodnotu pro π/4:

Řešení: Pro nalezení y’ je třeba si připomenout základní vzorce pro převod původní funkce na derivaci, totiž.
Předmět:„Derivace goniometrických funkcí“.
Typ lekce– lekce upevňování znalostí.
Forma lekce– integrovaná lekce.
Místo lekce v systému lekcí pro tuto sekci- obecná lekce.
Cíle jsou stanoveny komplexně:
- vzdělávací: znát pravidla derivování, umět aplikovat pravidla pro výpočet derivací při řešení rovnic a nerovnic; zlepšit předmět, včetně výpočetních, dovedností a schopností; Počítačové dovednosti;
- rozvíjející se: rozvoj intelektuálních a logických dovedností a kognitivních zájmů;
- vzdělávací: kultivovat přizpůsobivost moderní podmínky výcvik.
Metody:
- reprodukční a produktivní;
- praktické a slovní;
- samostatná práce;
- programované učení, T.S.O.;
- kombinace frontálních, skupinových a individuální práce;
- diferencované učení;
- induktivně-deduktivní.
Formy ovládání:
- ústní průzkum,
- naprogramované ovládání,
- samostatná práce,
- jednotlivé úkoly na počítači,
- vzájemné hodnocení pomocí diagnostické karty studenta.
BĚHEM lekcí
I. Organizační moment
II. Aktualizace referenčních znalostí
a) Komunikace cílů a záměrů:
- znát pravidla derivování, umět aplikovat pravidla pro výpočet derivací při řešení úloh, rovnic a nerovnic;
- zlepšit předmět, včetně výpočetních, dovedností a schopností; Počítačové dovednosti;
- rozvíjet intelektuální a logické dovednosti a kognitivní zájmy;
- kultivovat adaptabilitu na moderní podmínky učení.
b) Opakování výukového materiálu
Pravidla pro výpočet derivací (opakování vzorců na počítači se zvukem). doc.7.
- Co je derivace sinus?
- Co je derivace kosinu?
- Jaká je derivace tečny?
- Jaká je derivace kotangens?
III. Ústní práce
Najděte derivaci. |
|||
Možnost 1. |
Možnost 2. |
||
na = 2X + 5. |
na = 2X – 5. |
||
na= 4 cos X. |
na= 3 hříchy X. |
||
na= tg X+ctg X. |
na= tg X-ctg X. |
||
na= hřích 3 X. |
na= cos 4 X. |
||
Možnosti odpovědí. |
|||
– 4 hříchy X |
– 3 cos X |
||
1/cos 2 X+ 1/hřích 2 X |
1/cos 2 X-1/hřích 2 X |
1/hřích 2 X-1/cos 2 X |
|
– 4 hříchy 4 X |
– 3cos3 X |
||
Vyměňte sešity. V diagnostických kartách označte správně splněné úkoly znaménkem +, chybně splněné znaménkem –.
IV. Řešení rovnic pomocí derivace
– Jak najít body, ve kterých je derivace nulová?
Chcete-li najít body, ve kterých derivace tuto funkci rovná se nule, potřebujete:
- určit povahu funkce,
- najít oblast definice funkcí,
– najít derivaci této funkce,
- vyřešit rovnici F "(X) = 0,
- Vyberte správnou odpověď.
Úkol 1.
Vzhledem k tomu: na
= X-hřích X.
Nalézt: body, ve kterých je derivace nulová.
Řešení. Funkce je definována a diferencovatelná na množině všech reálných čísel, protože funkce jsou definovány a diferencovatelné na množině všech reálných čísel G(X) = X A t(X) = – hřích X.
Pomocí pravidel diferenciace dostaneme F
"(X) = (X-hřích X)" = (X)“ – (hřích X)" = 1 – cos X.
Li F "(X) = 0, pak 1 – cos X = 0.
cos X= 1/; zbavme se iracionality ve jmenovateli, dostaneme cos X
= /2.
Podle vzorce t= ± arccos A+ 2n, n Z, dostaneme: X= ± arccos /2 + 2n, n Z.
Odpovědět: x = ±/4 + 2n, nZ.
V. Řešení rovnic pomocí algoritmu
Najděte, ve kterých bodech derivace mizí.
F(X) = hřích X+ cos X |
F(X) = hřích 2 X – X |
F(X) = 2X+cos(4 X – ) |
Žák si může vybrat kterýkoli ze tří příkladů. První příklad je hodnocen " 3 ", druhý - " 4 ", Třetí - " 5 " Řešení v sešitech s následnou vzájemnou kontrolou. Jeden žák rozhoduje na radě. Pokud se ukáže, že řešení není správné, musí se student vrátit k algoritmu a pokusit se vyřešit znovu.
Naprogramované ovládání.
Možnost 1 |
Možnost 2 |
|||
y = 2X 3 |
y = 3X 2 |
|||
y = 1/4 X 4 + 2X 2 – 7 |
y = 1/2 X 4 + 4X + 5 |
|||
y = X 3 + 4X 2
– 3X. |
y = 2X 3 – 9X 2
+ 12X + 7. |
|||
y= hřích 2 X– protože 3 X. |
y= cos 2 X- hřích 3 X. |
|||
y= tg X–ctg( X + /4). |
y=ctg X+ tg( X – /4). |
|||
y= hřích 2 X. |
y= cos 2 X. |
|||
Možnosti odpovědí. |
||||
|
| ||||








