Definición. Sea una función f(x) definida en algún intervalo y x 0 sea un punto en este intervalo. Si , entonces se dice que f(x) es continua en el punto x 0 .
De la definición se deduce que podemos hablar de continuidad sólo en relación con aquellos puntos en los que se define f(x) (al definir el límite de una función, no se estableció tal condición). Para funciones continuas , es decir, las operaciones f y lim son conmutables. En consecuencia, a dos definiciones del límite de una función en un punto se les pueden dar dos definiciones de continuidad: "en el lenguaje de las secuencias" y "en el lenguaje de las desigualdades" (en el lenguaje de ε-δ). Se sugiere que lo haga usted mismo.
Para uso práctico, a veces es más conveniente definir la continuidad en el lenguaje de incrementos.
El valor Δx=x-x 0 se llama incremento del argumento, y Δy=f(x)-f(x 0) es el incremento de la función cuando se mueve del punto x 0 al punto x.
Definición. Definamos f(x) en el punto x 0 . Una función f(x) se llama continua en un punto x 0 si un incremento infinitesimal del argumento en este punto corresponde a un incremento infinitesimal de la función, es decir, Δy→0 para Δx→0.

Ejemplo 1. Demuestre que la función y=sinx es continua para cualquier valor de x.
Solución. Sea x 0 un punto arbitrario. Dándole un incremento Δx, obtenemos el punto x=x 0 +Δx. Entonces . Obtenemos .
Definición. La función y=f(x) se llama continua en el punto x 0 a la derecha (izquierda) si
.
Una función continua en un punto interior será continua tanto a derecha como a izquierda. Lo contrario también es cierto: si una función es continua en un punto a la izquierda y a la derecha, entonces será continua en ese punto. Sin embargo, una función sólo puede ser continua en un lado. Por ejemplo, para , , f(1)=1, por lo tanto, esta función es continua solo a la izquierda (para ver la gráfica de esta función, consulte el párrafo 5.7.2 anterior).
Definición. Una función se llama continua en algún intervalo si es continua en todos los puntos de ese intervalo.
En particular, si el intervalo es un segmento, entonces se implica continuidad unilateral en sus extremos.

Propiedades de funciones continuas

1. Todas las funciones elementales son continuas en su dominio de definición.
2. Si f(x) y φ(x), dados en un determinado intervalo, son continuas en el punto x 0 de este intervalo, entonces las funciones también serán continuas en este punto.
3. Si y=f(x) es continua en el punto x 0 de X, y z=φ(y) es continua en el punto correspondiente y 0 =f(x 0) de Y, entonces función compleja z=φ(f(x)) será continua en el punto x 0 .

Rupturas de funciones y su clasificación.

Un signo de continuidad de la función f(x) en el punto x 0 es la igualdad, lo que implica la presencia de tres condiciones:
1) f(x) se define en el punto x 0 ;
2) ;
3) .
Si se viola al menos uno de estos requisitos, entonces x 0 se denomina punto de ruptura de la función. En otras palabras, un punto de ruptura es un punto en el que esta función no es continua. De la definición de puntos de ruptura se deduce que los puntos de ruptura de una función son:
a) puntos pertenecientes al dominio de definición de la función en los que f(x) pierde la propiedad de continuidad,
b) puntos que no pertenecen al dominio de definición de f(x), que son puntos adyacentes de dos intervalos del dominio de definición de la función.
Por ejemplo, para una función, el punto x=0 es un punto de ruptura, ya que la función en este punto no está definida y la función tiene una discontinuidad en el punto x=1, que es adyacente a dos intervalos (-∞,1) y (1,∞) del dominio de definición de f(x) y no existe.

Se adopta la siguiente clasificación para los puntos de quiebre.
1) Si en el punto x 0 hay finitos Y , pero f(x 0 +0)≠f(x 0 -0), entonces x 0 se llama punto de discontinuidad de primer tipo , y se llama salto de función .

Ejemplo 2. Considere la función
La función sólo se puede romper en el punto x=2 (en los demás puntos es continua como cualquier polinomio).
Lo encontraremos , . Dado que los límites unilaterales son finitos, pero no iguales entre sí, entonces en el punto x=2 la función tiene una discontinuidad del primer tipo. Darse cuenta de , por lo tanto la función en este punto es continua por la derecha (Fig. 2).
2) Puntos de discontinuidad del segundo tipo. se llaman puntos en los que al menos uno de los límites unilaterales es igual a ∞ o no existe.

Ejemplo 3. La función y=2 1/ x es continua para todos los valores de x excepto x=0. Encontremos límites unilaterales: , , por lo tanto x=0 es un punto de discontinuidad del segundo tipo (Fig. 3).
3) El punto x=x 0 se llama punto de ruptura removible , si f(x 0 +0)=f(x 0 -0)≠f(x 0).
"Eliminaremos" la brecha en el sentido de que basta con cambiar (redefinir o redefinir) el valor de la función en este punto estableciendo , y la función se volverá continua en el punto x 0 .
Ejemplo 4. Se sabe que , y este límite no depende de la forma en que x tiende a cero. Pero la función en el punto x=0 no está definida. Si redefinimos la función estableciendo f(0)=1, entonces resulta ser continua en este punto (en otros puntos es continua como el cociente de las funciones continuas sinx y x).
Ejemplo 5. Examinar la continuidad de una función. .
Solución. Las funciones y=x 3 e y=2x están definidas y son continuas en todas partes, incluso en los intervalos indicados. Examinemos el punto de unión de los intervalos x=0:
, , . Obtenemos que , lo que implica que en el punto x=0 la función es continua.
Definición. Una función que es continua en un intervalo excepto por un número finito de puntos de discontinuidad del primer tipo o discontinuidad removible se llama continua por partes en este intervalo.

Ejemplos de funciones discontinuas

Ejemplo 1. La función está definida y es continua en (-∞,+∞) excepto en el punto x=2. Determinemos el tipo de descanso. Porque el Y , entonces en el punto x=2 hay una discontinuidad del segundo tipo (Fig. 6).
Ejemplo 2. La función está definida y es continua para todo x excepto x=0, donde el denominador es cero. Encontremos límites unilaterales en el punto x=0:
Los límites unilaterales son finitos y diferentes, por lo tanto, x=0 es un punto de discontinuidad del primer tipo (Fig. 7).
Ejemplo 3. Determinar en qué puntos y qué tipo de discontinuidades tiene la función.
Esta función está definida en [-2,2]. Dado que x 2 y 1/x son continuas en los intervalos [-2,0] y , respectivamente, la discontinuidad sólo puede ocurrir en la unión de los intervalos, es decir, en el punto x=0. Dado que x=0 es un punto de discontinuidad del segundo tipo.

Ejemplo 4. ¿Es posible eliminar las lagunas funcionales?
A) en el punto x=2;
b) en el punto x=2;
V) en el punto x=1?
Solución. Respecto al ejemplo a) podemos decir inmediatamente que la discontinuidad f(x) en el punto x=2 no se puede eliminar, ya que en este punto existen infinitos límites unilaterales (ver ejemplo 1).
b) La función g(x) aunque tiene límites finitos unilaterales en el punto x=2

(,),

pero no coinciden, por lo que tampoco se puede eliminar la brecha.
c) La función φ(x) en el punto de discontinuidad x=1 tiene límites finitos unilaterales iguales: . Por lo tanto, la brecha se puede eliminar redefiniendo la función en x=1 poniendo f(1)=1 en lugar de f(1)=2.

Ejemplo 5. Demuestre que la función de Dirichlet

discontinuo en cada punto del eje numérico.
Solución. Sea x 0 cualquier punto desde (-∞,+∞). En cualquiera de sus barrios hay puntos tanto racionales como irracionales. Esto significa que en cualquier vecindad de x 0 la función tendrá valores iguales a 0 y 1. En este caso, no puede haber un límite de la función en el punto x 0 ni a la izquierda ni a la derecha, lo que significa que la función de Dirichlet tiene discontinuidades del segundo tipo en cada punto del eje real.

Ejemplo 6. Encontrar puntos de interrupción de funciones

y determinar su tipo.
Solución. Los puntos sospechosos de romperse son los puntos x 1 =2, x 2 =5, x 3 =3.
En el punto x 1 =2 f(x) tiene una discontinuidad del segundo tipo, ya que
.
El punto x 2 =5 es un punto de continuidad, ya que el valor de la función en este punto y en sus proximidades está determinado por la segunda recta, y no por la primera: .
Examinemos el punto x 3 =3: , , de lo que se sigue que x=3 es un punto de discontinuidad del primer tipo.

Para decisión independiente.
Examine las funciones en busca de continuidad y determine el tipo de puntos de discontinuidad:
1) ; Respuesta: x=-1 – punto de discontinuidad removible;
2) ; Respuesta: Discontinuidad del segundo tipo en el punto x=8;
3) ; Respuesta: Discontinuidad del primer tipo en x=1;
4)
Respuesta: En el punto x 1 = -5 hay un espacio removible, en x 2 =1 hay un espacio del segundo tipo y en el punto x 3 =0 hay un espacio del primer tipo.
5) ¿Cómo se debe elegir el número A para que la función

¿sería continuo en x=0?
Respuesta: A=2.
6) ¿Es posible elegir el número A para que la función

¿sería continua en x=2?
Respuesta: no.

Continuidad de una función en un punto. Función y = f(x ) se llama imprevisto

desigual en el punto x 0 si:

1) esta función está definida en alguna vecindad del punto x0;

2) hay un limite f(x);

→x0

3) este límite igual al valor funciones en el punto x 0, es decir limf (x )= f (x 0 ) .
		x→x0
La última condición es equivalente a la condición lim.		y = 0, donde x = x − x 0 – cuando
	x→ 0
rotación del argumento, y = f (x 0 +	x )− f (x 0 ) – incremento de la función, correspondiente
incrementando el argumento	x, es decir función	f(x) es continua en x 0

si y sólo si en este punto un incremento infinitesimal del argumento corresponde a un incremento infinitesimal de la función.

Continuidad unidireccional. La función y = f (x) se llama continua

a la izquierda en el puntox 0 si está definido en algún medio intervalo (a ;x 0 ]

y lím f (x) = f (x 0).

x→ x0 − 0

Se dice que una función y = f (x) es continua por la derecha en el punto x 0 si es op-

se distribuye en un cierto semiintervalo [ x 0 ;a ) y limf (x )= f (x 0 ) .

x→ x0 + 0

Función y = f(x)		continua en el punto x 0			entonces y sólo cuando ella
continuo
limf (x)= limf (x)= limf (x)= f (x 0).
x→ x0 + 0	x→ x0 − 0	x→x0

Continuidad de una función en un conjunto. La función y = f (x) se llama

continuo en el set X si es continua en todos los puntos de este conjunto. Además, si se define una función al final de un determinado intervalo del eje numérico, entonces la continuidad en este punto se entiende como continuidad a la derecha o a la izquierda. En particular, la función y = f (x) se llama no-

discontinuo en el segmento [a; b] si ella

1) continuo en cada punto del intervalo(a;b);

2) es continuo en un punto a ;

3) se deja continuo en un punto b.

Puntos de ruptura de funciones. El punto x 0 que pertenece al dominio de definición de la función y = f (x) o que es el punto límite de este dominio se llama

punto de ruptura de esta función, iff(x) no es continua en ese punto.

Los puntos de discontinuidad se dividen en puntos de discontinuidad del primer y segundo tipo:

1) Si existen límites finitos lim f (x )= f (x 0 − 0) y

x→ x0 − 0

	f (x) = f (x 0 + 0), y no los tres números son f (x 0 − 0), f (x 0 + 0),		f (x 0 ) son iguales
x→ x0 + 0
entre ellos, entonces x 0		se llama punto de discontinuidad del primer tipo.
	En particular, si los límites izquierdo y derecho de la función en el punto x 0		igual entre
	tú mismo, pero	no son iguales al valor de la función en este punto:

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , entonces x 0 se llama punto de discontinuidad removible.

En este caso, estableciendo f (x 0 )= A, puede modificar la función en el punto x 0

para que se vuelva continuo ( redefinir la función por continuidad). La diferencia f (x 0 + 0) − f (x 0 − 0) se llama salto de una función en un punto x0.

El salto de función en el punto de discontinuidad removible es cero.

2) Los puntos de discontinuidad que no son puntos de discontinuidad del primer tipo se denominan puntos de interrupción del segundo tipo. En puntos de discontinuidad del segundo tipo, al menos uno de los límites unilaterales f (x 0 − 0) y f (x 0 + 0) no existe o es infinito.

Propiedades de funciones continuas en un punto.

		f(x)	y g (x) son continuas en el punto x 0, entonces las funciones
f(x)±g(x),	f(x)g(x) y	f(x)	(donde g (x)≠ 0) también son continuas en el punto x.
		gramo(x)

2) Si la función u (x) es continua en el punto x 0, y la función f (u) es continua

en el punto u 0 = u (x 0), entonces la función compleja f (u (x)) es continua en el punto x 0.

3) Todas las funciones elementales básicas (c, x a, a x, loga x, sinx, cosx, tgx, ctgx, secx, cosecx, arcsinx, arccosx, arctgx, arcctgx) son continuas en cada una

hasta el punto de sus dominios de definición.

De las propiedades 1) a 3) se deduce que todas las funciones elementales (funciones obtenidas a partir de funciones elementales básicas utilizando un número finito de operaciones aritméticas y operaciones de composición) también son continuas en cada punto de sus dominios de definición.

Propiedades de funciones continuas en un intervalo.

1) (teorema del valor intermedio) Definamos la función f(x)

y es continua en el segmento [a;b]. Entonces para cualquier número C encerrado

entre los números f (a) y f (b), (f (a)< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (Teorema de Bolzano-Cauchy

es discontinuo en el segmento [a;b] y toma valores de diferentes signos en sus extremos.

Entonces existe al menos un punto x 0 [ a ; b ] tal que f (x 0 )= 0 .

3) (1er Teorema de Weierstrass) Dejemos que la función f (x) esté definida y

rasgado en el segmento [a;b]. Entonces esta función está limitada a este segmento.

4) (2do Teorema de Weierstrass) Dejemos que la función f (x) esté definida y

prisa en el segmento		[a;b] . Entonces esta función alcanza el intervalo [ a ; b ]
la mayor		el menos	valores, es decir	existir
x1, x2 [a; b] ,		para cualquier	puntos x [a;b]	justo	desigualdades

f (x 1 )≤ f (x )≤ f (x 2 ) .

Ejemplo 5.17. Usando la definición de continuidad, demuestra que la función y = 3x 2 + 2x − 5 es continua en un punto arbitrario x 0 en la recta numérica.

Solución: Método 1: Sea x 0 un punto arbitrario en el eje numérico. Tú-

Primero calculamos el límite de la función f (x) como x → x 0, aplicando teoremas sobre el límite de la suma y producto de funciones:

lim f (x )= lim(3x 2 + 2x − 5)= 3(limx )2 + 2 limx − 5= 3x 2							− 5.
x→x0	x→x0	x→x0	x→x0
Luego calculamos el valor de la función en el punto x:f (x)= 3x 2							− 5 .
Comparando los resultados obtenidos, vemos				lim f (x)= f (x 0) que según
				x→x0

definición y significa la continuidad de la función considerada en el punto x 0.

Método 2: dejar		x – incremento del argumento en el puntox 0. Encontremos la correspondencia.
adecuado	incremento			y = f(x0 + x) − f(x0 ) =
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x − 5)
6 x x+ (x) 2	2x = (6x + 2)x + (x)2.
Calculemos ahora el límite del incremento de la función cuando el incremento del argumento
		se esfuerza

	y = límite (6x + 2)		x + (x )2 = (6x + 2) límite		x + (limx)2 = 0.
x→ 0	x→ 0			x→ 0	x→ 0

Por lo tanto, lim y = 0, lo que significa por definición continuidad

x→ 0

funciones para cualquier x 0 R .

Ejemplo 5.18. Encuentre los puntos de discontinuidad de la función f (x) y determine su tipo. EN

En el caso de una discontinuidad removible, defina la función por continuidad:

1) f (x) = 1− x 2 en x< 3;

5x cuando x ≥ 3

2) f (x)= x 2 + 4 x + 3;

x+1

	f(x)=
		x4 (x-2)
	f(x)= arctán
			(x-5)

Solución: 1) El dominio de definición de esta función es el número entero

Eje y (−∞;+∞). En los intervalos (−∞ ;3) ,(3;+∞ ) la función es continua. Una discontinuidad sólo es posible en el punto x = 3, en el que cambia la especificación analítica de la función.

Encontremos los límites unilaterales de la función en el punto indicado:

f (3− 0)= lím (1− x 2 )= 1− 9= 8;

x →3 −0

f (3+ 0)= lím 5x = 15.

x →3 +0

Vemos que los límites izquierdo y derecho son finitos, entonces x = 3
ruptura yo			f(x). Función saltar a
f (3+ 0)− f (3− 0)= 15− 8= 7 .
		f (3)= 5 3= 15= f (3+ 0) , por lo tanto en el punto		x = 3

f(x) es continua por la derecha.

2) La función es continua en toda la recta numérica excepto en el punto x = − 1, en el que no está definido. Transformemos la expresión para f (x), expandiendo el numerador.

fracciones en factores:		f(x)=			4 x +3			(x+1)(x+3)	X + 3 para x ≠ − 1.
					x+1			x+1
Encontremos los límites unilaterales de la función en el punto x = − 1:
	f(x)=lím	f(x)= lim(x + 3)= 2 .
x →−1−0	x →−1 +0		x →−1

Descubrimos que los límites izquierdo y derecho de la función en el punto en estudio existen, son finitos e iguales entre sí, por lo tanto x = − 1 es un punto removible

recta y = x + 3 con un punto “pinchado” M (− 1;2) . Para que la función se vuelva permanente

discontinuo, deberíamos poner f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 .

Así, habiendo definido aún más f (x) por continuidad en el punto x = − 1, obtuvimos la función f * (x) = x + 3 con el dominio de definición (−∞;+∞).

3) Esta función definido y continuo para todos x excepto puntos

x = 0,x = 2, en el que el denominador de la fracción se vuelve cero.

Considere el punto x = 0:

Dado que en una vecindad de cero suficientemente pequeña, la función solo toma

	para valores negativos, entonces f (− 0) = lim			= −∞ = f (+0)	Aquellos. punto
			(x-2)
	x →−0
	x = 0 es un punto de discontinuidad del segundo tipo de función		f(x).

Consideremos ahora el punto x = 2:

La función toma valores negativos cercanos a la izquierda del considerado.

	punto y los positivos están a la derecha, por lo tanto				f(2-0)=			= −∞,
							x4 (x-2)
						x →2 −0
	f (2+ 0)= límite			= +∞. Como en el caso anterior, en el puntox = 2
			(x-2)
	x →2 +0

ción no tiene límites finitos izquierdo ni derecho, es decir sufre una rotura tipo II en este punto.

x = 5 .

f (5− 0)= lím arctan

π ,f (5+ 0)= lím arctan

x = 5

(x-5)

(x-5)

x →5 −0

x →5 +0

ruptura de ka

f(5+ 0)− f(5− 0)=

π − (−

π )= π (ver Fig. 5.2).

Problemas para resolver de forma independiente.

5.174. Usando solo la definición, demuestre la continuidad de la función f (x) en

cada punto x 0 R :

a) f(x) = c= constante;		b)f(x)=x;
c) f(x)= x 3;		d) f(x)= 5x 2 − 4x + 1;
e) f (x)= senx.
5.175. Demuestre que la función	f(x) = x2	1 cuando x ≥ 0,	es continuo en
		1 en x< 0
toda la recta numérica. Construya una gráfica de esta función.
5.176. Demuestre que la función	f(x) = x2	1 cuando x ≥ 0,	no es continuo
		0 en x< 0

en el punto x = 0, pero es continua hacia la derecha en ese punto. Grafica la función f(x).

entrecortado en el punto x =

Pero en este punto es continuo por la izquierda. construir un gráfico

funciones f(x).

5.178. Funciones gráficas

a) y =

x+1

b) y=x+

x+1

x+1

x+1

¿Cuáles de las condiciones de continuidad en los puntos de interrupción de estas funciones se satisfacen y cuáles no?

5.179. Especificar el punto de interrupción de la función.

pecado x		Para x ≠ 0
		en x = 0

¿Cuáles de las condiciones de continuidad se cumplen en este punto y cuáles no?

Definición puntos de interrupción de funciones y sus tipos es una continuación del tema de la continuidad de la función. También se ofrece una explicación visual (gráfica) del significado de los puntos de ruptura de una función en contraste con el concepto de continuidad. Aprendamos a encontrar puntos de interrupción de una función y a determinar sus tipos. Y el nuestro nos ayudará con esto. amigos fieles- límites izquierdo y derecho, generalmente llamados límites unilaterales. Si alguien tiene algún temor a los límites unilaterales, pronto lo disiparemos.

Los puntos de una gráfica que no están conectados entre sí se llaman puntos de interrupción de funciones . La gráfica de dicha función, que sufre una discontinuidad en el punto x=2 - - en la siguiente figura.

Una generalización de lo anterior es la siguiente definición. Si una función no es continua en un punto, entonces tiene una discontinuidad en ese punto y el punto en sí se llama punto de quiebre . Las perturbaciones son del primer tipo y del segundo tipo. .

Para determinar tipos (carácter) de puntos de ruptura Las funciones deben encontrarse con confianza. límites, por lo que es una buena idea abrir la lección correspondiente en una nueva ventana. Pero en relación con los puntos de interrupción, tenemos algo nuevo e importante: límites unilaterales (izquierda y derecha). En general se escriben (límite derecho) y (límite izquierdo). Como en el caso de un límite en general, para encontrar el límite de una función, es necesario sustituir X en la expresión de la función por aquello a lo que tiende X. Pero, tal vez, te preguntes en qué se diferenciarán los límites derecho e izquierdo, si en el caso del derecho se suma algo a X, pero ese algo es cero, y en el caso del izquierdo se resta algo de X, pero este algo - ¿también cero? Y tendrás razón. En la mayoría de los casos.

Pero en la práctica de buscar puntos de discontinuidad de una función y determinar su tipo, hay dos casos típicos en los que los límites derecho e izquierdo no son iguales:

• una función tiene dos o más expresiones dependiendo de la porción de la recta numérica a la que pertenece x (estas expresiones generalmente se escriben entre llaves después F(X)= );
• como resultado de sustituir lo que tiende a X, obtenemos una fracción en cuyo denominador queda más cero (+0) o menos cero (-0) y, por lo tanto, dicha fracción significa más infinito o menos infinito, y estos son cosas completamente diferentes.

Puntos de discontinuidad del primer tipo.

Punto de ruptura del primer tipo: una función tiene un límite izquierdo finito (es decir, no igual al infinito) y un límite derecho finito, pero la función no está definida en un punto o los límites izquierdo y derecho son diferentes (no iguales).

Punto de discontinuidad removible del primer tipo. Los límites izquierdo y derecho son iguales. En este caso, es posible definir más la función en un punto. Definir una función en un punto, simplemente hablando, significa proporcionar una conexión de puntos entre los cuales hay un punto en el que los límites izquierdo y derecho son iguales entre sí. En este caso, la conexión debe representar sólo un punto en el que se debe encontrar el valor de la función.

Ejemplo 1. Determine el punto de interrupción de la función y el tipo (carácter) del punto de interrupción.

Puntos de discontinuidad del segundo tipo.

Punto de ruptura del segundo tipo: el punto en el que al menos uno de los límites (izquierdo o derecho) es infinito (igual al infinito).

Ejemplo 3.

Solución. De la expresión para la potencia en mi está claro que la función no está definida en ese punto. Encontremos los límites izquierdo y derecho de la función en este punto:

Uno de los límites es igual al infinito, por lo que el punto es un punto de discontinuidad del segundo tipo. La gráfica de una función con un punto de ruptura se encuentra debajo del ejemplo.

Encontrar puntos de interrupción de una función puede ser una tarea independiente o parte de Investigación y gráficos de funciones completas. .

Ejemplo 4. Determine el punto de interrupción de la función y el tipo (carácter) del punto de interrupción de la función

Solución. De la expresión para la potencia en 2 queda claro que la función no está definida en el punto. Encontremos los límites izquierdo y derecho de la función en este punto.

Hueco extraíble.

Definición. Punto a llamado punto de discontinuidad removible de la función y=f(x), si el límite de la función f(x) existe en este punto, pero en el punto a función f(x) o no está definido o tiene un significado privado fa), diferente del límite f(x) en este punto.

Ejemplo. Por ejemplo, la función

tiene en el punto x=0 brecha reparable. De hecho, el valor límite de esta función en el punto x=0 es igual a 1. El valor parcial es igual a 2.

Si la función f(x) tiene en el punto a brecha removible, entonces esta brecha se puede eliminar sin cambiar los valores de la función en puntos distintos a a. Para ello basta con poner el valor de la función en el punto a igual a su valor límite en este punto. Entonces, en el ejemplo considerado anteriormente, basta con poner f(0)=1 y luego , es decir. función f(x) se volverá continuo en el punto x=0.

Disrupción del primer tipo.

Definición. Punto a se llama punto de discontinuidad del primer tipo si en este punto la función f(x) tiene límites derecho e izquierdo finitos pero desiguales

Pongamos algunos ejemplos.

Ejemplo. Función y=sgn x tiene en el punto x=0 ruptura del primer tipo. De hecho, y por tanto estos límites no son iguales entre sí.

Ejemplo. Función , definido en todas partes excepto en el punto x=1, tiene en el punto x=1 ruptura del primer tipo. En efecto, .

Disrupción del segundo tipo.

Definición. Punto a se llama punto de discontinuidad de segundo tipo si en este punto la función f(x) no tiene al menos uno de los límites unilaterales o si al menos uno de los límites unilaterales es infinito.

Ejemplo. Función f(x)=tan x, obviamente, tiene una discontinuidad del segundo tipo en cada punto xk=π/2+πk, k=0, ± 1, ± 2,…, porque en cada uno de esos puntos

Ejemplo. La función tiene una discontinuidad del segundo tipo en el punto x=0, porque en este punto no tiene límites ni derecho ni izquierdo.

Continuidad de una función en un segmento.

Definición. Función definida en un intervalo y continua en cada uno de sus puntos se llama continua en este segmento.

Además, bajo continuidad en el punto a se entiende por continuidad por la derecha, y por continuidad en un punto b- continuidad por la izquierda.

Diremos que la función y=f(x), definido en el set (X) alcanza su borde superior (inferior) , si tal punto existe x0 ∈(x), Qué f(x 0)=β (f(x 0)=α).

Teorema de Weierstrass. Toda función continua en un intervalo está acotada y alcanza su límite superior y su límite inferior en él.

Teorema [Bolzano-Cauchy]. Si la función y=f(x) continuo en el segmento Y f(a)=A, f(b)=B, entonces para cualquier C, concluido entre A Y B, existe tal punto ξ∈ , Qué f(ξ)=C.

En otras palabras, una función continua en un intervalo, que toma dos valores cualesquiera, también toma cualquier valor que se encuentre entre ellos.

Consecuencia. Si una función es continua en un segmento y toma valores de diferentes signos en sus extremos, entonces hay al menos un punto en este segmento en el que la función desaparece.

Consecuencia. Deja que la función y=f(x) continuo en el segmento Y , . Entonces la función f(x) toma todos los valores del segmento y sólo estos valores.

Por tanto, el conjunto de todos los valores de una función que es dado y continuo en un determinado segmento también es un segmento.

Continuidad de función. Puntos de ruptura.

El toro camina, se balancea, suspira al andar:
- ¡Ay, el tablero se está acabando, ahora me voy a caer!

En esta lección examinaremos el concepto de continuidad de una función, la clasificación de puntos de discontinuidad y un problema práctico común. estudios de continuidad de funciones. Por el mismo nombre del tema, muchos adivinan intuitivamente lo que se discutirá y piensan que el material es bastante simple. Esto es cierto. Pero son las tareas simples las que más a menudo se castigan por negligencia y un enfoque superficial para resolverlas. Por eso, te recomiendo que estudies el artículo con mucha atención y captes todas las sutilezas y técnicas.

¿Qué necesitas saber y poder hacer? No mucho. Para aprender bien la lección, es necesario comprender de qué se trata. límite de una función. Lectores con nivel bajo la preparación es suficiente para comprender el artículo. Límites de función. Ejemplos de soluciones y mirar significado geométrico límite en el manual Gráficas y propiedades de funciones elementales.. También es recomendable familiarizarse con transformaciones geométricas de gráficos, ya que la práctica en la mayoría de los casos implica la construcción de un dibujo. Las perspectivas son optimistas para todos, e incluso una tetera llena podrá hacer frente a la tarea por sí sola en las próximas dos horas.

Continuidad de función. Puntos de interrupción y su clasificación.

Concepto de continuidad de función.

Consideremos alguna función que sea continua en toda la recta numérica:

O, para decirlo de manera más sucinta, nuestra función es continua en (el conjunto de los números reales).

¿Cuál es el criterio “filisteo” de continuidad? Obviamente el horario función continua Se puede dibujar sin levantar el lápiz del papel.

En este caso conviene distinguir claramente dos conceptos sencillos: dominio de una función Y continuidad de la función. EN caso general no es lo mismo. Por ejemplo:

Esta función se define en toda la recta numérica, es decir, para todos El significado de "x" tiene su propio significado de "y". En particular, si, entonces. Tenga en cuenta que el otro punto está puntuado, porque según la definición de una función, el valor del argumento debe corresponder a la única cosa valor de la función. De este modo, dominio nuestra función: .

Sin embargo ¡Esta función no es continua! Es bastante obvio que en el momento en que ella está sufriendo brecha. El término también es bastante inteligible y visual; de hecho, aquí de todos modos habrá que arrancar el lápiz del papel. Un poco más adelante veremos la clasificación de los puntos de interrupción.

Continuidad de una función en un punto y en un intervalo.

En un problema matemático particular, podemos hablar de la continuidad de una función en un punto, de la continuidad de una función en un intervalo, de un semiintervalo o de la continuidad de una función en un segmento. Eso es, no hay “mera continuidad”– la función puede ser continua EN ALGÚN LUGAR. Y el “elemento de construcción” fundamental de todo lo demás es continuidad de la función en el punto .

Teoría Análisis matemático da una definición de la continuidad de una función en un punto utilizando vecindades “delta” y “épsilon”, pero en la práctica se utiliza otra definición, a la que prestaremos mucha atención.

primero recordemos límites unilaterales que irrumpió en nuestras vidas en la primera lección sobre gráficas de funciones. Considere una situación cotidiana:

Si nos acercamos al eje al punto izquierda(flecha roja), luego los valores correspondientes de los "juegos" irán a lo largo del eje hasta el punto (flecha carmesí). Matemáticamente, este hecho se soluciona usando límite izquierdo:

Preste atención a la entrada (dice "x tiende a ka a la izquierda"). El “aditivo” “menos cero” simboliza Básicamente, esto significa que nos acercamos al número desde el lado izquierdo.

Del mismo modo, si te acercas al punto "ka" a la derecha(flecha azul), entonces los “juegos” llegarán al mismo valor, pero a lo largo de la flecha verde, y límite derecho tendrá el formato siguiente:

"Aditivo" simboliza , y la entrada dice: "x tiende a ka a la derecha".

Si los límites unilaterales son finitos e iguales(como en nuestro caso): , entonces diremos que hay un límite GENERAL. Es simple, el límite general es nuestro “habitual” límite de una función, igual a un número finito.

Tenga en cuenta que si la función no está definida en (punción punto negro en la rama del gráfico), entonces los cálculos anteriores siguen siendo válidos. Como ya se ha señalado varias veces, en particular en el artículo sobre funciones infinitesimales, las expresiones significan que "x" infinitamente cerca se acerca al punto, mientras NO IMPORTA, ya sea que la función en sí esté definida en un punto determinado o no. Buen ejemplo aparecerá en el siguiente párrafo, cuando se analice la función.

Definición: una función es continua en un punto si el límite de la función en un punto dado es igual al valor de la función en ese punto: .

La definición se detalla en siguientes condiciones:

1) La función debe estar definida en el punto, es decir, el valor debe existir.

2) Debe haber un límite general de la función. Como se señaló anteriormente, esto implica la existencia e igualdad de límites unilaterales: .

3) El límite de la función en un punto dado debe ser igual al valor de la función en este punto: .

Si se viola al menos uno de las tres condiciones, entonces la función pierde la propiedad de continuidad en el punto .

Continuidad de una función en un intervalo se formula de manera ingeniosa y muy simple: una función es continua en el intervalo si es continua en cada punto del intervalo dado.

En particular, muchas funciones son continuas en un intervalo infinito, es decir, en el conjunto de los números reales. Esta es una función lineal, polinomial, exponencial, seno, coseno, etc. Y en general, cualquier función elemental continuo en su dominio de definición, por ejemplo, una función logarítmica es continua en el intervalo . Espero que en este momento Tienes una idea bastante clara de cómo se ven las gráficas de las funciones principales. Más información detallada Su continuidad se puede deducir de persona amable por el apellido Fichtengolts.

Con la continuidad de una función en un segmento y semiintervalos, tampoco todo es difícil, pero es más apropiado hablar de esto en clase. sobre cómo encontrar los valores mínimo y máximo de una función en un segmento, pero por ahora no nos preocupemos por eso.

Clasificación de puntos de quiebre

La fascinante vida de las funciones es rica en todo tipo de momentos especiales, y los puntos de ruptura son sólo una de las páginas de su biografía.

Nota : por si acaso, me detendré en un punto elemental: el punto de ruptura siempre es punto único– no hay “varios puntos de quiebre seguidos”, es decir, no existe un “intervalo de quiebre”.

Estos puntos a su vez se dividen en dos grandes grupos: rupturas del primer tipo Y rupturas del segundo tipo. Cada tipo de brecha tiene su propia características que veremos ahora mismo:

Punto de discontinuidad del primer tipo.

Si se viola la condición de continuidad en un punto y límites unilaterales finito , entonces se llama punto de discontinuidad de primer tipo.

Empecemos por el caso más optimista. Según la idea original de la lección, quería contar la teoría “en vista general”, pero para demostrar la realidad del material, me decidí por la opción con personajes específicos.

Es triste, como una foto de recién casados ​​​​con el telón de fondo de la Llama Eterna, pero la siguiente toma es generalmente aceptada. Representemos la gráfica de la función en el dibujo:


Esta función es continua en toda la recta numérica, excepto en el punto. Y, de hecho, el denominador no puede ser igual a cero. Sin embargo, de acuerdo con el significado del límite, podemos infinitamente cerca acercarse a "cero" tanto por la izquierda como por la derecha, es decir, existen límites unilaterales y, obviamente, coinciden:
(Se cumple la condición N° 2 de continuidad).

Pero la función no está definida en el punto, por lo tanto, se viola la Condición No. 1 de continuidad, y la función sufre una discontinuidad en este punto.

Una ruptura de este tipo (con la existente límite general) son llamados brecha reparable. ¿Por qué removible? Porque la función puede redefinir en el punto de ruptura:

¿Parece raro? Tal vez. ¡Pero tal notación de función no contradice nada! Ahora la brecha se ha cerrado y todos están contentos:


Realicemos una verificación formal:

2) – existe un límite general;
3)

Por lo tanto, se cumplen las tres condiciones y la función es continua en un punto según la definición de continuidad de una función en un punto.

Sin embargo, los que odian a matan pueden definir la función de mala manera, por ejemplo :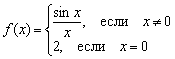


Es interesante que aquí se cumplan las dos primeras condiciones de continuidad:
1) – la función se define en un punto dado;
2) – hay un límite general.

Pero no se ha traspasado el tercer límite: , es decir, el límite de la función en el punto no es igual el valor de una función dada en un punto dado.

Así, en un punto la función sufre una discontinuidad.

El segundo caso, más triste, se llama ruptura del primer tipo con un salto. Y la tristeza es evocada por límites unilaterales que finito y diferente. En el segundo dibujo de la lección se muestra un ejemplo. Esta brecha suele ocurrir en funciones definidas por partes, que ya han sido mencionados en el artículo. sobre transformaciones de grafos.

Considere la función por partes y completaremos su dibujo. ¿Cómo construir un gráfico? Muy simple. En un medio intervalo dibujamos un fragmento de una parábola ( color verde), en el intervalo – un segmento de línea recta (rojo) y en un medio intervalo – una línea recta ( Color azul).

Además, debido a la desigualdad, el valor se determina para función cuadrática(punto verde), y debido a la desigualdad, el valor se determina para función lineal(punto azul):

En el caso más difícil, conviene recurrir a la construcción punto por punto de cada parte del gráfico (ver la primera lección sobre gráficas de funciones).

Ahora sólo nos interesará el punto. Examinemos la continuidad:

2) Calculemos límites unilaterales.

A la izquierda tenemos un segmento de línea roja, por lo que el límite del lado izquierdo es:

A la derecha está la línea recta azul y el límite derecho:

Como resultado, recibimos números finitos, y ellos no es igual. Desde límites unilaterales finito y diferente: , entonces nuestra función tolera discontinuidad del primer tipo con un salto.

Es lógico que la brecha no se pueda eliminar: la función realmente no se puede definir más y “pegar”, como en el ejemplo anterior.

Puntos de discontinuidad del segundo tipo.

Por lo general, todos los demás casos de rotura se clasifican inteligentemente en esta categoría. No enumeraré todo, porque en la práctica, en el 99% de los problemas encontrarás brecha sin fin– cuando es zurdo o diestro, y más a menudo, ambos límites son infinitos.

Y, por supuesto, la imagen más obvia es la hipérbola en el punto cero. Aquí ambos límites unilaterales son infinitos: , por tanto, la función sufre una discontinuidad de segundo tipo en el punto .

Intento llenar mis artículos con contenido lo más diverso posible, así que veamos la gráfica de una función que aún no se ha encontrado:

según el esquema estándar:

1) La función no está definida en este punto porque el denominador va a cero.

Por supuesto, podemos concluir inmediatamente que la función sufre una discontinuidad en el punto , pero sería bueno clasificar la naturaleza de la discontinuidad, que a menudo es requerida por la condición. Para esto:

Permítanme recordarles que por grabar queremos decir infinitesimal un numero negativo , y debajo de la entrada - número positivo infinitesimal.

Los límites unilaterales son infinitos, lo que significa que la función sufre una discontinuidad de segundo tipo en el punto . El eje y es asíntota vertical para el gráfico.

No es raro que existan ambos límites unilaterales, pero sólo uno de ellos sea infinito, por ejemplo:

Esta es la gráfica de la función.

Examinamos el punto de continuidad:

1) La función no está definida en este punto.

2) Calculemos límites unilaterales:

Hablaremos sobre el método para calcular tales límites unilaterales en los dos últimos ejemplos de la conferencia, aunque muchos lectores ya lo han visto y adivinado todo.

El límite de la izquierda es finito e igual a cero (no vamos al punto mismo), pero el límite de la derecha es infinito y la rama naranja de la gráfica se aproxima infinitamente a su asíntota vertical, dada por la ecuación (línea de puntos negra).

Entonces la función sufre discontinuidad de segundo tipo en el punto .

En cuanto a una discontinuidad del primer tipo, la función se puede definir en el propio punto de discontinuidad. Por ejemplo, para una función por partes Siéntase libre de poner un punto negro en negrita en el origen de las coordenadas. A la derecha hay una rama de una hipérbola y el límite de la derecha es infinito. Creo que casi todo el mundo tiene una idea de cómo se ve este gráfico.

Lo que todos esperaban:

¿Cómo examinar la continuidad de una función?

El estudio de una función para la continuidad en un punto se realiza según un esquema rutinario ya establecido, que consiste en comprobar tres condiciones de continuidad:

Ejemplo 1

Explorar función

Solución:

1) El único punto dentro del alcance es donde la función no está definida.

2) Calculemos límites unilaterales:

Los límites unilaterales son finitos e iguales.

Así, en ese punto la función sufre una discontinuidad removible.

¿Cómo es la gráfica de esta función?

me gustaria simplificar , y parece que se obtiene una parábola ordinaria. PERO la función original no está definida en el punto, por lo que se requiere la siguiente cláusula:

Hagamos el dibujo:

Respuesta: la función es continua en toda la recta numérica excepto en el punto en el que sufre una discontinuidad removible.

La función se puede definir mejor o no tan bien, pero según la condición esto no es necesario.

¿Dices que este es un ejemplo descabellado? De nada. Esto ha sucedido decenas de veces en la práctica. Casi todas las tareas del sitio provienen de pruebas y trabajos independientes reales.

Deshagámonos de nuestros módulos favoritos:

Ejemplo 2

Explorar función por la continuidad. Determine la naturaleza de las discontinuidades de la función, si existen. Ejecute el dibujo.

Solución: Por alguna razón, los estudiantes tienen miedo y no les gustan las funciones de un módulo, aunque no tienen nada de complicado. Ya hemos tocado un poco esas cosas en la lección. Transformaciones geométricas de gráficos.. Dado que el módulo no es negativo, se expande de la siguiente manera: , donde "alfa" es alguna expresión. EN en este caso, y nuestra función debe escribirse por partes: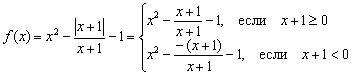

Pero las fracciones de ambas piezas deben reducirse en . La reducción, como en el ejemplo anterior, no se producirá sin consecuencias. La función original no está definida en el punto ya que el denominador va a cero. Por lo tanto, el sistema debería especificar adicionalmente la condición y hacer que la primera desigualdad sea estricta:

Ahora sobre el MUY Recepción útil soluciones: antes de finalizar la tarea sobre un borrador, es ventajoso hacer un dibujo (independientemente de si las condiciones lo exigen o no). Esto ayudará, en primer lugar, a ver inmediatamente los puntos de continuidad y los puntos de discontinuidad y, en segundo lugar, le protegerá al 100% de errores al encontrar límites unilaterales.

Hagamos el dibujo. De acuerdo con nuestros cálculos, a la izquierda del punto es necesario dibujar un fragmento de una parábola (color azul), y a la derecha, un trozo de parábola (color rojo), mientras que la función no está definida en el punto en sí:

En caso de duda, tome algunos valores de x e introdúzcalos en la función (recordando que el módulo destruye el posible signo menos) y revisa el gráfico.

Examinemos analíticamente la función de continuidad:

1) La función no está definida en el punto, por lo que podemos decir inmediatamente que no es continua en él.

2) Establezcamos la naturaleza de la discontinuidad, para ello calculamos límites unilaterales:

Los límites unilaterales son finitos y diferentes, lo que significa que la función sufre una discontinuidad de 1er tipo con un salto en el punto . Tenga en cuenta nuevamente que al encontrar límites, no importa si la función en el punto de ruptura está definida o no.

Ahora solo queda transferir el dibujo del borrador (se hizo como con la ayuda de una investigación ;-)) y completar la tarea:

Respuesta: la función es continua en toda la recta numérica excepto en el punto en el que sufre una discontinuidad de primer tipo con un salto.

En ocasiones requieren indicación adicional del salto de discontinuidad. Se calcula de forma sencilla: desde el límite derecho es necesario restar el límite izquierdo: , es decir, en el punto de ruptura nuestra función saltó 2 unidades hacia abajo (como nos indica el signo menos).

Ejemplo 3

Explorar función por la continuidad. Determine la naturaleza de las discontinuidades de la función, si existen. Haz un dibujo.

Este es un ejemplo para que lo resuelvas por tu cuenta, una solución de muestra al final de la lección.

Pasemos a la versión más popular y extendida de la tarea, cuando la función consta de tres partes:

Ejemplo 4

Examinar la continuidad de una función y trazar una gráfica de la función. .

Solución: es obvio que las tres partes de la función son continuas en los intervalos correspondientes, por lo que queda comprobar sólo dos puntos de “unión” entre las piezas. Primero, hagamos un borrador del dibujo, la técnica de construcción la comenté con suficiente detalle en la primera parte del artículo. Lo único es que debemos seguir cuidadosamente nuestros puntos singulares: debido a la desigualdad, el valor pertenece a la línea recta (punto verde), y debido a la desigualdad, el valor pertenece a la parábola (punto rojo):


Bueno, en principio todo está claro =) Solo queda formalizar la decisión. Para cada uno de los dos puntos de “unión”, comprobamos de forma estándar 3 condiciones de continuidad:

I) Examinamos el punto de continuidad.

1)

Los límites unilaterales son finitos y diferentes, lo que significa que la función sufre una discontinuidad de 1er tipo con un salto en el punto .

Calculemos el salto de discontinuidad como la diferencia entre los límites derecho e izquierdo:
, es decir, el gráfico subió una unidad.

II) Examinamos el punto de continuidad.

1) – la función se define en un punto dado.

2) Encuentra límites unilaterales:

– Los límites unilaterales son finitos e iguales, lo que significa que hay un límite general.

3) – el límite de una función en un punto es igual al valor de esta función en un punto dado.

En la etapa final, trasladamos el dibujo a la versión final, tras lo cual ponemos el acorde final:

Respuesta: la función es continua en toda la recta numérica, excepto en el punto en el que sufre una discontinuidad de primer tipo con un salto.

Ejemplo 5

Examinar la continuidad de una función y construir su gráfica. .

Este es un ejemplo para que lo resuelvas por tu cuenta, solución corta y una muestra aproximada de la tarea al final de la lección.

Puede tener la impresión de que en un punto la función debe ser continua y en otro debe haber una discontinuidad. En la práctica, este no es siempre el caso. Trate de no descuidar el resto de ejemplos: habrá varias características interesantes e importantes:

Ejemplo 6

Dada una función . Investigue la función para determinar la continuidad en los puntos. Construye un gráfico.

Solución: y nuevamente ejecute inmediatamente el dibujo en el borrador:

La peculiaridad de este gráfico es que la función por partes viene dada por la ecuación del eje de abscisas. Esta área está dibujada aquí. verde, y en un cuaderno se suele resaltar en negrita con un simple lápiz. Y, por supuesto, no te olvides de nuestros arietes: el valor pertenece a la rama tangente (punto rojo) y el valor pertenece a la recta.

Todo está claro en el dibujo: la función es continua a lo largo de toda la recta numérica, solo queda formalizar la solución, que se lleva a la automatización completa literalmente después de 3-4 ejemplos similares:

I) Examinamos el punto de continuidad.

1) – la función se define en un punto dado.

2) Calculemos límites unilaterales:

, lo que significa que hay un límite general.

Por si acaso, déjame recordarte un hecho trivial: el límite de una constante es igual a la constante misma. En este caso, el límite de cero es igual al propio cero (límite para zurdos).

3) – el límite de una función en un punto es igual al valor de esta función en un punto dado.

Por tanto, una función es continua en un punto según la definición de continuidad de una función en un punto.

II) Examinamos el punto de continuidad.

1) – la función se define en un punto dado.

2) Encuentra límites unilaterales:

Y aquí el límite de uno es igual a la unidad misma.

– hay un límite general.

3) – el límite de una función en un punto es igual al valor de esta función en un punto dado.

Por tanto, una función es continua en un punto según la definición de continuidad de una función en un punto.

Como es habitual, después de investigar transferimos nuestro dibujo a la versión final.

Respuesta: la función es continua en los puntos.

Tenga en cuenta que en la condición no se nos preguntó nada sobre el estudio de la continuidad de la función completa, y se considera una buena forma matemática formular preciso y claro la respuesta a la pregunta planteada. Por cierto, si la condición no requiere que construyas un gráfico, entonces tienes todo derecho no lo construyas (aunque el profesor puede obligarte a hacerlo más tarde).

Un pequeño “trabalenguas” matemático para resolverlo tú mismo:

Ejemplo 7

Dada una función . Investigue la función para determinar la continuidad en los puntos. Clasifique los puntos de interrupción, si los hay. Ejecute el dibujo.

Intente "pronunciar" todas las "palabras" correctamente =) Y dibuje el gráfico con mayor precisión, precisión, no será superfluo en todas partes;-)

Como recordarás, recomendé completar inmediatamente el dibujo como borrador, pero de vez en cuando te encuentras con ejemplos en los que no puedes entender de inmediato cómo se ve el gráfico. Por lo tanto, en algunos casos, es ventajoso encontrar primero los límites unilaterales y solo entonces, basándose en el estudio, representar las ramas. En los dos últimos ejemplos también aprenderemos una técnica para calcular algunos límites unilaterales:

Ejemplo 8

Examina la continuidad de la función y construye su gráfico esquemático.

Solución: los puntos malos son obvios: (reduce el denominador del exponente a cero) y (reduce el denominador de toda la fracción a cero). No está claro cómo se ve la gráfica de esta función, lo que significa que es mejor investigar un poco primero.