SISTEM PERSAMAAN LINEAR HOMOGENEUS
Sistem homogen persamaan linear dipanggil sistem bentuk
Adalah jelas bahawa dalam kes ini 
, kerana semua elemen salah satu lajur dalam penentu ini adalah sama dengan sifar.
Oleh kerana yang tidak diketahui ditemui mengikut formula 
, maka dalam kes apabila Δ ≠ 0, sistem mempunyai penyelesaian sifar yang unik x = y = z= 0. Namun, dalam banyak masalah persoalan yang menarik ialah sama ada sistem homogen penyelesaian selain sifar.
Teorem. Untuk sistem linear persamaan homogen mempunyai penyelesaian bukan sifar, adalah perlu dan mencukupi bahawa Δ ≠ 0.
Jadi, jika penentu Δ ≠ 0, maka sistem mempunyai penyelesaian yang unik. Jika Δ ≠ 0, maka sistem persamaan homogen linear mempunyai bilangan penyelesaian yang tidak terhingga.
Contoh.
Vektor eigen dan nilai eigen bagi matriks
Biarkan matriks segi empat sama diberikan 
, X– beberapa lajur matriks, ketinggiannya bertepatan dengan susunan matriks A. .
Dalam banyak masalah kita perlu mempertimbangkan persamaan untuk X
di mana λ ialah nombor tertentu. Adalah jelas bahawa untuk mana-mana λ persamaan ini mempunyai penyelesaian sifar.
Nombor λ yang mana persamaan ini mempunyai penyelesaian bukan sifar dipanggil nilai eigen matriks A, A X kerana λ sedemikian dipanggil eigenvector matriks A.
Mari kita cari vektor eigen bagi matriks A. Kerana ia E∙X = X, maka persamaan matriks boleh ditulis semula sebagai 
atau 
. Dalam bentuk diperluas, persamaan ini boleh ditulis semula sebagai sistem persamaan linear. sungguh 
.
Dan oleh itu 
Jadi, kami telah memperoleh sistem persamaan linear homogen untuk menentukan koordinat x 1, x 2, x 3 vektor X. Untuk sistem mempunyai penyelesaian bukan sifar adalah perlu dan mencukupi bahawa penentu sistem adalah sama dengan sifar, i.e.
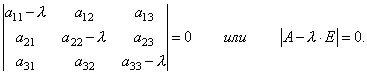
Ini ialah persamaan darjah ke-3 untuk λ. Ia dipanggil persamaan ciri matriks A dan berfungsi untuk menentukan nilai eigen λ.
Setiap nilai eigen λ sepadan dengan vektor eigen X, yang koordinatnya ditentukan daripada sistem pada nilai λ yang sepadan.
Contoh.
ALGEBRA VEKTOR. KONSEP VEKTOR
Apabila mengkaji pelbagai cabang fizik, terdapat kuantiti yang ditentukan sepenuhnya dengan menyatakan nilai berangkanya, contohnya, panjang, luas, jisim, suhu, dll. Kuantiti sedemikian dipanggil skalar. Walau bagaimanapun, sebagai tambahan kepada mereka, terdapat juga kuantiti, untuk menentukan yang, sebagai tambahan kepada nilai berangka, ia juga perlu untuk mengetahui arah mereka dalam ruang, sebagai contoh, daya yang bertindak pada badan, kelajuan dan pecutan badan apabila ia bergerak di angkasa, ketegangan medan magnet pada titik tertentu dalam ruang, dsb. Kuantiti sedemikian dipanggil kuantiti vektor.
Mari kita perkenalkan definisi yang ketat.
Segmen terarah Mari kita panggil segmen, berbanding dengan hujung yang diketahui mana antara mereka yang pertama dan yang kedua.
vektor dipanggil segmen terarah yang mempunyai panjang tertentu, i.e. Ini ialah segmen dengan panjang tertentu, di mana salah satu titik yang mengehadkannya diambil sebagai permulaan, dan yang kedua sebagai penghujung. Jika A– permulaan vektor, B adalah penghujungnya, maka vektor dilambangkan dengan simbol sebagai tambahan, vektor sering dilambangkan dengan satu huruf. Dalam rajah, vektor ditunjukkan oleh segmen, dan arahnya dengan anak panah.
Modul atau panjang Vektor dipanggil panjang segmen terarah yang mentakrifkannya. Ditandakan dengan || atau ||.
Kami juga akan memasukkan apa yang dipanggil vektor sifar, yang permulaan dan penghujungnya bertepatan, sebagai vektor. Ia ditetapkan. Vektor sifar tidak mempunyai arah tertentu dan modulusnya ialah sifar ||=0.
Vektor dipanggil kolinear, jika ia terletak pada garisan yang sama atau pada garisan selari. Selain itu, jika vektor dan berada dalam arah yang sama, kita akan menulis , bertentangan.
Vektor yang terletak pada garis lurus selari dengan satah yang sama dipanggil coplanar.
Kedua-dua vektor itu dipanggil sama rata, jika ia adalah kolinear, mempunyai arah yang sama dan sama panjang. Dalam kes ini mereka menulis.
Daripada takrifan kesamaan vektor, ia menunjukkan bahawa vektor boleh diangkut selari dengan dirinya sendiri, meletakkan asalnya di mana-mana titik dalam ruang.
Sebagai contoh.
OPERASI LINEAR PADA VEKTOR
- Mendarab vektor dengan nombor.
Hasil darab vektor dan nombor λ ialah vektor baharu supaya:
Hasil darab vektor dan nombor λ dilambangkan dengan .
Sebagai contoh, terdapat vektor yang diarahkan ke arah yang sama dengan vektor dan mempunyai panjang separuh daripada vektor.
Operasi yang diperkenalkan mempunyai perkara berikut harta benda:
- Penambahan vektor.
Biarkan dan menjadi dua vektor sewenang-wenangnya. Mari kita ambil titik sewenang-wenangnya O dan membina vektor. Selepas itu dari titik A mari kita ketepikan vektor. Vektor yang menghubungkan permulaan vektor pertama dengan penghujung vektor kedua dipanggil jumlah daripada vektor ini dan dilambangkan
.
Takrifan yang dirumuskan bagi penambahan vektor dipanggil peraturan selari, kerana jumlah vektor yang sama boleh diperoleh seperti berikut. Mari kita tangguhkan dari titik itu O vektor dan . Mari kita bina segi empat selari pada vektor ini OABC. Oleh kerana vektor, maka vektor, yang merupakan pepenjuru bagi segi empat selari yang dilukis daripada bucu O, jelas akan menjadi jumlah vektor.
Sangat mudah untuk menyemak perkara berikut sifat penambahan vektor.
- Perbezaan vektor.
Kolinear vektor kepada vektor tertentu, sama panjang dan arah bertentangan, dipanggil bertentangan vektor untuk vektor dan dilambangkan dengan . Vektor bertentangan boleh dianggap sebagai hasil darab vektor dengan nombor λ = –1: .
Definisi 9.3. vektor X dipanggil eigenvector matriks A, jika terdapat nombor sedemikian λ, bahawa persamaan itu dipegang: A X= λ X, iaitu hasil memohon kepada X penjelmaan linear yang ditentukan oleh matriks A, ialah pendaraban vektor ini dengan nombor λ . Nombor itu sendiri λ dipanggil nilai eigen matriks A.
Menggantikan kepada formula (9.3) x` j = λx j , kita memperoleh sistem persamaan untuk menentukan koordinat vektor eigen:
. (9.5)
Sistem homogen linear ini akan mempunyai penyelesaian bukan remeh hanya jika penentu utamanya ialah 0 (peraturan Cramer). Dengan menulis syarat ini dalam bentuk:
kita memperoleh persamaan untuk menentukan nilai eigen λ , dipanggil persamaan ciri. Secara ringkas ia boleh diwakili seperti berikut:
| A - λE | = 0, (9.6)
kerana bahagian kirinya mengandungi penentu matriks A-λE. relatif polinomial λ | A - λE| dipanggil polinomial ciri matriks A.
Sifat polinomial ciri:
1) Polinomial ciri penjelmaan linear tidak bergantung pada pilihan asas. Bukti. 
(lihat (9.4)), tetapi 
oleh itu, . Oleh itu, ia tidak bergantung kepada pilihan asas. Ini bermakna bahawa | A-λE| tidak berubah apabila berpindah ke asas baru.
2) Jika matriks A penjelmaan linear ialah simetri(mereka. dan ij =a ji), maka semua punca persamaan ciri (9.6) ialah nombor nyata.
Sifat nilai eigen dan vektor eigen:
1) Jika anda memilih asas daripada vektor eigen x 1, x 2, x 3 , sepadan dengan nilai eigen λ 1, λ 2, λ 3 matriks A, maka dalam asas ini penjelmaan linear A mempunyai matriks bentuk pepenjuru:
(9.7) Bukti sifat ini mengikut takrifan vektor eigen.
2) Jika nilai eigen bagi penjelmaan A adalah berbeza, maka vektor eigen yang sepadan adalah bebas secara linear.
3) Jika polinomial ciri matriks A mempunyai tiga pelbagai akar, maka dalam beberapa asas matriks A mempunyai rupa pepenjuru.
Mari kita cari nilai eigen dan vektor eigen bagi matriks Mari kita karang persamaan ciri: 
(1- λ
)(5 - λ
)(1 - λ
) + 6 - 9(5 - λ
) - (1 - λ
) - (1 - λ
) = 0, λ
³ - 7 λ
² + 36 = 0, λ
1 = -2, λ
2 = 3, λ
3 = 6.
Mari cari koordinat bagi vektor eigen yang sepadan dengan setiap nilai yang ditemui λ. Daripada (9.5) ia berikutan bahawa jika X (1) ={x 1 ,x 2 ,x 3) – vektor eigen sepadan λ 1 =-2, maka
- sistem koperasi tetapi tidak pasti. Penyelesaiannya boleh ditulis dalam bentuk X (1)
={a,0,-a), di mana a ialah sebarang nombor. Khususnya, jika kami memerlukan | x (1)
|=1, X (1)
=
Menggantikan ke dalam sistem (9.5) λ 2 =3, kita memperoleh sistem untuk menentukan koordinat bagi vektor eigen kedua - x (2) ={y 1 ,y 2 ,y 3}:
, di mana X (2)
={b,-b,b) atau, dengan syarat | x (2)
|=1, x (2)
= 
Untuk λ 3 = 6 cari vektor eigen x (3) ={z 1 , z 2 , z 3}:
, x (3)
={c,2c,c) atau dalam versi biasa
x (3) = 
Ia boleh diperhatikan bahawa X (1) X (2)
= ab–ab= 0, x (1) x (3)
= ac-ac= 0, x (2) x (3)
= bc- 2bc + bc= 0. Oleh itu, vektor eigen bagi matriks ini adalah ortogonal berpasangan.
Kuliah 10.
Bentuk kuadratik dan hubungannya dengan matriks simetri. Sifat vektor eigen dan nilai eigen bagi matriks simetri. Mengurangkan bentuk kuadratik kepada bentuk kanonik.
Definisi 10.1.Bentuk kuadratik pembolehubah sebenar x 1, x 2,…, x n dipanggil polinomial darjah kedua dalam pembolehubah ini yang tidak mengandungi sebutan bebas dan sebutan darjah pertama.
Contoh bentuk kuadratik:
(n = 2),
(n = 3). (10.1)
Mari kita ingat definisi matriks simetri yang diberikan dalam kuliah lepas:
Definisi 10.2. Matriks segi empat sama dipanggil simetri, jika , iaitu jika unsur matriks yang simetri tentang pepenjuru utama adalah sama.
Sifat nilai eigen dan vektor eigen bagi matriks simetri:
1) Semua nilai eigen bagi matriks simetri adalah nyata.
Bukti (untuk n = 2).
Biarkan matriks A mempunyai bentuk: 
. Mari kita buat persamaan ciri:
(10.2) Mari kita cari yang membezakan:
Oleh itu, persamaan hanya mempunyai punca sebenar.
2) Eigenvectors matriks simetri adalah ortogon.
Bukti (untuk n= 2).
Koordinat bagi vektor eigen dan mesti memenuhi persamaan.
www.site membolehkan anda mencari . Laman web melakukan pengiraan. Dalam beberapa saat pelayan akan memberikan penyelesaian yang betul. Persamaan ciri untuk matriks akan jadi ungkapan algebra, ditemui oleh peraturan untuk mengira penentu matriks matriks, manakala di sepanjang pepenjuru utama akan terdapat perbezaan dalam nilai unsur pepenjuru dan pembolehubah. Apabila mengira persamaan ciri untuk matriks dalam talian, setiap elemen matriks akan didarab dengan unsur-unsur lain yang sepadan matriks. Cari dalam mod dalam talian hanya mungkin untuk persegi matriks. Operasi mencari persamaan ciri untuk matriks dalam talian berkurang untuk mengira jumlah algebra hasil darab unsur matriks hasil daripada mencari penentu matriks, hanya untuk tujuan menentukan persamaan ciri untuk matriks dalam talian. Operasi ini menduduki tempat yang istimewa dalam teori matriks, membolehkan anda mencari nilai eigen dan vektor menggunakan akar. Tugas mencari persamaan ciri untuk matriks dalam talian terdiri daripada unsur pendaraban matriks diikuti dengan menjumlahkan produk ini mengikut peraturan tertentu. www.site jumpa persamaan ciri untuk matriks dimensi yang diberikan dalam mod dalam talian. Pengiraan persamaan ciri untuk matriks dalam talian memandangkan dimensinya, ini ialah mencari polinomial dengan pekali berangka atau simbolik, ditemui mengikut peraturan untuk mengira penentu matriks- sebagai jumlah hasil darab unsur yang sepadan matriks, hanya untuk tujuan menentukan persamaan ciri untuk matriks dalam talian. Mencari polinomial berkenaan dengan pembolehubah bagi kuadratik matriks, sebagai definisi persamaan ciri untuk matriks, biasa dalam teori matriks. Maksud akar bagi polinomial persamaan ciri untuk matriks dalam talian digunakan untuk menentukan vektor eigen dan nilai eigen untuk matriks. Lebih-lebih lagi, jika penentu matriks akan sama dengan sifar, maka persamaan ciri matriks akan tetap wujud, tidak seperti sebaliknya matriks. Untuk mengira persamaan ciri untuk matriks atau cari beberapa sekali gus persamaan ciri matriks, anda perlu menghabiskan banyak masa dan usaha, manakala pelayan kami akan mencari dalam masa beberapa saat persamaan ciri untuk matriks dalam talian. Dalam kes ini, jawapan untuk mencari persamaan ciri untuk matriks dalam talian akan betul dan dengan ketepatan yang mencukupi, walaupun nombor semasa mencari persamaan ciri untuk matriks dalam talian akan menjadi tidak rasional. Di tapak www.site entri aksara dibenarkan dalam elemen matriks, itu dia persamaan ciri untuk matriks dalam talian boleh diwakili dalam bentuk simbolik umum semasa mengira persamaan ciri matriks dalam talian. Adalah berguna untuk menyemak jawapan yang diperoleh semasa menyelesaikan masalah mencari persamaan ciri untuk matriks dalam talian menggunakan tapak www.site. Apabila melakukan operasi pengiraan polinomial - persamaan ciri matriks, anda perlu berhati-hati dan sangat fokus apabila menyelesaikan masalah ini. Sebaliknya, laman web kami akan membantu anda menyemak keputusan anda mengenai topik tersebut persamaan ciri matriks dalam talian. Jika anda tidak mempunyai masa untuk pemeriksaan panjang masalah yang diselesaikan, maka www.site sudah tentu akan menjadi alat yang mudah untuk menyemak apabila mencari dan mengira persamaan ciri untuk matriks dalam talian.
Vektor eigen bagi matriks segi empat sama ialah, apabila didarab dengan matriks tertentu, menghasilkan vektor kolinear. Dengan kata mudah, apabila mendarab matriks dengan vektor eigen, yang terakhir kekal sama, tetapi didarab dengan nombor tertentu.
Definisi
Vektor eigen ialah vektor bukan sifar V, yang, apabila didarab dengan matriks persegi M, menjadi sendiri meningkat dengan beberapa nombor λ. Dalam tatatanda algebra ia kelihatan seperti:
M × V = λ × V,
di mana λ ialah nilai eigen bagi matriks M.
Mari kita pertimbangkan contoh berangka. Untuk memudahkan rakaman, nombor dalam matriks akan dipisahkan dengan koma bertitik. Mari kita mempunyai matriks:
- M = 0; 4;
- 6; 10.
Mari kita darabkannya dengan vektor lajur:
- V = -2;
Apabila kita mendarab matriks dengan vektor lajur, kita juga mendapat vektor lajur. Tegas bahasa matematik Formula untuk mendarab matriks 2 × 2 dengan vektor lajur akan kelihatan seperti ini:
- M × V = M11 × V11 + M12 × V21;
- M21 × V11 + M22 × V21.
M11 bermaksud elemen matriks M yang terletak di baris pertama dan lajur pertama, dan M22 bermaksud elemen yang terletak di baris kedua dan lajur kedua. Untuk matriks kami, unsur-unsur ini adalah sama dengan M11 = 0, M12 = 4, M21 = 6, M22 10. Untuk vektor lajur, nilai-nilai ini adalah sama dengan V11 = –2, V21 = 1. Menurut formula ini, kita mendapat keputusan berikut hasil darab matriks segi empat sama dengan vektor:
- M × V = 0 × (-2) + (4) × (1) = 4;
- 6 × (-2) + 10 × (1) = -2.
Untuk kemudahan, mari tulis vektor lajur ke dalam satu baris. Jadi, kami mendarabkan matriks segi empat sama dengan vektor (-2; 1), menghasilkan vektor (4; -2). Jelas sekali, ini adalah vektor yang sama didarab dengan λ = -2. Lambda masuk dalam kes ini menandakan nilai eigen bagi matriks.
Vektor eigen bagi matriks ialah vektor kolinear, iaitu objek yang tidak mengubah kedudukannya dalam ruang apabila didarab dengan matriks. Konsep kolineariti dalam algebra vektor adalah serupa dengan istilah keselarian dalam geometri. Dalam tafsiran geometri, vektor kolinear ialah segmen terarah selari dengan panjang yang berbeza. Sejak zaman Euclid, kita tahu bahawa satu baris mempunyai bilangan garis tak terhingga yang selari dengannya, jadi adalah logik untuk mengandaikan bahawa setiap matriks mempunyai bilangan vektor eigen yang tidak terhingga.
Daripada contoh sebelumnya adalah jelas bahawa vektor eigen boleh menjadi (-8; 4), dan (16; -8), dan (32, -16). Ini semua adalah vektor kolinear yang sepadan dengan nilai eigen λ = -2. Apabila mendarab matriks asal dengan vektor ini, kita masih akan berakhir dengan vektor yang berbeza daripada asal sebanyak 2 kali. Itulah sebabnya, apabila menyelesaikan masalah mencari vektor eigen, adalah perlu untuk mencari hanya objek vektor bebas linear. Selalunya, untuk matriks n × n, terdapat n bilangan vektor eigen. Kalkulator kami direka untuk analisis matriks segi empat sama tertib kedua, jadi hampir selalu hasilnya akan menemui dua vektor eigen, kecuali untuk kes apabila ia bertepatan.
Dalam contoh di atas, kami mengetahui terlebih dahulu vektor eigen bagi matriks asal dan dengan jelas menentukan nombor lambda. Walau bagaimanapun, dalam amalan, segala-galanya berlaku sebaliknya: nilai eigen ditemui dahulu dan barulah vektor eigen.
Algoritma penyelesaian
Mari kita lihat semula matriks asal M dan cuba cari kedua-dua vektor eigennya. Jadi matriks kelihatan seperti:
- M = 0; 4;
- 6; 10.
Mula-mula kita perlu menentukan nilai eigen λ, yang memerlukan pengiraan penentu matriks berikut:
- (0 − λ); 4;
- 6; (10 − λ).
Matriks ini diperoleh dengan menolak λ yang tidak diketahui daripada unsur-unsur pada pepenjuru utama. Penentu ditentukan menggunakan formula piawai:
- detA = M11 × M21 − M12 × M22
- detA = (0 − λ) × (10 − λ) − 24
Oleh kerana vektor kami mestilah bukan sifar, kami menerima persamaan yang terhasil sebagai bersandar secara linear dan menyamakan detA penentu kami kepada sifar.
(0 − λ) × (10 − λ) − 24 = 0
Mari kita buka kurungan dan dapatkan persamaan ciri matriks:
λ 2 − 10λ − 24 = 0
Ini adalah standard persamaan kuadratik, yang perlu diselesaikan melalui diskriminasi.
D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196
Punca diskriminasi ialah sqrt(D) = 14, oleh itu λ1 = -2, λ2 = 12. Sekarang untuk setiap nilai lambda kita perlu mencari vektor eigen. Mari kita nyatakan pekali sistem untuk λ = -2.
- M − λ × E = 2; 4;
- 6; 12.
Dalam formula ini, E ialah matriks identiti. Berdasarkan matriks yang terhasil, kami mencipta sistem persamaan linear:
2x + 4y = 6x + 12y,
dengan x dan y ialah unsur vektor eigen.
Mari kumpulkan semua X di sebelah kiri dan semua Y di sebelah kanan. Jelas sekali - 4x = 8y. Bahagikan ungkapan dengan - 4 dan dapatkan x = –2y. Sekarang kita boleh menentukan vektor eigen pertama matriks, mengambil sebarang nilai yang tidak diketahui (ingat infiniti vektor eigen yang bergantung secara linear). Mari kita ambil y = 1, kemudian x = –2. Oleh itu, vektor eigen pertama kelihatan seperti V1 = (–2; 1). Kembali ke permulaan artikel. Objek vektor inilah yang kami darabkan dengan matriks untuk menunjukkan konsep vektor eigen.
Sekarang mari kita cari vektor eigen untuk λ = 12.
- M - λ × E = -12; 4
- 6; -2.
Mari kita cipta sistem persamaan linear yang sama;
- -12x + 4y = 6x − 2y
- -18x = -6y
- 3x = y.
Sekarang kita ambil x = 1, oleh itu y = 3. Oleh itu, vektor eigen kedua kelihatan seperti V2 = (1; 3). Apabila mendarab matriks asal dengan vektor tertentu, hasilnya akan sentiasa menjadi vektor yang sama didarab dengan 12. Di sinilah algoritma penyelesaian berakhir. Sekarang anda tahu cara menentukan vektor eigen bagi matriks secara manual.
- penentu;
- surih, iaitu jumlah unsur pada pepenjuru utama;
- pangkat, iaitu bilangan maksimum baris/lajur bebas linear.
Program ini beroperasi mengikut algoritma di atas, memendekkan proses penyelesaian sebanyak mungkin. Adalah penting untuk menunjukkan bahawa dalam program lambda ditetapkan oleh huruf "c". Mari kita lihat contoh berangka.
Contoh bagaimana program ini berfungsi
Mari cuba tentukan vektor eigen untuk matriks berikut:
- M = 5; 13;
- 4; 14.
Mari masukkan nilai ini ke dalam sel kalkulator dan dapatkan jawapan dalam bentuk berikut:
- Kedudukan matriks: 2;
- Penentu matriks: 18;
- Surih matriks: 19;
- Pengiraan vektor eigen: c 2 − 19.00c + 18.00 (persamaan ciri);
- Pengiraan vektor eigen: 18 (nilai lambda pertama);
- Pengiraan vektor eigen: 1 (nilai lambda kedua);
- Sistem persamaan untuk vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
- Sistem persamaan untuk vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
- Eigenvector 1: (1; 1);
- Eigenvector 2: (-3.25; 1).
Oleh itu, kami memperoleh dua vektor eigen bebas linear.
Kesimpulan
Algebra linear dan geometri analitik adalah mata pelajaran standard untuk mana-mana jurusan kejuruteraan pelajar baru. Bilangan besar vektor dan matriks adalah menakutkan, dan mudah untuk membuat kesilapan dalam pengiraan yang menyusahkan itu. Program kami akan membolehkan pelajar menyemak pengiraan mereka atau menyelesaikan masalah mencari vektor eigen secara automatik. Terdapat kalkulator algebra linear lain dalam katalog kami menggunakannya dalam pengajian atau kerja anda.
