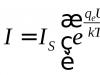અર્થશાસ્ત્રમાં ગેમ થિયરીનો ઉપયોગ. ગેમ થિયરીના ગાણિતિક મોડલ

3.4.1. ગેમ થિયરીની મૂળભૂત વિભાવનાઓ

હાલમાં, ઔદ્યોગિક, આર્થિક અથવા વ્યાપારી પ્રવૃત્તિઓમાં સમસ્યાઓના ઘણા ઉકેલો નિર્ણય લેનારના વ્યક્તિલક્ષી ગુણો પર આધારિત છે. અનિશ્ચિતતાની સ્થિતિમાં નિર્ણયો પસંદ કરતી વખતે, મનસ્વીતાનું તત્વ અને તેથી જોખમ હંમેશા અનિવાર્ય છે.

સંપૂર્ણ અથવા આંશિક અનિશ્ચિતતાની પરિસ્થિતિઓમાં નિર્ણય લેવાની સમસ્યાઓનો સામનો રમત સિદ્ધાંત દ્વારા કરવામાં આવે છે અને આંકડાકીય ઉકેલો. અનિશ્ચિતતા અન્ય પક્ષ તરફથી વિરોધનું સ્વરૂપ લઈ શકે છે, જે વિરોધી લક્ષ્યોને અનુસરે છે, અમુક ક્રિયાઓ અથવા રાજ્યોમાં દખલ કરે છે. બાહ્ય વાતાવરણ. આવા કિસ્સાઓમાં, વિરોધી પક્ષના વર્તન માટે સંભવિત વિકલ્પો ધ્યાનમાં લેવા જરૂરી છે.

બંને પક્ષો માટે સંભવિત વર્તન વિકલ્પો અને વિકલ્પો અને રાજ્યોના દરેક સંયોજન માટે તેમના પરિણામો ફોર્મમાં રજૂ કરી શકાય છે. ગાણિતિક મોડેલજેને રમત કહેવામાં આવે છે.સંઘર્ષના બંને પક્ષો પરસ્પર ક્રિયાઓની ચોક્કસ આગાહી કરી શકતા નથી. આવી અનિશ્ચિતતા હોવા છતાં, સંઘર્ષની દરેક બાજુએ નિર્ણયો લેવાના હોય છે.

ગેમ થિયરી- આ ગાણિતિક સિદ્ધાંત સંઘર્ષની પરિસ્થિતિઓ. આ સિદ્ધાંતની મુખ્ય મર્યાદાઓ દુશ્મનની સંપૂર્ણ ("આદર્શ") તર્કસંગતતાની ધારણા છે અને સંઘર્ષને ઉકેલતી વખતે સૌથી સાવચેત "પુનઃવીમા" નિર્ણયને અપનાવે છે.

વિરોધાભાસી પક્ષોને બોલાવવામાં આવે છે ખેલાડીઓ, રમતનું એક અમલીકરણ – પાર્ટી રમતનું પરિણામ - જીતવું કે હારવું.

ચાલ પરગેમ થિયરીમાં નિયમો અને તેના અમલીકરણ દ્વારા પૂરી પાડવામાં આવેલ ક્રિયાઓમાંથી એકની પસંદગી છે.

અંગત રીતેતેમાંથી એકની ખેલાડીની સભાન પસંદગી કહેવાય છે શક્ય વિકલ્પોક્રિયાઓ અને તેમના અમલીકરણ.

રેન્ડમ ચાલખેલાડીની પસંદગી કહેવાય છે જે બનાવવામાં આવી નથી સ્વૈચ્છિક નિર્ણય દ્વારાપ્લેયર, પરંતુ ક્રિયા અને તેના અમલીકરણ માટેના સંભવિત વિકલ્પોમાંથી એકની રેન્ડમ સિલેક્શન (સિક્કો ઉછાળવો, કાર્ડ ડીલિંગ વગેરે) ની કેટલીક પદ્ધતિ દ્વારા.

પ્લેયર વ્યૂહરચનાએ નિયમોનો સમૂહ છે જે રમત દરમિયાન ઊભી થતી પરિસ્થિતિના આધારે આ ખેલાડીની દરેક વ્યક્તિગત ચાલ માટે ક્રિયાની પસંદગી નક્કી કરે છે.

શ્રેષ્ઠ વ્યૂહરચનાપ્લેયર એ એક વ્યૂહરચના છે જે, જ્યારે વ્યક્તિગત અને રેન્ડમ મૂવ્સ ધરાવતી રમતમાં ઘણી વખત પુનરાવર્તિત થાય છે, ત્યારે તે ખેલાડીને શક્ય તેટલું મહત્તમ પ્રદાન કરે છે. સરેરાશજીત (અથવા, સમાન શું છે, શક્ય તેટલું ન્યૂનતમ સરેરાશનુકશાન).

પરિણામોની અનિશ્ચિતતાના કારણોના આધારે, રમતોને નીચેના મુખ્ય જૂથોમાં વિભાજિત કરી શકાય છે:

- કોમ્બિનેટરીયલરમતો જેમાં નિયમો, સૈદ્ધાંતિક રીતે, દરેક ખેલાડીને દરેક વસ્તુનું વિશ્લેષણ કરવાની મંજૂરી આપે છે વિવિધ વિકલ્પોવર્તન અને, આ વિકલ્પોની સરખામણી કરીને, શ્રેષ્ઠ પસંદ કરો. અહીં અનિશ્ચિતતા એ છે કે ઘણા બધા વિકલ્પો છે જેનું વિશ્લેષણ કરવાની જરૂર છે.

- જુગારરમતો જેમાં રેન્ડમ પરિબળોના પ્રભાવને લીધે પરિણામ અનિશ્ચિત હોય છે.

- વ્યૂહાત્મકરમત કે જેમાં પરિણામની અનિશ્ચિતતા એ હકીકતને કારણે થાય છે કે દરેક ખેલાડી, નિર્ણય લેતી વખતે, રમતમાં અન્ય સહભાગીઓ કઈ વ્યૂહરચનાનું પાલન કરશે તે જાણતા નથી, કારણ કે વિરોધી (ભાગીદાર) ની અનુગામી ક્રિયાઓ વિશે કોઈ માહિતી નથી ).

- આ રમતને ડબલ્સ કહેવામાં આવે છે, જો રમતમાં બે ખેલાડીઓ સામેલ હોય.

- રમતને બહુવિધ કહેવામાં આવે છે, જો રમતમાં બે કરતાં વધુ ખેલાડીઓ હોય.

- રમતને શૂન્ય રકમ કહેવામાં આવે છે, જો દરેક ખેલાડી અન્યના ભોગે જીતે છે, અને એક બાજુની જીત અને હારનો સરવાળો બીજી બાજુ સમાન છે.

- શૂન્ય-સમ ડબલ્સ રમતકહેવાય છે વિરોધી રમત.

- રમતને મર્યાદિત કહેવામાં આવે છે, જો દરેક ખેલાડી પાસે માત્ર મર્યાદિત સંખ્યામાં વ્યૂહરચના હોય. નહિંતર, તે એક રમત છે અનંત

- એક પગલું રમતોજ્યારે ખેલાડી વ્યૂહરચનામાંથી એક પસંદ કરે છે અને એક ચાલ કરે છે.

- મલ્ટિ-સ્ટેપ ગેમ્સમાંખેલાડીઓ તેમના લક્ષ્યોને હાંસલ કરવા માટે શ્રેણીબદ્ધ ચાલ કરે છે, જે રમતના નિયમો દ્વારા મર્યાદિત હોઈ શકે છે અથવા જ્યાં સુધી કોઈ એક ખેલાડી પાસે રમત ચાલુ રાખવા માટે કોઈ સંસાધનો બાકી ન હોય ત્યાં સુધી તે ચાલુ રહી શકે છે.

- વ્યાપાર રમતોવિવિધ સંસ્થાઓ અને સાહસોમાં સંસ્થાકીય અને આર્થિક ક્રિયાપ્રતિક્રિયાઓનું અનુકરણ કરો. વાસ્તવિક ઑબ્જેક્ટ પર રમત સિમ્યુલેશનના ફાયદા છે:

લીધેલા નિર્ણયોની પછીની અસરોની દૃશ્યતા;

ચલ સમય સ્કેલ;

સેટિંગ્સમાં ફેરફારો સાથે હાલના અનુભવનું પુનરાવર્તન;

અસાધારણ ઘટના અને વસ્તુઓનું ચલ કવરેજ.

તત્વો રમત મોડેલ છે:

- રમતના સહભાગીઓ.

- રમતના નિયમો.

- માહિતી એરે, મોડેલ કરેલ સિસ્ટમની સ્થિતિ અને હિલચાલને પ્રતિબિંબિત કરે છે.

વર્ગીકરણ અને રમતોના જૂથને વહન કરવાથી અમને શોધવાની મંજૂરી મળે છે સામાન્ય પદ્ધતિઓનિર્ણય લેવામાં વિકલ્પોની શોધ, પ્રવૃત્તિના વિવિધ ક્ષેત્રોમાં સંઘર્ષની પરિસ્થિતિઓના વિકાસ દરમિયાન ક્રિયાના સૌથી તર્કસંગત માર્ગ પર ભલામણો વિકસાવવી.

3.4.2. રમત હેતુઓ સુયોજિત

મર્યાદિત શૂન્ય-સમ જોડીઓની રમતનો વિચાર કરો. ખેલાડી A પાસે m વ્યૂહરચના છે (A 1 A 2 A m), અને ખેલાડી B પાસે n વ્યૂહરચના છે (B 1, B 2 Bn). આવી રમતને m x n પરિમાણની રમત કહેવામાં આવે છે. એવી પરિસ્થિતિમાં કે જ્યાં ખેલાડી A એ વ્યૂહરચના A i પસંદ કરી અને ખેલાડી B વ્યૂહરચના B j પસંદ કરે તેવી પરિસ્થિતિમાં ij ને ખેલાડી A ની ચૂકવણી થવા દો. આ પરિસ્થિતિમાં ખેલાડીનું વળતર b ij દ્વારા સૂચવવામાં આવશે. શૂન્ય-સરવાળા રમત, તેથી, a ij = - b ij . વિશ્લેષણ હાથ ધરવા માટે, ફક્ત એક ખેલાડીઓની ચૂકવણી જાણવી પૂરતી છે, એ કહે છે.

જો રમતમાં ફક્ત વ્યક્તિગત ચાલનો સમાવેશ થાય છે, તો પછી વ્યૂહરચના (A i, B j) ની પસંદગી રમતના પરિણામને વિશિષ્ટ રીતે નક્કી કરે છે. જો રમતમાં રેન્ડમ ચાલ પણ હોય, તો અપેક્ષિત જીત એ સરેરાશ મૂલ્ય છે (ગાણિતિક અપેક્ષા).

ચાલો ધારીએ કે ij ના મૂલ્યો વ્યૂહરચનાઓની દરેક જોડી (A i, B j) માટે જાણીતા છે. ચાલો એક લંબચોરસ કોષ્ટક બનાવીએ, જેની પંક્તિઓ ખેલાડી A ની વ્યૂહરચનાઓને અનુરૂપ છે અને કૉલમ્સ ખેલાડી Bની વ્યૂહરચનાઓને અનુરૂપ છે. આ કોષ્ટક કહેવામાં આવે છે. ચુકવણી મેટ્રિક્સ.

ખેલાડી A નો ધ્યેય તેની જીતને મહત્તમ કરવાનો છે, અને ખેલાડી B નો ધ્યેય તેની ખોટ ઘટાડવાનો છે.

આમ, ચુકવણી મેટ્રિક્સ આના જેવો દેખાય છે:

કાર્ય નક્કી કરવાનું છે:

1) A 1 A 2 A m વ્યૂહરચનાઓમાંથી ખેલાડી A ની શ્રેષ્ઠ (શ્રેષ્ઠ) વ્યૂહરચના;

2) B 1, B 2 Bn વ્યૂહરચનામાંથી ખેલાડી B ની શ્રેષ્ઠ (શ્રેષ્ઠ) વ્યૂહરચના.

સમસ્યાને હલ કરવા માટે, સિદ્ધાંત લાગુ કરવામાં આવે છે જે મુજબ રમતમાં સહભાગીઓ સમાન બુદ્ધિશાળી હોય છે અને તેમાંથી દરેક તેમના લક્ષ્યને પ્રાપ્ત કરવા માટે બધું જ કરે છે.

3.4.3. રમત સમસ્યાઓ ઉકેલવા માટેની પદ્ધતિઓ

મિનિમેક્સ સિદ્ધાંત

ચાલો આપણે ખેલાડી A ની દરેક વ્યૂહરચનાનું ક્રમિક વિશ્લેષણ કરીએ. જો ખેલાડી A વ્યૂહરચના A 1 પસંદ કરે છે, તો ખેલાડી B એવી વ્યૂહરચના B j પસંદ કરી શકે છે, જેમાં ખેલાડી A નું વળતર 1j ની સૌથી નાની સંખ્યાની બરાબર હશે. ચાલો તેને 1 સૂચવીએ:

એટલે કે, 1 એ પ્રથમ લીટીની તમામ સંખ્યાઓનું લઘુત્તમ મૂલ્ય છે.

આ તમામ પંક્તિઓ સુધી વિસ્તૃત કરી શકાય છે. તેથી, ખેલાડી A એ વ્યૂહરચના પસંદ કરવી જોઈએ જેના માટે a i મહત્તમ હોય.

મૂલ્ય a એ બાંયધરીકૃત જીત છે જે ખેલાડી B ના કોઈપણ વર્તન માટે ખેલાડી એ પોતાના માટે સુરક્ષિત કરી શકે છે. મૂલ્ય aને રમતની નીચી કિંમત કહેવામાં આવે છે.

ખેલાડી B તેની ખોટ ઘટાડવામાં રસ ધરાવે છે, એટલે કે ખેલાડી Aની જીતને ન્યૂનતમ ઘટાડવામાં. શ્રેષ્ઠ વ્યૂહરચના પસંદ કરવા માટે, તેણે દરેક કૉલમમાં મહત્તમ વળતર મૂલ્ય શોધવું જોઈએ અને તેમાંથી સૌથી નાનું પસંદ કરવું જોઈએ.

ચાલો દરેક કૉલમમાં મહત્તમ મૂલ્ય b j દ્વારા દર્શાવીએ:

ન્યૂનતમ મૂલ્ય b j દ્વારા સૂચવો.

b = લઘુત્તમ મહત્તમ a ij

b કહેવાય છે ઉપલી મર્યાદારમતો સિદ્ધાંત જે સૂચવે છે કે ખેલાડીઓ યોગ્ય વ્યૂહરચના પસંદ કરે છે તેને મિનિમેક્સ સિદ્ધાંત કહેવામાં આવે છે.

એવી મેટ્રિક્સ રમતો છે કે જેના માટે રમતની નીચી કિંમત ઉપલા ભાવની બરાબર હોય છે, આવી રમતોને સેડલ પોઈન્ટ ગેમ્સ કહેવામાં આવે છે. આ કિસ્સામાં, g=a=b ને રમતની ચોખ્ખી કિંમત કહેવામાં આવે છે, અને વ્યૂહરચનાઓ A * i, B * j જે આ મૂલ્યને હાંસલ કરવાની મંજૂરી આપે છે તેને શ્રેષ્ઠ કહેવાય છે. જોડી (A * i, B * j) ને મેટ્રિક્સનો સેડલ પોઈન્ટ કહેવામાં આવે છે, કારણ કે તત્વ a ij .= g વારાફરતી i-પંક્તિમાં લઘુત્તમ અને j-સ્તંભમાં મહત્તમ છે. શ્રેષ્ઠ વ્યૂહરચનાઓ A * i, B * j, અને ચોખ્ખી કિંમત એ શુદ્ધ વ્યૂહરચનાઓમાં રમતનો ઉકેલ છે, એટલે કે, રેન્ડમ સિલેક્શન મિકેનિઝમને સામેલ કર્યા વિના.

ઉદાહરણ 1.

પેમેન્ટ મેટ્રિક્સ આપવા દો. રમતનો ઉકેલ શોધો, એટલે કે રમતના નીચા અને ઉપલા ભાવ અને મિનિમેક્સ વ્યૂહરચના નક્કી કરો.

અહીં એક 1 = મિનિટ a 1 j = મિનિટ(5,3,8,2) =2

a = મહત્તમ મિનિટ a ij = મહત્તમ(2,1,4) =4

b = મિનિટ મહત્તમ a ij = મિનિટ(9,6,8,7) =6

આમ, ઓછી કિંમતરમતની (a=4) વ્યૂહરચના A 3 ને અનુરૂપ છે. આ વ્યૂહરચના પસંદ કરીને, ખેલાડી A, ખેલાડી B ના કોઈપણ વર્તન માટે ઓછામાં ઓછા 4 નું વળતર હાંસલ કરશે. રમતની ઉપલી કિંમત (b=6) ને અનુરૂપ છે. પ્લેયર બીની વ્યૂહરચના. આ વ્યૂહરચના મિનિમેક્સ છે. જો બંને પક્ષો આ વ્યૂહરચનાઓને અનુસરે છે, તો વળતર 4 (a 33) હશે.

ઉદાહરણ 2.

ચુકવણી મેટ્રિક્સ આપવામાં આવે છે. રમતના નીચલા અને ઉપલા ભાવો શોધો.

a = મહત્તમ મિનિટ a ij = મહત્તમ(1,2,3) =3

b = મિનિટ મહત્તમ a ij = મિનિટ(5,6,3) =3

તેથી, a =b=g=3. સેડલ પોઇન્ટ એ જોડી છે (A * 3, B * 3). જો મેટ્રિક્સ ગેમમાં સેડલ પોઈન્ટ હોય, તો તેનો ઉકેલ મિનિમેક્સ સિદ્ધાંતનો ઉપયોગ કરીને જોવા મળે છે.

મિશ્ર વ્યૂહરચના રમતો ઉકેલવા

જો ચુકવણી મેટ્રિક્સમાં સેડલ પોઈન્ટ (એ મિશ્ર વ્યૂહરચના.

મિશ્ર વ્યૂહરચનાનો ઉપયોગ કરવા માટે, નીચેની શરતો આવશ્યક છે:

1) રમતમાં કોઈ કાઠી બિંદુ નથી.

2) ખેલાડીઓ અનુરૂપ સંભાવનાઓ સાથે શુદ્ધ વ્યૂહરચનાના રેન્ડમ મિશ્રણનો ઉપયોગ કરે છે.

3) સમાન શરતો હેઠળ રમત ઘણી વખત પુનરાવર્તિત થાય છે.

4) દરેક ચાલ દરમિયાન, ખેલાડીને અન્ય ખેલાડી દ્વારા વ્યૂહરચના પસંદ કરવા વિશે જાણ કરવામાં આવતી નથી.

5) રમતના પરિણામોની સરેરાશ મંજૂરી છે.

ગેમ થિયરીમાં તે સાબિત થયું છે કે દરેક શૂન્ય-સરવાળા જોડીવાળી રમતમાં ઓછામાં ઓછો એક મિશ્ર વ્યૂહરચના ઉકેલ હોય છે, જે સૂચવે છે કે દરેક મર્યાદિત રમતની કિંમત g છે. જી- સરેરાશ જીત, બેચ દીઠ, સંતોષકારક સ્થિતિ એ<=g<=b . Оптимальное решение игры в смешанных стратегиях обладает следующим свойством: каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии.

ખેલાડીઓની તેમની શ્રેષ્ઠ મિશ્ર વ્યૂહરચનાઓને સક્રિય કહેવામાં આવે છે.

સક્રિય વ્યૂહરચના પર પ્રમેય.

શ્રેષ્ઠ મિશ્ર વ્યૂહરચનાનો ઉપયોગ ખેલાડીને રમત g ની કિંમતની સમાન મહત્તમ સરેરાશ જીત (અથવા ન્યૂનતમ સરેરાશ નુકસાન) પ્રદાન કરે છે, અન્ય ખેલાડી જે પગલાં લે છે તે ધ્યાનમાં લીધા વિના, જ્યાં સુધી તે મર્યાદાઓથી આગળ ન જાય ત્યાં સુધી તેની સક્રિય વ્યૂહરચના.

ચાલો નીચે આપેલ સૂચન રજૂ કરીએ:

P 1 P 2 ... P m - વ્યૂહરચનાનો ઉપયોગ કરીને ખેલાડી A ની સંભાવના A 1 A 2 ..... A m ;

Q 1 Q 2 … Q n વ્યૂહરચના B 1, B 2 નો ઉપયોગ કરીને ખેલાડી B ની સંભાવના….. Bn

અમે પ્લેયર A ની મિશ્ર વ્યૂહરચના ફોર્મમાં લખીએ છીએ:

A 1 A 2…. એક મી

Р 1 Р 2 … Р m

અમે ખેલાડી B ની મિશ્ર વ્યૂહરચના આ રીતે લખીએ છીએ:

B 1 B 2…. બીએન

ચુકવણી મેટ્રિક્સ A ને જાણીને, તમે સરેરાશ ચૂકવણી (ગાણિતિક અપેક્ષા) M(A,P,Q) નક્કી કરી શકો છો:

M(A,P,Q)=S Sa ij P i Q j

ખેલાડી A ની સરેરાશ જીત:

a = મહત્તમ minM(A,P,Q)

ખેલાડી B ની સરેરાશ ખોટ:

b = મિનિટ મહત્તમM(A,P,Q)

ચાલો P A * અને Q B * દ્વારા શ્રેષ્ઠ મિશ્ર વ્યૂહરચનાઓને અનુરૂપ વેક્ટર્સ સૂચવીએ જે હેઠળ:

મહત્તમ minM(A,P,Q) = ન્યૂનતમ મહત્તમM(A,P,Q) = M(A,P A *,Q B *)

આ કિસ્સામાં, નીચેની શરતો સંતુષ્ટ છે:

maxM(A,P,Q B*)<=maxМ(А,P А * ,Q В *)<= maxМ(А,P А * ,Q)

રમતને ઉકેલવાનો અર્થ એ છે કે રમતની કિંમત અને શ્રેષ્ઠ વ્યૂહરચના શોધવી.

રમતની કિંમતો અને શ્રેષ્ઠ વ્યૂહરચના નક્કી કરવા માટે ભૌમિતિક પદ્ધતિ

(રમત 2X2 માટે)

લંબાઈ 1 નો સેગમેન્ટ એબ્સીસા અક્ષ પર રચાયેલ છે.

y-અક્ષ એ 11 અને 12ની જીત દર્શાવે છે.

21 અને 22 ની જીતને બિંદુ 1 થી ઓર્ડિનેટ અક્ષની સમાંતર રેખા સાથે રચવામાં આવે છે.

જો ખેલાડી B વ્યૂહરચના B 1 નો ઉપયોગ કરે છે, તો પછી પોઈન્ટ a 11 અને a 21 ને જોડો, જો B 2, તો પછી પોઈન્ટ a 12 અને a 22 ને જોડો.

સરેરાશ જીતને બિંદુ N દ્વારા દર્શાવવામાં આવે છે, જે રેખાઓ B 1 B 1 અને B 2 B 2 ના આંતરછેદના બિંદુ છે. આ બિંદુનો એબ્સીસા P 2 ની બરાબર છે, અને રમતની કિંમતનો નિર્દેશ g છે.

અગાઉની તકનીકની તુલનામાં, લાભ 55% છે.

ગેમ થિયરી એ ગેમ્સમાં શ્રેષ્ઠ વ્યૂહરચનાનો અભ્યાસ કરવા માટેની ગાણિતિક પદ્ધતિ છે. "રમત" શબ્દને બે અથવા વધુ પક્ષોની ક્રિયાપ્રતિક્રિયા તરીકે સમજવો જોઈએ જેઓ તેમના હિતોને સાકાર કરવા માગે છે. દરેક પક્ષની પોતાની વ્યૂહરચના પણ હોય છે, જે જીત અથવા હાર તરફ દોરી શકે છે, જે ખેલાડીઓ કેવી રીતે વર્તે છે તેના પર નિર્ભર કરે છે. ગેમ થિયરી માટે આભાર, અન્ય ખેલાડીઓ અને તેમની સંભવિતતા વિશેના વિચારોને ધ્યાનમાં રાખીને, સૌથી અસરકારક વ્યૂહરચના શોધવાનું શક્ય બને છે.

ગેમ થિયરી ઓપરેશન સંશોધનની વિશેષ શાખા છે. મોટા ભાગના કિસ્સાઓમાં, ગેમ થિયરી પદ્ધતિઓનો ઉપયોગ અર્થશાસ્ત્રમાં થાય છે, પરંતુ કેટલીકવાર અન્ય સામાજિક વિજ્ઞાનમાં, ઉદાહરણ તરીકે, રાજકીય વિજ્ઞાન, સમાજશાસ્ત્ર, નીતિશાસ્ત્ર અને કેટલાક અન્ય. 20મી સદીના 70 ના દાયકાથી, જીવવિજ્ઞાનીઓ દ્વારા પ્રાણીઓના વર્તન અને ઉત્ક્રાંતિના સિદ્ધાંતનો અભ્યાસ કરવા માટે પણ તેનો ઉપયોગ કરવામાં આવે છે. વધુમાં, આજે ગેમ થિયરી સાયબરનેટિક્સના ક્ષેત્રમાં ખૂબ જ મહત્વપૂર્ણ છે અને. એટલા માટે અમે તમને તેના વિશે જણાવવા માંગીએ છીએ.

ગેમ થિયરીનો ઇતિહાસ

વૈજ્ઞાનિકોએ 18મી સદીમાં ગાણિતિક મોડેલિંગના ક્ષેત્રમાં સૌથી શ્રેષ્ઠ વ્યૂહરચનાનો પ્રસ્તાવ મૂક્યો હતો. 19મી સદીમાં, ઓછી સ્પર્ધાવાળા બજારમાં કિંમતો અને ઉત્પાદનની સમસ્યાઓ, જે પાછળથી ગેમ થિયરીના ઉત્તમ ઉદાહરણો બની હતી, તેને જોસેફ બર્ટ્રાન્ડ અને એન્ટોઈન કોર્નોટ જેવા વૈજ્ઞાનિકો દ્વારા ગણવામાં આવી હતી. અને 20મી સદીની શરૂઆતમાં, ઉત્કૃષ્ટ ગણિતશાસ્ત્રીઓ એમિલ બોરેલ અને અર્ન્સ્ટ ઝરમેલોએ હિતોના સંઘર્ષના ગાણિતિક સિદ્ધાંતનો વિચાર આગળ ધપાવ્યો.

ગાણિતિક રમત સિદ્ધાંતની ઉત્પત્તિ નિયોક્લાસિકલ અર્થશાસ્ત્રમાં શોધવી જોઈએ. શરૂઆતમાં, આ સિદ્ધાંતના પાયા અને પાસાઓ 1944માં ઓસ્કાર મોર્ગનસ્ટર્ન અને જ્હોન વોન ન્યુમેનના કાર્યમાં "ધ થિયરી ઓફ ગેમ્સ એન્ડ ઈકોનોમિક બિહેવિયર"માં દર્શાવેલ હતા.

પ્રસ્તુત ગાણિતિક ક્ષેત્રે સામાજિક સંસ્કૃતિમાં પણ થોડું પ્રતિબિંબ જોવા મળ્યું. ઉદાહરણ તરીકે, 1998 માં, સિલ્વિયા નાસર (અમેરિકન પત્રકાર અને લેખક) એ અર્થશાસ્ત્રમાં નોબેલ પારિતોષિક વિજેતા અને ગેમ થિયરીસ્ટ જ્હોન નેશને સમર્પિત પુસ્તક પ્રકાશિત કર્યું. 2001 માં, આ કાર્ય પર આધારિત, ફિલ્મ "એ બ્યુટીફુલ માઇન્ડ" બનાવવામાં આવી હતી. અને સંખ્યાબંધ અમેરિકન ટેલિવિઝન શો, જેમ કે “NUMB3RS”, “Alias” અને “Friend or Foe” પણ તેમના પ્રસારણમાં સમય સમય પર ગેમ થિયરીનો સંદર્ભ આપે છે.

પરંતુ જોન નેશ વિશે ખાસ ઉલ્લેખ કરવો જોઈએ.

1949 માં, તેમણે ગેમ થિયરી પર એક મહાનિબંધ લખ્યો, અને 45 વર્ષ પછી તેમને અર્થશાસ્ત્રમાં નોબેલ પુરસ્કાર એનાયત કરવામાં આવ્યો. ગેમ થિયરીના પ્રારંભિક ખ્યાલોમાં, વિરોધી પ્રકારની રમતોનું વિશ્લેષણ કરવામાં આવ્યું હતું, જેમાં એવા ખેલાડીઓ છે કે જેઓ હારનારાઓના ભોગે જીતે છે. પરંતુ જ્હોન નેશે વિશ્લેષણાત્મક પદ્ધતિઓ વિકસાવી જે મુજબ તમામ ખેલાડીઓ કાં તો હારે છે અથવા જીતે છે.

નેશ દ્વારા વિકસિત પરિસ્થિતિઓને પાછળથી "નેશ સંતુલન" કહેવામાં આવી. તેઓ અલગ પડે છે કે રમતની તમામ બાજુઓ સૌથી શ્રેષ્ઠ વ્યૂહરચનાનો ઉપયોગ કરે છે, જે સ્થિર સંતુલન બનાવે છે. સંતુલન જાળવવું એ ખેલાડીઓ માટે ખૂબ ફાયદાકારક છે, કારણ કે અન્યથા એક ફેરફાર તેમની સ્થિતિને નકારાત્મક અસર કરી શકે છે.

જ્હોન નેશના કાર્ય માટે આભાર, રમત સિદ્ધાંતને તેના વિકાસમાં એક શક્તિશાળી પ્રોત્સાહન મળ્યું. વધુમાં, આર્થિક મોડેલિંગના ગાણિતિક સાધનોમાં ગંભીરતાથી સુધારો કરવામાં આવ્યો છે. જ્હોન નેશ એ સાબિત કરવામાં સક્ષમ હતા કે સ્પર્ધાના મુદ્દા પર ક્લાસિકલ દૃષ્ટિકોણ, જ્યાં દરેક વ્યક્તિ ફક્ત પોતાના માટે રમે છે, તે શ્રેષ્ઠ નથી, અને સૌથી અસરકારક વ્યૂહરચના એ છે કે જેમાં ખેલાડીઓ શરૂઆતમાં અન્યને વધુ સારું બનાવીને પોતાને વધુ સારા બનાવે છે.

હકીકત એ છે કે રમત સિદ્ધાંતમાં શરૂઆતમાં તેના દૃષ્ટિકોણના ક્ષેત્રમાં આર્થિક મોડલનો સમાવેશ થતો હોવા છતાં, છેલ્લી સદીના 50 ના દાયકા સુધી તે માત્ર ગણિતના માળખા દ્વારા મર્યાદિત ઔપચારિક સિદ્ધાંત હતો. જો કે, 20મી સદીના ઉત્તરાર્ધથી, અર્થશાસ્ત્ર, માનવશાસ્ત્ર, ટેકનોલોજી, સાયબરનેટિક્સ અને જીવવિજ્ઞાનમાં તેનો ઉપયોગ કરવાનો પ્રયાસ કરવામાં આવ્યો છે. બીજા વિશ્વ યુદ્ધ દરમિયાન અને તેના અંત પછી, સૈન્ય દ્વારા રમત સિદ્ધાંતને ધ્યાનમાં લેવાનું શરૂ થયું, જેણે તેમાં વ્યૂહાત્મક નિર્ણયોના વિકાસ માટે એક ગંભીર ઉપકરણ જોયું.

60-70 ના દાયકા દરમિયાન, આ સિદ્ધાંતમાં રસ ઓછો થયો, તે હકીકત હોવા છતાં કે તે સારા ગાણિતિક પરિણામો આપે છે. પરંતુ 80 ના દાયકાથી, વ્યવહારમાં રમત સિદ્ધાંતનો સક્રિય ઉપયોગ શરૂ થયો, મુખ્યત્વે મેનેજમેન્ટ અને અર્થશાસ્ત્રમાં. છેલ્લા કેટલાક દાયકાઓમાં, તેની સુસંગતતા નોંધપાત્ર રીતે વધી છે, અને કેટલાક આધુનિક આર્થિક વલણો તેના વિના કલ્પના કરવી સંપૂર્ણપણે અશક્ય છે.

અર્થશાસ્ત્રમાં નોબેલ પારિતોષિક વિજેતા થોમસ શેલિંગ દ્વારા 2005 ની કૃતિ “સ્ટ્રેટેજી ઑફ કોન્ફ્લિક્ટ” દ્વારા ગેમ થિયરીના વિકાસમાં મહત્વપૂર્ણ યોગદાન આપવામાં આવ્યું હતું તે કહેવું પણ અનાવશ્યક રહેશે નહીં. તેમના કાર્યમાં, શેલિંગે સંઘર્ષની ક્રિયાપ્રતિક્રિયાઓમાં સહભાગીઓ દ્વારા ઉપયોગમાં લેવાતી ઘણી વ્યૂહરચનાઓની તપાસ કરી. આ વ્યૂહરચનાઓ સંઘર્ષ વ્યવસ્થાપન વ્યૂહરચના અને વિશ્લેષણાત્મક સિદ્ધાંતો સાથે સુસંગત છે, સાથે સાથે સંગઠનોમાં સંઘર્ષને સંચાલિત કરવા માટે ઉપયોગમાં લેવાતી યુક્તિઓ.

મનોવૈજ્ઞાનિક વિજ્ઞાન અને અન્ય સંખ્યાબંધ શાખાઓમાં, "રમત" ની વિભાવનાનો ગણિત કરતાં થોડો અલગ અર્થ છે. "ગેમ" શબ્દનું સાંસ્કૃતિક અર્થઘટન જોહાન હુઇઝિંગા દ્વારા પુસ્તક "હોમો લુડેન્સ" માં રજૂ કરવામાં આવ્યું હતું, જ્યાં લેખક નૈતિકતા, સંસ્કૃતિ અને ન્યાયમાં રમતોના ઉપયોગ વિશે વાત કરે છે, અને એ પણ નિર્દેશ કરે છે કે રમત પોતે નોંધપાત્ર રીતે શ્રેષ્ઠ છે. ઉંમરમાં માણસો, કારણ કે પ્રાણીઓ પણ ઝોક રમત છે.

ઉપરાંત, "ગેમ" ની વિભાવના એરિક બાયર્નની વિભાવનામાં મળી શકે છે, જે "" પુસ્તકમાંથી જાણીતી છે. અહીં, જો કે, અમે ફક્ત મનોવૈજ્ઞાનિક રમતો વિશે વાત કરી રહ્યા છીએ, જેનો આધાર વ્યવહાર વિશ્લેષણ છે.

ગેમ થિયરીનો ઉપયોગ

જો આપણે ગાણિતિક રમત સિદ્ધાંત વિશે વાત કરીએ, તો તે હાલમાં સક્રિય વિકાસના તબક્કે છે. પરંતુ ગાણિતિક આધાર સ્વાભાવિક રીતે ખૂબ જ ખર્ચાળ છે, આ કારણોસર તેનો ઉપયોગ મુખ્યત્વે ત્યારે જ થાય છે જ્યારે અંત માધ્યમોને ન્યાયી ઠેરવે છે, એટલે કે: રાજકારણમાં, એકાધિકારનું અર્થશાસ્ત્ર અને બજાર શક્તિનું વિતરણ વગેરે. નહિંતર, રમત સિદ્ધાંતનો ઉપયોગ મોટી સંખ્યામાં પરિસ્થિતિઓમાં માનવ અને પ્રાણીઓના વર્તનના અભ્યાસમાં થાય છે.

પહેલેથી જ ઉલ્લેખ કર્યો છે તેમ, ગેમ થિયરી સૌપ્રથમ આર્થિક વિજ્ઞાનની સીમાઓમાં વિકસિત થઈ, જે વિવિધ પરિસ્થિતિઓમાં આર્થિક એજન્ટોના વર્તનને નિર્ધારિત અને અર્થઘટન કરવાનું શક્ય બનાવે છે. પરંતુ પાછળથી, તેની એપ્લિકેશનનો અવકાશ નોંધપાત્ર રીતે વિસ્તર્યો અને ઘણા સામાજિક વિજ્ઞાનનો સમાવેશ કરવાનું શરૂ કર્યું, જેના કારણે આજે રમત સિદ્ધાંત મનોવિજ્ઞાન, સમાજશાસ્ત્ર અને રાજકીય વિજ્ઞાનમાં માનવ વર્તનને સમજાવે છે.

નિષ્ણાતો રમત સિદ્ધાંતનો ઉપયોગ માત્ર માનવ વર્તનને સમજાવવા અને આગાહી કરવા માટે જ કરતા નથી - બેન્ચમાર્ક વર્તન વિકસાવવા માટે આ સિદ્ધાંતનો ઉપયોગ કરવાના ઘણા પ્રયાસો કરવામાં આવ્યા છે. વધુમાં, ફિલસૂફો અને અર્થશાસ્ત્રીઓએ લાંબા સમયથી તેનો ઉપયોગ સારા કે યોગ્ય વર્તનને શક્ય તેટલી શ્રેષ્ઠ રીતે સમજવાનો પ્રયાસ કરવા માટે કર્યો છે.

આમ, આપણે નિષ્કર્ષ પર આવી શકીએ છીએ કે રમત સિદ્ધાંત ઘણા વિજ્ઞાનના વિકાસમાં એક વાસ્તવિક વળાંક બની ગયો છે, અને આજે તે માનવ વર્તનના વિવિધ પાસાઓનો અભ્યાસ કરવાની પ્રક્રિયાનો એક અભિન્ન ભાગ છે.

નિષ્કર્ષને બદલે:જેમ તમે નોંધ્યું છે તેમ, ગેમ થિયરી સંઘર્ષશાસ્ત્ર સાથે ખૂબ નજીકથી જોડાયેલી છે - એક વિજ્ઞાન જે સંઘર્ષની ક્રિયાપ્રતિક્રિયાની પ્રક્રિયામાં માનવ વર્તનના અભ્યાસને સમર્પિત છે. અને, અમારા મતે, આ ક્ષેત્ર માત્ર તેમાંથી એક સૌથી મહત્વપૂર્ણ છે કે જેમાં રમત સિદ્ધાંત લાગુ થવો જોઈએ, પરંતુ તેમાંથી પણ કે જેનો વ્યક્તિએ પોતે અભ્યાસ કરવો જોઈએ, કારણ કે તકરાર, ગમે તે કહે, તે આપણા જીવનનો ભાગ છે. .

જો તમે સામાન્ય રીતે કઈ વર્તણૂકલક્ષી વ્યૂહરચનાઓ અસ્તિત્વમાં છે તે સમજવા માંગતા હો, તો અમે તમને અમારો સ્વ-જ્ઞાન અભ્યાસક્રમ લેવાનું સૂચન કરીએ છીએ, જે તમને આવી માહિતી સંપૂર્ણ રીતે પ્રદાન કરશે. પરંતુ, વધુમાં, અમારો અભ્યાસક્રમ પૂર્ણ કર્યા પછી, તમે સામાન્ય રીતે તમારા વ્યક્તિત્વનું વ્યાપક મૂલ્યાંકન કરી શકશો. આનો અર્થ એ છે કે તમે જાણશો કે સંઘર્ષના કિસ્સામાં કેવી રીતે વર્તવું, અને તમારા વ્યક્તિગત ફાયદા અને ગેરફાયદા શું છે, જીવન મૂલ્યો અને પ્રાથમિકતાઓ, કાર્ય અને સર્જનાત્મકતા અને ઘણું બધું. સામાન્ય રીતે, વિકાસ માટે પ્રયત્નશીલ કોઈપણ માટે આ એક ખૂબ જ ઉપયોગી અને જરૂરી સાધન છે.

અમારો અભ્યાસક્રમ ચાલુ છે - સ્વ-જ્ઞાન શરૂ કરવા અને પોતાને સુધારવા માટે નિઃસંકોચ.

અમે તમને સફળતા અને કોઈપણ રમતમાં વિજેતા બનવાની ક્ષમતાની ઇચ્છા કરીએ છીએ!

ગેમ થિયરી વિભાગ ત્રણ દ્વારા રજૂ થાય છે ઓનલાઈન કેલ્ક્યુલેટર:

1. મેટ્રિક્સ રમત ઉકેલવી. આવી સમસ્યાઓમાં, ચુકવણી મેટ્રિક્સનો ઉલ્લેખ કરવામાં આવે છે. ખેલાડીઓની શુદ્ધ અથવા મિશ્રિત વ્યૂહરચના શોધવા જરૂરી છે અને, રમત કિંમત. ઉકેલવા માટે, તમારે મેટ્રિક્સનું પરિમાણ અને ઉકેલ પદ્ધતિનો ઉલ્લેખ કરવો આવશ્યક છે.
2. Bimatrix રમત. સામાન્ય રીતે આવી રમતમાં પ્રથમ અને બીજા ખેલાડીઓની ચૂકવણીના સમાન કદના બે મેટ્રિસિસનો ઉલ્લેખ કરવામાં આવે છે. આ મેટ્રિસિસની પંક્તિઓ પ્રથમ ખેલાડીની વ્યૂહરચનાઓને અનુરૂપ છે, અને મેટ્રિસિસના કૉલમ બીજા ખેલાડીની વ્યૂહરચનાઓને અનુરૂપ છે. આ કિસ્સામાં, પ્રથમ મેટ્રિક્સ પ્રથમ ખેલાડીની જીતનું પ્રતિનિધિત્વ કરે છે, અને બીજું મેટ્રિક્સ બીજાની જીતનું પ્રતિનિધિત્વ કરે છે.
3. પ્રકૃતિ સાથે રમતો. જ્યારે મેક્સિમેક્સ, બેયસ, લેપ્લેસ, વાલ્ડ, સેવેજ, હર્વિટ્ઝના માપદંડ અનુસાર મેનેજમેન્ટ નિર્ણય પસંદ કરવો જરૂરી હોય ત્યારે તેનો ઉપયોગ થાય છે.

વ્યવહારમાં, અમે ઘણીવાર સમસ્યાઓનો સામનો કરીએ છીએ જેમાં અનિશ્ચિતતાની પરિસ્થિતિઓમાં નિર્ણયો લેવા જરૂરી છે, એટલે કે. એવી પરિસ્થિતિઓ ઊભી થાય છે જેમાં બે પક્ષો જુદા જુદા ધ્યેયોને અનુસરે છે અને દરેક પક્ષની ક્રિયાઓના પરિણામો દુશ્મન (અથવા ભાગીદાર) ની પ્રવૃત્તિઓ પર આધાર રાખે છે.

એવી પરિસ્થિતિ કે જેમાં એક પક્ષ દ્વારા લેવામાં આવેલા નિર્ણયની અસરકારકતા બીજા પક્ષની ક્રિયાઓ પર આધાર રાખે છે તેને કહેવામાં આવે છે સંઘર્ષ. સંઘર્ષ હંમેશા અમુક પ્રકારના મતભેદ સાથે સંકળાયેલો હોય છે (આ જરૂરી નથી કે વિરોધી વિરોધાભાસ હોય).

સંઘર્ષની સ્થિતિ કહેવામાં આવે છે વિરોધી, જો ચોક્કસ રકમ દ્વારા એક પક્ષની જીતમાં વધારો એ જ રકમ દ્વારા બીજી બાજુની જીતમાં ઘટાડો તરફ દોરી જાય છે, અને ઊલટું.

અર્થશાસ્ત્રમાં, સંઘર્ષની પરિસ્થિતિઓ ઘણી વાર જોવા મળે છે અને તે વિવિધ પ્રકારની હોય છે. ઉદાહરણ તરીકે, સપ્લાયર અને ગ્રાહક, ખરીદનાર અને વિક્રેતા, બેંક અને ગ્રાહક વચ્ચેનો સંબંધ. તેમાંના દરેકની પોતાની રુચિઓ છે અને શ્રેષ્ઠ નિર્ણયો લેવાનો પ્રયત્ન કરે છે જે તેમના લક્ષ્યોને સૌથી વધુ હદ સુધી પ્રાપ્ત કરવામાં મદદ કરે છે. તે જ સમયે, દરેક વ્યક્તિએ ફક્ત તેમના પોતાના ધ્યેયો જ નહીં, પરંતુ તેમના જીવનસાથીના લક્ષ્યોને પણ ધ્યાનમાં લેવા જોઈએ અને આ ભાગીદારો જે નિર્ણયો લેશે તે ધ્યાનમાં લેવું જોઈએ (તેઓ અગાઉથી અજાણ હોઈ શકે છે). સંઘર્ષની પરિસ્થિતિઓમાં શ્રેષ્ઠ નિર્ણયો લેવા માટે, સંઘર્ષની પરિસ્થિતિઓનો ગાણિતિક સિદ્ધાંત બનાવવામાં આવ્યો છે, જેને કહેવામાં આવે છે. રમત સિદ્ધાંત . આ સિદ્ધાંતનો ઉદભવ 1944નો છે, જ્યારે જે. વોન ન્યુમેનનો મોનોગ્રાફ “ગેમ થિયરી એન્ડ ઈકોનોમિક બિહેવિયર” પ્રકાશિત થયો હતો.

આ રમત વાસ્તવિક સંઘર્ષની પરિસ્થિતિનું ગાણિતિક મોડેલ છે. સંઘર્ષમાં સામેલ પક્ષોને ખેલાડીઓ કહેવામાં આવે છે. સંઘર્ષના પરિણામને જીત કહેવામાં આવે છે. રમતના નિયમો એ શરતોની સિસ્ટમ છે જે ખેલાડીઓના ક્રિયા માટેના વિકલ્પો નક્કી કરે છે; દરેક ખેલાડી પાસે તેમના ભાગીદારોના વર્તન વિશેની માહિતીનો જથ્થો; ચૂકવણી કે જે ક્રિયાઓના દરેક સમૂહ તરફ દોરી જાય છે.

રમત કહેવાય છે સ્ટીમ રૂમ, જો તેમાં બે ખેલાડીઓ સામેલ હોય, અને બહુવિધ, જો ખેલાડીઓની સંખ્યા બે કરતા વધુ હોય. અમે ફક્ત ડબલ્સ રમતો પર વિચાર કરીશું. ખેલાડીઓ નિયુક્ત કરવામાં આવ્યા છે એઅને બી.

રમત કહેવાય છે વિરોધી (શૂન્ય રકમ), જો ખેલાડીઓમાંથી એકનો ફાયદો બીજાના નુકસાનની બરાબર હોય.

નિયમો દ્વારા પૂરા પાડવામાં આવેલ વિકલ્પોમાંથી એકની પસંદગી અને અમલીકરણ કહેવામાં આવે છે પ્રગતિખેલાડી ચાલ વ્યક્તિગત અને રેન્ડમ હોઈ શકે છે.
વ્યક્તિગત ચાલ- ક્રિયા માટેના વિકલ્પોમાંથી એકના ખેલાડી દ્વારા આ સભાન પસંદગી છે (ઉદાહરણ તરીકે, ચેસમાં).
રેન્ડમ ચાલઅવ્યવસ્થિત રીતે પસંદ કરેલી ક્રિયા છે (ઉદાહરણ તરીકે, ડાઇસ ફેંકવું). અમે ફક્ત વ્યક્તિગત ચાલ ધ્યાનમાં લઈશું.

પ્લેયર વ્યૂહરચનાનિયમોનો સમૂહ છે જે દરેક વ્યક્તિગત ચાલ દરમિયાન ખેલાડીની વર્તણૂક નક્કી કરે છે. સામાન્ય રીતે દરેક તબક્કે રમત દરમિયાન ખેલાડી ચોક્કસ પરિસ્થિતિના આધારે ચાલ પસંદ કરે છે. તે પણ શક્ય છે કે તમામ નિર્ણયો ખેલાડી દ્વારા અગાઉથી લેવામાં આવ્યા હોય (એટલે ​​કે ખેલાડીએ ચોક્કસ વ્યૂહરચના પસંદ કરી હોય).

રમત કહેવાય છે અંતિમ, જો દરેક ખેલાડી પાસે મર્યાદિત સંખ્યામાં વ્યૂહરચના હોય, અને અનંત- અન્યથા.

ગેમ થિયરીનો હેતુ- દરેક ખેલાડી માટે શ્રેષ્ઠ વ્યૂહરચના નક્કી કરવા માટે પદ્ધતિઓ વિકસાવો.

ખેલાડીની વ્યૂહરચના કહેવાય છે શ્રેષ્ઠ, જો તે આ ખેલાડીને રમતના બહુવિધ પુનરાવર્તનો સાથે મહત્તમ સંભવિત સરેરાશ જીત પ્રદાન કરે છે (અથવા પ્રતિસ્પર્ધીના વર્તનને ધ્યાનમાં લીધા વિના ન્યૂનતમ સંભવિત સરેરાશ નુકસાન).

ઉદાહરણ 1.ખેલાડીઓ દરેક એઅથવા બી, બીજાથી સ્વતંત્ર રીતે, 1, 2 અને 3 નંબરો લખી શકે છે. જો ખેલાડીઓ દ્વારા લખવામાં આવેલી સંખ્યાઓ વચ્ચેનો તફાવત હકારાત્મક હોય, તો એજીતેલી સંખ્યાઓ વચ્ચેના તફાવતની બરાબર પોઈન્ટની સંખ્યા. જો તફાવત 0 કરતા ઓછો હોય, તો તે જીતે છે બી. જો તફાવત 0 છે, તો તે ડ્રો છે.
પ્લેયર A પાસે ત્રણ વ્યૂહરચના (ક્રિયા વિકલ્પો): A 1 = 1 (1 લખો), A 2 = 2, A 3 = 3, ખેલાડી પાસે પણ ત્રણ વ્યૂહરચના છે: B 1, B 2, B 3.

બી એ	B 1 = 1	B2=2	B 3 =3
A 1 = 1	0	-1	-2
A 2 = 2	1	0	-1
A 3 = 3	2	1	0

પ્લેયર Aનું કાર્ય તેની જીતને મહત્તમ કરવાનું છે. પ્લેયર બીનું કાર્ય તેના નુકસાનને ઓછું કરવાનું છે, એટલે કે. લાભ એ ઓછો કરો. આ શૂન્ય-સમ ડબલ્સ રમત.

પ્રસ્તાવના

આ લેખનો હેતુ વાચકને ગેમ થિયરીના મૂળભૂત ખ્યાલોથી પરિચિત કરવાનો છે. લેખમાંથી, વાચક ગેમ થિયરી શું છે તે શીખશે, ગેમ થિયરીના સંક્ષિપ્ત ઈતિહાસને ધ્યાનમાં લેશે અને ગેમ થિયરીના મૂળભૂત સિદ્ધાંતોથી પરિચિત થશે, જેમાં રમતોના મુખ્ય પ્રકારો અને તેમની રજૂઆતના સ્વરૂપોનો સમાવેશ થાય છે. આ લેખ શાસ્ત્રીય સમસ્યા અને ગેમ થિયરીની મૂળભૂત સમસ્યાને સ્પર્શશે. લેખનો અંતિમ વિભાગ મેનેજમેન્ટના નિર્ણયો લેવા માટે ગેમ થિયરીનો ઉપયોગ કરવાની સમસ્યાઓ અને મેનેજમેન્ટમાં ગેમ થિયરીના વ્યવહારુ ઉપયોગને ધ્યાનમાં લેવા માટે સમર્પિત છે.

પરિચય.

21મી સદી. માહિતીનો યુગ, ઝડપથી વિકસતી માહિતી તકનીકો, નવીનતાઓ અને તકનીકી નવીનતાઓ. પરંતુ માહિતી યુગ શા માટે? સમાજમાં થતી લગભગ તમામ પ્રક્રિયાઓમાં માહિતી શા માટે મુખ્ય ભૂમિકા ભજવે છે? તે ખૂબ જ સરળ છે. માહિતી આપણને અમૂલ્ય સમય આપે છે, અને કેટલાક કિસ્સાઓમાં તે આગળ વધવાની તક પણ આપે છે. છેવટે, તે કોઈ રહસ્ય નથી કે જીવનમાં તમારે ઘણીવાર એવા કાર્યોનો સામનો કરવો પડે છે જેમાં તમારે અનિશ્ચિતતાની પરિસ્થિતિઓમાં નિર્ણયો લેવાની જરૂર હોય છે, તમારી ક્રિયાઓના પ્રતિસાદ વિશેની માહિતીની ગેરહાજરીમાં, એટલે કે પરિસ્થિતિઓ ઊભી થાય છે જેમાં બે (અથવા વધુ) પક્ષો હોય છે. જુદા જુદા ધ્યેયોનો પીછો કરો, અને દરેક પક્ષની કોઈપણ ક્રિયાના પરિણામો ભાગીદારની પ્રવૃત્તિઓ પર આધારિત છે. આવી પરિસ્થિતિઓ દરરોજ સર્જાય છે. ઉદાહરણ તરીકે, જ્યારે ચેસ, ચેકર્સ, ડોમિનોઝ અને તેથી વધુ રમતા. એ હકીકત હોવા છતાં કે રમતો મુખ્યત્વે પ્રકૃતિમાં મનોરંજક હોય છે, તેમના સ્વભાવ દ્વારા તેઓ સંઘર્ષની પરિસ્થિતિઓ સાથે સંબંધિત છે જેમાં સંઘર્ષ પહેલેથી જ રમતના લક્ષ્યમાં સહજ છે - ભાગીદારોમાંથી એકની જીત. તે જ સમયે, દરેક ખેલાડીની ચાલનું પરિણામ વિરોધીની પ્રતિક્રિયા ચાલ પર આધારિત છે. અર્થશાસ્ત્રમાં, સંઘર્ષની પરિસ્થિતિઓ ઘણી વાર જોવા મળે છે અને તે વૈવિધ્યસભર હોય છે, અને તેમની સંખ્યા એટલી મોટી છે કે ઓછામાં ઓછા એક દિવસમાં બજારમાં ઊભી થતી તમામ સંઘર્ષ પરિસ્થિતિઓની ગણતરી કરવી અશક્ય છે. અર્થતંત્રમાં સંઘર્ષની પરિસ્થિતિઓમાં, ઉદાહરણ તરીકે, સપ્લાયર અને ગ્રાહક, ખરીદનાર અને વેચનાર, બેંક અને ક્લાયન્ટ વચ્ચેના સંબંધોનો સમાવેશ થાય છે. ઉપરોક્ત તમામ ઉદાહરણોમાં, સંઘર્ષની પરિસ્થિતિ ભાગીદારોના હિતમાં તફાવત અને તેમાંથી દરેકની શ્રેષ્ઠ નિર્ણયો લેવાની ઇચ્છાથી ઉત્પન્ન થાય છે જે તેમના લક્ષ્યોને સૌથી વધુ હદ સુધી સાકાર કરે છે. તે જ સમયે, દરેક વ્યક્તિએ માત્ર તેમના પોતાના ધ્યેયો જ નહીં, પરંતુ તેમના જીવનસાથીના લક્ષ્યોને પણ ધ્યાનમાં લેવા જોઈએ, અને આ ભાગીદારો જે નિર્ણયો લેશે તે અગાઉથી અજાણ્યા નિર્ણયોને ધ્યાનમાં લેવા જોઈએ. સંઘર્ષની પરિસ્થિતિઓમાં સમસ્યાઓને સક્ષમ રીતે ઉકેલવા માટે, વૈજ્ઞાનિક રીતે આધારિત પદ્ધતિઓની જરૂર છે. આવી પદ્ધતિઓ સંઘર્ષ પરિસ્થિતિઓના ગાણિતિક સિદ્ધાંત દ્વારા વિકસાવવામાં આવે છે, જેને કહેવામાં આવે છે રમત સિદ્ધાંત.

ગેમ થિયરી શું છે?

ગેમ થિયરી એક જટિલ, બહુ-પરિમાણીય ખ્યાલ છે, તેથી માત્ર એક વ્યાખ્યાનો ઉપયોગ કરીને ગેમ થિયરીનું અર્થઘટન કરવું અશક્ય લાગે છે. ચાલો ગેમ થિયરીને વ્યાખ્યાયિત કરવા માટેના ત્રણ અભિગમો જોઈએ.

1.ગેમ થિયરી એ ગેમ્સમાં શ્રેષ્ઠ વ્યૂહરચનાનો અભ્યાસ કરવા માટેની ગાણિતિક પદ્ધતિ છે. રમત એ એક પ્રક્રિયા છે જેમાં બે અથવા વધુ પક્ષો ભાગ લે છે, તેમના હિતોની અનુભૂતિ માટે લડતા હોય છે. દરેક પક્ષનો પોતાનો ધ્યેય હોય છે અને તે કેટલીક વ્યૂહરચનાનો ઉપયોગ કરે છે જે અન્ય ખેલાડીઓની વર્તણૂકના આધારે - જીતવા અથવા હાર તરફ દોરી શકે છે. ગેમ થિયરી અન્ય સહભાગીઓ, તેમના સંસાધનો અને તેમની સંભવિત ક્રિયાઓ વિશેના વિચારોને ધ્યાનમાં લઈને શ્રેષ્ઠ વ્યૂહરચના પસંદ કરવામાં મદદ કરે છે.

2. ગેમ થિયરી એ એપ્લાઇડ મેથેમેટિક્સની શાખા છે, અથવા વધુ સ્પષ્ટ રીતે, ઓપરેશન સંશોધન. મોટેભાગે, રમત સિદ્ધાંત પદ્ધતિઓનો ઉપયોગ અર્થશાસ્ત્રમાં થાય છે, અને થોડી ઓછી વાર અન્ય સામાજિક વિજ્ઞાન - સમાજશાસ્ત્ર, રાજકીય વિજ્ઞાન, મનોવિજ્ઞાન, નીતિશાસ્ત્ર અને અન્યમાં. 1970 ના દાયકાથી, જીવવિજ્ઞાનીઓ દ્વારા પ્રાણીઓના વર્તન અને ઉત્ક્રાંતિના સિદ્ધાંતનો અભ્યાસ કરવા માટે તેને અપનાવવામાં આવ્યું છે. આર્ટિફિશિયલ ઇન્ટેલિજન્સ અને સાયબરનેટિક્સ માટે ગેમ થિયરી ખૂબ જ મહત્વપૂર્ણ છે.

3. સૌથી મહત્વપૂર્ણ ચલો પૈકી એક કે જેના પર સંસ્થાની સફળતા આધાર રાખે છે તે સ્પર્ધાત્મકતા છે. દેખીતી રીતે, સ્પર્ધકોની ક્રિયાઓની આગાહી કરવાની ક્ષમતાનો અર્થ કોઈપણ સંસ્થા માટે લાભ છે. ગેમ થિયરી એ સ્પર્ધકો પરના નિર્ણયની અસરનું મોડેલિંગ કરવાની પદ્ધતિ છે.

ગેમ થિયરીનો ઇતિહાસ

ગાણિતિક મોડેલિંગમાં શ્રેષ્ઠ ઉકેલો અથવા વ્યૂહરચનાઓ 18મી સદીમાં પ્રસ્તાવિત કરવામાં આવી હતી. ઓલિગોપોલી પરિસ્થિતિઓ હેઠળ ઉત્પાદન અને કિંમત નિર્ધારણની સમસ્યાઓ, જે પાછળથી ગેમ થિયરીના પાઠ્યપુસ્તકના ઉદાહરણો બની, 19મી સદીમાં ધ્યાનમાં લેવામાં આવી હતી. એ. કોર્નોટ અને જે. બર્ટ્રાન્ડ. 20મી સદીની શરૂઆતમાં. E. Lasker, E. Zermelo, E. Borel એ હિતોના સંઘર્ષના ગાણિતિક સિદ્ધાંતનો વિચાર આગળ ધપાવ્યો.

ગાણિતિક રમત સિદ્ધાંત નિયોક્લાસિકલ અર્થશાસ્ત્રમાંથી ઉદ્દભવે છે. જ્હોન વોન ન્યુમેન અને ઓસ્કાર મોર્ગનસ્ટર્ન, ગેમ થિયરી અને ઇકોનોમિક બિહેવિયર દ્વારા ક્લાસિક 1944 પુસ્તકમાં થિયરીના ગાણિતિક પાસાઓ અને એપ્લિકેશનો સૌપ્રથમ દર્શાવેલ છે.

જ્હોન નેશ, કાર્નેગી પોલિટેકનિક ઇન્સ્ટિટ્યૂટમાંથી બે ડિગ્રી - સ્નાતક અને માસ્ટર ડિગ્રી સાથે સ્નાતક થયા પછી પ્રિન્સટન યુનિવર્સિટીમાં પ્રવેશ્યા, જ્યાં તેમણે જ્હોન વોન ન્યુમેનના પ્રવચનોમાં હાજરી આપી. તેમના લખાણોમાં, નેશે "મેનેજરીયલ ડાયનેમિક્સ" ના સિદ્ધાંતો વિકસાવ્યા. ગેમ થિયરીની પ્રથમ વિભાવનાઓએ શૂન્ય-સમ રમતોનું વિશ્લેષણ કર્યું, જ્યાં તેમના ખર્ચે હારનારા અને વિજેતાઓ છે. નેશ વિશ્લેષણની પદ્ધતિઓ વિકસાવે છે જેમાં સામેલ દરેક વ્યક્તિ કાં તો જીતે છે અથવા હારે છે. આ પરિસ્થિતિઓને "નેશ સંતુલન" અથવા "બિન-સહકારી સંતુલન" કહેવામાં આવે છે, પરિસ્થિતિમાં, પક્ષો શ્રેષ્ઠ વ્યૂહરચનાનો ઉપયોગ કરે છે, જે સ્થિર સંતુલનની રચના તરફ દોરી જાય છે. ખેલાડીઓ માટે આ સંતુલન જાળવવું ફાયદાકારક છે, કારણ કે કોઈપણ ફેરફાર તેમની સ્થિતિને વધુ ખરાબ કરશે. નેશના આ કાર્યોએ ગેમ થિયરીના વિકાસમાં ગંભીર યોગદાન આપ્યું હતું અને આર્થિક મોડેલિંગના ગાણિતિક સાધનોમાં સુધારો કરવામાં આવ્યો હતો. જ્હોન નેશ દર્શાવે છે કે એ. સ્મિથનો સ્પર્ધા પ્રત્યેનો ઉત્તમ અભિગમ, જ્યાં દરેક વ્યક્તિ પોતાના માટે છે, તે સબઓપ્ટીમલ છે. વધુ શ્રેષ્ઠ વ્યૂહરચના એ છે જ્યારે દરેક વ્યક્તિ પોતાના માટે વધુ સારું કરવાનો પ્રયાસ કરે છે જ્યારે અન્ય લોકો માટે વધુ સારું કરે છે. 1949 માં, જ્હોન નેશે ગેમ થિયરી પર એક મહાનિબંધ લખ્યો, અને 45 વર્ષ પછી તેને અર્થશાસ્ત્રમાં નોબેલ પુરસ્કાર મળ્યો.

ગેમ થિયરી મૂળરૂપે આર્થિક મોડલ સાથે સંકળાયેલી હોવા છતાં, તે 1950 ના દાયકા સુધી ગણિતમાં એક ઔપચારિક સિદ્ધાંત રહી. પરંતુ પહેલેથી જ 1950 થી. માત્ર અર્થશાસ્ત્રમાં જ નહીં, પરંતુ જીવવિજ્ઞાન, સાયબરનેટિક્સ, ટેક્નોલોજી અને માનવશાસ્ત્રમાં ગેમ થિયરી પદ્ધતિઓ લાગુ કરવાના પ્રયાસો શરૂ થયા છે. બીજા વિશ્વયુદ્ધ દરમિયાન અને તેના પછી તરત જ, સૈન્યને ગેમ થિયરીમાં ગંભીરતાથી રસ પડ્યો, જેણે તેમાં વ્યૂહાત્મક નિર્ણયોનો અભ્યાસ કરવા માટે એક શક્તિશાળી સાધન જોયું.

1960 - 1970 માં તે સમય સુધીમાં નોંધપાત્ર ગાણિતિક પરિણામો પ્રાપ્ત થયા હોવા છતાં, ગેમ થિયરીમાં રસ ઓછો થઈ રહ્યો છે. 1980 ના દાયકાના મધ્યભાગથી. રમત સિદ્ધાંતનો સક્રિય વ્યવહારિક ઉપયોગ શરૂ થાય છે, ખાસ કરીને અર્થશાસ્ત્ર અને સંચાલનમાં. છેલ્લા 20 - 30 વર્ષોમાં, રમત સિદ્ધાંત અને રસનું મહત્વ નોંધપાત્ર રીતે વધી રહ્યું છે, આધુનિક આર્થિક સિદ્ધાંતના કેટલાક ક્ષેત્રો રમત સિદ્ધાંતના ઉપયોગ વિના રજૂ કરી શકાતા નથી;

2005માં અર્થશાસ્ત્રમાં નોબેલ પુરસ્કાર વિજેતા થોમસ શેલિંગનું કાર્ય "ધ સ્ટ્રેટેજી ઑફ કોન્ફ્લિક્ટ" હતું. ટી. શેલિંગ સંઘર્ષમાં સહભાગીઓની વર્તણૂકની વિવિધ "વ્યૂહરચના" ને ધ્યાનમાં લે છે. આ વ્યૂહરચનાઓ સંઘર્ષ વ્યવસ્થાપન યુક્તિઓ અને સંઘર્ષશાસ્ત્ર અને સંગઠનાત્મક સંઘર્ષ સંચાલનમાં સંઘર્ષ વિશ્લેષણના સિદ્ધાંતો સાથે સુસંગત છે.

રમત સિદ્ધાંતના મૂળભૂત સિદ્ધાંતો

ચાલો ગેમ થિયરીના મૂળભૂત ખ્યાલોથી પરિચિત થઈએ. સંઘર્ષની પરિસ્થિતિનું ગાણિતિક મોડેલ કહેવામાં આવે છે રમત,સંઘર્ષમાં સામેલ પક્ષો - ખેલાડીઓ. રમતનું વર્ણન કરવા માટે, તમારે પહેલા તેના સહભાગીઓ (ખેલાડીઓ) ને ઓળખવા જોઈએ. જ્યારે ચેસ વગેરે જેવી સામાન્ય રમતોની વાત આવે ત્યારે આ સ્થિતિ સરળતાથી પૂરી થાય છે. "માર્કેટ ગેમ્સ" સાથે પરિસ્થિતિ અલગ છે. અહીં બધા ખેલાડીઓને ઓળખવું હંમેશા સરળ નથી, એટલે કે. વર્તમાન અથવા સંભવિત સ્પર્ધકો. પ્રેક્ટિસ બતાવે છે કે તમામ ખેલાડીઓને ઓળખવા જરૂરી નથી; રમતો સામાન્ય રીતે કેટલાક સમયગાળામાં વિસ્તરે છે જે દરમિયાન ખેલાડીઓ ક્રમિક અથવા એક સાથે ક્રિયાઓ કરે છે. નિયમો દ્વારા પૂરી પાડવામાં આવેલ ક્રિયાઓમાંથી એકની પસંદગી અને અમલીકરણ કહેવામાં આવે છે પ્રગતિખેલાડી ચાલ વ્યક્તિગત અને રેન્ડમ હોઈ શકે છે. વ્યક્તિગત ચાલ- આ સંભવિત ક્રિયાઓમાંથી એકના ખેલાડી દ્વારા સભાન પસંદગી છે (ઉદાહરણ તરીકે, ચેસની રમતમાં ચાલ). રેન્ડમ ચાલરેન્ડમલી પસંદ કરેલી ક્રિયા છે (ઉદાહરણ તરીકે, શફલ્ડ ડેકમાંથી કાર્ડ પસંદ કરવું). ક્રિયાઓ કિંમતો, વેચાણની માત્રા, સંશોધન અને વિકાસ ખર્ચ વગેરે સાથે સંબંધિત હોઈ શકે છે. જે સમયગાળા દરમિયાન ખેલાડીઓ તેમની ચાલ કરે છે તેને કહેવામાં આવે છે તબક્કાઓરમતો દરેક તબક્કે પસંદ કરેલ ચાલ આખરે નક્કી કરે છે "ચુકવણીઓ"દરેક ખેલાડીની (જીત અથવા હાર), જે ભૌતિક સંપત્તિ અથવા પૈસામાં વ્યક્ત કરી શકાય છે. આ સિદ્ધાંતનો બીજો ખ્યાલ છે પ્લેયર વ્યૂહરચના. વ્યૂહરચનાખેલાડી એ નિયમોનો સમૂહ છે જે વર્તમાન પરિસ્થિતિના આધારે દરેક વ્યક્તિગત ચાલ પર તેની ક્રિયાની પસંદગી નક્કી કરે છે. સામાન્ય રીતે રમત દરમિયાન, દરેક વ્યક્તિગત ચાલ સાથે, ખેલાડી ચોક્કસ પરિસ્થિતિના આધારે પસંદગી કરે છે. જો કે, તે સૈદ્ધાંતિક રીતે શક્ય છે કે તમામ નિર્ણયો ખેલાડી દ્વારા અગાઉથી લેવામાં આવે (કોઈપણ પરિસ્થિતિના જવાબમાં). આનો અર્થ એ છે કે ખેલાડીએ ચોક્કસ વ્યૂહરચના પસંદ કરી છે, જે નિયમોની સૂચિ અથવા પ્રોગ્રામ તરીકે સ્પષ્ટ કરી શકાય છે. (આ રીતે તમે કમ્પ્યુટરનો ઉપયોગ કરીને ગેમ રમી શકો છો.) બીજા શબ્દોમાં કહીએ તો, વ્યૂહરચના એ સંભવિત ક્રિયાઓનો સંદર્ભ આપે છે જે રમતના દરેક તબક્કે ખેલાડીને અમુક વૈકલ્પિક વિકલ્પોમાંથી પસંદ કરવાની મંજૂરી આપે છે જે તેને અન્ય ખેલાડીઓની ક્રિયાઓ માટે "શ્રેષ્ઠ પ્રતિભાવ" લાગે છે. વ્યૂહરચનાની વિભાવના વિશે, એ નોંધવું જોઈએ કે ખેલાડી તેની ક્રિયાઓ માત્ર કોઈ ચોક્કસ રમત ખરેખર પહોંચેલા તબક્કાઓ માટે જ નહીં, પરંતુ આપેલ રમત દરમિયાન ઊભી ન થઈ શકે તે સહિતની તમામ પરિસ્થિતિઓ માટે પણ નક્કી કરે છે. રમત કહેવાય છે સ્ટીમ રૂમ, જો તેમાં બે ખેલાડીઓ સામેલ હોય, અને બહુવિધ, જો ખેલાડીઓની સંખ્યા બે કરતા વધુ હોય. દરેક ઔપચારિક રમત માટે, નિયમો રજૂ કરવામાં આવે છે, એટલે કે. શરતોની સિસ્ટમ જે નક્કી કરે છે: 1) ખેલાડીઓની ક્રિયાઓ માટેના વિકલ્પો; 2) દરેક ખેલાડી પાસે તેમના ભાગીદારોના વર્તન વિશેની માહિતીનો જથ્થો; 3) લાભ કે જે દરેક ક્રિયાઓના સમૂહ તરફ દોરી જાય છે. સામાન્ય રીતે, જીત (અથવા હાર)નું પ્રમાણ નક્કી કરી શકાય છે; ઉદાહરણ તરીકે, તમે નુકસાનને શૂન્ય, જીતને એક અને ડ્રોને ½ ગણી શકો છો. રમતને શૂન્ય-સમ રમત કહેવામાં આવે છે, અથવા વિરોધી, જો ખેલાડીઓમાંથી એકનો ફાયદો બીજાના નુકસાન સમાન હોય, એટલે કે, રમત પૂર્ણ કરવા માટે, તે તેમાંથી એકનું મૂલ્ય સૂચવવા માટે પૂરતું છે. જો આપણે નિયુક્ત કરીએ એ- ખેલાડીઓમાંથી એકની જીત, b- બીજાની જીત, પછી શૂન્ય રકમની રમત માટે b = -a,તેથી, ઉદાહરણ તરીકે, ધ્યાનમાં લેવા માટે તે પૂરતું છે એ.રમત કહેવાય છે અંતિમજો દરેક ખેલાડી પાસે મર્યાદિત સંખ્યામાં વ્યૂહરચના હોય, અને અનંત- અન્યથા. ક્રમમાં નક્કી કરોરમત, અથવા શોધો રમત ઉકેલ, તમારે દરેક ખેલાડી માટે એવી વ્યૂહરચના પસંદ કરવી જોઈએ જે સ્થિતિને સંતોષે શ્રેષ્ઠતાતે ખેલાડીઓમાંથી એકને પ્રાપ્ત કરવું આવશ્યક છે મહત્તમ જીતજ્યારે બીજો તેની વ્યૂહરચના પર વળગી રહે છે. તે જ સમયે, બીજા ખેલાડી પાસે હોવું આવશ્યક છે ન્યૂનતમ નુકસાન, જો પ્રથમ વ્યક્તિ તેની વ્યૂહરચના પર વળગી રહે છે. આવા વ્યૂહરચનાકહેવાય છે શ્રેષ્ઠ. શ્રેષ્ઠ વ્યૂહરચનાઓએ પણ સ્થિતિને સંતોષવી જોઈએ ટકાઉપણું, એટલે કે, કોઈપણ ખેલાડીઓ માટે આ રમતમાં તેમની વ્યૂહરચના છોડી દેવી તે હાનિકારક હોવું જોઈએ. જો રમત ઘણી વાર પુનરાવર્તિત થાય છે, તો પછી ખેલાડીઓ દરેક ચોક્કસ રમતમાં જીતવા અને હારવામાં નહીં, પરંતુ સરેરાશ જીત (હાર)તમામ બેચમાં. હેતુ રમત સિદ્ધાંત શ્રેષ્ઠ નક્કી કરવા માટે છે દરેક ખેલાડી માટે વ્યૂહરચના. શ્રેષ્ઠ વ્યૂહરચના પસંદ કરતી વખતે, એવું માનવું સ્વાભાવિક છે કે બંને ખેલાડીઓ તેમની રુચિઓના સંદર્ભમાં વ્યાજબી વર્તન કરે છે.

સહકારી અને બિન સહકારી

રમત સહકારી કહેવાય છે, અથવા ગઠબંધન, જો ખેલાડીઓ જૂથોમાં એક થઈ શકે છે, અન્ય ખેલાડીઓ પ્રત્યે કેટલીક જવાબદારીઓ લે છે અને તેમની ક્રિયાઓનું સંકલન કરી શકે છે. આ બિન-સહકારી રમતોથી અલગ છે જેમાં દરેક વ્યક્તિએ પોતાના માટે રમવું જોઈએ. મનોરંજન રમતો ભાગ્યે જ સહકારી હોય છે, પરંતુ રોજિંદા જીવનમાં આવી પદ્ધતિઓ અસામાન્ય નથી.

ઘણીવાર એવું માનવામાં આવે છે કે ખેલાડીઓની એકબીજા સાથે વાતચીત કરવાની ક્ષમતા એ સહકારી રમતોને અલગ બનાવે છે. સામાન્ય રીતે આ સાચું નથી. એવી રમતો છે જ્યાં વાતચીતની મંજૂરી છે, પરંતુ ખેલાડીઓ વ્યક્તિગત લક્ષ્યોને અનુસરે છે, અને ઊલટું.

બે પ્રકારની રમતોમાંથી, બિન-સહકારી રમતો પરિસ્થિતિનું વિગતવાર વર્ણન કરે છે અને વધુ સચોટ પરિણામો આપે છે. સહકારી સંસ્થાઓ સમગ્ર રમત પ્રક્રિયાને ધ્યાનમાં લે છે.

હાઇબ્રિડ રમતોમાં સહકારી અને બિન-સહકારી રમતોના ઘટકોનો સમાવેશ થાય છે. ઉદાહરણ તરીકે, ખેલાડીઓ જૂથો બનાવી શકે છે, પરંતુ રમત બિન-સહકારી શૈલીમાં રમવામાં આવશે. આનો અર્થ એ છે કે દરેક ખેલાડી તેના જૂથના હિતોને અનુસરશે, જ્યારે તે જ સમયે વ્યક્તિગત લાભ પ્રાપ્ત કરવાનો પ્રયાસ કરશે.

સપ્રમાણ અને અસમપ્રમાણ

અસમપ્રમાણતાવાળી રમત

જ્યારે ખેલાડીઓની અનુરૂપ વ્યૂહરચના સમાન હોય, એટલે કે, તેમની સમાન ચૂકવણી હોય ત્યારે રમત સપ્રમાણતાવાળી હશે. બીજા શબ્દોમાં કહીએ તો, જો ખેલાડીઓ સ્થાનો બદલી શકે છે અને સમાન ચાલ માટે તેમની જીત બદલાશે નહીં. અભ્યાસ કરેલ ઘણી બે-ખેલાડી રમતો સપ્રમાણ છે. ખાસ કરીને, આ છે: "કેદીની મૂંઝવણ", "હરણનો શિકાર". જમણી બાજુના ઉદાહરણમાં, સમાન વ્યૂહરચનાઓને લીધે રમત પ્રથમ નજરમાં સપ્રમાણ લાગે છે, પરંતુ આ કેસ નથી - છેવટે, વ્યૂહરચના પ્રોફાઇલ્સ (A, A) અને (B, B) સાથે બીજા ખેલાડીની ચૂકવણી પહેલા કરતા વધારે હશે.

શૂન્ય-સરવાળા અને બિન-શૂન્ય-સરવાળા

ઝીરો-સમ ગેમ્સ એ એક ખાસ પ્રકારની કોન્સ્ટન્ટ-સમ ગેમ્સ છે, એટલે કે જ્યાં ખેલાડીઓ ઉપલબ્ધ સંસાધનો અથવા ગેમ ફંડમાં વધારો કે ઘટાડો કરી શકતા નથી. આ કિસ્સામાં, તમામ જીતનો સરવાળો કોઈપણ ચાલ માટેના તમામ નુકસાનના સરવાળા સમાન છે. જમણી તરફ જુઓ - નંબરો ખેલાડીઓને ચૂકવણીનું પ્રતિનિધિત્વ કરે છે - અને દરેક કોષમાં તેમનો સરવાળો શૂન્ય છે. આવી રમતોના ઉદાહરણોમાં પોકરનો સમાવેશ થાય છે, જેમાં એક બીજાના તમામ દાવ જીતે છે; રિવર્સી, જ્યાં દુશ્મનના ટુકડાઓ કબજે કરવામાં આવે છે; અથવા મામૂલી ચોરી.

ગણિતશાસ્ત્રીઓ દ્વારા અભ્યાસ કરાયેલ ઘણી રમતો, જેમાં પહેલેથી જ ઉલ્લેખિત "કેદીની મૂંઝવણ"નો સમાવેશ થાય છે, તે અલગ પ્રકારની છે: બિન-શૂન્ય રકમની રમતોએક ખેલાડીની જીતનો અર્થ એ નથી કે બીજાની હાર અને તેનાથી ઊલટું. આવી રમતનું પરિણામ શૂન્ય કરતાં ઓછું કે વધુ હોઈ શકે છે. આવી રમતોને શૂન્ય રકમમાં રૂપાંતરિત કરી શકાય છે - આ પરિચય દ્વારા કરવામાં આવે છે કાલ્પનિક ખેલાડી, જે સરપ્લસને "યોગ્ય" બનાવે છે અથવા ભંડોળના અભાવ માટે બનાવે છે.

બિન-શૂન્ય રકમ સાથેની બીજી રમત છે વેપાર, જ્યાં દરેક સહભાગીને ફાયદો થાય છે. આમાં ચેકર્સ અને ચેસનો પણ સમાવેશ થાય છે; છેલ્લા બેમાં, ખેલાડી તેના સામાન્ય ભાગને વધુ મજબૂત બનાવી શકે છે, ફાયદો મેળવી શકે છે. આ બધા કિસ્સાઓમાં, રમતની રકમ વધે છે. જ્યાં તે ઘટે છે તેનું જાણીતું ઉદાહરણ છે યુદ્ધ.

સમાંતર અને સીરીયલ

સમાંતર રમતોમાં, ખેલાડીઓ એક સાથે આગળ વધે છે, અથવા ઓછામાં ઓછું તેઓ અન્યની પસંદગીઓ વિશે જાણતા નથી ત્યાં સુધી બધાતેમની ચાલ કરશે નહીં. અનુક્રમમાં, અથવા ગતિશીલરમતોમાં, સહભાગીઓ પૂર્વનિર્ધારિત અથવા રેન્ડમ ક્રમમાં ચાલ કરી શકે છે, પરંતુ તે જ સમયે તેઓ અન્યની અગાઉની ક્રિયાઓ વિશે કેટલીક માહિતી મેળવે છે. આ માહિતી પણ હોઈ શકે છે તદ્દન સંપૂર્ણ નથી, ઉદાહરણ તરીકે, એક ખેલાડી તેની દસ વ્યૂહરચનામાંથી તેના વિરોધીને શોધી શકે છે ચોક્કસપણે પસંદ કર્યું નથીપાંચમું, બીજાઓ વિશે કંઈપણ શીખ્યા વિના.

સમાંતર અને ક્રમિક રમતોની રજૂઆતમાં તફાવતો ઉપર ચર્ચા કરવામાં આવી હતી. ભૂતપૂર્વ સામાન્ય રીતે સામાન્ય સ્વરૂપમાં રજૂ કરવામાં આવે છે, અને બાદમાં વ્યાપક સ્વરૂપમાં.

સંપૂર્ણ અથવા અપૂર્ણ માહિતી સાથે

ક્રમિક રમતોનો એક મહત્વપૂર્ણ સબસેટ સંપૂર્ણ માહિતી સાથેની રમતો છે. આવી રમતમાં, સહભાગીઓ વર્તમાન ક્ષણ સુધી કરવામાં આવેલી તમામ ચાલ, તેમજ તેમના વિરોધીઓની સંભવિત વ્યૂહરચનાઓને જાણે છે, જે તેમને અમુક અંશે રમતના અનુગામી વિકાસની આગાહી કરવાની મંજૂરી આપે છે. સમાંતર રમતોમાં સંપૂર્ણ માહિતી ઉપલબ્ધ નથી, કારણ કે વિરોધીઓની વર્તમાન ચાલ અજાણ છે. ગણિતમાં અભ્યાસ કરવામાં આવતી મોટાભાગની રમતોમાં અધૂરી માહિતી હોય છે. ઉદાહરણ તરીકે, બધા "મીઠું" કેદીની દુવિધાઓતેની અપૂર્ણતામાં રહેલું છે.

સંપૂર્ણ માહિતી સાથે રમતોના ઉદાહરણો: ચેસ, ચેકર્સ અને અન્ય.

સંપૂર્ણ માહિતીની વિભાવના ઘણીવાર સમાન એક સાથે મૂંઝવણમાં આવે છે - સંપૂર્ણ માહિતી. બાદમાં માટે, વિરોધીઓ માટે ઉપલબ્ધ તમામ વ્યૂહરચનાઓ જાણવા માટે તે પૂરતું છે, તેમની બધી ચાલનું જ્ઞાન જરૂરી નથી.

અસંખ્ય પગલાં સાથેની રમતો

વાસ્તવિક દુનિયામાં રમતો, અથવા અર્થશાસ્ત્રમાં અભ્યાસ કરાયેલ રમતો, ટકી રહેવાનું વલણ ધરાવે છે અંતિમચાલની સંખ્યા. ગણિત એટલું મર્યાદિત નથી, અને સેટ થિયરી ખાસ કરીને રમતો સાથે સંબંધિત છે જે અનિશ્ચિત સમય સુધી ચાલુ રહી શકે છે. તદુપરાંત, તમામ ચાલના અંત સુધી વિજેતા અને તેની જીત નક્કી થતી નથી.

સામાન્ય રીતે આ કિસ્સામાં જે કાર્ય રજૂ કરવામાં આવે છે તે શ્રેષ્ઠ ઉકેલ શોધવાનું નથી, પરંતુ ઓછામાં ઓછી વિજેતા વ્યૂહરચના શોધવાનું છે.

અલગ અને સતત રમતો

મોટાભાગની રમતોનો અભ્યાસ કર્યો અલગ: તેમની પાસે ખેલાડીઓ, ચાલ, ઘટનાઓ, પરિણામો વગેરેની મર્યાદિત સંખ્યા છે. જો કે, આ ઘટકોને ઘણી વાસ્તવિક સંખ્યાઓ સુધી વિસ્તૃત કરી શકાય છે. જે રમતોમાં આવા તત્વોનો સમાવેશ થાય છે તેને ઘણી વખત વિભેદક રમતો કહેવામાં આવે છે. તેઓ અમુક પ્રકારના મટીરીયલ સ્કેલ (સામાન્ય રીતે ટાઈમ સ્કેલ) સાથે સંકળાયેલા છે, જો કે તેમાં બનતી ઘટનાઓ પ્રકૃતિમાં અલગ હોઈ શકે છે. ડિફરન્શિયલ ગેમ્સ એન્જિનિયરિંગ અને ટેક્નોલોજી, ફિઝિક્સમાં તેમની એપ્લિકેશન શોધે છે.

મેટાગેમ્સ

આ એવી રમતો છે જે અન્ય રમત માટે નિયમોના સમૂહમાં પરિણમે છે (કહેવાય છે લક્ષ્યઅથવા રમત-ઓબ્જેક્ટ). મેટાગેમ્સનો ધ્યેય આપેલ નિયમોની ઉપયોગિતા વધારવાનો છે.

રમત પ્રસ્તુતિ ફોર્મ

રમતના સિદ્ધાંતમાં, રમતોના વર્ગીકરણ સાથે, રમતની રજૂઆતનું સ્વરૂપ એક વિશાળ ભૂમિકા ભજવે છે. સામાન્ય રીતે, સામાન્ય અથવા મેટ્રિક્સ સ્વરૂપને અલગ પાડવામાં આવે છે અને વિસ્તૃત સ્વરૂપ, એક વૃક્ષના સ્વરૂપમાં નિર્દિષ્ટ કરવામાં આવે છે. સરળ રમત માટેના આ સ્વરૂપો ફિગમાં બતાવવામાં આવ્યા છે. 1a અને 1b.

નિયંત્રણના ક્ષેત્ર સાથે પ્રથમ જોડાણ સ્થાપિત કરવા માટે, રમતનું વર્ણન નીચે પ્રમાણે કરી શકાય છે. સમાન ઉત્પાદનોનું ઉત્પાદન કરતા બે સાહસોને પસંદગીનો સામનો કરવો પડે છે. એક કિસ્સામાં, તેઓ ઊંચી કિંમત નક્કી કરીને બજારમાં પગ જમાવી શકે છે, જે તેમને સરેરાશ કાર્ટેલ નફો P K પ્રદાન કરશે. જ્યારે ભીષણ સ્પર્ધામાં ઉતરે છે, ત્યારે બંનેને નફો મળે છે P W . જો સ્પર્ધકોમાંથી એક ઊંચી કિંમત નક્કી કરે છે, અને બીજો નીચી કિંમત નક્કી કરે છે, તો બાદમાં P M નો ઈજારો નફો મેળવે છે, જ્યારે બીજાને P G નુકસાન થાય છે. સમાન પરિસ્થિતિ ઊભી થઈ શકે છે, ઉદાહરણ તરીકે, જ્યારે બંને કંપનીઓએ તેમની કિંમત જાહેર કરવી જ જોઈએ, જે પછીથી સુધારી શકાતી નથી.

કડક શરતોની ગેરહાજરીમાં, બંને સાહસો માટે ઓછી કિંમત નક્કી કરવી ફાયદાકારક છે. કોઈપણ પેઢી માટે "ઓછી કિંમત" વ્યૂહરચના પ્રબળ છે: હરીફ પેઢી ગમે તે કિંમત પસંદ કરે, તે હંમેશા નીચી કિંમત નક્કી કરવાનું વધુ સારું છે. પરંતુ આ કિસ્સામાં, કંપનીઓ મૂંઝવણનો સામનો કરે છે, કારણ કે નફો P K (જે બંને ખેલાડીઓ માટે નફો P W કરતા વધારે છે) પ્રાપ્ત થતો નથી.

અનુરૂપ ચૂકવણીઓ સાથે “નીચા ભાવ/ઓછી કિંમતો” નું વ્યૂહાત્મક સંયોજન નેશ સંતુલનનું પ્રતિનિધિત્વ કરે છે, જેમાં કોઈ પણ ખેલાડી પસંદ કરેલી વ્યૂહરચનાથી અલગથી વિચલિત થવું તે નુકસાનકારક છે. સંતુલનનો આ ખ્યાલ વ્યૂહાત્મક પરિસ્થિતિઓને ઉકેલવા માટે મૂળભૂત છે, પરંતુ ચોક્કસ સંજોગોમાં તેને હજુ પણ સુધારણાની જરૂર છે.

ઉપરોક્ત મૂંઝવણ માટે, તેનું નિરાકરણ ખાસ કરીને, ખેલાડીઓની ચાલની મૌલિકતા પર આધારિત છે. જો એન્ટરપ્રાઇઝને તેના વ્યૂહાત્મક ચલ (આ કિસ્સામાં કિંમતમાં) પર પુનર્વિચાર કરવાની તક હોય, તો પછી ખેલાડીઓ વચ્ચેના કડક કરાર વિના પણ સમસ્યાનો સહકારી ઉકેલ શોધી શકાય છે. અંતર્જ્ઞાન સૂચવે છે કે ખેલાડીઓ વચ્ચે વારંવાર સંપર્ક સાથે, સ્વીકાર્ય "વળતર" પ્રાપ્ત કરવાની તકો ઊભી થાય છે. આમ, અમુક સંજોગોમાં, જો ભવિષ્યમાં "કિંમત યુદ્ધ" ઊભી થઈ શકે તો ભાવ ડમ્પિંગ દ્વારા ટૂંકા ગાળાના ઊંચા નફા માટે પ્રયત્ન કરવો અયોગ્ય છે.

નોંધ્યું છે તેમ, બંને ચિત્રો સમાન રમતનું લક્ષણ ધરાવે છે. સામાન્ય કિસ્સામાં રમતને સામાન્ય સ્વરૂપમાં રજૂ કરવી "સિંક્રોનિસિટી" દર્શાવે છે. જો કે, આનો અર્થ ઇવેન્ટ્સની "એકસાથે" નથી, પરંતુ સૂચવે છે કે ખેલાડીની વ્યૂહરચના પસંદ કરવાની વ્યૂહરચના વિરોધીની પસંદગીની અજ્ઞાનતામાં કરવામાં આવે છે. વિસ્તૃત સ્વરૂપમાં, આ પરિસ્થિતિ અંડાકાર જગ્યા (માહિતી ક્ષેત્ર) દ્વારા વ્યક્ત કરવામાં આવે છે. આ જગ્યાની ગેરહાજરીમાં, રમતની પરિસ્થિતિ અલગ પાત્ર ધારણ કરે છે: પ્રથમ, એક ખેલાડીએ નિર્ણય લેવો પડશે, અને બીજા તેના પછી તે કરી શકશે.

ગેમ થિયરીમાં ક્લાસિક સમસ્યા

ચાલો ગેમ થિયરીમાં ક્લાસિક સમસ્યાને ધ્યાનમાં લઈએ. હરણનો શિકારરમત સિદ્ધાંતમાંથી સહકારી સમપ્રમાણ રમત છે જે વ્યક્તિગત હિતો અને જાહેર હિતો વચ્ચેના સંઘર્ષનું વર્ણન કરે છે. આ રમતનું સૌપ્રથમ વર્ણન જીન-જેક્સ રૂસો દ્વારા 1755માં કરવામાં આવ્યું હતું:

"જો તેઓ હરણનો શિકાર કરતા હતા, તો પછી દરેક જણ સમજી ગયા કે આ માટે તે તેની પોસ્ટ પર રહેવા માટે બંધાયેલો છે; પરંતુ જો સસલું શિકારીઓમાંના એકની નજીક દોડે છે, તો તેમાં કોઈ શંકા નથી કે આ શિકારી, અંતરાત્માની ઝંખના વિના, કરશે. તેની પાછળ નીકળ્યા અને, શિકારથી આગળ નીકળી ગયા પછી, બહુ ઓછા લોકો શોક કરશે કે આ રીતે તેણે તેના સાથીઓને શિકારથી વંચિત રાખ્યા."

હરણનો શિકાર માણસને સ્વાર્થ માટે લલચાવીને જાહેર ભલાઈ પૂરી પાડવાના પડકારનું ઉત્તમ ઉદાહરણ છે. શું શિકારીએ તેના સાથીઓ સાથે રહેવું જોઈએ અને આખી આદિજાતિને મોટો શિકાર પહોંચાડવાની ઓછી અનુકૂળ તક પર શરત લગાવવી જોઈએ, અથવા તેના સાથીઓને છોડીને પોતાને વધુ વિશ્વસનીય તક સોંપવી જોઈએ જે તેના પોતાના કુટુંબને સસલું વચન આપે છે?

ગેમ થિયરીમાં મૂળભૂત સમસ્યા

ગેમ થિયરીમાં એક મૂળભૂત સમસ્યાનો વિચાર કરો જેને પ્રિઝનર્સ ડાઇલેમા કહેવાય છે.

કેદીની મૂંઝવણગેમ થિયરીમાં એક મૂળભૂત સમસ્યા, ખેલાડીઓ હંમેશા એકબીજાને સહકાર આપતા નથી, પછી ભલે તે તેમના શ્રેષ્ઠ હિતમાં હોય. ખેલાડી ("કેદી") અન્યના લાભની પરવા કર્યા વિના તેના પોતાના વળતરને મહત્તમ કરે તેવું માનવામાં આવે છે. સમસ્યાનો સાર 1950 માં મેરિલ ફ્લડ અને મેલ્વિન ડ્રેસર દ્વારા ઘડવામાં આવ્યો હતો. આ મૂંઝવણનું નામ ગણિતશાસ્ત્રી આલ્બર્ટ ટકર દ્વારા આપવામાં આવ્યું હતું.

કેદીની મૂંઝવણમાં, વિશ્વાસઘાત સખત પ્રભુત્વ ધરાવે છેસહકાર પર, તેથી એકમાત્ર સંભવિત સંતુલન એ બંને સહભાગીઓનો વિશ્વાસઘાત છે. સરળ શબ્દોમાં કહીએ તો, અન્ય ખેલાડી શું કરે છે તે કોઈ બાબત નથી, જો તેઓ દગો કરશે તો દરેક વધુ જીતશે. કોઈપણ પરિસ્થિતિમાં સહકાર આપવા કરતાં દગો કરવો વધુ નફાકારક હોવાથી, બધા તર્કસંગત ખેલાડીઓ વિશ્વાસઘાત પસંદ કરશે.

વ્યક્તિગત રીતે તર્કસંગત રીતે વર્તતી વખતે, સહભાગીઓ એકસાથે અતાર્કિક નિર્ણય પર આવે છે: જો બંને દગો કરે છે, તો તેઓ સહકાર આપે તેના કરતાં કુલ નાનું વળતર મેળવશે (આ રમતમાં એકમાત્ર સંતુલન આ તરફ દોરી જતું નથી. પેરેટો-શ્રેષ્ઠનિર્ણય, એટલે કે એક નિર્ણય કે જે અન્ય તત્વોની પરિસ્થિતિને બગાડ્યા વિના સુધારી શકાતો નથી.) એમાં જ મૂંઝવણ રહે છે.

પુનરાવર્તિત કેદીની મૂંઝવણમાં, રમત સમયાંતરે થાય છે, અને દરેક ખેલાડી અગાઉ સહકાર ન આપવા બદલ બીજાને "સજા" કરી શકે છે. આવી રમતમાં, સહકાર એક સંતુલન બની શકે છે, અને દગો કરવા માટેના પ્રોત્સાહનને સજાની ધમકીથી વધુ વજન આપી શકાય છે.

ઉત્તમ કેદીની મૂંઝવણ

તમામ ન્યાયિક પ્રણાલીઓમાં, ડાકુની સજા (સંગઠિત જૂથના ભાગ રૂપે ગુનાઓ કરવા) એ એકલા કરવામાં આવેલા સમાન ગુનાઓ કરતાં ઘણી ભારે હોય છે (તેથી વૈકલ્પિક નામ - "ધ ડાકુની મૂંઝવણ").

કેદીની મૂંઝવણની ઉત્તમ રચના છે:

બે ગુનેગારો, A અને B, સમાન ગુનાઓ માટે લગભગ એક જ સમયે પકડાયા હતા. એવું માનવા માટેનું કારણ છે કે તેઓએ કાવતરું કર્યું હતું, અને પોલીસ, તેમને એકબીજાથી અલગ કરીને, સમાન સોદાની ઓફર કરે છે: જો એક બીજા વિરુદ્ધ જુબાની આપે છે, અને તે મૌન રહે છે, તો પછી તપાસમાં મદદ કરવા માટે પ્રથમને મુક્ત કરવામાં આવે છે, અને બીજાને મહત્તમ સજા કેદ (10 વર્ષ) (20 વર્ષ) મળે છે. જો બંને મૌન હોય, તો તેમના કૃત્ય પર હળવા લેખ હેઠળ આરોપ મૂકવામાં આવે છે, અને તેમને 6 મહિના (1 વર્ષ) ની સજા કરવામાં આવે છે. જો બંને એકબીજા સામે જુબાની આપે તો તેમને ઓછામાં ઓછી 2 વર્ષની (5 વર્ષની) સજા થાય છે. દરેક કેદી ચૂપ રહેવું કે બીજા સામે જુબાની આપવી તે પસંદ કરે છે. જો કે, બેમાંથી કોઈને બરાબર ખબર નથી કે બીજા શું કરશે. શું થશે?

રમતને નીચેના કોષ્ટકના સ્વરૂપમાં રજૂ કરી શકાય છે:

દ્વિધા ઊભી થાય છે જો આપણે ધારીએ કે બંને ફક્ત તેમની પોતાની જેલની મુદત ઘટાડવા માટે ચિંતિત છે.

ચાલો એક કેદીના તર્કની કલ્પના કરીએ. જો તમારો સાથી મૌન છે, તો તેની સાથે દગો કરવો અને મુક્ત થવું વધુ સારું છે (અન્યથા - છ મહિના જેલમાં). જો ભાગીદાર જુબાની આપે છે, તો 2 વર્ષ (અન્યથા - 10 વર્ષ) મેળવવા માટે તેની સામે જુબાની આપવી પણ વધુ સારું છે. "સાક્ષી આપો" વ્યૂહરચના સખત રીતે "ચુપ રહો" વ્યૂહરચના પર પ્રભુત્વ ધરાવે છે. એ જ રીતે, અન્ય કેદી પણ આ જ નિષ્કર્ષ પર આવે છે.

જૂથના દૃષ્ટિકોણથી (આ બે કેદીઓ), એકબીજાને સહકાર આપવો, મૌન રહેવું અને દરેકને છ મહિનાનો સમય મળવો શ્રેષ્ઠ છે, કારણ કે આ જેલની કુલ મુદતમાં ઘટાડો કરશે. અન્ય કોઈપણ ઉકેલ ઓછા નફાકારક રહેશે.

સામાન્યકૃત સ્વરૂપ

1. આ રમતમાં બે ખેલાડીઓ અને એક બેંકરનો સમાવેશ થાય છે. દરેક ખેલાડી 2 કાર્ડ ધરાવે છે: એક કહે છે "સહકાર કરો", બીજો કહે છે "ખામી" (આ રમતની પ્રમાણભૂત પરિભાષા છે). દરેક ખેલાડી બેંકરની સામે એક કાર્ડ મોઢું નીચે મૂકે છે (એટલે ​​કે, કોઈ બીજાના નિર્ણયને જાણતું નથી, જો કે કોઈ બીજાના નિર્ણયને જાણવું પ્રભુત્વ વિશ્લેષણને અસર કરતું નથી). બેંકર કાર્ડ ખોલે છે અને જીત આપે છે.
2. જો બંને સહકાર આપવાનું પસંદ કરે છે, તો બંને પ્રાપ્ત કરે છે સી. જો કોઈએ "દગો" કરવાનું પસંદ કર્યું, તો બીજું "સહકાર આપવા" - પ્રથમ પ્રાપ્ત કરે છે ડી, બીજું સાથે. જો બંનેએ "દગો" પસંદ કર્યો, તો બંને પ્રાપ્ત કરે છે ડી.
3. C, D, c, d ચલોની કિંમતો કોઈપણ ચિહ્નની હોઈ શકે છે (ઉપરના ઉદાહરણમાં, બધા 0 કરતા ઓછા અથવા સમાન છે). અસમાનતા D > C > d > c રમતને પ્રિઝનર્સ ડાઇલેમા (PD) બનાવવા માટે સંતુષ્ટ હોવી આવશ્યક છે.
4. જો રમત પુનરાવર્તિત થાય છે, એટલે કે, એક પંક્તિમાં એક કરતા વધુ વખત રમવામાં આવે છે, તો સહકારની કુલ ચૂકવણી એવી પરિસ્થિતિમાં કુલ ચૂકવણી કરતાં વધુ હોવી જોઈએ જ્યાં એક દગો કરે છે અને બીજો ન કરે, એટલે કે 2C > D + c.

આ નિયમો ડગ્લાસ હોફસ્ટેડટર દ્વારા સ્થાપિત કરવામાં આવ્યા હતા અને સામાન્ય કેદીની મૂંઝવણનું પ્રમાણભૂત વર્ણન બનાવે છે.

સમાન પરંતુ અલગ રમત

હોફસ્ટેડરે સૂચવ્યું હતું કે લોકો કેદીની મૂંઝવણ જેવી સમસ્યાઓને વધુ સરળતાથી સમજે છે જો તેને અલગ રમત અથવા વેપાર પ્રક્રિયા તરીકે રજૂ કરવામાં આવે. એક ઉદાહરણ છે " બંધ થેલીઓનું વિનિમય»:

બે લોકો મળે છે અને બંધ બેગની આપ-લે કરે છે, તે સમજીને કે તેમાંના એકમાં પૈસા છે, બીજામાં સામાન છે. દરેક ખેલાડી સોદાને માન આપી શકે છે અને જે સંમત થયા હતા તે બેગમાં મૂકી શકે છે અથવા ખાલી બેગ આપીને ભાગીદારને છેતરે છે.

આ રમતમાં, છેતરપિંડી હંમેશા શ્રેષ્ઠ ઉકેલ હશે, જેનો અર્થ એ પણ છે કે તર્કસંગત ખેલાડીઓ ક્યારેય રમત રમશે નહીં અને બંધ બેગના વેપાર માટે કોઈ બજાર નહીં હોય.

વ્યૂહાત્મક સંચાલન નિર્ણયો લેવા માટે રમત સિદ્ધાંતનો ઉપયોગ

ઉદાહરણોમાં સૈદ્ધાંતિક કિંમત નીતિના અમલીકરણ, નવા બજારોમાં પ્રવેશ, સહકાર અને સંયુક્ત સાહસોની રચના, નવીનતાના ક્ષેત્રમાં નેતાઓ અને કલાકારોની ઓળખ, વર્ટિકલ એકીકરણ વગેરે અંગેના નિર્ણયોનો સમાવેશ થાય છે. ગેમ થિયરીના સિદ્ધાંતો સૈદ્ધાંતિક રીતે તમામ પ્રકારના નિર્ણયો માટે ઉપયોગમાં લઈ શકાય છે જો તેઓ અન્ય કલાકારોથી પ્રભાવિત હોય. આ વ્યક્તિઓ, અથવા ખેલાડીઓ, બજારના સ્પર્ધકો હોવા જરૂરી નથી; તેમની ભૂમિકા સબસપ્લાયર્સ, અગ્રણી ગ્રાહકો, સંસ્થાઓના કર્મચારીઓ તેમજ કામના સાથીદારો હોઈ શકે છે.

 જ્યારે પ્રક્રિયામાં સહભાગીઓ વચ્ચે મહત્વપૂર્ણ અવલંબન હોય ત્યારે ગેમ થિયરી ટૂલ્સનો ઉપયોગ કરવાની ખાસ કરીને સલાહ આપવામાં આવે છે. ચૂકવણીના ક્ષેત્રમાં. સંભવિત સ્પર્ધકો સાથેની પરિસ્થિતિ ફિગમાં બતાવવામાં આવી છે. 2.

 ચતુર્થાંશ 1 અને 2 એવી પરિસ્થિતિને દર્શાવો કે જ્યાં સ્પર્ધકોની પ્રતિક્રિયા કંપનીની ચૂકવણી પર નોંધપાત્ર અસર કરતી નથી. આ એવા કિસ્સાઓમાં થાય છે જ્યાં સ્પર્ધક પાસે કોઈ પ્રેરણા નથી (ક્ષેત્ર 1 ) અથવા ક્ષમતાઓ (ક્ષેત્ર 2 ) પાછા હડતાલ. તેથી, સ્પર્ધકોની પ્રેરિત ક્રિયાઓની વ્યૂહરચનાનું વિગતવાર વિશ્લેષણ કરવાની જરૂર નથી.

એક સમાન નિષ્કર્ષ અનુસરે છે, જોકે અલગ કારણોસર, અને ચતુર્થાંશ દ્વારા પ્રતિબિંબિત પરિસ્થિતિ માટે 3 . અહીં, સ્પર્ધકોની પ્રતિક્રિયા કંપની પર નોંધપાત્ર અસર કરી શકે છે, પરંતુ તેની પોતાની ક્રિયાઓ સ્પર્ધકની ચૂકવણીને મોટા પ્રમાણમાં અસર કરી શકતી નથી, તેથી તેની પ્રતિક્રિયાથી ડરવું જોઈએ નહીં. બજારના માળખામાં પ્રવેશવાના નિર્ણયોનું ઉદાહરણ છે: અમુક સંજોગોમાં, મોટા સ્પર્ધકો પાસે નાની કંપનીના આવા નિર્ણય પર પ્રતિક્રિયા આપવાનું કોઈ કારણ નથી.

માત્ર ચતુર્થાંશમાં દર્શાવેલ પરિસ્થિતિ 4 (બજાર ભાગીદારો દ્વારા બદલો લેવાના પગલાંની શક્યતા) માટે ગેમ થિયરી જોગવાઈઓનો ઉપયોગ જરૂરી છે. જો કે, આ માત્ર જરૂરી છે પરંતુ સ્પર્ધકોનો સામનો કરવા માટે ગેમ થિયરી ફ્રેમવર્કના ઉપયોગને યોગ્ય ઠેરવવા માટે પૂરતી શરતો નથી. એવી પરિસ્થિતિઓ હોય છે જ્યારે એક વ્યૂહરચના નિઃશંકપણે અન્ય તમામ પર પ્રભુત્વ મેળવશે, હરીફ જે પગલાં લે છે તે ધ્યાનમાં લીધા વિના. જો આપણે, ઉદાહરણ તરીકે, દવાનું બજાર લઈએ, તો કંપની માટે બજારમાં નવું ઉત્પાદન રજૂ કરનાર પ્રથમ બનવું ઘણીવાર મહત્વપૂર્ણ છે: "ફર્સ્ટ મૂવર" નો નફો એટલો નોંધપાત્ર છે કે અન્ય તમામ " ખેલાડીઓ" ફક્ત નવીનતા પ્રવૃત્તિઓને ઝડપથી તીવ્ર બનાવી શકે છે.

 રમત સિદ્ધાંતના દૃષ્ટિકોણથી "પ્રબળ વ્યૂહરચના" નું એક તુચ્છ ઉદાહરણ એ સંબંધિત નિર્ણય છે નવા બજારમાં પ્રવેશ.ચાલો એક એન્ટરપ્રાઇઝ લઈએ જે કોઈપણ બજારમાં એકાધિકાર તરીકે કાર્ય કરે છે (ઉદાહરણ તરીકે, 80 ના દાયકાની શરૂઆતમાં વ્યક્તિગત કમ્પ્યુટર બજારમાં IBM). અન્ય એન્ટરપ્રાઇઝ, ઓપરેટિંગ, ઉદાહરણ તરીકે, કમ્પ્યુટર પેરિફેરલ સાધનોના બજારમાં, તેના ઉત્પાદનને ફરીથી ગોઠવીને પર્સનલ કમ્પ્યુટર માર્કેટમાં પ્રવેશ કરવાના મુદ્દા પર વિચારણા કરી રહ્યું છે. બહારની કંપની બજારમાં પ્રવેશવાનો કે ન દાખલ કરવાનો નિર્ણય લઈ શકે છે. એક એકાધિકારવાદી કંપની નવા હરીફના ઉદભવ માટે આક્રમક અથવા મૈત્રીપૂર્ણ પ્રતિક્રિયા આપી શકે છે. બંને કંપનીઓ બે તબક્કાની રમતમાં પ્રવેશ કરે છે જેમાં બહારની કંપની પ્રથમ ચાલ કરે છે. ચૂકવણીનો સંકેત આપતી રમતની સ્થિતિ આકૃતિ 3 માં વૃક્ષના રૂપમાં બતાવવામાં આવી છે.

 સમાન રમતની સ્થિતિને સામાન્ય સ્વરૂપમાં રજૂ કરી શકાય છે (ફિગ. 4).

અહીં બે સ્થિતિઓ સૂચવવામાં આવી છે - "પ્રવેશ/મૈત્રીપૂર્ણ પ્રતિક્રિયા" અને "નોન-એન્ટ્રી/આક્રમક પ્રતિક્રિયા". દેખીતી રીતે, બીજું સંતુલન અસમર્થ છે. વિસ્તૃત સ્વરૂપથી તે અનુસરે છે કે જે કંપનીએ પહેલેથી જ બજારમાં પગ જમાવી લીધો છે, તે માટે નવા સ્પર્ધકના ઉદભવ પર આક્રમક પ્રતિક્રિયા આપવી અયોગ્ય છે: આક્રમક વર્તન સાથે, વર્તમાન મોનોપોલિસ્ટ 1 (ચુકવણી) મેળવે છે અને મૈત્રીપૂર્ણ સાથે વર્તન - 3. બહારની કંપની એ પણ જાણે છે કે એકાધિકારવાદી તેને વિસ્થાપિત કરવાની ક્રિયાઓ શરૂ કરે તે તર્કસંગત નથી અને તેથી તે બજારમાં પ્રવેશવાનું નક્કી કરે છે. બહારની કંપની (-1) નું જોખમી નુકસાન સહન કરશે નહીં.

આવા તર્કસંગત સંતુલન એ "આંશિક રીતે સુધારેલ" રમતની લાક્ષણિકતા છે, જે ઇરાદાપૂર્વક વાહિયાત ચાલને બાકાત રાખે છે. વ્યવહારમાં, આવી સંતુલન સ્થિતિઓ, સૈદ્ધાંતિક રીતે, શોધવા માટે એકદમ સરળ છે. સંતુલન રૂપરેખાંકનો કોઈપણ મર્યાદિત રમત માટે ઓપરેશન સંશોધનના ક્ષેત્રમાંથી વિશેષ અલ્ગોરિધમનો ઉપયોગ કરીને ઓળખી શકાય છે. નિર્ણય લેનાર નીચે પ્રમાણે આગળ વધે છે: પ્રથમ, રમતના છેલ્લા તબક્કામાં "શ્રેષ્ઠ" ચાલની પસંદગી કરવામાં આવે છે, પછી "શ્રેષ્ઠ" ચાલને પાછલા તબક્કે પસંદ કરવામાં આવે છે, છેલ્લા તબક્કાની પસંદગીને ધ્યાનમાં લેતા, અને તેથી વધુ, જ્યાં સુધી વૃક્ષના પ્રારંભિક નોડ સુધી રમતો ન પહોંચે ત્યાં સુધી.

ગેમ થિયરી આધારિત વિશ્લેષણથી કંપનીઓને કેવી રીતે ફાયદો થઈ શકે? ઉદાહરણ તરીકે, IBM અને Telex વચ્ચે હિતોના સંઘર્ષનો એક જાણીતો કિસ્સો છે. બજારમાં પ્રવેશવા માટે બાદમાંની પ્રારંભિક યોજનાઓની ઘોષણાના સંબંધમાં, IBM મેનેજમેન્ટની "કટોકટી" મીટિંગ યોજવામાં આવી હતી, જેમાં નવા હરીફને નવા બજારમાં પ્રવેશવાના તેના ઇરાદાને છોડી દેવા માટે દબાણ કરવાના હેતુથી પગલાંનું વિશ્લેષણ કરવામાં આવ્યું હતું. ટેલેક્સ દેખીતી રીતે આ ઘટનાઓથી વાકેફ થઈ ગયું. ગેમ થિયરી પર આધારિત પૃથ્થકરણ દર્શાવે છે કે ઊંચા ખર્ચને કારણે IBM માટે જોખમો પાયાવિહોણા છે. આ સૂચવે છે કે કંપનીઓ માટે તેમના ગેમિંગ ભાગીદારોની સંભવિત પ્રતિક્રિયાઓ ધ્યાનમાં લેવી ઉપયોગી છે. અલગ-અલગ આર્થિક ગણતરીઓ, તે પણ નિર્ણય લેવાની સિદ્ધાંત પર આધારિત હોય છે, ઘણીવાર, વર્ણવેલ પરિસ્થિતિમાં, પ્રકૃતિમાં મર્યાદિત હોય છે. આમ, બહારની કંપની "નોન-એન્ટ્રી" ચાલ પસંદ કરી શકે છે જો પ્રારંભિક વિશ્લેષણ તેને ખાતરી આપે કે બજારમાં પ્રવેશ મોનોપોલિસ્ટ તરફથી આક્રમક પ્રતિક્રિયાનું કારણ બનશે. આ કિસ્સામાં, અપેક્ષિત મૂલ્યના માપદંડ અનુસાર, 0.5 ના આક્રમક પ્રતિભાવની સંભાવના સાથે "બિન-હસ્તક્ષેપ" ચાલ પસંદ કરવાનું વાજબી છે.

 નીચેનું ઉદાહરણ ક્ષેત્રની કંપનીઓની હરીફાઈ સાથે સંબંધિત છે તકનીકી નેતૃત્વ.પ્રારંભિક પરિસ્થિતિ એ છે જ્યારે એન્ટરપ્રાઇઝ 1 અગાઉ તકનીકી શ્રેષ્ઠતા હતી, પરંતુ હાલમાં તેના હરીફ કરતા સંશોધન અને વિકાસ (R&D) માટે ઓછા નાણાકીય સંસાધનો છે. બંને કંપનીઓએ મોટા મૂડી રોકાણ દ્વારા પોતપોતાના ટેક્નોલોજી ક્ષેત્રે વૈશ્વિક બજારમાં પ્રભુત્વ હાંસલ કરવાનો પ્રયાસ કરવો કે કેમ તે નક્કી કરવું જોઈએ. જો બંને સ્પર્ધકો વ્યવસાયમાં મોટા પ્રમાણમાં નાણાંનું રોકાણ કરે છે, તો પછી એન્ટરપ્રાઇઝની સફળતાની સંભાવનાઓ 1 વધુ સારું રહેશે, જો કે તે મોટા નાણાકીય ખર્ચો (જેમ કે એન્ટરપ્રાઇઝ 2 ). ફિગ માં. 5 આ પરિસ્થિતિ નકારાત્મક મૂલ્યો સાથે ચૂકવણી દ્વારા દર્શાવવામાં આવે છે.

એન્ટરપ્રાઇઝ માટે 1 જો એન્ટરપ્રાઇઝ હોય તો તે શ્રેષ્ઠ રહેશે 2 સ્પર્ધા કરવાનો ઇનકાર કર્યો. આ કિસ્સામાં તેનો લાભ 3 (ચુકવણીઓ) હશે. મોટે ભાગે એન્ટરપ્રાઇઝ 2 જ્યારે એન્ટરપ્રાઇઝ સ્પર્ધા જીતશે 1 ઘટાડેલા રોકાણ કાર્યક્રમ અને એન્ટરપ્રાઇઝને સ્વીકારશે 2 - વિશાળ. આ સ્થિતિ મેટ્રિક્સના ઉપરના જમણા ચતુર્થાંશમાં પ્રતિબિંબિત થાય છે.

પરિસ્થિતિનું વિશ્લેષણ દર્શાવે છે કે એન્ટરપ્રાઇઝના ઊંચા આર એન્ડ ડી ખર્ચ પર સંતુલન થાય છે 2 અને ઓછા સાહસો 1 . અન્ય કોઈપણ સંજોગોમાં, સ્પર્ધકોમાંના એક પાસે વ્યૂહાત્મક સંયોજનથી વિચલિત થવાનું કારણ છે: ઉદાહરણ તરીકે, એન્ટરપ્રાઇઝ માટે 1 જો એન્ટરપ્રાઇઝ હોય તો ઓછું બજેટ પ્રાધાન્યક્ષમ છે 2 સ્પર્ધામાં ભાગ લેવાનો ઇનકાર કરશે; તે જ સમયે એન્ટરપ્રાઇઝ માટે 2 તે જાણીતું છે કે જ્યારે સ્પર્ધકનો ખર્ચ ઓછો હોય છે, ત્યારે તેના માટે સંશોધન અને વિકાસમાં રોકાણ કરવું નફાકારક છે.

તકનીકી લાભ ધરાવતું એન્ટરપ્રાઇઝ આખરે પોતાને માટે શ્રેષ્ઠ પરિણામ પ્રાપ્ત કરવા માટે ગેમ થિયરીના આધારે પરિસ્થિતિનું વિશ્લેષણ કરવાનો આશરો લઈ શકે છે. ચોક્કસ સંકેતની મદદથી, તેણે બતાવવું જોઈએ કે તે સંશોધન અને વિકાસ પર મોટો ખર્ચ કરવા માટે તૈયાર છે. જો આવા સંકેત પ્રાપ્ત થયા નથી, તો પછી એન્ટરપ્રાઇઝ માટે 2 તે સ્પષ્ટ છે કે એન્ટરપ્રાઇઝ 1 ઓછી કિંમતનો વિકલ્પ પસંદ કરે છે.

સિગ્નલની વિશ્વસનીયતા એન્ટરપ્રાઇઝની જવાબદારીઓ દ્વારા પુરાવા હોવી આવશ્યક છે. આ કિસ્સામાં, તે એન્ટરપ્રાઇઝનો નિર્ણય હોઈ શકે છે 1 નવી પ્રયોગશાળાઓની ખરીદી અથવા વધારાના સંશોધન કર્મચારીઓની ભરતી પર.

ગેમ થિયરીના દૃષ્ટિકોણથી, આવી જવાબદારીઓ રમતના કોર્સને બદલવાની સમાન છે: એક સાથે નિર્ણય લેવાની પરિસ્થિતિને ક્રમિક ચાલની પરિસ્થિતિ દ્વારા બદલવામાં આવે છે. એન્ટરપ્રાઇઝ 1 મોટા ખર્ચ, એન્ટરપ્રાઇઝ બનાવવાના ઇરાદાને નિશ્ચિતપણે દર્શાવે છે 2 આ પગલાની નોંધણી કરે છે અને તેની પાસે હવે હરીફાઈમાં ભાગ લેવાનું કોઈ કારણ નથી. નવું સંતુલન "એન્ટરપ્રાઇઝની બિન-ભાગીદારી"ના દૃશ્યને અનુસરે છે 2 "અને" એન્ટરપ્રાઇઝના સંશોધન અને વિકાસના ઊંચા ખર્ચ 1 ".

 ગેમ થિયરી પદ્ધતિઓના ઉપયોગના જાણીતા ક્ષેત્રોમાં પણ સમાવેશ થાય છે ભાવોની વ્યૂહરચના, સંયુક્ત સાહસોની રચના, નવા ઉત્પાદન વિકાસનો સમય.

ગેમ થિયરીના ઉપયોગ માટે મહત્વપૂર્ણ યોગદાન આવે છે પ્રાયોગિક કાર્ય. ઘણી સૈદ્ધાંતિક ગણતરીઓ પ્રયોગશાળાની પરિસ્થિતિઓમાં પરીક્ષણ કરવામાં આવે છે, અને પ્રાપ્ત પરિણામો પ્રેક્ટિશનરો માટે પ્રેરણા તરીકે સેવા આપે છે. સૈદ્ધાંતિક રીતે, તે સ્પષ્ટ કરવામાં આવ્યું હતું કે બે સ્વાર્થી વિચારોવાળા ભાગીદારો માટે કઈ પરિસ્થિતિઓમાં સહકાર આપવા અને પોતાના માટે વધુ સારા પરિણામો પ્રાપ્ત કરવા સલાહ આપવામાં આવે છે.

આ જ્ઞાનનો ઉપયોગ એન્ટરપ્રાઇઝ પ્રેક્ટિસમાં બે કંપનીઓને જીત/જીતની પરિસ્થિતિ પ્રાપ્ત કરવામાં મદદ કરવા માટે કરી શકાય છે. આજે, ગેમિંગ-પ્રશિક્ષિત સલાહકારો ઝડપથી અને સ્પષ્ટપણે એવી તકોને ઓળખે છે કે જેનો લાભ ગ્રાહકો, પેટા-સપ્લાયર્સ, વિકાસ ભાગીદારો અને તેના જેવા સાથે સ્થિર, લાંબા ગાળાના કરારો સુરક્ષિત કરવા માટે વ્યવસાયો લઈ શકે છે.

મેનેજમેન્ટમાં વ્યવહારુ ઉપયોગની સમસ્યાઓ

અલબત્ત, એ નોંધવું જોઈએ કે ગેમ થિયરીના વિશ્લેષણાત્મક સાધનોના ઉપયોગની અમુક મર્યાદાઓ છે. નીચેના કેસોમાં, વધારાની માહિતી મેળવવામાં આવે તો જ તેનો ઉપયોગ કરી શકાય છે.

પ્રથમ,આ તે કેસ છે જ્યારે વ્યવસાયો તેઓ જે રમત રમી રહ્યા છે તેના વિશે જુદા જુદા વિચારો ધરાવે છે અથવા જ્યારે તેઓ એકબીજાની ક્ષમતાઓ વિશે પૂરતા પ્રમાણમાં માહિતગાર નથી. ઉદાહરણ તરીકે, સ્પર્ધકની ચૂકવણી (કિંમત માળખું) વિશે અસ્પષ્ટ માહિતી હોઈ શકે છે. જો માહિતી કે જે ખૂબ જટિલ નથી તે અપૂર્ણતા દ્વારા વર્ગીકૃત થયેલ છે, તો પછી કોઈ ચોક્કસ તફાવતોને ધ્યાનમાં લઈને સમાન કેસોની તુલના કરીને કાર્ય કરી શકે છે.

બીજું,ગેમ થિયરી ઘણી સંતુલન પરિસ્થિતિઓમાં લાગુ કરવી મુશ્કેલ છે. આ સમસ્યા એક સાથે વ્યૂહાત્મક નિર્ણયો સાથે સરળ રમતો દરમિયાન પણ ઊભી થઈ શકે છે.

ત્રીજું,જો વ્યૂહાત્મક નિર્ણય લેવાની પરિસ્થિતિ ખૂબ જ જટિલ હોય, તો ખેલાડીઓ ઘણીવાર પોતાના માટે શ્રેષ્ઠ વિકલ્પો પસંદ કરી શકતા નથી. ઉપરોક્ત ચર્ચા કરતાં વધુ જટિલ બજારની ઘૂંસપેંઠ પરિસ્થિતિની કલ્પના કરવી સરળ છે. ઉદાહરણ તરીકે, ઘણા સાહસો જુદા જુદા સમયે બજારમાં પ્રવેશી શકે છે, અથવા ત્યાં પહેલેથી કાર્યરત સાહસોની પ્રતિક્રિયા આક્રમક અથવા મૈત્રીપૂર્ણ હોવા કરતાં વધુ જટિલ હોઈ શકે છે.

તે પ્રાયોગિક રીતે સાબિત થયું છે કે જ્યારે રમત દસ કે તેથી વધુ તબક્કાઓ સુધી વિસ્તરે છે, ત્યારે ખેલાડીઓ યોગ્ય અલ્ગોરિધમનો ઉપયોગ કરી શકતા નથી અને સંતુલન વ્યૂહરચના સાથે રમત ચાલુ રાખી શકતા નથી.

ગેમ થિયરીનો વારંવાર ઉપયોગ થતો નથી. કમનસીબે, વાસ્તવિક દુનિયાની પરિસ્થિતિઓ ઘણી વખત ખૂબ જ જટિલ હોય છે અને એટલી ઝડપથી બદલાતી રહે છે કે પેઢીની બદલાતી રણનીતિ પર પ્રતિસ્પર્ધીઓ કેવી પ્રતિક્રિયા આપશે તેની ચોક્કસ આગાહી કરવી અશક્ય છે. જો કે, સ્પર્ધાત્મક નિર્ણય લેવાની પરિસ્થિતિમાં ધ્યાનમાં લેવાના સૌથી મહત્વપૂર્ણ પરિબળોને ઓળખવાની વાત આવે ત્યારે ગેમ થિયરી ઉપયોગી છે. આ માહિતી મહત્વપૂર્ણ છે કારણ કે તે મેનેજમેન્ટને વધારાના ચલો અથવા પરિબળોને ધ્યાનમાં લેવાની મંજૂરી આપે છે જે પરિસ્થિતિને અસર કરી શકે છે, જેનાથી નિર્ણયની અસરકારકતા વધે છે.

નિષ્કર્ષમાં, તે ખાસ કરીને ભાર મૂકવો જોઈએ કે રમત સિદ્ધાંત એ જ્ઞાનનું ખૂબ જટિલ ક્ષેત્ર છે. તેને હેન્ડલ કરતી વખતે, તમારે સાવચેત રહેવું જોઈએ અને તેના ઉપયોગની મર્યાદાઓને સ્પષ્ટપણે જાણવી જોઈએ. ખૂબ સરળ અર્થઘટન, ભલે તે પેઢી દ્વારા અથવા સલાહકારોની મદદથી અપનાવવામાં આવે, તે છુપાયેલા જોખમોથી ભરપૂર છે. તેમની જટિલતાને લીધે, રમત સિદ્ધાંત વિશ્લેષણ અને પરામર્શ ફક્ત ખાસ કરીને મહત્વપૂર્ણ સમસ્યાવાળા વિસ્તારો માટે જ ભલામણ કરવામાં આવે છે. કંપનીઓનો અનુભવ દર્શાવે છે કે મોટા સહકાર કરારો તૈયાર કરતી વખતે એક વખતના, મૂળભૂત રીતે મહત્વપૂર્ણ આયોજિત વ્યૂહાત્મક નિર્ણયો લેતી વખતે યોગ્ય સાધનોનો ઉપયોગ કરવો વધુ સારું છે.

સંદર્ભો

1. ગેમ થિયરી એન્ડ ઇકોનોમિક બિહેવિયર, વોન ન્યુમેન જે., મોર્ગેનસ્ટર્ન ઓ., સાયન્સ પબ્લિશિંગ હાઉસ, 1970

2. Petrosyan L.A., Zenkevich N.A., સેમિના E.A. ગેમ થિયરી: પાઠ્યપુસ્તક. યુનિવર્સિટીઓ માટે માર્ગદર્શિકા - એમ.: ઉચ્ચ. શાળા, બુક હાઉસ "યુનિવર્સિટી", 1998

3. ડુબિના I. N. આર્થિક રમતોના સિદ્ધાંતના મૂળભૂત: પાઠ્યપુસ્તક - M.: KNORUS, 2010

4. જર્નલનું આર્કાઇવ "પ્રૉબ્લેમ્સ ઑફ થિયરી એન્ડ પ્રેક્ટિસ ઑફ મેનેજમેન્ટ", રેનર વોલકર

5. સંસ્થાકીય પ્રણાલીઓના સંચાલનમાં ગેમ થિયરી. 2જી આવૃત્તિ., ગુબકો એમ.વી., નોવિકોવ ડી.એ. 2005

- જે. જે. રૂસો.લોકો વચ્ચે અસમાનતાના મૂળ અને પાયા વિશે તર્ક // ટ્રીટીસ / અનુવાદ. ફ્રેન્ચમાંથી એ. ખયુતિના - એમ.: નૌકા, 1969. - પૃષ્ઠ 75.

વ્યાવહારિક પ્રવૃત્તિઓમાં, અન્ય પક્ષના વિરોધને ધ્યાનમાં રાખીને નિર્ણયો લેવા માટે ઘણીવાર જરૂરી હોય છે, જે વિરોધી અથવા વિવિધ ધ્યેયોને અનુસરી શકે છે અથવા અમુક ક્રિયાઓ અથવા બાહ્ય વાતાવરણની સ્થિતિઓ દ્વારા ઉદ્દેશિત ધ્યેયની સિદ્ધિને અવરોધે છે. તદુપરાંત, વિરુદ્ધ બાજુથી આ પ્રભાવો નિષ્ક્રિય અથવા સક્રિય હોઈ શકે છે. આવા કિસ્સાઓમાં, વિરોધી પક્ષના સંભવિત વર્તન વિકલ્પો, બદલો લેવાની ક્રિયાઓ અને તેના સંભવિત પરિણામોને ધ્યાનમાં લેવું જરૂરી છે.

બંને પક્ષો માટે સંભવિત વર્તન વિકલ્પો અને વિકલ્પો અને રાજ્યોના દરેક સંયોજન માટે તેમના પરિણામો ઘણીવાર ગાણિતિક મોડેલના સ્વરૂપમાં રજૂ કરવામાં આવે છે, જેને રમત કહેવામાં આવે છે .

જો વિરોધી પક્ષ એક નિષ્ક્રિય, નિષ્ક્રિય પક્ષ છે જે ઇચ્છિત ધ્યેયની સિદ્ધિનો સભાનપણે વિરોધ કરતો નથી, તો પછી આ રમત કહેવાય છે પ્રકૃતિ સાથે રમે છે. પ્રકૃતિને સામાન્ય રીતે સંજોગોના સમૂહ તરીકે સમજવામાં આવે છે જેમાં નિર્ણયો લેવાના હોય છે (હવામાનની સ્થિતિની અનિશ્ચિતતા, વ્યાપારી પ્રવૃત્તિઓમાં ગ્રાહકોનું અજ્ઞાત વર્તન, નવા પ્રકારના સામાન અને સેવાઓ પ્રત્યે વસ્તીની પ્રતિક્રિયાની અનિશ્ચિતતા વગેરે)

અન્ય પરિસ્થિતિઓમાં, વિરોધી પક્ષ સક્રિયપણે, સભાનપણે ઇચ્છિત ધ્યેયની સિદ્ધિનો વિરોધ કરે છે. આવા કિસ્સાઓમાં, વિરોધી હિતો, મંતવ્યો અને વિચારોનો ટકરાવ થાય છે. આવી પરિસ્થિતિઓ સંઘર્ષ કહેવાય છે , અને દુશ્મનના વર્તનની અનિશ્ચિતતાને કારણે સંઘર્ષની પરિસ્થિતિમાં નિર્ણય લેવાનું મુશ્કેલ છે. તે જાણીતું છે કે દુશ્મન ઇરાદાપૂર્વક સૌથી વધુ સફળતાની ખાતરી કરવા માટે તમારા માટે ઓછામાં ઓછા ફાયદાકારક પગલાં લેવા માંગે છે. પરિસ્થિતિ અને સંભવિત પરિણામોનું મૂલ્યાંકન કેવી રીતે કરવું, તે તમારી ક્ષમતાઓ અને ઇરાદાઓનું મૂલ્યાંકન કેવી રીતે કરે છે તે દુશ્મન કેટલી હદે જાણે છે તે અજાણ છે. બંને પક્ષો પરસ્પર ક્રિયાઓની આગાહી કરી શકતા નથી. આટલી અનિશ્ચિતતા હોવા છતાં, સંઘર્ષની દરેક બાજુએ નિર્ણય લેવાનો છે

અર્થશાસ્ત્રમાં, સંઘર્ષની પરિસ્થિતિઓ ઘણી વાર જોવા મળે છે અને તે વિવિધ પ્રકારની હોય છે. આમાં, ઉદાહરણ તરીકે, સપ્લાયર અને ઉપભોક્તા, ખરીદનાર અને વિક્રેતા, બેંક અને ક્લાયન્ટ, વગેરે વચ્ચેના સંબંધનો સમાવેશ થાય છે. આ બધા ઉદાહરણોમાં, સંઘર્ષની પરિસ્થિતિ ભાગીદારોના હિતમાં તફાવત અને તેમાંથી દરેકની ઇચ્છાને કારણે ઉત્પન્ન થાય છે. શ્રેષ્ઠ નિર્ણયો. તે જ સમયે, દરેક વ્યક્તિએ ફક્ત તેમના પોતાના ધ્યેયો જ નહીં, પરંતુ તેમના જીવનસાથીના લક્ષ્યોને પણ ધ્યાનમાં લેવા જોઈએ અને અગાઉથી અજાણ્યા તેની સંભવિત ક્રિયાઓને ધ્યાનમાં લેવી જોઈએ.

સંઘર્ષની પરિસ્થિતિઓમાં શ્રેષ્ઠ નિર્ણયોને ન્યાયી ઠેરવવાની જરૂરિયાત ઉદભવે છે રમત સિદ્ધાંત.

ગેમ થિયરી - આ સંઘર્ષની પરિસ્થિતિઓનો ગાણિતિક સિદ્ધાંત છે. આ સિદ્ધાંતના પ્રારંભિક મુદ્દાઓ એ દુશ્મનની સંપૂર્ણ "આદર્શ" તર્કસંગતતાની ધારણા અને સંઘર્ષને ઉકેલતી વખતે સૌથી સાવચેત નિર્ણય અપનાવવાનો છે.

વિરોધાભાસી પક્ષોને બોલાવવામાં આવે છે ખેલાડીઓ , રમતનું એક અમલીકરણ - પાર્ટી , રમતનું પરિણામ છે જીતવું કે હારવું . ખેલાડી (રમતના આપેલા નિયમોની અંદર) માટે શક્ય હોય તેવી કોઈપણ ક્રિયાને તેની કહેવામાં આવે છે વ્યૂહરચના .

રમતનો મુદ્દો એ છે કે દરેક ખેલાડી, રમતના આપેલા નિયમોની અંદર, તે વ્યૂહરચના લાગુ કરવાનો પ્રયાસ કરે છે જે તેના માટે શ્રેષ્ઠ હોય, એટલે કે તે વ્યૂહરચના જે તેના માટે શ્રેષ્ઠ પરિણામ તરફ દોરી જાય. શ્રેષ્ઠ (ઉચિત) વર્તનના સિદ્ધાંતોમાંનું એક એ સંતુલન પરિસ્થિતિની સિદ્ધિ છે, જેના ઉલ્લંઘનમાં કોઈ પણ ખેલાડીને રસ નથી.

તે સંતુલનની સ્થિતિ છે જે ખેલાડીઓ વચ્ચે સ્થિર કરારનો વિષય બની શકે છે. વધુમાં, સંતુલન પરિસ્થિતિઓ દરેક ખેલાડી માટે ફાયદાકારક હોય છે: સંતુલનની પરિસ્થિતિમાં, દરેક ખેલાડી તેના પર નિર્ભર હોય તે હદે સૌથી વધુ વળતર મેળવે છે.

સંઘર્ષની પરિસ્થિતિનું ગાણિતિક મોડેલ રમત કહેવાય છે , સંઘર્ષમાં સામેલ પક્ષો, ખેલાડીઓ કહેવાય છે.

દરેક ઔપચારિક રમત માટે, નિયમો રજૂ કરવામાં આવે છે. સામાન્ય રીતે, રમતના નિયમો ક્રિયા માટે ખેલાડીઓના વિકલ્પો સ્થાપિત કરે છે; દરેક ખેલાડી પાસે તેમના ભાગીદારોના વર્તન વિશેની માહિતીનો જથ્થો; ચૂકવણી કે જે ક્રિયાઓના દરેક સમૂહ તરફ દોરી જાય છે.

સમય જતાં રમતનો વિકાસ તબક્કામાં અથવા ચાલમાં ક્રમિક રીતે થાય છે. ગેમ થિયરીમાં ચાલ કહેવામાં આવે છે રમતના નિયમો અને તેના અમલીકરણ દ્વારા પૂરી પાડવામાં આવેલ ક્રિયાઓમાંથી એકની પસંદગી. ચાલ વ્યક્તિગત અને રેન્ડમ છે. અંગત રીતે ક્રિયા અને તેના અમલીકરણ માટે સંભવિત વિકલ્પોમાંથી એકની ખેલાડીની સભાન પસંદગીને કૉલ કરો. રેન્ડમ ચાલ તેઓ ખેલાડીના સ્વૈચ્છિક નિર્ણય દ્વારા નહીં, પરંતુ અમુક પ્રકારની રેન્ડમ સિલેક્શન મિકેનિઝમ (સિક્કો ઉછાળવો, પસાર કરવો, કાર્ડ ડીલિંગ વગેરે) દ્વારા કરવામાં આવેલી પસંદગીને બોલાવે છે.

પરિણામોની અનિશ્ચિતતાના કારણોના આધારે, રમતોને નીચેના મુખ્ય જૂથોમાં વિભાજિત કરી શકાય છે:

સંયુક્ત રમતો, જેમાં નિયમો, સૈદ્ધાંતિક રીતે, દરેક ખેલાડીને તેની વર્તણૂક માટેના તમામ વિવિધ વિકલ્પોનું વિશ્લેષણ કરવાની તક પૂરી પાડે છે અને આ વિકલ્પોની સરખામણી કરીને, આ ખેલાડી માટે શ્રેષ્ઠ પરિણામ તરફ દોરી જાય તેવો વિકલ્પ પસંદ કરો. પરિણામની અનિશ્ચિતતા સામાન્ય રીતે એ હકીકતને કારણે છે કે સંભવિત વર્તણૂક વિકલ્પો (ચાલ) ની સંખ્યા ખૂબ મોટી છે અને ખેલાડી તે બધાને સૉર્ટ કરવા અને તેનું વિશ્લેષણ કરવામાં વ્યવહારીક રીતે અસમર્થ છે.

જુગાર , જેમાં વિવિધ રેન્ડમ પરિબળોના પ્રભાવને લીધે પરિણામ અનિશ્ચિત છે. જુગારની રમતોમાં માત્ર રેન્ડમ ચાલનો સમાવેશ થાય છે, જેનું વિશ્લેષણ સંભવિતતાના સિદ્ધાંતનો ઉપયોગ કરે છે. મેથેમેટિકલ ગેમ થિયરી જુગાર સાથે વ્યવહાર કરતી નથી.

વ્યૂહરચના રમતો , જેમાં પસંદગીની સંપૂર્ણ અનિશ્ચિતતા એ હકીકત દ્વારા વાજબી છે કે દરેક ખેલાડી, જ્યારે આગામી ચાલની પસંદગી અંગે નિર્ણય લે છે, ત્યારે રમતમાં અન્ય સહભાગીઓ કઈ વ્યૂહરચનાનું પાલન કરશે તે જાણતા નથી, અને ખેલાડીની અજ્ઞાનતા. ભાગીદારોની વર્તણૂક અને ઇરાદા મૂળભૂત છે, કારણ કે દુશ્મન (ભાગીદાર) ની અનુગામી ક્રિયાઓ વિશે કોઈ માહિતી નથી.

એવી રમતો છે જે સંયુક્ત અને જુગારની રમતોના ગુણધર્મોને જોડે છે;

રમતમાં સહભાગીઓની સંખ્યા પર આધાર રાખે છે જોડી અને બહુવિધ વિભાજિત કરવામાં આવે છે. ડબલ્સ રમતમાં સહભાગીઓની સંખ્યા બે હોય છે, બહુવિધ રમતમાં સહભાગીઓની સંખ્યા બે કરતા વધુ હોય છે. બહુવિધ રમતમાં સહભાગીઓ ગઠબંધન બનાવી શકે છે. આ કિસ્સામાં રમતો કહેવામાં આવે છે ગઠબંધન . બહુવિધ રમત બેવડી રમત બની જાય છે જો તેના સહભાગીઓ બે કાયમી ગઠબંધન બનાવે છે.

ગેમ થિયરીના મૂળભૂત ખ્યાલોમાંની એક વ્યૂહરચના છે. પ્લેયર વ્યૂહરચના એ નિયમોનો સમૂહ છે જે રમત દરમિયાન ઊભી થતી પરિસ્થિતિના આધારે આ ખેલાડીની દરેક વ્યક્તિગત ચાલ માટે ક્રિયાની પસંદગી નક્કી કરે છે.

શ્રેષ્ઠ વ્યૂહરચના પ્લેયર એ એક વ્યૂહરચના છે જે, જ્યારે વ્યક્તિગત અને રેન્ડમ ચાલ ધરાવતી રમતમાં ઘણી વખત પુનરાવર્તિત થાય છે, ત્યારે ખેલાડીને પ્રતિસ્પર્ધીની વર્તણૂકને ધ્યાનમાં લીધા વિના મહત્તમ સંભવિત સરેરાશ જીત અથવા ન્યૂનતમ સંભવિત નુકસાન પ્રદાન કરે છે.

રમત કહેવાય છે અંતિમ , જો ખેલાડીઓની વ્યૂહરચનાઓની સંખ્યા મર્યાદિત હોય, અને અનંત , જો ઓછામાં ઓછા એક ખેલાડી પાસે અસંખ્ય વ્યૂહરચના હોય.

મલ્ટી-મૂવ ગેમ થિયરી સમસ્યાઓમાં, "વ્યૂહરચના" અને "સંભવિત ક્રિયાઓનો વિકલ્પ" ની વિભાવનાઓ એકબીજાથી નોંધપાત્ર રીતે અલગ છે. સરળ (એક-ચાલની) રમત સમસ્યાઓમાં, જ્યારે દરેક રમતમાં દરેક ખેલાડી એક ચાલ કરી શકે છે, ત્યારે આ ખ્યાલો એકરૂપ થાય છે, અને તેથી, ખેલાડીની વ્યૂહરચનાનો સમૂહ તમામ સંભવિત ક્રિયાઓને આવરી લે છે જે તે કોઈપણ સંભવિત પરિસ્થિતિમાં અને કોઈપણ સંભવિત હેઠળ લઈ શકે છે. વાસ્તવિક માહિતી.

રમતો પણ જીતની રકમ દ્વારા અલગ પડે છે. રમત કહેવાય છે શૂન્ય સાથે રમત સરવાળો મી, જો દરેક ખેલાડી અન્યના ભોગે જીતે છે, અને એક પક્ષની જીતની રકમ બીજી બાજુની હારની રકમ જેટલી છે. શૂન્ય-સમ ડબલ્સ રમતમાં, ખેલાડીઓના હિતોનો સીધો વિરોધ થાય છે. શૂન્ય-સમ જોડીઓની રમત કહેવાય છે આઈવિરોધી રમત .

એવી રમતો જેમાં એક ખેલાડીનો ફાયદો અને બીજાનો નુકશાન સમાન નથી કહેવાય છેબિન-શૂન્ય રકમની રમતો .

રમતોનું વર્ણન કરવાની બે રીત છે: સ્થિતિ અને સામાન્ય . સ્થિતિની પદ્ધતિ રમતના વિસ્તૃત સ્વરૂપ સાથે સંકળાયેલી છે અને ક્રમિક પગલાઓ (ગેમ ટ્રી) ના ગ્રાફ સુધી ઘટાડવામાં આવે છે. સામાન્ય રીત એ છે કે પ્લેયર વ્યૂહરચનાઓના સમૂહને સ્પષ્ટપણે રજૂ કરવું અને ચુકવણી કાર્ય . રમતમાં ચુકવણી કાર્ય ખેલાડીઓ દ્વારા પસંદ કરાયેલ વ્યૂહરચનાના દરેક સેટ માટે દરેક બાજુની જીત નક્કી કરે છે.