El mercado primario es el criterio de Fisher. El criterio de Fisher se utiliza para probar la hipótesis de que las varianzas de dos poblaciones son iguales - documento

Criterio de Fisher

El criterio de Fisher se utiliza para probar la hipótesis de que las varianzas de dos poblaciones generales, distribuido según la ley normal. Es un criterio paramétrico.

La prueba F de Fisher se llama razón de varianza porque se forma como la razón de dos estimaciones insesgadas de varianzas que se comparan.

Dejemos que se obtengan dos muestras como resultado de las observaciones. De ellos las variaciones y teniendo Y grados de libertad. Supondremos que la primera muestra se toma de una población con varianza , y el segundo es de la población general con varianza . Se plantea una hipótesis nula sobre la igualdad de las dos varianzas, es decir H0:
o . Para rechazar esta hipótesis, es necesario probar la significancia de la diferencia en un nivel de significancia dado.
.

El valor del criterio se calcula mediante la fórmula:

Evidentemente, si las varianzas son iguales, el valor del criterio será igual a uno. En otros casos será mayor (menor) que uno.

La prueba tiene una distribución de Fisher.
. Prueba de Fisher: prueba de dos colas e hipótesis nula
rechazado a favor de una alternativa
Si . Aqui donde
– el volumen de la primera y segunda muestra, respectivamente.

El sistema STATISTICA implementa una prueba de Fisher unilateral, es decir la variación máxima siempre se toma como calidad. En este caso, se rechaza la hipótesis nula a favor de la alternativa si.

Ejemplo

Fijémonos la tarea de comparar la eficacia de enseñar a dos grupos de estudiantes. El nivel de logro caracteriza el nivel de gestión del proceso de aprendizaje, y la dispersión es la calidad de la gestión del aprendizaje, el grado de organización del proceso de aprendizaje. Ambos indicadores son independientes y caso general deben considerarse en conjunto. El nivel de rendimiento académico (expectativa matemática) de cada grupo de estudiantes se caracteriza por promedios aritméticos y , y la calidad se caracteriza por las correspondientes varianzas muestrales de las estimaciones: y . Al evaluar el nivel de desempeño actual, resultó que era el mismo para ambos estudiantes: = = 4.0. Variaciones de muestra:
Y
. Números de grados de libertad correspondientes a estas estimaciones:
Y
. A partir de aquí, para establecer diferencias en la efectividad del aprendizaje podemos utilizar la estabilidad del rendimiento académico, es decir Probemos la hipótesis.

calculemos
(debe haber una gran variación en el numerador), . Según las tablas ( ESTADÍSTICA – ProbabilidadDistribuciónCalculadora) encontramos , que es menor que lo calculado, por lo tanto la hipótesis nula debe rechazarse a favor de la alternativa. Esta conclusión puede no satisfacer al investigador, ya que está interesado en el verdadero valor de la relación.
(siempre tenemos una gran variación en el numerador). Al comprobar un criterio unilateral, obtenemos que es menor que el valor calculado anteriormente. Por tanto, la hipótesis nula debe rechazarse en favor de la alternativa.

Prueba de Fisher en el programa STATISTICA en entorno Windows

Para un ejemplo de prueba de una hipótesis (criterio de Fisher), usamos (creamos) un archivo con dos variables (fisher.sta):

Arroz. 1. Tabla con dos variables independientes

Para probar la hipótesis es necesario en estadística básica ( BásicoEstadísticasyMesas) seleccione la prueba t para variables independientes. ( Prueba t, independiente, por variables.).

Arroz. 2. Prueba de hipótesis paramétricas

Después de seleccionar las variables y presionar la tecla Resumen Se calculan los valores de las desviaciones estándar y el criterio de Fisher. Además, se determina el nivel de significancia. pag, en el que la diferencia es insignificante.

Arroz. 3. Resultados de la prueba de hipótesis (prueba F)

Usando ProbabilidadCalculadora y al establecer los valores de los parámetros, puede construir un gráfico de la distribución de Fisher con el valor calculado marcado.

Arroz. 4. Área de aceptación (rechazo) de la hipótesis (criterio F)

Fuentes.

Probar hipótesis sobre la relación entre dos varianzas.

URL: /tryfonov3/terms3/testdi.htm

Conferencia 6. :8080/resources/math/mop/lections/lection_6.htm

F – Criterio de Fisher

URL: /home/portal/aplicaciones/Multivariatadvisor/F-Fisher/F-Fisheer.htm

Teoría y práctica de la investigación estadística probabilística.

URL: /active/referats/read/doc-3663-1.html

F – Criterio de Fisher

Criterio de Fisher le permite comparar las varianzas muestrales de dos muestras independientes. Para calcular F emp, necesita encontrar la relación de las varianzas de dos muestras, de modo que la varianza mayor esté en el numerador y la menor en el denominador. La fórmula para calcular el criterio de Fisher es:

donde están las varianzas de la primera y segunda muestra, respectivamente.

Dado que, según la condición del criterio, el valor del numerador debe ser mayor o igual que el valor del denominador, el valor de F emp siempre será mayor o igual a uno.

El número de grados de libertad también se determina de forma sencilla:

k 1 =n yo - 1 para la primera muestra (es decir, para la muestra cuya varianza es mayor) y k 2 = norte 2 - 1 para la segunda muestra.

En el Apéndice 1, los valores críticos del criterio de Fisher se encuentran mediante los valores de k 1 (línea superior de la tabla) y k 2 (columna izquierda de la tabla).

Si t em >t crit, entonces se acepta la hipótesis nula; en caso contrario, se acepta la alternativa.

Ejemplo 3. Las pruebas se realizaron en dos de tercer grado. desarrollo mental diez estudiantes en la prueba TURMSH. Los valores promedio obtenidos no difirieron significativamente, pero al psicólogo le interesa la cuestión de si existen diferencias en el grado de homogeneidad de los indicadores de desarrollo mental entre clases.

Solución. Para la prueba de Fisher, es necesario comparar las varianzas de las puntuaciones de las pruebas en ambas clases. Los resultados de la prueba se presentan en la tabla:

Tabla 3.

Estudiantes núms.	Primer grado	Segunda clase

Habiendo calculado las varianzas para las variables X e Y, obtenemos:

s X 2 =572,83; s y 2 =174,04

Luego, utilizando la fórmula (8) para el cálculo utilizando el criterio F de Fisher, encontramos:

Según la tabla del Apéndice 1 para el criterio F con grados de libertad en ambos casos iguales a k = 10 - 1 = 9, encontramos F crit = 3,18 (<3.29), следовательно, в терминах статистических гипотез можно утвер­ждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

6.2 Pruebas no paramétricas

Al comparar visualmente (por porcentaje) los resultados antes y después de cualquier impacto, el investigador llega a la conclusión de que si se observan diferencias, entonces hay una diferencia en las muestras que se comparan. Este enfoque es categóricamente inaceptable, ya que para porcentajes es imposible determinar el nivel de confiabilidad de las diferencias. Los porcentajes tomados por sí solos no permiten sacar conclusiones estadísticamente fiables. Para demostrar la eficacia de cualquier intervención, es necesario identificar una tendencia estadísticamente significativa en el sesgo (desplazamiento) de los indicadores. Para resolver tales problemas, un investigador puede utilizar varios criterios de discriminación. A continuación consideraremos pruebas no paramétricas: la prueba de signos y la prueba de chi-cuadrado.

)

Cálculo del criterio φ*

1. Determinar aquellos valores del atributo que serán el criterio para dividir a los sujetos en los que “tienen efecto” y los que “no tienen efecto”. Si la característica se mide cuantitativamente, utilice el criterio λ para encontrar el punto de separación óptimo.

2. Dibuje una tabla de cuatro celdas (sinónimo: cuatro campos) de dos columnas y dos filas. La primera columna es “hay un efecto”; segunda columna - "sin efecto"; primera línea desde arriba: 1 grupo (muestra); segunda línea - grupo 2 (muestra).

4. Cuente el número de sujetos de la primera muestra que “no tienen ningún efecto” e ingrese este número en la celda superior derecha de la tabla. Calcula la suma de las dos celdas superiores. Debe coincidir con el número de sujetos del primer grupo.

6. Cuente el número de sujetos de la segunda muestra que “no tienen ningún efecto” e ingrese este número en la celda inferior derecha de la tabla. Calcula la suma de las dos celdas inferiores. Debe coincidir con el número de sujetos del segundo grupo (muestra).

7. Determinar el porcentaje de sujetos que “tienen un efecto” relacionando su número con el número total de sujetos en un grupo determinado (muestra). Escriba los porcentajes resultantes en las celdas superior izquierda e inferior izquierda de la tabla entre paréntesis, respectivamente, para no confundirlos con valores absolutos.

8. Verifique si uno de los porcentajes que se comparan es igual a cero. Si este es el caso, intente cambiarlo moviendo el punto de separación del grupo en una dirección u otra. Si esto es imposible o indeseable, abandone el criterio φ* y utilice el criterio χ2.

9. Determinar según la tabla. XII Apéndice 1 ángulos φ para cada uno de los porcentajes comparados.

donde: φ1 - ángulo correspondiente al porcentaje mayor;

φ2 - ángulo correspondiente al porcentaje menor;

N1 - número de observaciones en la muestra 1;

N2: número de observaciones en la muestra 2.

11. Comparar el valor obtenido φ* con los valores críticos: φ* ≤1.64 (p<0,05) и φ* ≤2,31 (р<0,01).

Si φ*emp ≤φ*cr. Se rechaza H0.

Si es necesario, determine el nivel exacto de significancia del φ*emp resultante según la Tabla. XIII Apéndice 1.

Este método se describe en muchos manuales (Plokhinsky N.A., 1970; Gubler E.V., 1978; Ivanter E.V., Korosov A.V., 1992, etc.) Esta descripción se basa en la versión del método que fue desarrollado y presentado por E.V. Gubler.

Propósito del criterio φ*

El criterio de Fisher pretende comparar dos muestras según la frecuencia de aparición del efecto (indicador) de interés para el investigador. Cuanto más grande sea, más fiables serán las diferencias.

Descripción del criterio

El criterio evalúa la confiabilidad de las diferencias entre aquellos porcentajes de dos muestras en las que se registró el efecto (indicador) que nos interesa. En sentido figurado, comparamos las 2 mejores piezas cortadas de 2 pasteles y decidimos cuál es realmente más grande.

La esencia de la transformación angular de Fisher es convertir porcentajes en valores de ángulos centrales, que se miden en radianes. Un porcentaje mayor corresponderá a un ángulo mayor φ, y un porcentaje menor corresponderá a un ángulo menor, pero las relaciones aquí no son lineales:

donde P es el porcentaje expresado en fracciones de una unidad (ver Fig. 5.1).

Con una discrepancia creciente entre los ángulos φ 1 y φ 2 y al aumentar el número de muestras, aumenta el valor del criterio. Cuanto mayor sea el valor de φ*, más probable es que las diferencias sean significativas.

Hipótesis

h 0 : Proporción de personas, en el que se manifiesta el efecto estudiado, no hay más en la muestra 1 que en la muestra 2.

h 1 : La proporción de individuos que exhiben el efecto estudiado es mayor en la muestra 1 que en la muestra 2.

Representación gráfica del criterio. φ*

El método de transformación angular es algo más abstracto que los demás criterios.

La fórmula seguida por E.V. Gubler al calcular los valores de φ supone que el 100% constituye un ángulo φ=3,142, es decir, un valor redondeado π=3,14159... Esto nos permite presentar las muestras comparadas en forma de dos semicírculos, cada uno de los cuales simboliza el 100% de la población de su muestra. Los porcentajes de sujetos con “efecto” se representarán como sectores formados por los ángulos centrales φ. En la Fig. La figura 5.2 muestra dos semicírculos que ilustran el ejemplo 1. En la primera muestra, el 60% de los sujetos resolvió el problema. Este porcentaje corresponde al ángulo φ=1,772. En la segunda muestra, el 40% de los sujetos resolvió el problema. Este porcentaje corresponde al ángulo φ =1,369.

El criterio φ* le permite determinar si uno de los ángulos es de hecho estadísticamente significativamente superior al otro para tamaños de muestra determinados.

Limitaciones del criterio φ*

1. Ninguna de las proporciones que se comparan debe ser cero. Formalmente, no existen obstáculos para aplicar el método φ en los casos en que la proporción de observaciones en una de las muestras sea igual a 0. Sin embargo, en estos casos, el resultado puede resultar injustificadamente inflado (Gubler E.V., 1978, p. .86).

2. superior no hay límite en el criterio φ: las muestras pueden ser tan grandes como se desee.

Más bajo límite: 2 observaciones en una de las muestras. Sin embargo, se deben observar las siguientes proporciones en el número de dos muestras:

a) si una muestra tiene solo 2 observaciones, entonces la segunda debe tener al menos 30:

b) si una de las muestras tiene solo 3 observaciones, entonces la segunda debe tener al menos 7:

c) si una de las muestras tiene solo 4 observaciones, entonces la segunda debe tener al menos 5:

d) ennorte 1 , norte 2 ≥ 5 Cualquier comparación es posible.

En principio, también es posible comparar muestras que no cumplan esta condición, por ejemplo, con la relaciónnorte 1 =2, norte 2 = 15, pero en estos casos no será posible identificar diferencias significativas.

El criterio φ* no tiene otras restricciones.

Veamos algunos ejemplos para ilustrar las posibilidades.criterio φ*.

Ejemplo 1: comparación de muestras según una característica cualitativamente definida.

Ejemplo 2: comparación de muestras según una característica medida cuantitativamente.

Ejemplo 3: comparación de muestras tanto por nivel como por distribución de una característica.

Ejemplo 4: Uso del criterio φ* en combinación con el criterioX Kolmogorov-Smirnov para lograr el resultado más preciso.

Ejemplo 1: comparación de muestras según una característica determinada cualitativamente

En este uso del criterio, comparamos el porcentaje de sujetos en una muestra caracterizada por alguna cualidad con el porcentaje de sujetos en otra muestra caracterizada por la misma calidad.

Digamos que estamos interesados ​​en saber si dos grupos de estudiantes difieren en su éxito al resolver un nuevo problema experimental. En el primer grupo de 20 personas, 12 personas lo solucionaron, y en la segunda muestra de 25 personas, 10. En el primer caso, el porcentaje de quienes resolvieron el problema será 12/20·100%=60%, y en el segundo 10/25·100%= 40%. ¿Estos porcentajes difieren significativamente según los datos?norte 1 Ynorte 2 ?

Parecería que incluso “a simple vista” se puede determinar que el 60% es significativamente mayor que el 40%. Sin embargo, de hecho, estas diferencias, dados los datosnorte 1 , norte 2 faltón.

Vamos a ver. Como estamos interesados ​​en el hecho de resolver un problema, consideraremos el éxito en la resolución de un problema experimental como un “efecto” y el fracaso en su resolución como la ausencia de un efecto.

Formulemos hipótesis.

h 0 : Proporción de personasNo hubo más personas que completaron la tarea en el primer grupo que en el segundo grupo.

h 1 : La proporción de personas que completaron la tarea en el primer grupo es mayor que en el segundo grupo.

Ahora construyamos la llamada tabla de cuatro celdas o de cuatro campos, que en realidad es una tabla de frecuencias empíricas para dos valores del atributo: "hay un efecto" - "no hay ningún efecto".

Tabla 5.1

Tabla de cuatro celdas para calcular el criterio al comparar dos grupos de sujetos según el porcentaje de quienes resolvieron el problema.

Grupos	“Hay un efecto”: problema resuelto			"Sin efecto": el problema no se soluciona			Cantidades
	Cantidad asignaturas	% compartir		Cantidad asignaturas	% compartir
1 grupo		(60%)			(40%)
2do grupo		(40%)			(60%)
Cantidades

En una tabla de cuatro celdas, por regla general, las columnas "Hay un efecto" y "Sin efecto" están marcadas en la parte superior, y las filas "Grupo 1" y "Grupo 2" están a la izquierda. De hecho, en las comparaciones sólo participan los campos (celdas) A y B, es decir, los porcentajes en la columna "Hay un efecto".

Según la tabla.XIIEn el Apéndice 1 se determinan los valores de φ correspondientes a las participaciones porcentuales en cada uno de los grupos.

Ahora calculemos el valor empírico de φ* usando la fórmula:

donde φ 1 - ángulo correspondiente al porcentaje de participación mayor;

φ 2 - ángulo correspondiente al porcentaje menor;

norte 1 - número de observaciones en la muestra 1;

norte 2 - número de observaciones en la muestra 2.

En este caso:

Según la tabla.XIIIEn el Apéndice 1 determinamos qué nivel de significancia corresponde a φ* ellos=1,34:

p=0,09

También es posible establecer valores críticos de φ* correspondientes a los niveles aceptados en psicología. significancia estadística:

Construyamos un "eje de significación".

El valor empírico obtenido φ* se encuentra en la zona de insignificancia.

Respuesta: h 0 aceptado. El porcentaje de personas que completaron la tarea.Ven el primer grupo no más que en el segundo grupo.

Sólo se puede simpatizar con un investigador que considera significativas diferencias del 20% e incluso del 10% sin comprobar su fiabilidad mediante el criterio φ*. En este caso, por ejemplo, sólo serían significativas diferencias de al menos el 24,3%.

Parece que al comparar dos muestras sobre cualquier base cualitativa, el criterio φ puede entristecernos en lugar de alegrarnos. Lo que parecía significativo puede no serlo desde el punto de vista estadístico.

El criterio de Fisher tiene muchas más oportunidades de complacer al investigador cuando comparamos dos muestras según características medidas cuantitativamente y puede variar el "efecto".

Ejemplo 2: comparación de dos muestras según una característica medida cuantitativamente

En este uso del criterio, comparamos el porcentaje de sujetos de una muestra que alcanzan un cierto nivel de valor de atributo con el porcentaje de sujetos que alcanzan este nivel en otra muestra.

En un estudio de G. A. Tlegenova (1990), de 70 jóvenes estudiantes de escuelas vocacionales de entre 14 y 16 años, se seleccionaron en base a los resultados 10 sujetos con una puntuación alta en la escala de Agresión y 11 sujetos con una puntuación baja en la escala de Agresión. de una encuesta utilizando el Cuestionario de Personalidad de Friburgo. Es necesario determinar si los grupos de jóvenes agresivos y no agresivos difieren en cuanto a la distancia que eligen espontáneamente en una conversación con un compañero de estudios. Los datos de G. A. Tlegenova se presentan en la tabla. 5.2. Puedes notar que los jóvenes agresivos eligen con mayor frecuencia una distancia de 50cm o incluso menos, mientras que los niños no agresivos eligen con mayor frecuencia una distancia superior a 50 cm.

Ahora podemos considerar una distancia de 50 cm como crítica y asumir que si la distancia elegida por el sujeto es menor o igual a 50 cm, entonces “hay un efecto”, y si la distancia seleccionada es mayor a 50 cm, entonces "No hay ningún efecto". Vemos que en el grupo de jóvenes agresivos el efecto se observa en 7 de cada 10, es decir, en el 70% de los casos, y en el grupo de jóvenes no agresivos, en 2 de 11, es decir, en el 18,2% de los casos. . Estos porcentajes se pueden comparar mediante el método φ* para establecer la significancia de las diferencias entre ellos.

Tabla 5.2

Indicadores de la distancia (en cm) elegida por jóvenes agresivos y no agresivos en una conversación con un compañero de estudios (según G.A. Tlegenova, 1990)

	Grupo 1: chicos con puntuaciones altas en la escala de AgresiónFPI- R (norte 1 =10)		Grupo 2: chicos con valores bajos en la escala de AgresividadFPI- R (norte 2 =11)
	corriente continua metro )	% compartir	corriente continua METRO )	% compartir
"Comer Efecto" d≤50cm
				18,2%
"No efecto" d>50 cm
	80 QO			81,8%
Cantidades		100%		100%
Promedio	5b:o		77.3

Formulemos hipótesis.

h 0 d ≤ 50 cm, en el grupo de chicos agresivos no hay más que en el grupo de chicos no agresivos.

h 1 : Proporción de personas que eligen la distanciad≤ 50 cm, más en el grupo de jóvenes agresivos que en el grupo de jóvenes no agresivos. Ahora construyamos la llamada tabla de cuatro celdas.

Tabla 53

Tabla de cuatro celdas para calcular el criterio φ* al comparar grupos de agresivos (nf=10) y hombres jóvenes no agresivos (n2=11)

Grupos	"Hay un efecto": d≤50			"Sin efecto." d>50			Cantidades
	Número de sujetos	(% compartir)		Número de sujetos	(% compartir)
Grupo 1: jóvenes agresivos		(70%)			(30%)
Grupo 2: hombres jóvenes no agresivos		(180%)			(81,8%)
Suma

Según la tabla.XIIEl Apéndice 1 determina los valores de φ correspondientes a las participaciones porcentuales del “efecto” en cada uno de los grupos.

El valor empírico obtenido φ* se encuentra en la zona de significación.

Respuesta: h 0 rechazado. Aceptadoh 1 . La proporción de personas que eligen una distancia en la conversación menor o igual a 50 cm es mayor en el grupo de jóvenes agresivos que en el grupo de jóvenes no agresivos

Con base en los resultados obtenidos, podemos concluir que los jóvenes más agresivos eligen con mayor frecuencia una distancia inferior a medio metro, mientras que los jóvenes no agresivos eligen con mayor frecuencia una distancia superior a medio metro. Vemos que los jóvenes agresivos en realidad se comunican en el límite entre la zona íntima (0-46 cm) y la personal (a partir de 46 cm). Recordamos, sin embargo, que la distancia íntima entre socios es prerrogativa no sólo de relaciones buenas y cercanas, sino también deYcombate mano a mano (Salami. t., 1959).

Ejemplo 3: comparación de muestras tanto por nivel como por distribución de la característica.

En este caso de uso, primero podemos probar si los grupos difieren en los niveles de algún rasgo y luego comparar las distribuciones del rasgo en las dos muestras. Esta tarea puede ser relevante al analizar las diferencias en los rangos o la forma de la distribución de las evaluaciones obtenidas por los sujetos que utilizan cualquier técnica nueva.

En un estudio de R. T. Chirkina (1995), se utilizó por primera vez un cuestionario destinado a identificar la tendencia a reprimir de la memoria hechos, nombres, intenciones y métodos de acción debido a complejos personales, familiares y profesionales. El cuestionario fue elaborado con la participación de E.V. Sidorenko basándose en materiales del libro 3. Freud "Psicopatología de la vida cotidiana". Se examinó una muestra de 50 estudiantes del Instituto Pedagógico, solteros, sin hijos, con edades entre 17 y 20 años, mediante este cuestionario, así como la técnica de Menester-Corzini para identificar la intensidad del sentimiento de insuficiencia personal.o"complejo de inferioridad" (manásterGRAMO. j., CorsiniR. j., 1982).

Los resultados de la encuesta se presentan en la tabla. 5.4.

¿Es posible decir que existen relaciones significativas entre el indicador de energía de represión, diagnosticado mediante un cuestionario, y los indicadores de la intensidad del sentimiento de propia insuficiencia?

Tabla 5.4

Indicadores de la intensidad de los sentimientos de insuficiencia personal en grupos de estudiantes con alto (Nueva Jersey=18) y baja (n2=24) energía de desplazamiento

Grupo 1: energía de desplazamiento de 19 a 31 puntos (norte 1 =181		Grupo 2: energía de desplazamiento de 7 a 13 puntos (norte 2 =24)
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30; 30 50; 50 60; 60		0; 0 5; 5; 5; 5 10; 10; 10; 10; 10; 10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30
Cantidades Promedio	26,11	15,42

A pesar de que el valor medio en el grupo con represión más enérgica es superior, en él también se observan 5 valores cero. Si comparamos los histogramas de la distribución de calificaciones en las dos muestras, se revela un contraste sorprendente entre ellas (Fig. 5.3).

Para comparar dos distribuciones podríamos aplicar la prueba.χ 2 o criterioλ , pero para ello habría que ampliar las filas, y además, en ambas muestrasnorte <30.

El criterio φ* nos permitirá comprobar el efecto de la discrepancia entre dos distribuciones observadas en el gráfico si aceptamos asumir que “hay un efecto” si el indicador de sensación de insuficiencia toma muy bajo (0) o, por el contrario , valores muy altos (S30), y que “no hay efecto” si el indicador de sentimientos de insuficiencia toma valores medios, de 5 a 25.

Formulemos hipótesis.

h 0 : Los valores extremos del índice de deficiencia (0 o 30 o más) en el grupo con más represión enérgica no son más comunes que en el grupo con menos represión enérgica.

h 1 : Los valores extremos del índice de deficiencia (ya sea 0 o 30 o más) en el grupo con más represión enérgica son más comunes que en el grupo con menos represión enérgica.

Creemos una tabla de cuatro celdas conveniente para realizar más cálculos del criterio φ*.

Tabla 5.5

Tabla de cuatro celdas para calcular el criterio φ* al comparar grupos con mayor y menor energía de represión en función de la proporción de indicadores de insuficiencia

Grupos	“Hay un efecto”: el indicador de deficiencia es 0 o >30		“Sin efecto”: índice de fracaso de 5 a 25		Cantidades
		(88,9%)		(11,1%)
		(33,3%)		(66,7%)
Cantidades

Según la tabla.XIIEn el Apéndice 1 determinamos los valores de φ correspondientes a los porcentajes comparados:

Calculemos el valor empírico de φ*:

Valores críticos de φ* para cualquiernorte 1 , norte 2 , como recordamos del ejemplo anterior, son:

MesaXIIIEl Apéndice 1 nos permite determinar con mayor precisión el nivel de significancia del resultado obtenido: p<0,001.

Respuesta: h 0 rechazado. Aceptadoh 1 . Los valores extremos del índice de deficiencia (0 o 30 o más) en el grupo con mayor energía de represión ocurren con más frecuencia que en el grupo con menos energía de represión.

Así, los sujetos con mayor energía de represión pueden tener indicadores de sentimiento de propia insuficiencia tanto muy altos (30 o más) como muy bajos (cero). Se puede suponer que están reprimiendo tanto su insatisfacción como la necesidad de éxito en la vida. Estas suposiciones necesitan más pruebas.

El resultado obtenido, independientemente de su interpretación, confirma las capacidades del criterio φ* para evaluar diferencias en la forma de la distribución de un rasgo en dos muestras.

Había 50 personas en la muestra original, pero 8 de ellas fueron excluidas de la consideración por tener una puntuación media en el índice de anergia represiva (14-15). Sus indicadores de intensidad de los sentimientos de insuficiencia también son medios: 6 valores de 20 puntos cada uno y 2 valores de 25 puntos cada uno.

Las poderosas capacidades del criterio φ* pueden verificarse confirmando una hipótesis completamente diferente al analizar los materiales de este ejemplo. Podemos demostrar, por ejemplo, que en un grupo con mayor energía de represión la tasa de insuficiencia es aún mayor, a pesar de la naturaleza paradójica de su distribución en este grupo.

Formulemos nuevas hipótesis.

h 0 Los valores más altos del índice de deficiencia (30 o más) en el grupo con mayor energía de represión no son más comunes que en el grupo con menor energía de represión.

h 1 : Los valores más altos del índice de deficiencia (30 o más) en el grupo con mayor energía de represión ocurren con más frecuencia que en el grupo con menos energía de represión. Construyamos una tabla de cuatro campos usando los datos de Tabla. 5.4.

Tabla 5.6

Tabla de cuatro celdas para calcular el criterio φ* al comparar grupos con mayor y menor energía de represión según el nivel de indicador de insuficiencia

Grupos	“Hay efecto”* el indicador de falla es mayor o igual a 30		“Sin efecto”: la tasa de fracaso es menor 30		Cantidades
Grupo 1 - con mayor energía de desplazamiento		(61,1%)		(38.9%)
Grupo 2 - con menor energía de desplazamiento		(25.0%)		(75.0%)
Cantidades

Según la tabla.XIIIEn el Apéndice 1 determinamos que este resultado corresponde al nivel de significancia de p = 0,008.

Respuesta: Pero es rechazado. Aceptadohj: Los indicadores más altos de deficiencia (30 o más puntos) en el grupo.Concon mayor energía de desplazamiento ocurren con mayor frecuencia que en el grupo con menor energía de desplazamiento (p = 0,008).

Entonces pudimos demostrar queVgrupoConcon una represión más enérgica predominan los valores extremos del indicador de insuficiencia, y el hecho de que este indicador supere sus valoresalcanzaexactamente en este grupo.

Ahora podríamos intentar demostrar que en el grupo con mayor energía de represión son más habituales valores más bajos del índice de insuficiencia, a pesar de que el valor medioV este grupo tiene más (26,11 versus 15,42 en el grupoCon menor desplazamiento).

Formulemos hipótesis.

h 0 : Tasas de deficiencia más bajas (cero) en el grupoCon Las represiones con mayor energía no son más comunes que en el grupo.Con menor energía de desplazamiento.

h 1 : Se producen las tasas más bajas de deficiencia (cero)V grupo con mayor energía de represión con mayor frecuencia que en el grupoCon represión menos enérgica. Agrupemos los datos en una nueva tabla de cuatro celdas.

Tabla 5.7

Tabla de cuatro celdas para comparar grupos con diferentes energías de represión según la frecuencia de valores cero del indicador de deficiencia

Grupos	"Hay un efecto": el indicador de falla es 0		"Ningún efecto" de la insuficiencia	el indicador no es igual a 0	Cantidades
Grupo 1 - con mayor energía de desplazamiento		(27,8%)		(72,2%)
1 grupo - con menos energía de desplazamiento		(8,3%)		(91,7%)
Cantidades

Determinamos los valores de φ y calculamos el valor de φ*:

Respuesta: h 0 rechazado. Los índices más bajos de insuficiencia (cero) en el grupo con mayor energía de represión son más comunes que en el grupo con menor energía de represión (p<0,05).

En total, los resultados obtenidos pueden considerarse como evidencia de una coincidencia parcial de los conceptos de complejo en S. Freud y A. Adler.

Es significativo que entre el indicador de energía de represión y el indicador de intensidad del sentimiento de insuficiencia propia en el conjunto de la muestra se obtuvo una correlación lineal positiva (p = +0,491, p<0,01). Как мы можем убедиться, применение критерия φ* позволяет проникнуть в более тонкие и содержательно значимые соотношения между этими двумя показателями.

Ejemplo 4: uso del criterio φ* en combinación con el criterio λ Kolmogorov-Smirnov para lograr el máximo precisoresultado

Si las muestras se comparan según indicadores medidos cuantitativamente, surge el problema de identificar el punto de distribución que puede usarse como punto crítico para dividir a todos los sujetos entre aquellos que “tienen un efecto” y aquellos que “no tienen un efecto”.

En principio, el punto en el que dividiríamos el grupo en subgrupos donde hay un efecto y donde no hay efecto puede elegirse de forma bastante arbitraria. Nos puede interesar cualquier efecto y, por tanto, podemos dividir ambas muestras en dos partes en cualquier momento, siempre que tenga algún sentido.

Sin embargo, para maximizar la potencia de la prueba φ*, es necesario seleccionar el punto en el que las diferencias entre los dos grupos comparados son mayores. Con mayor precisión, podemos hacer esto usando un algoritmo para calcular el criterio.λ , permitiéndole detectar el punto de máxima discrepancia entre dos muestras.

Posibilidad de combinar criterios φ* yλ descrito por E.V. Gubler (1978, págs. 85-88). Intentemos utilizar este método para resolver el siguiente problema.

En un estudio conjunto de M.A. Kurochkina, E.V. Sidorenko y Yu.A. Churakov (1992) en el Reino Unido realizó una encuesta entre médicos generales ingleses de dos categorías: a) médicos que apoyaban la reforma médica y ya habían convertido sus oficinas de recepción en organizaciones tenedoras de fondos con su propio presupuesto; b) los médicos cuyos consultorios aún no cuentan con fondos propios y están financiados íntegramente por el presupuesto estatal. Se enviaron cuestionarios a una muestra de 200 médicos, representativa de la población general de médicos ingleses en términos de representación de personas de diferente género, edad, antigüedad en el servicio y lugar de trabajo, en grandes ciudades o en provincias.

Respondieron al cuestionario 78 médicos, de los cuales 50 trabajaban en salas de espera con fondos y 28 en salas de espera sin fondos. Cada uno de los médicos tuvo que predecir cuál sería la proporción de ingresos con fondos para el próximo año, 1993. Sólo 70 médicos de 78 que enviaron respuestas respondieron a esta pregunta. La distribución de sus pronósticos se presenta en la Tabla. 5.8 por separado para el grupo de médicos con fondos y el grupo de médicos sin fondos.

¿Los pronósticos de los médicos con fondos y de los médicos sin fondos son diferentes en algún aspecto?

Tabla 5.8

Distribución de las previsiones de los médicos generales sobre cuál será la proporción de urgencias con fondos en 1993

Participación proyectada
salas de recepción con fondos	médicos con el fondo (norte 1 =45)	médicos sin fondo (norte 2 =25)	Cantidades
1. de 0 a 20%	4	5	9
2. del 21 al 40%	15	Y	26
3. del 41 al 60%	18	5	23
4. del 61 al 80%	7	4	Y
5. del 81 al 100%	1	0	1
Cantidades	45	25	70

Determinemos el punto de máxima discrepancia entre las dos distribuciones de respuesta utilizando el Algoritmo 15 de la cláusula 4.3 (ver Tabla 5.9).

Tabla 5.9

Cálculo de la diferencia máxima de frecuencias acumuladas en las distribuciones de pronósticos de médicos de dos grupos.

Proporción proyectada de admisiones con fondos (%)	Frecuencias empíricas de elección para una categoría de respuesta determinada		Frecuencias empíricas		Frecuencias empíricas acumuladas		Diferencia (d)
	doctores con el fondo(norte 1 =45)	médicos sin fondo (norte 2 =25)	F* oh 1	F* a2	∑F* e1	∑F* a1
1. de 0 a 20% 2. del 21 al 40% 3. del 41 al 60% 4. del 61 al 80% 5. del 81 al 100%	4 15 18 7 1	5 11 5 4 0	0,089 0,333 0,400 0,156 0,022	0,200 0,440 0,200 0,160 0	0,089 0,422 0,822 0,978 1,000	0,200 0,640 0,840 1,000 1,000	0111 0,218 0,018 0,022 0

La diferencia máxima detectada entre dos frecuencias empíricas acumuladas es0,218.

Esta diferencia resulta acumulada en la segunda categoría del pronóstico. Intentemos utilizar el límite superior de esta categoría como criterio para dividir ambas muestras en un subgrupo donde "hay un efecto" y un subgrupo donde "no hay efecto". Supondremos que hay un “efecto” si un determinado médico predice entre el 41 y el 100% de los ingresos con fondos en1993 año, y que no hay “ningún efecto” si un determinado médico predice del 0 al 40% de los ingresos con fondos en1993 año. Combinamos las categorías de pronóstico 1 y 2 por un lado, y las categorías de pronóstico 3, 4 y 5 por el otro. La distribución resultante de pronósticos se presenta en la Tabla. 5.10.

Tabla 5.10

Distribución de pronósticos para médicos con fondos y médicos sin fondos.

Proporción proyectada de admisiones con fondos (%1	Frecuencias empíricas para elegir una categoría de pronóstico determinada		Cantidades
	doctores con el fondo(norte 1 =45)	doctores sin fondo(norte 2 =25)
1. de 0 a 40%	19	16	35
2. del 41 al 100%	26	9	35
Cantidades	45	25	70

Podemos usar la tabla resultante (Tabla 5.10) para probar diferentes hipótesis comparando dos de sus celdas. Recordamos que se trata de la denominada tabla de cuatro celdas o de cuatro campos.

Aquí, nos interesa saber si los médicos que ya tienen fondos predicen un mayor crecimiento futuro de este movimiento que los médicos que no tienen fondos. Por lo tanto, consideramos condicionalmente que “hay un efecto” cuando el pronóstico cae en la categoría del 41 al 100%. Para simplificar los cálculos, ahora necesitamos girar la mesa 90°, girándola en el sentido de las agujas del reloj. Incluso puedes hacerlo literalmente girando el libro junto con la mesa. Ahora podemos pasar a la hoja de trabajo para calcular el criterio φ*: Transformada angular de Fisher.

Mesa 5.11

Tabla de cuatro celdas para calcular la prueba φ* de Fisher para identificar diferencias en los pronósticos de dos grupos de médicos generales

Grupo	Hay un efecto: pronóstico del 41 al 100%	Sin efecto - previsión de 0 a 40%	Total
Igrupo - médicos que tomaron el fondo	26 (57.8%)	19 (42.2%)	45
IIgrupo - médicos que no aceptaron el fondo	9 (36.0%)	16 (64.0%)	25
Total	35	35	70

Formulemos hipótesis.

h 0 : Proporción de personasPrediciendo la distribución de fondos al 41%-100% de todos los consultorios médicos, en el grupo de médicos con fondos no hay más que en el grupo de médicos sin fondos.

h 1 : La proporción de personas que predicen la distribución de los fondos hasta el 41%-100% de todas las admisiones es mayor en el grupo de médicos con fondos que en el grupo de médicos sin fondos.

Determinando los valores de φ 1 y φ 2 según tablaXIIApéndice 1. Recuerde que φ 1 es siempre el ángulo correspondiente al mayor porcentaje.

Ahora determinemos el valor empírico del criterio φ*:

Según la tabla.XIIIEn el Apéndice 1 determinamos a qué nivel de significancia corresponde este valor: p = 0,039.

Utilizando la misma tabla del Apéndice 1, se pueden determinar los valores críticos del criterio φ*:

Respuesta: Pero se rechaza (p=0,039). La proporción de personas que predicen la distribución de fondos a41-100 % de todas las recepciones en el grupo de médicos que tomaron el fondo excede esta proporción en el grupo de médicos que no tomaron el fondo.

En otras palabras, los médicos que ya trabajan en sus salas de espera con un presupuesto separado predicen una mayor difusión de esta práctica este año que los médicos que aún no han aceptado pasar a un presupuesto independiente. Hay múltiples interpretaciones de este resultado. Por ejemplo, se puede suponer que los médicos de cada grupo inconscientemente consideran que su comportamiento es más típico. Esto también puede significar que los médicos que ya han adoptado la autofinanciación tienden a exagerar el alcance de este movimiento, ya que necesitan justificar su decisión. Las diferencias identificadas también pueden significar algo que está completamente fuera del alcance de las preguntas planteadas en el estudio. Por ejemplo, que la actividad de los médicos que trabajan con un presupuesto independiente contribuye a agudizar las diferencias en las posiciones de ambos grupos. Fueron más activos cuando aceptaron recibir los fondos, fueron más activos cuando se tomaron la molestia de responder el cuestionario por correo; son más activos cuando predicen que otros médicos serán más activos a la hora de recibir fondos.

De una forma u otra, podemos estar seguros de que el nivel detectado de diferencias estadísticas es el máximo posible para estos datos reales. Establecimos usando el criterioλ el punto de máxima divergencia entre las dos distribuciones, y fue en este punto que las muestras se dividieron en dos partes.

Tu marca.

La función FISCHER devuelve la transformada de Fisher de los argumentos a X . Esta transformación produce una función que tiene una distribución normal en lugar de sesgada. La función FISCHER se utiliza para probar la hipótesis utilizando el coeficiente de correlación.

Descripción de la función FISCHER en Excel

Al trabajar con esta función, debe establecer el valor de la variable. Vale la pena señalar de inmediato que hay algunas situaciones en las que esta función no dará resultados. Esto es posible si la variable:

• no es un número. En tal situación, la función FISCHER devolverá el valor de error #¡VALOR!;
• tiene un valor menor que -1 o mayor que 1. En este caso, la función FISCHER devolverá el valor de error #¡NUM!.

La ecuación que se utiliza para describir matemáticamente la función FISCHER es:

Z"=1/2*ln(1+x)/(1-x)

Veamos el uso de esta función usando 3 ejemplos específicos.



Estimación de la relación entre ganancias y costos utilizando la función de FISHER

Ejemplo 1. Utilizando datos sobre la actividad de organizaciones comerciales, es necesario evaluar la relación entre las ganancias Y (millones de rublos) y los costos X (millones de rublos) utilizados para el desarrollo de productos (que se muestran en la Tabla 1).

Tabla 1 – Datos iniciales:

№	X	Y
1	210.000.000,00 rublos	95.000.000,00 rublos
2	1.068.000.000,00 rublos	76.000.000,00 rublos
3	1.005.000.000,00 rublos	78.000.000,00 rublos
4	610.000.000,00 rublos	89.000.000,00 rublos
5	768.000.000,00 rublos	77.000.000,00 rublos
6	799.000.000,00 rublos	85.000.000,00 rublos

El esquema para resolver tales problemas es el siguiente:

1. Calculado coeficiente lineal correlaciones r xy ;
2. La importancia del coeficiente de correlación lineal se comprueba mediante la prueba t de Student. En este caso, se plantea y prueba la hipótesis de que el coeficiente de correlación es igual a cero. El estadístico t se utiliza para probar esta hipótesis. Si se confirma la hipótesis, el estadístico t tiene una distribución de Student. Si el valor calculado t p > t cr, entonces se rechaza la hipótesis, lo que indica la significancia del coeficiente de correlación lineal y, por tanto, la significancia estadística de la relación entre X e Y;
3. Se determina una estimación de intervalo para un coeficiente de correlación lineal estadísticamente significativo.
4. Se determina una estimación de intervalo para el coeficiente de correlación lineal basándose en la transformada z de Fisher inversa;
5. Se calcula el error estándar del coeficiente de correlación lineal.

Los resultados de resolver este problema con las funciones utilizadas en Excel se muestran en la Figura 1.

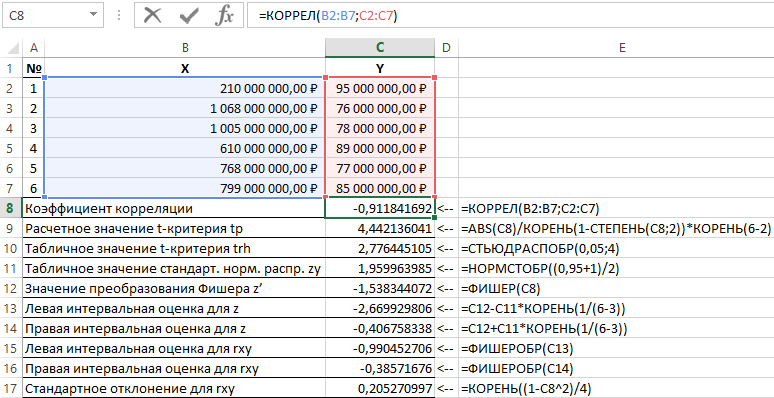
Figura 1 – Ejemplo de cálculos.

No.	Nombre del indicador	Fórmula de cálculo
1	Coeficiente de correlación	=CORRECCIÓN(B2:B7,C2:C7)
2	Valor de prueba t calculado tp	=ABS(C8)/SQRT(1-POWER(C8,2))*SQRT(6-2)
3	Valor de la tabla de la prueba t trh	= ESTUDIAR DESCUBRIR (0.05,4)
4	Valor de tabla del estándar. distribución normal zy	=SINVNORMA((0,95+1)/2)
5	Valor de transformación z de Fisher	=PESCADOR(C8)
6	Estimación del intervalo izquierdo para z	=C12-C11*RAÍZ(1/(6-3))
7	Estimación del intervalo derecho para z	=C12+C11*RAÍZ(1/(6-3))
8	Estimación del intervalo izquierdo para rxy	=PESCADORBR(C13)
9	Estimación del intervalo derecho para rxy	=PESCADORBR(C14)
10	Desviación estándar para rxy	=RAÍZ((1-C8^2)/4)

Así, con una probabilidad de 0,95, el coeficiente de correlación lineal se encuentra en el rango de (–0,386) a (–0,990) con un error estándar de 0,205.

Comprobación de la significancia estadística de la regresión utilizando la función MÁS RÁPIDO

Ejemplo 2: probar la significancia estadística de la ecuación regresión múltiple Utilizando la prueba F de Fisher, saque conclusiones.

Para comprobar la importancia de la ecuación en su conjunto, planteamos la hipótesis H 0 sobre la insignificancia estadística del coeficiente de determinación y la hipótesis opuesta H 1 sobre la importancia estadística del coeficiente de determinación:

H 1: R 2 ≠ 0.

Probemos las hipótesis utilizando la prueba F de Fisher. Los indicadores se muestran en la Tabla 2.

Tabla 2 - Datos iniciales

Para ello utilizamos la función en Excel:

MÁS RÁPIDO (α;p;n-p-1)

• α es la probabilidad asociada con una distribución dada;
• p y n son el numerador y denominador de los grados de libertad, respectivamente.

Sabiendo que α = 0,05, p = 2 y n = 53, obtenemos el siguiente valor para F crit (ver Figura 2).

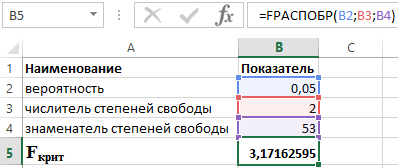
Figura 2 – Ejemplo de cálculos.

Así podemos decir que F calculado > F crítico. Como resultado, se acepta la hipótesis H 1 sobre la significancia estadística del coeficiente de determinación.

Calcular el valor del indicador de correlación en Excel.

Ejemplo 3. Utilizando datos de 23 empresas sobre: ​​X es el precio del producto A, en miles de rublos; Y es el beneficio de una empresa comercial, millones de rublos; se está estudiando su dependencia. Calificación Modelo de regresión dio lo siguiente: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. ¿Qué indicador de correlación se puede determinar a partir de estos datos? Calcule el valor del indicador de correlación y, utilizando el criterio de Fisher, saque una conclusión sobre la calidad del modelo de regresión.

Determinemos F crítico a partir de la expresión:

F calculado = R 2 /23*(1-R 2)

donde R es el coeficiente de determinación igual a 0,67.

Por tanto, el valor calculado F calc = 46.

Para determinar F crítico utilizamos la distribución de Fisher (ver Figura 3).

Figura 3 – Ejemplo de cálculos.

Por tanto, la estimación resultante de la ecuación de regresión es confiable.

La importancia de la ecuación de regresión múltiple en su conjunto, así como en la regresión pareada, se evalúa mediante el criterio de Fisher:

, (2.22)

Dónde
– factor suma de cuadrados por grado de libertad;
– suma residual de cuadrados por grado de libertad;
– coeficiente (índice) de determinación múltiple;
– número de parámetros para variables (V regresión lineal coincide con el número de factores incluidos en el modelo); – número de observaciones.

Se evalúa la importancia no sólo de la ecuación en su conjunto, sino también del factor incluido adicionalmente en el modelo de regresión. La necesidad de tal evaluación se debe al hecho de que no todos los factores incluidos en el modelo pueden aumentar significativamente la proporción de variación explicada en el rasgo resultante. Además, si hay varios factores en el modelo, se pueden ingresar en el modelo en diferentes secuencias. Debido a la correlación entre factores, la importancia de un mismo factor puede ser diferente dependiendo de la secuencia de su introducción en el modelo. La medida para evaluar la inclusión de un factor en el modelo es el precio privado
-criterio, es decir .

Privado
-El criterio se basa en comparar el aumento en la varianza del factor debido a la influencia de un factor incluido adicionalmente con la varianza residual por un grado de libertad para el modelo de regresión en su conjunto. EN vista general por factor privado
-el criterio se determinará como

, (2.23)

Dónde
– coeficiente de determinación múltiple para un modelo con un conjunto completo de factores,
– el mismo indicador, pero sin incluir el factor en el modelo ,– número de observaciones,
– número de parámetros en el modelo (sin término libre).

Valor real del cociente
- el criterio se compara con la tabla en el nivel de significancia
y número de grados de libertad: 1 y
. Si el valor real excede
, entonces la inclusión adicional del factor en el modelo está estadísticamente justificado y el coeficiente de regresión pura en factor Estadísticamente significante. Si el valor real es menor que el valor de la tabla, entonces inclusión adicional del factor en el modelo no aumenta significativamente la proporción de variación explicada en un rasgo , por lo tanto, no resulta apropiado incluirlo en el modelo; El coeficiente de regresión para este factor en este caso es estadísticamente insignificante.

Para una ecuación de dos factores, los cocientes
-los criterios tienen la forma:

,
. (2.23a)

Usando privado
-criterio, se puede verificar la significancia de todos los coeficientes de regresión bajo el supuesto de que cada factor correspondiente ingresado en último lugar en la ecuación de regresión múltiple.

-Prueba de Student para ecuación de regresión múltiple.

Privado
-El criterio evalúa la importancia de los coeficientes de regresión pura. Conociendo la magnitud , es posible determinar -criterio para el coeficiente de regresión en -factor m, , a saber:

. (2.24)

Evaluación de la importancia de los coeficientes de regresión pura mediante -La prueba t de Student se puede realizar sin calcular el parcial
-criterios. En este caso, como en la regresión por pares, se utiliza la fórmula para cada factor:

, (2.25)

Dónde – coeficiente de regresión puro en el factor ,– error cuadrático medio (estándar) del coeficiente de regresión .

Para una ecuación de regresión múltiple, el error cuadrático medio del coeficiente de regresión se puede determinar mediante la siguiente fórmula:

, (2.26)

Dónde ,– desviación estándar de la característica ,
– coeficiente de determinación de la ecuación de regresión múltiple,
– coeficiente de determinación de la dependencia del factor con todos los demás factores de la ecuación de regresión múltiple;
– número de grados de libertad para la suma residual de las desviaciones al cuadrado.

Como puede ver, para utilizar esta fórmula, necesita una matriz de correlación interfactorial y el cálculo de los coeficientes de determinación correspondientes con ella.
. Entonces, para la ecuación
Evaluación de la importancia de los coeficientes de regresión. ,,Implica el cálculo de tres coeficientes de determinación interfactorial:
,
,
.

La relación entre los indicadores del coeficiente de correlación parcial, parcial.
-criterios y -La prueba t de Student para coeficientes de regresión pura se puede utilizar en el procedimiento de selección de factores. La eliminación de factores al construir una ecuación de regresión mediante el método de eliminación prácticamente se puede realizar no solo mediante coeficientes de correlación parcial, excluyendo en cada paso el factor con el valor más pequeño e insignificante del coeficiente de correlación parcial, sino también mediante valores. Y . Privado
-El criterio se usa ampliamente al construir un modelo utilizando el método de inclusión de variables y el método de regresión por pasos.