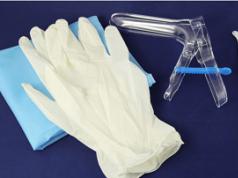
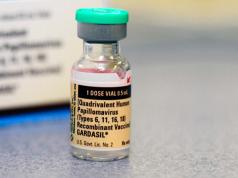
Pieņemsim, ka Ahillejs skrien desmit reizes ātrāk nekā bruņurupucis un ir tūkstoš soļu aiz tā. Laikā, kas nepieciešams Ahillam, lai noskrietu šo distanci, bruņurupucis rāpos simts soļus tajā pašā virzienā. Kad Ahillejs noskrien simts soļus, bruņurupucis rāpo vēl desmit soļus utt. Process turpināsies bezgalīgi, Ahillejs nekad nepanāks bruņurupuci.
Šī argumentācija kļuva par loģisku šoku visām nākamajām paaudzēm. Aristotelis, Diogēns, Kants, Hēgelis, Hilberts... Viņi visi tā vai citādi uzskatīja Zenona aporiju. Šoks bija tik spēcīgs, ka " ...diskusijas turpinās līdz pat šai dienai, lai panāktu vienotu viedokli par paradoksu būtību zinātnieku kopiena līdz šim tas nav bijis iespējams... bijām iesaistīti jautājuma izpētē matemātiskā analīze, kopu teorija, jaunas fizikālās un filozofiskās pieejas; neviens no tiem nekļuva par vispārpieņemtu problēmas risinājumu..."[Wikipedia, "Zeno's Aporia". Visi saprot, ka tiek muļķoti, bet neviens nesaprot, no kā sastāv maldināšana.
No matemātikas viedokļa Zenons savā aporijā skaidri demonstrēja pāreju no kvantitātes uz . Šī pāreja nozīmē piemērošanu, nevis pastāvīgus. Cik es saprotu, matemātiskais aparāts mainīgo mērvienību izmantošanai vai nu vēl nav izstrādāts, vai arī tas nav piemērots Zenona aporijai. Pielietojot mūsu ierasto loģiku, mēs nonākam slazdā. Mēs, pateicoties domāšanas inercei, abpusējai vērtībai piemērojam nemainīgas laika vienības. No fiziskā viedokļa tas izskatās pēc laika palēnināšanās, līdz tas pilnībā apstājas brīdī, kad Ahillejs panāk bruņurupuci. Ja laiks apstājas, Ahillejs vairs nevar apsteigt bruņurupuci.
Ja pagriežam savu ierasto loģiku otrādi, viss nostājas savās vietās. Ahillejs skrien ar nemainīgs ātrums. Katrs nākamais viņa ceļa posms ir desmit reizes īsāks nekā iepriekšējais. Attiecīgi tās pārvarēšanai pavadītais laiks ir desmit reizes mazāks nekā iepriekšējā. Ja šajā situācijā pielietojam jēdzienu “bezgalība”, tad būtu pareizi teikt: “Ahillejs bezgalīgi ātri panāks bruņurupuci”.
Kā izvairīties no šīs loģiskās lamatas? Palieciet nemainīgās laika vienībās un nepārslēdzieties uz abpusējām vienībām. Zenona valodā tas izskatās šādi:
Laikā, kas vajadzīgs Ahillam, lai noskrietu tūkstoš soļu, bruņurupucis rāpos simts soļus tajā pašā virzienā. Nākamajā laika intervālā, kas vienāds ar pirmo, Ahillejs noskrien vēl tūkstoš soļu, un bruņurupucis rāpos simts soļus. Tagad Ahillejs ir astoņsimt soļu priekšā bruņurupucim.
Šī pieeja adekvāti apraksta realitāti bez jebkādiem loģiskiem paradoksiem. Bet tā nav pilnīgs risinājums Problēmas. Einšteina apgalvojums par gaismas ātruma neatvairāmību ir ļoti līdzīgs Zenona aporijai “Ahillejs un bruņurupucis”. Mums šī problēma vēl ir jāpēta, jāpārdomā un jāatrisina. Un risinājums jāmeklē nevis bezgala lielos skaitļos, bet mērvienībās.
Vēl viena interesanta Zenona aporija stāsta par lidojošu bultu:
Lidojoša bulta ir nekustīga, jo tā atrodas miera stāvoklī katrā laika brīdī, un, tā kā tā atrodas miera stāvoklī, tā vienmēr atrodas miera stāvoklī.
Šajā aporijā loģiskais paradokss tiek pārvarēts ļoti vienkārši - pietiek precizēt, ka katrā laika brīdī dažādos telpas punktos atrodas lidojoša bulta, kas patiesībā ir kustība. Šeit ir jāatzīmē vēl viens punkts. No vienas automašīnas fotogrāfijas uz ceļa nav iespējams noteikt ne tās kustības faktu, ne attālumu līdz tai. Lai noteiktu, vai automašīna pārvietojas, ir nepieciešamas divas fotogrāfijas, kas uzņemtas no viena un tā paša punkta dažādos laika punktos, taču jūs nevarat noteikt attālumu no tām. Lai noteiktu attālumu līdz automašīnai, ir nepieciešamas divas fotogrāfijas, kas vienā brīdī uzņemtas no dažādiem telpas punktiem, bet no tām nevar noteikt kustības faktu (protams, joprojām ir nepieciešami papildu dati aprēķiniem, trigonometrija jums palīdzēs ). Uz ko vēlos norādīt Īpaša uzmanība, ir tas, ka divi punkti laikā un divi punkti telpā ir dažādas lietas, kuras nevajadzētu jaukt, jo tās sniedz dažādas izpētes iespējas.
Trešdiena, 2018. gada 4. jūlijs
Atšķirības starp kopu un multikopu ir ļoti labi aprakstītas Vikipēdijā. Paskatīsimies.
Kā redzat, “kopā nevar būt divi identiski elementi”, bet, ja komplektā ir identiski elementi, šādu kopu sauc par “multisetu”. Saprātīgas būtnes nekad nesapratīs tik absurdu loģiku. Tas ir runājošu papagaiļu un apmācītu pērtiķu līmenis, kuriem nav saprāta no vārda “pilnīgi”. Matemātiķi darbojas kā parasti pasniedzēji, sludinot mums savas absurdās idejas.
Kādreiz tiltu būvējušie inženieri, testējot tiltu, atradās laivā zem tilta. Ja tilts sabruka, viduvējais inženieris nomira zem viņa radītajām drupām. Ja tilts varēja izturēt slodzi, talantīgais inženieris uzbūvēja citus tiltus.
Neatkarīgi no tā, kā matemātiķi slēpjas aiz frāzes "piedomājiet pie manis, es esmu mājā" vai, pareizāk sakot, "matemātika pēta abstraktus jēdzienus", ir viena nabassaite, kas tos nesaraujami saista ar realitāti. Šī nabassaite ir nauda. Piemērojams matemātiskā teorija kopas pašiem matemātiķiem.
Ļoti labi mācījāmies matemātiku un tagad sēžam pie kases, izsniedzam algas. Tātad matemātiķis nāk pie mums par savu naudu. Mēs viņam noskaitām visu summu un izklājam uz sava galda dažādās kaudzēs, kurās ievietojam viena un tā paša nomināla banknotes. Pēc tam mēs paņemam vienu rēķinu no katras kaudzes un dodam matemātiķim viņa "matemātisko algas kopu". Paskaidrosim matemātiķim, ka atlikušos rēķinus viņš saņems tikai tad, kad pierādīs, ka kopa bez identiskiem elementiem nav vienāda ar kopu ar identiskiem elementiem. Šeit sākas jautrība.
Pirmkārt, derēs deputātu loģika: “Uz citiem to var attiecināt, bet uz mani nē!” Tad viņi sāks mūs pārliecināt, ka viena un tā paša nomināla vekseļiem ir dažādi vekseļu numuri, kas nozīmē, ka tos nevar uzskatīt par vienādiem elementiem. Labi, skaitīsim algas monētās – uz monētām nav skaitļu. Šeit matemātiķis sāks izmisīgi atcerēties fiziku: dažādās monētās ir atšķirīgs netīrumu daudzums, kristāla struktūra un atomu izvietojums katrai monētai ir unikāls...
Un tagad man ir interesantākais jautājums: kur ir tā robeža, aiz kuras multikopas elementi pārvēršas par kopas elementiem un otrādi? Tāda līnija neeksistē – visu izlemj šamaņi, zinātne te pat ne tuvu nemelo.
Apskatīt šeit. Mēs izvēlamies futbola stadioni ar tādu pašu lauka laukumu. Lauku platības ir vienādas – tas nozīmē, ka mums ir multikopa. Bet, ja paskatāmies uz šo pašu stadionu nosaukumiem, sanāk daudz, jo nosaukumi ir dažādi. Kā redzat, viena un tā pati elementu kopa ir gan kopa, gan multikopa. Kura ir pareiza? Un te matemātiķis-šamanis-sharpis izvelk no piedurknes trumpju dūzi un sāk mums stāstīt vai nu par setu, vai par multisetu. Jebkurā gadījumā viņš mūs pārliecinās, ka viņam ir taisnība.
Lai saprastu, kā mūsdienu šamaņi darbojas ar kopu teoriju, saistot to ar realitāti, pietiek atbildēt uz vienu jautājumu: kā vienas kopas elementi atšķiras no citas kopas elementiem? Es jums parādīšu bez "iedomājams kā viens veselums" vai "nav iedomājams kā vienots veselums".
Svētdiena, 2018. gada 18. marts
Skaitļa ciparu summa ir šamaņu deja ar tamburīnu, kam nav nekāda sakara ar matemātiku. Jā, matemātikas stundās mums māca atrast skaitļa ciparu summu un to izmantot, bet tāpēc viņi ir šamaņi, lai mācītu saviem pēcnācējiem prasmes un gudrību, pretējā gadījumā šamaņi vienkārši izmirs.
Vai jums ir nepieciešams pierādījums? Atveriet Wikipedia un mēģiniet atrast lapu "Ciparu ciparu summa". Viņa neeksistē. Matemātikā nav formulas, ar kuru var atrast jebkura skaitļa ciparu summu. Galu galā skaitļi ir grafiski simboli, ar kuriem mēs rakstām skaitļus, un matemātikas valodā uzdevums izklausās šādi: "Atrodiet grafisko simbolu summu, kas attēlo jebkuru skaitli." Matemātiķi nevar atrisināt šo problēmu, bet šamaņi to var viegli izdarīt.
Izdomāsim, ko un kā mēs darām, lai atrastu dotā skaitļa ciparu summu. Tātad, pieņemsim skaitli 12345. Kas jādara, lai atrastu šī skaitļa ciparu summu? Apsvērsim visas darbības secībā.
1. Uzrakstiet numuru uz papīra lapas. Ko mēs esam izdarījuši? Mēs esam pārveidojuši skaitli grafiskā skaitļa simbolā. Šī nav matemātiska darbība.
2. Mēs sagriežam vienu iegūto attēlu vairākos attēlos, kas satur atsevišķus skaitļus. Attēla izgriešana nav matemātiska darbība.
3. Pārvērtiet atsevišķus grafiskos simbolus skaitļos. Šī nav matemātiska darbība.
4. Pievienojiet iegūtos skaitļus. Tagad tā ir matemātika.
Skaitļa 12345 ciparu summa ir 15. Tie ir “griešanas un šūšanas kursi”, kurus māca šamaņi un kurus izmanto matemātiķi. Bet tas vēl nav viss.
No matemātiskā viedokļa nav nozīmes, kurā skaitļu sistēmā rakstām skaitli. Tātad, iekšā dažādas sistēmas Aprēķinos viena un tā paša skaitļa ciparu summa būs atšķirīga. Matemātikā skaitļu sistēma tiek norādīta kā apakšindekss pa labi no skaitļa. AR liels skaits 12345 Negribu mānīt galvu, paskatīsimies uz ciparu 26 no raksta par . Rakstīsim šo skaitli binārā, oktālā, decimālā un heksadecimālā skaitļu sistēmā. Mēs neskatīsimies uz katru soli mikroskopā; mēs to jau esam izdarījuši. Apskatīsim rezultātu.
Kā redzat, dažādās skaitļu sistēmās viena un tā paša skaitļa ciparu summa ir atšķirīga. Šim rezultātam nav nekāda sakara ar matemātiku. Tas ir tāpat kā, ja jūs noteiktu taisnstūra laukumu metros un centimetros, jūs iegūtu pilnīgi atšķirīgus rezultātus.
Nulle visās skaitļu sistēmās izskatās vienādi, un tai nav ciparu summas. Tas ir vēl viens arguments par labu tam, ka. Jautājums matemātiķiem: kā matemātikā tiek apzīmēts kaut kas, kas nav skaitlis? Matemātiķiem nekas neeksistē, izņemot skaitļus? Es to varu atļauties šamaņiem, bet ne zinātniekiem. Realitāte nav tikai skaitļi.
Iegūtais rezultāts jāuzskata par pierādījumu tam, ka skaitļu sistēmas ir skaitļu mērvienības. Galu galā mēs nevaram salīdzināt skaitļus ar dažādām mērvienībām. Ja vienas un tās pašas darbības ar dažādām viena un tā paša lieluma mērvienībām noved pie dažādiem rezultātiem pēc to salīdzināšanas, tad tam nav nekāda sakara ar matemātiku.
Kas ir īstā matemātika? Tas ir tad, kad matemātiskas darbības rezultāts nav atkarīgs no skaitļa lieluma, izmantotās mērvienības un no tā, kurš šo darbību veic.
Ak! Vai šī nav sieviešu tualete?
- Jauna sieviete! Šī ir laboratorija dvēseļu indefiliskā svētuma izpētei to pacelšanās debesīs laikā! Halo virsū un bulta uz augšu. Kāda vēl tualete?
Sieviete... Oreols augšpusē un bultiņa uz leju ir vīriešu kārtas.
Ja šāds dizaina mākslas darbs jūsu acu priekšā pazib vairākas reizes dienā,
Tad nav pārsteidzoši, ka pēkšņi savā automašīnā atrodat dīvainu ikonu:
Es personīgi cenšos saskatīt mīnus četrus grādus kakājošā cilvēkā (viena bilde) (vairāku bilžu kompozīcija: mīnusa zīme, cipars četri, grādu apzīmējums). Un es nedomāju, ka šī meitene ir muļķe, kas nezina fiziku. Viņai vienkārši ir spēcīgs stereotips par grafisko attēlu uztveri. Un matemātiķi mums to visu laiku māca. Šeit ir piemērs.
1A nav “mīnus četri grādi” vai “viens a”. Tas ir "kakājošs cilvēks" vai skaitlis "divdesmit seši" heksadecimālajā apzīmējumā. Tie cilvēki, kuri pastāvīgi strādā šajā ciparu sistēmā, automātiski uztver ciparu un burtu kā vienu grafisku simbolu.
Šajā video mēs analizēsim veselu lineāro vienādojumu kopu, kas tiek atrisinātas, izmantojot vienu un to pašu algoritmu - tāpēc tos sauc par vienkāršākajiem.
Pirmkārt, definēsim: kas ir lineārais vienādojums un kuru no tiem sauc par vienkāršāko?
Lineārs vienādojums ir tāds, kurā ir tikai viens mainīgais un tikai līdz pirmajai pakāpei.
Vienkāršākais vienādojums nozīmē konstrukciju:
Visi pārējie lineārie vienādojumi tiek reducēti līdz vienkāršākajiem, izmantojot algoritmu:
- Izvērsiet iekavas, ja tādas ir;
- Pārvietot terminus, kas satur mainīgo uz vienu vienādības zīmes pusi, un terminus bez mainīgā uz otru;
- Dodiet līdzīgus terminus pa kreisi un pa labi no vienādības zīmes;
- Sadaliet iegūto vienādojumu ar mainīgā $x$ koeficientu.
Protams, šis algoritms ne vienmēr palīdz. Fakts ir tāds, ka dažkārt pēc visām šīm mahinācijām mainīgā $x$ koeficients izrādās vienāds ar nulli. Šajā gadījumā ir iespējamas divas iespējas:
- Vienādojumam vispār nav atrisinājumu. Piemēram, kad izrādās kaut kas līdzīgs $0\cdot x=8$, t.i. kreisajā pusē ir nulle, bet labajā pusē ir skaitlis, kas nav nulle. Tālāk esošajā videoklipā apskatīsim vairākus iemeslus, kāpēc šāda situācija ir iespējama.
- Risinājums ir visi skaitļi. Vienīgais gadījums, kad tas ir iespējams, ir tad, kad vienādojums ir reducēts līdz konstrukcijai $0\cdot x=0$. Diezgan loģiski, ka neatkarīgi no tā, kādu $x$ mēs aizstātu, tomēr izrādīsies “nulle ir vienāda ar nulli”, t.i. pareiza skaitliskā vienādība.
Tagad redzēsim, kā tas viss darbojas, izmantojot reālas dzīves piemērus.
Vienādojumu risināšanas piemēri
Šodien mums ir darīšana ar lineāriem vienādojumiem un tikai visvienkāršākajiem. Kopumā lineārais vienādojums nozīmē jebkuru vienādību, kas satur tieši vienu mainīgo, un tas attiecas tikai uz pirmo pakāpi.
Šādas konstrukcijas tiek atrisinātas aptuveni tādā pašā veidā:
- Pirmkārt, jums ir jāpaplašina iekavas, ja tādas ir (kā mūsu pēdējā piemērā);
- Pēc tam apvienojiet līdzīgus
- Visbeidzot, izolējiet mainīgo, t.i. pārvietot visu, kas saistīts ar mainīgo — terminus, kuros tas ir ietverts — uz vienu pusi, un visu, kas paliek bez tā, uz otru pusi.
Tad, kā likums, katrā iegūtās vienādības pusē ir jāienes līdzīgi, un pēc tam atliek tikai dalīt ar koeficientu “x”, un mēs saņemsim galīgo atbildi.
Teorētiski tas izskatās skaisti un vienkārši, bet praksē pat pieredzējuši vidusskolēni var pieļaut aizvainojošas kļūdas diezgan vienkāršās lineārie vienādojumi. Parasti kļūdas tiek pieļautas, atverot iekavas vai aprēķinot “plusi” un “mīnusus”.
Turklāt gadās, ka lineāram vienādojumam vispār nav atrisinājumu vai arī risinājums ir visa skaitļa līnija, t.i. jebkurš skaitlis. Šīs smalkumus aplūkosim šodienas nodarbībā. Bet mēs sāksim, kā jūs jau sapratāt, ar pašu vienkāršus uzdevumus.
Vienkāršu lineāru vienādojumu risināšanas shēma
Pirmkārt, ļaujiet man vēlreiz uzrakstīt visu shēmu vienkāršāko lineāro vienādojumu risināšanai:
- Paplašiniet iekavas, ja tādas ir.
- Mēs izdalām mainīgos, t.i. Mēs pārvietojam visu, kas satur “X”, uz vienu pusi un visu bez “X” uz otru.
- Mēs piedāvājam līdzīgus terminus.
- Mēs visu sadalām ar koeficientu “x”.
Protams, šī shēma ne vienmēr darbojas, tajā ir daži smalkumi un triki, un tagad mēs tos iepazīsim.
Vienkāršu lineāro vienādojumu reālu piemēru risināšana
Uzdevums Nr.1
Pirmajā solī mums ir jāatver iekavas. Bet tie nav šajā piemērā, tāpēc mēs izlaižam šo soli. Otrajā solī mums ir jāizolē mainīgie. Lūdzu, ņemiet vērā: mēs runājam tikai par atsevišķiem noteikumiem. Pierakstīsim to:
Mēs piedāvājam līdzīgus terminus kreisajā un labajā pusē, taču tas jau ir izdarīts šeit. Tāpēc mēs pārejam uz ceturto soli: dala ar koeficientu:
\[\frac(6x)(6)=-\frac(72)(6)\]
Tātad mēs saņēmām atbildi.
Uzdevums Nr.2
Šajā uzdevumā mēs varam redzēt iekavas, tāpēc paplašināsim tās:
Gan pa kreisi, gan pa labi redzam aptuveni vienādu dizainu, bet rīkosimies pēc algoritma, t.i. atdalot mainīgos:
Šeit ir daži līdzīgi:
Pie kādām saknēm tas darbojas? Atbilde: jebkuram. Tāpēc mēs varam rakstīt, ka $x$ ir jebkurš skaitlis.
Uzdevums Nr.3
Trešais lineārais vienādojums ir interesantāks:
\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]
Šeit ir vairākas iekavas, bet tās nav reizinātas ar neko, vienkārši pirms tām ir dažādas zīmes. Sadalīsim tos:
Mēs veicam otro mums jau zināmo soli:
\[-x+x+2x=15-6-12+3\]
Aprēķināsim:
Mēs veicam pēdējo soli - visu sadalām ar koeficientu “x”:
\[\frac(2x)(x)=\frac(0)(2)\]
Lietas, kas jāatceras, risinot lineāros vienādojumus
Ja mēs ignorējam pārāk vienkāršus uzdevumus, es gribētu teikt sekojošo:
- Kā jau teicu iepriekš, ne katram lineārajam vienādojumam ir risinājums - dažreiz vienkārši nav sakņu;
- Pat ja ir saknes, starp tām var būt nulle - tur nav nekā slikta.
Nulle ir tāds pats skaitlis kā citi; jums nevajadzētu to nekādā veidā diskriminēt vai pieņemt, ka, ja jūs saņemat nulle, tad esat izdarījis kaut ko nepareizi.
Vēl viena iezīme ir saistīta ar kronšteinu atvēršanu. Lūdzu, ņemiet vērā: ja priekšā ir “mīnuss”, mēs to noņemam, bet iekavās mainām zīmes uz pretī. Un tad mēs varam to atvērt, izmantojot standarta algoritmus: mēs iegūsim to, ko redzējām iepriekš minētajos aprēķinos.
Izpratne par šo vienkāršo faktu palīdzēs izvairīties no stulbām un sāpinošām kļūdām vidusskolā, kad šādas lietas tiek uzskatītas par pašsaprotamām.
Sarežģītu lineāro vienādojumu risināšana
Pāriesim pie sarežģītākiem vienādojumiem. Tagad konstrukcijas kļūs sarežģītākas un, veicot dažādas transformācijas, parādīsies kvadrātiskā funkcija. Tomēr mums no tā nav jābaidās, jo, ja saskaņā ar autora plānu mēs risinām lineāru vienādojumu, tad transformācijas procesā noteikti tiks atcelti visi monomi, kas satur kvadrātfunkciju.
Piemērs Nr.1
Acīmredzot pirmais solis ir kronšteinu atvēršana. Darīsim to ļoti uzmanīgi:
Tagad apskatīsim privātumu:
\[-x+6((x)^(2))-6((x)^(2))+x=-12\]
Šeit ir daži līdzīgi:
Acīmredzot šim vienādojumam nav atrisinājumu, tāpēc mēs to rakstīsim atbildē:
\[\varnothing\]
vai arī nav sakņu.
Piemērs Nr.2
Mēs veicam tādas pašas darbības. Pirmais solis:
Pārvietosim visu ar mainīgo pa kreisi un bez tā - pa labi:
Šeit ir daži līdzīgi:
Acīmredzot šim lineārajam vienādojumam nav risinājuma, tāpēc mēs to rakstīsim šādi:
\[\varnothing\],
vai arī nav sakņu.
Risinājuma nianses
Abi vienādojumi ir pilnībā atrisināti. Izmantojot šīs divas izteiksmes kā piemēru, mēs vēlreiz pārliecinājāmies, ka pat visvienkāršākajos lineārajos vienādojumos viss var nebūt tik vienkārši: var būt vai nu viena, vai neviena, vai bezgalīgi daudz sakņu. Mūsu gadījumā mēs izskatījām divus vienādojumus, abiem vienkārši nav sakņu.
Bet es vēlos vērst jūsu uzmanību uz vēl vienu faktu: kā strādāt ar iekavām un kā tās atvērt, ja priekšā ir mīnusa zīme. Apsveriet šo izteiksmi:
Pirms atvēršanas viss jāreizina ar “X”. Lūdzu, ņemiet vērā: reizina katru atsevišķu terminu. Iekšpusē ir divi termini - attiecīgi divi termini un reizināts.
Un tikai pēc tam, kad ir pabeigtas šīs it kā elementārās, bet ļoti svarīgās un bīstamās pārvērtības, jūs varat atvērt kronšteinu no tā viedokļa, ka aiz tā ir mīnusa zīme. Jā, jā: tikai tagad, kad transformācijas ir pabeigtas, atceramies, ka iekavās priekšā ir mīnusa zīme, kas nozīmē, ka viss zemāk vienkārši maina zīmes. Tajā pašā laikā pazūd paši kronšteini un, pats galvenais, pazūd arī priekšējais "mīnuss".
Mēs darām to pašu ar otro vienādojumu:
Ne jau nejauši es pievēršu uzmanību šiem mazajiem, šķietami nenozīmīgajiem faktiem. Jo vienādojumu risināšana vienmēr ir elementāru pārveidojumu secība, kur nespēja skaidri un kompetenti veikt vienkāršas darbības noved pie tā, ka vidusskolēni nāk pie manis un atkal mācās risināt tik vienkāršus vienādojumus.
Protams, pienāks diena, kad šīs prasmes noslīpēsi līdz automātismam. Jums vairs nebūs katru reizi jāveic tik daudz pārveidojumu, jūs visu uzrakstīsit vienā rindā. Bet, kamēr jūs tikai mācāties, jums ir jāraksta katra darbība atsevišķi.
Vēl sarežģītāku lineāro vienādojumu risināšana
To, ko mēs tagad risināsim, diez vai var saukt par vienkāršāko uzdevumu, bet nozīme paliek nemainīga.
Uzdevums Nr.1
\[\kreisais(7x+1\labais)\kreisais(3x-1\labais)-21((x)^(2))=3\]
Sareizināsim visus elementus pirmajā daļā:
Padarīsim dažus privātuma pasākumus:
Šeit ir daži līdzīgi:
Pabeigsim pēdējo darbību:
\[\frac(-4x)(4)=\frac(4)(-4)\]
Šeit ir mūsu galīgā atbilde. Un, neskatoties uz to, ka risināšanas procesā mums bija koeficienti ar kvadrātfunkciju, tie viens otru atcēla, kas padara vienādojumu lineāru, nevis kvadrātisku.
Uzdevums Nr.2
\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]
Uzmanīgi veiksim pirmo soli: reiziniet katru elementu no pirmās iekavas ar katru elementu no otrās. Pēc pārveidojumiem vajadzētu būt pavisam četriem jauniem terminiem:
Tagad rūpīgi veiksim reizināšanu katrā terminā:
Pārvietosim terminus ar “X” pa kreisi un tos, kuriem nav – pa labi:
\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]
Šeit ir līdzīgi termini:
Atkal esam saņēmuši galīgo atbildi.
Risinājuma nianses
Vissvarīgākā piezīme par šiem diviem vienādojumiem ir šāda: tiklīdz mēs sākam reizināt iekavas, kas satur vairāk nekā vienu terminu, tas tiek darīts saskaņā ar šādu noteikumu: mēs ņemam pirmo vārdu no pirmā un reizinām ar katru elementu no otrais; tad ņemam otro elementu no pirmā un līdzīgi reizinām ar katru elementu no otrā. Rezultātā mums būs četri termiņi.
Par algebrisko summu
Ar šo pēdējo piemēru es vēlētos studentiem atgādināt, kas ir algebriskā summa. Klasiskajā matemātikā ar $1-7$ mēs domājam vienkāršu konstrukciju: no viena atņemiet septiņus. Algebrā ar to mēs saprotam sekojošo: skaitlim “viens” pievienojam citu skaitli, proti, “mīnus septiņi”. Tādējādi algebriskā summa atšķiras no parastās aritmētiskās summas.
Tiklīdz, veicot visas transformācijas, katru saskaitīšanu un reizināšanu, jūs sākat redzēt konstrukcijas, kas līdzīgas iepriekš aprakstītajām, jums vienkārši nebūs problēmu algebrā, strādājot ar polinomiem un vienādojumiem.
Visbeidzot, apskatīsim vēl dažus piemērus, kas būs vēl sarežģītāki par tiem, kurus mēs tikko apskatījām, un, lai tos atrisinātu, mums būs nedaudz jāpaplašina mūsu standarta algoritms.
Vienādojumu risināšana ar daļskaitļiem
Lai atrisinātu šādus uzdevumus, mums mūsu algoritmam būs jāpievieno vēl viens solis. Bet vispirms ļaujiet man jums atgādināt mūsu algoritmu:
- Atveriet kronšteinus.
- Atsevišķi mainīgie.
- Ņemiet līdzi līdzīgus.
- Sadaliet ar attiecību.
Diemžēl šis brīnišķīgais algoritms, neskatoties uz visu tā efektivitāti, izrādās ne visai piemērots, ja mums priekšā ir daļskaitļi. Un tajā, ko mēs redzēsim tālāk, mums abos vienādojumos ir daļa gan kreisajā, gan labajā pusē.
Kā šajā gadījumā strādāt? Jā, tas ir ļoti vienkārši! Lai to izdarītu, algoritmam jāpievieno vēl viens solis, ko var veikt gan pirms, gan pēc pirmās darbības, proti, atbrīvošanās no daļskaitļiem. Tātad algoritms būs šāds:
- Atbrīvojieties no frakcijām.
- Atveriet kronšteinus.
- Atsevišķi mainīgie.
- Ņemiet līdzi līdzīgus.
- Sadaliet ar attiecību.
Ko nozīmē “atbrīvoties no frakcijām”? Un kāpēc to var izdarīt gan pēc, gan pirms pirmā standarta soļa? Faktiski mūsu gadījumā visas daļskaitļi savā saucējā ir skaitliski, t.i. Visur saucējs ir tikai skaitlis. Tāpēc, ja mēs reizinām abas vienādojuma puses ar šo skaitli, mēs atbrīvosimies no daļām.
Piemērs Nr.1
\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]
Atbrīvosimies no daļām šajā vienādojumā:
\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]
Lūdzu, ņemiet vērā: viss tiek reizināts ar “četri”, t.i. tas, ka jums ir divas iekavas, nenozīmē, ka jums katra no tām ir jāreizina ar "četri". Pierakstīsim:
\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]
Tagad paplašināsim:
Mēs izslēdzam mainīgo:
Mēs veicam līdzīgu terminu samazināšanu:
\[-4x=-1\left| :\left(-4 \right) \right.\]
\[\frac(-4x)(-4)=\frac(-1)(-4)\]
Mēs saņēmām gala lēmums, pāriesim pie otrā vienādojuma.
Piemērs Nr.2
\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]
Šeit mēs veicam visas tās pašas darbības:
\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]
\[\frac(4x)(4)=\frac(4)(4)\]
Problēma ir atrisināta.
Tas patiesībā ir viss, ko es šodien gribēju jums pateikt.
Galvenie punkti
Galvenie atklājumi ir:
- Zināt lineāro vienādojumu risināšanas algoritmu.
- Spēja atvērt iekavas.
- Neuztraucieties, ja redzat kvadrātiskās funkcijas, visticamāk, turpmāko pārvērtību procesā tie samazināsies.
- Lineārajos vienādojumos ir trīs veidu saknes, pat visvienkāršākajos: viena sakne, visa skaitļu līnija ir sakne, un sakņu nav vispār.
Es ceru, ka šī nodarbība palīdzēs jums apgūt vienkāršu, bet ļoti svarīgu tēmu visas matemātikas tālākai izpratnei. Ja kaut kas nav skaidrs, dodieties uz vietni un atrisiniet tur sniegtos piemērus. Sekojiet līdzi jaunumiem, jūs gaida vēl daudz interesantu lietu!
Šī vienādojuma daļa ir izteiksme iekavās. Lai atvērtu iekavas, apskatiet zīmi iekavu priekšā. Ja ir plus zīme, iekavu atvēršana izteiksmē neko nemainīs: vienkārši noņemiet iekavas. Ja ir mīnusa zīme, atverot iekavas, ir jānomaina visas zīmes, kas sākotnēji bija iekavās, uz pretējām. Piemēram, -(2x-3)=-2x+3.
Reizinot divas iekavas.
Ja vienādojumā ir divu iekavu reizinājums, atverot iekavas saskaņā ar standarta noteikums. Katrs termins pirmajā iekavā tiek reizināts ar katru vārdu otrajā iekavā. Iegūtie skaitļi tiek summēti. Šajā gadījumā divu “plusu” vai divu “mīnusu” reizinājums piešķir terminam “plus” zīmi, un, ja faktoriem ir dažādas zīmes, pēc tam saņem mīnusa zīmi.
Apsvērsim.
(5x+1)(3x-4)=5x*3x-5x*4+1*3x-1*4=15x^2-20x+3x-4=15x^2-17x-4.
Atverot iekavas, dažreiz paaugstinot izteiksmi līdz . Kvadrātveida un kubošanas formulas ir jāzina no galvas un jāatceras.
(a+b)^2=a^2+2ab+b^2
(a-b)^2=a^2-2ab+b^2
(a+b)^3=a^3+3a^2*b+3ab^2+b^3
(a-b)^3=a^3-3a^2*b+3ab^2-b^3
Formulas izteiksmes, kas lielāka par trīs, konstruēšanai var veikt, izmantojot Paskāla trīsstūri.
Avoti:
- iekavas paplašināšanas formula
Iekļauts iekavās matemātiskās operācijas var saturēt mainīgos un izteiksmes dažādas pakāpes grūtības. Lai pavairotos šādas izteiksmes, jums būs jāmeklē risinājums vispārējs skats, atverot iekavas un vienkāršojot rezultātu. Ja iekavās ir darbības bez mainīgajiem, tikai ar skaitliskām vērtībām, tad iekavu atvēršana nav nepieciešama, jo, ja jums ir dators, tā lietotājam ir pieejami ļoti ievērojami skaitļošanas resursi - tos ir vieglāk izmantot, nekā vienkāršot izteiksmi.
Instrukcijas
Reiziniet secīgi katru (vai minuend ar ), kas atrodas vienā iekavā, ar visu pārējo iekavu saturu, ja vēlaties iegūt rezultātu vispārīgā formā. Piemēram, ļaujiet sākotnējo izteiksmi rakstīt šādi: (5+x)∗(6-x)∗(x+2). Tad secīga reizināšana (tas ir, atverot iekavas) dos šādu rezultātu: (5+x)∗(6-x)∗(x+2) = (5∗6-5∗x)∗(5∗x+ 5∗2) + (6∗x-x∗x)∗(x∗x+2∗x) = (5∗6∗5∗x+5∗6∗5∗2) - (5∗x∗5∗x+ 5∗x∗5∗2) + (6∗x∗x∗x+6∗x∗2∗x) - (x∗x∗x∗x+x∗x∗2∗x) = 5∗6∗5 ∗x + 5∗6∗5∗2 – 5∗x∗5∗x – 5∗x∗5∗2 + 6∗x∗x∗x + 6∗x∗2∗x – x∗x∗x∗x - x∗x∗2∗x = 150∗x + 300 – 25∗x² – 50∗x + 6∗x³ + 12∗x² – x∗x³ – 2∗x³.
Vienkāršojiet rezultātu, saīsinot izteiksmes. Piemēram, iepriekšējā solī iegūto izteiksmi var vienkāršot šādi: 150∗x + 300 - 25∗x² - 50∗x + 6∗x³ + 12∗x² - x∗x³ - 2∗x³ = 100∗x + 300 — 13∗ x² — 8∗x³ — x∗x³.
Izmantojiet kalkulatoru, ja jums jāreizina x ir vienāds ar 4,75, tas ir, (5+4,75)∗(6-4,75)∗(4,75+2). Lai aprēķinātu šo vērtību, dodieties uz Google vai Nigma meklētājprogrammas vietni un vaicājuma laukā ievadiet izteiksmi tās sākotnējā formā (5+4,75)*(6-4,75)*(4,75+2). Google parādīs 82.265625 uzreiz, neklikšķinot uz pogas, bet Nigma ar pogas klikšķi jānosūta dati uz serveri.
Iekavu galvenā funkcija ir mainīt darbību secību, aprēķinot vērtības. Piemēram, skaitliskā izteiksmē \(5·3+7\) vispirms tiks aprēķināts reizinājums un pēc tam saskaitīšana: \(5·3+7 =15+7=22\). Bet izteiksmē \(5·(3+7)\) vispirms tiks aprēķināta saskaitīšana iekavās un tikai pēc tam reizināšana: \(5·(3+7)=5·10=50\).

Piemērs.
Izvērsiet kronšteinu: \(-(4m+3)\).
Risinājums
: \(-(4m+3)=-4m-3\).
Piemērs.
Atveriet iekava un ievadiet līdzīgus terminus \(5-(3x+2)+(2+3x)\).
Risinājums
: \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).
Piemērs.
Izvērsiet iekavas \(5(3-x)\).
Risinājums
: iekavās ir \(3\) un \(-x\), un pirms iekavas ir piecinieks. Tas nozīmē, ka katrs iekavas elements tiek reizināts ar \(5\) — es jums to atgādinu Reizināšanas zīme starp skaitli un iekavām nav rakstīta matemātikā, lai samazinātu ierakstu lielumu.

Piemērs.
Izvērsiet iekavas \(-2(-3x+5)\).
Risinājums
: tāpat kā iepriekšējā piemērā, \(-3x\) un \(5\) iekavās tiek reizināti ar \(-2\).
Piemērs.
Vienkāršojiet izteiksmi: \(5(x+y)-2(x-y)\).
Risinājums
: \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).
Atliek apsvērt pēdējo situāciju.
Reizinot iekavu ar iekavu, katrs pirmās iekavas vārds tiek reizināts ar katru otrās iekavas vārdu:
\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)
Piemērs.
Izvērsiet iekavas \((2-x)(3x-1)\).
Risinājums
: Mums ir iekavu produkts, un to var nekavējoties paplašināt, izmantojot iepriekš minēto formulu. Bet, lai neapjuktu, darīsim visu soli pa solim.
1. darbība. Noņemiet pirmo iekavu — reiziniet katru tās vārdu ar otro iekava:
2. darbība. Izvērsiet iekavu un koeficienta produktus, kā aprakstīts iepriekš:
- Pirmās lietas vispirms...
Tad otrais.
3. darbība. Tagad mēs reizinām un parādām līdzīgus terminus:
Nav nepieciešams tik detalizēti aprakstīt visas pārvērtības, tās var pavairot uzreiz. Bet, ja jūs tikai mācāties atvērt iekavas, rakstiet detalizēti, būs mazāka iespēja kļūdīties.
Piezīme visai sadaļai. Patiesībā jums nav jāatceras visi četri noteikumi, jums ir jāatceras tikai viens, šis: \(c(a-b)=ca-cb\) . Kāpēc? Jo, ja c vietā aizstājat vienu, jūs iegūsit noteikumu \((a-b)=a-b\) . Un, ja mēs aizstājam mīnus viens, mēs iegūstam noteikumu \(-(a-b)=-a+b\) . Nu, ja aizstājat citu iekavu c vietā, varat iegūt pēdējo noteikumu.
Iekavas iekavās
Dažreiz praksē rodas problēmas ar iekavām, kas ir ligzdotas citās iekavās. Šeit ir šāda uzdevuma piemērs: vienkāršojiet izteiksmi \(7x+2(5-(3x+y))\).
Lai veiksmīgi atrisinātu šādus uzdevumus, jums ir nepieciešams:
- rūpīgi jāsaprot iekavu ligzdošana - kura kurā atrodas;
- secīgi atveriet kronšteinus, sākot, piemēram, ar visdziļāko.
Tas ir svarīgi, atverot kādu no kronšteiniem nepieskarieties pārējai izteiksmei, vienkārši pārrakstot to kā ir.
Kā piemēru aplūkosim iepriekš rakstīto uzdevumu.
Piemērs.
Atveriet iekavas un ievadiet līdzīgus vārdus \(7x+2(5-(3x+y))\).
Risinājums:
Piemērs.
Atveriet iekavas un ievadiet līdzīgus terminus \(-(x+3(2x-1+(x-5)))\).
Risinājums
:
|
\(-(x+3(2x-1\)\(+(x-5)\) \())\) |
Šeit ir trīskārša iekavu ligzda. Sāksim ar visdziļāko (izcelts zaļā krāsā). Kronšteina priekšā ir pluss, tāpēc tas vienkārši nāk nost. |
|
|
\(-(x+3(2x-1\)\(+x-5\) \())\) |
Tagad jums ir jāatver otrā kronšteina, starpposma. Bet pirms tam mēs vienkāršosim spokiem līdzīgo terminu izteiksmi šajā otrajā iekavā. |
|
|
\(=-(x\)\(+3(3x-6)\) \()=\) |
Tagad mēs atveram otro kronšteinu (izcelts zilā krāsā). Pirms iekava ir faktors – tāpēc katrs iekavās esošais termins tiek reizināts ar to. |
|
|
\(=-(x\)\(+9x-18\) \()=\) |
||
|
Un atveriet pēdējo iekava. Iekavas priekšā ir mīnusa zīme, tāpēc visas zīmes ir apgrieztas. |
||
Iekavu izvēršana ir matemātikas pamatprasme. Bez šīs prasmes 8. un 9. klasē nav iespējams iegūt atzīmi virs C. Tāpēc es iesaku jums labi izprast šo tēmu.
Šajā rakstā mēs detalizēti aplūkosim tik svarīgas tēmas pamatnoteikumus matemātikas kursā kā sākuma iekavas. Lai pareizi atrisinātu vienādojumus, kuros tie tiek izmantoti, jums jāzina iekavu atvēršanas noteikumi.
Kā pareizi atvērt iekavas pievienojot
Izvērsiet iekavas, pirms kurām ir “+” zīme
Šis ir vienkāršākais gadījums, jo, ja iekavām priekšā ir pievienošanas zīme, tad, atverot kronšteinus, zīmes to iekšpusē nemainās. Piemērs:
(9 + 3) + (1 - 6 + 9) = 9 + 3 + 1 - 6 + 9 = 16.
Kā izvērst iekavas, pirms kurām ir zīme "-".
IN šajā gadījumā jums ir jāpārraksta visi termini bez iekavām, bet tajā pašā laikā jāmaina visas to iekšpusē esošās zīmes uz pretējām. Zīmes mainās tikai tiem terminiem no tām iekavām, kurām priekšā ir zīme “-”. Piemērs:
(9 + 3) - (1 - 6 + 9) = 9 + 3 - 1 + 6 - 9 = 8.
Kā reizināšanas laikā atvērt iekavas
Pirms iekavām ir reizinātāja skaitlis
Šajā gadījumā jums ir jāreizina katrs termins ar koeficientu un jāatver iekavas, nemainot zīmes. Ja reizinātājam ir “-” zīme, tad reizināšanas laikā vārdu zīmes tiek apgrieztas. Piemērs:
3 * (1 - 6 + 9) = 3 * 1 - 3 * 6 + 3 * 9 = 3 - 18 + 27 = 12.
Kā atvērt divas iekavas ar reizināšanas zīmi starp tām
Šajā gadījumā jums ir jāreizina katrs vārds no pirmajām iekavām ar katru vārdu no otrajām iekavām un pēc tam jāpievieno rezultāti. Piemērs:
(9 + 3) * (1 - 6 + 9) = 9 * 1 + 9 * (- 6) + 9 * 9 + 3 * 1 + 3 * (- 6) + 3 * 9 = 9 - 54 + 81 + 3 - 18 + 27 = 48.
Kā kvadrātā atvērt iekavas
Ja divu vārdu summa vai starpība ir kvadrātā, iekavas jāatver pēc šādas formulas:
(x + y)^2 = x^2 + 2 * x * y + y^2.
Ja iekavās ir mīnuss, formula nemainās. Piemērs:
(9 + 3) ^ 2 = 9 ^ 2 + 2 * 9 * 3 + 3 ^ 2 = 144.
Kā paplašināt iekavas citā pakāpē
Ja terminu summa vai starpība tiek palielināta, piemēram, līdz 3. vai 4. pakāpei, tad jums vienkārši ir jāsadala iekavas jauda “kvadrātos”. Identisku faktoru pakāpes tiek saskaitītas, un, dalot, dalītāja jauda tiek atņemta no dividendes jaudas. Piemērs:
(9 + 3) ^ 3 = ((9 + 3) ^ 2) * (9 + 3) = (9 ^ 2 + 2 * 9 * 3 + 3 ^ 2) * 12 = 1728.
Kā atvērt 3 iekavas
Ir vienādojumi, kuros uzreiz tiek reizinātas 3 iekavas. Šajā gadījumā vispirms ir jāreizina pirmo divu iekavu vārdi un pēc tam jāreizina šī reizinājuma summa ar trešās iekavas vārdiem. Piemērs:
(1 + 2) * (3 + 4) * (5 - 6) = (3 + 4 + 6 + 8) * (5 - 6) = - 21.
Šie iekavu atvēršanas noteikumi vienlīdz attiecas gan uz lineāro, gan trigonometrisko vienādojumu risināšanu.