Nodarbība un prezentācija par tēmu: "Jaudas funkcijas. Īpašības. Grafiki"
Papildu materiāli
Cienījamie lietotāji, neaizmirstiet atstāt savus komentārus, atsauksmes, vēlmes! Visi materiāli ir pārbaudīti ar pretvīrusu programmu.
Mācību līdzekļi un simulatori Interneta veikalā Integral 11. klasei
Interaktīva rokasgrāmata 9.–11. klasei "Trigonometrija"
Interaktīva rokasgrāmata 10.–11. klasei "Logaritmi"
Jaudas funkcijas, definīcijas joma.
Puiši, pēdējā nodarbībā mēs iemācījāmies strādāt ar skaitļiem ar racionāliem eksponentiem. Šajā nodarbībā aplūkosim jaudas funkcijas un aprobežosimies ar gadījumu, kad eksponents ir racionāls.Apskatīsim šādas formas funkcijas: $y=x^(\frac(m)(n))$.
Vispirms apskatīsim funkcijas, kuru eksponents $\frac(m)(n)>1$.
Dosim mums īpašu funkciju $y=x^2*5$.
Saskaņā ar definīciju, ko sniedzām pēdējā nodarbībā: ja $x≥0$, tad mūsu funkcijas definīcijas domēns ir stars $(x)$. Shematiski attēlosim mūsu funkcijas grafiku.

Funkcijas $y=x^(\frac(m)(n))$, $0 īpašības 2. Tā nav ne pāra, ne nepāra.
3. Palielinās par $$,
b) $(2,10)$,
c) uz stara $$.
Risinājums.
Puiši, vai atceraties, kā mēs 10. klasē atradām segmenta lielāko un mazāko funkcijas vērtību?
Tieši tā, mēs izmantojām atvasinājumu. Atrisināsim mūsu piemēru un atkārtosim algoritmu, lai atrastu mazāko un augstākā vērtība.
1. Atrodiet dotās funkcijas atvasinājumu:
$y"=\frac(16)(5)*\frac(5)(2)x^(\frac(3)(2))-x^3=8x^(\frac(3)(2)) -x^3=8\sqrt(x^3)-x^3$.
2. Atvasinājums pastāv visā sākotnējās funkcijas definīcijas jomā, tad nav kritisko punktu. Atradīsim stacionārus punktus:
$y"=8\sqrt(x^3)-x^3=0$.
$8*\sqrt(x^3)=x^3$.
$64x^3=x^6$.
$x^6-64x^3=0$.
$x^3(x^3-64)=0$.
$x_1=0$ un $x_2=\sqrt(64)=4$.
Dotais segments satur tikai vienu risinājumu $x_2=4$.
Izveidosim tabulu ar mūsu funkcijas vērtībām segmenta galos un galējā punktā:
Atbilde: $y_(nosaukums)=-862.65$ pie $x=9$; $y_(maks.)=38,4$ pie $x=4$.
Piemērs. Atrisiniet vienādojumu: $x^(\frac(4)(3))=24-x$.
Risinājums. Funkcijas $y=x^(\frac(4)(3))$ grafiks palielinās, bet funkcijas $y=24-x$ grafiks samazinās. Puiši, jūs un es zinām: ja viena funkcija palielinās, bet otra samazinās, tad tās krustojas tikai vienā punktā, tas ir, mums ir tikai viens risinājums.
Piezīme:
$8^(\frac(4)(3))=\sqrt(8^4)=(\sqrt(8))^4=2^4=16$.
$24-8=16$.
Tas ir, ar $x=8$ mēs saņēmām pareizo vienādību $16=16$, tas ir mūsu vienādojuma risinājums.
Atbilde: $x=8$.
Piemērs.
Grafiksējiet funkciju: $y=(x-3)^\frac(3)(4)+2$.
Risinājums.
Mūsu funkcijas grafiks tiek iegūts no funkcijas $y=x^(\frac(3)(4))$ grafika, nobīdot to par 3 vienībām pa labi un 2 vienībām uz augšu. 
Piemērs. Uzrakstiet taisnes $y=x^(-\frac(4)(5))$ pieskares vienādojumu punktā $x=1$.
Risinājums. Pieskares vienādojumu nosaka pēc mums zināmās formulas:
$y=f(a)+f"(a)(x-a)$.
Mūsu gadījumā $a=1$.
$f(a)=f(1)=1^(-\frac(4)(5))=1$.
Atradīsim atvasinājumu:
$y"=-\frac(4)(5)x^(-\frac(9)(5))$.
Aprēķināsim:
$f"(a)=-\frac(4)(5)*1^(-\frac(9)(5))=-\frac(4)(5)$.
Atradīsim pieskares vienādojumu:
$y=1-\frac(4)(5)(x-1)=-\frac(4)(5)x+1\frac(4)(5)$.
Atbilde: $y=-\frac(4)(5)x+1\frac(4)(5)$.
Problēmas, kas jārisina patstāvīgi
1. Segmentā atrodiet funkcijas $y=x^\frac(4)(3)$ lielāko un mazāko vērtību:a) $$.
b) $(4,50) $.
c) uz stara $$.
3. Atrisiniet vienādojumu: $x^(\frac(1)(4))=18-x$.
4. Izveidojiet funkcijas grafiku: $y=(x+1)^(\frac(3)(2))-1$.
5. Izveidojiet vienādojumu taisnes $y=x^(-\frac(3)(7))$ pieskarei punktā $x=1$.
Funkcija kur X- mainīgs daudzums, A– tiek izsaukts norādīts numurs Jaudas funkcija .
Ja tad ir lineāra funkcija, tās grafiks ir taisna līnija (sk. 4.3. punktu, 4.7. att.).
Ja tad - kvadrātiskā funkcija, tā grafiks ir parabola (sk. 4.3. punktu, 4.8. att.).
Ja tad tā grafiks ir kubiskā parabola (sk. 4.3. punktu, 4.9. att.).
Šī ir apgrieztā funkcija
1. Domēns: ![]()
2. Vairākas nozīmes:![]()
3. Pāra un nepāra: funkcija ir nepāra.
4. Funkciju biežums: neperiodisks.
5. Funkcijas nulles: X= 0 – vienīgā nulle.
6. Funkcijai nav maksimālās vai minimālās vērtības.
7.
8. Funkcijas grafiks Simetrisks kubiskās parabolas grafikam attiecībā pret taisnu līniju Y=X un ir parādīts attēlā. 5.1.
 |
Jaudas funkcija
1. Domēns: ![]()
2. Vairākas nozīmes:
3. Pāra un nepāra: funkcija ir vienmērīga.
4. Funkciju biežums: neperiodisks.
5. Funkcijas nulles: viena nulle X = 0.
6. Funkcijas lielākās un mazākās vērtības:ņem mazāko vērtību X= 0, tas ir vienāds ar 0.
7. Intervālu palielināšana un samazināšana: funkcija samazinās intervālā un palielinās pēc intervāla
8. Funkcijas grafiks(katram N Î N) ir “līdzīgs” kvadrātparabolas grafikam (funkciju grafiki parādīti 5.2. att.).

Jaudas funkcija
1. Domēns: ![]()
2. Vairākas nozīmes: ![]()
3. Pāra un nepāra: funkcija ir nepāra.
4. Funkciju biežums: neperiodisks.
5. Funkcijas nulles: X= 0 – vienīgā nulle.
6. Augstākās un zemākās vērtības:
7. Intervālu palielināšana un samazināšana: funkcija palielinās visā definīcijas jomā.
8. Funkcijas grafiks(katram ) ir “līdzīgs” kubiskās parabolas grafikam (funkciju grafiki parādīti 5.3. attēlā).
 |
Jaudas funkcija![]()
1. Domēns:
2. Vairākas nozīmes:
3. Pāra un nepāra: funkcija ir nepāra.
4. Funkciju biežums: neperiodisks.
5. Funkcijas nulles: nav nulles.
6. Funkcijas lielākās un mazākās vērtības: funkcijai nav lielākās un mazākās vērtības nevienai
7. Intervālu palielināšana un samazināšana: funkcija samazinās tās definīcijas jomā.
8. Asimptotes:(ass OU) – vertikālā asimptote;
(ass Ak) – horizontālā asimptote.
9. Funkcijas grafiks(jebkuram N) ir “līdzīgs” hiperbolas grafikam (funkciju grafiki parādīti 5.4. att.).
 |
Jaudas funkcija
1. Domēns:
2. Vairākas nozīmes:
3. Pāra un nepāra: funkcija ir vienmērīga.
4. Funkciju biežums: neperiodisks.
5. Funkcijas lielākās un mazākās vērtības: funkcijai nav lielākās un mazākās vērtības nevienai
6. Intervālu palielināšana un samazināšana: funkcija palielinās par un samazinās par
7. Asimptotes: X= 0 (ass OU) – vertikālā asimptote;
Y= 0 (ass Ak) – horizontālā asimptote.
8. Funkciju grafiki Tās ir kvadrātveida hiperbolas (5.5. att.).
 |
Jaudas funkcija
1. Domēns:
2. Vairākas nozīmes:
3. Pāra un nepāra: funkcijai nav pāra un nepāra īpašības.
4. Funkciju biežums: neperiodisks.
5. Funkcijas nulles: X= 0 – vienīgā nulle.
6. Funkcijas lielākās un mazākās vērtības: funkcija iegūst mazāko vērtību, kas vienāda ar 0 punktā X= 0; nav svarīgākais.
7. Intervālu palielināšana un samazināšana: funkcija palielinās visā definīcijas jomā.
8. Katra šāda funkcija noteiktam eksponentam ir sniegtās funkcijas apgrieztā vērtība
9. Funkcijas grafiks"līdzinās" jebkuras funkcijas grafikam N un ir parādīts attēlā. 5.6.

Jaudas funkcija
1. Domēns: ![]()
2. Vairākas nozīmes:![]()
3. Pāra un nepāra: funkcija ir nepāra.
4. Funkciju biežums: neperiodisks.
5. Funkcijas nulles: X= 0 – vienīgā nulle.
6. Funkcijas lielākās un mazākās vērtības: funkcijai nav lielākās un mazākās vērtības nevienai
7. Intervālu palielināšana un samazināšana: funkcija palielinās visā definīcijas jomā.
8. Funkcijas grafiks Attēlā parādīts. 5.7.
 |
Atgādināsim jaudas funkciju īpašības un grafikus ar veselu skaitli negatīvs rādītājs.
Pat n, :
Funkcijas piemērs:
Visi šādu funkciju grafiki iet caur diviem fiksētiem punktiem: (1;1), (-1;1). Šāda veida funkciju īpatnība ir to paritāte; grafiki ir simetriski attiecībā pret op-amp asi.

Rīsi. 1. Funkcijas grafiks
Nepāra n, :
Funkcijas piemērs:
Visi šādu funkciju grafiki iet caur diviem fiksētiem punktiem: (1;1), (-1;-1). Šāda veida funkciju īpatnība ir tā, ka tās ir nepāra, grafiki ir simetriski attiecībā pret izcelsmi.

Rīsi. 2. Funkcijas grafiks
Atcerēsimies pamata definīciju.
Nenegatīva skaitļa a jaudu ar racionālu pozitīvu eksponentu sauc par skaitli.
Pozitīva skaitļa a jaudu ar racionālu negatīvu eksponentu sauc par skaitli.
Par vienlīdzību:
![]()
![]()
Piemēram: ![]() ; - izteiksme pēc definīcijas nepastāv pakāpei ar negatīvu racionālo eksponentu; pastāv, jo eksponents ir vesels skaitlis,
; - izteiksme pēc definīcijas nepastāv pakāpei ar negatīvu racionālo eksponentu; pastāv, jo eksponents ir vesels skaitlis, ![]()
Pāriesim pie jaudas funkciju izskatīšanas ar racionālu negatīvu eksponentu.
![]()
Piemēram:
Lai attēlotu šīs funkcijas grafiku, varat izveidot tabulu. Mēs to darīsim savādāk: vispirms izveidosim un izpētīsim saucēja grafiku - tas mums ir zināms (3. attēls).

Rīsi. 3. Funkcijas grafiks
Saucēja funkcijas grafiks iet caur fiksētu punktu (1;1). Uzzīmējot sākotnējo funkciju dots punkts paliek, kad arī sakne tiecas uz nulli, funkcija tiecas uz bezgalību. Un otrādi, tā kā x tiecas uz bezgalību, funkcijai ir tendence uz nulli (4. attēls).

Rīsi. 4. Funkciju grafiks
Apskatīsim vēl vienu funkciju no pētāmo funkciju saimes.
![]()
Ir svarīgi, ka pēc definīcijas
Apskatīsim funkcijas grafiku saucējā: , šīs funkcijas grafiks mums ir zināms, tas palielinās savā definīcijas apgabalā un iet caur punktu (1;1) (5. attēls).

Rīsi. 5. Funkcijas grafiks
Uzzīmējot sākotnējās funkcijas grafiku, punkts (1;1) paliek, savukārt sakne arī tiecas uz nulli, funkcija tiecas uz bezgalību. Un otrādi, tā kā x tiecas uz bezgalību, funkcijai ir tendence uz nulli (6. attēls).

Rīsi. 6. Funkcijas grafiks
Apskatītie piemēri palīdz saprast, kā grafs plūst un kādas ir pētāmās funkcijas - funkcijas ar negatīvu racionālo eksponentu - īpašības.
Šīs saimes funkciju grafiki iet caur punktu (1;1), funkcija samazinās visā definīcijas jomā.
Funkciju darbības joma: ![]()
Funkcija nav ierobežota no augšas, bet ir ierobežota no apakšas. Funkcijai nav ne lielākā, ne zemākā vērtība.
Funkcija ir nepārtraukta un ņem visas pozitīvās vērtības no nulles līdz plus bezgalībai.
Funkcija ir izliekta uz leju (15.7. attēls)
Punkti A un B tiek ņemti uz līknes, caur tiem tiek novilkts segments, visa līkne atrodas zem segmenta, šis nosacījums ir izpildīts patvaļīgiem diviem līknes punktiem, tāpēc funkcija ir izliekta uz leju. Rīsi. 7.

Rīsi. 7. Funkcijas izliekums
Ir svarīgi saprast, ka šīs ģimenes funkcijas no apakšas ierobežo nulle, bet tām nav mazākās vērtības.
1. piemērs — atrodiet funkcijas maksimumu un minimumu intervālā \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \]
Grafiks (2. att.).

2. attēls. Funkcijas $f\left(x\right)=x^(2n)$ grafiks
Jaudas funkcijas ar naturālu nepāra eksponentu īpašības
Definīcijas domēns ir visi reālie skaitļi.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ — funkcija ir nepāra.
$f(x)$ ir nepārtraukts visā definīcijas domēnā.
Diapazons ir visi reālie skaitļi.
$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Funkcija palielinās visā definīcijas jomā.
$f\left(x\right)0$, par $x\in (0,+\infty)$.
$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$
\ \
Funkcija ir ieliekta $x\in (-\infty ,0)$ un izliekta $x\in (0,+\infty)$.
Grafiks (3. att.).
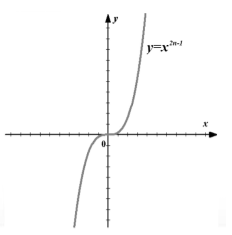
3. attēls. Funkcijas $f\left(x\right)=x^(2n-1)$ grafiks
Jaudas funkcija ar veselu eksponentu
Vispirms ieviesīsim pakāpes jēdzienu ar veselu eksponentu.
3. definīcija
Reāla skaitļa $a$ ar veselu eksponentu $n$ jaudu nosaka pēc formulas:

4. attēls.
Tagad apskatīsim jaudas funkciju ar veselu eksponentu, tās īpašības un grafiku.
4. definīcija
$f\left(x\right)=x^n$ ($n\in Z)$ sauc par jaudas funkciju ar veselu eksponentu.
Ja pakāpe ir lielāka par nulli, mēs nonākam pie pakāpes funkcijas gadījuma ar naturālo eksponentu. Mēs to jau apspriedām iepriekš. Par $n=0$ mēs saņemam lineārā funkcija$y=1$. Mēs to atstāsim lasītāja ziņā. Atliek apsvērt jaudas funkcijas īpašības ar negatīvu veselu eksponentu
Jaudas funkcijas ar negatīvu veselu eksponentu īpašības
Definīcijas domēns ir $\left(-\infty ,0\right)(0,+\infty)$.
Ja eksponents ir pāra, tad funkcija ir pāra, ja tā ir nepāra, tad funkcija ir nepāra.
$f(x)$ ir nepārtraukts visā definīcijas domēnā.
Darbības joma:
Ja eksponents ir pāra, tad $(0,+\infty)$; ja tas ir nepāra, tad $\left(-\infty ,0\right)(0,+\infty)$.
Nepāra eksponentam funkcija samazinās kā $x\in \left(-\infty ,0\right)(0,+\infty)$. Ja eksponents ir pāra, funkcija samazinās kā $x\in (0,+\infty)$. un palielinās kā $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ visā definīcijas domēnā








