ത്രികോണമിതി ഫംഗ്‌ഷനുകളുടെ ഡെറിവേറ്റീവുകൾ സോൾവിംഗ് സോൾവിംഗ് ഉദാഹരണങ്ങൾ. ലളിതമായ ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ ഡെറിവേറ്റീവുകൾ

കണ്ടുപിടിക്കാൻ ഒരു ത്രികോണമിതി പ്രവർത്തനത്തിന്റെ ഡെറിവേറ്റീവ് ഉപയോഗിക്കേണ്ടതുണ്ട് ഡെറിവേറ്റീവുകളുടെ പട്ടിക, അതായത് ഡെറിവേറ്റീവുകൾ 6-13.

നിങ്ങൾ കണ്ടെത്തുമ്പോൾ പ്രധാന ഡെറിവേറ്റീവുകൾ ത്രികോണമിതി പ്രവർത്തനങ്ങൾ സാധാരണ തെറ്റുകൾ ഒഴിവാക്കാൻ, നിങ്ങൾ ഇനിപ്പറയുന്ന പോയിന്റുകൾ ശ്രദ്ധിക്കണം:

• ഒരു ഫംഗ്‌ഷൻ എക്‌സ്‌പ്രഷനിൽ, നിബന്ധനകളിൽ ഒന്ന് പലപ്പോഴും സൈൻ, കോസൈൻ അല്ലെങ്കിൽ മറ്റ് ത്രികോണമിതി പ്രവർത്തനംഫംഗ്ഷന്റെ വാദത്തിൽ നിന്നല്ല, സംഖ്യയിൽ നിന്ന് (സ്ഥിരമായത്), അതിനാൽ ഈ പദത്തിന്റെ ഡെറിവേറ്റീവ് പൂജ്യത്തിന് തുല്യമാണ്;
• വ്യത്യാസത്തിന്റെ ഫലമായി ലഭിച്ച പദപ്രയോഗം നിങ്ങൾ എല്ലായ്പ്പോഴും ലളിതമാക്കേണ്ടതുണ്ട്, ഇതിനായി ഭിന്നസംഖ്യകളുള്ള പ്രവർത്തനങ്ങളെക്കുറിച്ചുള്ള അറിവ് നിങ്ങൾ ആത്മവിശ്വാസത്തോടെ ഉപയോഗിക്കേണ്ടതുണ്ട്;
• ഒരു പദപ്രയോഗം ലളിതമാക്കാൻ, നിങ്ങൾ മിക്കവാറും എല്ലായ്‌പ്പോഴും ത്രികോണമിതി ഐഡന്റിറ്റികൾ അറിയേണ്ടതുണ്ട്, ഉദാഹരണത്തിന്, ഫോർമുല ഇരട്ട കോൺസൈൻ, കോസൈൻ എന്നിവയുടെ വർഗ്ഗങ്ങളുടെ ആകെത്തുകയായി ഏകത്വത്തിനുള്ള സൂത്രവാക്യം.

ഉദാഹരണം 1.ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക

പരിഹാരം. കൂടെ പറയാം കോസൈന്റെ ഡെറിവേറ്റീവ്എല്ലാം വ്യക്തമാണ്, ഡെറിവേറ്റീവുകൾ പഠിക്കാൻ തുടങ്ങുന്ന പലരും പറയും. എന്തുപറ്റി സൈനിന്റെ ഡെറിവേറ്റീവ്പന്ത്രണ്ടിനെ പൈ കൊണ്ട് ഹരിച്ചോ? ഉത്തരം: ഇത് പൂജ്യത്തിന് തുല്യമായി കണക്കാക്കുക! ഇവിടെ സൈൻ (എല്ലാത്തിനുമുപരി ഒരു ഫംഗ്‌ഷൻ!) ഒരു കെണിയാണ്, കാരണം ആർഗ്യുമെന്റ് വേരിയബിൾ X അല്ലെങ്കിൽ മറ്റേതെങ്കിലും വേരിയബിളല്ല, മറിച്ച് ഒരു സംഖ്യയാണ്. അതായത്, ഈ സംഖ്യയുടെ സൈനും ഒരു സംഖ്യയാണ്. ഡെറിവേറ്റീവുകളുടെ പട്ടികയിൽ നിന്ന് നമുക്കറിയാവുന്ന ഒരു സംഖ്യയുടെ (സ്ഥിരമായ) ഡെറിവേറ്റീവ് പൂജ്യത്തിന് തുല്യമാണ്. അതിനാൽ, ഞങ്ങൾ X ന്റെ മൈനസ് സൈൻ മാത്രം ഉപേക്ഷിച്ച് അതിന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുന്നു, ചിഹ്നത്തെക്കുറിച്ച് മറക്കരുത്:

.

ഉദാഹരണം 2.ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക

.

പരിഹാരം. മുമ്പത്തെ ഉദാഹരണത്തിലെ ആദ്യ ടേമിന്റെ അതേ കേസാണ് രണ്ടാമത്തെ ടേം. അതായത്, ഇത് ഒരു സംഖ്യയാണ്, സംഖ്യയുടെ ഡെറിവേറ്റീവ് പൂജ്യമാണ്. രണ്ടാമത്തെ പദത്തിന്റെ ഡെറിവേറ്റീവ് ഘടകത്തിന്റെ ഡെറിവേറ്റീവായി ഞങ്ങൾ കണ്ടെത്തുന്നു:

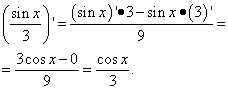
ഉദാഹരണം 3.ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക

പരിഹാരം. ഇത് മറ്റൊരു പ്രശ്‌നമാണ്: ഇവിടെ ആദ്യ പദത്തിൽ ആർക്‌സൈനോ മറ്റ് ട്രൈഗണോമെറ്റിക് ഫംഗ്‌ഷനോ ഇല്ല, എന്നാൽ x ഉണ്ട്, അതായത് ഇത് x ന്റെ ഒരു ഫംഗ്‌ഷൻ ആണ്. അതിനാൽ, ഫംഗ്‌ഷനുകളുടെ ആകെത്തുകയിൽ ഞങ്ങൾ അതിനെ ഒരു പദമായി വേർതിരിക്കുന്നു:

ഇവിടെ ഭിന്നസംഖ്യകളുള്ള പ്രവർത്തനങ്ങളിൽ കഴിവുകൾ ആവശ്യമാണ്, അതായത്, ഒരു ഭിന്നസംഖ്യയുടെ മൂന്ന്-നില ഘടന ഇല്ലാതാക്കുന്നതിൽ.

ഉദാഹരണം 4.ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക

.

പരിഹാരം. ഇവിടെ "phi" എന്ന അക്ഷരം മുമ്പത്തെ സന്ദർഭങ്ങളിൽ "x" എന്നതിന് സമാനമായ പങ്ക് വഹിക്കുന്നു (മറ്റു മിക്കവയിലും, എന്നാൽ എല്ലാം അല്ല) - സ്വതന്ത്ര വേരിയബിൾ. അതിനാൽ, ഫംഗ്‌ഷനുകളുടെ ഒരു ഉൽപ്പന്നത്തിന്റെ ഡെറിവേറ്റീവിനായി ഞങ്ങൾ തിരയുമ്പോൾ, പൂജ്യത്തിന് തുല്യമായ "ഫൈ" എന്ന റൂട്ടിന്റെ ഡെറിവേറ്റീവ് പ്രഖ്യാപിക്കാൻ ഞങ്ങൾ തിരക്കുകൂട്ടില്ല. അതിനാൽ:

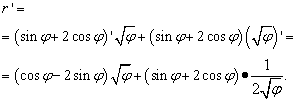
എന്നാൽ പരിഹാരം അവിടെ അവസാനിക്കുന്നില്ല. സമാന പദങ്ങൾ രണ്ട് ബ്രാക്കറ്റുകളിലായി ശേഖരിക്കുന്നതിനാൽ, ഞങ്ങൾ പദപ്രയോഗം രൂപാന്തരപ്പെടുത്തേണ്ടതുണ്ട് (ലളിതമാക്കുക). അതിനാൽ, ഞങ്ങൾ ബ്രാക്കറ്റുകളെ അവയുടെ പിന്നിലെ ഘടകങ്ങളാൽ ഗുണിക്കുന്നു, തുടർന്ന് ഞങ്ങൾ നിബന്ധനകൾ ഒരു പൊതു വിഭാഗത്തിലേക്ക് കൊണ്ടുവരികയും മറ്റ് പ്രാഥമിക പരിവർത്തനങ്ങൾ നടത്തുകയും ചെയ്യുന്നു:

ഉദാഹരണം 5.ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക

പരിഹാരം. ഈ ഉദാഹരണത്തിൽ, അത്തരമൊരു ത്രികോണമിതി ഫംഗ്‌ഷൻ - സെക്കന്റ് - അതിന്റെ സൂത്രവാക്യങ്ങളും കോസൈനിലൂടെ ഉണ്ടെന്ന വസ്തുത നാം അറിയേണ്ടതുണ്ട്. നമുക്ക് വേർതിരിക്കാം:

ഉദാഹരണം 6.ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക

.

പരിഹാരം. ഈ ഉദാഹരണത്തിൽ, സ്കൂളിൽ നിന്നുള്ള ഡബിൾ ആംഗിൾ ഫോർമുല നമ്മൾ ഓർക്കേണ്ടതുണ്ട്. എന്നാൽ ആദ്യം നമുക്ക് വേർതിരിക്കാം:

,

(ഇതാണ് ഡബിൾ ആംഗിൾ ഫോർമുല)

വിപരീത ത്രികോണമിതി ഫംഗ്‌ഷനുകളുടെ ഡെറിവേറ്റീവുകളും അവയുടെ ഫോർമുലകളുടെ ഡെറിവേറ്റേഷനും അവതരിപ്പിക്കുന്നു. ഉയർന്ന ഓർഡർ ഡെറിവേറ്റീവുകൾക്കുള്ള എക്സ്പ്രഷനുകളും നൽകിയിരിക്കുന്നു. ഫോർമുലകളുടെ വ്യുൽപ്പന്നത്തിന്റെ കൂടുതൽ വിശദമായ വിവരണമുള്ള പേജുകളിലേക്കുള്ള ലിങ്കുകൾ.

ആദ്യം, ആർക്സൈനിന്റെ ഡെറിവേറ്റീവിനുള്ള സൂത്രവാക്യം ഞങ്ങൾ കണ്ടെത്തുന്നു. അനുവദിക്കുക
y= ആർക്‌സിൻ x.
ആർക്സൈൻ സൈനിന്റെ വിപരീത പ്രവർത്തനമായതിനാൽ
.
ഇവിടെ y എന്നത് x ന്റെ ഒരു ഫങ്ഷനാണ്. x എന്ന വേരിയബിളുമായി ബന്ധപ്പെട്ട് വേർതിരിക്കുക:
.
ഞങ്ങൾ പ്രയോഗിക്കുന്നു:
.
അതിനാൽ ഞങ്ങൾ കണ്ടെത്തി:
.

കാരണം, അപ്പോൾ. പിന്നെ
.
മുമ്പത്തെ ഫോർമുല ഫോം എടുക്കുന്നു:
. ഇവിടെ നിന്ന്
.

കൃത്യമായി ഈ രീതിയിൽ, ആർക്ക് കോസൈന്റെ ഡെറിവേറ്റീവിനുള്ള ഫോർമുല നിങ്ങൾക്ക് ലഭിക്കും. എന്നിരുന്നാലും, വിപരീത ത്രികോണമിതി പ്രവർത്തനങ്ങളുമായി ബന്ധപ്പെട്ട ഒരു ഫോർമുല ഉപയോഗിക്കുന്നത് എളുപ്പമാണ്:
.
പിന്നെ
.

"ആർക്സൈൻ, ആർക്കോസൈൻ എന്നിവയുടെ ഡെറിവേറ്റീവുകളുടെ ഡെറിവേഷൻ" എന്ന പേജിൽ കൂടുതൽ വിശദമായ വിവരണം അവതരിപ്പിച്ചിരിക്കുന്നു. അവിടെ കൊടുത്തിരിക്കുന്നു രണ്ട് തരത്തിൽ ഡെറിവേറ്റീവുകളുടെ വ്യുൽപ്പന്നം- മുകളിൽ ചർച്ച ചെയ്തതും വിപരീത ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവിനുള്ള ഫോർമുല അനുസരിച്ചും.

ആർക്റ്റാൻജെന്റ്, ആർക്കോടാൻജെന്റ് എന്നിവയുടെ ഡെറിവേറ്റീവുകളുടെ ഡെറിവേറ്റീവ്

അതുപോലെ ആർക്റ്റാൻജന്റ്, ആർക്കോടാൻജെന്റ് എന്നിവയുടെ ഡെറിവേറ്റീവുകൾ നമുക്ക് കണ്ടെത്താം.

അനുവദിക്കുക
y= ആർക്റ്റാൻ x.
ടാൻജന്റിന്റെ വിപരീത പ്രവർത്തനമാണ് ആർക്റ്റഞ്ചന്റ്:
.
x എന്ന വേരിയബിളുമായി ബന്ധപ്പെട്ട് വേർതിരിക്കുക:
.
സങ്കീർണ്ണമായ ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവിനായി ഞങ്ങൾ ഫോർമുല പ്രയോഗിക്കുന്നു:
.
അതിനാൽ ഞങ്ങൾ കണ്ടെത്തി:
.

ആർക്ക് കോട്ടാൻജെന്റിന്റെ ഡെറിവേറ്റീവ്:
.

ആർക്സൈൻ ഡെറിവേറ്റീവുകൾ

അനുവദിക്കുക
.
ആർക്സൈനിന്റെ ഫസ്റ്റ്-ഓർഡർ ഡെറിവേറ്റീവ് ഞങ്ങൾ ഇതിനകം കണ്ടെത്തി:
.
വേർതിരിക്കുന്നതിലൂടെ, ഞങ്ങൾ രണ്ടാമത്തെ ഓർഡർ ഡെറിവേറ്റീവ് കണ്ടെത്തുന്നു:
;
.
ഇത് ഇനിപ്പറയുന്ന ഫോമിലും എഴുതാം:
.
ഇവിടെ നിന്ന് നമുക്ക് ലഭിക്കുന്നു ഡിഫറൻഷ്യൽ സമവാക്യം, ആദ്യത്തേയും രണ്ടാമത്തെയും ഓർഡറുകളുടെ ആർക്സൈൻ ഡെറിവേറ്റീവുകളാൽ സംതൃപ്തമാണ്:
.

ഈ സമവാക്യം വേർതിരിക്കുന്നതിലൂടെ, നമുക്ക് ഉയർന്ന ഓർഡർ ഡെറിവേറ്റീവുകൾ കണ്ടെത്താനാകും.

nth ഓർഡറിന്റെ ആർക്സൈനിന്റെ ഡെറിവേറ്റീവ്

n-ആം ക്രമത്തിന്റെ ആർക്സൈനിന്റെ ഡെറിവേറ്റീവിന് ഇനിപ്പറയുന്ന രൂപമുണ്ട്:
,
ഡിഗ്രിയുടെ ഒരു ബഹുപദം എവിടെയാണ്. ഇത് സൂത്രവാക്യങ്ങളാൽ നിർണ്ണയിക്കപ്പെടുന്നു:
;
.
ഇവിടെ .

ബഹുപദം ഡിഫറൻഷ്യൽ സമവാക്യത്തെ തൃപ്തിപ്പെടുത്തുന്നു:
.

എൻ-ആം ഓർഡറിന്റെ ആർക്കോസിൻ ഡെറിവേറ്റീവ്

ആർക്ക് കോസൈനിനുള്ള ഡെറിവേറ്റീവുകൾ ത്രികോണമിതി ഫോർമുല ഉപയോഗിച്ച് ആർക്ക് സൈനിനുള്ള ഡെറിവേറ്റീവുകളിൽ നിന്ന് ലഭിക്കുന്നു:
.
അതിനാൽ, ഈ ഫംഗ്‌ഷനുകളുടെ ഡെറിവേറ്റീവുകൾ ചിഹ്നത്തിൽ മാത്രം വ്യത്യാസപ്പെട്ടിരിക്കുന്നു:
.

ആർക്റ്റാൻജെന്റിന്റെ ഡെറിവേറ്റീവുകൾ

അനുവദിക്കുക. ആദ്യ ഓർഡറിന്റെ ആർക്ക് കോട്ടാൻജെന്റിന്റെ ഡെറിവേറ്റീവ് ഞങ്ങൾ കണ്ടെത്തി:
.

നമുക്ക് ഭിന്നസംഖ്യയെ അതിന്റെ ഏറ്റവും ലളിതമായ രൂപത്തിലേക്ക് വിഭജിക്കാം:

.
ഇവിടെ സാങ്കൽപ്പിക യൂണിറ്റ്, .

ഞങ്ങൾ ഒരിക്കൽ വേർതിരിച്ച് ഭിന്നസംഖ്യയെ ഒരു പൊതു വിഭാഗത്തിലേക്ക് കൊണ്ടുവരുന്നു:

.

പകരമായി, നമുക്ക് ലഭിക്കുന്നത്:
.

nth ഓർഡറിന്റെ ആർക്റ്റാൻജന്റ് എന്നതിന്റെ ഡെറിവേറ്റീവ്

അങ്ങനെ, n-ആം ഓർഡറിന്റെ ആർക്റ്റാൻജന്റ് ഡെറിവേറ്റീവ് പല തരത്തിൽ പ്രതിനിധീകരിക്കാം:
;
.

ആർക്ക് കോട്ടാൻജെന്റിന്റെ ഡെറിവേറ്റീവുകൾ

അത് ഇപ്പോൾ ആവട്ടെ. വിപരീത ത്രികോണമിതി പ്രവർത്തനങ്ങളെ ബന്ധിപ്പിക്കുന്ന ഫോർമുല നമുക്ക് പ്രയോഗിക്കാം:
.
അപ്പോൾ ആർക്ക് ടാൻജെന്റിന്റെ nth ഓർഡർ ഡെറിവേറ്റീവ് ആർക്ക് ടാൻജെന്റിന്റെ ഡെറിവേറ്റീവിൽ നിന്ന് ചിഹ്നത്തിൽ മാത്രം വ്യത്യാസപ്പെട്ടിരിക്കുന്നു:
.

പകരമായി, ഞങ്ങൾ കണ്ടെത്തുന്നു:
.

റഫറൻസുകൾ:
എൻ.എം. ഗുണ്ടർ, ആർ.ഒ. കുസ്മിൻ, ഉയർന്ന ഗണിതത്തിലെ പ്രശ്നങ്ങളുടെ ശേഖരം, "ലാൻ", 2003.

പട്ടികയുടെ ആദ്യ സൂത്രവാക്യം കണ്ടെത്തുമ്പോൾ, ഒരു പോയിന്റിലെ ഡെറിവേറ്റീവ് ഫംഗ്ഷന്റെ നിർവചനത്തിൽ നിന്ന് ഞങ്ങൾ മുന്നോട്ട് പോകും. എവിടേക്കെടുക്കാം x- ഏതെങ്കിലും യഥാർത്ഥ സംഖ്യ, അതായത്, x- ഫംഗ്‌ഷന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌നിൽ നിന്നുള്ള ഏതെങ്കിലും നമ്പർ. ഫംഗ്‌ഷന്റെ ഇൻക്രിമെന്റിന്റെയും ആർഗ്യുമെന്റിന്റെ ഇൻക്രിമെന്റിന്റെയും അനുപാതത്തിന്റെ പരിധി നമുക്ക് ഇവിടെ എഴുതാം:

പരിധി ചിഹ്നത്തിന് കീഴിൽ എക്സ്പ്രഷൻ ലഭിക്കുന്നത് ശ്രദ്ധിക്കേണ്ടതാണ്, ഇത് പൂജ്യത്തെ പൂജ്യത്താൽ ഹരിച്ചാൽ അനിശ്ചിതത്വമല്ല, കാരണം ന്യൂമറേറ്ററിൽ അനന്തമായ മൂല്യം അടങ്ങിയിട്ടില്ല, പക്ഷേ കൃത്യമായി പൂജ്യം. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, സ്ഥിരമായ പ്രവർത്തനത്തിന്റെ വർദ്ധനവ് എല്ലായ്പ്പോഴും പൂജ്യമാണ്.

അങ്ങനെ, സ്ഥിരമായ ഒരു പ്രവർത്തനത്തിന്റെ ഡെറിവേറ്റീവ്നിർവചനത്തിന്റെ മുഴുവൻ ഡൊമെയ്‌നിലുടനീളം പൂജ്യത്തിന് തുല്യമാണ്.

ഒരു പവർ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ്.

ഡെറിവേറ്റീവ് ഫോർമുല വൈദ്യുതി പ്രവർത്തനംപോലെ തോന്നുന്നു , എവിടെ ഘാതം പി- ഏതെങ്കിലും യഥാർത്ഥ സംഖ്യ.

നമുക്ക് ആദ്യം സ്വാഭാവിക ഘാതം, അതായത്, ഫോർമുല തെളിയിക്കാം p = 1, 2, 3, …

ഡെറിവേറ്റീവിന്റെ നിർവചനം ഞങ്ങൾ ഉപയോഗിക്കും. ഒരു പവർ ഫംഗ്‌ഷന്റെ ഇൻക്രിമെന്റിന്റെയും ആർഗ്യുമെന്റിന്റെ വർദ്ധനവിന്റെയും അനുപാതത്തിന്റെ പരിധി നമുക്ക് എഴുതാം:

ന്യൂമറേറ്ററിലെ പദപ്രയോഗം ലളിതമാക്കാൻ, ഞങ്ങൾ ന്യൂട്ടൺ ബൈനോമിയൽ ഫോർമുലയിലേക്ക് തിരിയുന്നു:

അതിനാൽ,

ഒരു സ്വാഭാവിക ഘാതകത്തിനായുള്ള ഒരു പവർ ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവിനുള്ള സൂത്രവാക്യം ഇത് തെളിയിക്കുന്നു.

ഒരു എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ്.

നിർവചനത്തെ അടിസ്ഥാനമാക്കി ഡെറിവേറ്റീവ് ഫോർമുലയുടെ വ്യുൽപ്പന്നം ഞങ്ങൾ അവതരിപ്പിക്കുന്നു:

ഞങ്ങൾ അനിശ്ചിതത്വത്തിൽ എത്തിയിരിക്കുന്നു. ഇത് വികസിപ്പിക്കുന്നതിന്, ഞങ്ങൾ ഒരു പുതിയ വേരിയബിൾ അവതരിപ്പിക്കുന്നു, കൂടാതെ . പിന്നെ . അവസാന സംക്രമണത്തിൽ, ഒരു പുതിയ ലോഗരിഥമിക് ബേസിലേക്ക് മാറുന്നതിനുള്ള ഫോർമുല ഞങ്ങൾ ഉപയോഗിച്ചു.

നമുക്ക് യഥാർത്ഥ പരിധിയിലേക്ക് മാറ്റിസ്ഥാപിക്കാം:

ശ്രദ്ധേയമായ രണ്ടാമത്തെ പരിധി ഞങ്ങൾ ഓർക്കുകയാണെങ്കിൽ, എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവിനുള്ള ഫോർമുലയിൽ ഞങ്ങൾ എത്തിച്ചേരുന്നു:

ഒരു ലോഗരിതമിക് ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവ്.

എല്ലാവർക്കുമായി ഒരു ലോഗരിഥമിക് ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവിനുള്ള ഫോർമുല നമുക്ക് തെളിയിക്കാം xനിർവചനത്തിന്റെ ഡൊമെയ്‌നിൽ നിന്നും അടിസ്ഥാനത്തിന്റെ എല്ലാ സാധുവായ മൂല്യങ്ങളിൽ നിന്നും എലോഗരിതം ഡെറിവേറ്റീവിന്റെ നിർവ്വചനം അനുസരിച്ച് ഞങ്ങൾക്ക് ഉണ്ട്:

നിങ്ങൾ ശ്രദ്ധിച്ചതുപോലെ, തെളിവ് സമയത്ത് ലോഗരിതത്തിന്റെ സവിശേഷതകൾ ഉപയോഗിച്ചാണ് പരിവർത്തനങ്ങൾ നടത്തിയത്. സമത്വം രണ്ടാമത്തെ ശ്രദ്ധേയമായ പരിധി കാരണം ശരിയാണ്.

ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ ഡെറിവേറ്റീവുകൾ.

ത്രികോണമിതി ഫംഗ്‌ഷനുകളുടെ ഡെറിവേറ്റീവുകൾക്കായുള്ള ഫോർമുലകൾ ലഭിക്കുന്നതിന്, ഞങ്ങൾ ചില ത്രികോണമിതി സൂത്രവാക്യങ്ങളും അതുപോലെ തന്നെ ആദ്യത്തെ ശ്രദ്ധേയമായ പരിധിയും ഓർക്കേണ്ടതുണ്ട്.

നമുക്കുള്ള സൈൻ ഫംഗ്‌ഷനുള്ള ഡെറിവേറ്റീവിന്റെ നിർവചനം പ്രകാരം .

നമുക്ക് സൈൻസ് ഫോർമുലയുടെ വ്യത്യാസം ഉപയോഗിക്കാം:

ആദ്യത്തെ ശ്രദ്ധേയമായ പരിധിയിലേക്ക് തിരിയാൻ ഇത് ശേഷിക്കുന്നു:

അങ്ങനെ, ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവ് പാപം xഇതുണ്ട് cos x.

കോസൈന്റെ ഡെറിവേറ്റീവിനുള്ള സൂത്രവാക്യം അതേ രീതിയിൽ തന്നെ തെളിയിക്കപ്പെട്ടിരിക്കുന്നു.

അതിനാൽ, പ്രവർത്തനത്തിന്റെ ഡെറിവേറ്റീവ് cos xഇതുണ്ട് – പാപം x.

തെളിയിക്കപ്പെട്ട ഡിഫറൻഷ്യേഷൻ നിയമങ്ങൾ (ഒരു ഭിന്നസംഖ്യയുടെ ഡെറിവേറ്റീവ്) ഉപയോഗിച്ച് ടാൻജെന്റിനും കോട്ടാൻജെന്റിനുമുള്ള ഡെറിവേറ്റീവുകളുടെ പട്ടികയ്ക്കായി ഞങ്ങൾ ഫോർമുലകൾ കണ്ടെത്തും.

ഹൈപ്പർബോളിക് ഫംഗ്ഷനുകളുടെ ഡെറിവേറ്റീവുകൾ.

ഡെറിവേറ്റീവുകളുടെ പട്ടികയിൽ നിന്ന് എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവിനുള്ള ഡിഫറൻഷ്യേഷൻ നിയമങ്ങളും ഫോർമുലയും ഹൈപ്പർബോളിക് സൈൻ, കോസൈൻ, ടാൻജെന്റ്, കോട്ടാൻജെന്റ് എന്നിവയുടെ ഡെറിവേറ്റീവുകൾക്കായി സൂത്രവാക്യങ്ങൾ രൂപപ്പെടുത്താൻ ഞങ്ങളെ അനുവദിക്കുന്നു.

വിപരീത പ്രവർത്തനത്തിന്റെ ഡെറിവേറ്റീവ്.

അവതരണ വേളയിൽ ആശയക്കുഴപ്പം ഒഴിവാക്കുന്നതിന്, വ്യതിരിക്തത നടപ്പിലാക്കുന്ന ഫംഗ്‌ഷന്റെ വാദം സബ്‌സ്‌ക്രിപ്‌റ്റിൽ സൂചിപ്പിക്കാം, അതായത്, ഇത് ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് ആണ് f(x)എഴുതിയത് x.

ഇനി നമുക്ക് രൂപപ്പെടുത്താം ഒരു വിപരീത പ്രവർത്തനത്തിന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുന്നതിനുള്ള നിയമം.

പ്രവർത്തനങ്ങൾ അനുവദിക്കുക y = f(x)ഒപ്പം x = g(y)പരസ്പരം വിപരീതമായി, യഥാക്രമം ഇടവേളകളിൽ നിർവചിച്ചിരിക്കുന്നു. ഒരു ബിന്ദുവിൽ ഫംഗ്‌ഷന്റെ പൂജ്യമല്ലാത്ത ഒരു പരിമിതമായ ഡെറിവേറ്റീവ് ഉണ്ടെങ്കിൽ f(x), അപ്പോൾ പോയിന്റിൽ വിപരീത പ്രവർത്തനത്തിന്റെ ഒരു പരിമിതമായ ഡെറിവേറ്റീവ് ഉണ്ട് g(y), ഒപ്പം . മറ്റൊരു പോസ്റ്റിൽ .

ഈ നിയമം ആർക്കും പരിഷ്കരിക്കാവുന്നതാണ് xഇടവേള മുതൽ, നമുക്ക് ലഭിക്കും .

ഈ ഫോർമുലകളുടെ സാധുത പരിശോധിക്കാം.

സ്വാഭാവിക ലോഗരിതത്തിന്റെ വിപരീത പ്രവർത്തനം നമുക്ക് കണ്ടെത്താം (ഇവിടെ വൈഒരു ഫംഗ്ഷൻ ആണ്, ഒപ്പം x- വാദം). എന്നതിനായുള്ള ഈ സമവാക്യം പരിഹരിച്ചു x, നമുക്ക് ലഭിക്കുന്നു (ഇവിടെ xഒരു ഫംഗ്ഷൻ ആണ്, ഒപ്പം വൈ- അവളുടെ വാദം). അതാണ്, പരസ്പരം വിപരീത പ്രവർത്തനങ്ങളും.

ഡെറിവേറ്റീവുകളുടെ പട്ടികയിൽ നിന്ന് നമുക്ക് അത് കാണാം ഒപ്പം .

വിപരീത ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവുകൾ കണ്ടെത്തുന്നതിനുള്ള സൂത്രവാക്യങ്ങൾ സമാന ഫലങ്ങളിലേക്ക് നമ്മെ നയിക്കുന്നുവെന്ന് ഉറപ്പാക്കാം:

ജ്യാമിതിയുടെയും ഗണിതശാസ്ത്രത്തിന്റെയും ഗതിയിൽ നിന്ന്, ഒരു രൂപത്തിന്റെ വിസ്തീർണ്ണം, വ്യത്യാസങ്ങൾ, പ്രവർത്തനങ്ങളുടെ പരിധികൾ, അതുപോലെ പരിധികൾ എന്നിവയിലൂടെ ഒരു ഡെറിവേറ്റീവ് എന്ന ആശയം അവരെ അറിയിക്കുന്നു എന്ന വസ്തുത സ്കൂൾ കുട്ടികൾ പരിചിതമാണ്. ഡെറിവേറ്റീവ് എന്ന ആശയം മറ്റൊരു കോണിൽ നിന്ന് നോക്കാനും ഡെറിവേറ്റീവ്, ത്രികോണമിതി ഫംഗ്ഷനുകൾ എങ്ങനെ ബന്ധിപ്പിക്കാമെന്ന് നിർണ്ണയിക്കാനും ശ്രമിക്കാം.

അതിനാൽ, y = f(x) എന്ന അമൂർത്ത ഫംഗ്‌ഷൻ വിവരിക്കുന്ന ചില അനിയന്ത്രിതമായ വക്രങ്ങൾ നമുക്ക് പരിഗണിക്കാം.

ഷെഡ്യൂൾ ഒരു ടൂറിസ്റ്റ് റൂട്ടിന്റെ ഭൂപടമാണെന്ന് സങ്കൽപ്പിക്കുക. ചിത്രത്തിലെ ഇൻക്രിമെന്റ് ∆x (ഡെൽറ്റ x) പാതയുടെ ഒരു നിശ്ചിത ദൂരമാണ്, കൂടാതെ ∆y എന്നത് സമുദ്രനിരപ്പിന് മുകളിലുള്ള പാതയുടെ ഉയരത്തിലെ മാറ്റമാണ്.
അപ്പോൾ ∆x/∆y എന്ന അനുപാതം റൂട്ടിന്റെ ഓരോ സെഗ്‌മെന്റിലെയും റൂട്ടിന്റെ സങ്കീർണ്ണതയെ ചിത്രീകരിക്കും. ഈ മൂല്യം മനസിലാക്കിയ ശേഷം, കയറ്റമോ ഇറക്കമോ കുത്തനെയുള്ളതാണോ, നിങ്ങൾക്ക് കയറാനുള്ള ഉപകരണങ്ങൾ ആവശ്യമുണ്ടോ, വിനോദസഞ്ചാരികൾക്ക് ഒരു നിശ്ചിത ആവശ്യമുണ്ടോ എന്ന് നിങ്ങൾക്ക് ആത്മവിശ്വാസത്തോടെ പറയാൻ കഴിയും കായികപരിശീലനം. എന്നാൽ ഈ സൂചകം ഒരു ചെറിയ ഇടവേള ∆x-ന് മാത്രമേ സാധുതയുള്ളൂ.

യാത്രയുടെ സംഘാടകൻ ട്രയലിന്റെ ആരംഭ, അവസാന പോയിന്റുകൾക്കുള്ള മൂല്യങ്ങൾ എടുക്കുകയാണെങ്കിൽ, അതായത്, ∆x റൂട്ടിന്റെ ദൈർഘ്യത്തിന് തുല്യമാണ്, തുടർന്ന് ബുദ്ധിമുട്ടിന്റെ അളവിനെക്കുറിച്ചുള്ള വസ്തുനിഷ്ഠമായ ഡാറ്റ നേടാൻ അദ്ദേഹത്തിന് കഴിയില്ല. യാത്രയുടെ. അതിനാൽ, പാതയിലെ മാറ്റങ്ങളുടെ വേഗതയും “ഗുണനിലവാരവും” ചിത്രീകരിക്കുന്ന മറ്റൊരു ഗ്രാഫ് നിർമ്മിക്കേണ്ടത് ആവശ്യമാണ്, മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, റൂട്ടിന്റെ ഓരോ “മീറ്ററിനും” ∆x/∆y അനുപാതം നിർണ്ണയിക്കുക.

ഈ ഗ്രാഫ് ഒരു നിർദ്ദിഷ്‌ട പാതയ്‌ക്കുള്ള ഒരു വിഷ്വൽ ഡെറിവേറ്റീവായിരിക്കും കൂടാതെ താൽപ്പര്യത്തിന്റെ ഓരോ ഇടവേളയിലും അതിന്റെ മാറ്റങ്ങളെ വസ്തുനിഷ്ഠമായി വിവരിക്കുകയും ചെയ്യും. ഇത് പരിശോധിക്കുന്നത് വളരെ ലളിതമാണ്; ∆x/∆y മൂല്യം x, y എന്നിവയുടെ ഒരു പ്രത്യേക മൂല്യത്തിന് വേണ്ടി എടുത്ത ഒരു വ്യത്യാസമല്ലാതെ മറ്റൊന്നുമല്ല. നിർദിഷ്ട കോർഡിനേറ്റുകളിലേക്കല്ല, മൊത്തത്തിലുള്ള ഫംഗ്‌ഷനിലേക്കാണ് നമുക്ക് വ്യത്യാസം പ്രയോഗിക്കുന്നത്:

ഡെറിവേറ്റീവ്, ത്രികോണമിതി പ്രവർത്തനങ്ങൾ

ത്രികോണമിതി പ്രവർത്തനങ്ങൾ ഡെറിവേറ്റീവുകളുമായി അഭേദ്യമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. ഇനിപ്പറയുന്ന ഡ്രോയിംഗിൽ നിന്ന് ഇത് മനസ്സിലാക്കാം. കോർഡിനേറ്റ് അച്ചുതണ്ടിന്റെ ചിത്രം Y = f (x) - നീല കർവ് ഫംഗ്ഷൻ കാണിക്കുന്നു.

K (x0; f (x0)) ഒരു അനിയന്ത്രിതമായ പോയിന്റാണ്, x0 + ∆x എന്നത് OX അക്ഷത്തോടൊപ്പമുള്ള ഇൻക്രിമെന്റാണ്, കൂടാതെ F (x0 + ∆x) എന്നത് ഒരു നിശ്ചിത പോയിന്റ് L-ൽ OY അക്ഷത്തിനൊപ്പം വർദ്ധനവുമാണ്.

K, L എന്നീ പോയിന്റുകളിലൂടെ ഒരു നേർരേഖ വരച്ച് നമുക്ക് നിർമ്മിക്കാം മട്ട ത്രികോണംകെ.എൽ.എൻ. നിങ്ങൾ Y = f (x) ഗ്രാഫിനൊപ്പം LN സെഗ്‌മെന്റ് മാനസികമായി നീക്കുകയാണെങ്കിൽ, L, N പോയിന്റുകൾ K (x0; f (x0)) മൂല്യങ്ങളിലേക്ക് ചായും. നമുക്ക് ഈ പോയിന്റിനെ ഗ്രാഫിന്റെ സോപാധികമായ തുടക്കം എന്ന് വിളിക്കാം - പരിധി; ഫംഗ്ഷൻ അനന്തമാണെങ്കിൽ, കുറഞ്ഞത് ഒരു ഇടവേളയിലെങ്കിലും, ഈ പ്രവണതയും അനന്തമായിരിക്കും, അതിന്റെ പരിമിത മൂല്യം 0 ന് അടുത്താണ്.

ഈ പ്രവണതയുടെ സ്വഭാവം തിരഞ്ഞെടുത്ത പോയിന്റ് y = kx + b അല്ലെങ്കിൽ യഥാർത്ഥ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവിന്റെ ഗ്രാഫ് ഉപയോഗിച്ചോ പച്ച നേർരേഖയിലോ വിവരിക്കാം.

എന്നാൽ ഇവിടെ ത്രികോണമിതി എവിടെയാണ്?! എല്ലാം വളരെ ലളിതമാണ്, വലത് ത്രികോണം KLN പരിഗണിക്കുക. ഒരു നിർദ്ദിഷ്‌ട ബിന്ദു K യുടെ ഡിഫറൻഷ്യൽ മൂല്യം ആംഗിൾ α അല്ലെങ്കിൽ ∠K ന്റെ ടാൻജന്റ് ആണ്:

ഈ രീതിയിൽ, നമുക്ക് ഡെറിവേറ്റീവിന്റെ ജ്യാമിതീയ അർത്ഥവും ത്രികോണമിതി പ്രവർത്തനങ്ങളുമായുള്ള ബന്ധവും വിവരിക്കാം.

ത്രികോണമിതി പ്രവർത്തനങ്ങൾക്കുള്ള ഡെറിവേറ്റീവ് ഫോർമുലകൾ

ഡെറിവേറ്റീവ് നിർണ്ണയിക്കുമ്പോൾ സൈൻ, കോസൈൻ, ടാൻജെന്റ്, കോട്ടാൻജെന്റ് എന്നിവയുടെ പരിവർത്തനങ്ങൾ ഓർമ്മിക്കേണ്ടതാണ്.

അവസാനത്തെ രണ്ട് സൂത്രവാക്യങ്ങൾ ഒരു പിശകല്ല, ഒരു ലളിതമായ ആർഗ്യുമെന്റിന്റെ ഡെറിവേറ്റീവും അതേ ശേഷിയിലുള്ള ഒരു ഫംഗ്ഷനും നിർവചിക്കുന്നത് തമ്മിൽ വ്യത്യാസമുണ്ടെന്നതാണ് കാര്യം.

സൈനസ്, കോസൈൻ, ടാൻജെന്റ്, കോട്ടാൻജെന്റ് എന്നിവയുടെ ഡെറിവേറ്റീവുകൾക്കായുള്ള ഫോർമുലകളുള്ള ഒരു താരതമ്യ പട്ടിക നോക്കാം:

ആർക്‌സൈൻ, ആർക്കോസിൻ, ആർക്‌റ്റഞ്ചന്റ്, ആർക്കോടാൻജെന്റ് എന്നിവയുടെ ഡെറിവേറ്റീവുകൾക്കായും ഫോർമുലകൾ ഉരുത്തിരിഞ്ഞുവന്നിട്ടുണ്ട്, എന്നിരുന്നാലും അവ വളരെ അപൂർവമായി മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ:

സാധാരണ USE ടാസ്‌ക്കുകൾ വിജയകരമായി പരിഹരിക്കുന്നതിന് മുകളിലുള്ള സൂത്രവാക്യങ്ങൾ പര്യാപ്തമല്ല എന്നത് ശ്രദ്ധിക്കേണ്ടതാണ്, ഇത് ഒരു ത്രികോണമിതി പദപ്രയോഗത്തിന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുന്നതിനുള്ള ഒരു നിർദ്ദിഷ്ട ഉദാഹരണം പരിഹരിക്കുമ്പോൾ പ്രദർശിപ്പിക്കും.

വ്യായാമം ചെയ്യുക: ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുകയും അതിന്റെ മൂല്യം π/4 ന് കണ്ടെത്തുകയും ചെയ്യേണ്ടത് ആവശ്യമാണ്:

പരിഹാരം: y' കണ്ടെത്തുന്നതിന് യഥാർത്ഥ ഫംഗ്‌ഷനെ ഒരു ഡെറിവേറ്റീവാക്കി മാറ്റുന്നതിനുള്ള അടിസ്ഥാന സൂത്രവാക്യങ്ങൾ ഓർമ്മിക്കേണ്ടത് ആവശ്യമാണ്, അതായത്.

വിഷയം:"ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ ഡെറിവേറ്റീവ്".
പാഠ തരം- അറിവ് ഏകീകരിക്കുന്നതിനുള്ള ഒരു പാഠം.
പാഠ രൂപം- സംയോജിത പാഠം.
ഈ വിഭാഗത്തിനായുള്ള പാഠ സംവിധാനത്തിൽ പാഠത്തിന്റെ സ്ഥാനം- പൊതു പാഠം.
ലക്ഷ്യങ്ങൾ സമഗ്രമായി സജ്ജീകരിച്ചിരിക്കുന്നു:

• വിദ്യാഭ്യാസപരമായ:വ്യത്യാസത്തിന്റെ നിയമങ്ങൾ അറിയുക, സമവാക്യങ്ങളും അസമത്വങ്ങളും പരിഹരിക്കുമ്പോൾ ഡെറിവേറ്റീവുകൾ കണക്കാക്കുന്നതിനുള്ള നിയമങ്ങൾ പ്രയോഗിക്കാൻ കഴിയും; കമ്പ്യൂട്ടേഷണൽ, കഴിവുകൾ, കഴിവുകൾ എന്നിവ ഉൾപ്പെടെ വിഷയം മെച്ചപ്പെടുത്തുക; കമ്പ്യൂട്ടർ കഴിവുകൾ;
• വികസിപ്പിക്കുന്നു:ബൗദ്ധികവും യുക്തിപരവുമായ കഴിവുകളുടെയും വൈജ്ഞാനിക താൽപ്പര്യങ്ങളുടെയും വികസനം;
• വിദ്യാഭ്യാസപരമായ:പൊരുത്തപ്പെടുത്താനുള്ള കഴിവ് വളർത്തിയെടുക്കുക ആധുനിക സാഹചര്യങ്ങൾപരിശീലനം.

രീതികൾ:

• പ്രത്യുൽപാദനവും ഉൽപാദനക്ഷമതയും;
• പ്രായോഗികവും വാക്കാലുള്ളതും;
• സ്വതന്ത്ര ജോലി;
• പ്രോഗ്രാം ചെയ്ത പഠനം, ടി.എസ്.ഒ.
• ഫ്രണ്ടൽ, ഗ്രൂപ്പ്, എന്നിവയുടെ സംയോജനം വ്യക്തിഗത ജോലി;
• വ്യത്യസ്തമായ പഠനം;
• ഇൻഡക്റ്റീവ്-ഡിഡക്റ്റീവ്.

നിയന്ത്രണ രൂപങ്ങൾ:

• വാക്കാലുള്ള സർവേ,
• പ്രോഗ്രാം ചെയ്ത നിയന്ത്രണം,
• സ്വതന്ത്ര ജോലി,
• കമ്പ്യൂട്ടറിലെ വ്യക്തിഗത ജോലികൾ,
• വിദ്യാർത്ഥിയുടെ ഡയഗ്നോസ്റ്റിക് കാർഡ് ഉപയോഗിച്ച് സമപ്രായക്കാരുടെ അവലോകനം.

ക്ലാസുകൾക്കിടയിൽ

I. സംഘടനാ നിമിഷം

II. റഫറൻസ് അറിവ് അപ്ഡേറ്റ് ചെയ്യുന്നു

a) ലക്ഷ്യങ്ങളും ലക്ഷ്യങ്ങളും ആശയവിനിമയം:

• വ്യത്യാസത്തിന്റെ നിയമങ്ങൾ അറിയുക, പ്രശ്നങ്ങൾ, സമവാക്യങ്ങൾ, അസമത്വങ്ങൾ എന്നിവ പരിഹരിക്കുമ്പോൾ ഡെറിവേറ്റീവുകൾ കണക്കാക്കുന്നതിനുള്ള നിയമങ്ങൾ പ്രയോഗിക്കാൻ കഴിയും;
• കമ്പ്യൂട്ടേഷണൽ, കഴിവുകൾ, കഴിവുകൾ എന്നിവ ഉൾപ്പെടെ വിഷയം മെച്ചപ്പെടുത്തുക; കമ്പ്യൂട്ടർ കഴിവുകൾ;
• ബുദ്ധിപരവും യുക്തിപരവുമായ കഴിവുകളും വൈജ്ഞാനിക താൽപ്പര്യങ്ങളും വികസിപ്പിക്കുക;
• ആധുനിക പഠന സാഹചര്യങ്ങളുമായി പൊരുത്തപ്പെടുത്തൽ വളർത്തുക.

ബി) വിദ്യാഭ്യാസ സാമഗ്രികളുടെ ആവർത്തനം

ഡെറിവേറ്റീവുകൾ കണക്കാക്കുന്നതിനുള്ള നിയമങ്ങൾ (ശബ്ദമുള്ള കമ്പ്യൂട്ടറിൽ ഫോർമുലകളുടെ ആവർത്തനം). ഡോക്.7.

1. സൈനിന്റെ ഡെറിവേറ്റീവ് എന്താണ്?
2. കോസൈന്റെ ഡെറിവേറ്റീവ് എന്താണ്?
3. സ്പർശനത്തിന്റെ ഡെറിവേറ്റീവ് എന്താണ്?
4. കോട്ടാൻജെന്റിന്റെ ഡെറിവേറ്റീവ് എന്താണ്?

III. വാക്കാലുള്ള ജോലി

നോട്ട്ബുക്കുകൾ കൈമാറ്റം ചെയ്യുക. ഡയഗ്നോസ്റ്റിക് കാർഡുകളിൽ, ശരിയായി പൂർത്തിയാക്കിയ ടാസ്ക്കുകൾ + ചിഹ്നം ഉപയോഗിച്ച് അടയാളപ്പെടുത്തുക, കൂടാതെ തെറ്റായി പൂർത്തിയാക്കിയ ടാസ്ക്കുകൾ - ചിഹ്നം ഉപയോഗിച്ച് അടയാളപ്പെടുത്തുക.

IV. ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് സമവാക്യങ്ങൾ പരിഹരിക്കുന്നു

– ഡെറിവേറ്റീവ് പൂജ്യമാകുന്ന പോയിന്റുകൾ എങ്ങനെ കണ്ടെത്താം?

ഡെറിവേറ്റീവ് ആയ പോയിന്റുകൾ കണ്ടെത്താൻ ഈ പ്രവർത്തനംപൂജ്യത്തിന് തുല്യമാണ്, നിങ്ങൾക്ക് ഇത് ആവശ്യമാണ്:

- പ്രവർത്തനത്തിന്റെ സ്വഭാവം നിർണ്ണയിക്കുക;
- പ്രദേശം കണ്ടെത്തുക ഫംഗ്ഷൻ നിർവചനങ്ങൾ,
- ഈ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക,
- സമവാക്യം പരിഹരിക്കുക എഫ് "(x) = 0,
- ശരിയായ ഉത്തരം തിരഞ്ഞെടുക്കുക.

ടാസ്ക് 1.

നൽകിയത്: ചെയ്തത് = എക്സ്- പാപം x.
കണ്ടെത്തുക:ഡെറിവേറ്റീവ് പൂജ്യമായ പോയിന്റുകൾ.
പരിഹാരം.എല്ലാ യഥാർത്ഥ സംഖ്യകളുടെയും ഗണത്തിൽ ഫംഗ്‌ഷനുകൾ നിർവചിക്കപ്പെടുകയും വ്യത്യാസപ്പെടുത്തുകയും ചെയ്യുന്നതിനാൽ, എല്ലാ യഥാർത്ഥ സംഖ്യകളുടെയും ഗണത്തിൽ ഫംഗ്‌ഷൻ നിർവചിക്കപ്പെടുകയും വ്യത്യാസപ്പെടുത്തുകയും ചെയ്യുന്നു. ജി(x) = xഒപ്പം ടി(x) = – പാപം x.
വ്യത്യസ്ത നിയമങ്ങൾ ഉപയോഗിച്ച്, നമുക്ക് ലഭിക്കും എഫ് "(x) = (x- പാപം x)" = (x)"- (പാപം x)" = 1 – കോസ് x.
എങ്കിൽ എഫ് "(x) = 0, പിന്നെ 1 - കോസ് x = 0.
കോസ് x= 1/; ഡിനോമിനേറ്ററിലെ യുക്തിരാഹിത്യത്തെ നമുക്ക് ഒഴിവാക്കാം, നമുക്ക് കോസ് ലഭിക്കും x = /2.
ഫോർമുല അനുസരിച്ച് ടി= ± ആർക്കോസ് എ+ 2n, n Z, നമുക്ക് ലഭിക്കുന്നത്: എക്സ്= ± ആർക്കോസ് /2 + 2n, n Z.
ഉത്തരം: x = ± /4 + 2n, n Z.

V. ഒരു അൽഗോരിതം ഉപയോഗിച്ച് സമവാക്യങ്ങൾ പരിഹരിക്കുന്നു

ഡെറിവേറ്റീവ് അപ്രത്യക്ഷമാകുന്ന പോയിന്റുകൾ കണ്ടെത്തുക.

വിദ്യാർത്ഥിക്ക് മൂന്ന് ഉദാഹരണങ്ങളിൽ ഏതെങ്കിലും തിരഞ്ഞെടുക്കാം. ആദ്യ ഉദാഹരണം റേറ്റുചെയ്തിരിക്കുന്നു " 3 ", രണ്ടാമത്തേത് -" 4 ", മൂന്നാമത് -" 5 " പരസ്പര പരിശോധനയ്ക്ക് ശേഷം നോട്ട്ബുക്കുകളിലെ പരിഹാരം. ഒരു വിദ്യാർത്ഥി ബോർഡിൽ തീരുമാനിക്കുന്നു. പരിഹാരം തെറ്റാണെന്ന് തെളിഞ്ഞാൽ, വിദ്യാർത്ഥി അൽഗോരിതത്തിലേക്ക് മടങ്ങി വീണ്ടും പരിഹരിക്കാൻ ശ്രമിക്കേണ്ടതുണ്ട്.

പ്രോഗ്രാം ചെയ്ത നിയന്ത്രണം.

ഓപ്ഷൻ 1		ഓപ്ഷൻ 2
വൈ = 2എക്സ് 3		വൈ = 3എക്സ് 2
വൈ = 1/4 എക്സ് 4 + 2എക്സ് 2 – 7		വൈ = 1/2 എക്സ് 4 + 4എക്സ് + 5
വൈ = എക്സ് 3 + 4എക്സ് 2 – 3എക്സ്. സമവാക്യം പരിഹരിക്കുക വൈ " = 0		വൈ = 2എക്സ് 3 – 9എക്സ് 2 + 12എക്സ് + 7. സമവാക്യം പരിഹരിക്കുക വൈ " = 0.
വൈ= പാപം 2 എക്സ്- ചെലവ് 3 എക്സ്.		വൈ= വില 2 എക്സ്- പാപം 3 എക്സ്.
വൈ= ടിജി എക്സ്-ctg( എക്സ് + /4).		വൈ=ctg എക്സ്+ tg( എക്സ് – /4).
വൈ= പാപം 2 എക്സ്.		വൈ= വില 2 എക്സ്.
ഉത്തര ഓപ്ഷനുകൾ.
പൾപ്പിറ്റിസ് പള്ളിയുടെയും വീട്ടിലെയും പ്രാർത്ഥനകളുടെ വിശദീകരണങ്ങൾ പൾപ്പിറ്റിസ് വലിയ ക്രിസ്ത്യൻ ലൈബ്രറി ഓർത്തോപീഡിക്സ് ഒരു പഴയ കത്തിച്ച പള്ളി മെഴുകുതിരി കണ്ടെത്തി സൈറ്റിൽ പുതിയത് എതിരാളികളുടെ അവലോകനങ്ങളുമായുള്ള ബന്ധങ്ങൾ നശിപ്പിക്കുന്നതിനുള്ള ശക്തമായ റൂണിക് ലാപ്പൽ റണ്ണുകൾ 29-ാം ചാന്ദ്ര ദിനത്തിൽ വഴക്ക്. ചന്ദ്ര ജന്മദിനം. ഇരുപത്തിയൊമ്പതാം ചാന്ദ്ര ദിനത്തിൽ ജനിച്ചവരുടെ സ്വഭാവഗുണങ്ങൾ സെന്റ് നിക്കോളാസ് ദി വണ്ടർ വർക്കറുടെ അവശിഷ്ടങ്ങൾ പാപമോചന ചടങ്ങിൽ എന്താണ് പറയേണ്ടത് കെരൂബ് എന്ന വാക്കിന്റെ അർത്ഥം എന്താണ് കെരൂബ് > ഏറ്റവും ജനപ്രിയമായ ബഹുമാനപ്പെട്ട ലിയോ, ഒപ്റ്റിന മിച്ചുറിൻ ബിഷപ്പ് ഹെർമോഗന്റെയും മോർഷയുടെയും ക്രിസ്തുമസ് സന്ദേശം ആർക്കിമാൻഡ്രൈറ്റ് ജെറോം (ഷുറിജിൻ): “കർത്താവ് എനിക്ക് സ്നേഹം നൽകണമെന്ന് ഞാൻ പ്രാർത്ഥിക്കുന്നു ജെറോം ഷുറിഗിന്റെ ജീവചരിത്രം രസകരമായ അന്വേഷണ ജോലികൾ വിദേശ കഥാകൃത്തുക്കൾ വിദേശ എഴുത്തുകാരുടെ കഥകളും കഥകളും © 2023. ഡെന്റൽ കൺസൾട്ടേഷൻ പോർട്ടൽ. ജനപ്രിയ വിഭാഗങ്ങൾ ഓർത്തോപീഡിക്സ് പൊതിഞ്ഞ നാവ് വായിൽ നിന്ന് മണം പ്രായപൂര്ത്തിയായിട്ടുവരുന്ന പല്ല് മോണകൾ സ്റ്റോമാറ്റിറ്റിസ് നീക്കം