Kira kamiran menggunakan kaedah pengamiran mengikut bahagian. Kalkulator dalam talian Kira kamiran tak tentu (antiterbitan)

Formula berikut dipanggil integrasi mengikut formula bahagian dalam kamiran tak tentu:

Untuk menggunakan formula penyepaduan mengikut bahagian, integrand mesti dibahagikan kepada dua faktor. Salah satunya dilambangkan dengan u, dan selebihnya merujuk kepada faktor kedua dan dilambangkan dengan dv. Kemudian dengan pembezaan kita dapati du dan integrasi - fungsi v. Pada masa yang sama, untuk u dv- bahagian integrand sedemikian yang boleh disepadukan dengan mudah.

Bilakah berfaedah untuk menggunakan kaedah penyepaduan mengikut bahagian? Jadi bila integrand mengandungi :

1) - fungsi logaritma, serta fungsi trigonometri songsang (dengan awalan "arka"), kemudian, berdasarkan pengalaman jangka panjang penyepaduan mengikut bahagian, fungsi ini dilambangkan dengan u;

2) , , - sinus, kosinus dan eksponen didarab dengan P(x) ialah polinomial arbitrari dalam x, maka fungsi ini dilambangkan dengan dv, dan polinomial adalah melalui u;

3) , , , , dalam kes ini penyepaduan mengikut bahagian digunakan dua kali.

Mari kita terangkan nilai kaedah penyepaduan mengikut bahagian menggunakan contoh kes pertama. Biarkan ungkapan di bawah tanda kamiran mengandungi fungsi logaritma (ini akan menjadi contoh 1). Dengan menggunakan pengamiran mengikut bahagian, kamiran sedemikian dikurangkan untuk mengira kamiran bagi fungsi algebra sahaja (paling kerap polinomial), iaitu, tidak mengandungi logaritma atau songsang. fungsi trigonometri. Menggunakan rumus penyepaduan mengikut bahagian yang diberikan pada awal pelajaran

kita memperoleh dalam sebutan pertama (tanpa kamiran) fungsi logaritma, dan dalam sebutan kedua (di bawah tanda kamiran) fungsi yang tidak mengandungi logaritma. Kamiran bagi fungsi algebra adalah jauh lebih mudah daripada kamiran di bawah tanda yang mana logaritma atau fungsi trigonometri songsang ditemui secara berasingan atau bersama-sama dengan faktor algebra.

Oleh itu, menggunakan penyepaduan mengikut formula bahagian pengamiran tidak dilakukan serta-merta: mencari kamiran yang diberikan dikurangkan kepada mencari yang lain. Maksud formula pengamiran mengikut bahagian ialah hasil daripada penggunaannya, kamiran baharu menjadi jadual atau sekurang-kurangnya menjadi lebih mudah daripada yang asal.

Kaedah penyepaduan mengikut bahagian adalah berdasarkan penggunaan formula untuk membezakan hasil darab dua fungsi:

maka ia boleh ditulis dalam bentuk

yang diberikan pada awal pelajaran.

Apabila mencari dengan menyepadukan fungsi v untuknya set tak terhingga fungsi antiterbitan diperolehi. Untuk menggunakan formula penyepaduan mengikut bahagian, anda boleh mengambil mana-mana daripadanya, dan oleh itu formula yang sepadan dengan pemalar sewenang-wenangnya DENGAN, sama dengan sifar. Oleh itu, apabila mencari fungsi v pemalar sewenang-wenangnya DENGAN tidak boleh dimasukkan.

Kaedah penyepaduan mengikut bahagian mempunyai aplikasi yang sangat istimewa: ia boleh digunakan untuk memperoleh formula berulang untuk mencari fungsi antiterbitan apabila perlu untuk mengurangkan tahap fungsi di bawah tanda kamiran. Mengurangkan darjah adalah perlu apabila tiada kamiran jadual untuk, contohnya, fungsi seperti sinus dan kosinus kepada kuasa yang lebih besar daripada kedua dan hasil keluarannya. Formula berulang ialah formula untuk mencari ahli urutan seterusnya melalui ahli sebelumnya. Untuk kes yang ditunjukkan, matlamat dicapai dengan menurunkan darjah berturut-turut. Jadi, jika kamiran dan ialah sinus kepada kuasa keempat x, maka dengan menyepadukan mengikut bahagian anda boleh mencari formula untuk kamiran sinus kepada kuasa ketiga, dan seterusnya. Perenggan terakhir pelajaran ini dikhaskan untuk tugas yang diterangkan.

Mengaplikasikan integrasi mengikut bahagian bersama-sama

Contoh 1. Cari kamiran tak tentu menggunakan kaedah pengamiran mengikut bahagian:

Penyelesaian. Dalam ungkapan integrand - logaritma, yang, seperti yang telah kita ketahui, boleh dilambangkan dengan munasabah dengan u. Kami percaya bahawa , .

Kami dapati (seperti yang telah disebutkan dalam penjelasan untuk rujukan teori, kami segera memperoleh fungsi logaritma dalam sebutan pertama (tanpa kamiran), dan fungsi yang tidak mengandungi logaritma dalam sebutan kedua (di bawah tanda kamiran):

Dan sekali lagi logaritma...

Contoh 2. Cari kamiran tak tentu:

Penyelesaian. Biarlah , .

Logaritma hadir dalam petak. Ini bermakna ia perlu dibezakan sebagai fungsi yang kompleks. Kita dapati
,
.

Kami sekali lagi mencari kamiran kedua mengikut bahagian dan memperoleh kelebihan yang telah disebutkan (dalam sebutan pertama (tanpa kamiran) terdapat fungsi logaritma, dan dalam sebutan kedua (di bawah tanda kamiran) terdapat fungsi yang tidak mengandungi a logaritma).

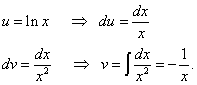
Kami dapati kamiran asal:

Contoh 3.

Penyelesaian. Arktangen, seperti logaritma, lebih baik dilambangkan dengan u. Jadi biarlah,.

Kemudian,
.

Menggunakan formula penyepaduan mengikut bahagian, kami memperoleh:

Kami mencari kamiran kedua dengan menukar pembolehubah.

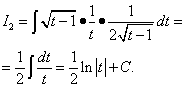
Berbalik kepada pembolehubah x, kita mendapatkan

.

Kami dapati kamiran asal:

.

Contoh 4. Cari kamiran tak tentu menggunakan kaedah pengamiran mengikut bahagian:

Penyelesaian. Adalah lebih baik untuk menandakan eksponen dengan dv. Kami membahagikan integrand kepada dua faktor. Percaya itu

Contoh 5. Cari kamiran tak tentu menggunakan kaedah pengamiran mengikut bahagian:

.

Penyelesaian. Biarlah , . Kemudian , .

Dengan menggunakan formula penyepaduan mengikut bahagian (1), kita dapati:

Contoh 6. Cari kamiran tak tentu melalui pengamiran mengikut bahagian:

Penyelesaian. Sinus, seperti eksponen, boleh dilambangkan dengan mudah dengan dv. Biarlah , .

Menggunakan formula penyepaduan mengikut bahagian, kami dapati:

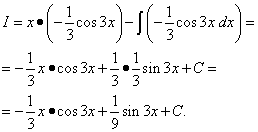
Kami menggunakan penyepaduan mengikut bahagian bersama-sama sekali lagi

Contoh 10. Cari kamiran tak tentu melalui pengamiran mengikut bahagian:

.

Penyelesaian. Seperti dalam semua kes yang serupa, adalah mudah untuk menandakan kosinus dengan dv. Kami menandakan , .

Kemudian , .

Dengan menggunakan formula penyepaduan mengikut bahagian, kami memperoleh:

Kami juga menggunakan penyepaduan mengikut bahagian pada penggal kedua. Kami menandakan , .

Menggunakan notasi ini, kami menyepadukan istilah yang disebutkan:

Sekarang kita dapati integral yang diperlukan:

Di antara kamiran yang boleh diselesaikan dengan kaedah pengamiran mengikut bahagian, terdapat juga yang tidak termasuk dalam mana-mana tiga kumpulan yang disebutkan dalam bahagian teori, yang mana ia diketahui dari amalan bahawa lebih baik dinyatakan dengan u, dan melalui apa dv. Oleh itu, dalam kes ini, anda perlu menggunakan pertimbangan kemudahan, juga diberikan dalam perenggan "Intipati kaedah penyepaduan mengikut bahagian": untuk u seseorang harus mengambil sebahagian daripada integrand yang tidak menjadi lebih rumit semasa pembezaan, tetapi dv- bahagian integrand sedemikian yang boleh disepadukan dengan mudah. Contoh terakhir pelajaran ini ialah penyelesaian bagi kamiran sedemikian.

Dengan kamiran yang pasti daripada fungsi berterusan f(x) pada segmen akhir [ a, b] (di mana ) ialah kenaikan beberapa antiderivatifnya pada segmen ini. (Secara umumnya, pemahaman akan menjadi lebih mudah jika anda mengulangi topik kamiran tak tentu) Dalam kes ini, tatatanda digunakan

Seperti yang boleh dilihat dalam graf di bawah (kenaikan fungsi antiterbitan ditunjukkan oleh ), kamiran pasti boleh sama ada positif atau nombor negatif (Ia dikira sebagai perbezaan antara nilai antiderivatif dalam had atas dan nilainya dalam had bawah, iaitu sebagai F(b) - F(a)).

Nombor a Dan b dipanggil had bawah dan atas penyepaduan, masing-masing, dan segmen [ a, b] – segmen integrasi.

Justeru, jika F(x) – beberapa fungsi antiterbitan untuk f(x), maka, mengikut definisi,

(38)

Persamaan (38) dipanggil Formula Newton-Leibniz . Beza F(b) – F(a) ditulis secara ringkas seperti berikut:

Oleh itu, kami akan menulis formula Newton-Leibniz seperti ini:

(39)

Mari kita buktikan bahawa kamiran pasti tidak bergantung pada antiterbitan bagi kamiran yang mana diambil semasa mengiranya. biarlah F(x) dan F( X) ialah antiderivatif arbitrari bagi integrand. Oleh kerana ini adalah antiterbitan fungsi yang sama, ia berbeza dengan sebutan tetap: Ф( X) = F(x) + C. sebab tu

Ini membuktikan bahawa pada segmen [ a, b] kenaikan semua antiderivatif fungsi f(x) padankan.

Oleh itu, untuk mengira kamiran pasti, adalah perlu untuk mencari sebarang antiterbitan bagi kamiran, i.e. Mula-mula anda perlu mencari kamiran tak tentu. berterusan DENGAN dikecualikan daripada pengiraan seterusnya. Kemudian formula Newton-Leibniz digunakan: nilai had atas digantikan ke dalam fungsi antiderivatif b , selanjutnya - nilai had bawah a dan perbezaan dikira F(b) - F(a) . Nombor yang terhasil akan menjadi kamiran pasti..

Pada a = b mengikut definisi diterima

Contoh 1.

Penyelesaian. Pertama, mari kita cari kamiran tak tentu:

Menggunakan formula Newton-Leibniz pada antiderivatif

(pada DENGAN= 0), kita dapat

Walau bagaimanapun, apabila mengira kamiran pasti, adalah lebih baik untuk tidak mencari antiterbitan secara berasingan, tetapi segera menulis kamiran dalam bentuk (39).

Contoh 2. Kira kamiran pasti

Penyelesaian. Menggunakan formula

Sifat kamiran pasti

Teorem 2.Nilai kamiran pasti tidak bergantung pada penetapan pembolehubah kamiran, iaitu

(40)

biarlah F(x) – antiderivatif untuk f(x). Untuk f(t) antiterbitan adalah fungsi yang sama F(t), di mana pembolehubah bebas hanya ditetapkan secara berbeza. Oleh itu,

Berdasarkan formula (39), kesamaan terakhir bermaksud kesamaan kamiran

Teorem 3.Faktor pemalar boleh dikeluarkan daripada tanda kamiran pasti, iaitu

(41)

Teorem 4.Kamiran pasti bagi hasil tambah algebra bagi bilangan terhingga fungsi adalah sama dengan hasil tambah algebra bagi kamiran pasti bagi fungsi ini, iaitu

(42)

Teorem 5.Jika segmen pengamiran dibahagikan kepada bahagian, maka kamiran pasti ke atas keseluruhan segmen sama dengan jumlah kamiran pasti di atas bahagian-bahagiannya, iaitu Jika

(43)

Teorem 6.Apabila menyusun semula had penyepaduan nilai mutlak kamiran pasti tidak berubah, tetapi hanya tandanya sahaja yang berubah, iaitu

(44)

Teorem 7(teorem nilai min). Kamiran pasti adalah sama dengan hasil darab panjang segmen kamiran dan nilai kamiran dan pada satu titik di dalamnya., iaitu

(45)

Teorem 8.Jika had atas pengamiran lebih besar daripada yang lebih rendah dan kamiran dan bukan negatif (positif), maka kamiran pasti juga bukan negatif (positif), i.e. Jika

Teorem 9.Jika had atas penyepaduan lebih besar daripada yang lebih rendah dan berfungsi dan berterusan, maka ketaksamaan

boleh diintegrasikan istilah demi istilah, iaitu

(46)

Sifat-sifat kamiran pasti memungkinkan untuk memudahkan pengiraan langsung kamiran.

Contoh 5. Kira kamiran pasti

Menggunakan Teorem 4 dan 3, dan apabila mencari antiterbitan - kamiran jadual (7) dan (6), kita memperoleh

Kamiran pasti dengan had atas pembolehubah

biarlah f(x) – berterusan pada segmen [ a, b] fungsi, dan F(x) ialah antiterbitannya. Pertimbangkan kamiran pasti

(47)

dan melalui t pembolehubah integrasi ditetapkan supaya tidak mengelirukannya had atas. Apabila ia berubah X kamiran pasti (47) juga berubah, i.e. ia adalah fungsi had atas penyepaduan X, yang kami nyatakan dengan F(X), iaitu

(48)

Mari kita buktikan bahawa fungsi F(X) ialah antiderivatif untuk f(x) = f(t). Sesungguhnya, membezakan F(X), kita mendapatkan

kerana F(x) – antiderivatif untuk f(x), A F(a) ialah nilai tetap.

Fungsi F(X) – salah satu daripada bilangan antiderivatif yang tidak terhingga untuk f(x), iaitu yang x = a pergi ke sifar. Pernyataan ini diperoleh jika dalam kesamaan (48) kita letakkan x = a dan gunakan Teorem 1 perenggan sebelumnya.

Pengiraan kamiran pasti dengan kaedah pengamiran mengikut bahagian dan kaedah perubahan pembolehubah

di mana, mengikut definisi, F(x) – antiderivatif untuk f(x). Jika kita menukar pembolehubah dalam integrand

maka, mengikut formula (16), kita boleh menulis

Dalam ungkapan ini

fungsi antiterbitan untuk

Malah, terbitannya, menurut peraturan pembezaan fungsi kompleks, adalah sama

Biarkan α dan β ialah nilai pembolehubah t, yang mana fungsi

mengambil nilai dengan sewajarnya a Dan b, iaitu

Tetapi, mengikut formula Newton-Leibniz, perbezaannya F(b) – F(a) Terdapat

Kaedah integrasi mengikut bahagian digunakan terutamanya apabila integrand terdiri daripada hasil darab dua faktor jenis tertentu. Formula integrasi mengikut bahagian kelihatan seperti:

Ia memungkinkan untuk mengurangkan pengiraan kamiran tertentu
kepada pengiraan kamiran
, yang ternyata lebih mudah daripada yang ini.

Kebanyakan kamiran yang dikira dengan kaedah pengamiran mengikut bahagian boleh dibahagikan kepada tiga kumpulan:

1. Kamiran bentuk
,
,
, Di mana
- polinomial,
– nombor tidak sama dengan sifar

Dalam kes ini, melalui menunjukkan polinomial

.

2. Kamiran bentuk
,
,
,
,
, Di mana
– polinomial.

Dalam kes ini, melalui
menandakan
, dan selebihnya integrand melalui :

3. Kamiran bentuk
,
, Di mana
– nombor.

Dalam kes ini, melalui menandakan
dan gunakan formula pengamiran mengikut bahagian dua kali, kembali sebagai hasilnya kepada kamiran asal, selepas itu kamiran asal dinyatakan daripada kesamaan.

Komen: Dalam sesetengah kes, untuk mencari kamiran tertentu, formula pengamiran mengikut bahagian mesti digunakan beberapa kali. Juga, kaedah penyepaduan mengikut bahagian digabungkan dengan kaedah lain.

Contoh 26.

Cari kamiran menggunakan kaedah mengikut bahagian: a)
; b)
.

Penyelesaian.

b)

3.1.4. Penyepaduan Fungsi Pecahan-Rasional

Fungsi rasional pecahan(pecahan rasional) ialah fungsi yang sama dengan nisbah dua polinomial:
, Di mana
– polinomial darjah
,
– polinomial darjah .

Pecahan rasional dipanggil betul, jika darjah polinomial dalam pengangka kurang daripada darjah polinomial dalam penyebut, i.e.
, jika tidak (jika
) pecahan rasional dipanggil salah.

Mana-mana pecahan rasional tak wajar boleh diwakili sebagai hasil tambah polinomial
dan betul pecahan rasional, membahagikan pengangka dengan penyebut mengikut peraturan untuk membahagi polinomial:

,

di mana
– keseluruhan bahagian daripada bahagian, - pecahan rasional wajar,
- baki bahagian.

Pecahan rasional wajar bagi bentuk:

saya. ;

II.
;

III.
;

IV.
,

di mana ,,
,
,,,
– nombor nyata dan
(mereka. trinomial kuadratik dalam penyebut III dan IV pecahan tidak mempunyai punca - diskriminasi adalah negatif) dipanggil pecahan rasional mudah I, II, III dan IV jenis.

Menggabungkan pecahan mudah

Kamiran bagi pecahan termudah bagi empat jenis dikira seperti berikut.

saya)
.

II),
.

III) Untuk menyepadukan pecahan termudah jenis III, pilih segi empat sama lengkap dalam penyebut dan gantikan
. Selepas penggantian, kamiran dibahagikan kepada dua kamiran. Kamiran pertama dikira dengan mengasingkan terbitan penyebut dalam pengangka, yang memberikan kamiran jadual, dan kamiran kedua ditukar kepada bentuk
, kerana
, yang juga memberikan kamiran jadual.

;

IV) Untuk menyepadukan pecahan termudah jenis IV, pilih segi empat sama lengkap dalam penyebut dan gantikan
. Selepas penggantian, kamiran dibahagikan kepada dua kamiran. Kamiran pertama dikira dengan penggantian
, dan yang kedua menggunakan hubungan berulang.

Contoh 27.

Cari kamiran pecahan mudah:

A)
; b)
; V)
.

Penyelesaian.

A)
.

Mana-mana pecahan rasional wajar yang penyebutnya boleh difaktorkan boleh diwakili sebagai jumlah pecahan mudah. Penguraian kepada hasil tambah pecahan mudah dijalankan menggunakan kaedah pekali tak tentu. Ia adalah seperti berikut:

sepadan dengan satu pecahan bentuk ;

– setiap faktor penyebut
sepadan dengan jumlahnya pecahan bentuk

sepadan dengan pecahan bentuk
;

– setiap faktor kuasa dua penyebut
sepadan dengan jumlahnya pecahan bentuk

di manakah pekali yang tidak ditentukan.

Untuk mencari pekali tak tentu, bahagian kanan dalam bentuk jumlah pecahan mudah dibawa kepada penyebut sepunya dan diubah. Hasilnya ialah pecahan dengan penyebut yang sama seperti di sebelah kiri persamaan. Kemudian penyebutnya dibuang dan pengangkanya disamakan. Hasilnya ialah kesamaan yang sama di mana bahagian kiri adalah polinomial dengan pekali yang diketahui, dan bahagian kanan– polinomial dengan pekali tidak ditentukan.

Terdapat dua cara untuk menentukan pekali yang tidak diketahui: kaedah pekali yang tidak diketahui dan kaedah nilai separa.

Kaedah pekali yang tidak ditentukan.

Kerana polinomial adalah sama, maka pekali pada kuasa yang sama adalah sama . Menyamakan pekali pada darjah yang sama dalam polinomial sisi kiri dan kanan, kita memperoleh sistem persamaan linear. Apabila menyelesaikan sistem, kami menentukan pekali yang tidak pasti.

Kaedah nilai peribadi.

Kerana polinomial adalah identik sama, kemudian, menggantikan di sebelah kiri dan kanan sebarang nombor, kita memperoleh kesamaan sebenar, linear berkenaan dengan pekali yang tidak diketahui. Menggantikan begitu banyak nilai , berapa banyak pekali yang tidak diketahui terdapat, kita memperoleh sistem persamaan linear. Sebaliknya Anda boleh menggantikan sebarang nombor ke bahagian kiri dan kanan, tetapi lebih mudah untuk menggantikan punca penyebut pecahan.

Selepas mencari nilai pekali yang tidak diketahui, pecahan asal ditulis sebagai jumlah pecahan mudah dalam kamiran dan pengamiran yang dibincangkan sebelum ini dijalankan ke atas setiap pecahan mudah.

Skim integrasi pecahan rasional:

1. Jika kamiran dan tidak betul, maka ia adalah perlu untuk membentangkannya sebagai hasil tambah polinomial dan pecahan rasional wajar (iaitu, bahagikan polinomial pengangka dengan polinomial penyebut dengan baki). Jika integrand adalah betul, kita terus ke titik kedua rajah.

2. Faktorkan penyebut bagi pecahan rasional wajar, jika boleh.

3. Uraikan pecahan rasional wajar kepada hasil tambah pecahan rasional mudah menggunakan kaedah pekali tak tentu.

4. Sepadukan hasil tambah pecahan polinomial dan pecahan mudah.

Contoh 28.

Cari kamiran pecahan rasional:

A)
; b)
; V)
.

Penyelesaian.

A)
.

Kerana integrand ialah pecahan rasional tak wajar, maka kita pilih keseluruhan bahagian, i.e. Mari kita bayangkan ia sebagai hasil tambah polinomial dan pecahan rasional wajar. Bahagikan polinomial dalam pengangka dengan polinomial dalam penyebut menggunakan sudut.

Kamiran asal akan mengambil bentuk:
.

Marilah kita menguraikan pecahan rasional wajar kepada jumlah pecahan mudah menggunakan kaedah pekali tak tentu:

, kita mendapatkan:

Menyelesaikan sistem persamaan linear, kami memperoleh nilai pekali yang tidak pasti: A = 1; DALAM = 3.

Kemudian pengembangan yang diperlukan mempunyai bentuk:
.

=
.

b)
.

.

Mari kita buang penyebut dan samakan sisi kiri dan kanan:

Menyamakan pekali pada darjah yang sama , kami mendapat sistem:

Dengan menyelesaikan sistem lima persamaan linear, kita dapati pekali yang tidak ditentukan:

.

Mari cari kamiran asal, dengan mengambil kira pengembangan yang terhasil:

.

V)
.

Mari kita kembangkan kamiran (pecahan rasional wajar) kepada jumlah pecahan mudah menggunakan kaedah pekali tak tentu. Kami mencari penguraian dalam bentuk:

.

Mengurangkan kepada penyebut biasa, kita mendapat:

Mari kita buang penyebut dan samakan sisi kiri dan kanan:

Untuk mencari pekali tidak pasti, kami menggunakan kaedah nilai separa. Jom tambah nilai separa, di mana faktor hilang, iaitu, kita menggantikan nilai ini ke dalam ungkapan terakhir dan mendapatkan tiga persamaan:

;
;

;
;

;
.

Kemudian pengembangan yang diperlukan mempunyai bentuk:

Mari cari kamiran asal, dengan mengambil kira pengembangan yang terhasil:

Fungsi F(x) boleh dibezakan dalam selang X tertentu dipanggil antiderivatif fungsi f(x), atau kamiran f(x), jika bagi setiap x ∈X persamaan berikut dipegang:

F " (x) = f(x). (8.1)

Mencari semua antiderivatif untuk fungsi tertentu dipanggilnya integrasi. Fungsi kamiran tak tentu f(x) pada selang tertentu X ialah set semua fungsi antiterbitan untuk fungsi f(x); jawatan -

Jika F(x) ialah beberapa antiterbitan untuk fungsi f(x), maka ∫ f(x)dx = F(x) + C, (8.2)

di mana C ialah pemalar arbitrari.

Jadual kamiran

Secara langsung dari definisi kita memperoleh sifat utama tidak kamiran pasti dan senarai kamiran jadual:

1) d∫f(x)dx=f(x)

2)∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Senarai kamiran jadual

1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sin x + C

7. = arctan x + C

8. = arcsin x + C

10. = - ctg x + C

Penggantian boleh ubah

Untuk menyepadukan banyak fungsi, gunakan kaedah penggantian pembolehubah atau penggantian, membolehkan anda mengurangkan kamiran kepada bentuk jadual.

Jika fungsi f(z) selanjar pada [α,β], fungsi z =g(x) mempunyai terbitan selanjar dan α ≤ g(x) ≤ β, maka

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

Selain itu, selepas pengamiran di sebelah kanan, penggantian z=g(x) hendaklah dibuat.

Untuk membuktikannya, cukup menulis kamiran asal dalam bentuk:

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Sebagai contoh:

Kaedah penyepaduan mengikut bahagian

Biarkan u = f(x) dan v = g(x) ialah fungsi yang mempunyai selanjar . Kemudian, mengikut kerja,

d(uv))= udv + vdu atau udv = d(uv) - vdu.

Untuk ungkapan d(uv), antiterbitan jelas akan menjadi uv, jadi formulanya memegang:

∫ udv = uv - ∫ vdu (8.4.)

Formula ini menyatakan peraturan integrasi mengikut bahagian. Ia membawa penyepaduan ungkapan udv=uv"dx kepada penyepaduan ungkapan vdu=vu"dx.

Biarkan, sebagai contoh, anda ingin mencari ∫xcosx dx. Mari kita letakkan u = x, dv = cosxdx, jadi du=dx, v=sinx. Kemudian

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

Peraturan penyepaduan mengikut bahagian mempunyai skop yang lebih terhad daripada penggantian pembolehubah. Tetapi terdapat keseluruhan kelas kamiran, sebagai contoh,

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax dan lain-lain, yang dikira dengan tepat menggunakan pengamiran mengikut bahagian.

Kamiran pasti

Konsep kamiran pasti diperkenalkan seperti berikut. Biarkan fungsi f(x) ditakrifkan pada selang. Mari kita bahagikan segmen [a,b] kepada n bahagian dengan titik a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i =x i - x i-1. Jumlah bagi bentuk f(ξ i)Δ x i dipanggil jumlah integral, dan hadnya pada λ = maxΔx i → 0, jika ia wujud dan terhingga, dipanggil kamiran pasti fungsi f(x) daripada a sebelum ini b dan ditetapkan:

F(ξ i)Δx i (8.5).

Fungsi f(x) dalam kes ini dipanggil boleh diintegrasikan pada selang waktu, nombor a dan b dipanggil had bawah dan atas kamiran.

Untuk kamiran pasti sifat-sifat berikut adalah sah:

4), (k = const, k∈R);

5)

6)

7) f(ξ)(b-a) (ξ∈).

Harta terakhir dipanggil teorem nilai min.

Biarkan f(x) selanjar pada . Kemudian pada segmen ini terdapat kamiran tak tentu

∫f(x)dx = F(x) + C

dan berlaku Formula Newton-Leibniz, menghubungkan kamiran pasti dengan kamiran tak tentu:

F(b) - F(a). (8.6)

Tafsiran geometri: kamiran pasti ialah luas trapezium lengkung yang dibatasi dari atas oleh lengkung y=f(x), garis lurus x = a dan x = b dan segmen paksi lembu.

Kamiran tidak wajar

Kamiran dengan had tak terhingga dan kamiran bagi fungsi tak selanjar (tidak terhad) dipanggil bukan milik anda. Kamiran tak wajar jenis pertama - ini adalah kamiran sepanjang selang tak terhingga, ditakrifkan seperti berikut:

(8.7)

Jika had ini wujud dan terhad, maka ia dipanggil kamiran tak wajar penumpuan bagi f(x) pada selang [a+ ∞), dan fungsi f(x) dipanggil boleh diintegrasikan dalam selang waktu yang tidak terhingga[a+ ∞). Jika tidak, kamiran dikatakan sebagai tidak wujud atau menyimpang.

Kamiran tak wajar pada selang (-∞,b] dan (-∞, + ∞) ditakrifkan secara serupa:

Mari kita takrifkan konsep kamiran bagi fungsi tak terbatas. Jika f(x) adalah selanjar untuk semua nilai x segmen , kecuali untuk titik c, di mana f(x) mempunyai ketakselanjaran tak terhingga, kemudian kamiran tak wajar jenis kedua f(x) bermula dari a hingga b jumlahnya dipanggil:

jika had ini wujud dan terhad. Jawatan:

Contoh pengiraan kamiran

Contoh 3.30. Kira ∫dx/(x+2).

Penyelesaian. Mari kita nyatakan t = x+2, kemudian dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.

Contoh 3.31. Cari ∫ tgxdx.

Penyelesaian.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Biarkan t=cosx, kemudian ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Contoh3.32 . Cari ∫dx/sinx

Penyelesaian.

Contoh3.33. Cari .

Penyelesaian. = .

Contoh3.34 . Cari ∫arctgxdx.

Penyelesaian. Mari kita sepadukan mengikut bahagian. Mari kita nyatakan u=arctgx, dv=dx. Kemudian du = dx/(x 2 +1), v=x, dari mana ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; kerana
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Contoh3.35 . Kira ∫lnxdx.

Penyelesaian. Menggunakan formula penyepaduan mengikut bahagian, kami memperoleh:
u=lnx, dv=dx, du=1/x dx, v=x. Kemudian ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Contoh3.36 . Hitung ∫e x sinxdx.

Penyelesaian. Mari kita nyatakan u = e x, dv = sinxdx, kemudian du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Kami juga menyepadukan kamiran ∫e x cosxdx mengikut bahagian: u = e x , dv = cosxdx, du=e x dx, v=sinx. Kami ada:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Kami memperoleh hubungan ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, dari mana 2∫e x sinx dx = - e x cosx + e x sinx + C.

Contoh 3.37. Kira J = ∫cos(lnx)dx/x.

Penyelesaian. Oleh kerana dx/x = dlnx, maka J= ∫cos(lnx)d(lnx). Menggantikan lnx melalui t, kita tiba di jadual kamiran J = ∫ costdt = sint + C = sin(lnx) + C.

Contoh 3.38 . Kira J = .

Penyelesaian. Memandangkan = d(lnx), kita gantikan lnx = t. Kemudian J = .

Contoh 3.39 . Hitung kamiran J = .

Penyelesaian. Kami ada: . Oleh itu =
=
=. dimasukkan seperti ini: sqrt(tan(x/2)).

Dan jika dalam tetingkap hasil anda mengklik pada Tunjukkan langkah di sudut kanan atas, anda akan mendapat penyelesaian terperinci.

Formula integrasi mengikut bahagian kelihatan seperti:
.

Kaedah penyepaduan mengikut bahagian terdiri daripada menggunakan formula ini. Dalam aplikasi praktikal, perlu diperhatikan bahawa u dan v ialah fungsi pembolehubah penyepaduan. Biarkan pembolehubah pengamiran ditetapkan sebagai x (simbol selepas tanda pembezaan d pada akhir tatatanda kamiran). Maka u dan v ialah fungsi bagi x: u(x) dan v(x) .
Kemudian
, .
Dan formula untuk penyepaduan mengikut bahagian mengambil bentuk:
.

Iaitu, fungsi integrand mesti terdiri daripada hasil darab dua fungsi:
,
satu daripadanya kita nyatakan sebagai u: g(x) = u, dan untuk satu lagi kamiran mesti dikira (lebih tepat lagi, antiterbitan mesti ditemui):
, maka dv = f(x) dx .

Dalam sesetengah kes f(x) = 1 . Iaitu, dalam kamiran
,
kita boleh meletakkan g(x) = u, x = v .

Ringkasan

Jadi, dalam kaedah ini, formula integrasi mengikut bahagian harus diingat dan digunakan dalam dua bentuk:
;
.

Kamiran dikira dengan pengamiran mengikut bahagian

Kamiran yang mengandungi logaritma dan fungsi trigonometri songsang (hiperbola).

Kamiran yang mengandungi logaritma dan fungsi trigonometri songsang atau hiperbolik sering disepadukan oleh bahagian. Dalam kes ini, bahagian yang mengandungi logaritma atau fungsi trigonometri songsang (hiperbolik) dilambangkan dengan u, bahagian yang tinggal dengan dv.

Berikut adalah contoh kamiran tersebut, yang dikira dengan kaedah penyepaduan mengikut bahagian:
, , , , , , .

Kamiran yang mengandungi hasil darab polinomial dan sin x, cos x atau e x

Menggunakan formula pengamiran mengikut bahagian, kamiran bentuk ditemui:
, , ,
di mana P(x) ialah polinomial dalam x. Apabila menyepadukan, polinomial P(x) dilambangkan dengan u, dan e ax dx, cos ax dx atau dosa kapak dx- melalui dv.

Berikut adalah contoh kamiran tersebut:
, , .

Contoh pengiraan kamiran menggunakan kaedah pengamiran mengikut bahagian

Contoh kamiran yang mengandungi logaritma dan fungsi trigonometri songsang

Contoh

Hitung kamiran:

Penyelesaian terperinci

Di sini integrand mengandungi logaritma. Membuat penggantian
u = ln x,
dv = x 2 dx.
Kemudian
,
.

Kami mengira kamiran yang tinggal:
.
Kemudian
.
Pada akhir pengiraan, adalah perlu untuk menambah pemalar C, kerana kamiran tak tentu ialah set semua antiderivatif. Ia juga boleh ditambah dalam pengiraan pertengahan, tetapi ini hanya akan mengacaukan pengiraan.

Penyelesaian yang lebih pendek

Anda boleh membentangkan penyelesaian dalam versi yang lebih pendek. Untuk melakukan ini, anda tidak perlu membuat penggantian dengan u dan v, tetapi anda boleh mengumpulkan faktor dan menggunakan formula penyepaduan mengikut bahagian dalam bentuk kedua.

.

Jawab

Contoh kamiran yang mengandungi hasil darab polinomial dan sin x, cos x atau ex

Contoh

Hitung kamiran:
.

Penyelesaian

Mari kita perkenalkan eksponen di bawah tanda pembezaan:
e - x dx = - e - x d(-x) = - d(e - x).

Mari kita sepadukan mengikut bahagian.
.
Kami juga menggunakan kaedah penyepaduan mengikut bahagian.
.
.
.
Akhirnya kita ada.