Lekcja i prezentacja na temat: „Funkcje potęgowe. Właściwości. Wykresy”
Dodatkowe materiały
Drodzy użytkownicy, nie zapomnijcie zostawić swoich komentarzy, recenzji i życzeń! Wszystkie materiały zostały sprawdzone programem antywirusowym.
Pomoce dydaktyczne i symulatory w sklepie internetowym Integral dla klasy 11
Podręcznik interaktywny dla klas 9–11 „Trygonometria”
Podręcznik interaktywny dla klas 10–11 „Logarity”
Funkcje potęgowe, dziedzina definicji.
Chłopaki, na ostatniej lekcji nauczyliśmy się pracować z liczbami z wymiernymi wykładnikami. W tej lekcji przyjrzymy się funkcjom potęgowym i ograniczymy się do przypadku, gdy wykładnik jest wymierny.Rozważymy funkcje postaci: $y=x^(\frac(m)(n))$.
Rozważmy najpierw funkcje, których wykładnik $\frac(m)(n)>1$.
Dana nam będzie konkretna funkcja $y=x^2*5$.
Zgodnie z definicją, którą podaliśmy na ostatniej lekcji: jeśli $x≥0$, to dziedziną definicji naszej funkcji jest promień $(x)$. Przedstawmy schematycznie nasz wykres funkcji.

Własności funkcji $y=x^(\frac(m)(n))$, $0 2. Nie jest ona ani parzysta, ani nieparzysta.
3. Zwiększa się o $$,
b) $(2,10)$,
c) na promieniu $$.
Rozwiązanie.
Chłopaki, pamiętacie, jak w 10. klasie znaleźliśmy największą i najmniejszą wartość funkcji w segmencie?
Zgadza się, użyliśmy pochodnej. Rozwiążmy nasz przykład i powtórzmy algorytm znajdowania najmniejszego i najwyższa wartość.
1. Znajdź pochodną danej funkcji:
$y"=\frac(16)(5)*\frac(5)(2)x^(\frac(3)(2))-x^3=8x^(\frac(3)(2)) -x^3=8\sqrt(x^3)-x^3$.
2. Pochodna istnieje w całym obszarze definicji funkcji pierwotnej, wówczas nie ma punktów krytycznych. Znajdźmy punkty stacjonarne:
$y"=8\sqrt(x^3)-x^3=0$.
$8*\sqrt(x^3)=x^3$.
64 $ x ^ 3 = x ^ 6 $.
$x^6-64x^3=0$.
$x^3(x^3-64)=0$.
$x_1=0$ i $x_2=\sqrt(64)=4$.
Dany segment zawiera tylko jedno rozwiązanie $x_2=4$.
Zbudujmy tabelę wartości naszej funkcji na końcach segmentu i w punkcie ekstremalnym:
Odpowiedź: $y_(imię)=-862,65$ przy $x=9$; $y_(maks.)=38,4$ przy $x=4$.
Przykład. Rozwiąż równanie: $x^(\frac(4)(3))=24-x$.
Rozwiązanie. Wykres funkcji $y=x^(\frac(4)(3))$ rośnie, a wykres funkcji $y=24-x$ maleje. Chłopaki, ty i ja wiemy: jeśli jedna funkcja rośnie, a druga maleje, to przecinają się tylko w jednym punkcie, to znaczy mamy tylko jedno rozwiązanie.
Notatka:
$8^(\frac(4)(3))=\sqrt(8^4)=(\sqrt(8))^4=2^4=16$.
$24-8=16$.
Oznacza to, że przy $x=8$ otrzymaliśmy poprawną równość $16=16$, to jest rozwiązanie naszego równania.
Odpowiedź: $x = 8 $.
Przykład.
Narysuj wykres funkcji: $y=(x-3)^\frac(3)(4)+2$.
Rozwiązanie.
Wykres naszej funkcji otrzymujemy z wykresu funkcji $y=x^(\frac(3)(4))$, przesuwając go o 3 jednostki w prawo i 2 jednostki w górę. 
Przykład. Zapisz równanie stycznej do prostej $y=x^(-\frac(4)(5))$ w punkcie $x=1$.
Rozwiązanie. Równanie styczne wyznacza się ze znanego nam wzoru:
$y=f(a)+f”(a)(x-a)$.
W naszym przypadku $a=1$.
$f(a)=f(1)=1^(-\frac(4)(5))=1$.
Znajdźmy pochodną:
$y"=-\frac(4)(5)x^(-\frac(9)(5))$.
Obliczmy:
$f"(a)=-\frac(4)(5)*1^(-\frac(9)(5))=-\frac(4)(5)$.
Znajdźmy równanie styczne:
$y=1-\frac(4)(5)(x-1)=-\frac(4)(5)x+1\frac(4)(5)$.
Odpowiedź: $y=-\frac(4)(5)x+1\frac(4)(5)$.
Problemy do samodzielnego rozwiązania
1. Znajdź największą i najmniejszą wartość funkcji: $y=x^\frac(4)(3)$ na odcinku:a) $$.
b) $(4,50)$.
c) na promieniu $$.
3. Rozwiąż równanie: $x^(\frac(1)(4))=18-x$.
4. Skonstruuj wykres funkcji: $y=(x+1)^(\frac(3)(2))-1$.
5. Utwórz równanie na styczną do prostej $y=x^(-\frac(3)(7))$ w punkcie $x=1$.
Funkcja gdzie X– zmienna ilość, A– wywoływany jest dany numer Funkcja zasilania .
Jeżeli jest to funkcja liniowa, to jej wykres jest linią prostą (patrz paragraf 4.3, rys. 4.7).
Jeśli następnie - funkcja kwadratowa, jego wykres jest parabolą (patrz akapit 4.3, ryc. 4.8).
Jeśli wówczas jego wykres jest parabolą sześcienną (patrz akapit 4.3, ryc. 4.9).
To jest funkcja odwrotna dla
1. Domena: ![]()
2. Wiele znaczeń:![]()
3. Parzyste i nieparzyste: funkcja jest nieparzysta.
4. Częstotliwość funkcji: nieokresowe.
5. Funkcja zerowa: X= 0 – jedyne zero.
6. Funkcja nie ma wartości maksymalnej ani minimalnej.
7.
8. Wykres funkcji Symetryczny do wykresu paraboli sześciennej względem linii prostej T=X i pokazano na rys. 5.1.
 |
Funkcja zasilania
1. Domena: ![]()
2. Wiele znaczeń:
3. Parzyste i nieparzyste: funkcja jest parzysta.
4. Częstotliwość funkcji: nieokresowe.
5. Funkcja zerowa: pojedyncze zero X = 0.
6. Największe i najmniejsze wartości funkcji: przyjmuje najmniejszą wartość dla X= 0, jest równe 0.
7. Zwiększaj i zmniejszaj interwały: funkcja maleje na przedziale i rośnie na przedziale
8. Wykres funkcji(dla każdego N Î N) jest „podobny” do wykresu paraboli kwadratowej (wykresy funkcji pokazano na rys. 5.2).

Funkcja zasilania
1. Domena: ![]()
2. Wiele znaczeń: ![]()
3. Parzyste i nieparzyste: funkcja jest nieparzysta.
4. Częstotliwość funkcji: nieokresowe.
5. Funkcja zerowa: X= 0 – jedyne zero.
6. Najwyższe i najniższe wartości:
7. Zwiększaj i zmniejszaj interwały: funkcja rośnie w całym obszarze definicji.
8. Wykres funkcji(dla każdego ) jest „podobny” do wykresu paraboli sześciennej (wykresy funkcji pokazano na rys. 5.3).
 |
Funkcja zasilania![]()
1. Domena:
2. Wiele znaczeń:
3. Parzyste i nieparzyste: funkcja jest nieparzysta.
4. Częstotliwość funkcji: nieokresowe.
5. Funkcja zerowa: nie ma zer.
6. Największe i najmniejsze wartości funkcji: funkcja nie ma dla żadnej wartości największej i najmniejszej
7. Zwiększaj i zmniejszaj interwały: funkcja jest malejąca w swojej dziedzinie definicji.
8. Asymptoty:(oś Jednostka organizacyjna) - pionowa asymptota;
(oś Oh) - asymptota pozioma.
9. Wykres funkcji(dla kazdego N) jest „podobny” do wykresu hiperboli (wykresy funkcji pokazano na ryc. 5.4).
 |
Funkcja zasilania
1. Domena:
2. Wiele znaczeń:
3. Parzyste i nieparzyste: funkcja jest parzysta.
4. Częstotliwość funkcji: nieokresowe.
5. Największe i najmniejsze wartości funkcji: funkcja nie ma dla żadnej wartości największej i najmniejszej
6. Zwiększaj i zmniejszaj interwały: funkcja rośnie i maleje o
7. Asymptoty: X= 0 (oś Jednostka organizacyjna) - pionowa asymptota;
Y= 0 (oś Oh) - asymptota pozioma.
8. Wykresy funkcji Są to hiperbole kwadratowe (ryc. 5.5).
 |
Funkcja zasilania
1. Domena:
2. Wiele znaczeń:
3. Parzyste i nieparzyste: funkcja nie ma własności parzystej i nieparzystej.
4. Częstotliwość funkcji: nieokresowe.
5. Funkcja zerowa: X= 0 – jedyne zero.
6. Największe i najmniejsze wartości funkcji: funkcja przyjmuje w tym punkcie najmniejszą wartość równą 0 X= 0; nie ma większego znaczenia.
7. Zwiększaj i zmniejszaj interwały: funkcja rośnie w całym obszarze definicji.
8. Każda taka funkcja dla pewnego wykładnika jest odwrotnością podanej funkcji
9. Wykres funkcji„przypomina” wykres funkcji dowolnego N i pokazano na rys. 5.6.

Funkcja zasilania
1. Domena: ![]()
2. Wiele znaczeń:![]()
3. Parzyste i nieparzyste: funkcja jest nieparzysta.
4. Częstotliwość funkcji: nieokresowe.
5. Funkcja zerowa: X= 0 – jedyne zero.
6. Największe i najmniejsze wartości funkcji: funkcja nie ma dla żadnej wartości największej i najmniejszej
7. Zwiększaj i zmniejszaj interwały: funkcja rośnie w całym obszarze definicji.
8. Wykres funkcji Pokazane na ryc. 5.7.
 |
Przypomnijmy sobie właściwości i wykresy funkcji potęgowych z liczbą całkowitą wskaźnik negatywny.
Dla nawet n:
Przykładowa funkcja:
Wszystkie wykresy takich funkcji przechodzą przez dwa stałe punkty: (1;1), (-1;1). Cechą charakterystyczną funkcji tego typu jest ich parzystość, wykresy są symetryczne względem osi wzmacniacza operacyjnego.

Ryż. 1. Wykres funkcji
Dla nieparzystego n:
Przykładowa funkcja:
Wszystkie wykresy takich funkcji przechodzą przez dwa stałe punkty: (1;1), (-1;-1). Cechą charakterystyczną funkcji tego typu jest to, że są one nieparzyste, a wykresy są symetryczne względem początku.

Ryż. 2. Wykres funkcji
Przypomnijmy podstawową definicję.
Potęga liczby nieujemnej a z wymiernym dodatnim wykładnikiem nazywana jest liczbą.
Potęga liczby dodatniej a z wymiernym wykładnikiem ujemnym nazywana jest liczbą.
Dla równości:
![]()
![]()
Na przykład: ![]() ; - nie istnieje wyrażenie z definicji stopnia o ujemnym wykładniku wymiernym; istnieje, ponieważ wykładnik jest liczbą całkowitą,
; - nie istnieje wyrażenie z definicji stopnia o ujemnym wykładniku wymiernym; istnieje, ponieważ wykładnik jest liczbą całkowitą, ![]()
Przejdźmy do rozważania funkcji potęgowych z wymiernym wykładnikiem ujemnym.
![]()
Na przykład:
Aby wykreślić wykres tej funkcji, możesz utworzyć tabelę. Zrobimy to inaczej: najpierw zbudujemy i przestudiujemy wykres mianownika - jest on nam znany (rysunek 3).

Ryż. 3. Wykres funkcji
Wykres funkcji mianownika przechodzi przez stały punkt (1;1). Podczas kreślenia oryginalnej funkcji dany punkt pozostaje, gdy pierwiastek również dąży do zera, funkcja dąży do nieskończoności. I odwrotnie, gdy x dąży do nieskończoności, funkcja dąży do zera (rysunek 4).

Ryż. 4. Wykres funkcji
Rozważmy inną funkcję z rodziny badanych funkcji.
![]()
Ważne, że z definicji
Rozważmy wykres funkcji w mianowniku: , wykres tej funkcji jest nam znany, rośnie ona w swojej dziedzinie definicji i przechodzi przez punkt (1;1) (rysunek 5).

Ryż. 5. Wykres funkcji
Podczas rysowania wykresu pierwotnej funkcji pozostaje punkt (1;1), pierwiastek również dąży do zera, a funkcja dąży do nieskończoności. I odwrotnie, gdy x dąży do nieskończoności, funkcja dąży do zera (rysunek 6).

Ryż. 6. Wykres funkcji
Rozważane przykłady pomagają zrozumieć, jak przebiega wykres i jakie są właściwości badanej funkcji - funkcji o ujemnym wykładniku wymiernym.
Wykresy funkcji tej rodziny przechodzą przez punkt (1;1), funkcja maleje w całym obszarze definicji.
Zakres funkcji: ![]()
Funkcja nie jest ograniczona od góry, ale jest ograniczona od dołu. Funkcja nie ma największej ani najniższa wartość.
Funkcja jest ciągła i przyjmuje wszystkie wartości dodatnie od zera do plus nieskończoności.
Funkcja jest wypukła w dół (rysunek 15.7)
Na krzywej pobiera się punkty A i B, przez nie przeciąga się odcinek, cała krzywa znajduje się pod odcinkiem, ten warunek jest spełniony dla dowolnych dwóch punktów na krzywej, zatem funkcja jest wypukła w dół. Ryż. 7.

Ryż. 7. Wypukłość funkcji
Ważne jest, aby zrozumieć, że funkcje tej rodziny są ograniczone od dołu przez zero, ale nie mają najmniejszej wartości.
Przykład 1 - znajdź maksimum i minimum funkcji na przedziale \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \]
Wykres (ryc. 2).

Rysunek 2. Wykres funkcji $f\left(x\right)=x^(2n)$
Własności funkcji potęgowej z wykładnikiem naturalnym nieparzystym
Dziedziną definicji są wszystkie liczby rzeczywiste.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- funkcja jest nieparzysta.
$f(x)$ jest ciągłe w całym obszarze definicji.
Cały zakres to liczby rzeczywiste.
$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Funkcja rośnie w całym obszarze definicji.
$f\lewo(x\prawo)0$, dla $x\in (0,+\infty)$.
$f(""\lewo(x\prawo))=(\lewo(\lewo(2n-1\prawo)\cdot x^(2\lewo(n-1\prawo))\prawo))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$
\ \
Funkcja jest wklęsła dla $x\in (-\infty ,0)$ i wypukła dla $x\in (0,+\infty)$.
Wykres (ryc. 3).
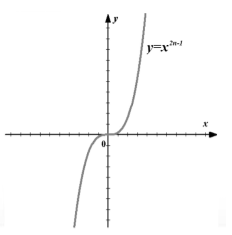
Rysunek 3. Wykres funkcji $f\left(x\right)=x^(2n-1)$
Funkcja potęgowa z wykładnikiem całkowitym
Najpierw wprowadźmy pojęcie stopnia z wykładnikiem całkowitym.
Definicja 3
Potęgę liczby rzeczywistej $a$ z wykładnikiem całkowitym $n$ określa się ze wzoru:

Rysunek 4.
Rozważmy teraz funkcję potęgową z wykładnikiem całkowitym, jej właściwości i wykres.
Definicja 4
$f\left(x\right)=x^n$ ($n\in Z)$ nazywa się funkcją potęgową z wykładnikiem całkowitym.
Jeśli stopień jest większy od zera, wówczas dochodzimy do przypadku funkcji potęgowej z wykładnikiem naturalnym. Omówiliśmy to już powyżej. Dla $n=0$ otrzymujemy funkcja liniowa$y=1$. Rozważania pozostawimy czytelnikowi. Pozostaje rozważyć właściwości funkcji potęgowej z ujemnym wykładnikiem całkowitym
Właściwości funkcji potęgowej z ujemnym wykładnikiem całkowitym
Dziedziną definicji jest $\left(-\infty,0\right)(0,+\infty)$.
Jeśli wykładnik jest parzysty, to funkcja jest parzysta, jeśli jest nieparzysta, to funkcja jest nieparzysta.
$f(x)$ jest ciągłe w całym obszarze definicji.
Zakres:
Jeśli wykładnik jest parzysty, to $(0,+\infty)$; jeśli jest nieparzysty, to $\left(-\infty ,0\right)(0,+\infty)$.
W przypadku wykładnika nieparzystego funkcja maleje jako $x\in \left(-\infty ,0\right)(0,+\infty)$. Jeśli wykładnik jest parzysty, funkcja maleje jako $x\in (0,+\infty)$. i rośnie o $x\in \left(-\infty,0\right)$.
$f(x)\ge 0$ w całym obszarze definicji