تعريف. دع الدالة f(x) يتم تعريفها على فترة معينة وأن تكون x 0 نقطة في هذه الفترة. إذا كان f(x) يقال أنه مستمر عند النقطة x 0 .
يترتب على التعريف أنه لا يمكننا التحدث عن الاستمرارية إلا فيما يتعلق بتلك النقاط التي يتم عندها تعريف f(x) (عند تحديد حد الدالة، لم يتم تعيين مثل هذا الشرط). للوظائف المستمرة أي أن العمليات f وlim قابلة للتبديل. وبناء على ذلك، يمكن إعطاء تعريفين لحد الدالة عند نقطة ما تعريفين للاستمرارية - "في لغة المتواليات" و"في لغة عدم المساواة" (في لغة ε-δ). ويقترح أن تفعل ذلك بنفسك.
للاستخدام العملي، يكون من المناسب أحيانًا تعريف الاستمرارية بلغة الزيادات.
تسمى القيمة Δx=x-x 0 بزيادة الوسيطة، وΔy=f(x)-f(x 0) هي زيادة الدالة عند الانتقال من النقطة x 0 إلى النقطة x.
تعريف. دع f(x) يتم تعريفه عند النقطة x 0 . تسمى الدالة f(x) مستمرة عند نقطة x 0 إذا كانت الزيادة المتناهية الصغر في الوسيطة عند هذه النقطة تتوافق مع زيادة متناهية الصغر في الدالة، أي Δy→0 لـ Δx→0.

مثال 1. أثبت أن الدالة y=sinx متصلة لأي قيمة لـ x.
حل. دع x 0 تكون نقطة تعسفية. بإعطائها زيادة Δx، نحصل على النقطة x=x 0 +Δx. ثم . نحن نحصل .
تعريف. تسمى الدالة y=f(x) مستمرة عند النقطة x 0 على اليمين (يسار) إذا
.
الدالة المستمرة عند نقطة داخلية ستكون مستمرة في اليمين واليسار. والعكس صحيح أيضًا: إذا كانت الدالة متصلة عند نقطة على اليسار واليمين، فستكون متصلة عند تلك النقطة. ومع ذلك، يمكن أن تكون الدالة متصلة على جانب واحد فقط. على سبيل المثال، ل , ، f(1)=1، وبالتالي فإن هذه الدالة مستمرة فقط على اليسار (للاطلاع على الرسم البياني لهذه الدالة، انظر أعلاه في الفقرة 5.7.2).
تعريف. تسمى الدالة متصلة على فترة ما إذا كانت متصلة عند كل نقطة من هذه الفترة.
على وجه الخصوص، إذا كانت الفترة عبارة عن قطعة، فإن الاستمرارية من جانب واحد تكون ضمنية عند طرفيها.

خصائص الدوال المستمرة

1. جميع الوظائف الأولية مستمرة في مجال تعريفها.
2. إذا كانت f(x) وφ(x)، المعطاة في فترة معينة، متصلتين عند النقطة x 0 من هذه الفترة، فستكون الدوال متصلة أيضًا عند هذه النقطة.
3. إذا كانت y=f(x) متصلة عند النقطة x 0 من X، وz=φ(y) مستمرة عند النقطة المقابلة y 0 =f(x 0) من Y، إذن وظيفة معقدة z=φ(f(x)) ستكون مستمرة عند النقطة x 0 .

فواصل الوظائف وتصنيفها

علامة استمرارية الدالة f(x) عند النقطة x 0 هي المساواة، مما يعني وجود ثلاثة شروط:
1) يتم تعريف f(x) عند النقطة x 0 ;
2) ;
3) .
إذا تم انتهاك واحد على الأقل من هذه المتطلبات، فإن x 0 تسمى نقطة توقف الدالة. بمعنى آخر، نقطة التوقف هي النقطة التي لا تكون فيها هذه الوظيفة متصلة. ويترتب على تعريف نقاط التوقف أن نقاط التوقف للدالة هي:
أ) النقاط التي تنتمي إلى مجال تعريف الوظيفة التي تفقد فيها f(x) خاصية الاستمرارية،
ب) نقاط لا تنتمي إلى مجال تعريف f(x)، وهي نقاط متجاورة لفترتين من مجال تعريف الدالة.
على سبيل المثال، بالنسبة للدالة، النقطة x=0 هي نقطة فاصل، نظرًا لأن الدالة عند هذه النقطة غير محددة، والدالة لديه انقطاع عند النقطة x=1، المجاورة لفترتين (-∞,1) و (1,∞) من مجال تعريف f(x) وغير موجود.

تم اعتماد التصنيف التالي لنقاط الاستراحة.
1) إذا كان هناك حدود عند النقطة × 0 و ، ولكن f(x 0 +0)≠f(x 0 -0)، ثم يتم استدعاء x 0 نقطة انقطاع من النوع الأول ، ويسمى قفزة الوظيفة .

مثال 2. النظر في الوظيفة
لا يمكن تقسيم الدالة إلا عند النقطة x=2 (وفي نقاط أخرى تكون متصلة مثل أي كثيرة حدود).
سوف نجد , . بما أن النهايات أحادية الجانب محدودة، ولكنها غير متساوية، فعند النقطة x=2 يكون للدالة انقطاع من النوع الأول. لاحظ أن وبالتالي فإن الدالة عند هذه النقطة مستمرة على اليمين (الشكل 2).
2) نقاط الانقطاع من النوع الثاني تسمى النقاط التي تكون فيها إحدى النهايات أحادية الجانب على الأقل مساوية لـ ∞ أو غير موجودة.

مثال 3. الدالة y=2 1/ x متصلة لجميع قيم x باستثناء x=0. دعونا نجد الحدود من جانب واحد: , وبالتالي فإن x=0 هي نقطة انقطاع من النوع الثاني (الشكل 3).
3) تسمى النقطة x=x0 نقطة انقطاع قابلة للإزالة ، إذا كان f(x 0 +0)=f(x 0 -0)≠f(x 0).
سنقوم "بإزالة" الفجوة بمعنى أنه يكفي تغيير (إعادة تعريف أو إعادة تعريف) قيمة الدالة عند هذه النقطة عن طريق الإعداد، وستصبح الدالة مستمرة عند النقطة x 0 .
مثال 4. ومن المعروف أن ، ولا يعتمد هذا الحد على الطريقة التي تتجه بها x إلى الصفر. لكن الدالة عند النقطة x=0 غير محددة. إذا قمنا بإعادة تعريف الدالة عن طريق تحديد f(0)=1، فسيتبين أنها مستمرة عند هذه النقطة (وفي نقاط أخرى تكون مستمرة كحاصل الدوال المستمرة sinx و x).
مثال 5. فحص استمرارية الوظيفة .
حل. يتم تعريف الوظائف y=x 3 و y=2x ومستمرة في كل مكان، بما في ذلك الفواصل الزمنية المشار إليها. دعونا نتفحص نقطة الوصل للفترات x=0:
, ، . نحصل على ذلك، مما يعني أن الدالة مستمرة عند النقطة x=0.
تعريف. تسمى الدالة المستمرة على فترة ما عدا عدد محدود من نقاط عدم الاستمرارية من النوع الأول أو عدم الاستمرارية القابلة للإزالة، بالتابعة المتعددة التعريف على هذه الفترة.

أمثلة على الوظائف المتقطعة

مثال 1. الدالة معرفة ومستمرة على (-∞,+∞) إلا عند النقطة x=2. دعونا نحدد نوع الاستراحة. بسبب ال و فعند النقطة x=2 يوجد انقطاع من النوع الثاني (الشكل 6).
مثال 2. الدالة محددة ومستمرة لجميع x باستثناء x=0، حيث يكون المقام صفرًا. دعونا نجد الحدود من جانب واحد عند النقطة x=0:
الحدود أحادية الجانب محدودة ومختلفة، وبالتالي فإن x=0 هي نقطة انقطاع من النوع الأول (الشكل 7).
مثال 3. حدد عند أي نقاط ونوع الانقطاعات الموجودة في الوظيفة
تم تعريف هذه الوظيفة على [-2,2]. بما أن x 2 و 1/x متصلان في الفواصل الزمنية [-2,0] و، على التوالي، يمكن أن يحدث الانقطاع فقط عند تقاطع الفواصل الزمنية، أي عند النقطة x=0. وبما أن x=0 هي نقطة انقطاع من النوع الثاني.

مثال 4. هل من الممكن القضاء على الفجوات الوظيفية:
أ) عند النقطة س=2؛
ب) عند النقطة س=2؛
الخامس) عند النقطة x=1 ؟
حل. فيما يتعلق بالمثال أ) يمكننا أن نقول على الفور أن الانقطاع f(x) عند النقطة x=2 لا يمكن حذفه، لأنه عند هذه النقطة توجد حدود لا نهائية من جانب واحد (انظر المثال 1).
ب) الدالة g(x) على الرغم من أن لها حدود محدودة من جانب واحد عند النقطة x=2

(,),

لكنهما لا يتطابقان، لذلك لا يمكن إزالة الفجوة أيضًا.
ج) الدالة φ(x) عند نقطة الانقطاع x=1 لها حدود محدودة من جانب واحد متساوية: . ولذلك، يمكن إزالة الفجوة عن طريق إعادة تعريف الدالة عند x=1 وذلك بوضع f(1)=1 بدلاً من f(1)=2.

مثال 5. تبين أن وظيفة ديريشليت

متقطع عند كل نقطة على المحور العددي.
حل. دع x 0 يكون أي نقطة من (-∞،+∞). في أي من أحيائها توجد نقاط عقلانية وغير عقلانية. هذا يعني أنه في أي حي x 0 ستكون للدالة قيم تساوي 0 و 1. في هذه الحالة، لا يمكن أن توجد نهاية الدالة عند النقطة x 0 سواء على اليسار أو على اليمين، مما يعني أن تحتوي دالة ديريشليت على انقطاعات من النوع الثاني عند كل نقطة على المحور الحقيقي.

مثال 6. البحث عن نقاط توقف الوظيفة

وتحديد نوعها.
حل. النقاط المشتبه في كسرها هي النقاط x 1 = 2، x 2 = 5، x 3 = 3.
عند النقطة x 1 =2 f(x) يوجد انقطاع من النوع الثاني، منذ ذلك الحين
.
النقطة x 2 =5 هي نقطة تواصل، إذ أن قيمة الدالة عند هذه النقطة وفي جوارها تتحدد بالسطر الثاني وليس الأول: .
دعونا نتفحص النقطة x 3 =3 : , ، ويترتب على ذلك أن x=3 هي نقطة انقطاع من النوع الأول.

ل قرار مستقل.
فحص دوال الاستمرارية وتحديد نوع نقاط الانقطاع:
1) ; الإجابة: x=-1 - نقطة الانقطاع القابلة للإزالة؛
2) ; الجواب: انقطاع من النوع الثاني عند النقطة x=8؛
3) ; الجواب: الانقطاع من النوع الأول عند x=1؛
4)
الجواب: عند النقطة x 1 = -5 توجد فجوة قابلة للإزالة، وعند x 2 = 1 توجد فجوة من النوع الثاني، وعند النقطة x 3 = 0 توجد فجوة من النوع الأول.
5) كيف يجب اختيار الرقم A حتى تكون الدالة

ستكون مستمرة عند x=0؟
الجواب: أ=2.
6) هل من الممكن اختيار الرقم A بحيث تكون الوظيفة

ستكون مستمرة عند x=2؟
الجواب: لا.

استمرارية الدالة عند نقطة ما. الدالة ص = و(س ) يسمى غير مسبق

متشنج عند النقطة × 0 إذا:

1) يتم تعريف هذه الوظيفة في بعض أحياء النقطةس 0 ;

2) هناك حد ليمو (خ)؛

→ × 0

3) هذا الحد يساوي القيمةوظائف عند النقطة × 0، أي. الحافة (x )= و (x 0 ) .
		س → س0
الشرط الأخير يعادل الشرط ليم		ص = 0، حيث س = س − س 0 - متى
	س → 0
دوران الوسيطة، y = f (x 0 +	x )− f (x 0 ) – زيادة الدالة المقابلة
زيادة الحجة	س، أي. وظيفة	f(x) مستمر عند x 0

إذا وفقط إذا كانت الزيادة المتناهية الصغر في هذه النقطة تقابل زيادة متناهية الصغر في الدالة.

الاستمرارية في اتجاه واحد.الدالة y = f (x) تسمى مستمرة

على اليسار عند النقطةx 0 إذا تم تعريفها على فترة نصفية (a ;x 0 ]

و ليم و (س)= و (س 0).

س→ س0 - 0

يقال إن الدالة y = f (x) متصلة بشكل صحيح عند النقطة x 0 إذا كانت OP

يتم توزيعها على نصف فترة معينة [ x 0 ;a ) و limf (x )= f (x 0 ) .

س → س0 + 0

الدالة ص = و(خ)		مستمر عند النقطة × 0			ثم وفقط عندما تكون
مستمر
ليم و (س) = ليمف (س) = ليمف (س) = و (س 0).
س → س0 + 0	س→ س0 - 0	س → س0

استمرارية الدالة في المجموعة يتم استدعاء الدالة y = f (x).

مستمر على المجموعة X إذا كانت مستمرة عند كل نقطة من هذه المجموعة. علاوة على ذلك، إذا تم تعريف الدالة في نهاية فترة معينة من خط الأعداد، فإن الاستمرارية عند هذه النقطة تُفهم على أنها استمرارية على اليمين أو اليسار. على وجه الخصوص، تسمى الدالة y = f (x) غير

متقطع على الجزء [أ؛ ب] إذا كانت

1) مستمر في كل نقطة من الفاصل الزمني(أ؛ب)؛

2) هو حق مستمر عند نقطة ماأ؛

3) ويترك مستمرا عند نقطة ماب.

نقاط توقف الوظيفةتسمى النقطة x 0 التي تنتمي إلى مجال تعريف الدالة y = f (x) أو كونها النقطة الحدودية لهذا المجال

نقطة انقطاع هذه الوظيفة، iff(x) ليس مستمرًا عند هذه النقطة.

تنقسم نقاط الانقطاع إلى نقاط انقطاع من النوع الأول والثاني:

1) إذا كانت هناك حدود محدودة lim f (x )= f (x 0 − 0) و

س→ س0 - 0

	f (x)= f (x 0 + 0)، وليست جميع الأرقام الثلاثة هي f (x 0 − 0)، f (x 0 + 0)،		f (x 0 ) متساويان
س → س0 + 0
فيما بينهم، ثم × 0		وتسمى نقطة الانقطاع من النوع الأول.
	على وجه الخصوص، إذا كانت الحدود اليسرى واليمنى للدالة عند النقطة x 0		متساوي بين
	نفسك ولكن	لا تساوي قيمة الدالة في هذه المرحلة:

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) ، ثم x 0 تسمى نقطة انقطاع قابلة للإزالة.

في هذه الحالة، من خلال ضبط f (x 0) = A، يمكنك تعديل الدالة عند النقطة x 0

حتى يصبح مستمرا ( إعادة تعريف الوظيفة بالاستمرارية). يسمى الفرق f (x 0 + 0)− f (x 0 − 0). قفزة دالة عند نقطة ما× 0 .

قفزة الدالة عند نقطة الانقطاع القابلة للإزالة هي صفر.

2) تسمى نقاط الانقطاع التي ليست نقاط انقطاع من النوع الأول نقاط التوقف من النوع الثاني. عند نقاط الانقطاع من النوع الثاني، على الأقل واحدة من الحدود أحادية الجانب f (x 0 − 0) و f (x 0 + 0) غير موجودة أو لا نهائية.

خصائص الدوال المستمرة عند نقطة ما.

		و (خ)	و g (x) متواصلة عند النقطة x 0، ثم الدوال
و (س) ± ز (خ)،	و(خ)ز(خ) و	و (خ)	(حيث g (x) ≠ 0) مستمرة أيضًا عند النقطة x.
		ز (خ)

2) إذا كانت الدالة u (x) متصلة عند النقطة x 0، والدالة f (u) متصلة

عند النقطة u 0 = u (x 0)، فإن الدالة المعقدة f (u (x)) مستمرة عند النقطة x 0.

3) جميع الوظائف الأولية الأساسية (c، x a، a x، loga x، sinx، cosx، tgx، ctgx، secx، cosecx، arcsinx، arccosx، arctgx، arcctgx) مستمرة في كل منها

إلى حد مجالات تعريفهم.

من الخصائص 1)-3) يترتب على ذلك أن جميع الوظائف الأولية (الوظائف التي تم الحصول عليها من الوظائف الأولية الأساسية باستخدام عدد محدود من العمليات الحسابية وعمليات التركيب) تكون أيضًا مستمرة عند كل نقطة من مجالات تعريفها.

خصائص الدوال المستمرة على فترة.

1) (نظرية القيمة المتوسطة) دع الدالة f(x) تحدد

على ومستمر على القطعة [a;b]. ثم لأي رقم C مغلق

بين الأرقام f (a) و f (b)، (f (a)< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (نظرية بولزانو-كوشي

متقطع على القطعة [a;b] ويأخذ قيم الإشارات المختلفة عند طرفيه.

ثم هناك نقطة واحدة على الأقل x 0 [ a ; b ] بحيث f (x 0 )= 0 .

3) (1 نظرية ويرستراس) دع الدالة f (x) يتم تعريفها و

ممزقة على الجزء [أ، ب]. ثم تقتصر هذه الوظيفة على هذا الجزء.

4) (الثاني نظرية ويرستراس) دع الدالة f (x) يتم تعريفها و

الاندفاع على هذا الجزء		[أ ؛ ب] . ثم تصل هذه الدالة في الفاصل الزمني [ a ;
أعظم		الأقل	القيم، أي	يخرج
×1، ×2 [أ؛ ب] ،		لأي	النقاط س [أ؛ب]	عدل	عدم المساواة

و (x 1 )≥ و (x )≥ و (x 2 ) .

مثال 5.17. باستخدام تعريف الاستمرارية، أثبت أن الدالة y = 3x 2 + 2x − 5 متصلة عند نقطة اختيارية x 0 على خط الأعداد.

الحل: الطريقة الأولى: اجعل x 0 نقطة عشوائية على محور الرقم. أنت-

نحسب أولاً نهاية الدالة f (x) على أنها x → x 0، مع تطبيق النظريات على حد مجموع وحاصل ضرب الدوال:

ليم f (x )= ليم(3x 2 + 2x − 5)= 3(ليمكس )2 + 2 ليمكس − 5= 3x 2							− 5.
س → س0	س → س0	س → س0	س → س0
ثم نحسب قيمة الدالة عند النقطة x:f (x)= 3x 2							− 5 .
مقارنة النتائج التي تم الحصول عليها، ونحن نرى				ليم f (x )= f (x 0 ) الذي وفقا ل
				س → س0

التعريف ويعني استمرارية الوظيفة قيد النظر عند النقطة × 0.

الطريقة الثانية: دع		x - زيادة الوسيطة عند النقطة x 0. دعونا نجد المراسلات
ملائم	زيادة راتب			ص = و(x0 + س) − و(x0 ) =
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x − 5)
6 × س+ (خ) 2	2س = (6س + 2)س + (س)2.
دعونا الآن نحسب حد زيادة الدالة عند زيادة الوسيطة
		الفتن

	ص = الحد (6س + 2)		س + (س)2 = (6س + 2) ليم		س + (ليمكس)2 = 0.
س → 0	س → 0			س → 0	س → 0

وبالتالي، lim y = 0، وهو ما يعني الاستمرارية بالتعريف

س → 0

وظائف لأي x 0 R .

مثال 5.18. أوجد نقاط انقطاع الدالة f (x) وحدد نوعها. في

في حالة عدم الاستمرارية القابلة للإزالة، حدد الوظيفة بالاستمرارية:

1) f (x) = 1− x 2 عند x< 3;

5x عندما x ≥ 3

2) و (س)= س 2 + 4 س + 3؛

س+1

	و(خ)=
		س4 (س− 2)
	f(x)= القطب الشمالي
			(س − 5)

الحل: 1) مجال تعريف هذه الدالة هو العدد الكامل

المحور ص (−∞ ;+∞ ) . على الفترات (−∞ ;3) ,(3;+∞ ) تكون الدالة متصلة. يكون الانقطاع ممكنًا فقط عند النقطة x = 3، حيث تتغير المواصفات التحليلية للوظيفة.

دعونا نجد الحدود من جانب واحد للدالة عند النقطة المشار إليها:

و (3− 0)= ليم (1− x 2 )= 1− 9= 8;

س →3 −0

و (3+ 0)= الحد 5س = 15.

س →3 +0

نرى أن الحدين الأيسر والأيمن محدودان، لذا فإن x = 3
تمزق أنا			و (خ). وظيفة الانتقال إلى
و (3+ 0)− و (3− 0)= 15− 8= 7 .
		f (3)= 5 3= 15= f (3+ 0) ، عند هذه النقطة		س = 3

f(x) مستقيم مستمر.

2) الدالة متصلة على خط الأعداد بأكمله ما عدا النقطة x = − 1، حيث لم يتم تعريفه. لنقم بتحويل التعبير الخاص بـ f (x) عن طريق توسيع البسط

الكسور إلى عوامل:		و(خ)=			4 × +3			(س + 1) (س + 3)	X + 3 لـ x ≠ − 1.
					س+1			س+1
دعونا نوجد النهايات الأحادية الجانب للدالة عند النقطة x = − 1:
	f(x)=lim	و (x )= ليم(x + 3)= 2 .
س →−1−0	س →−1 +0		س →−1

لقد اكتشفنا أن الحدين الأيسر والأيمن للدالة عند النقطة قيد الدراسة موجودان، ومحدودان ومتساويان، وبالتالي فإن x = − 1 هي نقطة قابلة للإزالة

خط مستقيم y = x + 3 بنقطة "مثقوبة" M (− 1;2) . لكي تصبح الوظيفة دائمة

متقطع، يجب أن نضع f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 .

وبالتالي، بعد تعريف f (x) بالاستمرارية عند النقطة x = − 1، حصلنا على الدالة f * (x)= x + 3 بمجال التعريف (−∞ ;+∞ ) .

3) هذه الوظيفةمحددة ومستمرة للجميع× باستثناء النقاط

x = 0,x = 2، حيث يصبح مقام الكسر صفرًا.

خذ بعين الاعتبار النقطة x = 0:

نظرًا لأنه في حي صغير بما فيه الكفاية من الصفر، فإن الوظيفة تستغرق فقط

	للقيم السالبة، ثم f (− 0)= lim			= −∞ = و (+0)	أولئك. نقطة
			(س − 2)
	س →−0
	x = 0 هي نقطة انقطاع للنوع الثاني من الوظائف		و (خ).

اعتبر الآن النقطة x = 2:

تأخذ الدالة قيمًا سالبة قريبة من يسار المدروس

	النقطة والإيجابية على اليمين، لذلك				و (2− 0)=			= −∞,
							س4 (س− 2)
						س →2 −0
	و (2+ 0)= الحد			= +∞ . كما في الحالة السابقة، عند النقطةx = 2
			(س − 2)
	س →2 +0

ليس للنشوء حدود محدودة يسارًا أو يمينًا، أي. يعاني من تمزق من النوع الثاني في هذه المرحلة.

س = 5 .

و (5− 0)= ليم أركتان

π ,f (5+ 0)= ليم القطب الشمالي

س = 5

(س − 5)

(س − 5)

س →5 −0

س →5 +0

كا تمزق

و (5+ 0)− و (5− 0)=

π − (−

π )= π (انظر الشكل 5.2).

مشاكل لحلها بشكل مستقل

5.174. باستخدام التعريف فقط، أثبت استمرارية الدالة f (x) في

كل نقطة × 0 ر :

أ) f(x) = c= const;		ب) و (س)= س؛
ج) و (س)= × 3؛		د) و (س)= 5س 2 − 4س + 1؛
ه) و (س)= الخطيئة.
5.175. اثبات أن الدالة	و(خ) = س2	1 عندما س ≥ 0،	مستمر على
		1 في س< 0
خط الأعداد بأكمله. قم بإنشاء رسم بياني لهذه الوظيفة.
5.176. اثبات أن الدالة	و(خ) = س2	1 عندما س ≥ 0،	ليست مستمرة
		0 في س< 0

عند النقطة x = 0، ولكنها مستمرة عند تلك النقطة. ارسم بيانيًا الدالة f(x).

متشنج عند النقطة x =

ولكنها مستمرة على اليسار عند هذه النقطة. قم ببناء رسم بياني

وظائف و (خ).

5.178. وظائف الرسم البياني

أ) ذ =

س+1

ب) ص = س+

س+1

س+1

س+1

أي من شروط الاستمرارية عند نقاط توقف هذه الوظائف مستوفاة وأيها غير مستوفي؟

5.179. تحديد نقطة توقف الدالة

الخطيئة س		ل س ≠ 0
		عند س = 0

أي من شروط الاستمرارية قد تم استيفاءه في هذه المرحلة وأيها لم يتم استيفاءه؟

تعريف نقاط انقطاع الوظيفة وأنواعها هي استمرار لموضوع استمرارية الوظيفة. يتم أيضًا تقديم شرح مرئي (رسومي) لمعنى نقاط التوقف للدالة على النقيض من مفهوم الاستمرارية. دعونا نتعلم كيفية العثور على نقاط التوقف للدالة وتحديد أنواعها. وسوف يساعدنا بلدنا في هذا الأصدقاء المخلصين- الحدود اليسرى واليمنى، وتسمى عمومًا الحدود أحادية الجانب. إذا كان لدى أي شخص أي مخاوف من الحدود الأحادية الجانب، فسنبددها قريبًا.

تسمى النقاط الموجودة على الرسم البياني غير المرتبطة ببعضها البعض نقاط انقطاع الوظيفة . الرسم البياني لهذه الدالة التي تعاني من انقطاع عند النقطة x=2 - - في الشكل أدناه.

تعميم ما ورد أعلاه هو التعريف التالي. إذا كانت الدالة غير متصلة عند نقطة ما، فهي غير متصلة عند هذه النقطة وتسمى النقطة نفسها نقطة الاستراحة . هناك فواصل من النوع الأول والنوع الثاني .

من أجل تحديد أنواع (شخصية) نقاط التوقف يجب العثور على الوظائف بثقة حدود، لذا من الجيد فتح الدرس المقابل في نافذة جديدة. ولكن فيما يتعلق بنقاط التوقف، لدينا شيء جديد ومهم - الحدود أحادية الجانب (اليسار واليمين). بشكل عام يتم كتابتها (الحد الأيمن) و (الحد الأيسر). كما هو الحال في حالة النهاية بشكل عام، لكي تجد نهاية الدالة، عليك استبدال X في تعبير الدالة بما تميل إليه X. لكن ربما تسأل كيف سيختلف الحد الأيمن عن الحد الأيسر، إذا كان في حالة الحد الأيمن يضاف شيء إلى X، ولكن هذا شيء صفر، وفي حالة الحد الأيسر يتم طرح شيء من X، ولكن هذا شيء - صفر أيضا؟ وستكون على حق. في معظم الحالات.

ولكن في ممارسة البحث عن نقاط انقطاع الدالة وتحديد نوعها، هناك حالتان نموذجيتان عندما لا يكون الحدان الأيمن والأيسر متساويين:

• تحتوي الدالة على تعبيرين أو أكثر اعتمادًا على جزء سطر الأرقام الذي تنتمي إليه x (عادةً ما تتم كتابة هذه التعبيرات بين قوسين متعرجين بعد F(س)= );
• ونتيجة لاستبدال ما تميل إليه X، نحصل على كسر في مقامه يبقى إما زائد صفر (+0) أو ناقص صفر (-0) وبالتالي فإن مثل هذا الكسر يعني إما زائد ما لا نهاية أو ناقص ما لا نهاية، وهذه هي أشياء مختلفة تماما.

نقاط الانقطاع من النوع الأول

نقطة الكسر من النوع الأول: تحتوي الدالة على حد يسار محدود (أي لا يساوي اللانهاية) وحد أيمن منته، ولكن الدالة غير محددة عند نقطة ما أو أن الحدين الأيسر والأيمن مختلفان (غير متساويين).

نقطة الانقطاع القابلة للإزالة من النوع الأول.الحدود اليسرى واليمنى متساوية. في هذه الحالة، من الممكن تحديد الوظيفة بشكل أكبر عند نقطة ما. إن تعريف دالة عند نقطة ما، يعني ببساطة توفير اتصال بين النقاط التي توجد بينها نقطة يكون عندها الحد الأيسر والأيمن متساويين مع بعضهما البعض. في هذه الحالة، يجب أن يمثل الاتصال نقطة واحدة فقط يجب العثور عندها على قيمة الدالة.

مثال 1.تحديد نقطة انقطاع الدالة ونوع (حرف) نقطة التوقف.

نقاط الانقطاع من النوع الثاني

نقطة الكسر من النوع الثاني: النقطة التي يكون عندها أحد النهايتين على الأقل (يسارًا أو يمينًا) لانهائيًا (يساوي ما لا نهاية).

مثال 3.

حل. من إعراب القوة في هفمن الواضح أن الوظيفة لم يتم تعريفها عند هذه النقطة. لنجد الحدين الأيسر والأيمن للدالة عند هذه النقطة:

أحد النهايتين يساوي ما لا نهاية، وبالتالي فإن النقطة هي نقطة انقطاع من النوع الثاني. الرسم البياني للدالة ذات نقطة التوقف موجود أسفل المثال.

يمكن أن يكون العثور على نقاط التوقف لوظيفة إما مهمة مستقلة أو جزءًا منها وظيفة كاملة للبحث والرسوم البيانية .

مثال 4.تحديد نقطة فاصل الدالة ونوع (حرف) نقطة فاصل الدالة

حل. من التعبير عن القوة عند 2، من الواضح أن الوظيفة غير محددة عند هذه النقطة. دعونا نجد الحدين الأيسر والأيمن للدالة عند هذه النقطة.

فجوة قابلة للإزالة.

تعريف. نقطة أتسمى نقطة الانقطاع القابلة للإزالة للوظيفة ص = و (س)، إذا كان الحد من الوظيفة و (خ)موجود عند هذه النقطة، ولكن عند هذه النقطة أوظيفة و (خ)إما غير محددة أو لها معنى خاص و (أ)، يختلف عن الحد و (خ)عند هذه النقطة.

مثال. على سبيل المثال، الدالة

لديه عند النقطة س = 0فجوة قابلة للإصلاح. والواقع أن القيمة الحدية لهذه الوظيفة عند هذه النقطة س = 0تساوي 1. القيمة الجزئية تساوي 2.

إذا كانت الوظيفة و (خ)لديه عند النقطة أفجوة قابلة للإزالة، فيمكن إزالة هذه الفجوة دون تغيير قيم الدالة عند نقاط أخرى غير أ. للقيام بذلك، يكفي وضع قيمة الوظيفة عند هذه النقطة أمساوية لقيمته الحدية عند هذه النقطة. لذلك، في المثال المذكور أعلاه يكفي أن نضع و(0)=1وثم ، أي. وظيفة و (خ)سوف تصبح مستمرة عند هذه النقطة س = 0.

الاضطراب من النوع الأول.

تعريف. نقطة أتسمى نقطة الانقطاع من النوع الأول إذا كانت الوظيفة عند هذه النقطة و (خ)له حدود محدودة ولكن غير متساوية لليمين واليسار

دعونا نعطي بعض الأمثلة.

مثال. وظيفة ص = SGN سلديه عند النقطة س = 0تمزق من النوع الأول. وبالفعل، وبالتالي فإن هذه الحدود ليست متساوية مع بعضها البعض.

مثال. وظيفة ، محددة في كل مكان باستثناء النقطة س = 1، عند هذه النقطة س = 1تمزق من النوع الأول. بالفعل، .

الاضطراب من النوع الثاني.

تعريف. نقطة أتسمى نقطة الانقطاع من النوع الثاني إذا كانت الوظيفة عند هذه النقطة و (خ)لا يحتوي على حد واحد على الأقل من النهايات من جانب واحد أو إذا كان أحد النهايات من جانب واحد على الأقل لا نهائيًا.

مثال. وظيفة و(س)=تان سومن الواضح أن لديه انقطاعًا من النوع الثاني عند كل نقطة س ك =π/2+π ك, ك=0، ± 1، ± 2،…لأنه في كل نقطة من هذا القبيل

مثال. الدالة لها انقطاع من النوع الثاني عند النقطة س = 0لأنه في هذه المرحلة ليس له حدود يمينية ولا يسرية.

استمرارية الدالة على القطعة

تعريف. وظيفة محددة على فترة زمنية والمستمر في كل نقطة من نقاطه يسمى مستمرا على هذه القطعة.

وعلاوة على ذلك، في ظل الاستمرارية عند هذه النقطة أيُفهم على أنه الاستمرارية على اليمين، وبالاستمرارية عند نقطة ما ب- الاستمرارية على اليسار.

سنقول أن الوظيفة ص = و (س)، محددة على المجموعة (خ)يصل إلى حافته العليا (السفلية) عليه ، في حالة وجود مثل هذه النقطة س 0 ∈(س)، ماذا و(س 0)=β (و(س 0)=α).

[فايرستراس] نظرية. كل دالة متصلة على فترة تكون محدودة وتصل إلى حدها الأعلى وحدها الأدنى عليها.

نظرية [بولزانو-كوشي]. إذا كانت الوظيفة ص = و (س)المستمر على الجزء و و(أ)=أ, و(ب)=ب، ثم لأي ج، خلص بين أو ب، هناك مثل هذه النقطة ξ∈ ، ماذا و(ξ)=C.

بمعنى آخر، الدالة المستمرة على فترة ما، والتي تأخذ أي قيمتين، تأخذ أيضًا أي قيمة تقع بينهما.

عاقبة. إذا كانت الدالة متصلة على قطعة ما وتأخذ قيم إشارات مختلفة في طرفيها، فهناك نقطة واحدة على الأقل على هذه القطعة تختفي عندها الدالة.

عاقبة. دع الوظيفة ص = و (س)المستمر على الجزء و , . ثم الوظيفة و (خ)يأخذ كافة القيم من الجزء وهذه القيم فقط.

وبالتالي فإن مجموعة جميع قيم الدالة المعطاة والمستمرة على قطعة معينة هي أيضًا قطعة.

استمرارية الوظيفة. نقاط الانهيار.

الثور يمشي ويتمايل ويتنهد وهو يمشي:
- أوه، اللوحة تنفد، والآن سأسقط!

سنتناول في هذا الدرس مفهوم استمرارية الدالة وتصنيف نقاط الانقطاع ومشكلة عملية شائعة دراسات استمرارية الوظائف. من اسم الموضوع، يخمن الكثيرون بشكل حدسي ما سيتم مناقشته ويعتقدون أن المادة بسيطة للغاية. هذا صحيح. لكن المهام البسيطة هي التي تُعاقب في أغلب الأحيان بسبب الإهمال والنهج السطحي لحلها. لذلك أنصحك بدراسة المقالة بعناية فائقة والتعرف على كل التفاصيل الدقيقة والتقنيات.

ما الذي تحتاج إلى معرفته وتكون قادرًا على فعله؟ليس كثيرا. لكي تتعلم الدرس جيدًا، عليك أن تفهم ما هو عليه حد الوظيفة. القراء مع مستوى منخفضالتحضير يكفي لاستيعاب المقال حدود الوظيفة. أمثلة على الحلولوالنظر معنى هندسيالحد في الدليل الرسوم البيانية وخصائص الوظائف الأولية. ومن المستحسن أيضًا أن تتعرف عليها التحولات الهندسية للرسوم البيانية، نظرًا لأن الممارسة في معظم الحالات تتضمن إنشاء رسم. التوقعات متفائلة للجميع، وحتى الغلاية الكاملة ستكون قادرة على التعامل مع المهمة بمفردها خلال الساعة أو الساعتين التاليتين!

استمرارية الوظيفة. نقاط التوقف وتصنيفها

مفهوم استمرارية الوظيفة

لنفكر في دالة متصلة على خط الأعداد بأكمله:

أو بعبارة أكثر إيجازًا، الدالة متصلة على (مجموعة الأعداد الحقيقية).

ما هو المعيار "الضيق الأفق" للاستمرارية؟ ومن الواضح أن الجدول الزمني وظيفة مستمرةيمكن الرسم دون رفع القلم الرصاص عن الورقة.

في هذه الحالة، يجب التمييز بوضوح بين مفهومين بسيطين: مجال الوظيفةو استمرارية الوظيفة. في الحالة العامة إنه ليس نفس الشيء. على سبيل المثال:

يتم تعريف هذه الوظيفة على خط الأعداد بأكمله، أي ل الجميعمعنى "x" له معناه الخاص "y". على وجه الخصوص، إذا، ثم. لاحظ أن النقطة الأخرى موضوعة بعلامات ترقيم، لأنه من خلال تعريف الدالة، يجب أن تتوافق قيمة الوسيطة معها الشيء الوحيدقيمة الوظيفة. هكذا، اِختِصاصوظيفتنا : .

لكن هذه الوظيفة ليست مستمرة!ومن الواضح تمامًا أنها تعاني في هذه المرحلة فجوة. المصطلح أيضًا واضح ومرئي تمامًا، هنا يجب أن يتم تمزيق قلم الرصاص من الورقة على أي حال. بعد ذلك بقليل سننظر في تصنيف نقاط التوقف.

استمرارية الدالة عند نقطة وعلى فترة

في مسألة رياضية معينة، يمكننا التحدث عن استمرارية دالة عند نقطة ما، أو استمرارية دالة على فترة، أو نصف فاصل، أو استمرارية دالة على قطعة. إنه، لا يوجد "مجرد استمرارية"- يمكن أن تكون الوظيفة مستمرة في مكان ما. و"لبنة البناء" الأساسية لكل شيء آخر هي استمرارية الوظيفة عند هذه النقطة .

نظرية التحليل الرياضييعطي تعريفًا لاستمرارية دالة عند نقطة ما باستخدام الأحياء "دلتا" و"إبسيلون"، ولكن عمليًا هناك تعريف آخر قيد الاستخدام، والذي سنوليه اهتمامًا وثيقًا.

أولا دعونا نتذكر حدود من جانب واحدالذي اقتحم حياتنا في الدرس الأول حول الرسوم البيانية الوظيفية. فكر في موقف يومي:

إذا اقتربنا من المحور إلى هذه النقطة غادر(السهم الأحمر)، فإن القيم المقابلة لـ "الألعاب" ستمتد على طول المحور إلى النقطة (السهم القرمزي). رياضيا، تم إصلاح هذه الحقيقة باستخدام الحد الأيسر:

انتبه إلى الإدخال (يقرأ "x يميل إلى ka على اليسار"). يرمز "المضاف" "ناقص صفر". ، وهذا يعني في الأساس أننا نقترب من الرقم من الجانب الأيسر.

وبالمثل، إذا اقتربت من النقطة "كا" على اليمين(السهم الأزرق)، فإن "الألعاب" ستصل إلى نفس القيمة، ولكن على طول السهم الأخضر، و الحد الأيمنسيتم تنسيقها على النحو التالي:

"المضاف" يرمز ، ويقول الإدخال: "x يميل إلى ka على اليمين."

إذا كانت النهايات من جهة واحدة منتهية ومتساوية(كما في حالتنا): فسنقول أن هناك حدًا عامًا. الأمر بسيط، الحد العام هو "المعتاد" لدينا حد الوظيفة، يساوي عددا منتهيا.

لاحظ أنه إذا لم يتم تعريف الدالة عند (ثقب نقطة سوداءعلى فرع الرسم البياني)، فإن الحسابات المذكورة أعلاه تظل صالحة. كما سبق أن أشرنا عدة مرات، ولا سيما في المقال على وظائف متناهية الصغر، التعبيرات تعني أن "x" قريبة بلا حدوديقترب من هذه النقطة، في حين لا يهم، سواء تم تعريف الوظيفة نفسها عند نقطة معينة أم لا. مثال جيدسوف تظهر في الفقرة التالية، عندما يتم تحليل الوظيفة.

تعريف: تكون الدالة متصلة عند نقطة ما إذا كانت نهاية الدالة عند نقطة معينة تساوي قيمة الدالة عند تلك النقطة: .

التعريف مفصل في وفقا للشروط:

1) يجب تعريف الدالة عند النقطة، أي أن القيمة يجب أن تكون موجودة.

2) يجب أن يكون هناك حد عام للوظيفة. وكما ذكر أعلاه، فإن هذا يعني وجود ومساواة الحدود من جانب واحد: .

3) نهاية الدالة عند نقطة معينة يجب أن تكون مساوية لقيمة الدالة عند هذه النقطة: .

إذا انتهكت مرة على الأقللثلاثة شروط، تفقد الدالة خاصية الاستمرارية عند النقطة .

استمرارية الدالة خلال فترة زمنيةتمت صياغتها ببراعة وبساطة شديدة: تكون الدالة متصلة على الفترة إذا كانت متصلة عند كل نقطة من الفترة المعطاة.

على وجه الخصوص، العديد من الدوال تكون متصلة على فترة لا نهائية، أي على مجموعة الأعداد الحقيقية. هذه دالة خطية، متعددة الحدود، أسية، جيب التمام، جيب التمام، إلخ. وبشكل عام، أي وظيفة أوليةالمستمر عليها مجال التعريفعلى سبيل المثال، تكون الدالة اللوغاريتمية متصلة على الفترة. آمل أن بهذه اللحظةلديك فكرة جيدة عن الشكل الذي تبدو عليه الرسوم البيانية للوظائف الرئيسية. أكثر معلومات مفصلةيمكن استخلاص استمراريتها من شخص لطيفباللقب Fichtengolts.

مع استمرارية الدالة على قطعة وأنصاف الفترات، فإن كل شيء ليس صعبًا أيضًا، ولكن من المناسب التحدث عن ذلك في الفصل حول العثور على الحد الأدنى والحد الأقصى لقيم دالة على مقطع ماولكن في الوقت الحالي دعونا لا نقلق بشأن ذلك.

تصنيف نقاط التوقف

إن الحياة الرائعة للوظائف غنية بجميع أنواع النقاط الخاصة، ونقاط الاستراحة ليست سوى صفحة واحدة من صفحات سيرتهم الذاتية.

ملحوظة : في حالة حدوث ذلك، سأتناول نقطة أولية: نقطة الانهيار هي دائمًا نقطة واحدة- لا يوجد "عدة نقاط استراحة متتالية"، أي أنه لا يوجد شيء اسمه "فاصل فاصل".

وتنقسم هذه النقاط بدورها إلى قسمين مجموعات كبيرة: تمزقات من النوع الأولو تمزقات من النوع الثاني. كل نوع من الفجوة له خاصته صفاتوالتي سننظر إليها الآن:

نقطة الانقطاع من النوع الأول

إذا تم انتهاك شرط الاستمرارية عند نقطة ما وحدود من جانب واحد محدود ، ثم يطلق عليه نقطة انقطاع من النوع الأول.

لنبدأ بالحالة الأكثر تفاؤلاً. وفقا للفكرة الأصلية للدرس، أردت أن أقول النظرية "في منظر عام"، ولكن من أجل إظهار حقيقة المادة، استقريت على الخيار بشخصيات محددة.

إنه لأمر محزن، مثل صورة للعروسين على خلفية الشعلة الأبدية، ولكن اللقطة التالية مقبولة بشكل عام. دعونا نصور الرسم البياني للوظيفة في الرسم:


هذه الدالة متصلة على خط الأعداد بأكمله، باستثناء النقطة. وفي الواقع، لا يمكن أن يساوي المقام صفرًا. ومع ذلك، وفقا لمعنى الحد، نستطيع قريبة بلا حدودالاقتراب من "الصفر" من اليسار ومن اليمين، أي أن الحدود أحادية الجانب موجودة، ومن الواضح أنها تتزامن:
(تم استيفاء الشرط رقم 2 الخاص بالاستمرارية).

لكن الدالة لم يتم تعريفها عند هذه النقطة، لذلك تم انتهاك الشرط رقم 1 من الاستمرارية، وتعاني الدالة من عدم الاستمرارية عند هذه النقطة.

استراحة من هذا النوع (مع الموجود الحد العام) وتسمى فجوة قابلة للإصلاح. لماذا قابلة للإزالة؟ لأن الوظيفة يمكن إعادة تعريفعند نقطة الانهيار:

هل يبدو الأمر غريبا؟ ربما. لكن مثل هذا التدوين الوظيفي لا يتعارض مع أي شيء! والآن أغلقت الفجوة وأصبح الجميع سعداء:


لنجري فحصًا رسميًا:

2) - هناك حد عام؛
3)

وبذلك تتحقق الشروط الثلاثة، وتكون الدالة متصلة عند نقطة حسب تعريف استمرارية الدالة عند نقطة.

ومع ذلك، يمكن لمكرهي الماتان تعريف الوظيفة بطريقة سيئة، على سبيل المثال :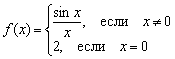


ومن المثير للاهتمام أن شرطي الاستمرارية الأولين قد تم استيفاءهما هنا:
1) - يتم تعريف الوظيفة عند نقطة معينة؛
2) - هناك حد عام.

لكن الحد الثالث لم يتم تجاوزه: أي حد الدالة عند النقطة غير متساويقيمة دالة معينة عند نقطة معينة.

وبالتالي، عند نقطة ما تعاني الوظيفة من انقطاع.

الحالة الثانية الأكثر حزنا تسمى تمزق من النوع الأول مع قفزة. والحزن يثيره حدود من جانب واحد محدودة ومختلفة. يظهر مثال في الرسم الثاني للدرس. عادة ما تحدث مثل هذه الفجوة في وظائف محددة جزئيا، والتي سبق ذكرها في المقال حول التحولات الرسم البياني.

خذ بعين الاعتبار الدالة متعددة التعريف وسنكمل رسمها. كيفية بناء الرسم البياني؟ بسيط جدا. على نصف فاصل نرسم جزءًا من القطع المكافئ ( اللون الاخضر)، على الفاصل الزمني – قطعة خط مستقيم (أحمر) وعلى نصف الفاصل – خط مستقيم ( لون ازرق).

علاوة على ذلك، بسبب عدم المساواة، يتم تحديد القيمة ل وظيفة من الدرجة الثانية(النقطة الخضراء)، وبسبب عدم المساواة، يتم تحديد القيمة ل دالة خطية(نقطة زرقاء):

في الحالة الأكثر صعوبة، يجب عليك اللجوء إلى البناء نقطة بنقطة لكل جزء من الرسم البياني (انظر الأول درس حول الرسوم البيانية للوظائف).

الآن سنكون مهتمين فقط بهذه النقطة. دعونا نفحصها من أجل الاستمرارية:

2) دعونا نحسب الحدود من جانب واحد.

على اليسار لدينا قطعة خط أحمر، وبالتالي فإن الحد من الجانب الأيسر هو:

على اليمين يوجد الخط المستقيم الأزرق، والحد الأيمن:

ونتيجة لذلك، تلقينا أعداد محدودة، و هم غير متساوي. منذ حدود من جانب واحد محدودة ومختلفة: ، فإن وظيفتنا تتحمل انقطاع من النوع الأول مع قفزة.

من المنطقي أنه لا يمكن إزالة هذه الفجوة - فالوظيفة في الواقع لا يمكن تعريفها بشكل أكبر و"لصقها معًا"، كما في المثال السابق.

نقاط الانقطاع من النوع الثاني

عادة، يتم تصنيف جميع حالات التمزق الأخرى بذكاء ضمن هذه الفئة. لن أدرج كل شيء، لأنه في الممارسة العملية، ستواجه 99٪ من المشاكل فجوة لا نهاية لها- عندما يكون الشخص أعسر أو أيمن، وفي أغلب الأحيان، يكون كلا الحدين لا نهائيين.

وبالطبع، الصورة الأكثر وضوحًا هي القطع الزائد عند النقطة صفر. هنا كلا الحدين من جانب واحد لا نهائيان: ولذلك تعاني الدالة من انقطاع من النوع الثاني عند النقطة .

أحاول ملء مقالاتي بمحتوى متنوع قدر الإمكان، لذلك دعونا نلقي نظرة على الرسم البياني للدالة التي لم يتم رؤيتها بعد:

وفقًا للمخطط القياسي:

1) لم يتم تعريف الدالة في هذه المرحلة لأن المقام يذهب إلى الصفر.

بالطبع، يمكننا أن نستنتج على الفور أن الدالة تعاني من انقطاع عند النقطة، ولكن سيكون من الجيد تصنيف طبيعة الانقطاع، والذي غالبًا ما يتطلبه الشرط. لهذا:

اسمحوا لي أن أذكركم أننا نعني بالتسجيل متناهي الصغر رقم سلبي ، وتحت الإدخال - عدد موجب متناهية الصغر.

الحدود من جانب واحد لا نهائية، مما يعني أن الدالة تعاني من انقطاع من النوع الثاني عند النقطة . المحور y هو الخط المقارب الرأسيللرسم البياني.

ليس من غير المألوف وجود كلا النهايتين من جانب واحد، ولكن أحدهما فقط لانهائي، على سبيل المثال:

هذا هو الرسم البياني للوظيفة.

نحن ندرس نقطة الاستمرارية:

1) لم يتم تعريف الوظيفة في هذه المرحلة.

2) دعونا نحسب الحدود من جانب واحد:

سنتحدث عن طريقة حساب هذه الحدود أحادية الجانب في المثالين الأخيرين من المحاضرة، على الرغم من أن العديد من القراء قد رأوا كل شيء وخمنوه بالفعل.

الحد الأيسر محدود ويساوي الصفر (نحن "لا نذهب إلى النقطة نفسها")، لكن الحد الأيمن لا نهائي ويقترب الفرع البرتقالي من الرسم البياني من مسافة لا نهائية الخط المقارب الرأسي، تعطى بالمعادلة (خط منقط أسود).

وبالتالي فإن الوظيفة تعاني انقطاع النوع الثانيعند نقطة .

أما بالنسبة للانقطاع من النوع الأول فيمكن تعريف الدالة عند نقطة الانقطاع نفسها. على سبيل المثال، لوظيفة متعددة التعريف لا تتردد في وضع نقطة سوداء غامقة عند أصل الإحداثيات. على اليمين فرع من القطع الزائد، والحد الأيمن لا نهائي. أعتقد أن الجميع تقريبًا لديه فكرة عما يبدو عليه هذا الرسم البياني.

ما كان الجميع يتطلع إليه:

كيفية فحص وظيفة للاستمرارية؟

يتم إجراء دراسة دالة الاستمرارية عند نقطة ما وفقًا لمخطط روتيني محدد بالفعل، والذي يتكون من التحقق من ثلاثة شروط للاستمرارية:

مثال 1

استكشاف الوظيفة

حل:

1) النقطة الوحيدة داخل النطاق هي حيث لم يتم تعريف الوظيفة.

2) دعونا نحسب الحدود من جانب واحد:

الحدود من جانب واحد محدودة ومتساوية.

وبالتالي، عند هذه النقطة تعاني الوظيفة من انقطاع قابل للإزالة.

كيف يبدو الرسم البياني لهذه الوظيفة؟

أود أن أبسط ، ويبدو أنه تم الحصول على قطع مكافئ عادي. لكنلم يتم تعريف الوظيفة الأصلية عند النقطة، لذلك مطلوب العبارة التالية:

لنقم بالرسم:

إجابة: تكون الدالة متصلة على خط الأعداد بأكمله باستثناء النقطة التي تعاني فيها من انقطاع قابل للإزالة.

يمكن تعريف الوظيفة بشكل أكبر بطريقة جيدة أو غير جيدة، ولكن وفقًا للشرط، فإن هذا غير مطلوب.

هل تقول أن هذا مثال بعيد المنال؟ مُطْلَقاً. لقد حدث هذا عشرات المرات في الممارسة العملية. تأتي جميع مهام الموقع تقريبًا من عمل واختبارات حقيقية مستقلة.

دعونا نتخلص من الوحدات المفضلة لدينا:

مثال 2

استكشاف الوظيفة من أجل الاستمرارية. تحديد طبيعة الانقطاعات الوظيفية إن وجدت. نفذ الرسم.

حل: لسبب ما، يشعر الطلاب بالخوف ولا يحبون الوظائف التي تحتوي على وحدة نمطية، على الرغم من عدم وجود شيء معقد فيها. لقد تطرقنا بالفعل إلى مثل هذه الأشياء قليلاً في الدرس. التحولات الهندسية للرسوم البيانية. وبما أن الوحدة غير سلبية، يتم توسيعها على النحو التالي: ، حيث "ألفا" هي بعض التعبيرات. في في هذه الحالة، ويجب كتابة وظيفتنا بالقطعة: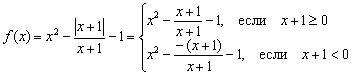

ولكن يجب تقليل كسور كلا القطعتين بمقدار . التخفيض، كما في المثال السابق، لن يتم دون عواقب. لم يتم تعريف الدالة الأصلية عند هذه النقطة لأن المقام يصل إلى الصفر. لذلك، يجب على النظام بالإضافة إلى ذلك تحديد الشرط، وجعل عدم المساواة الأولى صارمة:

الآن عن جدا استقبال مفيدحلول: قبل الانتهاء من المهمة على المسودة، من المفيد إجراء رسم (بغض النظر عما إذا كانت الشروط مطلوبة أم لا). سيساعد ذلك، أولا، على رؤية نقاط الاستمرارية ونقاط الانقطاع على الفور، وثانيا، سوف يحميك بنسبة 100٪ من الأخطاء عند العثور على حدود من جانب واحد.

دعونا نفعل الرسم. وفقًا لحساباتنا، من الضروري رسم جزء من القطع المكافئ (اللون الأزرق) على يسار النقطة، وعلى اليمين - قطعة من القطع المكافئ (اللون الأحمر)، بينما لم يتم تعريف الوظيفة عند نقطة نفسها:

إذا كنت في شك، فخذ بعض قيم x وقم بتوصيلها بالوظيفة (تذكر أن الوحدة تدمر علامة الطرح المحتملة) وتحقق من الرسم البياني.

دعونا نفحص وظيفة الاستمرارية تحليليا:

1) الدالة غير محددة عند النقطة، لذلك يمكننا القول على الفور أنها غير متصلة عندها.

2) لنحدد طبيعة الانقطاع، وللقيام بذلك، نحسب الحدود من جانب واحد:

النهايات أحادية الجانب منتهية ومختلفة، مما يعني أن الدالة تعاني من انقطاع من النوع الأول مع القفز عند النقطة . لاحظ مرة أخرى أنه عند إيجاد الحدود، لا يهم ما إذا كانت الدالة عند نقطة التوقف محددة أم لا.

الآن كل ما تبقى هو نقل الرسم من المسودة (تم إجراؤه كما لو كان بمساعدة البحث ؛-)) وإكمال المهمة:

إجابة: تكون الدالة متصلة على خط الأعداد بأكمله باستثناء النقطة التي تعاني فيها من انقطاع من النوع الأول مع قفزة.

في بعض الأحيان يحتاجون إلى إشارة إضافية إلى قفزة التوقف. يتم حسابه ببساطة - من الحد الأيمن تحتاج إلى طرح الحد الأيسر: أي أنه عند نقطة الاستراحة قفزت وظيفتنا بمقدار وحدتين (كما تخبرنا علامة الطرح).

مثال 3

استكشاف الوظيفة من أجل الاستمرارية. تحديد طبيعة الانقطاعات الوظيفية إن وجدت. جعل الرسم.

هذا مثال يمكنك حله بنفسك، وهو نموذج للحل في نهاية الدرس.

دعنا ننتقل إلى الإصدار الأكثر شيوعًا وانتشارًا للمهمة، حيث تتكون الوظيفة من ثلاثة أجزاء:

مثال 4

فحص دالة للاستمرارية ورسم رسم بياني للوظيفة .

حل: من الواضح أن الأجزاء الثلاثة للدالة متصلة على الفواصل الزمنية المقابلة، لذلك يبقى التحقق من نقطتي "التقاطع" فقط بين القطع. أولاً، لنقم بعمل مسودة رسم، لقد علقت على تقنية البناء بتفاصيل كافية في الجزء الأول من المقالة. الشيء الوحيد هو أننا بحاجة إلى متابعة النقاط الفردية بعناية: بسبب عدم المساواة، تنتمي القيمة إلى الخط المستقيم (النقطة الخضراء)، وبسبب عدم المساواة، تنتمي القيمة إلى القطع المكافئ (النقطة الحمراء):


حسنًا، من حيث المبدأ، كل شيء واضح =) كل ما تبقى هو إضفاء الطابع الرسمي على القرار. لكل نقطة من نقطتي "الانضمام"، نتحقق بشكل قياسي من 3 شروط للاستمرارية:

أنا)نحن ندرس نقطة الاستمرارية

1)

النهايات أحادية الجانب منتهية ومختلفة، مما يعني أن الدالة تعاني من انقطاع من النوع الأول مع القفز عند النقطة .

دعونا نحسب قفزة التوقف كالفرق بين الحدين الأيمن والأيسر:
أي أن الرسم البياني قد ارتفع بمقدار وحدة واحدة.

ثانيا)نحن ندرس نقطة الاستمرارية

1) - يتم تعريف الوظيفة عند نقطة معينة.

2) البحث عن حدود من جانب واحد:

- النهايات من جهة واحدة منتهية ومتساوية، مما يعني أن هناك نهاية عامة.

3) - نهاية الدالة عند نقطة ما تساوي قيمة هذه الدالة عند نقطة معينة.

في المرحلة النهائية ننقل الرسم إلى النسخة النهائية وبعد ذلك نضع الوتر النهائي:

إجابة: تكون الدالة متصلة على خط الأعداد بأكمله، باستثناء النقطة التي تعاني فيها من انقطاع من النوع الأول مع قفزة.

مثال 5

فحص دالة للاستمرارية وإنشاء الرسم البياني الخاص بها .

هذا مثال عليك حله بنفسك حل قصيروعينة تقريبية للمهمة في نهاية الدرس.

قد يتولد لديك انطباع بأن الدالة في مرحلة ما يجب أن تكون مستمرة، وفي نقطة أخرى يجب أن يكون هناك انقطاع. في الممارسة العملية، هذا ليس هو الحال دائما. حاول ألا تهمل الأمثلة المتبقية - سيكون هناك العديد من الميزات المثيرة للاهتمام والمهمة:

مثال 6

نظرا لوظيفة . التحقيق في وظيفة الاستمرارية عند النقاط. قم ببناء رسم بياني.

حل: ومرة ​​أخرى قم بتنفيذ الرسم على المسودة على الفور:

تكمن خصوصية هذا الرسم البياني في أن الدالة المتعددة التعريف تُعطى بواسطة معادلة محور الإحداثي السيني. يتم رسم هذه المنطقة هنا أخضر، وعادة ما يتم تمييزه في دفتر الملاحظات بالخط العريض باستخدام قلم رصاص بسيط. وبالطبع، لا ننسى كباشنا: القيمة تنتمي إلى فرع المماس (النقطة الحمراء)، والقيمة تنتمي إلى الخط المستقيم.

كل شيء واضح من الرسم - الوظيفة مستمرة على طول خط الأعداد بأكمله، ولا يبقى سوى إضفاء الطابع الرسمي على الحل، والذي يتم جلبه إلى الأتمتة الكاملة حرفيًا بعد 3-4 أمثلة مماثلة:

أنا)نحن ندرس نقطة الاستمرارية

1) - يتم تعريف الوظيفة عند نقطة معينة.

2) دعونا نحسب الحدود من جانب واحد:

مما يعني أن هناك حدًا عامًا.

فقط في حالة حدوث ذلك، دعني أذكرك بحقيقة تافهة: نهاية الثابت تساوي الثابت نفسه. في هذه الحالة، نهاية الصفر تساوي الصفر نفسه (الحد الأيسر).

3) - نهاية الدالة عند نقطة ما تساوي قيمة هذه الدالة عند نقطة معينة.

وبالتالي، تكون الدالة مستمرة عند نقطة ما حسب تعريف استمرارية الدالة عند نقطة ما.

ثانيا)نحن ندرس نقطة الاستمرارية

1) - يتم تعريف الوظيفة عند نقطة معينة.

2) البحث عن حدود من جانب واحد:

وهنا - نهاية الواحد تساوي الوحدة نفسها.

- هناك حد عام.

3) - نهاية الدالة عند نقطة ما تساوي قيمة هذه الدالة عند نقطة معينة.

وبالتالي، تكون الدالة مستمرة عند نقطة ما حسب تعريف استمرارية الدالة عند نقطة ما.

كالعادة، بعد البحث ننقل رسمنا إلى النسخة النهائية.

إجابة: الدالة مستمرة عند النقاط.

يرجى ملاحظة أنه في الحالة لم يطلب منا أي شيء عن دراسة الدالة بأكملها للاستمرارية، وتعتبر صيغة رياضية جيدة لصياغتها دقيقة وواضحةالجواب على السؤال المطروح. بالمناسبة، إذا كان الشرط لا يتطلب منك إنشاء رسم بياني، فهذا يعني أنك قمت بذلك كل الحقلا تقم ببنائها (على الرغم من أن المعلم يمكن أن يجبرك على القيام بذلك لاحقًا).

"إعصار اللسان" الرياضي الصغير لحلها بنفسك:

مثال 7

نظرا لوظيفة . التحقيق في وظيفة الاستمرارية عند النقاط. تصنيف نقاط التوقف، إن وجدت. نفذ الرسم.

حاول "نطق" كل "الكلمات" بشكل صحيح =) وارسم الرسم البياني بشكل أكثر دقة، ودقة، لن تكون زائدة عن الحاجة في كل مكان؛-)

كما تتذكر، أوصيت بإكمال الرسم على الفور كمسودة، ولكن من وقت لآخر تصادف أمثلة لا يمكنك فيها على الفور معرفة شكل الرسم البياني. لذلك، في بعض الحالات، من المفيد أولاً العثور على حدود من جانب واحد وبعد ذلك فقط، بناءً على الدراسة، قم بتصوير الفروع. في المثالين الأخيرين، سنتعلم أيضًا تقنية لحساب بعض النهايات أحادية الجانب:

مثال 8

فحص الدالة للاستمرارية وإنشاء الرسم البياني التخطيطي لها.

حل: النقاط السيئة واضحة: (يخفض مقام الأس إلى الصفر) و (يخفض مقام الكسر بأكمله إلى الصفر). ليس من الواضح كيف يبدو الرسم البياني لهذه الوظيفة، مما يعني أنه من الأفضل إجراء بعض الأبحاث أولاً.