أولاً، دعونا نفكر في حالة دالة مكونة من متغيرين. الحد الأقصى الشرطي للدالة $z=f(x,y)$ عند النقطة $M_0(x_0;y_0)$ هو الحد الأقصى لهذه الوظيفة، ويتم تحقيقه بشرط أن يكون المتغيران $x$ و $y$ في إن محيط هذه النقطة يحقق معادلة الاتصال $\ varphi (x,y)=0$.

يرجع اسم الحد الأقصى "الشرطي" إلى حقيقة أنه تم فرض شرط إضافي $\varphi(x,y)=0$ على المتغيرات. إذا كان من الممكن التعبير عن متغير واحد من معادلة الاتصال من خلال آخر، فإن مشكلة تحديد الحد الأقصى الشرطي تتلخص في مشكلة تحديد الحد الأقصى المعتاد لدالة متغير واحد. على سبيل المثال، إذا كانت معادلة الاتصال تتضمن $y=\psi(x)$، فعند استبدال $y=\psi(x)$ إلى $z=f(x,y)$، نحصل على دالة بمتغير واحد $z =f\left (x,\psi(x)\right)$. في الحالة العامةومع ذلك، فإن هذه الطريقة قليلة الفائدة، لذا يلزم إدخال خوارزمية جديدة.

طريقة مضاعف لاغرانج لوظائف متغيرين.

تتكون طريقة مضاعف لاغرانج من إنشاء دالة لاغرانج للعثور على الحد الأقصى الشرطي: $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ (تسمى المعلمة $\lambda$ مضاعف لاغرانج). يتم تحديد الشروط اللازمة للطرف الأقصى من خلال نظام المعادلات التي يتم من خلالها تحديد النقاط الثابتة:

$$ \left \( \begin(محاذاة) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \varphi (x,y)=0.\end(محاذاة) \right.$$

الشرط الكافي الذي يمكن من خلاله تحديد طبيعة الطرف الأقصى هو العلامة $d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy) ^("" )دي^2$. إذا كانت عند نقطة ثابتة $d^2F > 0$، فإن الدالة $z=f(x,y)$ لها حد أدنى شرطي عند هذه النقطة، ولكن إذا $d^2F< 0$, то условный максимум.

هناك طريقة أخرى لتحديد طبيعة الحد الأقصى. من معادلة الاقتران نحصل على: $\varphi_(x)^(")dx+\varphi_(y)^(")dy=0$, $dy=-\frac(\varphi_(x)^("))( \varphi_ (y)^("))dx$، وبالتالي عند أي نقطة ثابتة لدينا:

$$d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=F_(xx)^( "")dx^2+2F_(xy)^("")dx\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\right)+ F_(yy)^("")\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\right)^2=\\ =-\frac (dx^2)(\left(\varphi_(y)^(") \right)^2)\cdot\left(-(\varphi_(y)^("))^2 F_(xx)^(" ")+2\varphi_(x)^(")\varphi_(y)^(")F_(xy)^("")-(\varphi_(x)^("))^2 F_(yy)^ ("") \يمين)$$

أما العامل الثاني (الموجود بين قوسين) فيمكن تمثيله بهذا الشكل:

يتم تمييز عناصر المحدد $\left| باللون الأحمر. \begin(array) (cc) F_(xx)^("") & F_(xy)^("") \\ F_(xy)^("") & F_(yy)^("") \end (array)\right|$، وهي دالة هسي لدالة لاغرانج. إذا كان $H > 0$، فإن $d^2F< 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F >0 دولار، أي لدينا الحد الأدنى الشرطي للدالة $z=f(x,y)$.

ملاحظة بخصوص تدوين المحدد $H$. اظهر المخفي

$$ H=-\left|\begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_ (xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \ النهاية(صفيف) \يمين| $$

في هذه الحالة، ستتغير القاعدة المذكورة أعلاه على النحو التالي: إذا كان $H > 0$، فإن الدالة لها حد أدنى شرطي، وإذا كان $H< 0$ получим условный максимум функции $z=f(x,y)$. При решении задач следует учитывать такие нюансы.

خوارزمية لدراسة دالة لمتغيرين لأقصى شرطي

1. إنشاء دالة لاغرانج $F(x,y)=f(x,y)+\lambda\varphi(x,y)$
2. حل النظام $ \left \( \begin(aligned) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \ varphi (x,y)=0.\end(محاذاة) \right.$
3. حدد طبيعة الحد الأقصى عند كل نقطة من النقاط الثابتة الموجودة في الفقرة السابقة. للقيام بذلك، استخدم إحدى الطرق التالية:
   • قم بتكوين محدد $H$ واكتشف إشارته
   • مع الأخذ بعين الاعتبار معادلة الاقتران، احسب إشارة $d^2F$

طريقة لاغرانج المضاعف لوظائف المتغيرات n

لنفترض أن لدينا دالة مكونة من متغيرات $n$ $z=f(x_1,x_2,\ldots,x_n)$ ومعادلات اقتران $m$ ($n > m$):

$$\varphi_1(x_1,x_2,\ldots,x_n)=0; \; \varphi_2(x_1,x_2,\ldots,x_n)=0,\ldots,\varphi_m(x_1,x_2,\ldots,x_n)=0.$$

بالإشارة إلى مضاعفات لاغرانج كـ $\lambda_1,\lambda_2,\ldots,\lambda_m$، نقوم بتكوين دالة لاغرانج:

$$F(x_1,x_2,\ldots,x_n,\lambda_1,\lambda_2,\ldots,\lambda_m)=f+\lambda_1\varphi_1+\lambda_2\varphi_2+\ldots+\lambda_m\varphi_m$$

يتم توفير الشروط اللازمة لوجود الحد الأقصى الشرطي من خلال نظام المعادلات التي يتم من خلالها العثور على إحداثيات النقاط الثابتة وقيم مضاعفات لاغرانج:

$$\left\(\begin(aligned) & \frac(\partial F)(\partial x_i)=0; (i=\overline(1,n))\\ & \varphi_j=0; (j=\ overline(1,m)) \end(محاذاة) \right.$$

يمكنك معرفة ما إذا كانت الدالة تحتوي على حد أدنى شرطي أو حد أقصى شرطي عند النقطة التي تم العثور عليها، كما كان من قبل، باستخدام العلامة $d^2F$. إذا كان عند النقطة التي تم العثور عليها $d^2F > 0$، فإن الدالة لها حد أدنى شرطي، ولكن إذا كان $d^2F< 0$, - то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:

محدد المصفوفة $\left| \begin(array) (ccccc) \frac(\partial^2F)(\partial x_(1)^(2)) & \frac(\partial^2F)(\partial x_(1)\partial x_(2) ) & \frac(\جزئي^2F)(\جزئي x_(1)\جزئي x_(3)) &\ldots & \frac(\جزئي^2F)(\جزئي x_(1)\جزئي x_(n)) \\ \frac(\جزئي^2F)(\جزئي x_(2)\جزئي x_1) & \frac(\جزئي^2F)(\جزئي x_(2)^(2)) & \frac(\جزئي^2F) )(\جزئي x_(2)\جزئي x_(3)) &\ldots & \frac(\جزئي^2F)(\جزئي x_(2)\جزئي x_(n))\\ \frac(\جزئي^2F) )(\جزئي x_(3) \جزئي x_(1)) & \frac(\جزئي^2F)(\جزئي x_(3)\جزئي x_(2)) & \frac(\جزئي^2F)(\جزئي x_(3)^(2)) &\ldots & \frac(\partial^2F)(\partial x_(3)\جزئي x_(n))\\ \ldots & \ldots & \ldots &\ldots & \ ldots\\ \frac(\partial^2F)(\جزئي x_(n)\جزئي x_(1)) & \frac(\جزئي^2F)(\جزئي x_(n)\جزئي x_(2)) & \ frac(\جزئي^2F)(\جزئي x_(n)\جزئي x_(3)) &\ldots & \frac(\جزئي^2F)(\جزئي x_(n)^(2))\\ \end( array) \right|$، المميزة باللون الأحمر في المصفوفة $L$، هي الدالة Hessian لدالة Lagrange. نستخدم القاعدة التالية:

• إذا كانت علامات الزاوية الصغرى $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ المصفوفات $L$ تتزامن مع إشارة $(-1)^m$، فإن النقطة الثابتة قيد الدراسة هي النقطة الدنيا المشروطة للدالة $ z=f(x_1,x_2 ,x_3,\ldots,x_n)$.
• إذا كانت علامات الزاوية الصغرى $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ بديلة، وإشارة الصغير $H_(2m+1)$ تتطابق مع إشارة الرقم $(-1)^(m+1) )$، فإن النقطة الثابتة هي النقطة القصوى المشروطة للدالة $z=f(x_1,x_2,x_3,\ldots,x_n)$.

المثال رقم 1

أوجد الحد الأقصى الشرطي للدالة $z(x,y)=x+3y$ تحت الشرط $x^2+y^2=10$.

التفسير الهندسي لهذه المشكلة هو كما يلي: مطلوب إيجاد أكبر وأصغر قيم لتطبيق المستوى $z=x+3y$ لنقاط تقاطعه مع الاسطوانة $x^2+y ^2=10$.

من الصعب إلى حد ما التعبير عن متغير من خلال متغير آخر من معادلة الاقتران واستبداله في الدالة $z(x,y)=x+3y$، لذلك سوف نستخدم طريقة لاغرانج.

للإشارة إلى $\varphi(x,y)=x^2+y^2-10$، نقوم بتكوين دالة Lagrange:

$$ F(x,y)=z(x,y)+\lambda \varphi(x,y)=x+3y+\lambda(x^2+y^2-10);\\ \frac(\جزئي) F)(\جزئي x)=1+2\لامدا x; \frac(\partial F)(\partial y)=3+2\lambda y. $$

دعونا نكتب نظامًا من المعادلات لتحديد النقاط الثابتة لدالة لاغرانج:

$$ \left \( \begin(محاذاة) & 1+2\lambda x=0;\\ & 3+2\lambda y=0;\\ & x^2+y^2-10=0. \end (محاذاة)\يمين.$$

إذا افترضنا $\lambda=0$، تصبح المعادلة الأولى: $1=0$. يشير التناقض الناتج إلى أن $\lambda\neq 0$. تحت الشرط $\lambda\neq 0$، من المعادلتين الأولى والثانية لدينا: $x=-\frac(1)(2\lambda)$, $y=-\frac(3)(2\lambda) $. بتعويض القيم التي تم الحصول عليها في المعادلة الثالثة نحصل على:

$$ \left(-\frac(1)(2\lambda) \right)^2+\left(-\frac(3)(2\lambda) \right)^2-10=0;\\ \frac (1)(4\لامدا^2)+\فارك(9)(4\لامدا^2)=10; \lambda^2=\frac(1)(4); \left[ \begin(محاذاة) & \lambda_1=-\frac(1)(2);\\ & \lambda_2=\frac(1)(2). \end(محاذاة) \right.\\ \begin(محاذاة) & \lambda_1=-\frac(1)(2); \; x_1=-\frac(1)(2\lambda_1)=1; \; y_1=-\frac(3)(2\lambda_1)=3;\\ & \lambda_2=\frac(1)(2); \; x_2=-\frac(1)(2\lambda_2)=-1; \; y_2=-\frac(3)(2\lambda_2)=-3.\end(محاذاة) $$

لذلك، لدى النظام حلان: $x_1=1;\; y_1=3;\; \lambda_1=-\frac(1)(2)$ و $x_2=-1;\; y_2=-3;\; \lambda_2=\frac(1)(2)$. دعونا نتعرف على طبيعة الحد الأقصى عند كل نقطة ثابتة: $M_1(1;3)$ و$M_2(-1;-3)$. للقيام بذلك، نحسب محدد $H$ عند كل نقطة.

$$ \varphi_(x)^(")=2x;\; \varphi_(y)^(")=2y;\; F_(xx)^("")=2\lambda;\; F_(xy)^("")=0;\; F_(yy)^("")=2\lambda.\\ H=\left| \begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \end(array) \right|= \يسار| \begin(array) (ccc) 0 & 2x & 2y\\ 2x & 2\lambda & 0 \\ 2y & 0 & 2\lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right| $$

عند النقطة $M_1(1;3)$ نحصل على: $H=8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & 1 & 3\\ 1 & -1/2 & 0 \\ 3 & 0 & -1/2 \end(array) \right|=40 > 0$، لذا في النقطة الدالة $M_1(1;3)$ $z(x,y)=x+3y$ لها حد أقصى شرطي، $z_(\max)=z(1;3)=10$.

وبالمثل، عند النقطة $M_2(-1,-3)$ نجد: $H=8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \end(array) \right|=-40$. منذ $H< 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{\min}=z(-1;-3)=-10$.

ألاحظ أنه بدلاً من حساب قيمة المحدد $H$ عند كل نقطة، فمن الملائم أكثر توسيعه منظر عام. لكي لا تشوش النص بالتفاصيل، سأخفي هذه الطريقة تحت الملاحظة.

كتابة المحدد $H$ بشكل عام. اظهر المخفي

$$ H=8\cdot\left|\begin(array)(ccc)0&x&y\\x&\lambda&0\\y&0&\lambda\end(array)\right| =8\cdot\left(-\lambda(y^2)-\lambda(x^2)\right) =-8\lambda\cdot\left(y^2+x^2\right). $$

من حيث المبدأ، من الواضح بالفعل ما هي العلامة $H$. نظرًا لعدم تطابق أي من النقاط $M_1$ أو $M_2$ مع الأصل، فإن $y^2+x^2>0$. ولذلك، فإن علامة $H$ تكون معاكسة لعلامة $\lambda$. يمكنك إكمال الحسابات:

$$ \begin(aligned) &H(M_1)=-8\cdot\left(-\frac(1)(2)\right)\cdot\left(3^2+1^2\right)=40;\ \ &H(M_2)=-8\cdot\frac(1)(2)\cdot\left((-3)^2+(-1)^2\right)=-40. \end(محاذاة) $$

يمكن حل السؤال حول طبيعة الحد الأقصى عند النقطتين الثابتتين $M_1(1;3)$ و $M_2(-1;-3)$ دون استخدام المحدد $H$. دعونا نجد علامة $d^2F$ عند كل نقطة ثابتة:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=2\lambda \left( dx^2+dy^2\يمين) $$

اسمحوا لي أن أشير إلى أن الترميز $dx^2$ يعني بالضبط $dx$ مرفوعًا إلى القوة الثانية، أي. $\left(dx \right)^2$. وبالتالي لدينا: $dx^2+dy^2>0$، وبالتالي، مع $\lambda_1=-\frac(1)(2)$ نحصل على $d^2F< 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.

إجابة: عند النقطة $(-1;-3)$، يكون للدالة حد أدنى شرطي، $z_(\min)=-10$. عند النقطة $(1;3)$، يكون للدالة حد أقصى شرطي، $z_(\max)=10$

المثال رقم 2

أوجد الحد الأقصى الشرطي للدالة $z(x,y)=3y^3+4x^2-xy$ تحت الشرط $x+y=0$.

الطريقة الأولى (طريقة مضاعف لاغرانج)

للدلالة على $\varphi(x,y)=x+y$، نؤلف دالة Lagrange: $F(x,y)=z(x,y)+\lambda \varphi(x,y)=3y^3+ 4x^2 -xy+\lambda(x+y)$.

$$ \frac(\partial F)(\partial x)=8x-y+\lambda; \; \frac(\partial F)(\partial y)=9y^2-x+\lambda.\\ \left \( \begin(aligned) & 8x-y+\lambda=0;\\ & 9y^2-x+\ lambda=0; \\ & x+y=0.\end(محاذاة) \right.$$

بعد حل النظام، نحصل على: $x_1=0$، $y_1=0$، $\lambda_1=0$ و $x_2=\frac(10)(9)$, $y_2=-\frac(10)( 9)$ , $\lambda_2=-10$. لدينا نقطتان ثابتتان: $M_1(0;0)$ و $M_2 \left(\frac(10)(9);-\frac(10)(9) \right)$. دعونا نتعرف على طبيعة الحد الأقصى عند كل نقطة ثابتة باستخدام المحدد $H$.

$$H=\left| \begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \end(array) \right|= \يسار| \begin(array) (ccc) 0 & 1 & 1\\ 1 & 8 & -1 \\ 1 & -1 & 18y \end(array) \right|=-10-18y $$

عند النقطة $M_1(0;0)$ $H=-10-18\cdot 0=-10< 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{\min}=0$. В точке $M_2\left(\frac{10}{9};-\frac{10}{9}\right)$ $H=10 >0$، وبالتالي فإن الدالة عند هذه النقطة لها حد أقصى مشروط، $z_(\max)=\frac(500)(243)$.

نحن نتحقق من طبيعة الطرف الأقصى عند كل نقطة باستخدام طريقة مختلفة، بناءً على إشارة $d^2F$:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=8dx^2-2dxdy+ 18ydy ^2 $$

من معادلة الاتصال $x+y=0$ لدينا: $d(x+y)=0$، $dx+dy=0$، $dy=-dx$.

$$ د^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2 $$

بما أن $ d^2F \Bigr|_(M_1)=10 dx^2 > 0$، فإن $M_1(0;0)$ هي النقطة الدنيا الشرطية للدالة $z(x,y)=3y^3+ 4x^2-xy$. وبالمثل، $d^2F \Bigr|_(M_2)=-10 dx^2< 0$, т.е. $M_2\left(\frac{10}{9}; -\frac{10}{9} \right)$ - точка условного максимума.

الطريقة الثانية

من معادلة الاتصال $x+y=0$ نحصل على: $y=-x$. باستبدال $y=-x$ في الدالة $z(x,y)=3y^3+4x^2-xy$، نحصل على بعض دوال المتغير $x$. لنشير إلى هذه الوظيفة بالرمز $u(x)$:

$$ u(x)=z(x,-x)=3\cdot(-x)^3+4x^2-x\cdot(-x)=-3x^3+5x^2. $$

وهكذا قمنا بتقليص مشكلة إيجاد الحد الأقصى الشرطي لدالة لمتغيرين إلى مشكلة تحديد الحد الأقصى لدالة لمتغير واحد.

$$ u_(x)^(")=-9x^2+10x;\\ -9x^2+10x=0; \; x\cdot(-9x+10)=0;\\ x_1=0; \ ; y_1=-x_1=0;\\ x_2=\frac(10)(9);\; y_2=-x_2=-\frac(10)(9).$$

لقد حصلنا على النقاط $M_1(0;0)$ و$M_2\left(\frac(10)(9); -\frac(10)(9)\right)$. يُعرف المزيد من البحث من خلال حساب التفاضل والتكامل لوظائف متغير واحد. من خلال فحص إشارة $u_(xx)^("")$ عند كل نقطة ثابتة أو التحقق من التغيير في إشارة $u_(x)^(")$ عند النقاط التي تم العثور عليها، نحصل على نفس الاستنتاجات عندما حل الطريقة الأولى، على سبيل المثال، سوف نتحقق من العلامة $u_(xx)^("")$:

$$u_(xx)^("")=-18x+10;\\ u_(xx)^("")(M_1)=10;\;u_(xx)^("")(M_2)=- 10.$$

بما أن $u_(xx)^("")(M_1)>0$، فإن $M_1$ هي النقطة الدنيا للدالة $u(x)$، و $u_(\min)=u(0)=0 $ . منذ $u_(xx)^("")(M_2)<0$, то $M_2$ - точка максимума функции $u(x)$, причём $u_{\max}=u\left(\frac{10}{9}\right)=\frac{500}{243}$.

تتطابق قيم الدالة $u(x)$ لحالة اتصال معينة مع قيم الدالة $z(x,y)$، أي الحدود القصوى التي تم العثور عليها للدالة $u(x)$ هي الحدود القصوى الشرطية المطلوبة للدالة $z(x,y)$.

إجابة: عند النقطة $(0;0)$، يكون للدالة حد أدنى شرطي، $z_(\min)=0$. عند النقطة $\left(\frac(10)(9); -\frac(10)(9) \right)$ يكون للدالة حد أقصى شرطي، $z_(\max)=\frac(500)(243) )$.

لنفكر في مثال آخر سنوضح فيه طبيعة الحد الأقصى من خلال تحديد إشارة $d^2F$.

المثال رقم 3

أوجد القيم الأكبر والأصغر للدالة $z=5xy-4$ إذا كان المتغيران $x$ و $y$ موجبين ويحققان معادلة الاقتران $\frac(x^2)(8)+\frac( ص^2)(2) -1=0$.

لنقم بتكوين دالة لاغرانج: $F=5xy-4+\lambda \left(\frac(x^2)(8)+\frac(y^2)(2)-1 \right)$. دعونا نجد النقاط الثابتة لوظيفة لاغرانج:

$$ F_(x)^(")=5y+\frac(\lambda x)(4); \; F_(y)^(")=5x+\lambda y.\\ \left \( \begin(محاذاة) & 5y+\frac(\lambda x)(4)=0;\\ & 5x+\lambda y=0;\\ & \frac(x^2)(8)+\frac(y^2)(2)- 1=0;\\ & x > 0; \;y > 0. \end(محاذاة) \right. $$

يتم تنفيذ جميع التحويلات الإضافية مع الأخذ بعين الاعتبار $x > 0; \; y > 0$ (تم تحديد هذا في بيان المشكلة). من المعادلة الثانية نعبر عن $\lambda=-\frac(5x)(y)$ ونعوض بالقيمة التي تم العثور عليها في المعادلة الأولى: $5y-\frac(5x)(y)\cdot \frac(x)(4) )=0$ , $4y^2-x^2=0$, $x=2y$. بالتعويض $x=2y$ في المعادلة الثالثة، نحصل على: $\frac(4y^2)(8)+\frac(y^2)(2)-1=0$، $y^2=1$، $ص =1$.

بما أن $y=1$، فإن $x=2$، $\lambda=-10$. نحدد طبيعة الحد الأقصى عند النقطة $(2;1)$ بناءً على إشارة $d^2F$.

$$ F_(xx)^("")=\frac(\lambda)(4); \; F_(xy)^("")=5; \; F_(yy)^("")=\lambda. $$

بما أن $\frac(x^2)(8)+\frac(y^2)(2)-1=0$، إذن:

$$ d\left(\frac(x^2)(8)+\frac(y^2)(2)-1\right)=0; \; d\left(\frac(x^2)(8) \right)+d\left(\frac(y^2)(2) \right)=0; \; \frac(x)(4)dx+ydy=0; \; دى=-\فارك(xdx)(4y). $$

من حيث المبدأ، هنا يمكنك على الفور استبدال إحداثيات النقطة الثابتة $x=2$، $y=1$ والمعلمة $\lambda=-10$، والحصول على:

$$ F_(xx)^("")=\frac(-5)(2); \; F_(xy)^("")=-10; \; dy=-\frac(dx)(2).\\ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^(" ")dy^2=-\frac(5)(2)dx^2+10dx\cdot \left(-\frac(dx)(2) \right)-10\cdot \left(-\frac(dx) (2) \يمين)^2=\\ =-\frac(5)(2)dx^2-5dx^2-\frac(5)(2)dx^2=-10dx^2. $$

ومع ذلك، في مشاكل أخرى على الحد الأقصى المشروط قد يكون هناك عدة نقاط ثابتة. في مثل هذه الحالات، من الأفضل تمثيل $d^2F$ بشكل عام، ثم استبدال إحداثيات كل نقطة ثابتة تم العثور عليها في التعبير الناتج:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=\frac(\lambda) (4)dx^2+10\cdot dx\cdot \frac(-xdx)(4y) +\lambda\cdot \left(-\frac(xdx)(4y) \right)^2=\\ =\frac (\lambda)(4)dx^2-\frac(5x)(2y)dx^2+\lambda \cdot \frac(x^2dx^2)(16y^2)=\left(\frac(\lambda) )(4)-\frac(5x)(2y)+\frac(\lambda \cdot x^2)(16y^2) \right)\cdot dx^2 $$

بالتعويض $x=2$، $y=1$، $\lambda=-10$، نحصل على:

$$ d^2 F=\left(\frac(-10)(4)-\frac(10)(2)-\frac(10 \cdot 4)(16) \right)\cdot dx^2=- 10دx^2. $$

منذ $d^2F=-10\cdot dx^2< 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{\max}=10-4=6$.

إجابة: عند النقطة $(2;1)$، يكون للدالة حد أقصى شرطي، $z_(\max)=6$.

في الجزء التالي سوف نتناول تطبيق طريقة لاغرانج على دوال ذات عدد أكبر من المتغيرات.

الحدود القصوى لوظائف عدة متغيرات. شرط ضروري للأقصى. حالة كافية للأقصى. الحد الأقصى المشروط. طريقة لاغرانج المضاعف. العثور على أكبر وأصغر القيم.

محاضرة 5.

التعريف 5.1.نقطة م 0 (س 0، ص 0)مُسَمًّى النقطة القصوىالمهام ض = و (س، ص)،لو و (س س، ص س) > و (س، ص)لجميع النقاط (س، ص) م 0.

التعريف 5.2.نقطة م 0 (س 0، ص 0)مُسَمًّى نقطة الحد الأدنىالمهام ض = و (س، ص)،لو و (س س، ص س) < و (س، ص)لجميع النقاط (س، ص)من بعض المناطق المجاورة لنقطة ما م 0.

ملاحظة 1. يتم استدعاء الحد الأقصى والحد الأدنى من النقاط النقاط القصوىوظائف العديد من المتغيرات.

الملاحظة 2. يتم تحديد النقطة القصوى لوظيفة أي عدد من المتغيرات بطريقة مماثلة.

نظرية 5.1(الشروط اللازمة للأقصى). لو م 0 (س 0، ص 0)- النقطة القصوى للوظيفة ض = و (س، ص)،عند هذه النقطة تكون المشتقات الجزئية من الدرجة الأولى لهذه الدالة تساوي صفرًا أو لا وجود لها.

دليل.

دعونا إصلاح قيمة المتغير في، العد ص = ص 0. ثم الوظيفة و (س، ص 0)ستكون دالة لمتغير واحد X، لأي منهم س = س 0هي النقطة القصوى. لذلك، وفقا لنظرية فيرما، أو غير موجود. وقد ثبت نفس البيان بالمثل ل .

التعريف 5.3.تسمى النقاط التي تنتمي إلى مجال دالة ذات عدة متغيرات تكون عندها المشتقات الجزئية للدالة مساوية للصفر أو غير موجودة نقاط ثابتةهذه الوظيفة.

تعليق. وبالتالي، لا يمكن الوصول إلى الحد الأقصى إلا عند نقاط ثابتة، ولكن ليس بالضرورة أن يتم ملاحظته عند كل منها.

نظرية 5.2(شروط كافية للحد الأقصى). اسمحوا في بعض حي هذه النقطة م 0 (س 0، ص 0)، وهي نقطة ثابتة للوظيفة ض = و (س، ص)،هذه الدالة لها مشتقات جزئية متصلة حتى الدرجة الثالثة ضمنا. فلنشير إذن إلى:

1) و (س، ص)لديه عند هذه النقطة م 0الحد الأقصى إذا أ-ب² > 0, أ < 0;

2) و (س، ص)لديه عند هذه النقطة م 0الحد الأدنى إذا أ-ب² > 0, أ > 0;

3) لا يوجد حد أقصى عند النقطة الحرجة إذا أ-ب² < 0;

4) إذا أ-ب² = 0، هناك حاجة إلى مزيد من البحث.

دليل.

دعونا نكتب صيغة تايلور من الدرجة الثانية للدالة و (س، ص)،تذكر أنه عند نقطة ثابتة تكون المشتقات الجزئية من الدرجة الأولى تساوي الصفر:

أين إذا كانت الزاوية بين القطعة م 0 م، أين م (× 0 +Δ س، ص 0 +Δ في) والمحور O Xتشير إلى φ، ثم Δ س =Δ ρ كوس φ, Δ ص =Δρالخطيئة. في هذه الحالة، صيغة تايلور سوف تأخذ الشكل: . دعونا بعد ذلك يمكننا قسمة وضرب التعبير بين قوسين أ. نحن نحصل:

دعونا الآن نفكر في أربعة الحالات المحتملة:

1) ايه سي-بي² > 0, أ < 0. Тогда , и في صغيرة بما فيه الكفاية Δρ. لذلك في بعض الأحياء م 0 و (س 0 + Δ س، ص 0 +Δ ذ)< و (س 0، ص 0)، إنه م 0- النقطة القصوى.

2) دع أ-ب² > 0, أ> 0.ثم ، و م 0- نقطة الحد الأدنى.

3) دع ايه سي-بي² < 0, أ> 0. ضع في اعتبارك زيادة الوسائط على طول الشعاع φ = 0. ثم من (5.1) يتبع ذلك أي أنه عند التحرك على طول هذا الشعاع تزداد الدالة. إذا تحركنا على طول شعاع بحيث tg φ 0 = -أ/ب،الذي - التي لذلك، عند التحرك على طول هذا الشعاع، تقل الدالة. لذا، الفترة م 0ليست نقطة متطرفة.

3`) متى أ-ب² < 0, أ < 0 доказательство отсутствия экстремума проводится

مماثلة للسابقة.

3``) إذا أ-ب² < 0, أ= 0 ثم . حيث . ثم لصغير بما فيه الكفاية φ التعبير 2 بكوسφ + ج sinφ قريب من 2 فيأي أنها تحتفظ بإشارة ثابتة، ولكن علامة sinφ تغير بالقرب من النقطة م 0.وهذا يعني أن زيادة دالة التغييرات تشير إلى محيط نقطة ثابتة، وهي بالتالي ليست نقطة متطرفة.

4) إذا أ-ب² = 0، و , أي أن علامة الزيادة تتحدد بعلامة 2α 0. وفي الوقت نفسه، من الضروري إجراء مزيد من البحث لتوضيح مسألة وجود الحد الأقصى.

مثال. دعونا نجد النقاط القصوى للوظيفة ض = س² - 2 س ص + 2ذ² + 2 س.للعثور على نقاط ثابتة، نحل النظام . إذن النقطة الثابتة هي (-2،-1). حيث أ = 2, في = -2, مع= 4. ثم أ-ب² = 4 > 0، وبالتالي، عند نقطة ثابتة يتم الوصول إلى الحد الأقصى، أي الحد الأدنى (منذ أ > 0).

التعريف 5.4.إذا كانت الحجج الدالة و (× 1، × 2،…، × ن)متصل شروط إضافيةمثل مالمعادلات ( م< n) :

φ 1 ( × 1، × 2،…، × ن) = 0, φ 2 ( × 1، × 2،…، × ن) = 0، …، φ م ( × 1، × 2،…، × ن) = 0, (5.2)

حيث أن الدوال φ i لها مشتقات جزئية متصلة، فتسمى المعادلات (5.2). معادلات الاتصال.

التعريف 5.5.الحد الأقصى للوظيفة و (× 1، × 2،…، × ن)عند استيفاء الشروط (5.2)، يتم استدعاؤه أقصى مشروط.

تعليق. يمكننا تقديم التفسير الهندسي التالي للقيمة القصوى الشرطية لدالة ذات متغيرين: دع وسيطات الدالة و (س، ص)المرتبطة بالمعادلة φ (س، ص)= 0، تحديد بعض المنحنى في المستوى O xy. إعادة بناء الخطوط المتعامدة على المستوى O من كل نقطة من هذا المنحنى xyحتى يتقاطع مع السطح ض = و (س، ص)،نحصل على منحنى مكاني ملقى على السطح فوق المنحنى φ (س، ص)= 0. المهمة هي العثور على النقاط القصوى للمنحنى الناتج، والتي، بالطبع، في الحالة العامة لا تتطابق مع النقاط القصوى غير المشروطة للدالة و (س، ص).

دعونا نحدد الشروط اللازمة لحد أقصى مشروط لدالة ذات متغيرين من خلال تقديم التعريف التالي أولاً:

التعريف 5.6.وظيفة L (x 1 , x 2 ,…, x n) = f (x 1 , x 2 ,…, x n) + lect 1 φ 1 (x 1 , x 2 ,…, x n) +

+ lect 2 φ 2 (x 1 , x 2 ,…, x n) +…+lect m φ m (x 1 , x 2 ,…, x n), (5.3)

أين lecti –بعضها ثابت، يسمى وظيفة لاغرانج، والأرقام χ ط– مضاعفات لاغرانج لأجل غير مسمى.

نظرية 5.3(الشروط اللازمة لحد أقصى مشروط). الحد الأقصى الشرطي للدالة ض = و (س، ص)في وجود معادلة الاقتران φ ( س، ص)لا يمكن تحقيق = 0 إلا عند النقاط الثابتة لوظيفة لاغرانج L (س، ص) = و (س، ص) + φ (س، ص).

دليل. تحدد معادلة الاقتران علاقة ضمنية فيمن Xلذلك سنفترض ذلك فيهناك وظيفة من X: ص = ص(س).ثم ضهنالك وظيفة معقدةمن X، ويتم تحديد نقاطها الحرجة بالشرط: . (5.4) من معادلة الاقتران يتبع ذلك . (5.5)

دعونا نضرب المساواة (5.5) في عدد ما ونضيفه إلى (5.4). نحن نحصل:

، أو .

يجب تحقيق المساواة الأخيرة عند النقاط الثابتة، والتي منها يلي:

(5.6)

تم الحصول على نظام من ثلاث معادلات لثلاثة مجهولين: س، صو، والمعادلتان الأوليتان هما شروط النقطة الثابتة لدالة لاغرانج. من خلال حذف المجهول المساعد lect من النظام (5.6)، نجد إحداثيات النقاط التي يمكن أن يكون للدالة الأصلية عندها حد مشروط.

الملاحظة 1. يمكن التحقق من وجود الحد الأقصى الشرطي عند النقطة التي تم العثور عليها من خلال دراسة المشتقات الجزئية من الدرجة الثانية لدالة لاغرانج عن طريق القياس مع النظرية 5.2.

الملاحظة 2. النقاط التي يمكن عندها الوصول إلى الحد الأقصى المشروط للدالة و (× 1، × 2،…، × ن)عند استيفاء الشروط (5.2)، يمكن تعريفها كحلول للنظام (5.7)

مثال. دعونا نجد الحد الأقصى الشرطي للدالة ض = س صبشرط س + ص= 1. دعونا نؤلف دالة لاغرانج L(x, y) = xy + lect (x + y – 1). يبدو النظام (5.6) كما يلي:

حيث -2lect=1، lect=-0.5، س = ص = -π = 0.5. حيث ل (س، ص)يمكن تمثيلها في النموذج ل(س، ص) = - 0,5 (س – ص)² + 0.5 ≥ 0.5، وبالتالي عند النقطة الثابتة التي تم العثور عليها ل (س، ص)لديه الحد الأقصى و ض = س ص –الحد الأقصى المشروط.

تعريف1: يقال أن الدالة لها قيمة عظمى محلية عند نقطة ما إذا كان هناك جوار للنقطة مثل أي نقطة ممع الإحداثيات (س، ص)يحمل عدم المساواة: . في هذه الحالة، أي زيادة الوظيفة< 0.

التعريف2: يقال أن الدالة لها قيمة صغرى محلية عند نقطة ما إذا كان هناك جوار للنقطة مثل أي نقطة ممع الإحداثيات (س، ص)يحمل عدم المساواة: . في هذه الحالة، أي زيادة الدالة > 0.

التعريف 3: يتم استدعاء نقاط الحد الأدنى والحد الأقصى المحلية النقاط القصوى.

النهايات الشرطية

عند البحث عن القيم القصوى لدالة ذات العديد من المتغيرات، غالبًا ما تنشأ مشاكل تتعلق بما يسمى أقصى مشروط.يمكن شرح هذا المفهوم باستخدام مثال دالة ذات متغيرين.

دع الوظيفة والخط يعطى لعلى السطح 0xy. المهمة هي الوصول إلى الخط لالعثور على مثل هذه النقطة ف(س، ص)،حيث تكون قيمة الدالة هي الأكبر أو الأصغر مقارنة بقيم هذه الدالة عند نقاط على الخط ل، يقع بالقرب من النقطة ص. مثل هذه النقاط صوتسمى النقاط القصوى المشروطةوظائف على الخط ل. وعلى النقيض من نقطة النهاية المعتادة، تتم مقارنة قيمة الدالة عند نقطة النهاية الشرطية مع قيم الدالة ليس في جميع النقاط المجاورة لها، ولكن فقط عند تلك التي تقع على الخط ل.

من الواضح تمامًا أن نقطة الحد الأقصى المعتادة (يقولون أيضًا أقصى غير مشروط) هي أيضًا نقطة قصوى مشروطة لأي خط يمر عبر هذه النقطة. والعكس بالطبع ليس صحيحا: فالنقطة القصوى المشروطة قد لا تكون هي النقطة القصوى العادية. اسمحوا لي أن أشرح ما قلته بمثال بسيط. الرسم البياني للوظيفة هو نصف الكرة العلوي (الملحق 3 (الشكل 3)).

هذه الدالة لها حد أقصى عند نقطة الأصل؛ الرأس يتوافق معها منصفي الكرة الأرضية. إذا كان الخط لهناك خط يمر عبر النقاط أو في(معادلة لها س+ص-1=0)، فمن الواضح هندسيًا أنه بالنسبة لنقاط هذا الخط أعلى قيمةتتحقق الوظيفة عند نقطة تقع في المنتصف بين النقاط أو في.هذه هي نقطة الحد الأقصى الشرطي (الحد الأقصى) للدالة على هذا الخط؛ إنه يتوافق مع النقطة M 1 في نصف الكرة الأرضية، ومن الشكل يتضح أنه لا يمكن الحديث عن أي طرف عادي هنا.

لاحظ أنه في الجزء الأخير من مشكلة العثور على أكبر وأصغر قيم للدالة منطقة مغلقةعلينا إيجاد القيم المتطرفة للدالة عند حدود هذه المنطقة، أي على سطر ما، وبالتالي حل مشكلة الحدود القصوى المشروطة.

لننتقل الآن إلى البحث العملي عن النقاط القصوى الشرطية للدالة Z= f(x, y) بشرط أن يكون المتغيران x وy مرتبطان بالمعادلة (x, y) = 0. وسوف نسمي هذه العلاقة معادلة الاتصال. إذا كان من الممكن التعبير عن y من معادلة الاقتران بشكل صريح من حيث x: y=(x)، فإننا نحصل على دالة لمتغير واحد Z= f(x, (x)) = Ф(x).

بعد العثور على القيمة x التي تصل عندها هذه الدالة إلى الحد الأقصى، ثم تحديد قيم y المقابلة من معادلة الاتصال، نحصل على النقاط المطلوبة من الحد الأقصى الشرطي.

لذا، في المثال أعلاه، من معادلة العلاقة x+y-1=0 لدينا y=1-x. من هنا

من السهل التحقق من أن z يصل إلى الحد الأقصى عند x = 0.5؛ ولكن بعد ذلك من معادلة الاتصال y = 0.5، نحصل بالضبط على النقطة P، التي تم العثور عليها من الاعتبارات الهندسية.

يمكن حل مشكلة الحد الأقصى الشرطي بسهولة شديدة حتى عندما يكون من الممكن تمثيل معادلة الاتصال المعادلات البارامتريةس=س(ر)، ص=ص(ر). باستبدال تعبيرات x وy في هذه الوظيفة، نأتي مرة أخرى إلى مشكلة إيجاد الحد الأقصى لدالة لمتغير واحد.

إذا كانت معادلة الاقتران تحتوي على أكثر من نظرة معقدةونحن غير قادرين على التعبير بشكل صريح عن متغير واحد بدلالة متغير آخر، أو استبداله بمعادلات بارامترية، فإن مهمة إيجاد الحد الأقصى الشرطي تصبح أكثر صعوبة. سنستمر في افتراض أنه في تعبير الدالة z= f(x, y) المتغير (x, y) = 0. المشتق الإجمالي للدالة z= f(x, y) يساوي:

حيث تم العثور على المشتق y باستخدام قاعدة اشتقاق الدالة الضمنية. عند نقاط الحد الأقصى الشرطي، يجب أن يكون المشتق الإجمالي الموجود مساويًا للصفر؛ هذا يعطي معادلة واحدة تتعلق بـ x و y. وبما أنه يجب عليهم أيضًا تحقيق معادلة الاقتران، فسنحصل على نظام من معادلتين بمجهولين

دعونا نحول هذا النظام إلى نظام أكثر ملاءمة من خلال كتابة المعادلة الأولى في شكل نسبة وإدخال مجهول مساعد جديد:

(علامة الطرح الموجودة في المقدمة هي من أجل الراحة). ومن هذه المساواة يسهل الانتقال إلى النظام التالي:

f` x =(x,y)+` x (x,y)=0, f` y (x,y)+` y (x,y)=0 (*),

والتي، مع معادلة الاتصال (x، y) = 0، تشكل نظامًا من ثلاث معادلات ذات مجاهيل x، y و.

من الأسهل تذكر هذه المعادلات (*) باستخدام القاعدة التالية: للعثور على النقاط التي يمكن أن تكون نقاط الحد الأقصى الشرطي للدالة

Z= f(x, y) مع معادلة الاتصال (x, y) = 0، تحتاج إلى تكوين دالة مساعدة

و(س،ص)=و(س،ص)+(س،ص)

أين يوجد بعض الثوابت، وقم بإنشاء معادلات للعثور على النقاط القصوى لهذه الدالة.

يوفر نظام المعادلات المشار إليه، كقاعدة عامة، الشروط الضرورية فقط، أي. ليس كل زوج من القيم x و y الذي يرضي هذا النظام هو بالضرورة نقطة متطرفة مشروطة. لن أعطي شروطًا كافية لنقاط الحد الأقصى المشروط؛ في كثير من الأحيان يشير المحتوى المحدد للمشكلة نفسها إلى النقطة التي تم العثور عليها. تسمى التقنية الموصوفة لحل المشكلات على الحد الأقصى المشروط بطريقة لاغرانج المضاعف.

مثال

أوجد الحد الأقصى للدالة بشرط ذلك Xو فيترتبط بالعلاقة : . هندسيا، المشكلة تعني ما يلي: على القطع الناقص
طائرة
.

يمكن حل هذه المشكلة بهذه الطريقة: من المعادلة
نجد
X:

بشرط
، تم اختصارها إلى مشكلة العثور على الحد الأقصى لدالة لمتغير واحد في الفترة
.

هندسيا، المشكلة تعني ما يلي: على القطع الناقص ، تم الحصول عليها عن طريق عبور الاسطوانة
طائرة
، فأنت بحاجة إلى العثور على الحد الأقصى أو الأدنى لقيمة الطلب (الشكل 9). يمكن حل هذه المشكلة بهذه الطريقة: من المعادلة
نجد
. بتعويض القيمة التي تم العثور عليها لـ y في معادلة المستوى، نحصل على دالة لمتغير واحد X:

ومن هنا جاءت مشكلة إيجاد الحد الأقصى للدالة
بشرط
، تم اختصارها إلى مشكلة العثور على الحد الأقصى لدالة لمتغير واحد على فترة زمنية.

لذا، مشكلة إيجاد الحد الأقصى المشروط- هذه هي مشكلة إيجاد الحد الأقصى للدالة الموضوعية
بشرط أن تكون المتغيرات Xو فيخاضعة للقيود
، مُسَمًّى معادلة الاتصال.

دعنا نقول ذلك نقطة
، إرضاء معادلة الاقتران ، هي نقطة الحد الأقصى المشروط المحلي (الحد الأدنى)، إذا كان هناك حي
بحيث لأية نقاط
، التي تحقق إحداثياتها معادلة الاتصال، يتم استيفاء عدم المساواة.

إذا كان من الممكن العثور على تعبير لـ من معادلة الاقتران في، ثم باستبدال هذا التعبير في الدالة الأصلية، نحول الأخيرة إلى دالة معقدة ذات متغير واحد X.

الطريقة العامة لحل مسألة الحدود القصوى المشروطة هي طريقة لاغرانج المضاعف. لنقم بإنشاء وظيفة مساعدة، حيث - بعض الأرقام. تسمى هذه الوظيفة وظيفة لاغرانج، أ ─ مضاعف لاغرانج. وبالتالي، فقد تم تقليص مهمة إيجاد الحد الأقصى الشرطي إلى إيجاد نقاط الحد الأقصى المحلية لدالة لاغرانج. للعثور على النقاط القصوى المحتملة، عليك حل نظام من ثلاث معادلات بثلاثة مجاهيل س، صو.

ثم يجب عليك استخدام الشرط الكافي التالي للحصول على أقصى حد.

نظرية. لتكن النقطة نقطة قصوى محتملة لدالة لاغرانج. لنفترض أنه على مقربة من هذه النقطة
هناك مشتقات جزئية مستمرة من الدرجة الثانية من الوظائف و . دعونا نشير

ثم إذا
، الذي - التي
─ النقطة القصوى الشرطية للوظيفة
مع معادلة الاقتران
في هذه الحالة، إذا
، الذي - التي
─ نقطة الحد الأدنى المشروط، إذا
، الذي - التي
─ النقطة القصوى المشروطة.

§8. التدرج ومشتق الاتجاه

دع الوظيفة
محددة في بعض المناطق (المفتوحة). النظر في أي نقطة
هذه المنطقة وأي خط مستقيم موجه (المحور) مروراً بهذه النقطة (الشكل 1). يترك
- نقطة أخرى على هذا المحور،
- طول القطعة بين
و
، مأخوذة بعلامة زائد، إذا كان الاتجاه
يتزامن مع اتجاه المحور وعلامة الطرح إذا كان اتجاههما متعاكسين.

يترك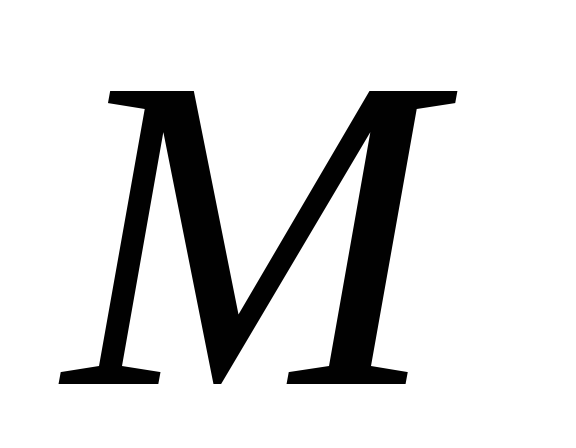
يقترب إلى أجل غير مسمى
. حد

مُسَمًّى مشتق من وظيفة
تجاه (أو على طول المحور ) ويشار إليه على النحو التالي:

.

يصف هذا المشتق "معدل التغير" للدالة عند النقطة
تجاه . وعلى وجه الخصوص، المشتقات الجزئية العادية ,يمكن أيضًا اعتبارها مشتقات "فيما يتعلق بالاتجاه".

لنفترض الآن أن الدالة
لديها مشتقات جزئية مستمرة في المنطقة قيد النظر. دع المحور يشكل زوايا ذات محاور الإحداثيات
و . في ظل الافتراضات المقدمة، مشتق الاتجاه موجود ويتم التعبير عنه بالصيغة

.

إذا كان ناقلات
نظرا لإحداثياتها
، ثم مشتقة الدالة
في اتجاه المتجه
يمكن حسابها باستخدام الصيغة:

.

ناقل مع الإحداثيات
مُسَمًّى ناقلات التدرجالمهام
عند هذه النقطة
. يشير متجه التدرج إلى اتجاه أسرع زيادة في الوظيفة عند نقطة معينة.

مثال

بالنظر إلى دالة، النقطة A(1, 1) والمتجه
. البحث عن: 1) غراد ض عند النقطة أ؛ 2) المشتق عند النقطة A في اتجاه المتجه .

المشتقات الجزئية لدالة معينة عند نقطة ما
:

;
.

ثم يكون متجه التدرج للدالة عند هذه النقطة هو:
. يمكن أيضًا كتابة متجه التدرج باستخدام تحليل المتجهات و :

. مشتق من وظيفة في اتجاه المتجه :

لذا،
,
.◄

الحد الأقصى المشروط.

الحدود القصوى لدالة ذات عدة متغيرات

طريقة المربع الأصغر.

أقصى المحليةفنب

دع الوظيفة تعطى و= F(ف)، РÎDÌR نودع النقطة P 0 ( أ 1 , أ 2 , ..., ص) –داخلينقطة المجموعة د

التعريف 9.4.

1) يتم استدعاء النقطة P 0 النقطة القصوى المهام و= F(P)، إذا كان هناك جوار لهذه النقطة U(P 0) М D بحيث يكون لأي نقطة P( X 1 , X 2 , ..., س ن)O U(P 0) , Р¹Р 0 , الشرط مستوفي F(ف) جنيه استرليني F(ف0) . معنى Fيتم استدعاء الدالة (P0) عند النقطة القصوى الحد الأقصى للوظيفة ويتم تعيينه F(P0) = الحد الأقصى F(ف) .

2) يتم استدعاء النقطة P 0 نقطة الحد الأدنى المهام و= F(P)، إذا كان هناك جوار لهذه النقطة U(P 0)Ì D بحيث يكون لأي نقطة P( X 1 , X 2 , ..., س ن)ОU(P 0), Р¹Р 0 ، الشرط مستوفي F(ف)³ F(ف0) . معنى Fيتم استدعاء الدالة (P0) عند النقطة الدنيا وظيفة الحد الأدنى ويتم تعيينه F(ف 0) = دقيقة F(ع).

يتم استدعاء الحد الأدنى والحد الأقصى لنقاط الوظيفة النقاط القصوى، يتم استدعاء قيم الدالة عند النقاط القصوى الحد الأقصى للوظيفة.

على النحو التالي من التعريف، وعدم المساواة F(ف) جنيه استرليني F(ف 0) , F(ف)³ F(P 0) يجب أن تتحقق فقط في منطقة معينة من النقطة P 0، وليس في مجال تعريف الدالة بأكمله، مما يعني أن الدالة يمكن أن يكون لها عدة نقاط متطرفة من نفس النوع (عدة حدود صغرى، عدة حدود قصوى) . لذلك، تسمى الحدود القصوى المحددة أعلاه محلي(المحلية) المتطرفة.

نظرية 9.1.( شرط ضروريالحد الأقصى للحزب الوطني التقدمي)

إذا كانت الوظيفة و= F(X 1 , X 2 , ..., س ن) له حد أقصى عند النقطة P 0 ، فإن مشتقاته الجزئية من الدرجة الأولى عند هذه النقطة إما تساوي الصفر أو غير موجودة.

دليل.دع عند النقطة P 0 ( أ 1 , أ 2 , ..., ص) وظيفة و= F(P) لها حد أقصى، على سبيل المثال، حد أقصى. دعونا إصلاح الحجج X 2 , ..., س ن، وضع X 2 =أ 2 ,..., س ن = ص. ثم و= F(ف) = F 1 ((X 1 , أ 2 , ..., ص) هي دالة لمتغير واحد X 1 . منذ هذه الوظيفة لديها X 1 = أ 1 أقصى (الحد الأقصى)، ثم F 1 ¢ = 0 أو غير موجود متى X 1 =أ 1 (شرط ضروري لوجود أقصى دالة لمتغير واحد). لكن هذا يعني أو أنه غير موجود عند النقطة P 0 - النقطة القصوى. وبالمثل، يمكننا النظر في المشتقات الجزئية فيما يتعلق بالمتغيرات الأخرى. CTD.

تسمى النقاط في مجال الدالة التي تكون فيها المشتقات الجزئية من الدرجة الأولى مساوية للصفر أو غير موجودة نقاط حرجة هذه الوظيفة.

كما يلي من النظرية 9.1، يجب البحث عن النقاط القصوى للـ FNP من بين النقاط الحرجة للدالة. ولكن، بالنسبة لدالة ذات متغير واحد، ليست كل نقطة حرجة هي نقطة متطرفة.

النظرية 9.2 (شرط كافي لأقصى FNP)

اجعل P 0 هي النقطة الحرجة للدالة و= F(ع) و هو التفاضل من الدرجة الثانية لهذه الوظيفة. ثم

و إذا د 2 ش(P 0) > 0 عند، ثم P 0 نقطة الحد الأدنىالمهام و= F(ف)؛

ب) إذا د 2 ش(ف0)< 0 при , то Р 0 – точка أقصىالمهام و= F(ف)؛

ج) إذا د 2 ش(P 0) غير محدد بالعلامة، وبالتالي فإن P 0 ليست نقطة متطرفة؛

سننظر في هذه النظرية بدون دليل.

لاحظ أن النظرية لا تأخذ في الاعتبار الحالة عندما د 2 ش(ف 0) = 0 أو غير موجود. هذا يعني أن مسألة وجود الحد الأقصى عند النقطة P 0 في ظل هذه الظروف تظل مفتوحة - نحتاجها أبحاث إضافيةعلى سبيل المثال، دراسة زيادة دالة عند هذه النقطة.

في دورات الرياضيات الأكثر تفصيلا ثبت ذلك، ولا سيما بالنسبة للوظيفة ض = و(س,ذ) من متغيرين، التفاضل من الدرجة الثانية هو مجموع النموذج

يمكن تبسيط دراسة وجود الحد الأقصى عند النقطة الحرجة P 0.

دعونا نشير ، ، . دعونا نؤلف المحدد

.

يتحول:

د 2 ض> 0 عند النقطة P 0، أي. P 0 – النقطة الدنيا إذا أ(ف 0) > 0 و د(ف 0) > 0؛

د 2 ض < 0 в точке Р 0 , т.е. Р 0 – точка максимума, если أ(ف0)< 0 , а D(Р 0) > 0;

إذا د(ف 0)< 0, то د 2 ضفي محيط النقطة P 0 تتغير الإشارة ولا يوجد حد أقصى عند النقطة P 0؛

وإذا كانت D(Р 0) = 0، يلزم أيضًا إجراء دراسات إضافية للوظيفة بالقرب من النقطة الحرجة Р 0.

وهكذا بالنسبة للوظيفة ض = و(س,ذ) لمتغيرين لدينا الخوارزمية التالية (دعنا نسميها "الخوارزمية D") لإيجاد الحد الأقصى:

1) ابحث عن مجال التعريف D( F) المهام.

2) البحث عن النقاط الحرجة، أي. نقاط من د( F)، والتي وتساوي الصفر أو غير موجودة.

3) عند كل نقطة حرجة P 0، تحقق من الشروط الكافية للحد الأقصى. للقيام بذلك، ابحث عن ، حيث ، وحساب D(P 0) و أ(ف0).ثم:

إذا كان D(P 0) >0، عند النقطة P 0 يوجد حد أقصى، وإذا أ(P 0) > 0 – فهذا هو الحد الأدنى، وإذا أ(ف 0)< 0 – максимум;

إذا د(ف 0)< 0, то в точке Р­ 0 нет экстремума;

إذا كان D(P 0) = 0، فستكون هناك حاجة إلى مزيد من البحث.

4) عند النقاط القصوى التي تم العثور عليها، احسب قيمة الدالة.

مثال 1.

أوجد الحد الأقصى للدالة ض = س 3 + 8ذ 3 – 3xy .

حل.مجال تعريف هذه الوظيفة هو المستوى الإحداثي بأكمله. دعونا نجد النقاط الحرجة.

, , Þ ف 0 (0,0) , .

دعونا نتحقق من استيفاء الشروط الكافية للحد الأقصى. سوف نجد

6X, = -3, = 48فيو = 288xy – 9.

ثم D(P 0) = 288×0×0 – 9 = -9< 0 , значит, в точке Р 0 экстремума нет.

D(Р 1) = 36-9>0 - عند النقطة Р 1 يوجد حد أقصى، ومنذ ذلك الحين أ(P 1) = 3 >0، فهذا الحد الأقصى هو الحد الأدنى. دقيقة جدا ض=ض(ف1) = .

مثال 2.

أوجد الحد الأقصى للدالة .

الحل: د( F) = ر 2 . نقاط حرجة: ; غير موجود عندما في= 0، مما يعني أن P 0 (0,0) هي النقطة الحرجة لهذه الوظيفة.

2, = 0, = , = ، لكن D(P 0) غير محددة، لذا فإن دراسة إشارتها مستحيلة.

لنفس السبب، من المستحيل تطبيق النظرية 9.2 مباشرة - د 2 ضغير موجود في هذه المرحلة.

دعونا نفكر في زيادة الوظيفة F(س, ذ) عند النقطة P 0. إذا د F =F(ف) – F(P 0)>0 "P، فإن P 0 هي النقطة الدنيا، ولكن إذا كانت D F < 0, то Р 0 – точка максимума.

في حالتنا لدينا

د F = F(س, ذ) – F(0, 0) = F(0+د س,0+د ذ) – F(0, 0) = .

عند د س= 0.1 و د ذ= -0.008 نحصل على D F = 0,01 – 0,2 < 0, а при Dس= 0.1 و د ذ= 0.001 د F= 0.01 + 0.1 > 0، أي وعلى مقربة من النقطة P 0، لا يتم استيفاء أي من الشرطين D F <0 (т.е. F(س, ذ) < F(0، 0) وبالتالي فإن P 0 ليست نقطة عظمى)، ولا الشرط D F>0 (أي F(س, ذ) > F(0، 0) ثم P 0 ليست نقطة دنيا). لذا، حسب تعريف الحد الأقصى، هذه الوظيفةليس لديه التطرف.

الحد الأقصى المشروط.

يسمى الحد الأقصى للوظيفة غير مشروط، نظرًا لعدم فرض أي قيود (شروط) على وسيطات الوظيفة.

التعريف 9.2.الحد الأقصى للوظيفة و = F(X 1 , X 2 , ... , س ن)، وجدت بشرط أن حججها X 1 , X 2 , ... , س نحقق المعادلات ي 1 ( X 1 , X 2 , ... , س ن) = 0، …، ي ت(X 1 , X 2 , ... , س ن) = 0، حيث P ( X 1 , X 2 , ... , س ن) يا د( F)، مُسَمًّى أقصى مشروط .

المعادلات ي ك(X 1 , X 2 , ... , س ن) = 0 , ك = 1, 2,..., م، وتسمى معادلات الاتصال.

دعونا نلقي نظرة على الوظائف ض = و(س,ذ) متغيرين. إذا كانت معادلة الاتصال واحدة، أي. ، فإن العثور على الحد الأقصى الشرطي يعني أنه لا يتم البحث عن الحد الأقصى في مجال تعريف الوظيفة بالكامل، ولكن على بعض المنحنى الموجود في D( F) (أي أنه ليس أعلى أو أدنى نقطة من السطح هي التي يتم البحث عنها ض = و(س,ذ)، وأعلى أو أدنى النقاط بين نقاط تقاطع هذا السطح مع الاسطوانة، شكل 5).

الحد الأقصى الشرطي للدالة ض = و(س,ذ) من متغيرين يمكن العثور عليهما بالطريقة التالية ( طريقة القضاء). من المعادلة، عبر عن أحد المتغيرات كدالة لمتغير آخر (على سبيل المثال، اكتب ) وبعد استبدال قيمة المتغير هذه في الدالة، اكتب الأخير كدالة لمتغير واحد (في الحالة المعنية ). أوجد الحد الأقصى للدالة الناتجة لمتغير واحد.