Урок и презентация на тема: "Степенни функции. Свойства. Графики"
Допълнителни материали
Уважаеми потребители, не забравяйте да оставите вашите коментари, отзиви, пожелания! Всички материали са проверени с антивирусна програма.
Учебни помагала и тренажори в онлайн магазин Интеграл за 11 клас
Интерактивно помагало за 9–11 клас „Тригонометрия“
Интерактивно ръководство за 10–11 клас „Логаритми“
Степенни функции, област на дефиниране.
Момчета, в последния урок научихме как да работим с числа с рационални степени. В този урок ще разгледаме степенните функции и ще се ограничим до случая, когато показателят е рационален.Ще разгледаме функции от вида: $y=x^(\frac(m)(n))$.
Нека първо разгледаме функции, чийто показател $\frac(m)(n)>1$.
Нека ни е дадена конкретна функция $y=x^2*5$.
Според дефиницията, която дадохме в миналия урок: ако $x≥0$, то дефиниционната област на нашата функция е лъчът $(x)$. Нека начертаем графиката на нашата функция.

Свойства на функцията $y=x^(\frac(m)(n))$, $0 2. Тя не е нито четна, нито нечетна.
3. Увеличава се с $$,
б) $(2,10)$,
в) на лъч $$.
Решение.
Момчета, помните ли как намерихме най-голямата и най-малката стойност на функция върху отсечка в 10 клас?
Точно така, използвахме производната. Нека решим нашия пример и повторим алгоритъма за намиране на най-малкото и най-висока стойност.
1. Намерете производната на дадената функция:
$y"=\frac(16)(5)*\frac(5)(2)x^(\frac(3)(2))-x^3=8x^(\frac(3)(2)) -x^3=8\sqrt(x^3)-x^3$.
2. Производната съществува в цялата област на дефиниране на оригиналната функция, тогава няма критични точки. Да намерим стационарни точки:
$y"=8\sqrt(x^3)-x^3=0$.
$8*\sqrt(x^3)=x^3$.
$64x^3=x^6$.
$x^6-64x^3=0$.
$x^3(x^3-64)=0$.
$x_1=0$ и $x_2=\sqrt(64)=4$.
Даден сегмент съдържа само едно решение $x_2=4$.
Нека изградим таблица със стойностите на нашата функция в краищата на сегмента и в екстремалната точка:
Отговор: $y_(име)=-862,65$ при $x=9$; $y_(макс.)=38,4$ при $x=4$.
Пример. Решете уравнението: $x^(\frac(4)(3))=24-x$.
Решение. Графиката на функцията $y=x^(\frac(4)(3))$ нараства, а графиката на функцията $y=24-x$ намалява. Момчета, вие и аз знаем: ако една функция нараства, а другата намалява, тогава те се пресичат само в една точка, тоест имаме само едно решение.
Забележка:
$8^(\frac(4)(3))=\sqrt(8^4)=(\sqrt(8))^4=2^4=16$.
$24-8=16$.
Тоест, с $x=8$ получихме правилното равенство $16=16$, това е решението на нашето уравнение.
Отговор: $x=8$.
Пример.
Графика на функцията: $y=(x-3)^\frac(3)(4)+2$.
Решение.
Графиката на нашата функция се получава от графиката на функцията $y=x^(\frac(3)(4))$, премествайки я 3 единици надясно и 2 единици нагоре. 
Пример. Напишете уравнение за допирателната към правата $y=x^(-\frac(4)(5))$ в точката $x=1$.
Решение. Уравнението на допирателната се определя от известната ни формула:
$y=f(a)+f"(a)(x-a)$.
В нашия случай $a=1$.
$f(a)=f(1)=1^(-\frac(4)(5))=1$.
Нека намерим производната:
$y"=-\frac(4)(5)x^(-\frac(9)(5))$.
Нека изчислим:
$f"(a)=-\frac(4)(5)*1^(-\frac(9)(5))=-\frac(4)(5)$.
Нека намерим уравнението на допирателната:
$y=1-\frac(4)(5)(x-1)=-\frac(4)(5)x+1\frac(4)(5)$.
Отговор: $y=-\frac(4)(5)x+1\frac(4)(5)$.
Проблеми за самостоятелно решаване
1. Намерете най-голямата и най-малката стойност на функцията: $y=x^\frac(4)(3)$ на отсечката:а) $$.
б) $(4,50) $.
в) на лъч $$.
3. Решете уравнението: $x^(\frac(1)(4))=18-x$.
4. Постройте графика на функцията: $y=(x+1)^(\frac(3)(2))-1$.
5. Създайте уравнение за допирателната към правата $y=x^(-\frac(3)(7))$ в точката $x=1$.
Функция къде х– променливо количество, А– извиква се даден номер Силова функция .
Ако тогава е линейна функция, нейната графика е права линия (вижте параграф 4.3, Фиг. 4.7).
Ако тогава - квадратична функция, неговата графика е парабола (виж параграф 4.3, Фиг. 4.8).
Ако тогава нейната графика е кубична парабола (виж параграф 4.3, фиг. 4.9).
Това е обратната функция за
1. Домейн: ![]()
2. Множество значения:![]()
3. Четно и нечетно:функцията е странна.
4. Функционална честота:непериодични.
5. Функционални нули: х= 0 – единствената нула.
6. Функцията няма максимална или минимална стойност.
7.
8. Графика на функцияСиметричен на графиката на кубична парабола спрямо права линия Y=хи е показано на фиг. 5.1.
 |
Силова функция
1. Домейн: ![]()
2. Множество значения:
3. Четно и нечетно:функцията е четна.
4. Функционална честота:непериодични.
5. Функционални нули:единична нула х = 0.
6. Най-големите и най-малките стойности на функцията:приема най-малката стойност за х= 0, то е равно на 0.
7. Интервали на нарастване и намаляване:функцията е намаляваща на интервала и нарастваща на интервала
8. Графика на функция(за всеки н Î н) е „подобна“ на графиката на квадратна парабола (функционалните графики са показани на фиг. 5.2).

Силова функция
1. Домейн: ![]()
2. Множество значения: ![]()
3. Четно и нечетно:функцията е странна.
4. Функционална честота:непериодични.
5. Функционални нули: х= 0 – единствената нула.
6. Най-високи и най-ниски стойности:
7. Интервали на нарастване и намаляване:функцията нараства в цялата област на дефиниция.
8. Графика на функция(за всяко ) е „подобно“ на графиката на кубична парабола (функционалните графики са показани на фиг. 5.3).
 |
Силова функция![]()
1. Домейн:
2. Множество значения:
3. Четно и нечетно:функцията е странна.
4. Функционална честота:непериодични.
5. Функционални нули:няма нули.
6. Най-големите и най-малките стойности на функцията:функцията няма най-големите и най-малките стойности за никоя
7. Интервали на нарастване и намаляване:функцията намалява в своята област на дефиниция.
8. Асимптоти:(ос OU) – вертикална асимптота;
(ос о) – хоризонтална асимптота.
9. Графика на функция(за всеки н) е „подобна“ на графиката на хипербола (функционалните графики са показани на фиг. 5.4).
 |
Силова функция
1. Домейн:
2. Множество значения:
3. Четно и нечетно:функцията е четна.
4. Функционална честота:непериодични.
5. Най-големите и най-малките стойности на функцията:функцията няма най-големите и най-малките стойности за никоя
6. Интервали на нарастване и намаляване:функцията нараства с и намалява с
7. Асимптоти: х= 0 (ос OU) – вертикална асимптота;
Y= 0 (ос о) – хоризонтална асимптота.
8. Функционални графикиТе са квадратни хиперболи (фиг. 5.5).
 |
Силова функция
1. Домейн:
2. Множество значения:
3. Четно и нечетно:функцията няма свойството четно и нечетно.
4. Функционална честота:непериодични.
5. Функционални нули: х= 0 – единствената нула.
6. Най-големите и най-малките стойности на функцията:най-малката стойност, равна на 0, функцията приема в точката х= 0; няма най-голямо значение.
7. Интервали на нарастване и намаляване:функцията нараства в цялата област на дефиниция.
8. Всяка такава функция за определен показател е обратна на предоставената функция
9. Графика на функция"наподобява" графиката на функция за всяка ни е показано на фиг. 5.6.

Силова функция
1. Домейн: ![]()
2. Множество значения:![]()
3. Четно и нечетно:функцията е странна.
4. Функционална честота:непериодични.
5. Функционални нули: х= 0 – единствената нула.
6. Най-големите и най-малките стойности на функцията:функцията няма най-големите и най-малките стойности за никоя
7. Интервали на нарастване и намаляване:функцията нараства в цялата област на дефиниция.
8. Графика на функцияПоказано на фиг. 5.7.
 |
Нека си припомним свойствата и графиките на степенните функции с цяло число отрицателен показател.
За четно n, :
Примерна функция:
Всички графики на такива функции преминават през две фиксирани точки: (1;1), (-1;1). Особеността на функциите от този тип е тяхната четност; графиките са симетрични спрямо оста на операционния усилвател.

Ориз. 1. Графика на функция
За нечетно n, :
Примерна функция:
Всички графики на такива функции преминават през две фиксирани точки: (1;1), (-1;-1). Особеността на функциите от този тип е, че те са нечетни по отношение на началото.

Ориз. 2. Графика на функция
Нека си припомним основното определение.
Степента на неотрицателно число a с рационален положителен показател се нарича число.
Степента на положително число a с рационален отрицателен показател се нарича число.
За равенството:
![]()
![]()
Например: ![]() ; - изразът не съществува по дефиниция на степен с отрицателен рационален показател; съществува, защото експонентата е цяло число,
; - изразът не съществува по дефиниция на степен с отрицателен рационален показател; съществува, защото експонентата е цяло число, ![]()
Нека да преминем към разглеждане на степенни функции с рационален отрицателен показател.
![]()
Например:
За да начертаете графика на тази функция, можете да създадете таблица. Ще го направим по различен начин: първо ще изградим и изучим графиката на знаменателя - тя ни е известна (Фигура 3).

Ориз. 3. Графика на функция
Графиката на функцията знаменател минава през фиксирана точка (1;1). При изчертаване на оригиналната функция дадена точкаостава, когато коренът също клони към нула, функцията клони към безкрайност. И обратно, когато x клони към безкрайност, функцията клони към нула (Фигура 4).

Ориз. 4. Функционална графика
Нека разгледаме друга функция от семейството на изучаваните функции.
![]()
Важно е, че по дефиниция
Нека разгледаме графиката на функцията в знаменателя: , графиката на тази функция ни е известна, тя нараства в своята област на дефиниране и преминава през точката (1;1) (Фигура 5).

Ориз. 5. Графика на функция
При начертаване на графиката на оригиналната функция точката (1;1) остава, докато коренът също клони към нула, функцията клони към безкрайност. И обратно, когато x клони към безкрайност, функцията клони към нула (Фигура 6).

Ориз. 6. Графика на функция
Разгледаните примери помагат да се разбере как протича графиката и какви са свойствата на изучаваната функция - функция с отрицателен рационален показател.
Графиките на функциите на това семейство преминават през точката (1;1), функцията намалява по цялата област на дефиниция.
Обхват на дефиницията на функцията: ![]()
Функцията не е ограничена отгоре, но е ограничена отдолу. Функцията няма нито най-голямо, нито най-ниска стойност.
Функцията е непрекъсната и приема всички положителни стойности от нула до плюс безкрайност.
Функцията е изпъкнала надолу (Фигура 15.7)
Точките A и B са взети на кривата, през тях е начертан сегмент, цялата крива е под сегмента, това състояниее изпълнено за произволни две точки на кривата, следователно функцията е изпъкнала надолу. Ориз. 7.

Ориз. 7. Изпъкналост на функцията
Важно е да се разбере, че функциите на това семейство са ограничени отдолу с нула, но нямат най-малка стойност.
Пример 1 - намерете максимума и минимума на функция в интервала \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \]
Графика (фиг. 2).

Фигура 2. Графика на функцията $f\left(x\right)=x^(2n)$
Свойства на степенна функция с естествен нечетен показател
Областта на дефиниция са всички реални числа.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- функцията е странна.
$f(x)$ е непрекъснат в цялата област на дефиниция.
Диапазонът е изцяло реални числа.
$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Функцията нараства в цялата област на дефиниция.
$f\left(x\right)0$, за $x\in (0,+\infty)$.
$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$
\ \
Функцията е вдлъбната за $x\in (-\infty ,0)$ и изпъкнала за $x\in (0,+\infty)$.
Графика (фиг. 3).
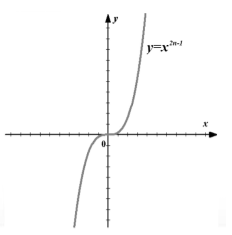
Фигура 3. Графика на функцията $f\left(x\right)=x^(2n-1)$
Степенна функция с цяло число
Първо, нека въведем концепцията за степен с цяло число.
Определение 3
Степента на реално число $a$ с цяло число $n$ се определя по формулата:

Фигура 4.
Нека сега разгледаме степенна функция с цяло число, нейните свойства и графика.
Определение 4
$f\left(x\right)=x^n$ ($n\in Z)$ се нарича степенна функция с цяло число.
Ако степента е по-голяма от нула, тогава стигаме до случай на степенна функция с естествен показател. Вече го обсъдихме по-горе. За $n=0$ получаваме линейна функция$y=1$. Разглеждането му ще оставим на читателя. Остава да разгледаме свойствата на степенна функция с отрицателен цяло число
Свойства на степенна функция с цяло отрицателно число
Домейнът на дефиницията е $\left(-\infty ,0\right)(0,+\infty)$.
Ако показателят е четен, тогава функцията е четна; ако е нечетна, тогава функцията е нечетна.
$f(x)$ е непрекъснат в цялата област на дефиниция.
Обхват:
Ако показателят е четен, тогава $(0,+\infty)$; ако е нечетен, тогава $\left(-\infty ,0\right)(0,+\infty)$.
За нечетен показател функцията намалява като $x\in \left(-\infty ,0\right)(0,+\infty)$. Ако показателят е четен, функцията намалява като $x\in (0,+\infty)$. и нараства като $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ върху цялата област на дефиниция








