ವ್ಯಾಖ್ಯಾನದಿಂದ ನಾವು ಎಫ್ (x) ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಿದ ಬಿಂದುಗಳಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಮಾತ್ರ ನಿರಂತರತೆಯ ಬಗ್ಗೆ ಮಾತನಾಡಬಹುದು (ಕಾರ್ಯದ ಮಿತಿಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವಾಗ, ಅಂತಹ ಸ್ಥಿತಿಯನ್ನು ಹೊಂದಿಸಲಾಗಿಲ್ಲ). ನಿರಂತರ ಕಾರ್ಯಗಳಿಗಾಗಿ
, ಅಂದರೆ, f ಮತ್ತು lim ಕಾರ್ಯಾಚರಣೆಗಳು ಪರಿವರ್ತಿತವಾಗಿವೆ. ಅಂತೆಯೇ, ಒಂದು ಹಂತದಲ್ಲಿ ಕ್ರಿಯೆಯ ಮಿತಿಯ ಎರಡು ವ್ಯಾಖ್ಯಾನಗಳನ್ನು ನಿರಂತರತೆಯ ಎರಡು ವ್ಯಾಖ್ಯಾನಗಳನ್ನು ನೀಡಬಹುದು - "ಅನುಕ್ರಮಗಳ ಭಾಷೆಯಲ್ಲಿ" ಮತ್ತು "ಅಸಮಾನತೆಗಳ ಭಾಷೆಯಲ್ಲಿ" (ε-δ ಭಾಷೆಯಲ್ಲಿ). ಇದನ್ನು ನೀವೇ ಮಾಡಲು ಸೂಚಿಸಲಾಗಿದೆ. ಪ್ರಾಯೋಗಿಕ ಬಳಕೆಗಾಗಿ, ಏರಿಕೆಗಳ ಭಾಷೆಯಲ್ಲಿ ನಿರಂತರತೆಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲು ಕೆಲವೊಮ್ಮೆ ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿರುತ್ತದೆ.
Δx=x-x 0 ಮೌಲ್ಯವನ್ನು ಆರ್ಗ್ಯುಮೆಂಟ್‌ನ ಇನ್‌ಕ್ರಿಮೆಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು Δy=f(x)-f(x 0) ಎಂಬುದು x 0 ರಿಂದ ಪಾಯಿಂಟ್ x ಗೆ ಚಲಿಸುವಾಗ ಕ್ರಿಯೆಯ ಹೆಚ್ಚಳವಾಗಿದೆ.
ವ್ಯಾಖ್ಯಾನ. x 0 ಬಿಂದುವಿನಲ್ಲಿ f(x) ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸೋಣ. ಈ ಹಂತದಲ್ಲಿ ಆರ್ಗ್ಯುಮೆಂಟ್‌ನ ಅಪರಿಮಿತ ಹೆಚ್ಚಳವು ಫಂಕ್ಷನ್‌ನ ಅಪರಿಮಿತ ಹೆಚ್ಚಳಕ್ಕೆ ಅನುರೂಪವಾಗಿದ್ದರೆ, Δx→0 ಗಾಗಿ Δy→0 ಅನ್ನು ಒಂದು ಹಂತದಲ್ಲಿ x 0 ನಲ್ಲಿ ನಿರಂತರವಾಗಿ f(x) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಉದಾಹರಣೆ 1.
x ನ ಯಾವುದೇ ಮೌಲ್ಯಕ್ಕೆ y=sinx ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ ಎಂದು ಸಾಬೀತುಪಡಿಸಿ.
ಪರಿಹಾರ.
x 0 ಅನಿಯಂತ್ರಿತ ಬಿಂದುವಾಗಿರಲಿ. ಇದಕ್ಕೆ Δx ಅನ್ನು ಹೆಚ್ಚಿಸಿದರೆ, ನಾವು x=x 0 +Δx ಬಿಂದುವನ್ನು ಪಡೆಯುತ್ತೇವೆ. ನಂತರ 
. ನಾವು ಪಡೆಯುತ್ತೇವೆ 
.
ವ್ಯಾಖ್ಯಾನ.
y=f(x) ಕಾರ್ಯವನ್ನು ಬಲಭಾಗದಲ್ಲಿ (ಎಡ) x 0 ಬಿಂದುವಿನಲ್ಲಿ ನಿರಂತರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ
.
ಆಂತರಿಕ ಹಂತದಲ್ಲಿ ನಿರಂತರವಾದ ಕಾರ್ಯವು ಬಲ ಮತ್ತು ಎಡ ನಿರಂತರವಾಗಿರುತ್ತದೆ. ಸಂಭಾಷಣೆಯು ಸಹ ನಿಜವಾಗಿದೆ: ಎಡ ಮತ್ತು ಬಲದ ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿದ್ದರೆ, ಅದು ಆ ಹಂತದಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಒಂದು ಕಾರ್ಯವು ಒಂದು ಬದಿಯಲ್ಲಿ ಮಾತ್ರ ನಿರಂತರವಾಗಿರುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಫಾರ್ 
, 
, f(1)=1, ಆದ್ದರಿಂದ, ಈ ಕಾರ್ಯವು ಎಡಭಾಗದಲ್ಲಿ ಮಾತ್ರ ನಿರಂತರವಾಗಿರುತ್ತದೆ (ಈ ಕಾರ್ಯದ ಗ್ರಾಫ್‌ಗಾಗಿ, ಮೇಲಿನ ಪ್ಯಾರಾಗ್ರಾಫ್ 5.7.2 ನೋಡಿ).
ವ್ಯಾಖ್ಯಾನ.
ಈ ಮಧ್ಯಂತರದ ಪ್ರತಿ ಹಂತದಲ್ಲಿಯೂ ನಿರಂತರವಾಗಿದ್ದರೆ ಕೆಲವು ಮಧ್ಯಂತರದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ನಿರಂತರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ನಿರ್ದಿಷ್ಟವಾಗಿ ಹೇಳುವುದಾದರೆ, ಮಧ್ಯಂತರವು ಒಂದು ವಿಭಾಗವಾಗಿದ್ದರೆ, ಅದರ ತುದಿಗಳಲ್ಲಿ ಏಕಪಕ್ಷೀಯ ನಿರಂತರತೆಯನ್ನು ಸೂಚಿಸಲಾಗುತ್ತದೆ.
ನಿರಂತರ ಕಾರ್ಯಗಳ ಗುಣಲಕ್ಷಣಗಳು
1. ಎಲ್ಲಾ ಪ್ರಾಥಮಿಕ ಕಾರ್ಯಗಳು ಅವುಗಳ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತವೆ.2. ನಿರ್ದಿಷ್ಟ ಮಧ್ಯಂತರದಲ್ಲಿ ನೀಡಲಾದ f(x) ಮತ್ತು φ(x), ಈ ಮಧ್ಯಂತರದ ಬಿಂದು x 0 ನಲ್ಲಿ ನಿರಂತರವಾಗಿದ್ದರೆ, ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯಗಳು ಸಹ ನಿರಂತರವಾಗಿರುತ್ತವೆ.
3. X ನಿಂದ x 0 ಬಿಂದುವಿನಲ್ಲಿ y=f(x) ನಿರಂತರವಾಗಿದ್ದರೆ ಮತ್ತು z=φ(y) Y ಯಿಂದ ಅನುಗುಣವಾದ ಬಿಂದು y 0 =f(x 0) ನಲ್ಲಿ ನಿರಂತರವಾಗಿದ್ದರೆ, ಆಗ ಸಂಕೀರ್ಣ ಕಾರ್ಯ z=φ(f(x)) ಬಿಂದು x 0 ನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ.
ಕಾರ್ಯ ವಿರಾಮಗಳು ಮತ್ತು ಅವುಗಳ ವರ್ಗೀಕರಣ
x 0 ಹಂತದಲ್ಲಿ ಎಫ್(x) ಕಾರ್ಯದ ನಿರಂತರತೆಯ ಸಂಕೇತವು ಸಮಾನತೆಯಾಗಿದೆ, ಇದು ಮೂರು ಷರತ್ತುಗಳ ಉಪಸ್ಥಿತಿಯನ್ನು ಸೂಚಿಸುತ್ತದೆ:1) f(x) ಅನ್ನು ಪಾಯಿಂಟ್ x 0 ನಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ;
2)
;
3) .
ಈ ಅವಶ್ಯಕತೆಗಳಲ್ಲಿ ಕನಿಷ್ಠ ಒಂದನ್ನು ಉಲ್ಲಂಘಿಸಿದರೆ, x 0 ಅನ್ನು ಕಾರ್ಯದ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ ಈ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿ ಇಲ್ಲದಿರುವ ಬಿಂದುವಾಗಿದೆ. ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳ ವ್ಯಾಖ್ಯಾನದಿಂದ ಇದು ಫಂಕ್ಷನ್‌ನ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್‌ಗಳನ್ನು ಅನುಸರಿಸುತ್ತದೆ:
a) ನಿರಂತರತೆಯ ಆಸ್ತಿಯನ್ನು f(x) ಕಳೆದುಕೊಳ್ಳುವ ಕಾರ್ಯದ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ಗೆ ಸೇರಿದ ಅಂಕಗಳು,
ಬಿ) ಎಫ್ (x) ನ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ಗೆ ಸೇರದ ಅಂಕಗಳು, ಅವು ಕಾರ್ಯದ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ನ ಎರಡು ಮಧ್ಯಂತರಗಳ ಪಕ್ಕದ ಬಿಂದುಗಳಾಗಿವೆ.
ಉದಾಹರಣೆಗೆ, ಒಂದು ಫಂಕ್ಷನ್‌ಗೆ, ಪಾಯಿಂಟ್ x=0 ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ ಆಗಿದೆ, ಏಕೆಂದರೆ ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ, ಮತ್ತು ಫಂಕ್ಷನ್
x=1 ಬಿಂದುವಿನಲ್ಲಿ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿದೆ, ಇದು f(x) ನ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ನ ಎರಡು ಮಧ್ಯಂತರಗಳ (-∞,1) ಮತ್ತು (1,∞) ಪಕ್ಕದಲ್ಲಿದೆ ಮತ್ತು ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ. ಬ್ರೇಕ್ ಪಾಯಿಂಟ್‌ಗಳಿಗೆ ಕೆಳಗಿನ ವರ್ಗೀಕರಣವನ್ನು ಅಳವಡಿಸಲಾಗಿದೆ.
1) x 0 ಬಿಂದುವಿನಲ್ಲಿ ಸೀಮಿತವಾಗಿದ್ದರೆ 
ಮತ್ತು 
, ಆದರೆ f(x 0 +0)≠f(x 0 -0), ನಂತರ x 0 ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತದ ಬಿಂದು
, ಮತ್ತು ಕರೆಯಲಾಗುತ್ತದೆ ಕಾರ್ಯ ಜಂಪ್
.
ಉದಾಹರಣೆ 2.
ಕಾರ್ಯವನ್ನು ಪರಿಗಣಿಸಿ 
ಕಾರ್ಯವನ್ನು x=2 ಬಿಂದುವಿನಲ್ಲಿ ಮಾತ್ರ ಮುರಿಯಬಹುದು (ಇತರ ಬಿಂದುಗಳಲ್ಲಿ ಇದು ಯಾವುದೇ ಬಹುಪದೋಕ್ತಿಯಂತೆ ನಿರಂತರವಾಗಿರುತ್ತದೆ). 
ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ 
, 
. ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಸೀಮಿತವಾಗಿರುವುದರಿಂದ, ಆದರೆ ಪರಸ್ಪರ ಸಮಾನವಾಗಿರುವುದಿಲ್ಲ, ನಂತರ x=2 ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಅದನ್ನು ಗಮನಿಸು 
, ಆದ್ದರಿಂದ ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ಬಲಭಾಗದಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ (ಚಿತ್ರ 2).
2) ಎರಡನೇ ವಿಧದ ಅಸಂಯಮ ಬಿಂದುಗಳು
ಕನಿಷ್ಠ ಒಂದು-ಬದಿಯ ಮಿತಿಗಳು ∞ ಗೆ ಸಮಾನವಾಗಿರುವ ಅಥವಾ ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲದ ಬಿಂದುಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ.
ಉದಾಹರಣೆ 3.
x = 0 ಹೊರತುಪಡಿಸಿ x ನ ಎಲ್ಲಾ ಮೌಲ್ಯಗಳಿಗೆ y=2 1/ x ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ. ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ: 
, 
, ಆದ್ದರಿಂದ x=0 ಎಂಬುದು ಎರಡನೇ ವಿಧದ ಒಂದು ಸ್ಥಗಿತ ಬಿಂದುವಾಗಿದೆ (ಚಿತ್ರ 3).
3) ಪಾಯಿಂಟ್ x=x 0 ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ತೆಗೆಯಬಹುದಾದ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್
, f(x 0 +0)=f(x 0 -0)≠f(x 0).
ಹೊಂದಿಸುವ ಮೂಲಕ ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮೌಲ್ಯವನ್ನು ಬದಲಾಯಿಸಲು (ಮರುವ್ಯಾಖ್ಯಾನಿಸಲು ಅಥವಾ ಮರುವ್ಯಾಖ್ಯಾನಿಸಲು) ಸಾಕು ಎಂಬ ಅರ್ಥದಲ್ಲಿ ನಾವು ಅಂತರವನ್ನು "ನಿರ್ಮೂಲನೆ ಮಾಡುತ್ತೇವೆ" ಮತ್ತು ಕಾರ್ಯವು x 0 ಹಂತದಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ. 
ಉದಾಹರಣೆ 4.
ಎಂದು ತಿಳಿದುಬಂದಿದೆ 
, ಮತ್ತು ಈ ಮಿತಿಯು x ಶೂನ್ಯಕ್ಕೆ ಒಲವು ತೋರುವ ವಿಧಾನವನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ. ಆದರೆ ಪಾಯಿಂಟ್ x=0 ನಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ. ನಾವು f(0)=1 ಅನ್ನು ಹೊಂದಿಸುವ ಮೂಲಕ ಕಾರ್ಯವನ್ನು ಮರುವ್ಯಾಖ್ಯಾನಿಸಿದರೆ, ಈ ಹಂತದಲ್ಲಿ ಅದು ನಿರಂತರವಾಗಿರುತ್ತದೆ (ಇತರ ಬಿಂದುಗಳಲ್ಲಿ ಇದು ನಿರಂತರ ಕಾರ್ಯಗಳಾದ sinx ಮತ್ತು x ನ ಅಂಶವಾಗಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ). 
ಉದಾಹರಣೆ 5.
ಕಾರ್ಯದ ನಿರಂತರತೆಯನ್ನು ಪರೀಕ್ಷಿಸಿ 
.
ಪರಿಹಾರ.
y=x 3 ಮತ್ತು y=2x ಕಾರ್ಯಗಳನ್ನು ಸೂಚಿಸಿದ ಮಧ್ಯಂತರಗಳನ್ನು ಒಳಗೊಂಡಂತೆ ಎಲ್ಲೆಡೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಮತ್ತು ನಿರಂತರವಾಗಿರುತ್ತದೆ. x=0 ಮಧ್ಯಂತರಗಳ ಜಂಕ್ಷನ್ ಪಾಯಿಂಟ್ ಅನ್ನು ಪರಿಶೀಲಿಸೋಣ: 
, 
, ನಾವು ಅದನ್ನು ಪಡೆಯುತ್ತೇವೆ, ಇದು x=0 ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ ಎಂದು ಸೂಚಿಸುತ್ತದೆ.
ವ್ಯಾಖ್ಯಾನ.
ಮೊದಲ ವಿಧದ ಅಥವಾ ತೆಗೆಯಬಹುದಾದ ಸ್ಥಗಿತದ ಸೀಮಿತ ಸಂಖ್ಯೆಯ ಸ್ಥಗಿತ ಬಿಂದುಗಳನ್ನು ಹೊರತುಪಡಿಸಿ ಮಧ್ಯಂತರದಲ್ಲಿ ನಿರಂತರವಾಗಿರುವ ಕಾರ್ಯವನ್ನು ಈ ಮಧ್ಯಂತರದಲ್ಲಿ ತುಣುಕು ನಿರಂತರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ನಿರಂತರ ಕಾರ್ಯಗಳ ಉದಾಹರಣೆಗಳು
ಉದಾಹರಣೆ 1.
x=2 ಬಿಂದುವನ್ನು ಹೊರತುಪಡಿಸಿ (-∞,+∞) ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಮತ್ತು ನಿರಂತರವಾಗಿರುತ್ತದೆ. ವಿರಾಮದ ಪ್ರಕಾರವನ್ನು ನಿರ್ಧರಿಸೋಣ. ಏಕೆಂದರೆ ದಿ 
ಮತ್ತು 
, ನಂತರ x=2 ಬಿಂದುವಿನಲ್ಲಿ ಎರಡನೇ ವಿಧದ (ಚಿತ್ರ 6) ಸ್ಥಗಿತಗೊಳ್ಳುತ್ತದೆ. 
ಉದಾಹರಣೆ 2.
ಛೇದವು ಶೂನ್ಯವಾಗಿರುವ x=0 ಹೊರತುಪಡಿಸಿ ಎಲ್ಲಾ x ಗೆ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಮತ್ತು ನಿರಂತರವಾಗಿರುತ್ತದೆ. x=0 ಬಿಂದುವಿನಲ್ಲಿ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ: ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಸೀಮಿತವಾಗಿರುತ್ತವೆ ಮತ್ತು ವಿಭಿನ್ನವಾಗಿವೆ, ಆದ್ದರಿಂದ, x=0 ಎಂಬುದು ಮೊದಲ ವಿಧದ ಸ್ಥಗಿತದ ಬಿಂದುವಾಗಿದೆ (ಚಿತ್ರ 7).
ಉದಾಹರಣೆ 3.
ಕಾರ್ಯವು ಯಾವ ಹಂತಗಳಲ್ಲಿ ಮತ್ತು ಯಾವ ರೀತಿಯ ಸ್ಥಗಿತಗಳನ್ನು ಹೊಂದಿದೆ ಎಂಬುದನ್ನು ನಿರ್ಧರಿಸಿ 
ಈ ಕಾರ್ಯವನ್ನು [-2,2] ರಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. x 2 ಮತ್ತು 1/x ಕ್ರಮವಾಗಿ [-2,0] ಮತ್ತು , ಮಧ್ಯಂತರಗಳಲ್ಲಿ ನಿರಂತರವಾಗಿರುವುದರಿಂದ, ಸ್ಥಗಿತವು ಮಧ್ಯಂತರಗಳ ಜಂಕ್ಷನ್‌ನಲ್ಲಿ ಮಾತ್ರ ಸಂಭವಿಸಬಹುದು, ಅಂದರೆ x=0 ಬಿಂದುವಿನಲ್ಲಿ. ರಿಂದ, ನಂತರ x=0 ಎರಡನೇ ವಿಧದ ಸ್ಥಗಿತ ಬಿಂದುವಾಗಿದೆ.
ಉದಾಹರಣೆ 4.
ಕಾರ್ಯದ ಅಂತರವನ್ನು ತೊಡೆದುಹಾಕಲು ಸಾಧ್ಯವೇ:
ಎ) 
ಬಿಂದು x=2 ನಲ್ಲಿ;
b) 
ಬಿಂದು x=2 ನಲ್ಲಿ;
ವಿ) 
ಪಾಯಿಂಟ್ x=1 ನಲ್ಲಿ?
ಪರಿಹಾರ.
ಉದಾಹರಣೆಗೆ ಸಂಬಂಧಿಸಿದಂತೆ a) x=2 ಬಿಂದುವಿನಲ್ಲಿ f(x) ಸ್ಥಗಿತವನ್ನು ತೆಗೆದುಹಾಕಲಾಗುವುದಿಲ್ಲ ಎಂದು ನಾವು ತಕ್ಷಣವೇ ಹೇಳಬಹುದು, ಏಕೆಂದರೆ ಈ ಹಂತದಲ್ಲಿ ಅನಂತ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳಿವೆ (ಉದಾಹರಣೆ 1 ನೋಡಿ).
b) g(x) ಕಾರ್ಯವು x=2 ಬಿಂದುವಿನಲ್ಲಿ ಸೀಮಿತ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಹೊಂದಿದೆ
(
,
),
ಆದರೆ ಅವು ಹೊಂದಿಕೆಯಾಗುವುದಿಲ್ಲ, ಆದ್ದರಿಂದ ಅಂತರವನ್ನು ತೆಗೆದುಹಾಕಲಾಗುವುದಿಲ್ಲ.
c) x=1 ಸ್ಥಗಿತ ಬಿಂದುವಿನಲ್ಲಿ φ(x) ಕಾರ್ಯವು ಸಮಾನವಾದ ಏಕಪಕ್ಷೀಯ ಸೀಮಿತ ಮಿತಿಗಳನ್ನು ಹೊಂದಿದೆ: ಆದ್ದರಿಂದ, f(1)=2 ಬದಲಿಗೆ f(1)=1 ಅನ್ನು ಹಾಕುವ ಮೂಲಕ x=1 ನಲ್ಲಿ ಕಾರ್ಯವನ್ನು ಮರು ವ್ಯಾಖ್ಯಾನಿಸುವ ಮೂಲಕ ಅಂತರವನ್ನು ತೆಗೆದುಹಾಕಬಹುದು.
ಉದಾಹರಣೆ 5. ಡಿರಿಚ್ಲೆಟ್ ಕಾರ್ಯವನ್ನು ತೋರಿಸಿ
ಸಂಖ್ಯಾತ್ಮಕ ಅಕ್ಷದ ಪ್ರತಿ ಹಂತದಲ್ಲೂ ನಿರಂತರ.
ಪರಿಹಾರ. (-∞,+∞) ನಿಂದ x 0 ಯಾವುದೇ ಬಿಂದುವಾಗಿರಲಿ. ಅದರ ಯಾವುದೇ ನೆರೆಹೊರೆಯಲ್ಲಿ ತರ್ಕಬದ್ಧ ಮತ್ತು ಅಭಾಗಲಬ್ಧ ಅಂಶಗಳಿವೆ. ಇದರರ್ಥ x 0 ರ ಯಾವುದೇ ನೆರೆಹೊರೆಯಲ್ಲಿ ಕಾರ್ಯವು 0 ಮತ್ತು 1 ಕ್ಕೆ ಸಮಾನವಾದ ಮೌಲ್ಯಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಎಡ ಅಥವಾ ಬಲಭಾಗದಲ್ಲಿ x 0 ಬಿಂದುವಿನಲ್ಲಿ ಕಾರ್ಯದ ಮಿತಿ ಇರುವಂತಿಲ್ಲ, ಅಂದರೆ ಡಿರಿಚ್ಲೆಟ್ ಕಾರ್ಯವು ನೈಜ ಅಕ್ಷದ ಪ್ರತಿ ಬಿಂದುವಿನಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತಗಳನ್ನು ಹೊಂದಿದೆ.
ಉದಾಹರಣೆ 6. ಫಂಕ್ಷನ್ ಬ್ರೇಕ್‌ಪಾಯಿಂಟ್‌ಗಳನ್ನು ಹುಡುಕಿ
ಮತ್ತು ಅವುಗಳ ಪ್ರಕಾರವನ್ನು ನಿರ್ಧರಿಸಿ.
ಪರಿಹಾರ. ಮುರಿಯುವ ಶಂಕಿತ ಬಿಂದುಗಳು x 1 =2, x 2 =5, x 3 =3.
ಬಿಂದುವಿನಲ್ಲಿ x 1 =2 f(x) ಎರಡನೆಯ ವಿಧದ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿದೆ
.
ಪಾಯಿಂಟ್ x 2 =5 ನಿರಂತರತೆಯ ಬಿಂದುವಾಗಿದೆ, ಏಕೆಂದರೆ ಈ ಹಂತದಲ್ಲಿ ಮತ್ತು ಅದರ ಸುತ್ತಮುತ್ತಲಿನ ಕಾರ್ಯದ ಮೌಲ್ಯವನ್ನು ಎರಡನೇ ಸಾಲಿನಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಮೊದಲನೆಯದಲ್ಲ: .
x 3 =3 ಬಿಂದುವನ್ನು ಪರಿಶೀಲಿಸೋಣ:,
, ಇದು x=3 ಮೊದಲ ವಿಧದ ಸ್ಥಗಿತ ಬಿಂದು ಎಂದು ಅನುಸರಿಸುತ್ತದೆ. ಫಾರ್ ಸ್ವತಂತ್ರ ನಿರ್ಧಾರ.
ನಿರಂತರತೆಗಾಗಿ ಕಾರ್ಯಗಳನ್ನು ಪರೀಕ್ಷಿಸಿ ಮತ್ತು ಸ್ಥಗಿತದ ಬಿಂದುಗಳ ಪ್ರಕಾರವನ್ನು ನಿರ್ಧರಿಸಿ:
1) 
; ಉತ್ತರ: x=-1 - ತೆಗೆಯಬಹುದಾದ ಸ್ಥಗಿತದ ಬಿಂದು;
2) 
; ಉತ್ತರ: x=8 ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತ;
3) 
; ಉತ್ತರ: x=1 ನಲ್ಲಿ ಮೊದಲ ವಿಧದ ಸ್ಥಗಿತ;
4) 
ಉತ್ತರ: x 1 =-5 ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ತೆಗೆಯಬಹುದಾದ ಅಂತರವಿದೆ, x 2 =1 ನಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಅಂತರವಿದೆ ಮತ್ತು x 3 =0 ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಮೊದಲ ವಿಧದ ಅಂತರವಿದೆ.
5) A ಸಂಖ್ಯೆಯನ್ನು ಹೇಗೆ ಆರಿಸಬೇಕು ಆದ್ದರಿಂದ ಕಾರ್ಯ 
x=0 ನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆಯೇ?
ಉತ್ತರ: A=2.
6) A ಸಂಖ್ಯೆಯನ್ನು ಆಯ್ಕೆ ಮಾಡಲು ಸಾಧ್ಯವೇ ಇದರಿಂದ ಕಾರ್ಯ 
x=2 ನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆಯೇ?
ಉತ್ತರ: ಇಲ್ಲ.
ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮುಂದುವರಿಕೆ. ಕಾರ್ಯ y = f(x ) ಪೂರ್ವ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ
ಬಿಂದು x 0 ನಲ್ಲಿ ಜರ್ಕಿ ಇದ್ದರೆ:
1) ಈ ಕಾರ್ಯವನ್ನು ಬಿಂದುವಿನ ಕೆಲವು ನೆರೆಹೊರೆಯಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ x 0;
2) ಮಿತಿಯ ಮಿತಿ ಇದೆ f(x);
→ x 0
3) ಈ ಮಿತಿ ಮೌಲ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆಪಾಯಿಂಟ್ x 0 ನಲ್ಲಿ ಕಾರ್ಯಗಳು, ಅಂದರೆ. limf (x )= f (x 0 ) . |
||
x→x0 |
||
ಕೊನೆಯ ಸ್ಥಿತಿಯು ಲಿಮ್ ಸ್ಥಿತಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ | y = 0, ಅಲ್ಲಿ x = x - x 0 - ಯಾವಾಗ |
|
x→ 0 | ||
ವಾದದ ತಿರುಗುವಿಕೆ, y = f (x 0 + | x )− f (x 0 ) – ಕ್ರಿಯೆಯ ಹೆಚ್ಚಳ, ಅನುಗುಣವಾದ |
|
ವಾದವನ್ನು ಹೆಚ್ಚಿಸುವುದು | x, ಅಂದರೆ. ಕಾರ್ಯ | f(x) x 0 ನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ |
ಒಂದು ವೇಳೆ ಮತ್ತು ಈ ಹಂತದಲ್ಲಿ ವಾದದ ಅನಂತವಾದ ಹೆಚ್ಚಳವು ಕಾರ್ಯದ ಅನಂತವಾದ ಹೆಚ್ಚಳಕ್ಕೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ.
ಏಕಮುಖ ನಿರಂತರತೆ. y = f (x) ಕಾರ್ಯವನ್ನು ನಿರಂತರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ
ಪಾಯಿಂಟ್ಎಕ್ಸ್ 0 ನಲ್ಲಿ ಎಡಭಾಗದಲ್ಲಿ ಕೆಲವು ಅರ್ಧ-ಮಧ್ಯಂತರದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಿದರೆ (a ;x 0 ]
ಮತ್ತು lim f (x)= f (x 0).
x→ x0 − 0
ಒಂದು ಫಂಕ್ಷನ್ y = f (x) op- ಆಗಿದ್ದರೆ x 0 ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಸರಿಯಾದ ನಿರಂತರವಾಗಿರುತ್ತದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ.
ನಿರ್ದಿಷ್ಟ ಅರ್ಧ ಮಧ್ಯಂತರದಲ್ಲಿ ವಿತರಿಸಲಾಗುತ್ತದೆ [ x 0 ;a ) ಮತ್ತು limf (x )= f (x 0 ) .
x→ x0 + 0
ಕಾರ್ಯ y = f(x) | ಬಿಂದು x 0 ನಲ್ಲಿ ನಿರಂತರ | ನಂತರ ಮತ್ತು ಅವಳು ಮಾತ್ರ |
||||||
ನಿರಂತರ | ||||||||
lim f (x)= limf (x)= limf (x)= f (x 0). | ||||||||
x→ x0 + 0 | x→ x0 − 0 | x→x0 | ||||||
ಒಂದು ಸೆಟ್ನಲ್ಲಿ ಕಾರ್ಯದ ಮುಂದುವರಿಕೆ. y = f (x) ಕಾರ್ಯವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ
ಸೆಟ್ನಲ್ಲಿ ನಿರಂತರ X ಈ ಸೆಟ್‌ನ ಪ್ರತಿಯೊಂದು ಹಂತದಲ್ಲಿಯೂ ನಿರಂತರವಾಗಿದ್ದರೆ. ಇದಲ್ಲದೆ, ಸಂಖ್ಯಾ ರೇಖೆಯ ನಿರ್ದಿಷ್ಟ ಮಧ್ಯಂತರದ ಕೊನೆಯಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಿದರೆ, ಈ ಹಂತದಲ್ಲಿ ನಿರಂತರತೆಯನ್ನು ಬಲ ಅಥವಾ ಎಡಭಾಗದಲ್ಲಿ ನಿರಂತರತೆ ಎಂದು ಅರ್ಥೈಸಲಾಗುತ್ತದೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ, y = f (x) ಕಾರ್ಯವನ್ನು ಅಲ್ಲದ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ
ವಿಭಾಗದಲ್ಲಿ ನಿರಂತರ [ಎ; b] ಅವಳು ಇದ್ದರೆ
1) ಮಧ್ಯಂತರದ ಪ್ರತಿ ಹಂತದಲ್ಲಿ ನಿರಂತರ(ಎ; ಬಿ);
2) ಒಂದು ಹಂತದಲ್ಲಿ ಸರಿಯಾದ ನಿರಂತರವಾಗಿರುತ್ತದೆ a ;
3) ಒಂದು ಹಂತದಲ್ಲಿ ನಿರಂತರವಾಗಿ ಬಿಡಲಾಗುತ್ತದೆಬಿ.
ಫಂಕ್ಷನ್ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳು. y = f (x) ಕಾರ್ಯದ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ಗೆ ಸೇರಿದ ಪಾಯಿಂಟ್ x 0 ಅಥವಾ ಈ ಡೊಮೇನ್‌ನ ಗಡಿ ಬಿಂದು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ
ಈ ಕಾರ್ಯದ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್, iff(x) ಆ ಹಂತದಲ್ಲಿ ನಿರಂತರವಾಗಿರುವುದಿಲ್ಲ.
ಸ್ಥಗಿತದ ಬಿಂದುಗಳನ್ನು ಮೊದಲ ಮತ್ತು ಎರಡನೆಯ ವಿಧದ ಸ್ಥಗಿತ ಬಿಂದುಗಳಾಗಿ ವಿಂಗಡಿಸಲಾಗಿದೆ:
1) ಸೀಮಿತ ಮಿತಿಗಳಿದ್ದರೆ lim f (x )= f (x 0 - 0) ಮತ್ತು
x→ x0 − 0
f (x)= f (x 0 + 0), ಮತ್ತು ಎಲ್ಲಾ ಮೂರು ಸಂಖ್ಯೆಗಳು f (x 0 - 0), f (x 0 + 0), | f (x 0) ಸಮಾನವಾಗಿರುತ್ತದೆ |
||
x→ x0 + 0 | |||
ತಮ್ಮ ನಡುವೆ, ನಂತರ x 0 | ಮೊದಲ ವಿಧದ ಸ್ಥಗಿತ ಬಿಂದು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. | ||
ನಿರ್ದಿಷ್ಟವಾಗಿ, x 0 ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳು | ನಡುವೆ ಸಮಾನವಾಗಿರುತ್ತದೆ |
||
ನೀವೇ, ಆದರೆ | ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯ ಮೌಲ್ಯಕ್ಕೆ ಸಮನಾಗಿರುವುದಿಲ್ಲ: |
||
f (x0 - 0) = f(x0 + 0) = A≠ f(x0 ) , ನಂತರ x 0 ಅನ್ನು ತೆಗೆಯಬಹುದಾದ ಸ್ಥಗಿತ ಬಿಂದು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಈ ಸಂದರ್ಭದಲ್ಲಿ, f (x 0 )= A ಅನ್ನು ಹೊಂದಿಸುವ ಮೂಲಕ, ನೀವು ಪಾಯಿಂಟ್ x 0 ನಲ್ಲಿ ಕಾರ್ಯವನ್ನು ಮಾರ್ಪಡಿಸಬಹುದು
ಇದರಿಂದ ಅದು ನಿರಂತರವಾಗಿರುತ್ತದೆ ( ನಿರಂತರತೆಯಿಂದ ಕಾರ್ಯವನ್ನು ಮರು ವ್ಯಾಖ್ಯಾನಿಸಿ) ವ್ಯತ್ಯಾಸ f (x 0 + 0)− f (x 0 - 0) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಜಂಪ್ x 0
ತೆಗೆಯಬಹುದಾದ ಸ್ಥಗಿತದ ಹಂತದಲ್ಲಿ ಕಾರ್ಯ ಜಂಪ್ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ.
2) ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತ ಬಿಂದುಗಳಲ್ಲದ ಸ್ಥಗಿತ ಬಿಂದುಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಎರಡನೇ ರೀತಿಯ ಬ್ರೇಕ್‌ಪಾಯಿಂಟ್‌ಗಳು. ಎರಡನೆಯ ವಿಧದ ಸ್ಥಗಿತದ ಬಿಂದುಗಳಲ್ಲಿ, ಕನಿಷ್ಠ ಒಂದು ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು f (x 0 - 0) ಮತ್ತು f (x 0 + 0) ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ ಅಥವಾ ಅನಂತವಾಗಿರುತ್ತದೆ.
ಒಂದು ಹಂತದಲ್ಲಿ ನಿರಂತರವಾದ ಕಾರ್ಯಗಳ ಗುಣಲಕ್ಷಣಗಳು.
f(x) | ಮತ್ತು g (x) ಬಿಂದು x 0 ನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ, ನಂತರ ಕಾರ್ಯಗಳು |
||
f(x) ±g(x), | f(x)g(x) ಮತ್ತು | f(x) | (ಇಲ್ಲಿ g (x)≠ 0) ಸಹ ಬಿಂದು x ನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ. |
g(x) | |||
2) u (x) ಕಾರ್ಯವು x 0 ಹಂತದಲ್ಲಿ ನಿರಂತರವಾಗಿದ್ದರೆ ಮತ್ತು f (u) ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ
ಬಿಂದು u 0 = u (x 0), ನಂತರ ಸಂಕೀರ್ಣ ಕಾರ್ಯ f (u (x)) ಬಿಂದು x 0 ನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ.
3) ಎಲ್ಲಾ ಮೂಲಭೂತ ಪ್ರಾಥಮಿಕ ಕಾರ್ಯಗಳು (c, x a, a x, loga x, sinx, cosx, tgx, ctgx, secx, cosecx, arcsinx, arccosx, arctgx, arcctgx) ಪ್ರತಿಯೊಂದರಲ್ಲೂ ನಿರಂತರವಾಗಿರುತ್ತವೆ
ಅವರ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ಗಳ ಹಂತಕ್ಕೆ.
ಗುಣಲಕ್ಷಣಗಳಿಂದ 1)–3) ಎಲ್ಲಾ ಪ್ರಾಥಮಿಕ ಕಾರ್ಯಗಳು (ಸೀಮಿತ ಸಂಖ್ಯೆಯ ಅಂಕಗಣಿತದ ಕಾರ್ಯಾಚರಣೆಗಳು ಮತ್ತು ಸಂಯೋಜನೆಯ ಕಾರ್ಯಾಚರಣೆಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಮೂಲಭೂತ ಪ್ರಾಥಮಿಕ ಕಾರ್ಯಗಳಿಂದ ಪಡೆದ ಕಾರ್ಯಗಳು) ಅವುಗಳ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ಗಳ ಪ್ರತಿ ಹಂತದಲ್ಲಿಯೂ ಸಹ ನಿರಂತರವಾಗಿರುತ್ತವೆ.
ಮಧ್ಯಂತರದಲ್ಲಿ ನಿರಂತರವಾದ ಕಾರ್ಯಗಳ ಗುಣಲಕ್ಷಣಗಳು.
1) (ಮಧ್ಯಂತರ ಮೌಲ್ಯ ಪ್ರಮೇಯ) f(x) ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸೋಣ
ಆನ್ ಮತ್ತು ವಿಭಾಗದಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ [a;b]. ನಂತರ ಯಾವುದೇ ಸಂಖ್ಯೆಗೆ C ಅನ್ನು ಲಗತ್ತಿಸಲಾಗಿದೆ
ಸಂಖ್ಯೆಗಳ ನಡುವೆ f (a) ಮತ್ತು f (b), (f (a)< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .
2) (ಬೊಲ್ಜಾನೊ-ಕೌಚಿ ಪ್ರಮೇಯ
ಸೆಗ್ಮೆಂಟ್ [a;b] ನಲ್ಲಿ ಸ್ಥಗಿತಗೊಳ್ಳುತ್ತದೆ ಮತ್ತು ಅದರ ತುದಿಗಳಲ್ಲಿ ವಿಭಿನ್ನ ಚಿಹ್ನೆಗಳ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ.
ನಂತರ ಕನಿಷ್ಠ ಒಂದು ಬಿಂದು x 0 [a; b] ಇರುತ್ತದೆ ಅಂದರೆ f (x 0)= 0 .
3) (1 ನೇ ವೈರ್‌ಸ್ಟ್ರಾಸ್ ಪ್ರಮೇಯಎಫ್ (x) ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸೋಣ ಮತ್ತು
ವಿಭಾಗದಲ್ಲಿ ಹರಿದಿದೆ [a;b]. ನಂತರ ಈ ಕಾರ್ಯವು ಈ ವಿಭಾಗದಲ್ಲಿ ಸೀಮಿತವಾಗಿದೆ.
4) (2ನೇ ವೈರ್‌ಸ್ಟ್ರಾಸ್ ಪ್ರಮೇಯಎಫ್ (x) ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸೋಣ ಮತ್ತು
ವಿಭಾಗದಲ್ಲಿ ಹೊರದಬ್ಬುವುದು | [ಎ; ಬಿ] . ನಂತರ ಈ ಕಾರ್ಯವು ಮಧ್ಯಂತರವನ್ನು ತಲುಪುತ್ತದೆ [a; b] | |||||
ಶ್ರೇಷ್ಠ | ಕನಿಷ್ಠ | ಮೌಲ್ಯಗಳು, ಅಂದರೆ. | ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ | |||
x1, x2 [a; ಬಿ], | ಯಾವುದಕ್ಕಾದರೂ | ಅಂಕಗಳು x [a;b] | ನ್ಯಾಯೋಚಿತ | ಅಸಮಾನತೆಗಳು |
||
f (x 1 )≤ f (x )≤ f (x 2 ) .
ಉದಾಹರಣೆ 5.17. ನಿರಂತರತೆಯ ವ್ಯಾಖ್ಯಾನವನ್ನು ಬಳಸಿಕೊಂಡು, y = 3x 2 + 2x - 5 ಕಾರ್ಯವು ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ x 0 ಅನಿಯಂತ್ರಿತ ಹಂತದಲ್ಲಿ ನಿರಂತರವಾಗಿದೆ ಎಂದು ಸಾಬೀತುಪಡಿಸಿ.
ಪರಿಹಾರ: ವಿಧಾನ 1: ಸಂಖ್ಯೆಯ ಅಕ್ಷದ ಮೇಲೆ x 0 ಅನಿಯಂತ್ರಿತ ಬಿಂದುವಾಗಿರಲಿ. ನೀವು -
ನಾವು ಮೊದಲು ಫಂಕ್ಷನ್‌ಗಳ ಮೊತ್ತ ಮತ್ತು ಉತ್ಪನ್ನದ ಮಿತಿಯ ಮೇಲೆ ಪ್ರಮೇಯಗಳನ್ನು ಅನ್ವಯಿಸುವ ಮೂಲಕ f (x) ಕಾರ್ಯದ ಮಿತಿಯನ್ನು x → x 0 ಎಂದು ಲೆಕ್ಕಾಚಾರ ಮಾಡುತ್ತೇವೆ:
lim f (x )= lim(3x 2 + 2x - 5)= 3(limx )2 + 2 limx - 5= 3x 2 | − 5. |
||||||
x→x0 | x→x0 | x→x0 | x→x0 | ||||
ನಂತರ ನಾವು x:f (x)= 3x 2 ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಕಾರ್ಯದ ಮೌಲ್ಯವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುತ್ತೇವೆ | − 5 . |
||||||
ಪಡೆದ ಫಲಿತಾಂಶಗಳನ್ನು ಹೋಲಿಸಿ, ನಾವು ನೋಡುತ್ತೇವೆ | lim f (x)= f (x 0) ಅದರ ಪ್ರಕಾರ |
||||||
x→x0 | |||||||
ವ್ಯಾಖ್ಯಾನ ಮತ್ತು ಎಂದರೆ x 0 ಹಂತದಲ್ಲಿ ಪರಿಗಣನೆಯಲ್ಲಿರುವ ಕಾರ್ಯದ ನಿರಂತರತೆ.
ವಿಧಾನ 2: ಅವಕಾಶ | x - ಪಾಯಿಂಟ್ಎಕ್ಸ್ 0 ನಲ್ಲಿ ಆರ್ಗ್ಯುಮೆಂಟ್‌ನ ಹೆಚ್ಚಳ. ಪತ್ರವ್ಯವಹಾರವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ |
|||
ಸೂಕ್ತ | ಹೆಚ್ಚಳ | y = f(x0 + x) - f(x0 ) = |
||
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x - 5) | ||||
6 x x+ (x) 2 | 2x = (6x + 2)x + (x)2. | |||
ಆರ್ಗ್ಯುಮೆಂಟ್‌ನ ಇನ್‌ಕ್ರಿಮೆಂಟ್ ಮಾಡಿದಾಗ ಫಂಕ್ಷನ್ ಇನ್‌ಕ್ರಿಮೆಂಟ್‌ನ ಮಿತಿಯನ್ನು ಈಗ ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ |
||||
ಶ್ರಮಿಸುತ್ತದೆ | ||||
y = ಲಿಮ್ (6x + 2) | x + (x )2 = (6x + 2) ಲಿಮ್ | x + (limx)2 = 0. |
|||
x→ 0 | x→ 0 | x→ 0 | x→ 0 |
||
ಹೀಗಾಗಿ, ಲಿಮ್ y = 0, ಅಂದರೆ ವ್ಯಾಖ್ಯಾನ ನಿರಂತರತೆ
x→ 0
ಯಾವುದೇ x 0 R ಗಾಗಿ ಕಾರ್ಯಗಳು.
ಉದಾಹರಣೆ 5.18. ಫಂಕ್ಷನ್ f (x) ನ ಸ್ಥಗಿತ ಬಿಂದುಗಳನ್ನು ಹುಡುಕಿ ಮತ್ತು ಅವುಗಳ ಪ್ರಕಾರವನ್ನು ನಿರ್ಧರಿಸಿ. IN
ತೆಗೆಯಬಹುದಾದ ಸ್ಥಗಿತದ ಸಂದರ್ಭದಲ್ಲಿ, ನಿರಂತರತೆಯ ಮೂಲಕ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಿ:
1) f (x) = 1− x 2 ನಲ್ಲಿ x< 3;
5x ಯಾವಾಗ x ≥ 3
2) f (x)= x 2 + 4 x + 3;
x+1
f(x)= | |||||
x4 (x− 2) |
|||||
f(x)= ಆರ್ಕ್ಟಾನ್ | |||||
(x - 5) |
|||||
ಪರಿಹಾರ: 1) ಈ ಕಾರ್ಯದ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್ ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯಾಗಿದೆ
y ಅಕ್ಷ (-∞ ;+∞) . ಮಧ್ಯಂತರಗಳಲ್ಲಿ (−∞ ;3) ,(3;+∞ ) ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ. x = 3 ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಮಾತ್ರ ಸ್ಥಗಿತಗೊಳಿಸುವಿಕೆ ಸಾಧ್ಯ, ಇದರಲ್ಲಿ ಕಾರ್ಯದ ವಿಶ್ಲೇಷಣಾತ್ಮಕ ವಿವರಣೆಯು ಬದಲಾಗುತ್ತದೆ.
ಸೂಚಿಸಿದ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:
f (3− 0)= ಲಿಮ್ (1− x 2 )= 1− 9= 8;
x →3 -0
f (3+ 0)= ಲಿಮ್ 5x = 15.
x →3 +0
ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳು ಸೀಮಿತವಾಗಿವೆ ಎಂದು ನಾವು ನೋಡುತ್ತೇವೆ, ಆದ್ದರಿಂದ x = 3 | |||||
ಛಿದ್ರ I | f(x) ಕಾರ್ಯ ಜಂಪ್ | ||||
f (3+ 0)− f (3− 0)= 15− 8= 7 . | |||||
f (3)= 5 3= 15= f (3+ 0) , ಆದ್ದರಿಂದ ಹಂತದಲ್ಲಿ | x = 3 | ||||
f(x) ಸರಿಯಾದ ನಿರಂತರವಾಗಿದೆ.
2) ಪಾಯಿಂಟ್ ಹೊರತುಪಡಿಸಿ ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ x = - 1, ಇದರಲ್ಲಿ ಅದನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ. ಎಫ್ (x) ಗಾಗಿ ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ಪರಿವರ್ತಿಸೋಣ, ಅಂಶವನ್ನು ವಿಸ್ತರಿಸೋಣ
ಅಂಶಗಳಾಗಿ ಭಿನ್ನರಾಶಿಗಳು: | f(x)= | 4 x +3 | (x + 1)(x + 3) | x ≠ − 1 ಗೆ X + 3. |
|||||
x+1 | x+1 |
||||||||
x = − 1 ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಕಾರ್ಯದ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ: |
|||||||||
f(x)=lim | f (x )= lim (x + 3)= 2 . | ||||||||
x →−1−0 | x →−1 +0 | x →−1 | |||||||
ಅಧ್ಯಯನದ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ ಎಂದು ನಾವು ಕಂಡುಕೊಂಡಿದ್ದೇವೆ, ಸೀಮಿತ ಮತ್ತು ಪರಸ್ಪರ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ x = - 1 ತೆಗೆಯಬಹುದಾದ ಬಿಂದುವಾಗಿದೆ
ನೇರ ರೇಖೆ y = x + 3 ಜೊತೆಗೆ "ಪಂಕ್ಚರ್ಡ್" ಪಾಯಿಂಟ್ M (- 1;2) . ಕಾರ್ಯವು ಶಾಶ್ವತವಾಗಲು
ನಿರಂತರ, ನಾವು f (- 1)= f (- 1− 0)= f (- 1+ 0)= 2 ಅನ್ನು ಹಾಕಬೇಕು.
ಹೀಗಾಗಿ, x = - 1 ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ನಿರಂತರತೆಯ ಮೂಲಕ f (x) ಅನ್ನು ಮತ್ತಷ್ಟು ವ್ಯಾಖ್ಯಾನಿಸಿದ ನಂತರ, ನಾವು ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್‌ನೊಂದಿಗೆ f * (x)= x + 3 ಕಾರ್ಯವನ್ನು ಪಡೆದುಕೊಂಡಿದ್ದೇವೆ (−∞ ;+∞ ) .
3) ಈ ಕಾರ್ಯಎಲ್ಲರಿಗೂ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಮತ್ತು ನಿರಂತರವಾಗಿದೆ x ಅಂಕಗಳನ್ನು ಹೊರತುಪಡಿಸಿ
x = 0,x = 2, ಇದರಲ್ಲಿ ಭಿನ್ನರಾಶಿಯ ಛೇದವು ಶೂನ್ಯವಾಗುತ್ತದೆ.
x = 0 ಬಿಂದುವನ್ನು ಪರಿಗಣಿಸಿ:
ಸೊನ್ನೆಯ ಸಾಕಷ್ಟು ಸಣ್ಣ ನೆರೆಹೊರೆಯಲ್ಲಿ ಕಾರ್ಯವು ಮಾತ್ರ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ
ಋಣಾತ್ಮಕ ಮೌಲ್ಯಗಳಿಗೆ, ನಂತರ f (- 0)= lim | = -∞ = f (+0) | ಆ. ಚುಕ್ಕೆ |
|||
(x - 2) |
|||||
x →−0 | |||||
x = 0 ಎಂಬುದು ಎರಡನೇ ರೀತಿಯ ಕಾರ್ಯದ ಸ್ಥಗಿತದ ಬಿಂದುವಾಗಿದೆ | f(x) | ||||
ಈಗ ಪಾಯಿಂಟ್ x = 2 ಅನ್ನು ಪರಿಗಣಿಸಿ:
ಕಾರ್ಯವು ಋಣಾತ್ಮಕ ಮೌಲ್ಯಗಳನ್ನು ಪರಿಗಣಿಸಿದ ಎಡಕ್ಕೆ ಹತ್ತಿರ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ
ಪಾಯಿಂಟ್ ಮತ್ತು ಧನಾತ್ಮಕವಾದವುಗಳು ಬಲಭಾಗದಲ್ಲಿವೆ | f (2− 0)= | = −∞, |
||||||
x4 (x− 2) |
||||||||
x →2 -0 | ||||||||
f (2+ 0)= ಲಿಮ್ | = +∞ . ಹಿಂದಿನ ಪ್ರಕರಣದಂತೆ, ಪಾಯಿಂಟ್ಎಕ್ಸ್ = 2 ನಲ್ಲಿ | |||||||
(x - 2) |
||||||||
x →2 +0 | ||||||||
tion ಎಡ ಅಥವಾ ಬಲ ಸೀಮಿತ ಮಿತಿಗಳನ್ನು ಹೊಂದಿಲ್ಲ, ಅಂದರೆ. ಈ ಹಂತದಲ್ಲಿ II ವಿಧದ ಛಿದ್ರವನ್ನು ಅನುಭವಿಸುತ್ತದೆ.
x = 5 | ||||||||||||||||||
f (5− 0)= ಲಿಮ್ ಆರ್ಕ್ಟಾನ್ | π ,f (5+ 0)= ಲಿಮ್ ಆರ್ಕ್ಟಾನ್ | x = 5 | ||||||||||||||||
(x - 5) | (x - 5) | |||||||||||||||||
x →5 -0 | x →5 +0 | |||||||||||||||||
ಕಾ ಛಿದ್ರ | ||||||||||||||||||
f (5+ 0)− f (5− 0)= | π − (− | π )= π (ಚಿತ್ರ 5.2 ನೋಡಿ). | ||||||||||||||||
ಸ್ವತಂತ್ರವಾಗಿ ಪರಿಹರಿಸಲು ಸಮಸ್ಯೆಗಳು
5.174. ಕೇವಲ ವ್ಯಾಖ್ಯಾನವನ್ನು ಬಳಸಿ, f (x) in ಫಂಕ್ಷನ್‌ನ ನಿರಂತರತೆಯನ್ನು ಸಾಬೀತುಪಡಿಸಿ
ಪ್ರತಿ ಪಾಯಿಂಟ್ x 0 R:
a) f(x) = c= const; | b) f (x)= x; | ||
c) f (x)= x 3; | d) f (x)= 5x 2 - 4x + 1; |
||
e) f (x)= sinx. | |||
5.175. ಕಾರ್ಯವನ್ನು ಸಾಬೀತುಪಡಿಸಿ | f(x) = x2 | 1 ಯಾವಾಗ x ≥ 0, | ನಿರಂತರವಾಗಿರುತ್ತದೆ |
1 ನಲ್ಲಿ x< 0 | |||
ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲು. ಈ ಕಾರ್ಯದ ಗ್ರಾಫ್ ಅನ್ನು ನಿರ್ಮಿಸಿ. | |||
5.176. ಕಾರ್ಯವನ್ನು ಸಾಬೀತುಪಡಿಸಿ | f(x) = x2 | 1 ಯಾವಾಗ x ≥ 0, | ನಿರಂತರವಲ್ಲ |
x ನಲ್ಲಿ 0< 0 | |||
x = 0 ಬಿಂದುವಿನಲ್ಲಿ, ಆದರೆ ಆ ಹಂತದಲ್ಲಿ ಸರಿಯಾದ ನಿರಂತರವಾಗಿರುತ್ತದೆ. f(x) ಕಾರ್ಯವನ್ನು ಗ್ರಾಫ್ ಮಾಡಿ.
x = ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಜರ್ಕಿ | ಆದರೆ ಈ ಹಂತದಲ್ಲಿ ಎಡಭಾಗದಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ. ಗ್ರಾಫ್ ಅನ್ನು ನಿರ್ಮಿಸಿ |
|||||||||||||
ಕಾರ್ಯಗಳು f(x). | ||||||||||||||
5.178. ಗ್ರಾಫ್ ಕಾರ್ಯಗಳು | ||||||||||||||
a) y = | x+1 | b) y= x+ | x+1 | |||||||||||
x+1 | x+1 | |||||||||||||
ಈ ಕಾರ್ಯಗಳ ಬ್ರೇಕ್‌ಪಾಯಿಂಟ್‌ಗಳಲ್ಲಿ ಯಾವ ನಿರಂತರತೆಯ ಪರಿಸ್ಥಿತಿಗಳು ತೃಪ್ತವಾಗಿವೆ ಮತ್ತು ಯಾವುದು ತೃಪ್ತಿ ಹೊಂದಿಲ್ಲ?
5.179. ಕಾರ್ಯದ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ ಅನ್ನು ಸೂಚಿಸಿ
ಪಾಪ x | x ≠ 0 ಗಾಗಿ | ||
x = 0 ನಲ್ಲಿ | |||
ಈ ಹಂತದಲ್ಲಿ ಯಾವ ನಿರಂತರತೆಯ ಷರತ್ತುಗಳನ್ನು ಪೂರೈಸಲಾಗಿದೆ ಮತ್ತು ಯಾವುದನ್ನು ಪೂರೈಸಲಾಗಿಲ್ಲ?
ವ್ಯಾಖ್ಯಾನ ಫಂಕ್ಷನ್ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳು ಮತ್ತು ಅವುಗಳ ಪ್ರಕಾರಗಳು ಕಾರ್ಯದ ನಿರಂತರತೆಯ ವಿಷಯದ ಮುಂದುವರಿಕೆಯಾಗಿದೆ. ಕಾರ್ಯದ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳ ಅರ್ಥದ ದೃಶ್ಯ (ಗ್ರಾಫಿಕಲ್) ವಿವರಣೆಯನ್ನು ನಿರಂತರತೆಯ ಪರಿಕಲ್ಪನೆಯೊಂದಿಗೆ ವ್ಯತಿರಿಕ್ತವಾಗಿ ನೀಡಲಾಗಿದೆ. ಫಂಕ್ಷನ್‌ನ ಬ್ರೇಕ್‌ಪಾಯಿಂಟ್‌ಗಳನ್ನು ಹೇಗೆ ಕಂಡುಹಿಡಿಯುವುದು ಮತ್ತು ಅವುಗಳ ಪ್ರಕಾರಗಳನ್ನು ನಿರ್ಧರಿಸುವುದು ಹೇಗೆ ಎಂದು ತಿಳಿಯೋಣ. ಮತ್ತು ನಮ್ಮದು ಇದಕ್ಕೆ ಸಹಾಯ ಮಾಡುತ್ತದೆ ನಿಷ್ಠಾವಂತ ಸ್ನೇಹಿತರು- ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳ ಬಗ್ಗೆ ಯಾರಿಗಾದರೂ ಯಾವುದೇ ಭಯವಿದ್ದರೆ, ನಾವು ಅದನ್ನು ಶೀಘ್ರದಲ್ಲೇ ಹೋಗಲಾಡಿಸುತ್ತೇವೆ.
ಒಂದಕ್ಕೊಂದು ಸಂಪರ್ಕ ಹೊಂದಿರದ ಗ್ರಾಫ್‌ನಲ್ಲಿರುವ ಪಾಯಿಂಟ್‌ಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಫಂಕ್ಷನ್ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳು . ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ x=2 - - ಬಿಂದುವಿನಲ್ಲಿ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುವ ಇಂತಹ ಕಾರ್ಯದ ಗ್ರಾಫ್.
ಮೇಲಿನ ಸಾಮಾನ್ಯೀಕರಣವು ಈ ಕೆಳಗಿನ ವ್ಯಾಖ್ಯಾನವಾಗಿದೆ. ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿಲ್ಲದಿದ್ದರೆ, ಈ ಹಂತದಲ್ಲಿ ಅದು ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿರುತ್ತದೆ ಮತ್ತು ಬಿಂದುವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ . ಅಡೆತಡೆಗಳು ಮೊದಲ ವಿಧ ಮತ್ತು ಎರಡನೆಯದು .
ನಿರ್ಧರಿಸುವ ಸಲುವಾಗಿ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳ ಪ್ರಕಾರಗಳು (ಪಾತ್ರ). ಕಾರ್ಯಗಳನ್ನು ವಿಶ್ವಾಸದಿಂದ ಕಂಡುಹಿಡಿಯಬೇಕು ಮಿತಿಗಳು, ಆದ್ದರಿಂದ ಹೊಸ ವಿಂಡೋದಲ್ಲಿ ಅನುಗುಣವಾದ ಪಾಠವನ್ನು ತೆರೆಯುವುದು ಒಳ್ಳೆಯದು. ಆದರೆ ಬ್ರೇಕ್‌ಪಾಯಿಂಟ್‌ಗಳಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ, ನಾವು ಹೊಸ ಮತ್ತು ಮುಖ್ಯವಾದದ್ದನ್ನು ಹೊಂದಿದ್ದೇವೆ - ಏಕಪಕ್ಷೀಯ (ಎಡ ಮತ್ತು ಬಲ) ಮಿತಿಗಳು. ಸಾಮಾನ್ಯವಾಗಿ ಅವುಗಳನ್ನು ಬರೆಯಲಾಗುತ್ತದೆ (ಬಲ ಮಿತಿ) ಮತ್ತು (ಎಡ ಮಿತಿ). ಸಾಮಾನ್ಯವಾಗಿ ಮಿತಿಯ ಸಂದರ್ಭದಲ್ಲಿ, ಒಂದು ಕಾರ್ಯದ ಮಿತಿಯನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನೀವು X ಅನ್ನು ಕಾರ್ಯದ ಅಭಿವ್ಯಕ್ತಿಯಲ್ಲಿ X ಅನ್ನು ಬದಲಿಸಬೇಕಾಗುತ್ತದೆ. ಆದರೆ, ಬಹುಶಃ, ನೀವು ಕೇಳುತ್ತೀರಿ, ಬಲ ಮತ್ತು ಎಡ ಮಿತಿಗಳು ಹೇಗೆ ಭಿನ್ನವಾಗಿರುತ್ತವೆ, ಸರಿಯಾದ ಸಂದರ್ಭದಲ್ಲಿ X ಗೆ ಏನನ್ನಾದರೂ ಸೇರಿಸಿದರೆ, ಆದರೆ ಇದು ಶೂನ್ಯವಾಗಿರುತ್ತದೆ ಮತ್ತು ಎಡಭಾಗದಲ್ಲಿ ಏನನ್ನಾದರೂ X ನಿಂದ ಕಳೆಯಲಾಗುತ್ತದೆ, ಆದರೆ ಈ ಏನೋ - ಸಹ ಶೂನ್ಯ? ಮತ್ತು ನೀವು ಸರಿಯಾಗಿರುತ್ತೀರಿ. ಹೆಚ್ಚಿನ ಸಂದರ್ಭಗಳಲ್ಲಿ.
ಆದರೆ ಕಾರ್ಯದ ಸ್ಥಗಿತ ಬಿಂದುಗಳನ್ನು ಹುಡುಕುವ ಮತ್ತು ಅವುಗಳ ಪ್ರಕಾರವನ್ನು ನಿರ್ಧರಿಸುವ ಅಭ್ಯಾಸದಲ್ಲಿ, ಬಲ ಮತ್ತು ಎಡ ಮಿತಿಗಳು ಸಮಾನವಾಗಿರದಿದ್ದಾಗ ಎರಡು ವಿಶಿಷ್ಟ ಪ್ರಕರಣಗಳಿವೆ:
- ಒಂದು ಕಾರ್ಯವು x ಸೇರಿರುವ ಸಂಖ್ಯೆಯ ರೇಖೆಯ ಭಾಗವನ್ನು ಅವಲಂಬಿಸಿ ಎರಡು ಅಥವಾ ಹೆಚ್ಚಿನ ಅಭಿವ್ಯಕ್ತಿಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ (ಈ ಅಭಿವ್ಯಕ್ತಿಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಕರ್ಲಿ ಬ್ರಾಕೆಟ್‌ಗಳಲ್ಲಿ ಬರೆಯಲಾಗುತ್ತದೆ f(X)= );
- X ಪ್ರವೃತ್ತಿಯನ್ನು ಬದಲಿಸುವ ಪರಿಣಾಮವಾಗಿ, ನಾವು ಛೇದದಲ್ಲಿ ಒಂದು ಭಾಗವನ್ನು ಪಡೆಯುತ್ತೇವೆ, ಅದರ ಜೊತೆಗೆ ಶೂನ್ಯ (+0) ಅಥವಾ ಮೈನಸ್ ಶೂನ್ಯ (-0) ಆಗಿರುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ ಅಂತಹ ಭಿನ್ನರಾಶಿ ಎಂದರೆ ಪ್ಲಸ್ ಅನಂತ ಅಥವಾ ಮೈನಸ್ ಅನಂತ, ಮತ್ತು ಇವುಗಳು ಸಂಪೂರ್ಣವಾಗಿ ವಿಭಿನ್ನ ವಿಷಯಗಳು.
ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತದ ಬಿಂದುಗಳು
ಮೊದಲ ವಿಧದ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್: ಒಂದು ಕಾರ್ಯವು ಸೀಮಿತ (ಅಂದರೆ, ಅನಂತಕ್ಕೆ ಸಮಾನವಾಗಿಲ್ಲ) ಎಡ ಮಿತಿ ಮತ್ತು ಸೀಮಿತ ಬಲ ಮಿತಿ ಎರಡನ್ನೂ ಹೊಂದಿದೆ, ಆದರೆ ಕಾರ್ಯವನ್ನು ಒಂದು ಹಂತದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ ಅಥವಾ ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳು ವಿಭಿನ್ನವಾಗಿವೆ (ಸಮಾನವಾಗಿಲ್ಲ).
ಮೊದಲ ರೀತಿಯ ತೆಗೆಯಬಹುದಾದ ಸ್ಥಗಿತದ ಪಾಯಿಂಟ್.ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳು ಸಮಾನವಾಗಿರುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ಮತ್ತಷ್ಟು ವ್ಯಾಖ್ಯಾನಿಸಲು ಸಾಧ್ಯವಿದೆ. ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲು, ಸರಳವಾಗಿ ಹೇಳುವುದಾದರೆ, ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳು ಪರಸ್ಪರ ಸಮಾನವಾಗಿ ಕಂಡುಬರುವ ಬಿಂದುಗಳ ನಡುವೆ ಬಿಂದುಗಳ ಸಂಪರ್ಕವನ್ನು ಒದಗಿಸುವುದು ಎಂದರ್ಥ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಸಂಪರ್ಕವು ಕಾರ್ಯದ ಮೌಲ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕಾದ ಒಂದು ಬಿಂದುವನ್ನು ಮಾತ್ರ ಪ್ರತಿನಿಧಿಸಬೇಕು.
ಉದಾಹರಣೆ 1.ಕ್ರಿಯೆಯ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ ಮತ್ತು ಬ್ರೇಕ್ ಪಾಯಿಂಟ್‌ನ ಪ್ರಕಾರವನ್ನು (ಪಾತ್ರ) ನಿರ್ಧರಿಸಿ.
ಎರಡನೇ ವಿಧದ ಅಸಂಯಮ ಬಿಂದುಗಳು
ಎರಡನೇ ವಿಧದ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್: ಕನಿಷ್ಠ ಒಂದು ಮಿತಿ (ಎಡ ಅಥವಾ ಬಲ) ಅನಂತವಾಗಿರುವ ಬಿಂದು (ಅನಂತಕ್ಕೆ ಸಮ).
ಉದಾಹರಣೆ 3.
ಪರಿಹಾರ. ನಲ್ಲಿ ಶಕ್ತಿಯ ಅಭಿವ್ಯಕ್ತಿಯಿಂದ ಇಕಾರ್ಯವನ್ನು ಹಂತದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ. ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:
ಮಿತಿಗಳಲ್ಲಿ ಒಂದು ಅನಂತತೆಗೆ ಸಮನಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ಬಿಂದುವು ಎರಡನೇ ವಿಧದ ಸ್ಥಗಿತದ ಬಿಂದುವಾಗಿದೆ. ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ ಹೊಂದಿರುವ ಫಂಕ್ಷನ್‌ನ ಗ್ರಾಫ್ ಉದಾಹರಣೆಯ ಕೆಳಗೆ ಇದೆ.
ಕ್ರಿಯೆಯ ಬ್ರೇಕ್‌ಪಾಯಿಂಟ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಸ್ವತಂತ್ರ ಕಾರ್ಯ ಅಥವಾ ಭಾಗವಾಗಿರಬಹುದು ಪೂರ್ಣ ಕಾರ್ಯ ಸಂಶೋಧನೆ ಮತ್ತು ಗ್ರಾಫಿಂಗ್ .
ಉದಾಹರಣೆ 4.ಫಂಕ್ಷನ್‌ನ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ ಮತ್ತು ಫಂಕ್ಷನ್‌ಗಾಗಿ ಬ್ರೇಕ್ ಪಾಯಿಂಟ್‌ನ ಪ್ರಕಾರವನ್ನು (ಪಾತ್ರ) ನಿರ್ಧರಿಸಿ
ಪರಿಹಾರ. 2 ನಲ್ಲಿನ ಶಕ್ತಿಯ ಅಭಿವ್ಯಕ್ತಿಯಿಂದ ಕಾರ್ಯವನ್ನು ಹಂತದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ. ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಎಡ ಮತ್ತು ಬಲ ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.
ತೆಗೆಯಬಹುದಾದ ಅಂತರ.
ವ್ಯಾಖ್ಯಾನ. ಡಾಟ್ ಎಫಂಕ್ಷನ್‌ನ ತೆಗೆಯಬಹುದಾದ ಸ್ಥಗಿತ ಬಿಂದು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ y=f(x), ಕಾರ್ಯದ ಮಿತಿಯಾಗಿದ್ದರೆ f(x)ಈ ಹಂತದಲ್ಲಿ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ, ಆದರೆ ಹಂತದಲ್ಲಿ ಎಕಾರ್ಯ f(x)ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ ಅಥವಾ ಖಾಸಗಿ ಅರ್ಥವನ್ನು ಹೊಂದಿದೆ f(a), ಮಿತಿಯಿಂದ ಭಿನ್ನವಾಗಿದೆ f(x)ಈ ಸಮಯದಲ್ಲಿ.
ಉದಾಹರಣೆ. ಉದಾಹರಣೆಗೆ, ಕಾರ್ಯ
ಹಂತದಲ್ಲಿ ಹೊಂದಿದೆ x=0ಸರಿಪಡಿಸಬಹುದಾದ ಅಂತರ. ವಾಸ್ತವವಾಗಿ, ಹಂತದಲ್ಲಿ ಈ ಕಾರ್ಯದ ಸೀಮಿತಗೊಳಿಸುವ ಮೌಲ್ಯ x=0 1 ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಭಾಗಶಃ ಮೌಲ್ಯವು 2 ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಕಾರ್ಯ ವೇಳೆ f(x)ಹಂತದಲ್ಲಿ ಹೊಂದಿದೆ ಎತೆಗೆಯಬಹುದಾದ ಅಂತರ, ನಂತರ ಬೇರೆ ಬಿಂದುಗಳಲ್ಲಿ ಕಾರ್ಯದ ಮೌಲ್ಯಗಳನ್ನು ಬದಲಾಯಿಸದೆ ಈ ಅಂತರವನ್ನು ತೆಗೆದುಹಾಕಬಹುದು ಎ. ಇದನ್ನು ಮಾಡಲು, ಕಾರ್ಯದ ಮೌಲ್ಯವನ್ನು ಹಂತದಲ್ಲಿ ಹಾಕಲು ಸಾಕು ಎಈ ಹಂತದಲ್ಲಿ ಅದರ ಮಿತಿ ಮೌಲ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ, ಮೇಲೆ ಪರಿಗಣಿಸಲಾದ ಉದಾಹರಣೆಯಲ್ಲಿ ಅದನ್ನು ಹಾಕಲು ಸಾಕು f(0)=1ತದನಂತರ 
, ಅಂದರೆ ಕಾರ್ಯ f(x)ಬಿಂದುವಿನಲ್ಲಿ ನಿರಂತರವಾಗುತ್ತದೆ x=0.
ಮೊದಲ ರೀತಿಯ ಅಡ್ಡಿ.
ವ್ಯಾಖ್ಯಾನ. ಡಾಟ್ ಎಈ ಹಂತದಲ್ಲಿ ಫಂಕ್ಷನ್ ಆಗಿದ್ದರೆ ಮೊದಲ ರೀತಿಯ ಡಿಸ್ಕಂಟಿನ್ಯೂಟಿ ಪಾಯಿಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ f(x)ಸೀಮಿತ ಆದರೆ ಅಸಮಾನ ಬಲ ಮತ್ತು ಎಡ ಮಿತಿಗಳನ್ನು ಹೊಂದಿದೆ
ಕೆಲವು ಉದಾಹರಣೆಗಳನ್ನು ನೀಡೋಣ.
ಉದಾಹರಣೆ. ಕಾರ್ಯ y=sgn xಹಂತದಲ್ಲಿ ಹೊಂದಿದೆ x=0ಮೊದಲ ರೀತಿಯ ಛಿದ್ರ. ವಾಸ್ತವವಾಗಿ, ಮತ್ತು ಆದ್ದರಿಂದ ಈ ಮಿತಿಗಳು ಪರಸ್ಪರ ಸಮಾನವಾಗಿರುವುದಿಲ್ಲ.
ಉದಾಹರಣೆ. ಕಾರ್ಯ 
, ಪಾಯಿಂಟ್ ಹೊರತುಪಡಿಸಿ ಎಲ್ಲೆಡೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ x=1, ಹಂತದಲ್ಲಿ ಹೊಂದಿದೆ x=1ಮೊದಲ ರೀತಿಯ ಛಿದ್ರ. ವಾಸ್ತವವಾಗಿ, .
ಎರಡನೇ ರೀತಿಯ ಅಡ್ಡಿ.
ವ್ಯಾಖ್ಯಾನ. ಡಾಟ್ ಎಈ ಹಂತದಲ್ಲಿ ಫಂಕ್ಷನ್ ಆಗಿದ್ದರೆ ಎರಡನೇ ರೀತಿಯ ಡಿಸ್ಕಂಟಿನ್ಯೂಟಿ ಪಾಯಿಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ f(x)ಕನಿಷ್ಠ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳಲ್ಲಿ ಒಂದನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ ಅಥವಾ ಕನಿಷ್ಠ ಒಂದು ಕಡೆಯ ಮಿತಿಗಳು ಅನಂತವಾಗಿದ್ದರೆ.
ಉದಾಹರಣೆ. ಕಾರ್ಯ f(x)=tan x, ನಿಸ್ಸಂಶಯವಾಗಿ, ಪ್ರತಿ ಹಂತದಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿದೆ x k =π/2+π k, k=0, ± 1, ± 2,..., ಏಕೆಂದರೆ ಅಂತಹ ಪ್ರತಿಯೊಂದು ಹಂತದಲ್ಲಿ
ಉದಾಹರಣೆ. ಕಾರ್ಯವು ಹಂತದಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿದೆ x=0, ಏಕೆಂದರೆ ಈ ಹಂತದಲ್ಲಿ ಅದು ಬಲ ಅಥವಾ ಎಡ ಮಿತಿಗಳನ್ನು ಹೊಂದಿಲ್ಲ.
ಒಂದು ವಿಭಾಗದಲ್ಲಿ ಕಾರ್ಯದ ಮುಂದುವರಿಕೆ
ವ್ಯಾಖ್ಯಾನ. ಕಾರ್ಯವನ್ನು ಮಧ್ಯಂತರದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಮತ್ತು ಅದರ ಪ್ರತಿಯೊಂದು ಬಿಂದುಗಳಲ್ಲಿ ನಿರಂತರವನ್ನು ಈ ವಿಭಾಗದಲ್ಲಿ ನಿರಂತರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಇದಲ್ಲದೆ, ಹಂತದಲ್ಲಿ ನಿರಂತರತೆಯ ಅಡಿಯಲ್ಲಿ ಎಬಲಭಾಗದಲ್ಲಿ ನಿರಂತರತೆ ಮತ್ತು ಒಂದು ಹಂತದಲ್ಲಿ ನಿರಂತರತೆ ಎಂದು ಅರ್ಥೈಸಲಾಗುತ್ತದೆ ಬಿ- ಎಡಭಾಗದಲ್ಲಿ ನಿರಂತರತೆ.
ಕಾರ್ಯ ಎಂದು ಹೇಳುತ್ತೇವೆ y=f(x), ಸೆಟ್ನಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ (X)ಅದರ ಮೇಲೆ ಅದರ ಮೇಲಿನ (ಕೆಳಗಿನ) ಅಂಚನ್ನು ತಲುಪುತ್ತದೆ 
, ಅಂತಹ ಒಂದು ಬಿಂದು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ x 0 ∈(x), ಏನು f(x 0)=β (f(x 0)=α).
[ವೀರ್‌ಸ್ಟ್ರಾಸ್] ಪ್ರಮೇಯ. ಒಂದು ಮಧ್ಯಂತರದಲ್ಲಿ ನಿರಂತರವಾದ ಪ್ರತಿಯೊಂದು ಕಾರ್ಯವು ಬಂಧಿತವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅದರ ಮೇಲಿನ ಮಿತಿಯನ್ನು ಮತ್ತು ಅದರ ಮೇಲಿನ ಬೌಂಡ್ ಅನ್ನು ತಲುಪುತ್ತದೆ.
ಪ್ರಮೇಯ [ಬೊಲ್ಜಾನೊ-ಕೌಚಿ]. ಕಾರ್ಯ ವೇಳೆ y=f(x)ವಿಭಾಗದಲ್ಲಿ ನಿರಂತರ ಮತ್ತು f(a)=A, f(b)=B, ನಂತರ ಯಾವುದೇ ಸಿ, ನಡುವೆ ತೀರ್ಮಾನಿಸಲಾಗಿದೆ ಎಮತ್ತು ಬಿ, ಅಂತಹ ಒಂದು ಅಂಶವಿದೆ ξ∈ , ಏನು f(ξ)=C.
ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಯಾವುದೇ ಎರಡು ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಮಧ್ಯಂತರದಲ್ಲಿ ನಿರಂತರವಾದ ಕಾರ್ಯವು ಅವುಗಳ ನಡುವೆ ಇರುವ ಯಾವುದೇ ಮೌಲ್ಯವನ್ನು ಸಹ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ.
ಪರಿಣಾಮ. ಒಂದು ವಿಭಾಗದಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿದ್ದರೆ ಮತ್ತು ಅದರ ತುದಿಗಳಲ್ಲಿ ವಿಭಿನ್ನ ಚಿಹ್ನೆಗಳ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಂಡರೆ, ಈ ವಿಭಾಗದಲ್ಲಿ ಕನಿಷ್ಠ ಒಂದು ಬಿಂದುವಿದೆ, ಇದರಲ್ಲಿ ಕಾರ್ಯವು ಕಣ್ಮರೆಯಾಗುತ್ತದೆ.
ಪರಿಣಾಮ. ಕಾರ್ಯ ಮಾಡಲಿ y=f(x)ವಿಭಾಗದಲ್ಲಿ ನಿರಂತರ
ಮತ್ತು 
, 
. ನಂತರ ಕಾರ್ಯ f(x)ವಿಭಾಗದಿಂದ ಎಲ್ಲಾ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ
ಮತ್ತು ಈ ಮೌಲ್ಯಗಳು ಮಾತ್ರ.
ಹೀಗಾಗಿ, ನಿರ್ದಿಷ್ಟ ವಿಭಾಗದಲ್ಲಿ ನೀಡಲಾದ ಮತ್ತು ನಿರಂತರವಾದ ಕಾರ್ಯದ ಎಲ್ಲಾ ಮೌಲ್ಯಗಳ ಸೆಟ್ ಕೂಡ ಒಂದು ವಿಭಾಗವಾಗಿದೆ.
ಕಾರ್ಯದ ನಿರಂತರತೆ. ಬ್ರೇಕಿಂಗ್ ಪಾಯಿಂಟ್ಗಳು.
ಅವನು ಹೋಗುವಾಗ ಬುಲ್ ನಡೆಯುತ್ತಾನೆ, ತೂಗಾಡುತ್ತಾನೆ, ನಿಟ್ಟುಸಿರು ಬಿಡುತ್ತಾನೆ:
- ಓಹ್, ಬೋರ್ಡ್ ಖಾಲಿಯಾಗುತ್ತಿದೆ, ಈಗ ನಾನು ಬೀಳಲಿದ್ದೇನೆ!
ಈ ಪಾಠದಲ್ಲಿ ನಾವು ಕಾರ್ಯದ ನಿರಂತರತೆಯ ಪರಿಕಲ್ಪನೆ, ಸ್ಥಗಿತ ಬಿಂದುಗಳ ವರ್ಗೀಕರಣ ಮತ್ತು ಸಾಮಾನ್ಯ ಪ್ರಾಯೋಗಿಕ ಸಮಸ್ಯೆಯನ್ನು ಪರಿಶೀಲಿಸುತ್ತೇವೆ ಕಾರ್ಯಗಳ ನಿರಂತರತೆಯ ಅಧ್ಯಯನಗಳು. ವಿಷಯದ ಹೆಸರಿನಿಂದಲೇ, ಅನೇಕರು ಅಂತರ್ಬೋಧೆಯಿಂದ ಏನನ್ನು ಚರ್ಚಿಸಲಾಗುವುದು ಎಂದು ಊಹಿಸುತ್ತಾರೆ ಮತ್ತು ವಸ್ತುವು ತುಂಬಾ ಸರಳವಾಗಿದೆ ಎಂದು ಭಾವಿಸುತ್ತಾರೆ. ಇದು ಸತ್ಯ. ಆದರೆ ಇದು ಸರಳವಾದ ಕಾರ್ಯಗಳು ನಿರ್ಲಕ್ಷ್ಯಕ್ಕಾಗಿ ಹೆಚ್ಚಾಗಿ ಶಿಕ್ಷಿಸಲ್ಪಡುತ್ತವೆ ಮತ್ತು ಅವುಗಳನ್ನು ಪರಿಹರಿಸುವ ಬಾಹ್ಯ ವಿಧಾನವಾಗಿದೆ. ಆದ್ದರಿಂದ, ನೀವು ಲೇಖನವನ್ನು ಬಹಳ ಎಚ್ಚರಿಕೆಯಿಂದ ಅಧ್ಯಯನ ಮಾಡಲು ಮತ್ತು ಎಲ್ಲಾ ಸೂಕ್ಷ್ಮತೆಗಳನ್ನು ಮತ್ತು ತಂತ್ರಗಳನ್ನು ಹಿಡಿಯಲು ನಾನು ಶಿಫಾರಸು ಮಾಡುತ್ತೇವೆ.
ನೀವು ಏನು ತಿಳಿದುಕೊಳ್ಳಬೇಕು ಮತ್ತು ಮಾಡಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ?ತುಂಬಾ ಅಲ್ಲ. ಪಾಠವನ್ನು ಚೆನ್ನಾಗಿ ಕಲಿಯಲು, ಅದು ಏನೆಂದು ನೀವು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಬೇಕು ಕಾರ್ಯದ ಮಿತಿ. ಜೊತೆ ಓದುಗರು ಕಡಿಮೆ ಮಟ್ಟದಲೇಖನವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ತಯಾರಿ ಸಾಕು ಕಾರ್ಯ ಮಿತಿಗಳು. ಪರಿಹಾರಗಳ ಉದಾಹರಣೆಗಳುಮತ್ತು ನೋಡಲು ಜ್ಯಾಮಿತೀಯ ಅರ್ಥಕೈಪಿಡಿಯಲ್ಲಿ ಮಿತಿ ಪ್ರಾಥಮಿಕ ಕಾರ್ಯಗಳ ಗ್ರಾಫ್‌ಗಳು ಮತ್ತು ಗುಣಲಕ್ಷಣಗಳು. ನೀವೇ ಪರಿಚಿತರಾಗಲು ಸಹ ಸಲಹೆ ನೀಡಲಾಗುತ್ತದೆ ಗ್ರಾಫ್ಗಳ ಜ್ಯಾಮಿತೀಯ ರೂಪಾಂತರಗಳು, ಹೆಚ್ಚಿನ ಸಂದರ್ಭಗಳಲ್ಲಿ ಅಭ್ಯಾಸವು ರೇಖಾಚಿತ್ರವನ್ನು ನಿರ್ಮಿಸುವುದನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ. ಭವಿಷ್ಯವು ಎಲ್ಲರಿಗೂ ಆಶಾವಾದಿಯಾಗಿದೆ, ಮತ್ತು ಪೂರ್ಣ ಕೆಟಲ್ ಸಹ ಮುಂದಿನ ಗಂಟೆ ಅಥವಾ ಎರಡು ಗಂಟೆಗಳಲ್ಲಿ ತನ್ನದೇ ಆದ ಕೆಲಸವನ್ನು ನಿಭಾಯಿಸಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ!
ಕಾರ್ಯದ ನಿರಂತರತೆ. ಬ್ರೇಕ್‌ಪಾಯಿಂಟ್‌ಗಳು ಮತ್ತು ಅವುಗಳ ವರ್ಗೀಕರಣ
ಕಾರ್ಯದ ನಿರಂತರತೆಯ ಪರಿಕಲ್ಪನೆ
ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ ನಿರಂತರವಾಗಿರುವ ಕೆಲವು ಕಾರ್ಯಗಳನ್ನು ಪರಿಗಣಿಸೋಣ: 
ಅಥವಾ, ಇದನ್ನು ಹೆಚ್ಚು ಸಂಕ್ಷಿಪ್ತವಾಗಿ ಹೇಳುವುದಾದರೆ, ನಮ್ಮ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ (ನೈಜ ಸಂಖ್ಯೆಗಳ ಸೆಟ್).
ನಿರಂತರತೆಯ "ಫಿಲಿಸ್ಟಿನ್" ಮಾನದಂಡ ಯಾವುದು? ನಿಸ್ಸಂಶಯವಾಗಿ ವೇಳಾಪಟ್ಟಿ ನಿರಂತರ ಕಾರ್ಯಕಾಗದದಿಂದ ಪೆನ್ಸಿಲ್ ಅನ್ನು ಎತ್ತದೆಯೇ ಎಳೆಯಬಹುದು.
ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಎರಡು ಸರಳ ಪರಿಕಲ್ಪನೆಗಳನ್ನು ಸ್ಪಷ್ಟವಾಗಿ ಪ್ರತ್ಯೇಕಿಸಬೇಕು: ಕಾರ್ಯದ ಡೊಮೇನ್ಮತ್ತು ಕಾರ್ಯದ ನಿರಂತರತೆ. IN ಸಾಮಾನ್ಯ ಪ್ರಕರಣ ಇದು ಒಂದೇ ಅಲ್ಲ. ಉದಾಹರಣೆಗೆ: 
ಈ ಕಾರ್ಯವನ್ನು ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ, ಅಂದರೆ ಎಲ್ಲರೂ"x" ನ ಅರ್ಥವು "y" ಗೆ ತನ್ನದೇ ಆದ ಅರ್ಥವನ್ನು ಹೊಂದಿದೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ, ವೇಳೆ , ನಂತರ . ಇನ್ನೊಂದು ಅಂಶವು ವಿರಾಮಚಿಹ್ನೆಯನ್ನು ಹೊಂದಿದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ, ಏಕೆಂದರೆ ಕಾರ್ಯದ ವ್ಯಾಖ್ಯಾನದಿಂದ, ವಾದದ ಮೌಲ್ಯವು ಇದಕ್ಕೆ ಅನುಗುಣವಾಗಿರಬೇಕು ಒಂದೇ ವಿಷಯಕಾರ್ಯ ಮೌಲ್ಯ. ಹೀಗಾಗಿ, ಡೊಮೇನ್ನಮ್ಮ ಕಾರ್ಯ: .
ಆದಾಗ್ಯೂ ಈ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುವುದಿಲ್ಲ!ಆ ಸಮಯದಲ್ಲಿ ಅವಳು ಬಳಲುತ್ತಿದ್ದಾಳೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ ಅಂತರ. ಪದವು ಸಾಕಷ್ಟು ಗ್ರಹಿಸಬಹುದಾದ ಮತ್ತು ದೃಷ್ಟಿಗೋಚರವಾಗಿದೆ; ವಾಸ್ತವವಾಗಿ, ಇಲ್ಲಿ ಪೆನ್ಸಿಲ್ ಅನ್ನು ಹೇಗಾದರೂ ಕಾಗದದಿಂದ ಹರಿದು ಹಾಕಬೇಕಾಗುತ್ತದೆ. ಸ್ವಲ್ಪ ಸಮಯದ ನಂತರ ನಾವು ಬ್ರೇಕ್ಪಾಯಿಂಟ್ಗಳ ವರ್ಗೀಕರಣವನ್ನು ನೋಡುತ್ತೇವೆ.
ಒಂದು ಹಂತದಲ್ಲಿ ಮತ್ತು ಮಧ್ಯಂತರದಲ್ಲಿ ಕಾರ್ಯದ ಮುಂದುವರಿಕೆ
ನಿರ್ದಿಷ್ಟ ಗಣಿತದ ಸಮಸ್ಯೆಯಲ್ಲಿ, ನಾವು ಒಂದು ಹಂತದಲ್ಲಿ ಕ್ರಿಯೆಯ ನಿರಂತರತೆ, ಮಧ್ಯಂತರದಲ್ಲಿ ಕ್ರಿಯೆಯ ನಿರಂತರತೆ, ಅರ್ಧ-ಮಧ್ಯಂತರ, ಅಥವಾ ಒಂದು ವಿಭಾಗದಲ್ಲಿ ಕಾರ್ಯದ ನಿರಂತರತೆಯ ಬಗ್ಗೆ ಮಾತನಾಡಬಹುದು. ಅದು, "ಕೇವಲ ನಿರಂತರತೆ" ಇಲ್ಲ- ಕಾರ್ಯವು ಎಲ್ಲೋ ನಿರಂತರವಾಗಿರಬಹುದು. ಮತ್ತು ಎಲ್ಲದರ ಮೂಲಭೂತ "ಬಿಲ್ಡಿಂಗ್ ಬ್ಲಾಕ್" ಆಗಿದೆ ಕಾರ್ಯದ ನಿರಂತರತೆ ಹಂತದಲ್ಲಿ .
ಸಿದ್ಧಾಂತ ಗಣಿತದ ವಿಶ್ಲೇಷಣೆ"ಡೆಲ್ಟಾ" ಮತ್ತು "ಎಪ್ಸಿಲಾನ್" ನೆರೆಹೊರೆಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಒಂದು ಹಂತದಲ್ಲಿ ಒಂದು ಕಾರ್ಯದ ನಿರಂತರತೆಯ ವ್ಯಾಖ್ಯಾನವನ್ನು ನೀಡುತ್ತದೆ, ಆದರೆ ಪ್ರಾಯೋಗಿಕವಾಗಿ ಮತ್ತೊಂದು ವ್ಯಾಖ್ಯಾನವು ಬಳಕೆಯಲ್ಲಿದೆ, ಅದನ್ನು ನಾವು ಹೆಚ್ಚು ಗಮನ ಹರಿಸುತ್ತೇವೆ.
ಮೊದಲು ನೆನಪಿಸಿಕೊಳ್ಳೋಣ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳುಮೊದಲ ಪಾಠದಲ್ಲಿ ನಮ್ಮ ಜೀವನದಲ್ಲಿ ಸಿಡಿದವನು ಕಾರ್ಯ ಗ್ರಾಫ್ಗಳ ಬಗ್ಗೆ. ದೈನಂದಿನ ಪರಿಸ್ಥಿತಿಯನ್ನು ಪರಿಗಣಿಸಿ: 
ನಾವು ಬಿಂದುವಿಗೆ ಅಕ್ಷವನ್ನು ಸಮೀಪಿಸಿದರೆ ಬಿಟ್ಟರು(ಕೆಂಪು ಬಾಣ), ನಂತರ "ಆಟಗಳ" ಅನುಗುಣವಾದ ಮೌಲ್ಯಗಳು ಅಕ್ಷದ ಉದ್ದಕ್ಕೂ ಬಿಂದುವಿಗೆ (ಕಡುಗೆಂಪು ಬಾಣ) ಹೋಗುತ್ತದೆ. ಗಣಿತದ ಪ್ರಕಾರ, ಈ ಸತ್ಯವನ್ನು ಬಳಸಿಕೊಂಡು ಸರಿಪಡಿಸಲಾಗಿದೆ ಎಡಗೈ ಮಿತಿ:
ಪ್ರವೇಶಕ್ಕೆ ಗಮನ ಕೊಡಿ ("ಎಡಭಾಗದಲ್ಲಿ x ಒಲವು ಕಾಗೆ" ಎಂದು ಓದುತ್ತದೆ). "ಸಂಯೋಜಕ" "ಮೈನಸ್ ಶೂನ್ಯ" ಸಂಕೇತಿಸುತ್ತದೆ , ಮೂಲಭೂತವಾಗಿ ಇದರರ್ಥ ನಾವು ಎಡಭಾಗದಿಂದ ಸಂಖ್ಯೆಯನ್ನು ಸಮೀಪಿಸುತ್ತಿದ್ದೇವೆ.
ಅಂತೆಯೇ, ನೀವು "ಕಾ" ಬಿಂದುವನ್ನು ಸಮೀಪಿಸಿದರೆ ಬಲಭಾಗದಲ್ಲಿ(ನೀಲಿ ಬಾಣ), ನಂತರ "ಆಟಗಳು" ಅದೇ ಮೌಲ್ಯಕ್ಕೆ ಬರುತ್ತವೆ, ಆದರೆ ಹಸಿರು ಬಾಣದ ಉದ್ದಕ್ಕೂ, ಮತ್ತು ಬಲಗೈ ಮಿತಿಈ ಕೆಳಗಿನಂತೆ ಫಾರ್ಮ್ಯಾಟ್ ಮಾಡಲಾಗುವುದು:
"ಸಂಯೋಜಕ" ಸಂಕೇತಿಸುತ್ತದೆ , ಮತ್ತು ನಮೂದು ಹೀಗಿದೆ: "x ಬಲಭಾಗದಲ್ಲಿ ka ಗೆ ಒಲವು ತೋರುತ್ತದೆ."
ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಸೀಮಿತ ಮತ್ತು ಸಮಾನವಾಗಿದ್ದರೆ(ನಮ್ಮ ಸಂದರ್ಭದಲ್ಲಿ ಇದ್ದಂತೆ): 
, ನಂತರ ನಾವು ಸಾಮಾನ್ಯ ಮಿತಿ ಇದೆ ಎಂದು ಹೇಳುತ್ತೇವೆ. ಇದು ಸರಳವಾಗಿದೆ, ಸಾಮಾನ್ಯ ಮಿತಿ ನಮ್ಮ "ಸಾಮಾನ್ಯ" ಕಾರ್ಯದ ಮಿತಿ, ಸೀಮಿತ ಸಂಖ್ಯೆಗೆ ಸಮನಾಗಿರುತ್ತದೆ.
(ಪಂಕ್ಚರ್) ನಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸದಿದ್ದರೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ ಕಪ್ಪು ಚುಕ್ಕೆಗ್ರಾಫ್ ಶಾಖೆಯಲ್ಲಿ), ನಂತರ ಮೇಲಿನ ಲೆಕ್ಕಾಚಾರಗಳು ಮಾನ್ಯವಾಗಿರುತ್ತವೆ. ಈಗಾಗಲೇ ಹಲವಾರು ಬಾರಿ ಗಮನಿಸಿದಂತೆ, ನಿರ್ದಿಷ್ಟವಾಗಿ ಲೇಖನದಲ್ಲಿ ಅನಂತವಾದ ಕಾರ್ಯಗಳ ಮೇಲೆ, ಅಭಿವ್ಯಕ್ತಿಗಳ ಅರ್ಥ "x" ಅನಂತ ಹತ್ತಿರಬಿಂದುವನ್ನು ಸಮೀಪಿಸುತ್ತದೆ, ಆದರೆ ಪರವಾಗಿಲ್ಲ, ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ಸ್ವತಃ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆಯೇ ಅಥವಾ ಇಲ್ಲವೇ. ಉತ್ತಮ ಉದಾಹರಣೆಕಾರ್ಯವನ್ನು ವಿಶ್ಲೇಷಿಸಿದಾಗ ಮುಂದಿನ ಪ್ಯಾರಾಗ್ರಾಫ್‌ನಲ್ಲಿ ಕಾಣಿಸುತ್ತದೆ.
ವ್ಯಾಖ್ಯಾನ: ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮಿತಿಯು ಆ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮೌಲ್ಯಕ್ಕೆ ಸಮನಾಗಿದ್ದರೆ ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ: .
ವ್ಯಾಖ್ಯಾನವನ್ನು ವಿವರಿಸಲಾಗಿದೆ ಕೆಳಗಿನ ಷರತ್ತುಗಳು:
1) ಕಾರ್ಯವನ್ನು ಹಂತದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಬೇಕು, ಅಂದರೆ ಮೌಲ್ಯವು ಅಸ್ತಿತ್ವದಲ್ಲಿರಬೇಕು.
2) ಕಾರ್ಯದ ಸಾಮಾನ್ಯ ಮಿತಿ ಇರಬೇಕು. ಮೇಲೆ ಗಮನಿಸಿದಂತೆ, ಇದು ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳ ಅಸ್ತಿತ್ವ ಮತ್ತು ಸಮಾನತೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ: 
.
3) ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮಿತಿಯು ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮೌಲ್ಯಕ್ಕೆ ಸಮನಾಗಿರಬೇಕು: .
ಉಲ್ಲಂಘಿಸಿದರೆ ಕನಿಷ್ಠ ಒಂದುಮೂರು ಷರತ್ತುಗಳಲ್ಲಿ, ನಂತರ ಕಾರ್ಯವು ಬಿಂದುವಿನಲ್ಲಿ ನಿರಂತರತೆಯ ಆಸ್ತಿಯನ್ನು ಕಳೆದುಕೊಳ್ಳುತ್ತದೆ.
ಮಧ್ಯಂತರದಲ್ಲಿ ಕಾರ್ಯದ ಮುಂದುವರಿಕೆಚತುರವಾಗಿ ಮತ್ತು ಸರಳವಾಗಿ ರೂಪಿಸಲಾಗಿದೆ: ನಿರ್ದಿಷ್ಟ ಮಧ್ಯಂತರದ ಪ್ರತಿಯೊಂದು ಹಂತದಲ್ಲಿಯೂ ನಿರಂತರವಾಗಿದ್ದರೆ, ಮಧ್ಯಂತರದಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ.
ನಿರ್ದಿಷ್ಟವಾಗಿ, ಅನೇಕ ಕಾರ್ಯಗಳು ಅನಂತ ಮಧ್ಯಂತರದಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತವೆ, ಅಂದರೆ, ನೈಜ ಸಂಖ್ಯೆಗಳ ಸೆಟ್ನಲ್ಲಿ. ಇದು ರೇಖೀಯ ಕಾರ್ಯ, ಬಹುಪದಗಳು, ಘಾತೀಯ, ಸೈನ್, ಕೊಸೈನ್, ಇತ್ಯಾದಿ. ಮತ್ತು ಸಾಮಾನ್ಯವಾಗಿ, ಯಾವುದೇ ಪ್ರಾಥಮಿಕ ಕಾರ್ಯಅದರ ಮೇಲೆ ನಿರಂತರ ವ್ಯಾಖ್ಯಾನದ ಡೊಮೇನ್, ಉದಾಹರಣೆಗೆ, ಲಾಗರಿಥಮಿಕ್ ಕಾರ್ಯವು ಮಧ್ಯಂತರದಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ. ನಾನು ಭಾವಿಸುತ್ತೇವೆ ಈ ಕ್ಷಣದಲ್ಲಿಮುಖ್ಯ ಕಾರ್ಯಗಳ ಗ್ರಾಫ್‌ಗಳು ಹೇಗೆ ಕಾಣುತ್ತವೆ ಎಂಬುದರ ಕುರಿತು ನಿಮಗೆ ಒಳ್ಳೆಯ ಕಲ್ಪನೆ ಇದೆ. ಇನ್ನಷ್ಟು ವಿವರವಾದ ಮಾಹಿತಿಅವುಗಳ ನಿರಂತರತೆಯನ್ನು ಪಡೆದುಕೊಳ್ಳಬಹುದು ಕರುಣಾಮಯಿ Fichtengolts ಎಂಬ ಉಪನಾಮದಿಂದ.
ಒಂದು ವಿಭಾಗ ಮತ್ತು ಅರ್ಧ-ಮಧ್ಯಂತರಗಳ ಮೇಲೆ ಕಾರ್ಯದ ನಿರಂತರತೆಯೊಂದಿಗೆ, ಎಲ್ಲವೂ ಸಹ ಕಷ್ಟಕರವಲ್ಲ, ಆದರೆ ತರಗತಿಯಲ್ಲಿ ಈ ಬಗ್ಗೆ ಮಾತನಾಡುವುದು ಹೆಚ್ಚು ಸೂಕ್ತವಾಗಿದೆ ಒಂದು ವಿಭಾಗದಲ್ಲಿ ಕಾರ್ಯದ ಕನಿಷ್ಠ ಮತ್ತು ಗರಿಷ್ಠ ಮೌಲ್ಯಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವ ಬಗ್ಗೆ, ಆದರೆ ಈಗ ಅದರ ಬಗ್ಗೆ ಚಿಂತಿಸಬೇಡಿ.
ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳ ವರ್ಗೀಕರಣ
ಕಾರ್ಯಗಳ ಆಕರ್ಷಕ ಜೀವನವು ಎಲ್ಲಾ ರೀತಿಯ ವಿಶೇಷ ಅಂಶಗಳಲ್ಲಿ ಸಮೃದ್ಧವಾಗಿದೆ ಮತ್ತು ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳು ಅವರ ಜೀವನಚರಿತ್ರೆಯ ಪುಟಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ.
ಸೂಚನೆ : ಒಂದು ವೇಳೆ, ನಾನು ಪ್ರಾಥಮಿಕ ಹಂತದಲ್ಲಿ ವಾಸಿಸುತ್ತೇನೆ: ಬ್ರೇಕಿಂಗ್ ಪಾಯಿಂಟ್ ಯಾವಾಗಲೂ ಒಂದೇ ಪಾಯಿಂಟ್- "ಸತತವಾಗಿ ಹಲವಾರು ಬ್ರೇಕ್ ಪಾಯಿಂಟ್ಗಳು" ಇಲ್ಲ, ಅಂದರೆ, "ಬ್ರೇಕ್ ಇಂಟರ್ವಲ್" ನಂತಹ ಯಾವುದೇ ವಿಷಯಗಳಿಲ್ಲ.
ಈ ಅಂಕಗಳನ್ನು ಪ್ರತಿಯಾಗಿ ಎರಡು ವಿಂಗಡಿಸಲಾಗಿದೆ ದೊಡ್ಡ ಗುಂಪುಗಳು: ಮೊದಲ ರೀತಿಯ ಬಿರುಕುಗಳುಮತ್ತು ಎರಡನೇ ರೀತಿಯ ಬಿರುಕುಗಳು. ಪ್ರತಿಯೊಂದು ರೀತಿಯ ಅಂತರವು ತನ್ನದೇ ಆದ ಹೊಂದಿದೆ ಗುಣಲಕ್ಷಣಗಳುನಾವು ಇದೀಗ ನೋಡೋಣ:
ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತದ ಬಿಂದು
ಒಂದು ಹಂತದಲ್ಲಿ ನಿರಂತರತೆಯ ಸ್ಥಿತಿಯನ್ನು ಉಲ್ಲಂಘಿಸಿದರೆ ಮತ್ತು ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಸೀಮಿತ , ನಂತರ ಅದನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತದ ಬಿಂದು.
ಅತ್ಯಂತ ಆಶಾವಾದಿ ಪ್ರಕರಣದೊಂದಿಗೆ ಪ್ರಾರಂಭಿಸೋಣ. ಪಾಠದ ಮೂಲ ಕಲ್ಪನೆಯ ಪ್ರಕಾರ, ನಾನು "ಇನ್" ಸಿದ್ಧಾಂತವನ್ನು ಹೇಳಲು ಬಯಸುತ್ತೇನೆ ಸಾಮಾನ್ಯ ನೋಟ”, ಆದರೆ ವಸ್ತುವಿನ ವಾಸ್ತವತೆಯನ್ನು ಪ್ರದರ್ಶಿಸುವ ಸಲುವಾಗಿ, ನಾನು ನಿರ್ದಿಷ್ಟ ಅಕ್ಷರಗಳೊಂದಿಗೆ ಆಯ್ಕೆಯನ್ನು ನಿರ್ಧರಿಸಿದೆ.
ಇದು ದುಃಖಕರವಾಗಿದೆ, ಎಟರ್ನಲ್ ಜ್ವಾಲೆಯ ಹಿನ್ನೆಲೆಯಲ್ಲಿ ನವವಿವಾಹಿತರ ಫೋಟೋದಂತೆ, ಆದರೆ ಕೆಳಗಿನ ಶಾಟ್ ಅನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಸ್ವೀಕರಿಸಲಾಗುತ್ತದೆ. ರೇಖಾಚಿತ್ರದಲ್ಲಿ ಕಾರ್ಯದ ಗ್ರಾಫ್ ಅನ್ನು ನಾವು ಚಿತ್ರಿಸೋಣ: 
ಈ ಕಾರ್ಯವು ಬಿಂದುವನ್ನು ಹೊರತುಪಡಿಸಿ ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ. ಮತ್ತು ವಾಸ್ತವವಾಗಿ, ಛೇದವು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುವುದಿಲ್ಲ. ಆದಾಗ್ಯೂ, ಮಿತಿಯ ಅರ್ಥಕ್ಕೆ ಅನುಗುಣವಾಗಿ, ನಾವು ಮಾಡಬಹುದು ಅನಂತ ಹತ್ತಿರಎಡ ಮತ್ತು ಬಲದಿಂದ "ಶೂನ್ಯ" ಅನುಸಂಧಾನ, ಅಂದರೆ, ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ ಮತ್ತು, ನಿಸ್ಸಂಶಯವಾಗಿ, ಹೊಂದಿಕೆಯಾಗುತ್ತವೆ: 
(ನಿರಂತರತೆಯ ಷರತ್ತು ಸಂಖ್ಯೆ 2 ತೃಪ್ತಿಗೊಂಡಿದೆ).
ಆದರೆ ಕಾರ್ಯವನ್ನು ಹಂತದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ, ಆದ್ದರಿಂದ, ನಿರಂತರತೆಯ ಷರತ್ತು ಸಂಖ್ಯೆ 1 ಅನ್ನು ಉಲ್ಲಂಘಿಸಲಾಗಿದೆ ಮತ್ತು ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ಸ್ಥಗಿತಗೊಳ್ಳುತ್ತದೆ.
ಈ ಪ್ರಕಾರದ ವಿರಾಮ (ಅಸ್ತಿತ್ವದಲ್ಲಿರುವವುಗಳೊಂದಿಗೆ ಸಾಮಾನ್ಯ ಮಿತಿ) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಸರಿಪಡಿಸಬಹುದಾದ ಅಂತರ. ಏಕೆ ತೆಗೆಯಬಹುದಾದ? ಏಕೆಂದರೆ ಕಾರ್ಯವು ಮಾಡಬಹುದು ಮರುವ್ಯಾಖ್ಯಾನಿಸಿಒಡೆಯುವ ಹಂತದಲ್ಲಿ: 
ಇದು ವಿಚಿತ್ರವಾಗಿ ಕಾಣುತ್ತಿದೆಯೇ? ಇರಬಹುದು. ಆದರೆ ಅಂತಹ ಕಾರ್ಯ ಸಂಕೇತವು ಯಾವುದನ್ನೂ ವಿರೋಧಿಸುವುದಿಲ್ಲ! ಈಗ ಅಂತರವನ್ನು ಮುಚ್ಚಲಾಗಿದೆ ಮತ್ತು ಎಲ್ಲರೂ ಸಂತೋಷವಾಗಿದ್ದಾರೆ: 
ಔಪಚಾರಿಕ ಪರಿಶೀಲನೆಯನ್ನು ಮಾಡೋಣ:
2) 
- ಸಾಮಾನ್ಯ ಮಿತಿ ಇದೆ;
3)
ಹೀಗಾಗಿ, ಎಲ್ಲಾ ಮೂರು ಷರತ್ತುಗಳನ್ನು ಪೂರೈಸಲಾಗುತ್ತದೆ ಮತ್ತು ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ನಿರಂತರತೆಯ ವ್ಯಾಖ್ಯಾನದಿಂದ ಕಾರ್ಯವು ಒಂದು ಹಂತದಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ.
ಆದಾಗ್ಯೂ, ಮಾತನ್ ದ್ವೇಷಿಗಳು ಕಾರ್ಯವನ್ನು ಕೆಟ್ಟ ರೀತಿಯಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು, ಉದಾಹರಣೆಗೆ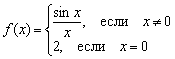 
:
ಮೊದಲ ಎರಡು ನಿರಂತರತೆಯ ಷರತ್ತುಗಳನ್ನು ಇಲ್ಲಿ ತೃಪ್ತಿಪಡಿಸಲಾಗಿದೆ ಎಂಬುದು ಕುತೂಹಲಕಾರಿಯಾಗಿದೆ:
1) - ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ;
2) 
- ಸಾಮಾನ್ಯ ಮಿತಿ ಇದೆ.
ಆದರೆ ಮೂರನೇ ಗಡಿಯನ್ನು ರವಾನಿಸಲಾಗಿಲ್ಲ: , ಅಂದರೆ, ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮಿತಿ ಸಮಾನವಾಗಿಲ್ಲನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ನೀಡಿದ ಕಾರ್ಯದ ಮೌಲ್ಯ.
ಹೀಗಾಗಿ, ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ಸ್ಥಗಿತಗೊಳ್ಳುತ್ತದೆ.
ಎರಡನೆಯದು, ದುಃಖಕರವಾದ ಪ್ರಕರಣವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಮೊದಲ ರೀತಿಯ ಛಿದ್ರ ಒಂದು ಜಿಗಿತದೊಂದಿಗೆ. ಮತ್ತು ದುಃಖವು ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳಿಂದ ಉಂಟಾಗುತ್ತದೆ ಸೀಮಿತ ಮತ್ತು ವಿಭಿನ್ನ. ಪಾಠದ ಎರಡನೇ ರೇಖಾಚಿತ್ರದಲ್ಲಿ ಉದಾಹರಣೆಯನ್ನು ತೋರಿಸಲಾಗಿದೆ. ಅಂತಹ ಅಂತರವು ಸಾಮಾನ್ಯವಾಗಿ ಸಂಭವಿಸುತ್ತದೆ ಭಾಗವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ಕಾರ್ಯಗಳು, ಇದನ್ನು ಈಗಾಗಲೇ ಲೇಖನದಲ್ಲಿ ಉಲ್ಲೇಖಿಸಲಾಗಿದೆ ಗ್ರಾಫ್ ರೂಪಾಂತರಗಳ ಬಗ್ಗೆ.
ತುಣುಕು ಕಾರ್ಯವನ್ನು ಪರಿಗಣಿಸಿ 
ಮತ್ತು ನಾವು ಅದರ ರೇಖಾಚಿತ್ರವನ್ನು ಪೂರ್ಣಗೊಳಿಸುತ್ತೇವೆ. ಗ್ರಾಫ್ ಅನ್ನು ಹೇಗೆ ನಿರ್ಮಿಸುವುದು? ತುಂಬಾ ಸರಳ. ಅರ್ಧ ಮಧ್ಯಂತರದಲ್ಲಿ ನಾವು ಪ್ಯಾರಾಬೋಲಾದ ತುಣುಕನ್ನು ಸೆಳೆಯುತ್ತೇವೆ ( ಹಸಿರು ಬಣ್ಣ), ಮಧ್ಯಂತರದಲ್ಲಿ - ನೇರ ರೇಖೆಯ ವಿಭಾಗ (ಕೆಂಪು) ಮತ್ತು ಅರ್ಧ ಮಧ್ಯಂತರದಲ್ಲಿ - ನೇರ ರೇಖೆ ( ನೀಲಿ ಬಣ್ಣ).
ಇದಲ್ಲದೆ, ಅಸಮಾನತೆಯಿಂದಾಗಿ, ಮೌಲ್ಯವನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ಚತುರ್ಭುಜ ಕಾರ್ಯ(ಹಸಿರು ಚುಕ್ಕೆ), ಮತ್ತು ಅಸಮಾನತೆಯ ಕಾರಣದಿಂದಾಗಿ, ಮೌಲ್ಯವನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ರೇಖೀಯ ಕಾರ್ಯ(ನೀಲಿ ಚುಕ್ಕೆ): 
ಅತ್ಯಂತ ಕಷ್ಟಕರವಾದ ಸಂದರ್ಭದಲ್ಲಿ, ನೀವು ಗ್ರಾಫ್ನ ಪ್ರತಿಯೊಂದು ತುಣುಕಿನ ಪಾಯಿಂಟ್-ಬೈ-ಪಾಯಿಂಟ್ ನಿರ್ಮಾಣವನ್ನು ಆಶ್ರಯಿಸಬೇಕು (ಮೊದಲನೆಯದನ್ನು ನೋಡಿ ಕಾರ್ಯಗಳ ಗ್ರಾಫ್ಗಳ ಬಗ್ಗೆ ಪಾಠ).
ಈಗ ನಾವು ವಿಷಯದಲ್ಲಿ ಮಾತ್ರ ಆಸಕ್ತಿ ವಹಿಸುತ್ತೇವೆ. ನಿರಂತರತೆಗಾಗಿ ಅದನ್ನು ಪರಿಶೀಲಿಸೋಣ:
2) ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ.
ಎಡಭಾಗದಲ್ಲಿ ನಾವು ಕೆಂಪು ರೇಖೆಯ ವಿಭಾಗವನ್ನು ಹೊಂದಿದ್ದೇವೆ, ಆದ್ದರಿಂದ ಎಡ-ಬದಿಯ ಮಿತಿ: 
ಬಲಭಾಗದಲ್ಲಿ ನೀಲಿ ನೇರ ರೇಖೆ, ಮತ್ತು ಬಲಗೈ ಮಿತಿ: 
ಪರಿಣಾಮವಾಗಿ, ನಾವು ಸ್ವೀಕರಿಸಿದ್ದೇವೆ ಸೀಮಿತ ಸಂಖ್ಯೆಗಳು, ಮತ್ತು ಅವರು ಸಮಾನವಾಗಿಲ್ಲ. ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳಿಂದ ಸೀಮಿತ ಮತ್ತು ವಿಭಿನ್ನ: 
, ನಂತರ ನಮ್ಮ ಕಾರ್ಯವನ್ನು ಸಹಿಸಿಕೊಳ್ಳುತ್ತದೆ ಜಂಪ್ನೊಂದಿಗೆ ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತಗೊಳಿಸುವಿಕೆ.
ಅಂತರವನ್ನು ತೊಡೆದುಹಾಕಲು ಸಾಧ್ಯವಿಲ್ಲ ಎಂಬುದು ತಾರ್ಕಿಕವಾಗಿದೆ - ಹಿಂದಿನ ಉದಾಹರಣೆಯಂತೆ ಕಾರ್ಯವನ್ನು ನಿಜವಾಗಿಯೂ ಮತ್ತಷ್ಟು ವ್ಯಾಖ್ಯಾನಿಸಲು ಮತ್ತು "ಒಟ್ಟಿಗೆ ಅಂಟಿಸಲು" ಸಾಧ್ಯವಿಲ್ಲ.
ಎರಡನೇ ವಿಧದ ಅಸಂಯಮ ಬಿಂದುಗಳು
ಸಾಮಾನ್ಯವಾಗಿ, ಛಿದ್ರತೆಯ ಎಲ್ಲಾ ಇತರ ಪ್ರಕರಣಗಳನ್ನು ಜಾಣತನದಿಂದ ಈ ವರ್ಗಕ್ಕೆ ವರ್ಗೀಕರಿಸಲಾಗಿದೆ. ನಾನು ಎಲ್ಲವನ್ನೂ ಪಟ್ಟಿ ಮಾಡುವುದಿಲ್ಲ, ಏಕೆಂದರೆ ಪ್ರಾಯೋಗಿಕವಾಗಿ, 99% ಸಮಸ್ಯೆಗಳಲ್ಲಿ ನೀವು ಎದುರಿಸುತ್ತೀರಿ ಅಂತ್ಯವಿಲ್ಲದ ಅಂತರ- ಎಡಗೈ ಅಥವಾ ಬಲಗೈ, ಮತ್ತು ಹೆಚ್ಚಾಗಿ, ಎರಡೂ ಮಿತಿಗಳು ಅನಂತವಾಗಿರುತ್ತವೆ.
ಮತ್ತು, ಸಹಜವಾಗಿ, ಅತ್ಯಂತ ಸ್ಪಷ್ಟವಾದ ಚಿತ್ರವೆಂದರೆ ಶೂನ್ಯದಲ್ಲಿ ಹೈಪರ್ಬೋಲಾ. ಇಲ್ಲಿ ಎರಡೂ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಅನಂತವಾಗಿವೆ: 
, ಆದ್ದರಿಂದ, ಕಾರ್ಯವು ಹಂತದಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುತ್ತದೆ.
ನನ್ನ ಲೇಖನಗಳನ್ನು ಸಾಧ್ಯವಾದಷ್ಟು ವೈವಿಧ್ಯಮಯ ವಿಷಯದೊಂದಿಗೆ ತುಂಬಲು ನಾನು ಪ್ರಯತ್ನಿಸುತ್ತೇನೆ, ಆದ್ದರಿಂದ ಇನ್ನೂ ಎದುರಿಸದ ಕಾರ್ಯದ ಗ್ರಾಫ್ ಅನ್ನು ನೋಡೋಣ: 
ಪ್ರಮಾಣಿತ ಯೋಜನೆಯ ಪ್ರಕಾರ:
1) ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ ಏಕೆಂದರೆ ಛೇದವು ಶೂನ್ಯಕ್ಕೆ ಹೋಗುತ್ತದೆ.
ಸಹಜವಾಗಿ, ಕಾರ್ಯವು ಒಂದು ಹಂತದಲ್ಲಿ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುತ್ತದೆ ಎಂದು ನಾವು ತಕ್ಷಣ ತೀರ್ಮಾನಿಸಬಹುದು , ಆದರೆ ಸ್ಥಗಿತದ ಸ್ವರೂಪವನ್ನು ವರ್ಗೀಕರಿಸುವುದು ಒಳ್ಳೆಯದು, ಇದು ಆಗಾಗ್ಗೆ ಸ್ಥಿತಿಯಿಂದ ಅಗತ್ಯವಾಗಿರುತ್ತದೆ. ಇದಕ್ಕಾಗಿ:
ರೆಕಾರ್ಡಿಂಗ್ ಮೂಲಕ ನಾವು ಅರ್ಥಮಾಡಿಕೊಂಡಿದ್ದೇವೆ ಎಂದು ನಾನು ನಿಮಗೆ ನೆನಪಿಸುತ್ತೇನೆ ಅಪರಿಮಿತ ನಕಾರಾತ್ಮಕ ಸಂಖ್ಯೆ
, ಮತ್ತು ಪ್ರವೇಶದ ಅಡಿಯಲ್ಲಿ - ಅಪರಿಮಿತ ಧನಾತ್ಮಕ ಸಂಖ್ಯೆ.
ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಅನಂತವಾಗಿವೆ, ಅಂದರೆ ಕಾರ್ಯವು ಹಂತದಲ್ಲಿ 2 ನೇ ರೀತಿಯ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುತ್ತದೆ. y-ಆಕ್ಸಿಸ್ ಆಗಿದೆ ಲಂಬವಾದ ಲಕ್ಷಣಗ್ರಾಫ್ಗಾಗಿ.
ಎರಡೂ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿರಲು ಅಸಾಮಾನ್ಯವೇನಲ್ಲ, ಆದರೆ ಅವುಗಳಲ್ಲಿ ಒಂದು ಮಾತ್ರ ಅನಂತವಾಗಿರುತ್ತದೆ, ಉದಾಹರಣೆಗೆ: 
ಇದು ಕಾರ್ಯದ ಗ್ರಾಫ್ ಆಗಿದೆ.
ನಾವು ನಿರಂತರತೆಯ ಬಿಂದುವನ್ನು ಪರಿಶೀಲಿಸುತ್ತೇವೆ:
1) ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ.
2) ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ: 
ಉಪನ್ಯಾಸದ ಕೊನೆಯ ಎರಡು ಉದಾಹರಣೆಗಳಲ್ಲಿ ಅಂತಹ ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ವಿಧಾನದ ಬಗ್ಗೆ ನಾವು ಮಾತನಾಡುತ್ತೇವೆ, ಆದಾಗ್ಯೂ ಅನೇಕ ಓದುಗರು ಈಗಾಗಲೇ ಎಲ್ಲವನ್ನೂ ನೋಡಿದ್ದಾರೆ ಮತ್ತು ಊಹಿಸಿದ್ದಾರೆ.
ಎಡಗೈ ಮಿತಿಯು ಸೀಮಿತವಾಗಿದೆ ಮತ್ತು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ (ನಾವು "ಬಿಂದುವಿಗೆ ಹೋಗುವುದಿಲ್ಲ"), ಆದರೆ ಬಲಗೈ ಮಿತಿಯು ಅನಂತವಾಗಿದೆ ಮತ್ತು ಗ್ರಾಫ್ನ ಕಿತ್ತಳೆ ಶಾಖೆಯು ಅದರ ಸಮೀಪಕ್ಕೆ ಅನಂತವಾಗಿ ಸಮೀಪಿಸುತ್ತದೆ ಲಂಬವಾದ ಲಕ್ಷಣ, ಸಮೀಕರಣದಿಂದ ನೀಡಲಾಗಿದೆ (ಕಪ್ಪು ಚುಕ್ಕೆಗಳ ರೇಖೆ).
ಆದ್ದರಿಂದ ಕಾರ್ಯವು ನರಳುತ್ತದೆ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತಹಂತದಲ್ಲಿ.
1 ನೇ ವಿಧದ ಸ್ಥಗಿತಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ, ಕಾರ್ಯವನ್ನು ಸ್ಥಗಿತದ ಹಂತದಲ್ಲಿಯೇ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ, ಒಂದು ತುಣುಕು ಕಾರ್ಯಕ್ಕಾಗಿ 
ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲದಲ್ಲಿ ಕಪ್ಪು ದಪ್ಪ ಚುಕ್ಕೆ ಹಾಕಲು ಹಿಂಜರಿಯಬೇಡಿ. ಬಲಭಾಗದಲ್ಲಿ ಹೈಪರ್ಬೋಲಾದ ಶಾಖೆಯಿದೆ, ಮತ್ತು ಬಲಗೈ ಮಿತಿಯು ಅನಂತವಾಗಿದೆ. ಈ ಗ್ರಾಫ್ ಹೇಗಿರುತ್ತದೆ ಎಂಬ ಕಲ್ಪನೆ ಬಹುತೇಕ ಎಲ್ಲರಿಗೂ ಇದೆ ಎಂದು ನಾನು ಭಾವಿಸುತ್ತೇನೆ.
ಎಲ್ಲರೂ ಏನನ್ನು ಎದುರು ನೋಡುತ್ತಿದ್ದರು:
ನಿರಂತರತೆಗಾಗಿ ಕಾರ್ಯವನ್ನು ಹೇಗೆ ಪರಿಶೀಲಿಸುವುದು?
ಒಂದು ಹಂತದಲ್ಲಿ ನಿರಂತರತೆಗಾಗಿ ಕಾರ್ಯದ ಅಧ್ಯಯನವನ್ನು ಈಗಾಗಲೇ ಸ್ಥಾಪಿಸಲಾದ ವಾಡಿಕೆಯ ಯೋಜನೆಯ ಪ್ರಕಾರ ನಡೆಸಲಾಗುತ್ತದೆ, ಇದು ನಿರಂತರತೆಯ ಮೂರು ಷರತ್ತುಗಳನ್ನು ಪರಿಶೀಲಿಸುತ್ತದೆ:
ಉದಾಹರಣೆ 1
ಕಾರ್ಯವನ್ನು ಅನ್ವೇಷಿಸಿ 
ಪರಿಹಾರ:
1) ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸದಿರುವ ಏಕೈಕ ಅಂಶವೆಂದರೆ ವ್ಯಾಪ್ತಿಯೊಳಗೆ.
2) ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ: 
ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಸೀಮಿತ ಮತ್ತು ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಹೀಗಾಗಿ, ಈ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ತೆಗೆದುಹಾಕಬಹುದಾದ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುತ್ತದೆ.
ಈ ಕಾರ್ಯದ ಗ್ರಾಫ್ ಹೇಗೆ ಕಾಣುತ್ತದೆ?
ನಾನು ಸರಳೀಕರಿಸಲು ಬಯಸುತ್ತೇನೆ 
, ಮತ್ತು ಇದು ಸಾಮಾನ್ಯ ಪ್ಯಾರಾಬೋಲಾವನ್ನು ಪಡೆದಂತೆ ತೋರುತ್ತದೆ. ಆದರೆಮೂಲ ಕಾರ್ಯವನ್ನು ಹಂತದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ, ಆದ್ದರಿಂದ ಈ ಕೆಳಗಿನ ಷರತ್ತು ಅಗತ್ಯವಿದೆ:
ರೇಖಾಚಿತ್ರವನ್ನು ಮಾಡೋಣ: 
ಉತ್ತರ: ಕಾರ್ಯವು ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ, ಅದು ತೆಗೆದುಹಾಕಬಹುದಾದ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುವ ಬಿಂದುವನ್ನು ಹೊರತುಪಡಿಸಿ.
ಕಾರ್ಯವನ್ನು ಉತ್ತಮ ಅಥವಾ ಉತ್ತಮ ರೀತಿಯಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು, ಆದರೆ ಸ್ಥಿತಿಯ ಪ್ರಕಾರ ಇದು ಅಗತ್ಯವಿಲ್ಲ.
ಇದು ದೂರದ ಉದಾಹರಣೆ ಎಂದು ನೀವು ಹೇಳುತ್ತೀರಾ? ಇಲ್ಲವೇ ಇಲ್ಲ. ಇದು ಆಚರಣೆಯಲ್ಲಿ ಹತ್ತಾರು ಬಾರಿ ಸಂಭವಿಸಿದೆ. ಸೈಟ್ನ ಬಹುತೇಕ ಎಲ್ಲಾ ಕಾರ್ಯಗಳು ನಿಜವಾದ ಸ್ವತಂತ್ರ ಕೆಲಸ ಮತ್ತು ಪರೀಕ್ಷೆಗಳಿಂದ ಬರುತ್ತವೆ.
ನಮ್ಮ ನೆಚ್ಚಿನ ಮಾಡ್ಯೂಲ್‌ಗಳನ್ನು ತೊಡೆದುಹಾಕೋಣ:
ಉದಾಹರಣೆ 2
ಕಾರ್ಯವನ್ನು ಅನ್ವೇಷಿಸಿ 
ನಿರಂತರತೆಗಾಗಿ. ಕಾರ್ಯ ಸ್ಥಗಿತಗೊಳಿಸುವಿಕೆಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ ಅವುಗಳ ಸ್ವರೂಪವನ್ನು ನಿರ್ಧರಿಸಿ. ರೇಖಾಚಿತ್ರವನ್ನು ಕಾರ್ಯಗತಗೊಳಿಸಿ.
ಪರಿಹಾರ: ಕೆಲವು ಕಾರಣಗಳಿಗಾಗಿ, ವಿದ್ಯಾರ್ಥಿಗಳು ಭಯಪಡುತ್ತಾರೆ ಮತ್ತು ಮಾಡ್ಯೂಲ್ನೊಂದಿಗೆ ಕಾರ್ಯಗಳನ್ನು ಇಷ್ಟಪಡುವುದಿಲ್ಲ, ಆದಾಗ್ಯೂ ಅವರ ಬಗ್ಗೆ ಏನೂ ಸಂಕೀರ್ಣವಾಗಿಲ್ಲ. ನಾವು ಈಗಾಗಲೇ ಪಾಠದಲ್ಲಿ ಅಂತಹ ವಿಷಯಗಳನ್ನು ಸ್ವಲ್ಪ ಸ್ಪರ್ಶಿಸಿದ್ದೇವೆ. ಗ್ರಾಫ್ಗಳ ಜ್ಯಾಮಿತೀಯ ರೂಪಾಂತರಗಳು. ಮಾಡ್ಯೂಲ್ ಋಣಾತ್ಮಕವಲ್ಲದ ಕಾರಣ, ಅದನ್ನು ಈ ಕೆಳಗಿನಂತೆ ವಿಸ್ತರಿಸಲಾಗಿದೆ: 
, ಅಲ್ಲಿ "ಆಲ್ಫಾ" ಕೆಲವು ಅಭಿವ್ಯಕ್ತಿಯಾಗಿದೆ. IN ಈ ವಿಷಯದಲ್ಲಿ, ಮತ್ತು ನಮ್ಮ ಕಾರ್ಯವನ್ನು ತುಂಡುಗಳಾಗಿ ಬರೆಯಬೇಕು: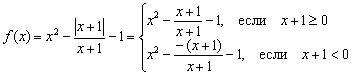 
ಆದರೆ ಎರಡೂ ತುಣುಕುಗಳ ಭಿನ್ನರಾಶಿಗಳನ್ನು ಕಡಿಮೆ ಮಾಡಬೇಕು. ಹಿಂದಿನ ಉದಾಹರಣೆಯಲ್ಲಿರುವಂತೆ ಕಡಿತವು ಪರಿಣಾಮಗಳಿಲ್ಲದೆ ನಡೆಯುವುದಿಲ್ಲ. ಛೇದವು ಶೂನ್ಯಕ್ಕೆ ಹೋಗುವುದರಿಂದ ಮೂಲ ಕಾರ್ಯವನ್ನು ಬಿಂದುವಿನಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ. ಆದ್ದರಿಂದ, ಸಿಸ್ಟಮ್ ಹೆಚ್ಚುವರಿಯಾಗಿ ಸ್ಥಿತಿಯನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಬೇಕು ಮತ್ತು ಮೊದಲ ಅಸಮಾನತೆಯನ್ನು ಕಟ್ಟುನಿಟ್ಟಾಗಿ ಮಾಡಬೇಕು: 
ಈಗ ಬಹಳ ಬಗ್ಗೆ ಉಪಯುಕ್ತ ಸ್ವಾಗತಪರಿಹಾರಗಳು: ಡ್ರಾಫ್ಟ್‌ನಲ್ಲಿ ಕಾರ್ಯವನ್ನು ಅಂತಿಮಗೊಳಿಸುವ ಮೊದಲು, ರೇಖಾಚಿತ್ರವನ್ನು ಮಾಡುವುದು ಅನುಕೂಲಕರವಾಗಿದೆ (ಅದು ಷರತ್ತುಗಳಿಂದ ಅಗತ್ಯವಿದೆಯೇ ಅಥವಾ ಇಲ್ಲವೇ ಎಂಬುದನ್ನು ಲೆಕ್ಕಿಸದೆ). ಇದು ಮೊದಲನೆಯದಾಗಿ, ನಿರಂತರತೆಯ ಬಿಂದುಗಳು ಮತ್ತು ಸ್ಥಗಿತದ ಬಿಂದುಗಳನ್ನು ತಕ್ಷಣವೇ ನೋಡಲು ಸಹಾಯ ಮಾಡುತ್ತದೆ ಮತ್ತು ಎರಡನೆಯದಾಗಿ, ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವಾಗ ಇದು 100% ದೋಷಗಳಿಂದ ನಿಮ್ಮನ್ನು ರಕ್ಷಿಸುತ್ತದೆ.
ಡ್ರಾಯಿಂಗ್ ಮಾಡೋಣ. ನಮ್ಮ ಲೆಕ್ಕಾಚಾರಗಳಿಗೆ ಅನುಗುಣವಾಗಿ, ಪಾಯಿಂಟ್‌ನ ಎಡಕ್ಕೆ ಪ್ಯಾರಾಬೋಲಾದ (ನೀಲಿ ಬಣ್ಣ) ತುಣುಕನ್ನು ಸೆಳೆಯುವುದು ಅವಶ್ಯಕ, ಮತ್ತು ಬಲಕ್ಕೆ - ಪ್ಯಾರಾಬೋಲಾದ ತುಂಡು (ಕೆಂಪು ಬಣ್ಣ), ಆದರೆ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ ಸ್ವತಃ ಸೂಚಿಸಿ: 
ಸಂದೇಹವಿದ್ದರೆ, ಕೆಲವು x ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಂಡು ಅವುಗಳನ್ನು ಕಾರ್ಯಕ್ಕೆ ಪ್ಲಗ್ ಮಾಡಿ 
(ಮಾಡ್ಯೂಲ್ ಸಂಭವನೀಯ ಮೈನಸ್ ಚಿಹ್ನೆಯನ್ನು ನಾಶಪಡಿಸುತ್ತದೆ ಎಂದು ನೆನಪಿಸಿಕೊಳ್ಳಿ) ಮತ್ತು ಗ್ರಾಫ್ ಅನ್ನು ಪರಿಶೀಲಿಸಿ.
ವಿಶ್ಲೇಷಣಾತ್ಮಕವಾಗಿ ನಿರಂತರತೆಯ ಕಾರ್ಯವನ್ನು ನಾವು ಪರಿಶೀಲಿಸೋಣ:
1) ಕಾರ್ಯವನ್ನು ಹಂತದಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ, ಆದ್ದರಿಂದ ನಾವು ಅದರಲ್ಲಿ ನಿರಂತರವಾಗಿಲ್ಲ ಎಂದು ತಕ್ಷಣವೇ ಹೇಳಬಹುದು.
2) ಸ್ಥಗಿತದ ಸ್ವರೂಪವನ್ನು ಸ್ಥಾಪಿಸೋಣ; ಇದನ್ನು ಮಾಡಲು, ನಾವು ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಲೆಕ್ಕ ಹಾಕುತ್ತೇವೆ: 
ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಸೀಮಿತವಾಗಿವೆ ಮತ್ತು ವಿಭಿನ್ನವಾಗಿವೆ, ಅಂದರೆ ಕಾರ್ಯವು 1 ನೇ ವಿಧದ ಸ್ಥಗಿತವನ್ನು ಹಂತದಲ್ಲಿ ಜಂಪ್ನೊಂದಿಗೆ ಅನುಭವಿಸುತ್ತದೆ. ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವಾಗ, ಬ್ರೇಕ್ ಪಾಯಿಂಟ್‌ನಲ್ಲಿನ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆಯೇ ಅಥವಾ ಇಲ್ಲವೇ ಎಂಬುದು ಅಪ್ರಸ್ತುತವಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಮತ್ತೊಮ್ಮೆ ಗಮನಿಸಿ.
ಈಗ ಉಳಿದಿರುವುದು ಡ್ರಾಫ್ಟ್‌ನಿಂದ ಡ್ರಾಯಿಂಗ್ ಅನ್ನು ವರ್ಗಾಯಿಸುವುದು (ಅದನ್ನು ಸಂಶೋಧನೆಯ ಸಹಾಯದಿಂದ ಮಾಡಲಾಗಿದೆ ;-)) ಮತ್ತು ಕಾರ್ಯವನ್ನು ಪೂರ್ಣಗೊಳಿಸಿ:
ಉತ್ತರ: ಜಂಪ್ನೊಂದಿಗೆ ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುವ ಹಂತವನ್ನು ಹೊರತುಪಡಿಸಿ ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ.
ಕೆಲವೊಮ್ಮೆ ಅವರಿಗೆ ಸ್ಥಗಿತದ ಜಂಪ್‌ನ ಹೆಚ್ಚುವರಿ ಸೂಚನೆಯ ಅಗತ್ಯವಿರುತ್ತದೆ. ಇದನ್ನು ಸರಳವಾಗಿ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ - ಬಲ ಮಿತಿಯಿಂದ ನೀವು ಎಡ ಮಿತಿಯನ್ನು ಕಳೆಯಬೇಕಾಗಿದೆ: , ಅಂದರೆ, ವಿರಾಮದ ಹಂತದಲ್ಲಿ ನಮ್ಮ ಕಾರ್ಯವು 2 ಘಟಕಗಳನ್ನು ಕೆಳಗೆ ಜಿಗಿದಿದೆ (ಮೈನಸ್ ಚಿಹ್ನೆಯು ನಮಗೆ ಹೇಳುವಂತೆ).
ಉದಾಹರಣೆ 3
ಕಾರ್ಯವನ್ನು ಅನ್ವೇಷಿಸಿ 
ನಿರಂತರತೆಗಾಗಿ. ಕಾರ್ಯ ಸ್ಥಗಿತಗೊಳಿಸುವಿಕೆಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ ಅವುಗಳ ಸ್ವರೂಪವನ್ನು ನಿರ್ಧರಿಸಿ. ಡ್ರಾಯಿಂಗ್ ಮಾಡಿ.
ನಿಮ್ಮದೇ ಆದ ಮೇಲೆ ಪರಿಹರಿಸಲು ಇದು ಒಂದು ಉದಾಹರಣೆಯಾಗಿದೆ, ಪಾಠದ ಕೊನೆಯಲ್ಲಿ ಮಾದರಿ ಪರಿಹಾರವಾಗಿದೆ.
ಕಾರ್ಯವು ಮೂರು ಭಾಗಗಳನ್ನು ಒಳಗೊಂಡಿರುವಾಗ ಕಾರ್ಯದ ಅತ್ಯಂತ ಜನಪ್ರಿಯ ಮತ್ತು ವ್ಯಾಪಕ ಆವೃತ್ತಿಗೆ ಹೋಗೋಣ:
ಉದಾಹರಣೆ 4
ನಿರಂತರತೆಗಾಗಿ ಕಾರ್ಯವನ್ನು ಪರೀಕ್ಷಿಸಿ ಮತ್ತು ಕಾರ್ಯದ ಗ್ರಾಫ್ ಅನ್ನು ರೂಪಿಸಿ 
.
ಪರಿಹಾರ: ಕಾರ್ಯದ ಎಲ್ಲಾ ಮೂರು ಭಾಗಗಳು ಅನುಗುಣವಾದ ಮಧ್ಯಂತರಗಳಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತವೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ, ಆದ್ದರಿಂದ ತುಣುಕುಗಳ ನಡುವೆ "ಜಂಕ್ಷನ್" ನ ಎರಡು ಬಿಂದುಗಳನ್ನು ಮಾತ್ರ ಪರಿಶೀಲಿಸಲು ಇದು ಉಳಿದಿದೆ. ಮೊದಲಿಗೆ, ಡ್ರಾಫ್ಟ್ ಡ್ರಾಯಿಂಗ್ ಮಾಡೋಣ; ಲೇಖನದ ಮೊದಲ ಭಾಗದಲ್ಲಿ ನಾನು ನಿರ್ಮಾಣ ತಂತ್ರದ ಬಗ್ಗೆ ಸಾಕಷ್ಟು ವಿವರವಾಗಿ ಕಾಮೆಂಟ್ ಮಾಡಿದ್ದೇನೆ. ಒಂದೇ ವಿಷಯವೆಂದರೆ ನಾವು ನಮ್ಮ ಏಕವಚನ ಬಿಂದುಗಳನ್ನು ಎಚ್ಚರಿಕೆಯಿಂದ ಅನುಸರಿಸಬೇಕು: ಅಸಮಾನತೆಯಿಂದಾಗಿ, ಮೌಲ್ಯವು ಸರಳ ರೇಖೆಗೆ (ಹಸಿರು ಚುಕ್ಕೆ) ಸೇರಿದೆ ಮತ್ತು ಅಸಮಾನತೆಯ ಕಾರಣದಿಂದಾಗಿ ಮೌಲ್ಯವು ಪ್ಯಾರಾಬೋಲಾ (ಕೆಂಪು ಚುಕ್ಕೆ) ಗೆ ಸೇರಿದೆ: 
ಸರಿ, ತಾತ್ವಿಕವಾಗಿ, ಎಲ್ಲವೂ ಸ್ಪಷ್ಟವಾಗಿದೆ =) ನಿರ್ಧಾರವನ್ನು ಔಪಚಾರಿಕಗೊಳಿಸುವುದು ಮಾತ್ರ ಉಳಿದಿದೆ. ಪ್ರತಿ ಎರಡು "ಸೇರುವ" ಬಿಂದುಗಳಿಗೆ, ನಾವು 3 ನಿರಂತರತೆಯ ಪರಿಸ್ಥಿತಿಗಳನ್ನು ಪ್ರಮಾಣಿತವಾಗಿ ಪರಿಶೀಲಿಸುತ್ತೇವೆ:
I)ನಾವು ನಿರಂತರತೆಯ ಬಿಂದುವನ್ನು ಪರಿಶೀಲಿಸುತ್ತೇವೆ
1) 
ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಸೀಮಿತವಾಗಿವೆ ಮತ್ತು ವಿಭಿನ್ನವಾಗಿವೆ, ಅಂದರೆ ಕಾರ್ಯವು 1 ನೇ ವಿಧದ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುತ್ತದೆ ಮತ್ತು ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಜಂಪ್ ಆಗುತ್ತದೆ.
ನಾವು ಸ್ಥಗಿತದ ಜಂಪ್ ಅನ್ನು ಬಲ ಮತ್ತು ಎಡ ಮಿತಿಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸವಾಗಿ ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ:
, ಅಂದರೆ, ಗ್ರಾಫ್ ಒಂದು ಘಟಕವನ್ನು ಎಳೆದಿದೆ.
II)ನಾವು ನಿರಂತರತೆಯ ಬಿಂದುವನ್ನು ಪರಿಶೀಲಿಸುತ್ತೇವೆ
1) 
- ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ.
2) ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಹುಡುಕಿ: 
- ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳು ಸೀಮಿತ ಮತ್ತು ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ ಸಾಮಾನ್ಯ ಮಿತಿ ಇದೆ.
3) 
- ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮಿತಿಯು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಈ ಕಾರ್ಯದ ಮೌಲ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಅಂತಿಮ ಹಂತದಲ್ಲಿ, ನಾವು ಡ್ರಾಯಿಂಗ್ ಅನ್ನು ಅಂತಿಮ ಆವೃತ್ತಿಗೆ ವರ್ಗಾಯಿಸುತ್ತೇವೆ, ಅದರ ನಂತರ ನಾವು ಅಂತಿಮ ಸ್ವರಮೇಳವನ್ನು ಹಾಕುತ್ತೇವೆ:
ಉತ್ತರ: ಕಾರ್ಯವು ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ, ಇದು ಜಂಪ್ನೊಂದಿಗೆ ಮೊದಲ ರೀತಿಯ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುವ ಹಂತವನ್ನು ಹೊರತುಪಡಿಸಿ.
ಉದಾಹರಣೆ 5
ನಿರಂತರತೆಗಾಗಿ ಕಾರ್ಯವನ್ನು ಪರೀಕ್ಷಿಸಿ ಮತ್ತು ಅದರ ಗ್ರಾಫ್ ಅನ್ನು ನಿರ್ಮಿಸಿ 
.
ನೀವೇ ಪರಿಹರಿಸಲು ಇದು ಒಂದು ಉದಾಹರಣೆಯಾಗಿದೆ, ಸಣ್ಣ ಪರಿಹಾರಮತ್ತು ಪಾಠದ ಕೊನೆಯಲ್ಲಿ ಕಾರ್ಯದ ಅಂದಾಜು ಮಾದರಿ.
ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರಬೇಕು ಮತ್ತು ಇನ್ನೊಂದರಲ್ಲಿ ಸ್ಥಗಿತಗೊಳ್ಳಬೇಕು ಎಂಬ ಅನಿಸಿಕೆ ನಿಮಗೆ ಬರಬಹುದು. ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಇದು ಯಾವಾಗಲೂ ಅಲ್ಲ. ಉಳಿದ ಉದಾಹರಣೆಗಳನ್ನು ನಿರ್ಲಕ್ಷಿಸದಿರಲು ಪ್ರಯತ್ನಿಸಿ - ಹಲವಾರು ಆಸಕ್ತಿದಾಯಕ ಮತ್ತು ಪ್ರಮುಖ ವೈಶಿಷ್ಟ್ಯಗಳಿವೆ:
ಉದಾಹರಣೆ 6
ಕಾರ್ಯವನ್ನು ನೀಡಲಾಗಿದೆ 
. ಬಿಂದುಗಳಲ್ಲಿ ನಿರಂತರತೆಗಾಗಿ ಕಾರ್ಯವನ್ನು ತನಿಖೆ ಮಾಡಿ. ಗ್ರಾಫ್ ಅನ್ನು ನಿರ್ಮಿಸಿ.
ಪರಿಹಾರ: ಮತ್ತು ಮತ್ತೆ ತಕ್ಷಣವೇ ಡ್ರಾಫ್ಟ್‌ನಲ್ಲಿ ಡ್ರಾಯಿಂಗ್ ಅನ್ನು ಕಾರ್ಯಗತಗೊಳಿಸಿ: 
ಈ ಗ್ರಾಫ್ನ ವಿಶಿಷ್ಟತೆಯೆಂದರೆ ಅಬ್ಸಿಸ್ಸಾ ಅಕ್ಷದ ಸಮೀಕರಣದಿಂದ ತುಂಡು ಕಾರ್ಯವನ್ನು ನೀಡಲಾಗುತ್ತದೆ. ಈ ಪ್ರದೇಶವನ್ನು ಇಲ್ಲಿ ಚಿತ್ರಿಸಲಾಗಿದೆ ಹಸಿರು, ಮತ್ತು ನೋಟ್ಬುಕ್ನಲ್ಲಿ ಇದನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಸರಳವಾದ ಪೆನ್ಸಿಲ್ನೊಂದಿಗೆ ದಪ್ಪದಲ್ಲಿ ಹೈಲೈಟ್ ಮಾಡಲಾಗುತ್ತದೆ. ಮತ್ತು, ಸಹಜವಾಗಿ, ನಮ್ಮ ರಾಮ್ಗಳ ಬಗ್ಗೆ ಮರೆಯಬೇಡಿ: ಮೌಲ್ಯವು ಸ್ಪರ್ಶಕ ಶಾಖೆಗೆ (ಕೆಂಪು ಚುಕ್ಕೆ) ಸೇರಿದೆ, ಮತ್ತು ಮೌಲ್ಯವು ನೇರ ರೇಖೆಗೆ ಸೇರಿದೆ.
ರೇಖಾಚಿತ್ರದಿಂದ ಎಲ್ಲವೂ ಸ್ಪಷ್ಟವಾಗಿದೆ - ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ರೇಖೆಯ ಉದ್ದಕ್ಕೂ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ, ಪರಿಹಾರವನ್ನು ಔಪಚಾರಿಕಗೊಳಿಸುವುದು ಮಾತ್ರ ಉಳಿದಿದೆ, ಇದನ್ನು 3-4 ರೀತಿಯ ಉದಾಹರಣೆಗಳ ನಂತರ ಅಕ್ಷರಶಃ ಪೂರ್ಣ ಯಾಂತ್ರೀಕೃತಗೊಳಿಸುವಿಕೆಗೆ ತರಲಾಗುತ್ತದೆ:
I)ನಾವು ನಿರಂತರತೆಯ ಬಿಂದುವನ್ನು ಪರಿಶೀಲಿಸುತ್ತೇವೆ
1) - ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ.
2) ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ: 
, ಅಂದರೆ ಸಾಮಾನ್ಯ ಮಿತಿ ಇದೆ.
ಒಂದು ವೇಳೆ, ನಾನು ನಿಮಗೆ ಒಂದು ಕ್ಷುಲ್ಲಕ ಸಂಗತಿಯನ್ನು ನೆನಪಿಸುತ್ತೇನೆ: ಸ್ಥಿರದ ಮಿತಿಯು ಸ್ಥಿರತೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಶೂನ್ಯದ ಮಿತಿಯು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ (ಎಡಗೈ ಮಿತಿ).
3) 
- ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮಿತಿಯು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಈ ಕಾರ್ಯದ ಮೌಲ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಹೀಗಾಗಿ, ಒಂದು ಹಂತದಲ್ಲಿ ಕ್ರಿಯೆಯ ನಿರಂತರತೆಯ ವ್ಯಾಖ್ಯಾನದಿಂದ ಒಂದು ಹಂತದಲ್ಲಿ ಒಂದು ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ.
II)ನಾವು ನಿರಂತರತೆಯ ಬಿಂದುವನ್ನು ಪರಿಶೀಲಿಸುತ್ತೇವೆ
1) - ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ.
2) ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಹುಡುಕಿ: 
ಮತ್ತು ಇಲ್ಲಿ - ಒಂದರ ಮಿತಿಯು ಘಟಕಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
- ಸಾಮಾನ್ಯ ಮಿತಿ ಇದೆ.
3) 
- ಒಂದು ಹಂತದಲ್ಲಿ ಕಾರ್ಯದ ಮಿತಿಯು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಈ ಕಾರ್ಯದ ಮೌಲ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಹೀಗಾಗಿ, ಒಂದು ಹಂತದಲ್ಲಿ ಕ್ರಿಯೆಯ ನಿರಂತರತೆಯ ವ್ಯಾಖ್ಯಾನದಿಂದ ಒಂದು ಹಂತದಲ್ಲಿ ಒಂದು ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ.
ಎಂದಿನಂತೆ, ಸಂಶೋಧನೆಯ ನಂತರ ನಾವು ನಮ್ಮ ರೇಖಾಚಿತ್ರವನ್ನು ಅಂತಿಮ ಆವೃತ್ತಿಗೆ ವರ್ಗಾಯಿಸುತ್ತೇವೆ.
ಉತ್ತರ: ಕಾರ್ಯವು ಬಿಂದುಗಳಲ್ಲಿ ನಿರಂತರವಾಗಿರುತ್ತದೆ.
ಈ ಸ್ಥಿತಿಯಲ್ಲಿ ನಾವು ನಿರಂತರತೆಗಾಗಿ ಸಂಪೂರ್ಣ ಕಾರ್ಯವನ್ನು ಅಧ್ಯಯನ ಮಾಡುವ ಬಗ್ಗೆ ಏನನ್ನೂ ಕೇಳಲಿಲ್ಲ ಮತ್ತು ಅದನ್ನು ರೂಪಿಸಲು ಉತ್ತಮ ಗಣಿತದ ರೂಪವೆಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ ಎಂಬುದನ್ನು ದಯವಿಟ್ಟು ಗಮನಿಸಿ. ನಿಖರ ಮತ್ತು ಸ್ಪಷ್ಟಕೇಳಿದ ಪ್ರಶ್ನೆಗೆ ಉತ್ತರ. ಮೂಲಕ, ಸ್ಥಿತಿಯು ನಿಮಗೆ ಗ್ರಾಫ್ ಅನ್ನು ನಿರ್ಮಿಸಲು ಅಗತ್ಯವಿಲ್ಲದಿದ್ದರೆ, ನೀವು ಹೊಂದಿದ್ದೀರಿ ಪ್ರತಿ ಹಕ್ಕುಅದನ್ನು ನಿರ್ಮಿಸಬೇಡಿ (ಶಿಕ್ಷಕರು ಅದನ್ನು ನಂತರ ಮಾಡಲು ನಿಮ್ಮನ್ನು ಒತ್ತಾಯಿಸಬಹುದು).
ಅದನ್ನು ನೀವೇ ಪರಿಹರಿಸಲು ಸಣ್ಣ ಗಣಿತದ "ನಾಲಿಗೆ ಟ್ವಿಸ್ಟರ್":
ಉದಾಹರಣೆ 7
ಕಾರ್ಯವನ್ನು ನೀಡಲಾಗಿದೆ 
. ಬಿಂದುಗಳಲ್ಲಿ ನಿರಂತರತೆಗಾಗಿ ಕಾರ್ಯವನ್ನು ತನಿಖೆ ಮಾಡಿ. ಬ್ರೇಕ್‌ಪಾಯಿಂಟ್‌ಗಳು ಯಾವುದಾದರೂ ಇದ್ದರೆ ವರ್ಗೀಕರಿಸಿ. ರೇಖಾಚಿತ್ರವನ್ನು ಕಾರ್ಯಗತಗೊಳಿಸಿ.
ಎಲ್ಲಾ "ಪದಗಳನ್ನು" ಸರಿಯಾಗಿ "ಉಚ್ಚರಿಸಲು" ಪ್ರಯತ್ನಿಸಿ =) ಮತ್ತು ಗ್ರಾಫ್ ಅನ್ನು ಹೆಚ್ಚು ನಿಖರವಾಗಿ ಸೆಳೆಯಿರಿ, ನಿಖರತೆ, ಅದು ಎಲ್ಲೆಡೆ ಅತಿಯಾಗಿರುವುದಿಲ್ಲ;-)
ನಿಮಗೆ ನೆನಪಿರುವಂತೆ, ಡ್ರಾಫ್ಟ್‌ನಂತೆ ಡ್ರಾಯಿಂಗ್ ಅನ್ನು ತಕ್ಷಣವೇ ಪೂರ್ಣಗೊಳಿಸಲು ನಾನು ಶಿಫಾರಸು ಮಾಡಿದ್ದೇನೆ, ಆದರೆ ಕಾಲಕಾಲಕ್ಕೆ ನೀವು ಗ್ರಾಫ್ ಹೇಗಿರುತ್ತದೆ ಎಂಬುದನ್ನು ತಕ್ಷಣವೇ ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸಾಧ್ಯವಾಗದ ಉದಾಹರಣೆಗಳನ್ನು ನೀವು ನೋಡುತ್ತೀರಿ. ಆದ್ದರಿಂದ, ಹಲವಾರು ಸಂದರ್ಭಗಳಲ್ಲಿ, ಮೊದಲು ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಅನುಕೂಲಕರವಾಗಿದೆ ಮತ್ತು ನಂತರ ಮಾತ್ರ, ಅಧ್ಯಯನದ ಆಧಾರದ ಮೇಲೆ, ಶಾಖೆಗಳನ್ನು ಚಿತ್ರಿಸುತ್ತದೆ. ಅಂತಿಮ ಎರಡು ಉದಾಹರಣೆಗಳಲ್ಲಿ ನಾವು ಕೆಲವು ಏಕಪಕ್ಷೀಯ ಮಿತಿಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ತಂತ್ರವನ್ನು ಸಹ ಕಲಿಯುತ್ತೇವೆ:
ಉದಾಹರಣೆ 8
ನಿರಂತರತೆಗಾಗಿ ಕಾರ್ಯವನ್ನು ಪರೀಕ್ಷಿಸಿ ಮತ್ತು ಅದರ ಸ್ಕೀಮ್ಯಾಟಿಕ್ ಗ್ರಾಫ್ ಅನ್ನು ನಿರ್ಮಿಸಿ.
ಪರಿಹಾರ: ಕೆಟ್ಟ ಅಂಕಗಳು ಸ್ಪಷ್ಟವಾಗಿವೆ: (ಘಾತದ ಛೇದವನ್ನು ಶೂನ್ಯಕ್ಕೆ ತಗ್ಗಿಸುತ್ತದೆ) ಮತ್ತು (ಇಡೀ ಭಾಗದ ಛೇದವನ್ನು ಶೂನ್ಯಕ್ಕೆ ತಗ್ಗಿಸುತ್ತದೆ). ಈ ಕಾರ್ಯದ ಗ್ರಾಫ್ ಹೇಗೆ ಕಾಣುತ್ತದೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿಲ್ಲ, ಅಂದರೆ ಮೊದಲು ಸ್ವಲ್ಪ ಸಂಶೋಧನೆ ಮಾಡುವುದು ಉತ್ತಮ.
