Atrast trigonometriskās funkcijas atvasinājums nepieciešams lietot atvasinājumu tabula, proti, atvasinājumi 6-13.
Kad atrodat primārie atvasinājumi trigonometriskās funkcijas Lai izvairītos no izplatītām kļūdām, jums jāpievērš uzmanība šādiem punktiem:
- funkcijas izteiksmē viens no terminiem bieži ir sinusa, kosinusa vai cita trigonometriska funkcija nevis no funkcijas argumenta, bet no skaitļa (konstantes), tāpēc šī vārda atvasinājums ir vienāds ar nulli;
- gandrīz vienmēr ir jāvienkāršo diferenciācijas rezultātā iegūtā izteiksme, un šim nolūkam jums ir pārliecinoši jāizmanto zināšanas par darbībām ar daļskaitļiem;
- Lai vienkāršotu izteiksmi, gandrīz vienmēr ir jāzina trigonometriskās identitātes, piemēram, formula dubults leņķis un vienotības formula kā sinusa un kosinusa kvadrātu summa.
1. piemērs. Atrodiet funkcijas atvasinājumu
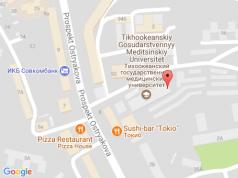
Risinājums. Teiksim ar kosinusa atvasinājums viss ir skaidrs, teiks daudzi, kas sāks pētīt atvasinājumus. Par ko sinusa atvasinājums divpadsmit dalīts ar pi? Atbilde: uzskata, ka tas ir vienāds ar nulli! Šeit sinuss (funkcija!) ir slazds, jo arguments nav mainīgais X vai kāds cits mainīgais, bet tikai skaitlis. Tas ir, šī skaitļa sinuss ir arī skaitlis. Un skaitļa atvasinājums (konstante), kā mēs zinām no atvasinājumu tabulas, ir vienāds ar nulli. Tātad, mēs atstājam tikai X mīnus sinusu un atrodam tā atvasinājumu, neaizmirstot par zīmi:
![]() .
.
2. piemērs. Atrodiet funkcijas atvasinājumu
![]() .
.
Risinājums. Otrais termins ir tāds pats gadījums kā pirmais termins iepriekšējā piemērā. Tas ir, tas ir skaitlis, un skaitļa atvasinājums ir nulle. Mēs atrodam otrā vārda atvasinājumu kā koeficienta atvasinājumu:
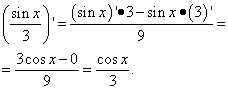
3. piemērs. Atrodiet funkcijas atvasinājumu
Risinājums. Šī ir vēl viena problēma: šeit pirmajā terminā nav arcsinusa vai citas trigonometriskas funkcijas, bet ir x, kas nozīmē, ka tā ir x funkcija. Tāpēc mēs to atšķiram kā terminu funkciju summā:

Šeit bija nepieciešamas iemaņas darbībās ar daļskaitļiem, proti, daļskaitļa trīsstāvu struktūras likvidēšanā.
4. piemērs. Atrodiet funkcijas atvasinājumu
![]() .
.
Risinājums. Šeit burts "phi" spēlē tādu pašu lomu kā "x" iepriekšējos gadījumos (un vairumā citu, bet ne visos) - neatkarīgais mainīgais. Tāpēc, meklējot funkciju reizinājuma atvasinājumu, mēs nesteigsimies pasludināt “phi” saknes atvasinājumu par vienādu ar nulli. Tātad:
Bet ar to risinājums nebeidzas. Tā kā līdzīgi termini ir apkopoti divās iekavās, mums joprojām ir jāpārveido (jāvienkāršo) izteiksme. Tāpēc mēs reizinām iekavas ar faktoriem, kas ir aiz tām, un pēc tam mēs apvienojam terminus līdz kopsaucējam un veicam citas elementāras transformācijas:

5. piemērs. Atrodiet funkcijas atvasinājumu
Risinājums. Šajā piemērā mums būs jāzina fakts, ka pastāv šāda trigonometriskā funkcija - secants - un tās formulas, izmantojot kosinusu. Atšķirsim:

6. piemērs. Atrodiet funkcijas atvasinājumu
![]() .
.
Risinājums. Šajā piemērā mums būs jāatceras dubultā leņķa formula no skolas. Bet vispirms atšķirsim:

![]() ,
,
(šī ir dubultā leņķa formula)
Tiek parādīti apgriezto trigonometrisko funkciju atvasinājumi un to formulu atvasinājumi. Ir dotas arī augstākas kārtas atvasinājumu izteiksmes. Saites uz lapām ar detalizētāku formulu atvasināšanas aprakstu.
Pirmkārt, mēs iegūstam arcsīna atvasinājuma formulu. Ļaujiet
y = arcsin x.
Tā kā arcsīns ir sinusa apgrieztā funkcija, tad
.
Šeit y ir x funkcija. Diferencēt attiecībā pret mainīgo x:
.
Mēs piesakāmies:
.
Tātad mēs atradām:
.
Jo tad. Tad
.
Un iepriekšējai formulai ir šāda forma:
. No šejienes
.
Tieši šādā veidā jūs varat iegūt formulu loka kosinusa atvasinājumam. Tomēr ir vieglāk izmantot formulu, kas attiecas uz apgrieztām trigonometriskām funkcijām:
.
Tad
.
Detalizētāks apraksts ir sniegts lapā “Arksīna un arkosīna atvasinājumu atvasinājumi”. Tur tas ir dots atvasinājumu atvasināšana divos veidos- apspriests iepriekš un saskaņā ar apgrieztās funkcijas atvasinājuma formulu.
Arktangenta un arkotangenta atvasinājumu atvasināšana
Tādā pašā veidā mēs atradīsim arktangenta un arkotangenta atvasinājumus.
Ļaujiet
y = arctan x.
Arktangenss ir pieskares apgrieztā funkcija:
.
Diferencēt attiecībā pret mainīgo x:
.
Mēs izmantojam kompleksas funkcijas atvasinājuma formulu:
.
Tātad mēs atradām:
.
Loka kotangensa atvasinājums:
.
Arcsīna atvasinājumi
Ļaujiet
.
Mēs jau esam atraduši arksīna pirmās kārtas atvasinājumu:
.
Atšķirot, mēs atrodam otrās kārtas atvasinājumu:
;
.
To var uzrakstīt arī šādā formā:
.
No šejienes mēs iegūstam diferenciālvienādojums, ko apmierina pirmās un otrās kārtas arcsīna atvasinājumi:
.
Diferencējot šo vienādojumu, mēs varam atrast augstākas kārtas atvasinājumus.
N-tās kārtas arcsīna atvasinājums
N-tās kārtas arcsinusa atvasinājumam ir šāda forma:
,
kur ir pakāpes polinoms. To nosaka pēc formulām:
;
.
Šeit .
Polinoms apmierina diferenciālvienādojumu:
.
N-tās kārtas arkosīna atvasinājums
Atvasinājumus loka kosinusam iegūst no loka sinusa atvasinājumiem, izmantojot trigonometrisko formulu:
.
Tāpēc šo funkciju atvasinājumi atšķiras tikai pēc zīmes:
.
Arktangenta atvasinājumi
Ļaujiet . Mēs atradām pirmās kārtas loka kotangensa atvasinājumu:
.
Sadalīsim frakciju tās vienkāršākajā formā:
.
Šeit ir iedomātā vienība, .
Mēs atšķiram vienreiz un apvienojam daļskaitli ar kopsaucēju:
.
Aizstājot, mēs iegūstam:
.
N-tās kārtas arktangenta atvasinājums
Tādējādi n-tās kārtas arktangenta atvasinājumu var attēlot vairākos veidos:
;
.
Loka kotangences atvasinājumi
Ļaujiet tam būt tagad. Izmantosim formulu, kas savieno apgrieztās trigonometriskās funkcijas:
.
Tad loka tangensa n-tās kārtas atvasinājums tikai pēc zīmes atšķiras no loka tangensa atvasinājuma:
.
Aizstājot , mēs atrodam:
.
Atsauces:
N.M. Ginters, R.O. Kuzmins, Augstākās matemātikas uzdevumu krājums, “Lan”, 2003.
Atvasinot pirmo tabulas formulu, mēs pāriesim no atvasinātās funkcijas definīcijas punktā. Ņemsim kur x- jebkurš reāls skaitlis, tas ir, x– jebkurš skaitlis no funkcijas definīcijas apgabala. Pierakstīsim funkcijas pieauguma un argumenta pieauguma attiecības robežu: ![]()
Jāņem vērā, ka zem robežzīmes tiek iegūta izteiksme, kas nav nulles nenoteiktība, kas dalīta ar nulli, jo skaitītājs nesatur bezgalīgi mazu vērtību, bet gan precīzi nulle. Citiem vārdiem sakot, nemainīgas funkcijas pieaugums vienmēr ir nulle.
Tādējādi konstantas funkcijas atvasinājumsir vienāds ar nulli visā definīcijas jomā.
Jaudas funkcijas atvasinājums.
Atvasinātā formula jaudas funkcija izskatās kā ![]() , kur eksponents lpp- jebkurš reāls skaitlis.
, kur eksponents lpp- jebkurš reāls skaitlis.
Vispirms pierādīsim naturālā eksponenta formulu, tas ir, for p = 1, 2, 3, …
Mēs izmantosim atvasinājuma definīciju. Pierakstīsim jaudas funkcijas pieauguma un argumenta pieauguma attiecības robežu: 
Lai vienkāršotu izteiksmi skaitītājā, mēs pievēršamies Ņūtona binominālajai formulai: 
Tāpēc 
Tas pierāda formulu pakāpes funkcijas atvasināšanai naturālajam eksponentam.
Eksponenciālās funkcijas atvasinājums.
Mēs piedāvājam atvasinātās formulas atvasinājumu, pamatojoties uz definīciju:
Mēs esam nonākuši pie nenoteiktības. Lai to paplašinātu, mēs ieviešam jaunu mainīgo un pie . Tad . Pēdējā pārejā mēs izmantojām formulu pārejai uz jaunu logaritmisko bāzi.
Aizstāsim ar sākotnējo ierobežojumu: 
Ja atceramies otro ievērojamo robežu, mēs nonākam pie eksponenciālās funkcijas atvasinājuma formulas: 
Logaritmiskās funkcijas atvasinājums.
Pierādīsim logaritmiskās funkcijas atvasinājuma formulu visiem x no definīcijas domēna un visām derīgajām bāzes vērtībām a logaritms Pēc atvasinājuma definīcijas mums ir: 
Kā jūs pamanījāt, pierādīšanas laikā transformācijas tika veiktas, izmantojot logaritma īpašības. Vienlīdzība  ir taisnība otrās ievērojamās robežas dēļ.
ir taisnība otrās ievērojamās robežas dēļ.
Trigonometrisko funkciju atvasinājumi.
Lai iegūtu formulas trigonometrisko funkciju atvasinājumiem, mums būs jāatgādina dažas trigonometrijas formulas, kā arī pirmā ievērojamā robeža.
Pēc sinusa funkcijas atvasinājuma definīcijas mums ir ![]() .
.
Izmantosim sinusu starpības formulu: 
Atliek pievērsties pirmajam ievērojamajam ierobežojumam: 
Tādējādi funkcijas atvasinājums grēks x Tur ir cos x.
Tieši tādā pašā veidā tiek pierādīta arī kosinusa atvasinājuma formula. 
Tāpēc funkcijas atvasinājums cos x Tur ir – grēks x.
Izmantojot pārbaudītus diferenciācijas noteikumus (daļskaitļa atvasinājumu), mēs atvasināsim formulas tangensas un kotangensas atvasinājumu tabulai. 
Hiperbolisko funkciju atvasinājumi.
Diferenciācijas noteikumi un eksponenciālās funkcijas atvasinājuma formula no atvasinājumu tabulas ļauj atvasināt formulas hiperboliskā sinusa, kosinusa, pieskares un kotangensa atvasinājumiem. 
Apgrieztās funkcijas atvasinājums.
Lai izvairītos no neskaidrībām prezentācijas laikā, apakšindeksā apzīmēsim funkcijas argumentu, ar kuru tiek veikta diferencēšana, tas ir, tas ir funkcijas atvasinājums f(x) Autors x.
Tagad formulēsim noteikums apgrieztās funkcijas atvasinājuma atrašanai.
Ļaujiet funkcijām y = f(x) Un x = g(y) savstarpēji apgriezti, noteikti uz intervāliem un attiecīgi. Ja kādā punktā ir funkcijas galīgs nulles atvasinājums f(x), tad punktā ir apgrieztās funkcijas galīgs atvasinājums g(y), un ![]() . Citā ierakstā
. Citā ierakstā ![]() .
.
Šo noteikumu var pārformulēt jebkuram x no intervāla , tad mēs iegūstam  .
.
Pārbaudīsim šo formulu derīgumu.
Atradīsim naturālā logaritma apgriezto funkciju ![]() (Šeit y ir funkcija un x- arguments). Atrisinot šo vienādojumu priekš x, mēs saņemam (šeit x ir funkcija un y– viņas arguments). Tas ir,
(Šeit y ir funkcija un x- arguments). Atrisinot šo vienādojumu priekš x, mēs saņemam (šeit x ir funkcija un y– viņas arguments). Tas ir, ![]() un savstarpēji apgrieztas funkcijas.
un savstarpēji apgrieztas funkcijas.
No atvasinājumu tabulas mēs to redzam ![]() Un
Un ![]() .
.
Pārliecināsimies, ka apgrieztās funkcijas atvasinājumu atrašanas formulas noved pie tādiem pašiem rezultātiem: 
No ģeometrijas un matemātikas kursa skolēni ir pieraduši pie tā, ka atvasinājuma jēdziens viņiem tiek nodots caur figūras laukumu, diferenciāļiem, funkciju ierobežojumiem, kā arī ierobežojumiem. Mēģināsim aplūkot atvasinājuma jēdzienu no cita leņķa un noteikt, kā var saistīt atvasinātās un trigonometriskās funkcijas.
Tātad, aplūkosim kādu patvaļīgu līkni, ko apraksta abstraktā funkcija y = f(x).
Iedomāsimies, ka grafiks ir tūrisma maršruta karte. Pieaugums ∆x (delta x) attēlā ir noteikts ceļa attālums, un ∆y ir ceļa augstuma izmaiņas virs jūras līmeņa.
Tad izrādās, ka attiecība ∆x/∆y raksturos maršruta sarežģītību katrā maršruta posmā. Uzzinot šo vērtību, varat droši teikt, vai kāpums/nokāpums ir stāvs, vai jums būs nepieciešams kāpšanas aprīkojums un vai tūristiem ir nepieciešams noteikts fiziskā sagatavotība. Bet šis rādītājs būs derīgs tikai vienam nelielam intervālam ∆x.
Ja brauciena organizators ņem takas sākuma un beigu punktu vērtības, tas ir, ∆x ir vienāds ar maršruta garumu, tad viņš nevarēs iegūt objektīvus datus par grūtības pakāpi. no ceļojuma. Tāpēc nepieciešams izveidot citu grafiku, kas raksturos trases izmaiņu ātrumu un “kvalitāti”, citiem vārdiem sakot, katram maršruta “metram” nosaka attiecību ∆x/∆y.
Šis grafiks būs vizuāls atvasinājums konkrētam ceļam un objektīvi aprakstīs tā izmaiņas katrā interesējošajā intervālā. To ir ļoti vienkārši pārbaudīt; vērtība ∆x/∆y nav nekas cits kā diferenciālis, kas ņemts noteiktai x un y vērtībai. Piemērosim diferenciāciju nevis konkrētām koordinātām, bet gan funkcijai kopumā:

Atvasinātās un trigonometriskās funkcijas
Trigonometriskās funkcijas ir nesaraujami saistītas ar atvasinājumiem. To var saprast no nākamā zīmējuma. Koordinātu ass attēlā redzama funkcija Y = f (x) - zilā līkne.
K (x0; f (x0)) ir patvaļīgs punkts, x0 + ∆x ir pieaugums pa OX asi, un f (x0 + ∆x) ir pieaugums pa OY asi noteiktā punktā L.

Novelkam taisni caur punktiem K un L un konstruēsim taisnleņķa trīsstūris KLN. Ja jūs garīgi pārvietojat segmentu LN pa grafiku Y = f (x), tad punkti L un N tiecas uz vērtībām K (x0; f (x0)). Sauksim šo punktu par grafa nosacīto sākumu – robežu, ja funkcija ir bezgalīga, vismaz vienā no intervāliem arī šī tendence būs bezgalīga, un tās robežvērtība ir tuvu 0.
Šīs tendences būtību var aprakstīt ar izvēlētā punkta y = kx + b pieskari vai ar sākotnējās funkcijas dy atvasinājuma grafiku - zaļo taisni.
Bet kur te ir trigonometrija?! Viss ir ļoti vienkārši, apsveriet taisnstūra trīsstūri KLN. Diferenciālā vērtība konkrētam punktam K ir leņķa α vai ∠K tangenss:

Tādā veidā varam aprakstīt atvasinājuma ģeometrisko nozīmi un saistību ar trigonometriskajām funkcijām.
Trigonometrisko funkciju atvasinātās formulas
Nosakot atvasinājumu, ir jāiegaumē sinusa, kosinusa, tangensa un kotangenta pārvērtības.

Pēdējās divas formulas nav kļūda, jo runa ir par to, ka pastāv atšķirība starp vienkārša argumenta atvasinājuma un funkcijas definēšanu tādā pašā kvalitātē.
Apskatīsim salīdzinošo tabulu ar formulām sinusa, kosinusa, tangensa un kotangensa atvasinājumiem:

Formulas ir iegūtas arī arcsīna, arkosīna, arktangenta un arkotangenta atvasinājumiem, lai gan tās tiek izmantotas ārkārtīgi reti:

Ir vērts atzīmēt, ka ar iepriekšminētajām formulām nepārprotami nepietiek, lai veiksmīgi atrisinātu tipiskus USE uzdevumus, kas tiks parādīti, risinot konkrētu piemēru trigonometriskās izteiksmes atvasinājuma atrašanai.
Vingrinājums: jāatrod funkcijas atvasinājums un jāatrod tā vērtība π/4:

Risinājums: Lai atrastu y’, ir jāatgādina pamatformulas sākotnējās funkcijas pārvēršanai atvasinājumā, proti.
Temats:"Trigonometrisko funkciju atvasinājums".
Nodarbības veids– nodarbība zināšanu nostiprināšanā.
Nodarbības forma– integrētā nodarbība.
Nodarbības vieta šīs sadaļas nodarbību sistēmā- vispārējā nodarbība.
Mērķi ir noteikti visaptveroši:
- izglītojošs: pārzināt diferenciācijas likumus, prast pielietot atvasinājumu aprēķināšanas noteikumus, risinot vienādojumus un nevienādības; uzlabot mācību priekšmetu, tostarp skaitļošanas prasmes un iemaņas; Datorprasmes;
- izstrādājot: intelektuālo un loģisko prasmju un izziņas interešu attīstība;
- izglītojošs: audzināt pielāgošanās spēju mūsdienu apstākļos apmācību.
Metodes:
- reproduktīvs un produktīvs;
- praktiski un verbāli;
- patstāvīgs darbs;
- programmētās mācības, T.S.O.;
- kombinācija frontālo, grupu un individuālais darbs;
- diferencēta mācīšanās;
- induktīvi-deduktīvi.
Kontroles formas:
- mutiska aptauja,
- programmēta vadība,
- patstāvīgs darbs,
- individuālie uzdevumi datorā,
- salīdzinošā pārskatīšana, izmantojot studenta diagnostikas karti.
NODARBĪBU LAIKĀ
I. Organizatoriskais moments
II. Atsauces zināšanu papildināšana
a) Mērķu un uzdevumu paziņošana:
- pārzināt diferenciācijas likumus, prast pielietot atvasinājumu aprēķināšanas noteikumus, risinot uzdevumus, vienādojumus un nevienādības;
- uzlabot mācību priekšmetu, tostarp skaitļošanas prasmes un iemaņas; Datorprasmes;
- attīstīt intelektuālās un loģiskās prasmes un izziņas intereses;
- attīstīt spēju pielāgoties mūsdienu mācību apstākļiem.
b) Mācību materiāla atkārtošana
Atvasinājumu aprēķināšanas noteikumi (formulu atkārtošana datorā ar skaņu). dok.7.
- Kas ir sinusa atvasinājums?
- Kas ir kosinusa atvasinājums?
- Kāds ir pieskares atvasinājums?
- Kāds ir kotangensa atvasinājums?
III. Mutisks darbs
Atrodiet atvasinājumu. |
|||
1. iespēja. |
2. iespēja. |
||
plkst = 2X + 5. |
plkst = 2X – 5. |
||
plkst= 4cos X. |
plkst= 3 grēks X. |
||
plkst= tg X+ctg X. |
plkst= tg X-ctg X. |
||
plkst= grēks 3 X. |
plkst= cos 4 X. |
||
Atbilžu iespējas. |
|||
– 4 grēks X |
– 3 cos X |
||
1/cos 2 X+ 1/grēks 2 X |
1/cos 2 X–1/grēks 2 X |
1/grēks 2 X–1/cos 2 X |
|
– 4sin4 X |
– 3cos3 X |
||
Mainiet piezīmju grāmatiņas. Diagnostikas kartēs pareizi izpildītus uzdevumus atzīmē ar + zīmi, bet nepareizi izpildītus ar – zīmi.
IV. Vienādojumu atrisināšana, izmantojot atvasinājumu
– Kā atrast punktus, kuros atvasinājums ir nulle?
Lai atrastu punktus, kuros atvasinājums šī funkcija ir vienāds ar nulli, jums ir nepieciešams:
– noteikt funkcijas raksturu,
- atrast apgabalu funkciju definīcijas,
- atrast šīs funkcijas atvasinājumu,
- atrisināt vienādojumu f "(x) = 0,
- Izvēlies pareizo atbildi.
1. uzdevums.
Ņemot vērā: plkst
= X- grēks x.
Atrast: punkti, kuros atvasinājums ir nulle.
Risinājums. Funkcija ir definēta un diferencējama visu reālo skaitļu kopā, jo funkcijas ir definētas un diferencējamas visu reālo skaitļu kopā g(x) = x Un t(x) = – grēks x.
Izmantojot diferenciācijas noteikumus, mēs iegūstam f
"(x) = (x- grēks x)" = (x)" – (grēks x)" = 1 — cos x.
Ja f "(x) = 0, tad 1 – cos x = 0.
cos x= 1/; atbrīvosimies no iracionalitātes saucējā, iegūstam cos x
= /2.
Pēc formulas t= ± arccos a+ 2n, n Z, mēs iegūstam: X= ± arccos /2 + 2n, n Z.
Atbilde: x = ± /4 + 2n, n Z.
V. Vienādojumu risināšana, izmantojot algoritmu
Atrodiet, kuros punktos atvasinājums pazūd.
f(x) = grēks x+cos x |
f(x) = grēks 2 x – x |
f(x) = 2x+cos(4 x – ) |
Students var izvēlēties jebkuru no trim piemēriem. Pirmais piemērs ir novērtēts 3 ", otrais - " 4 ", trešais - " 5 " Risinājums piezīmju grāmatiņās, kam seko savstarpēja pārbaude. Viens students pieņem lēmumu pie padomes. Ja risinājums izrādās nepareizs, skolēnam jāatgriežas pie algoritma un jāmēģina atrisināt vēlreiz.
Programmēta vadība.
1. iespēja |
2. iespēja |
|||
y = 2X 3 |
y = 3X 2 |
|||
y = 1/4 X 4 + 2X 2 – 7 |
y = 1/2 X 4 + 4X + 5 |
|||
y = X 3 + 4X 2
– 3X. |
y = 2X 3 – 9X 2
+ 12X + 7. |
|||
y= grēks 2 X- cos 3 X. |
y= cos 2 X- grēks 3 X. |
|||
y= tg X-ctg ( X + /4). |
y=ctg X+ tg( X – /4). |
|||
y= grēks 2 X. |
y= cos 2 X. |
|||
Atbilžu iespējas. |
||||
|
| ||||