Изчисляване на интеграли чрез метода на интегриране по части. Онлайн калкулатор Изчисляване на неопределен интеграл (антипроизводна).

Извиква се следната формула формула за интегриране по части в неопределен интеграл:

За да се приложи формулата за интегриране по части, интегралната функция трябва да бъде разделена на два фактора. Един от тях е означен с u, а остатъкът се отнася за втория фактор и се означава с дв. След това чрез диференциране намираме дуи интеграция – функция v. В същото време за u дв- такава част от интегранта, която може лесно да се интегрира.

Кога е полезно да се използва методът на интегриране по части? Тогава когато интеграндът съдържа :

1) - логаритмични функции, както и обратни тригонометрични функции (с префикса "дъга"), след това, въз основа на дългогодишен опит на интегриране по части, тези функции се означават с u;

2) , , - синус, косинус и експонента, умножени по П(х) е произволен полином от x, тогава тези функции се означават с дв, а полиномът е през u;

3) , , , , в този случай интегрирането по части се прилага два пъти.

Нека обясним стойността на метода на интегриране по части, използвайки примера на първия случай. Нека изразът под знака за интеграл съдържа логаритмична функция (това ще бъде пример 1). Чрез използването на интегриране по части такъв интеграл се свежда до изчисляване на интеграла само на алгебрични функции (най-често полином), тоест несъдържащ логаритмичен или обратен тригонометрична функция. Използване на формулата за интегриране по части, дадена в самото начало на урока

получаваме в първия член (без интеграл) логаритмична функция, а във втория член (под знака на интеграла) функция, която не съдържа логаритъм. Интегралът на алгебрична функция е много по-прост от интеграла, под чийто знак се намира логаритмична или обратна тригонометрична функция отделно или заедно с алгебричен фактор.

По този начин, използвайки интегриране по части формули интегрирането не се извършва веднага: намирането на даден интеграл се свежда до намиране на друг. Смисълът на формулата за интегриране по части е, че в резултат на нейното прилагане новият интеграл се оказва табличен или поне става по-опростен от първоначалния.

Методът на интегриране по части се основава на използването на формулата за диференциране на продукта на две функции:

тогава може да се запише във формата

който беше даден в самото начало на урока.

При намиране чрез интегриране на функцията vза него се получава безкраен набор от първообразни функции. За да приложите формулата за интегриране по части, можете да вземете всяка от тях и следователно тази, която съответства на произволна константа СЪС, равно на нула. Следователно при намиране на функцията vпроизволна константа СЪСне трябва да се въвежда.

Методът на интегриране по части има много специално приложение: той може да се използва за извеждане на рекурентни формули за намиране на първообразни функции, когато е необходимо да се намали степента на функциите под интегралния знак. Намаляването на степента е необходимо, когато няма таблични интеграли за, например, функции като синуси и косинуси до степени, по-големи от секундата и техните произведения. Рекурентна формула е формула за намиране на следващия член на последователност чрез предишния член. За посочените случаи целта се постига с последователно понижаване на степента. Така че, ако интеграндът е синус на четвърта степен от х, тогава чрез интегриране по части можете да намерите формула за интеграла на синус на трета степен и т.н. Последният параграф от този урок е посветен на описаната задача.

Прилагане на интеграция по части заедно

Пример 1. Намерете неопределения интеграл, като използвате метода на интегриране по части:

Решение. В израза на интегранд - логаритъма, който, както вече знаем, може разумно да бъде обозначен с u. Вярваме, че ,.

Намираме (както вече беше споменато в обяснението за теоретичната справка, веднага получаваме логаритмична функция в първия член (без интеграл) и функция, която не съдържа логаритъм във втория член (под интегралния знак):):

И пак логаритъм...

Пример 2.Намерете неопределения интеграл:

Решение. Позволявам , .

Логаритъмът присъства в квадрата. Това означава, че трябва да се обособи като сложна функция. Намираме
,
.

Отново намираме втория интеграл по части и получаваме вече споменатото предимство (в първия член (без интеграла) има логаритмична функция, а във втория член (под знака на интеграла) има функция, която не съдържа логаритъм).

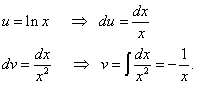
Намираме първоначалния интеграл:

Пример 3.

Решение. Арктангенсът, подобно на логаритъма, е по-добре да се означава с u. Така че нека,.

Тогава ,
.

Прилагайки формулата за интегриране по части, получаваме:

Намираме втория интеграл чрез промяна на променлива.

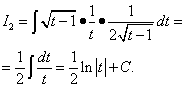
Връщане към променливата х, получаваме

.

Намираме първоначалния интеграл:

.

Пример 4. Намерете неопределения интеграл, като използвате метода на интегриране по части:

Решение. По-добре е степента да се обозначи с дв. Разделяме интегранта на два фактора. Вярвайки в това

Пример 5. Намерете неопределения интеграл, като използвате метода на интегриране по части:

.

Решение. Позволявам , . Тогава , .

Използвайки формулата за интегриране по части (1), намираме:

Пример 6.Намерете неопределения интеграл чрез интегриране по части:

Решение. Синусът, подобно на експоненциала, може удобно да се обозначи с дв. Позволявам , .

Използвайки формулата за интегриране по части, намираме:

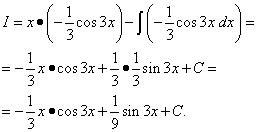
Отново прилагаме интегриране по части заедно

Пример 10.Намерете неопределения интеграл чрез интегриране по части:

.

Решение. Както във всички подобни случаи, удобно е косинусът да се обозначи с дв. Означаваме , .

Тогава , .

Използвайки формулата за интегриране по части, получаваме:

Също така прилагаме интегриране по части към втория член. Означаваме , .

Използвайки тези обозначения, ние интегрираме споменатия термин:

Сега намираме необходимия интеграл:

Сред интегралите, които могат да се решават чрез метода на интегриране по части, има и такива, които не са включени в нито една от трите групи, посочени в теоретичната част, за които е известно от практиката, че е по-добре да се означават с u, и през какво дв. Следователно в тези случаи трябва да използвате съображението за удобство, също дадено в параграфа „Същността на метода на интегриране по части“: за uтрябва да се вземе част от интегранта, която не става много по-сложна по време на диференцирането, но дв- такава част от интегранта, която може лесно да се интегрира. Последният пример от този урок е решението на точно такъв интеграл.

Чрез определен интеграл от непрекъсната функция f(х) на последния сегмент [ а, b] (където ) е увеличението на някои от неговите антипроизводни на този сегмент. (Като цяло разбирането ще бъде значително по-лесно, ако повторите темата за неопределения интеграл) В този случай се използва нотацията

Както може да се види на графиките по-долу (увеличението на антипроизводната функция е обозначено с), определеният интеграл може да бъде или положителен, или отрицателно число (Изчислява се като разликата между стойността на антипроизводното в горната граница и нейната стойност в долната граница, т.е. като Е(b) - Е(а)).

Числа аИ bсе наричат ​​съответно долна и горна граница на интегриране, а сегментът [ а, b] – сегмент на интеграция.

По този начин, ако Е(х) – някаква антипроизводна функция за f(х), тогава според определението,

(38)

Равенството (38) се нарича Формула на Нютон-Лайбниц . Разлика Е(b) – Е(а) се записва накратко, както следва:

Следователно ще запишем формулата на Нютон-Лайбниц така:

(39)

Нека докажем, че определеният интеграл не зависи от това коя първоизводна на подинтегралната функция е взета при изчисляването му. Позволявам Е(х) и F( х) са произволни първоизводни на интегранта. Тъй като това са антипроизводни на една и съща функция, те се различават с постоянен член: Ф( х) = Е(х) + ° С. Ето защо

Това установява, че на отсечката [ а, b] увеличения на всички първоизводни на функцията f(х) съвпада.

По този начин, за да се изчисли определен интеграл, е необходимо да се намери всяка антипроизводна на интегранта, т.е. Първо трябва да намерите неопределения интеграл. Константа СЪС изключени от следващите изчисления. След това се прилага формулата на Нютон-Лайбниц: стойността на горната граница се замества в антипроизводната функция b , по-нататък - стойността на долната граница а и се изчислява разликата F(b) - F(a) . Полученото число ще бъде определен интеграл..

При а = bпо дефиниция прието

Пример 1.

Решение. Първо, нека намерим неопределения интеграл:

Прилагане на формулата на Нютон-Лайбниц към първоизводната

(при СЪС= 0), получаваме

Въпреки това, когато изчислявате определен интеграл, е по-добре да не намирате първоизводната отделно, а веднага да напишете интеграла във формата (39).

Пример 2.Изчислете определен интеграл

Решение. Използване на формула

Свойства на определения интеграл

Теорема 2.Стойността на определения интеграл не зависи от обозначението на интегриращата променлива, т.е.

(40)

Позволявам Е(х) – противопроизводно за f(х). За f(T) антипроизводното е същата функция Е(T), в които независимата променлива е само обозначена по различен начин. следователно

Въз основа на формула (39) последното равенство означава равенство на интегралите

Теорема 3.Постоянният множител може да бъде изваден от знака на определения интеграл, т.е.

(41)

Теорема 4.Определеният интеграл на алгебрична сума от краен брой функции е равен на алгебричната сума на определени интеграли на тези функции, т.е.

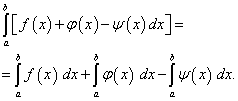(42)

Теорема 5.Ако интеграционният сегмент е разделен на части, тогава определен интеграл върху целия сегмент равно на суматаопределени интеграли по неговите части, т.е. Ако

(43)

Теорема 6.При пренареждане на границите на интеграция абсолютна стойностопределеният интеграл не се променя, а само знакът му, т.е.

(44)

Теорема 7(теорема за средната стойност). Определеният интеграл е равен на произведението от дължината на интегралния сегмент и стойността на интегралното изражение в дадена точка вътре в него, т.е.

(45)

Теорема 8.Ако горната граница на интегриране е по-голяма от долната и подинтегралната функция е неотрицателна (положителна), то определеният интеграл също е неотрицателен (положителен), т.е. Ако

Теорема 9.Ако горната граница на интегриране е по-голяма от долната и функциите и са непрекъснати, тогава неравенството

може да се интегрира термин по термин, т.е.

(46)

Свойствата на определения интеграл позволяват да се опрости директното изчисляване на интегралите.

Пример 5.Изчислете определен интеграл

Използвайки теореми 4 и 3, и при намиране на първоизводни - таблични интеграли (7) и (6), получаваме

Определен интеграл с променлива горна граница

Позволявам f(х) – непрекъснат на отсечката [ а, b] функция и Е(х) е неговата антипроизводна. Разгледайте определения интеграл

(47)

и чрез Tинтеграционната променлива е обозначена така, че да не се бърка с горен лимит. Когато се промени хпроменя се и определеният интеграл (47), т.е. това е функция на горната граница на интегриране х, което означаваме с Е(х), т.е.

(48)

Нека докажем, че функцията Е(х) е противопроизводно на f(х) = f(T). Наистина, диференциране Е(х), получаваме

защото Е(х) – противопроизводно за f(х), А Е(а) е постоянна стойност.

функция Е(х) – един от безкрайния брой антипроизводни на f(х), а именно този, който х = аотива на нула. Това твърдение се получава, ако в равенството (48) поставим х = аи използвайте теорема 1 от предходния параграф.

Изчисляване на определени интеграли чрез метода на интегриране по части и метода на промяна на променлива

където по дефиниция Е(х) – противопроизводно за f(х). Ако променим променливата в интегранта

тогава, в съответствие с формула (16), можем да запишем

В този израз

антипроизводна функция за

Всъщност неговата производна, според правило за диференциране на сложни функции, е равно

Нека α и β са стойностите на променливата T, за които функцията

приема стойности съответно аИ b, т.е.

Но според формулата на Нютон-Лайбниц разликата Е(b) – Е(а) Има

Методът на интегриране по части се използва главно когато интегралната функция се състои от произведението на два фактора от определен тип. Формулата за интегриране по части изглежда така:

Той дава възможност да се намали изчисляването на даден интеграл
към изчисляването на интеграла
, което се оказва по-просто от това.

Повечето от интегралите, изчислени чрез метода на интегриране по части, могат да бъдат разделени на три групи:

1. Интеграли на формата
,
,
, Където
– полином,
– число, което не е равно на нула

В този случай чрез обозначават полином

.

2. Интеграли на формата
,
,
,
,
, Където
– полином.

В този случай чрез
обозначавам
, а останалата част от интегранта през :

3. Интеграли на формата
,
, Където
– числа.

В този случай чрез обозначавам
и приложете формулата за интегриране по части два пъти, като резултатът се връща към първоначалния интеграл, след което първоначалният интеграл се изразява от равенството.

Коментирайте: В някои случаи, за да се намери даден интеграл, формулата за интегриране по части трябва да се приложи няколко пъти. Също така методът на интегриране по части се комбинира с други методи.

Пример 26.

Намерете интеграли, като използвате метода по части: а)
; б)
.

Решение.

б)

3.1.4. Интегриране на дробно-рационални функции

Дробна рационална функция(рационална дроб) е функция, равна на отношението на два полинома:
, Където
– полином на степен
,
– полином на степен .

Рационалната дроб се нарича правилно, ако степента на полинома в числителя е по-малка от степента на полинома в знаменателя, т.е.
, в противен случай (ако
) се нарича рационална дроб грешно.

Всяка неправилна рационална дроб може да бъде представена като сбор от полином
и правилно рационална дроб, разделяйки числителя на знаменателя според правилото за деление на полиноми:

,

Където
– цяла частот разделението, – правилна рационална дроб,
- остатък от делението.

Правилни рационални дроби от вида:

аз ;

II.
;

III.
;

IV.
,

Където ,,
,
,,,
– реални числа и
(тези. квадратен тричленв знаменателя III и IV на дробите няма корени - дискриминантът е отрицателен) се наричат прости рационални дроби I, II, III и IV видове.

Интегриране на прости дроби

Интегралите на най-простите дроби от четири вида се изчисляват, както следва.

аз)
.

II),
.

III) За да интегрирате най-простата дроб от тип III, изберете пълен квадрат в знаменателя и го заменете
. След заместването интегралът се разделя на два интеграла. Първият интеграл се изчислява чрез изолиране на производната на знаменателя в числителя, което дава табличен интеграл, а вторият интеграл се преобразува във формата
, защото
, което също дава табличния интеграл.

;

IV) За да интегрирате най-простата дроб от тип IV, изберете пълен квадрат в знаменателя и го заменете
. След заместването интегралът се разделя на два интеграла. Първият интеграл се изчислява чрез заместване
, а вторият използва рекурентни отношения.

Пример 27.

Намерете интеграли на прости дроби:

а)
; б)
; V)
.

Решение.

а)
.

Всяка правилна рационална дроб, чийто знаменател може да бъде факторизиран, може да бъде представена като сбор от прости дроби. Разлагането на сумата от прости дроби се извършва по метода на неопределените коефициенти. Той е както следва:

съответства на една част от формата ;

– всеки множител на знаменателя
отговаря на сумата дроби от формата

съответства на част от формата
;

– всеки квадратен множител на знаменателя
отговаря на сумата дроби от формата

където са неопределените коефициенти.

За да се намерят неопределени коефициенти, дясната страна под формата на сбор от прости дроби се привежда към общ знаменател и се трансформира. Резултатът е дроб със същия знаменател като в лявата страна на уравнението. След това знаменателите се изхвърлят и числителите се изравняват. Резултатът е идентично равенство, в което лявата страна е полином с известни коефициенти и дясна част– полином с неопределени коефициенти.

Има два начина за определяне на неизвестни коефициенти: методът на неизвестните коефициенти и методът на частичните стойности.

Метод на неопределените коефициенти.

защото полиномите са идентично равни, тогава коефициентите при еднакви степени са равни . Приравняване на коефициенти при еднакви степени в полиномите на лявата и дясната страна, получаваме системата линейни уравнения. При решаването на системата определяме несигурните коефициенти.

Метод на частните ценности.

защото полиноми са идентично равни, тогава замествайки от лявата и дясната страна на всяко число, получаваме истинско равенство, линейно по отношение на неизвестните коефициенти. Подмяна на толкова много стойности , колко неизвестни коефициента има, получаваме система от линейни уравнения. Вместо Можете да замените всякакви числа в лявата и дясната страна, но е по-удобно да замените корените на знаменателите на дробите.

След намиране на стойностите на неизвестните коефициенти, първоначалната дроб се записва като сбор от прости дроби в интегранта и обсъжданото по-рано интегриране се извършва върху всяка проста дроб.

Интеграционна схема рационални дроби:

1. Ако интегралната функция е неправилна, тогава е необходимо да се представи като сума от полином и правилна рационална дроб (т.е. разделете полинома на числителя на полинома на знаменателя с остатък). Ако интегралната функция е правилна, веднага преминаваме към втората точка на диаграмата.

2. Разложете на множители знаменателя на правилна рационална дроб, ако е възможно.

3. Разложете правилна рационална дроб на сбора от прости рационални дроби, като използвате метода на неопределените коефициенти.

4. Интегрирайте получената сума от полинома и простите дроби.

Пример 28.

Намерете интеграли на рационални дроби:

а)
; б)
; V)
.

Решение.

а)
.

защото интеграндът е неправилна рационална дроб, тогава избираме цялата част, т.е. Нека си го представим като сбор от полином и правилна рационална дроб. Разделете полинома в числителя на полинома в знаменателя с помощта на ъгъл.

Оригиналният интеграл ще приеме формата:
.

Нека разложим правилна рационална дроб на сбор от прости дроби, използвайки метода на неопределените коефициенти:

, получаваме:

Решавайки системата от линейни уравнения, получаваме стойностите на несигурните коефициенти: А = 1; IN = 3.

Тогава необходимото разширение има формата:
.

=
.

б)
.

.

Нека изхвърлим знаменателите и приравним лявата и дясната страна:

Приравняване на коефициенти при еднакви степени , получаваме системата:

Чрез решаване на система от пет линейни уравнения намираме неопределените коефициенти:

.

Нека намерим първоначалния интеграл, като вземем предвид полученото разширение:

.

V)
.

Нека разширим интегранта (правилната рационална дроб) в сбор от прости дроби, използвайки метода на неопределените коефициенти. Търсим разлагане във формата:

.

Привеждайки до общ знаменател, получаваме:

Нека изхвърлим знаменателите и приравним лявата и дясната страна:

За да намерим несигурни коефициенти, прилагаме метода на частичната стойност. Нека добавим частични стойности, при които факторите изчезват, т.е. заместваме тези стойности в последния израз и получаваме три уравнения:

;
;

;
;

;
.

Тогава необходимото разширение има формата:

Нека намерим първоначалния интеграл, като вземем предвид полученото разширение:

Извиква се функция F(x), диференцируема в даден интервал X първоизводна на функцията f(x) или интеграла на f(x), ако за всяко x ∈X е валидно следното равенство:

F " (x) = f(x). (8.1)

Намирането на всички първоизводни за дадена функция се нарича нейна интеграция. Неопределена интегрална функция f(x) на даден интервал X е множеството от всички първообразни функции за функцията f(x); обозначаване -

Ако F(x) е някакво първообразно на функцията f(x), тогава ∫ f(x)dx = F(x) + C, (8.2)

където C е произволна константа.

Таблица на интегралите

Директно от определението получаваме основните свойства Не определен интеграли списък с таблични интеграли:

1) d∫f(x)dx=f(x)

2) ∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Списък на табличните интеграли

1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sin x + C

7. = арктан x + C

8. = arcsin x + C

10. = - ctg x + C

Замяна на променливи

За да интегрирате много функции, използвайте метода за заместване на променливи или замествания,което ви позволява да намалите интегралите до таблична форма.

Ако функцията f(z) е непрекъсната върху [α,β], функцията z =g(x) има непрекъсната производна и α ≤ g(x) ≤ β, тогава

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

Освен това, след интегриране от дясната страна, трябва да се направи заместването z=g(x).

За да го докажете, достатъчно е да напишете оригиналния интеграл във формата:

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Например:

Метод на интегриране по части

Нека u = f(x) и v = g(x) са функции, които имат непрекъснато . Тогава, според работата,

d(uv))= udv + vdu или udv = d(uv) - vdu.

За израза d(uv) антипроизводното очевидно ще бъде uv, така че формулата е валидна:

∫ udv = uv - ∫ vdu (8.4.)

Тази формула изразява правилото интеграция по части. Това води интегрирането на израза udv=uv"dx до интегрирането на израза vdu=vu"dx.

Нека, например, искате да намерите ∫xcosx dx. Нека поставим u = x, dv = cosxdx, така че du=dx, v=sinx. Тогава

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

Правилото за интегриране по части има по-ограничен обхват от заместването на променливи. Но има цели класове интеграли, напр.

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и други, които се изчисляват точно с помощта на интегриране по части.

Определен интеграл

Концепцията за определен интеграл се въвежда по следния начин. Нека функция f(x) е дефинирана на интервал. Нека разделим сегмента [a,b] на нчасти по точки a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i = x i - x i-1. Извиква се сума от формата f(ξ i)Δ x i интегрална сума, а неговата граница при λ = maxΔx i → 0, ако съществува и е крайна, се нарича определен интегралфункции f(x) на апреди bи се обозначава:

F(ξ i)Δx i (8.5).

Функцията f(x) в този случай се извиква интегрируеми на интервала, се наричат ​​числата a и b долна и горна граница на интеграла.

Следните свойства са верни за определен интеграл:

4), (k = const, k∈R);

5)

6)

7) f(ξ)(b-a) (ξ∈).

Последното свойство се нарича теорема за средната стойност.

Нека f(x) е непрекъснато върху . Тогава на този сегмент има неопределен интеграл

∫f(x)dx = F(x) + C

и се провежда Формула на Нютон-Лайбниц, свързващ определения интеграл с неопределения интеграл:

F(b) - F(a). (8,6)

Геометрична интерпретация: определеният интеграл е площта на криволинеен трапец, ограничен отгоре от кривата y=f(x), прави x = a и x = b и сегмент от оста вол.

Неправилни интеграли

Интеграли с безкрайни граници и интеграли на прекъснати (неограничени) функции се наричат не твоя собствена. Неправилни интеграли от първи род -Това са интеграли върху безкраен интервал, дефиниран както следва:

(8.7)

Ако тази граница съществува и е крайна, тогава тя се нарича конвергентен неправилен интеграл на f(x)на интервала [a,+ ∞), и се извиква функцията f(x). интегрируеми в безкраен интервал[a,+ ∞). В противен случай се казва, че интегралът е не съществува или се разминава.

Неправилните интеграли на интервалите (-∞,b] и (-∞, + ∞) се дефинират по подобен начин:

Нека дефинираме понятието интеграл на неограничена функция. Ако f(x) е непрекъснато за всички стойности хсегмент , с изключение на точката c, в която f(x) има безкраен прекъсване, тогава неправилен интеграл от втория вид f(x) вариращи от a до bсумата се нарича:

ако тези граници съществуват и са крайни. Обозначаване:

Примери за интегрални изчисления

Пример 3.30.Изчислете ∫dx/(x+2).

Решение.Нека означим t = x+2, тогава dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.

Пример 3.31. Намерете ∫ tgxdx.

Решение.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Нека t=cosx, тогава ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Пример3.32 . Намерете ∫dx/sinx

Решение.

Пример3.33. Намирам .

Решение. = .

Пример3.34 . Намерете ∫arctgxdx.

Решение. Нека интегрираме по части. Нека означим u=arctgx, dv=dx. Тогава du = dx/(x 2 +1), v=x, откъдето ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; защото
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Пример3.35 . Изчислете ∫lnxdx.

Решение.Прилагайки формулата за интегриране по части, получаваме:
u=lnx, dv=dx, du=1/x dx, v=x. Тогава ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Пример3.36 . Изчислете ∫e x sinxdx.

Решение.Нека означим u = e x, dv = sinxdx, тогава du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Също така интегрираме интеграла ∫e x cosxdx по части: u = e x, dv = cosxdx, du=e x dx, v=sinx. Ние имаме:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Получихме отношението ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, от което 2∫e x sinx dx = - e x cosx + e x sinx + C.

Пример 3.37. Изчислете J = ∫cos(lnx)dx/x.

Решение.Тъй като dx/x = dlnx, тогава J= ∫cos(lnx)d(lnx). Заменяйки lnx с t, стигаме до интеграла на таблицата J = ∫ costdt = sint + C = sin(lnx) + C.

Пример 3.38 . Изчислете J = .

Решение.Като се има предвид, че = d(lnx), заместваме lnx = t. Тогава J = .

Пример 3.39 . Изчислете интеграла J = .

Решение.Ние имаме: . Следователно =
=
=. въведено по този начин: sqrt(tan(x/2)).

И ако в прозореца с резултати щракнете върху Покажи стъпки в горния десен ъгъл, ще получите подробно решение.

Формулата за интегриране по части изглежда така:
.

Методът на интегриране по части се състои в прилагането на тази формула. При практическо приложение си струва да се отбележи, че u и v са функции на интегриращата променлива. Нека променливата за интегриране бъде обозначена като x (символът след диференциалния знак d в края на интегралната нотация). Тогава u и v са функции на x: u(x) и v(x) .
Тогава
, .
А формулата за интегриране по части приема формата:
.

Тоест функцията интегранд трябва да се състои от произведението на две функции:
,
едното от които означаваме като u: g(x) = u, а за другото трябва да се изчисли интегралът (по-точно трябва да се намери първоизводната):
, тогава dv = f(x) dx .

В някои случаи f(x) = 1 . Тоест в интеграла
,
можем да поставим g(x) = u, x = v.

Резюме

Така че при този метод формулата за интегриране по части трябва да се запомни и приложи в две форми:
;
.

Интеграли, изчислени чрез интегриране по части

Интеграли, съдържащи логаритми и обратни тригонометрични (хиперболични) функции

Интегралите, съдържащи логаритми и обратни тригонометрични или хиперболични функции, често се интегрират по части. В този случай частта, която съдържа логаритъм или обратни тригонометрични (хиперболични) функции, се означава с u, а останалата част с dv.

Ето примери за такива интеграли, които се изчисляват по метода на интегриране по части:
, , , , , , .

Интеграли, съдържащи произведението на полином и sin x, cos x или e x

С помощта на формулата за интегриране по части се намират интеграли от вида:
, , ,
където P(x) е полином от x. При интегриране полиномът P(x) се означава с u и e ax dx, cos ax dxили sin ax dx- чрез dv.

Ето примери за такива интеграли:
, , .

Примери за изчисляване на интеграли с помощта на метода на интегриране по части

Примери за интеграли, съдържащи логаритми и обратни тригонометрични функции

Пример

Изчислете интеграла:

Подробно решение

Тук подинтегралната функция съдържа логаритъм. Правене на замествания
u = в х,
dv = x 2 dx.
Тогава
,
.

Изчисляваме оставащия интеграл:
.
Тогава
.
В края на изчисленията е необходимо да добавите константата C, тъй като неопределеният интеграл е множеството от всички първоизводни. Може да се добави и в междинни изчисления, но това само би затрупало изчисленията.

По-кратко решение

Можете да представите решението в по-кратък вариант. За да направите това, не е необходимо да правите замествания с u и v, но можете да групирате факторите и да приложите формулата за интегриране по части във втората форма.

.

Отговор

Примери за интеграли, съдържащи произведението на полином и sin x, cos x или ex

Пример

Изчислете интеграла:
.

Решение

Нека въведем показателя под диференциалния знак:
e - x dx = - e - x d(-x) = - d(e - x).

Нека интегрираме по части.
.
Използваме и метода на интегриране по части.
.
.
.
Най-накрая имаме.