বাড়ি প্রতিরোধ ফাংশনের বিরতি পয়েন্ট উল্লেখ করুন। ফাংশন বিচ্ছিন্নতা পয়েন্টের শ্রেণীবিভাগ

প্রতিরোধ

ফাংশনের বিরতি পয়েন্ট উল্লেখ করুন। ফাংশন বিচ্ছিন্নতা পয়েন্টের শ্রেণীবিভাগ

সংজ্ঞা। একটি ফাংশন f(x) কিছু ব্যবধানে সংজ্ঞায়িত করা যাক এবং x 0 এই ব্যবধানে একটি বিন্দু হবে। যদি, তাহলে f(x) x 0 বিন্দুতে অবিচ্ছিন্ন বলা হয়।
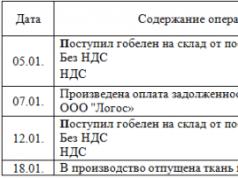
সংজ্ঞা থেকে এটি অনুসরণ করে যে আমরা ধারাবাহিকতা সম্পর্কে কেবলমাত্র সেই পয়েন্টগুলির সাথেই কথা বলতে পারি যেখানে f(x) সংজ্ঞায়িত করা হয়েছে (একটি ফাংশনের সীমা সংজ্ঞায়িত করার সময়, এই ধরনের শর্ত সেট করা হয়নি)। ক্রমাগত ফাংশন জন্য

, অর্থাৎ, অপারেশন f এবং lim পরিবর্তনযোগ্য। তদনুসারে, একটি বিন্দুতে একটি ফাংশনের সীমার দুটি সংজ্ঞাকে ধারাবাহিকতার দুটি সংজ্ঞা দেওয়া যেতে পারে - "অনুক্রমের ভাষায়" এবং "অসমতার ভাষায়" (ε-δ এর ভাষায়)। এটা আপনি নিজেই এটি করার পরামর্শ দেওয়া হয়.
ব্যবহারিক ব্যবহারের জন্য, কখনও কখনও বৃদ্ধির ভাষায় ধারাবাহিকতা সংজ্ঞায়িত করা আরও সুবিধাজনক।
মান Δx=x-x 0 কে আর্গুমেন্টের বৃদ্ধি বলা হয় এবং Δy=f(x)-f(x 0) হল ফাংশনের বৃদ্ধি যখন বিন্দু x 0 থেকে বিন্দু x এ চলে যায়।
সংজ্ঞা। f(x) কে x 0 বিন্দুতে সংজ্ঞায়িত করা যাক। একটি ফাংশন f(x) একটি বিন্দু x 0 এ অবিচ্ছিন্ন বলা হয় যদি এই বিন্দুতে আর্গুমেন্টের একটি অসীম বৃদ্ধি ফাংশনের একটি অসীম বৃদ্ধির সাথে মিলে যায়, অর্থাৎ, Δx→0 এর জন্য Δy→0।

উদাহরণ 1. প্রমাণ করুন যে x এর যেকোনো মানের জন্য y=sinx ফাংশন অবিচ্ছিন্ন।
সমাধান। x 0 একটি নির্বিচারে বিন্দু হতে দিন। এটিকে একটি বৃদ্ধি Δx দিলে, আমরা x=x 0 +Δx বিন্দু পাই। তারপর . আমরা পেতে .
সংজ্ঞা। y=f(x) ফাংশনটিকে ডানে (বামে) x 0 বিন্দুতে অবিচ্ছিন্ন বলা হয় যদি
.
একটি অভ্যন্তরীণ বিন্দুতে অবিচ্ছিন্ন একটি ফাংশন ডান এবং বাম উভয়ই অবিচ্ছিন্ন হবে। কথোপকথনটিও সত্য: যদি একটি ফাংশন বাম এবং ডানদিকে একটি বিন্দুতে অবিচ্ছিন্ন থাকে, তবে এটি সেই বিন্দুতে অবিচ্ছিন্ন থাকবে। যাইহোক, একটি ফাংশন শুধুমাত্র এক দিকে অবিচ্ছিন্ন হতে পারে। উদাহরণস্বরূপ, জন্য , , f(1)=1, অতএব, এই ফাংশনটি শুধুমাত্র বাম দিকে অবিচ্ছিন্ন (এই ফাংশনের গ্রাফের জন্য, উপরে অনুচ্ছেদ 5.7.2 দেখুন)।
সংজ্ঞা। একটি ফাংশন কিছু ব্যবধানে অবিচ্ছিন্ন বলা হয় যদি এটি এই ব্যবধানের প্রতিটি বিন্দুতে অবিচ্ছিন্ন থাকে।
বিশেষ করে, যদি ব্যবধানটি একটি সেগমেন্ট হয়, তাহলে একতরফা ধারাবাহিকতা তার প্রান্তে নিহিত থাকে।

ক্রমাগত ফাংশন বৈশিষ্ট্য

1. সমস্ত প্রাথমিক ফাংশন তাদের সংজ্ঞার ডোমেনে অবিচ্ছিন্ন।
2. যদি f(x) এবং φ(x), একটি নির্দিষ্ট ব্যবধানে প্রদত্ত, এই ব্যবধানের x 0 বিন্দুতে অবিচ্ছিন্ন থাকে, তাহলে ফাংশনগুলিও এই বিন্দুতে অবিচ্ছিন্ন থাকবে।
3. যদি X থেকে x 0 বিন্দুতে y=f(x) অবিচ্ছিন্ন থাকে এবং Y থেকে সংশ্লিষ্ট বিন্দু y 0 =f(x 0) এ z=φ(y) অবিচ্ছিন্ন থাকে, তাহলে জটিল ফাংশন z=φ(f(x)) x 0 বিন্দুতে একটানা থাকবে।

ফাংশন বিরতি এবং তাদের শ্রেণীবিভাগ

x 0 বিন্দুতে f(x) ফাংশনের ধারাবাহিকতার একটি চিহ্ন হল সমতা, যা তিনটি শর্তের উপস্থিতি বোঝায়:
1) f(x) বিন্দু x 0 এ সংজ্ঞায়িত করা হয়;
2)

;
3) .
যদি এই প্রয়োজনীয়তার অন্তত একটি লঙ্ঘন করা হয়, তাহলে x 0 কে ফাংশনের বিরতি পয়েন্ট বলা হয়। অন্য কথায়, একটি বিরতি পয়েন্ট এমন একটি বিন্দু যেখানে এই ফাংশনটি অবিচ্ছিন্ন নয়। বিরতি পয়েন্টের সংজ্ঞা থেকে এটি অনুসরণ করে যে একটি ফাংশনের বিরতি পয়েন্টগুলি হল:
ক) ফাংশনের সংজ্ঞার ডোমেনের অন্তর্গত পয়েন্ট যেখানে f(x) ধারাবাহিকতার বৈশিষ্ট্য হারায়,
b) পয়েন্টগুলি f(x) এর সংজ্ঞার ডোমেনের অন্তর্গত নয়, যা ফাংশনের সংজ্ঞার ডোমেনের দুটি ব্যবধানের সন্নিহিত বিন্দু।
উদাহরণস্বরূপ, একটি ফাংশনের জন্য, বিন্দু x=0 একটি বিরতি বিন্দু, যেহেতু এই বিন্দুতে ফাংশনটি সংজ্ঞায়িত করা হয়নি, এবং ফাংশন

x=1 বিন্দুতে একটি বিচ্ছিন্নতা রয়েছে, যা f(x) এর সংজ্ঞার ডোমেনের দুটি ব্যবধান (-∞,1) এবং (1,∞) এর সংলগ্ন এবং বিদ্যমান নেই।

নিম্নলিখিত শ্রেণীবিভাগ বিরতি পয়েন্ট জন্য গৃহীত হয়.
1) যদি x 0 বিন্দুতে সসীম থাকে এবং , কিন্তু f(x 0 +0)≠f(x 0 -0), তারপর x 0 বলা হয় প্রথম ধরনের বিচ্ছিন্নতা বিন্দু , এবং বলা হয় ফাংশন জাম্প .

উদাহরণ 2। ফাংশন বিবেচনা করুন
ফাংশনটি শুধুমাত্র x=2 বিন্দুতে ভাঙ্গা যেতে পারে (অন্যান্য বিন্দুতে এটি যেকোনো বহুপদীর মতো অবিচ্ছিন্ন)।
আমরা খুঁজে নেব , . যেহেতু একতরফা সীমাগুলি সসীম, কিন্তু একে অপরের সমান নয়, তাহলে x=2 বিন্দুতে ফাংশনটির প্রথম ধরণের একটি বিচ্ছিন্নতা রয়েছে। লক্ষ্য করুন , তাই এই বিন্দুতে ফাংশনটি ডানদিকে অবিচ্ছিন্ন (চিত্র 2)।
2) দ্বিতীয় ধরনের বিচ্ছিন্নতা পয়েন্ট বিন্দু বলা হয় যেখানে অন্তত একটি একতরফা সীমা ∞ সমান বা বিদ্যমান নেই।

উদাহরণ 3. y=2 1/ x ফাংশনটি x=0 ছাড়া x এর সকল মানের জন্য অবিচ্ছিন্ন। আসুন একতরফা সীমা খুঁজে বের করা যাক: , , তাই x=0 হল দ্বিতীয় প্রকারের একটি বিচ্ছিন্নতা বিন্দু (চিত্র 3)।
3) বিন্দু x=x 0 বলা হয় অপসারণযোগ্য বিরতি পয়েন্ট , যদি f(x 0 +0)=f(x 0 -0)≠f(x 0)।
আমরা এই ব্যবধানটিকে "বাতিল" করব এই অর্থে যে এটি সেট করার মাধ্যমে এই পয়েন্টে ফাংশনের মান পরিবর্তন করা (পুনরায় সংজ্ঞায়িত বা পুনরায় সংজ্ঞায়িত করা) যথেষ্ট, এবং ফাংশনটি x 0 বিন্দুতে অবিচ্ছিন্ন হয়ে যাবে।
উদাহরণ 4. জানা গেছে যে , এবং এই সীমা x যেভাবে শূন্যের দিকে থাকে তার উপর নির্ভর করে না। কিন্তু x=0 বিন্দুতে ফাংশনটি সংজ্ঞায়িত করা হয়নি। যদি আমরা f(0)=1 সেট করে ফাংশনটিকে পুনরায় সংজ্ঞায়িত করি, তাহলে এটি এই বিন্দুতে অবিচ্ছিন্ন হতে দেখা যায় (অন্যান্য বিন্দুতে এটি অবিচ্ছিন্ন ফাংশন sinx এবং x এর ভাগফল হিসাবে অবিচ্ছিন্ন)।
উদাহরণ 5। একটি ফাংশনের ধারাবাহিকতা পরীক্ষা করুন .
সমাধান। y=x 3 এবং y=2x ফাংশনগুলি নির্দেশিত ব্যবধান সহ সর্বত্র সংজ্ঞায়িত এবং অবিচ্ছিন্ন। চলুন x=0 ব্যবধানের সংযোগ বিন্দু পরীক্ষা করা যাক:
, , আমরা এটি পাই, যা বোঝায় যে x=0 বিন্দুতে ফাংশনটি অবিচ্ছিন্ন।
সংজ্ঞা। প্রথম ধরণের বা অপসারণযোগ্য বিচ্ছিন্নতার সীমিত সংখ্যক বিচ্ছিন্নতা বিন্দু ব্যতীত একটি ব্যবধানে অবিচ্ছিন্ন একটি ফাংশনকে এই ব্যবধানে পিসওয়াইজ অবিচ্ছিন্ন বলা হয়।

অবিচ্ছিন্ন ফাংশন উদাহরণ

উদাহরণ 1. x=2 বিন্দু ছাড়া (-∞,+∞) ফাংশনটি সংজ্ঞায়িত এবং অবিচ্ছিন্ন। বিরতির ধরন নির্ধারণ করা যাক। কারন

এবং

, তারপর x=2 বিন্দুতে দ্বিতীয় ধরণের একটি বিচ্ছিন্নতা রয়েছে (চিত্র 6)।

উদাহরণ 2। x=0 ছাড়া সকল x এর জন্য ফাংশনটি সংজ্ঞায়িত এবং অবিচ্ছিন্ন, যেখানে হর শূন্য। আসুন x=0 বিন্দুতে একতরফা সীমা খুঁজে পাই:
একতরফা সীমা সীমিত এবং ভিন্ন, তাই, x=0 হল প্রথম ধরণের একটি বিচ্ছিন্নতা বিন্দু (চিত্র 7)।

উদাহরণ 3. ফাংশনটি কোন পয়েন্টে এবং কি ধরনের বিচ্ছিন্নতা রয়েছে তা নির্ধারণ করুন

এই ফাংশনটি [-2,2] এ সংজ্ঞায়িত করা হয়েছে। যেহেতু x 2 এবং 1/x ব্যবধানে অবিচ্ছিন্ন [-2,0] এবং, যথাক্রমে, বিরতি শুধুমাত্র ব্যবধানের সংযোগস্থলে, অর্থাৎ x=0 বিন্দুতে ঘটতে পারে। যেহেতু, তাহলে x=0 হল দ্বিতীয় ধরনের একটি বিচ্ছিন্নতা বিন্দু।

উদাহরণ 4. ফাংশন ফাঁক দূর করা কি সম্ভব:
ক) বিন্দু x = 2 এ;
খ) বিন্দু x = 2 এ;
ভি) বিন্দু x = 1 এ?
সমাধান। উদাহরণ সম্পর্কে ক) আমরা অবিলম্বে বলতে পারি যে x=2 বিন্দুতে বিচ্ছিন্নতা f(x) দূর করা যাবে না, যেহেতু এই বিন্দুতে অসীম একতরফা সীমা রয়েছে (উদাহরণ 1 দেখুন)।
b) ফাংশন g(x) যদিও x=2 বিন্দুতে সসীম একতরফা সীমা রয়েছে

(,),

কিন্তু তারা একত্রিত হয় না, তাই ব্যবধানটিও দূর করা যায় না।
c) বিচ্ছিন্নতা বিন্দুতে φ(x) ফাংশন x=1 এর সমান একতরফা সসীম সীমা রয়েছে: অতএব, f(1)=2 এর পরিবর্তে f(1)=1 বসিয়ে x=1-এ ফাংশনটিকে পুনরায় সংজ্ঞায়িত করে ফাঁকটি দূর করা যেতে পারে।

উদাহরণ 5। দেখাও যে Dirichlet ফাংশন

সাংখ্যিক অক্ষের প্রতিটি বিন্দুতে বিচ্ছিন্ন।
সমাধান। ধরা যাক x 0 (-∞,+∞) থেকে যেকোনো বিন্দু। এর যেকোন আশেপাশে যৌক্তিক এবং অযৌক্তিক উভয় পয়েন্ট রয়েছে। এর মানে হল x 0-এর যেকোন আশেপাশে ফাংশনের মান 0 এবং 1 এর সমান হবে। এই ক্ষেত্রে, বাম বা ডানদিকে x 0 বিন্দুতে ফাংশনের একটি সীমা থাকতে পারে না, যার মানে যে ডিরিচলেট ফাংশনটি বাস্তব অক্ষের প্রতিটি বিন্দুতে দ্বিতীয় ধরণের বিচ্ছিন্নতা রয়েছে।

উদাহরণ 6. ফাংশন ব্রেকপয়েন্ট খুঁজুন

এবং তাদের ধরন নির্ধারণ করুন।
সমাধান। বিন্দুগুলি ভাঙার সন্দেহজনক পয়েন্টগুলি হল x 1 =2, x 2 =5, x 3 =3।
x 1 =2 f(x) বিন্দুতে দ্বিতীয় ধরনের একটি বিচ্ছিন্নতা আছে, যেহেতু
.
বিন্দু x 2 =5 হল ধারাবাহিকতার একটি বিন্দু, যেহেতু এই বিন্দুতে এবং এর আশেপাশে ফাংশনের মান দ্বিতীয় লাইন দ্বারা নির্ধারিত হয়, প্রথমটি নয়:।
আসুন x 3 =3 বিন্দু পরীক্ষা করি: ,

, যা থেকে এটি অনুসরণ করে যে x=3 হল প্রথম ধরণের একটি বিচ্ছিন্নতা বিন্দু।

জন্য স্বাধীন সিদ্ধান্ত.
ধারাবাহিকতার জন্য ফাংশন পরীক্ষা করুন এবং বিচ্ছিন্নতা বিন্দুর ধরন নির্ধারণ করুন:
1) ; উত্তর: x=-1 - অপসারণযোগ্য বিচ্ছিন্নতার বিন্দু;
2) ; উত্তর: x=8 বিন্দুতে দ্বিতীয় ধরণের বিচ্ছিন্নতা;
3) ; উত্তর: x=1-এ প্রথম ধরনের বিচ্ছিন্নতা;
4)
উত্তর: x 1 =-5 বিন্দুতে একটি অপসারণযোগ্য ব্যবধান আছে, x 2 =1 বিন্দুতে দ্বিতীয় ধরনের একটি ফাঁক রয়েছে এবং x 3 =0 বিন্দুতে প্রথম ধরনের একটি ফাঁক রয়েছে।
5) কিভাবে A সংখ্যাটি নির্বাচন করা উচিত যাতে ফাংশনটি

x=0 এ একটানা থাকবে?
উত্তরঃ A=2।
6) সংখ্যা A নির্বাচন করা সম্ভব যাতে ফাংশন

x=2 এ একটানা থাকবে?
উত্তরঃ না।

একটি বিন্দুতে একটি ফাংশনের ধারাবাহিকতা। ফাংশন y = f(x ) বলা হয় unpre-

বিন্দু x 0 এ ঝাঁকুনি যদি:

1) এই ফাংশন বিন্দু কিছু আশেপাশে সংজ্ঞায়িত করা হয় x 0;

2) একটা সীমা আছে f(x);

→ x 0

3) এই সীমা মানের সমান x 0 বিন্দুতে ফাংশন, যেমন limf (x ) = f (x 0 )।
		x→x0
শেষ শর্তটি শর্ত লিমের সমতুল্য		y = 0, যেখানে x = x − x 0 – কখন
	x→ 0
আর্গুমেন্টের ঘূর্ণন, y = f (x 0 +	x )− f (x 0 ) – ফাংশনের বৃদ্ধি, অনুরূপ
যুক্তি বৃদ্ধি	x, অর্থাৎ ফাংশন	f(x) x 0 এ একটানা থাকে

যদি এবং শুধুমাত্র এই সময়ে আর্গুমেন্টের একটি অসীম বৃদ্ধি ফাংশনের একটি অসীম বৃদ্ধির সাথে মিলে যায়।

একমুখী ধারাবাহিকতা।ফাংশন y = f(x) কে একটানা বলে

পয়েন্টএক্স 0 এ বাম দিকে যদি এটি কিছু অর্ধ-ব্যবধানে সংজ্ঞায়িত করা হয় (a ;x 0 ]

এবং লিম f (x) = f (x 0)।

x→ x0 − 0

একটি ফাংশন y = f (x) x 0 বিন্দুতে ডান অবিচ্ছিন্ন বলা হয় যদি এটি op- হয়।

একটি নির্দিষ্ট অর্ধ-ব্যবধানে বিতরণ করা হয় [ x 0 ;a ) এবং limf (x )= f (x 0 )।

x→ x0 + 0

ফাংশন y = f(x)		বিন্দু x 0 এ অবিচ্ছিন্ন	তারপর এবং শুধুমাত্র যখন সে
একটানা
lim f (x) = limf (x) = limf (x) = f (x 0)।
x→ x0 + 0	x→ x0 − 0	x→x0

একটি সেটে একটি ফাংশনের ধারাবাহিকতা। ফাংশন y = f(x) বলা হয়

সেটে একটানা X যদি এটি এই সেটের প্রতিটি বিন্দুতে অবিচ্ছিন্ন থাকে। অধিকন্তু, যদি একটি ফাংশনকে সাংখ্যিক অক্ষের একটি নির্দিষ্ট ব্যবধানের শেষে সংজ্ঞায়িত করা হয়, তবে এই বিন্দুতে ধারাবাহিকতা ডান বা বাম দিকে ধারাবাহিকতা হিসাবে বোঝা যায়। বিশেষ করে, ফাংশন y = f (x) বলা হয় অ-

সেগমেন্টে বিচ্ছিন্ন [ক; b] যদি সে

1) বিরতির প্রতিটি পয়েন্টে একটানা(a;b);

2) একটি বিন্দুতে সঠিক অবিচ্ছিন্ন a;

3) একটি বিন্দুতে অবিচ্ছিন্ন রেখে দেওয়া হয়খ.

ফাংশন বিরতি পয়েন্ট. y = f (x) ফাংশনের সংজ্ঞার ডোমেনের অন্তর্গত x 0 পয়েন্ট বা এই ডোমেনের সীমানা বিন্দু বলা হয়

এই ফাংশনের বিরতি পয়েন্ট, iff(x) সেই বিন্দুতে একটানা থাকে না।

বিচ্ছিন্নতা পয়েন্টগুলি প্রথম এবং দ্বিতীয় ধরণের বিচ্ছিন্নতা বিন্দুতে বিভক্ত:

1) যদি সসীম সীমা থাকে lim f (x )= f (x 0 − 0) এবং

x→ x0 − 0

	f (x)= f (x 0 + 0), এবং তিনটি সংখ্যাই f (x 0 − 0), f (x 0 + 0),		f (x 0 ) সমান
x→ x0 + 0
নিজেদের মধ্যে, তারপর x 0		প্রথম ধরনের একটি discontinuity পয়েন্ট বলা হয়.
	বিশেষ করে, যদি x 0 বিন্দুতে ফাংশনের বাম এবং ডান সীমা থাকে		মধ্যে সমান
	নিজেকে, কিন্তু	এই সময়ে ফাংশন মানের সমান নয়:

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , তারপর x 0 কে একটি অপসারণযোগ্য বিচ্ছিন্নতা বিন্দু বলা হয়।

এই ক্ষেত্রে, f (x 0 )= A সেট করে, আপনি x 0 বিন্দুতে ফাংশনটি পরিবর্তন করতে পারেন

যাতে এটি ক্রমাগত হয়ে যায় ( ধারাবাহিকতা দ্বারা ফাংশন পুনরায় সংজ্ঞায়িত করুন) পার্থক্য f (x 0 + 0)− f (x 0 − 0) বলা হয় একটি বিন্দুতে একটি ফাংশন জাম্প x 0।

অপসারণযোগ্য বিচ্ছিন্নতা বিন্দুতে ফাংশন জাম্প শূন্য।

2) বিচ্ছিন্নতা বিন্দুগুলিকে বলা হয় যেগুলি প্রথম ধরণের বিচ্ছিন্নতা বিন্দু নয় দ্বিতীয় ধরনের ব্রেকপয়েন্ট. দ্বিতীয় প্রকারের বিচ্ছিন্নতার বিন্দুতে, f (x 0 − 0) এবং f (x 0 + 0) একতরফা সীমার মধ্যে অন্তত একটি বিদ্যমান নেই বা অসীম।

একটি বিন্দুতে ক্রমাগত ফাংশনের বৈশিষ্ট্য।

		f(x)	এবং g (x) x 0 বিন্দুতে একটানা থাকে, তারপর ফাংশন
f(x)±g(x),	f(x)g(x) এবং	f(x)	(যেখানে g (x)≠ 0) x বিন্দুতেও একটানা থাকে।
f(x)±g(x),	f(x)g(x) এবং		(যেখানে g (x)≠ 0) x বিন্দুতেও একটানা থাকে।
		g(x)
		g(x)

2) যদি x 0 বিন্দুতে u (x) ফাংশনটি অবিচ্ছিন্ন হয় এবং ফাংশন f (u) অবিচ্ছিন্ন হয়

u 0 = u (x 0) বিন্দুতে, তারপর x 0 বিন্দুতে জটিল ফাংশন f (u (x)) অবিচ্ছিন্ন।

3) সমস্ত মৌলিক প্রাথমিক ফাংশন (c, x a, a x, loga x, sinx, cosx, tgx, ctgx, secx, cosecx, arcsinx, arccosx, arctgx, arcctgx) প্রতিটিতে অবিচ্ছিন্ন

তাদের সংজ্ঞার ডোমেনের বিন্দুতে।

বৈশিষ্ট্য থেকে 1)–3) এটি অনুসরণ করে যে সমস্ত প্রাথমিক ফাংশন (মূল প্রাথমিক ফাংশনগুলি থেকে প্রাপ্ত ফাংশনগুলি একটি সীমিত সংখ্যক গাণিতিক ক্রিয়াকলাপ এবং রচনা ক্রিয়াকলাপ ব্যবহার করে) তাদের সংজ্ঞার ডোমেনের প্রতিটি বিন্দুতেও অবিচ্ছিন্ন থাকে।

একটি ব্যবধানে ক্রমাগত ফাংশনের বৈশিষ্ট্য।

1) (মধ্যবর্তী মান উপপাদ্য) ফাংশন f(x) সংজ্ঞায়িত করা যাক

অন এবং সেগমেন্টে একটানা আছে [a;b]। তারপর যেকোন নম্বরের জন্য C ঢেকে দেওয়া হয়েছে

f (a) এবং f (b), (f (a) সংখ্যার মধ্যে< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (বলজানো-কচি উপপাদ্য

সেগমেন্ট [a;b] এ বিচ্ছিন্ন এবং এর প্রান্তে বিভিন্ন চিহ্নের মান গ্রহণ করে।

তারপরে কমপক্ষে একটি বিন্দু x 0 [ a ; b ] যেমন f (x 0 )= 0।

3) (1ম উইয়েরস্ট্রাসের উপপাদ্য) ফাংশন f (x) সংজ্ঞায়িত করা যাক এবং

অংশে ছেঁড়া [a;b]। তারপর এই ফাংশন এই বিভাগে সীমাবদ্ধ.

4) (২য় উইয়েরস্ট্রাসের উপপাদ্য) ফাংশন f (x) সংজ্ঞায়িত করা যাক এবং

সেগমেন্টে তাড়াহুড়ো	[ক;খ]। তারপর এই ফাংশনটি ব্যবধানে পৌঁছায় [ a ; b ]
সর্বশ্রেষ্ঠ	অন্তত	মান, যেমন	বিদ্যমান
x1, x2 [a; খ],	কোন জন্য	পয়েন্ট x [a;b]	ন্যায্য	অসমতা

f (x 1 )≤ f (x )≤ f (x 2 )।

উদাহরণ 5.17। ধারাবাহিকতার সংজ্ঞা ব্যবহার করে প্রমাণ করুন যে ফাংশন y = 3x 2 + 2x − 5 সংখ্যারেখার একটি নির্বিচারে x 0 এ অবিচ্ছিন্ন।

সমাধান: পদ্ধতি 1: x 0 কে সংখ্যা অক্ষের একটি নির্বিচারে বিন্দু হতে দিন। আপনি-

আমরা প্রথমে f (x) ফাংশনের সীমাকে x → x 0 হিসাবে গণনা করি, ফাংশনের যোগফল এবং গুণফলের সীমার উপর উপপাদ্য প্রয়োগ করে:

lim f (x )= lim(3x 2 + 2x − 5)= 3(limx )2 + 2 limx − 5= 3x 2					− 5.
x→x0	x→x0	x→x0	x→x0
x→x0	x→x0	x→x0	x→x0
তারপরে আমরা x:f (x) = 3x 2 পয়েন্টে ফাংশনের মান গণনা করি					− 5 .

প্রাপ্ত ফলাফল তুলনা, আমরা দেখতে				lim f (x) = f (x 0) যা অনুযায়ী
				x→x0

সংজ্ঞা এবং অর্থ x 0 বিন্দুতে বিবেচনাধীন ফাংশনের ধারাবাহিকতা।

পদ্ধতি 2: যাক		x – পয়েন্টএক্স 0 এ আর্গুমেন্টের বৃদ্ধি। চলুন চিঠিপত্র খুঁজে
যথাযথ	বৃদ্ধি		y = f(x0 + x) − f(x0 ) =
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x −5)

6 x x+ (x) 2	2x = (6x + 2)x + (x)2।

এখন আর্গুমেন্টের বৃদ্ধির সময় ফাংশন বৃদ্ধির সীমা গণনা করা যাক
		চেষ্টা করে

	y = লিম (6x + 2)	x + (x )2 = (6x + 2) lim		x + (limx)2 = 0।
x→ 0	x→ 0		x→ 0	x→ 0

সুতরাং, lim y = 0, যার অর্থ সংজ্ঞা ধারাবাহিকতা দ্বারা

x→ 0

যেকোনো x 0 R এর জন্য ফাংশন।

উদাহরণ 5.18। f (x) ফাংশনের বিচ্ছিন্নতা বিন্দুগুলি খুঁজুন এবং তাদের ধরন নির্ধারণ করুন। ভিতরে

একটি অপসারণযোগ্য বিচ্ছিন্নতার ক্ষেত্রে, ধারাবাহিকতা দ্বারা ফাংশনটি সংজ্ঞায়িত করুন:

1) f (x) = 1− x 2 এ x< 3;

5x যখন x ≥ 3

2) f (x) = x 2 + 4 x + 3;

x+1



f(x)=
	x4 (x− 2)
f(x)= আর্কটান
		(x − 5)

সমাধান: 1) এই ফাংশনের সংজ্ঞার ডোমেইন হল সম্পূর্ণ সংখ্যা

y অক্ষ (−∞ ;+∞ )। ব্যবধানে (−∞ ;3), (3;+∞ ) ফাংশনটি অবিচ্ছিন্ন। একটি বিচ্ছিন্নতা শুধুমাত্র x = 3 বিন্দুতে সম্ভব, যেখানে ফাংশনের বিশ্লেষণাত্মক স্পেসিফিকেশন পরিবর্তিত হয়।

আসুন নির্দেশিত বিন্দুতে ফাংশনের একতরফা সীমা খুঁজে পাই:

f (3− 0)= lim (1− x 2 )= 1− 9= 8;

x →3 −0

f (3+ 0)= lim 5x = 15।

x →3 +0

আমরা দেখি যে বাম এবং ডান সীমা সীমাবদ্ধ, তাই x = 3
ফেটে যাওয়া I		f(x)। ফাংশন লাফ
f (3+ 0)− f (3− 0)= 15− 8= 7।
	f (3)= 5 3= 15= f (3+ 0) , তাই বিন্দুতে		x = 3

f(x) সঠিক অবিচ্ছিন্ন।

2) বিন্দু ব্যতীত সমগ্র সংখ্যারেখায় ফাংশনটি অবিচ্ছিন্ন x = − 1, যেখানে এটি সংজ্ঞায়িত করা হয়নি। লব প্রসারিত করে f(x) এর রাশিটিকে রূপান্তর করা যাক

উপাদানে ভগ্নাংশ:		f(x)=		4 x +3	(x + 1)(x + 3)	x ≠ − 1 এর জন্য X + 3।
				x+1	x+1

x = −1 বিন্দুতে ফাংশনের একতরফা সীমা খুঁজে বের করা যাক:
	f(x)=lim	f (x )= lim(x + 3)= 2।
x →−1−0	x →−1 +0		x →−1

আমরা খুঁজে পেয়েছি যে অধ্যয়নের অধীনে বিন্দুতে ফাংশনের বাম এবং ডান সীমা বিদ্যমান, সীমাবদ্ধ এবং একে অপরের সমান, তাই x = −1 একটি অপসারণযোগ্য বিন্দু

সরলরেখা y = x + 3 একটি "খোঁচা" বিন্দু M (− 1;2) সহ। ফাংশনটি স্থায়ী হওয়ার জন্য

অবিচ্ছিন্ন, আমাদের f (− 1) = f (− 1− 0) = f (− 1 + 0) = 2 বসানো উচিত।

এইভাবে, x = − 1 বিন্দুতে ধারাবাহিকতা দ্বারা f (x) কে আরও সংজ্ঞায়িত করার পরে, আমরা সংজ্ঞার ডোমেন (−∞ ;+∞ ) সহ f * (x) = x + 3 ফাংশনটি পেয়েছি।

3) এই ফাংশনপ্রত্যেকের জন্য সংজ্ঞায়িত এবং অবিচ্ছিন্ন x পয়েন্ট ছাড়া

x = 0,x = 2, যেখানে ভগ্নাংশের হর শূন্য হয়ে যায়।

বিন্দু x = 0 বিবেচনা করুন:

যেহেতু শূন্যের একটি যথেষ্ট ছোট আশেপাশে ফাংশনটি শুধুমাত্র লাগে

ঋণাত্মক মানের জন্য, তারপর f (− 0) = lim		= −∞ = f (+0)	সেগুলো. বিন্দু
	(x − 2)
x →−0
x = 0 হল দ্বিতীয় ধরণের ফাংশনের একটি বিচ্ছিন্নতা বিন্দু	f(x)।

এখন বিন্দু x = 2 বিবেচনা করুন:

ফাংশনটি বিবেচনার বাম দিকে নেতিবাচক মান নেয়

পয়েন্ট এবং ইতিবাচক বেশী ডানদিকে, তাই			f (2− 0)=			= −∞,
					x4 (x− 2)
				x →2 −0
f (2+ 0) = লিম		= +∞। আগের ক্ষেত্রে যেমন, পয়েন্টএক্স = 2 এ
	(x − 2)
x →2 +0

tion এর বাম বা ডান কোন সীমাবদ্ধ সীমা নেই, অর্থাৎ এই সময়ে টাইপ II ফেটে যায়।

x = 5।

f (5− 0) = লিম আর্কটান

π,f (5+ 0)= লিম আর্কটান

x = 5

(x − 5)

x →5 −0

x →5 +0

কা ফেটে যাওয়া

f (5+ 0)− f (5− 0)=

π − (−

π ) = π (চিত্র 5.2 দেখুন)।

স্বাধীনভাবে সমাধান করতে সমস্যা

5.174। শুধুমাত্র সংজ্ঞা ব্যবহার করে, f(x) in ফাংশনের ধারাবাহিকতা প্রমাণ করুন

প্রতিটি পয়েন্ট x 0 R :

ক) f(x) = c= const;		খ) f (x) = x;
গ) f (x) = x 3;		d) f (x)= 5x 2 − 4x + 1;
e) f (x) = sinx.
5.175। যে ফাংশন প্রমাণ করুন	f(x) = x2	1 যখন x ≥ 0,	অবিরত আছে
		1 এ x< 0
সম্পূর্ণ সংখ্যা লাইন। এই ফাংশনের একটি গ্রাফ তৈরি করুন।
5.176। যে ফাংশন প্রমাণ করুন	f(x) = x2	1 যখন x ≥ 0,	অবিচ্ছিন্ন নয়
		x এ 0< 0

x = 0 বিন্দুতে, কিন্তু সেই বিন্দুতে অবিচ্ছিন্ন ডান। ফাংশন গ্রাফ করুন f(x)।

x = বিন্দুতে ঝাঁকুনি

কিন্তু এই মুহুর্তে বাম দিকে একটানা আছে। একটি গ্রাফ তৈরি করুন

ফাংশন f(x)।

5.178। গ্রাফ ফাংশন

ক) y =

x+1

খ) y= x+

x+1

এই ফাংশনের ব্রেকপয়েন্টে ধারাবাহিকতার শর্তগুলির মধ্যে কোনটি সন্তুষ্ট এবং কোনটি সন্তুষ্ট নয়?

5.179। ফাংশনের বিরতি পয়েন্ট উল্লেখ করুন

পাপ x		x ≠ 0 এর জন্য


		x = 0 এ

ধারাবাহিকতার শর্তগুলির মধ্যে কোনটি এই সময়ে সন্তুষ্ট এবং কোনটি পূরণ হয় না?

সংজ্ঞা ফাংশন বিরতি পয়েন্ট এবং তাদের প্রকারগুলি ফাংশনের ধারাবাহিকতার থিমের ধারাবাহিকতা। ধারাবাহিকতার ধারণার বিপরীতে একটি ফাংশনের বিরতি পয়েন্টের অর্থের একটি চাক্ষুষ (গ্রাফিক্যাল) ব্যাখ্যাও দেওয়া হয়। আসুন শিখি কিভাবে একটি ফাংশনের ব্রেকপয়েন্ট খুঁজে বের করতে হয় এবং তাদের প্রকারগুলি নির্ধারণ করতে হয়। এবং আমাদের এটি আমাদের সাহায্য করবে বিশ্বস্ত বন্ধুরা- বাম এবং ডান সীমা, সাধারণত একতরফা সীমা বলা হয়। যদি কারও একতরফা সীমাবদ্ধতার ভয় থাকে, আমরা শীঘ্রই তা দূর করব।

একটি গ্রাফের যে বিন্দুগুলি একে অপরের সাথে সংযুক্ত নয় তাকে বলা হয় ফাংশন বিরতি পয়েন্ট . এই ধরনের একটি ফাংশনের গ্রাফ, যা x=2 - বিন্দুতে বিচ্ছিন্নতা ভোগ করে - নীচের চিত্রে।

উপরের একটি সাধারণীকরণ নিম্নলিখিত সংজ্ঞা. যদি একটি ফাংশন একটি বিন্দুতে অবিচ্ছিন্ন না হয় তবে এই বিন্দুতে এটির একটি বিচ্ছিন্নতা থাকে এবং বিন্দুটিকে নিজেই বলা হয় বিরতি পয়েন্ট . বাধাগুলি প্রথম ধরণের এবং দ্বিতীয় ধরণের .

নির্ধারণ করার জন্য বিরতি পয়েন্টের প্রকার (চরিত্র) ফাংশন আত্মবিশ্বাসের সাথে খুঁজে পাওয়া প্রয়োজন সীমা, তাই একটি নতুন উইন্ডোতে সংশ্লিষ্ট পাঠ খোলার জন্য এটি একটি ভাল ধারণা। কিন্তু ব্রেকপয়েন্টের সাথে আমাদের কিছু নতুন এবং গুরুত্বপূর্ণ - একতরফা (বাম এবং ডান) সীমা রয়েছে। সাধারণভাবে এগুলি লেখা হয় (ডান সীমা) এবং (বাম সীমা)। সাধারণভাবে একটি সীমার ক্ষেত্রে যেমন, একটি ফাংশনের সীমা খুঁজে বের করার জন্য, আপনাকে X এর প্রতিস্থাপনের জন্য ফাংশনের অভিব্যক্তিতে X-কে প্রতিস্থাপন করতে হবে। কিন্তু, সম্ভবত, আপনি জিজ্ঞাসা করেন, ডান এবং বাম সীমার পার্থক্য কীভাবে হবে, যদি ডানের ক্ষেত্রে X-তে কিছু যোগ করা হয়, কিন্তু এটি শূন্য হয়, এবং বামটির ক্ষেত্রে X থেকে কিছু বিয়োগ করা হয়, কিন্তু এই কিছু - এছাড়াও শূন্য? এবং আপনি ঠিক হবে. অধিকাংশ ক্ষেত্রে.

কিন্তু একটি ফাংশনের বিচ্ছিন্নতা বিন্দু অনুসন্ধান এবং তাদের ধরন নির্ধারণের অনুশীলনে, দুটি সাধারণ ক্ষেত্রে রয়েছে যখন ডান এবং বাম সীমা সমান নয়:

একটি ফাংশনের সংখ্যা রেখার অংশের উপর নির্ভর করে দুটি বা ততোধিক রাশি থাকে যা x এর সাথে সম্পর্কিত (এই অভিব্যক্তিগুলি সাধারণত কোঁকড়া বন্ধনীতে লেখা হয় চ(এক্স)= );
X এর প্রতিস্থাপনের ফলস্বরূপ, আমরা হরটিতে একটি ভগ্নাংশ পাই যার হয় যোগ শূন্য (+0) বা বিয়োগ শূন্য (-0) থাকে এবং তাই এই ধরনের ভগ্নাংশের অর্থ হয় প্লাস ইনফিনিটি বা মাইনাস ইনফিনিটি, এবং এইগুলি হল সম্পূর্ণ ভিন্ন জিনিস।

প্রথম ধরনের বিচ্ছিন্নতা পয়েন্ট

প্রথম ধরনের ব্রেক পয়েন্ট: একটি ফাংশনের একটি সসীম (অর্থাৎ, অসীমের সমান নয়) বাম সীমা এবং একটি সসীম ডান সীমা উভয়ই রয়েছে, তবে ফাংশনটি একটি বিন্দুতে সংজ্ঞায়িত করা হয় না বা বাম এবং ডান সীমা আলাদা (সমান নয়)।

প্রথম ধরনের অপসারণযোগ্য বিচ্ছিন্নতার পয়েন্ট।বাম এবং ডান সীমা সমান। এই ক্ষেত্রে, একটি বিন্দুতে ফাংশনটিকে আরও সংজ্ঞায়িত করা সম্ভব। একটি বিন্দুতে একটি ফাংশন সংজ্ঞায়িত করার জন্য, সহজভাবে বলতে গেলে, বিন্দুগুলির একটি সংযোগ প্রদান করা যার মধ্যে একটি বিন্দু আছে যেখানে বাম এবং ডান সীমা একে অপরের সমান পাওয়া যায়। এই ক্ষেত্রে, সংযোগ শুধুমাত্র একটি বিন্দু প্রতিনিধিত্ব করা উচিত যেখানে ফাংশনের মান পাওয়া উচিত।

উদাহরণ 1.ফাংশনের ব্রেক পয়েন্ট এবং ব্রেক পয়েন্টের ধরন (চরিত্র) নির্ধারণ করুন।

দ্বিতীয় ধরনের বিচ্ছিন্নতা পয়েন্ট

দ্বিতীয় ধরণের ব্রেক পয়েন্ট: যে বিন্দুতে কমপক্ষে একটি সীমা (বাম বা ডান) অসীম (অনন্তের সমান)।

উদাহরণ 3.

সমাধান। এ ক্ষমতা জন্য অভিব্যক্তি থেকে eএটা স্পষ্ট যে ফাংশন বিন্দুতে সংজ্ঞায়িত করা হয় না। এই সময়ে ফাংশনের বাম এবং ডান সীমা খুঁজে বের করা যাক:

একটি সীমা অসীমের সমান, তাই বিন্দুটি দ্বিতীয় ধরণের একটি বিচ্ছিন্নতা বিন্দু। একটি ব্রেক পয়েন্ট সহ একটি ফাংশনের গ্রাফ উদাহরণের নীচে রয়েছে।

একটি ফাংশনের ব্রেকপয়েন্ট খোঁজা হয় একটি স্বাধীন কাজ বা এর অংশ হতে পারে সম্পূর্ণ ফাংশন গবেষণা এবং গ্রাফিং .

উদাহরণ 4.ফাংশনের ব্রেক পয়েন্ট এবং ফাংশনের জন্য ব্রেক পয়েন্টের ধরন (চরিত্র) নির্ধারণ করুন

সমাধান। 2 এ পাওয়ারের অভিব্যক্তি থেকে এটা স্পষ্ট যে ফাংশনটি বিন্দুতে সংজ্ঞায়িত করা হয়নি। এই পয়েন্টে ফাংশনের বাম এবং ডান সীমা খুঁজে বের করা যাক।

অপসারণযোগ্য ফাঁক।

সংজ্ঞা. ডট কফাংশনের অপসারণযোগ্য বিচ্ছিন্নতা বিন্দু বলা হয় y=f(x), যদি ফাংশনের সীমা থাকে f(x)এই সময়ে বিদ্যমান, কিন্তু বিন্দুতে কফাংশন f(x)হয় সংজ্ঞায়িত নয় বা একটি ব্যক্তিগত অর্থ আছে চ(ক), সীমা থেকে ভিন্ন f(x)এই মুহূর্তে.

উদাহরণ. উদাহরণস্বরূপ, ফাংশন

পয়েন্ট এ আছে x=0মেরামতযোগ্য ফাঁক। প্রকৃতপক্ষে, বিন্দুতে এই ফাংশনের সীমিত মান x=0 1 এর সমান। আংশিক মান 2 এর সমান।

যদি ফাংশন f(x)পয়েন্ট এ আছে কঅপসারণযোগ্য ফাঁক, তাহলে এই ব্যবধানটি অন্য পয়েন্টে ফাংশনের মান পরিবর্তন না করেই দূর করা যেতে পারে ক. এটি করার জন্য, বিন্দুতে ফাংশনের মান রাখা যথেষ্ট কএই সময়ে তার সীমা মানের সমান। সুতরাং, উপরে বিবেচনা করা উদাহরণে এটি করা যথেষ্ট f(0)=1এবং তারপর , অর্থাৎ ফাংশন f(x)বিন্দুতে অবিচ্ছিন্ন হয়ে যাবে x=0.

প্রথম ধরণের ব্যাঘাত।

সংজ্ঞা. ডট কএই বিন্দুতে ফাংশন হলে প্রথম ধরনের একটি বিচ্ছিন্নতা বিন্দু বলা হয় f(x)সসীম কিন্তু অসম ডান এবং বাম সীমা আছে

কিছু উদাহরণ দেওয়া যাক।

উদাহরণ. ফাংশন y=sgn xপয়েন্ট এ আছে x=0প্রথম ধরনের ফেটে যাওয়া। প্রকৃতপক্ষে, এবং এইভাবে এই সীমাগুলি একে অপরের সমান নয়।

উদাহরণ. ফাংশন , বিন্দু ছাড়া সর্বত্র সংজ্ঞায়িত x=1, বিন্দুতে আছে x=1প্রথম ধরনের ফেটে যাওয়া। প্রকৃতপক্ষে, .

দ্বিতীয় প্রকারের ব্যাঘাত।

সংজ্ঞা. ডট কএই বিন্দুতে ফাংশন থাকলে একে দ্বিতীয় ধরণের বিচ্ছিন্নতা বিন্দু বলা হয় f(x)একতরফা সীমার অন্তত একটি থাকে না বা যদি অন্তত একটি একতরফা সীমা অসীম হয়।

উদাহরণ. ফাংশন f(x) = tan x, স্পষ্টতই, প্রতিটি বিন্দুতে দ্বিতীয় ধরণের একটি বিচ্ছিন্নতা রয়েছে x k =π/2+π k, k=0, ± 1, ± 2,…, কারণ এই ধরনের প্রতিটি পয়েন্টে

উদাহরণ. ফাংশন বিন্দুতে দ্বিতীয় ধরনের একটি বিরতি আছে x=0, কারণ এই মুহুর্তে এটির ডান বা বাম সীমা নেই।

একটি অংশে একটি ফাংশনের ধারাবাহিকতা

সংজ্ঞা. একটি ব্যবধানে সংজ্ঞায়িত ফাংশন এবং এর প্রতিটি বিন্দুতে অবিরতকে এই অংশে অবিচ্ছিন্ন বলা হয়।

তদুপরি, পয়েন্টে ধারাবাহিকতার অধীনে কডানদিকে ধারাবাহিকতা এবং একটি বিন্দুতে ধারাবাহিকতা দ্বারা বোঝা যায় খ- বাম দিকে ধারাবাহিকতা।

আমরা বলব যে ফাংশন y=f(x), সেটে সংজ্ঞায়িত (এক্স)এটির উপরের (নিম্ন) প্রান্তে পৌঁছায় , যদি এমন একটি বিন্দু বিদ্যমান থাকে x 0 ∈(x), কি f(x 0)=β (f(x 0)=α).

[ওয়েয়ারস্ট্রাস] উপপাদ্য. একটি ব্যবধানে ক্রমাগত প্রতিটি ফাংশন সীমাবদ্ধ থাকে এবং তার উপরের সীমানায় এবং এটির নীচের সীমানায় পৌঁছে যায়।

উপপাদ্য [বোলজানো-কচি]. যদি ফাংশন y=f(x)সেগমেন্টে একটানা এবং f(a)=A, f(b)=B, তারপর যে কোনো জন্য গ, মধ্যে উপসংহার কএবং খ, যেমন একটি বিন্দু আছে ξ∈ , কি f(ξ)=C.

অন্য কথায়, একটি ব্যবধানে অবিচ্ছিন্ন একটি ফাংশন, যেকোনো দুটি মান গ্রহণ করে, তাদের মধ্যে থাকা যেকোনো মানও নেয়।

পরিণতি. যদি একটি ফাংশন একটি সেগমেন্টের উপর অবিচ্ছিন্ন থাকে এবং তার প্রান্তে বিভিন্ন চিহ্নের মান গ্রহণ করে, তাহলে এই সেগমেন্টে অন্তত একটি বিন্দু আছে যেখানে ফাংশনটি অদৃশ্য হয়ে যায়।

পরিণতি. ফাংশন যাক y=f(x)সেগমেন্টে একটানা এবং , . তারপর ফাংশন f(x)সেগমেন্ট থেকে সমস্ত মান নেয় এবং শুধুমাত্র এই মান.

এইভাবে, একটি ফাংশনের সমস্ত মানের সেট যা একটি নির্দিষ্ট সেগমেন্টে দেওয়া এবং অবিচ্ছিন্ন থাকে সেটিও একটি সেগমেন্ট।

ফাংশনের ধারাবাহিকতা। ব্রেকিং পয়েন্ট।

ষাঁড় হাঁটছে, দোল খাচ্ছে, দীর্ঘশ্বাস ফেলে যাচ্ছে:
- ওহ, বোর্ড ফুরিয়ে যাচ্ছে, এখন আমি পড়ে যাচ্ছি!

এই পাঠে আমরা একটি ফাংশনের ধারাবাহিকতার ধারণা, বিচ্ছিন্নতা বিন্দুর শ্রেণীবিভাগ এবং একটি সাধারণ ব্যবহারিক সমস্যা পরীক্ষা করব। ফাংশনের ধারাবাহিকতা অধ্যয়ন. বিষয়টির নাম থেকেই, অনেকে স্বজ্ঞাতভাবে অনুমান করে যে কী আলোচনা করা হবে এবং মনে করেন যে উপাদানটি বেশ সহজ। এটা সত্য. তবে এটি সাধারণ কাজ যা প্রায়শই অবহেলার জন্য শাস্তি দেওয়া হয় এবং সেগুলি সমাধান করার জন্য একটি সুপারফিশিয়াল পদ্ধতির। অতএব, আমি সুপারিশ করি যে আপনি নিবন্ধটি খুব সাবধানে অধ্যয়ন করুন এবং সমস্ত সূক্ষ্মতা এবং কৌশলগুলি ধরুন।

আপনি কি জানতে এবং করতে সক্ষম হতে হবে?খুব বেশী না. পাঠটি ভালভাবে শিখতে, আপনাকে এটি কী তা বুঝতে হবে একটি ফাংশনের সীমা. সঙ্গে পাঠক নিম্ন স্তরেরনিবন্ধটি বোঝার জন্য প্রস্তুতি যথেষ্ট ফাংশন সীমা। সমাধানের উদাহরণএবং দেখতে জ্যামিতিক অর্থম্যানুয়াল মধ্যে সীমা গ্রাফ এবং প্রাথমিক ফাংশন বৈশিষ্ট্য. এর সাথে নিজেকে পরিচিত করাও যুক্তিযুক্ত গ্রাফের জ্যামিতিক রূপান্তর, যেহেতু বেশিরভাগ ক্ষেত্রে অনুশীলনের সাথে একটি অঙ্কন তৈরি করা জড়িত। সম্ভাবনা প্রত্যেকের জন্য আশাবাদী, এবং এমনকি একটি পূর্ণ কেটলি পরবর্তী ঘন্টা বা দুই ঘন্টার মধ্যে নিজেই কাজটি মোকাবেলা করতে সক্ষম হবে!

ফাংশনের ধারাবাহিকতা। ব্রেকপয়েন্ট এবং তাদের শ্রেণীবিভাগ

ফাংশনের ধারাবাহিকতার ধারণা

আসুন কিছু ফাংশন বিবেচনা করি যা পুরো সংখ্যা লাইনে অবিচ্ছিন্ন:

অথবা, আরও সংক্ষিপ্তভাবে বলতে গেলে, আমাদের ফাংশন ক্রমাগত চালু থাকে (বাস্তব সংখ্যার সেট)।

ধারাবাহিকতার "ফিলিস্টাইন" মানদণ্ড কী? স্পষ্টতই শিডিউল ক্রমাগত ফাংশনকাগজ থেকে পেন্সিল উত্তোলন ছাড়া আঁকা যাবে.

এই ক্ষেত্রে, দুটি সহজ ধারণা পরিষ্কারভাবে আলাদা করা উচিত: একটি ফাংশনের ডোমেইনএবং ফাংশনের ধারাবাহিকতা. ভিতরে সাধারণ ক্ষেত্রে এটা একই জিনিস না. উদাহরণ স্বরূপ:

এই ফাংশনটি সম্পূর্ণ সংখ্যা লাইনে সংজ্ঞায়িত করা হয়েছে, অর্থাৎ এর জন্য সবাই"x" এর অর্থ "y" এর নিজস্ব অর্থ রয়েছে। বিশেষ করে, যদি, তাহলে। মনে রাখবেন যে অন্য বিন্দুটি বিরাম চিহ্নযুক্ত, কারণ একটি ফাংশনের সংজ্ঞা অনুসারে, আর্গুমেন্টের মান অবশ্যই সঙ্গতিপূর্ণ হতে হবে একমাত্র জিনিসফাংশন মান। এইভাবে, ডোমেইনআমাদের ফাংশন:।

যাহোক এই ফাংশন ক্রমাগত চালু হয় না!এটা মোটামুটি স্পষ্ট যে এই মুহুর্তে সে কষ্ট পাচ্ছে ফাঁক. শব্দটিও বেশ বোধগম্য এবং চাক্ষুষ; প্রকৃতপক্ষে, এখানে পেন্সিলটি যেভাবেই হোক কাগজটি ছিঁড়ে ফেলতে হবে। একটু পরে আমরা ব্রেকপয়েন্টের শ্রেণীবিভাগ দেখব।

একটি বিন্দুতে এবং একটি ব্যবধানে একটি ফাংশনের ধারাবাহিকতা

একটি নির্দিষ্ট গাণিতিক সমস্যায়, আমরা একটি বিন্দুতে একটি ফাংশনের ধারাবাহিকতা, একটি ব্যবধানে একটি ফাংশনের ধারাবাহিকতা, একটি অর্ধ-ব্যবধান, বা একটি অংশে একটি ফাংশনের ধারাবাহিকতা সম্পর্কে কথা বলতে পারি। এটাই, কোন "শুধু ধারাবাহিকতা" নেই- ফাংশনটি কোথাও একটানা চলতে পারে। আর সব কিছুর মৌলিক "বিল্ডিং ব্লক" হল ফাংশনের ধারাবাহিকতা বিন্দুতে .

তত্ত্ব গাণিতিক বিশ্লেষণ"ডেল্টা" এবং "এপসিলন" পাড়া ব্যবহার করে একটি বিন্দুতে একটি ফাংশনের ধারাবাহিকতার একটি সংজ্ঞা দেয়, কিন্তু বাস্তবে আরেকটি সংজ্ঞা ব্যবহার করা হচ্ছে, যার প্রতি আমরা গভীর মনোযোগ দেব।

প্রথমে মনে রাখা যাক একতরফা সীমাযারা প্রথম পাঠে আমাদের জীবনে ফেটে পড়ে ফাংশন গ্রাফ সম্পর্কে. একটি দৈনন্দিন পরিস্থিতি বিবেচনা করুন:

যদি আমরা বিন্দুতে অক্ষের কাছে যাই বাম(লাল তীর), তারপর "গেমস" এর সংশ্লিষ্ট মানগুলি অক্ষ বরাবর বিন্দুতে যাবে (লাল তীর)। গাণিতিকভাবে, এই সত্যটি ব্যবহার করে স্থির করা হয়েছে বাম হাতের সীমা:

এন্ট্রিতে মনোযোগ দিন (পড়ে "x বাম দিকে কা-এর দিকে থাকে")। "যোগ" "বিয়োগ শূন্য" এর প্রতীক , মূলত এর মানে হল যে আমরা বাম দিক থেকে সংখ্যাটির কাছে যাচ্ছি।

একইভাবে, আপনি যদি "কা" বিন্দুর কাছে যান ডানে(নীল তীর), তারপর "গেমস" একই মান আসবে, কিন্তু সবুজ তীর বরাবর, এবং ডান হাতের সীমানিম্নরূপ বিন্যাস করা হবে:

"অ্যাডিটিভ" প্রতীক , এবং এন্ট্রিতে লেখা আছে: "x ডানদিকে ka-এর দিকে ঝোঁক।"

যদি একতরফা সীমা সসীম এবং সমান হয়(আমাদের ক্ষেত্রে যেমন): , তারপর আমরা বলব যে একটি সাধারণ সীমা আছে। এটা সহজ, সাধারণ সীমা আমাদের "স্বাভাবিক" একটি ফাংশনের সীমা, একটি সসীম সংখ্যার সমান।

লক্ষ্য করুন যে যদি ফাংশনটি সংজ্ঞায়িত করা না থাকে (পঞ্চার কালো ফোটাগ্রাফ শাখায়), তাহলে উপরের গণনা বৈধ থাকবে। যেমনটি ইতিমধ্যে বেশ কয়েকবার উল্লেখ করা হয়েছে, বিশেষ করে নিবন্ধে অসীম ফাংশন উপর, অভিব্যক্তি মানে যে "x" অসীম বন্ধপয়েন্টের কাছাকাছি, যখন ব্যাপার না, ফাংশন নিজেই একটি নির্দিষ্ট বিন্দুতে সংজ্ঞায়িত করা হয় বা না। ভালো উদাহরণপরবর্তী অনুচ্ছেদে প্রদর্শিত হবে, যখন ফাংশন বিশ্লেষণ করা হয়।

সংজ্ঞা: একটি ফাংশন একটি বিন্দুতে অবিচ্ছিন্ন থাকে যদি একটি নির্দিষ্ট বিন্দুতে ফাংশনের সীমা সেই বিন্দুতে ফাংশনের মানের সমান হয়: .

সংজ্ঞা বিস্তারিত আছে নিম্নলিখিত শর্তাবলী:

1) ফাংশনটি অবশ্যই বিন্দুতে সংজ্ঞায়িত করতে হবে, অর্থাৎ মানটি অবশ্যই বিদ্যমান থাকতে হবে।

2) ফাংশনের একটি সাধারণ সীমা থাকতে হবে। উপরে উল্লিখিত হিসাবে, এটি একতরফা সীমার অস্তিত্ব এবং সমতা বোঝায়: .

3) একটি নির্দিষ্ট বিন্দুতে ফাংশনের সীমা এই বিন্দুতে ফাংশনের মানের সমান হতে হবে: .

লঙ্ঘন হলে অন্তত একটাতিনটি শর্তের মধ্যে, তারপর ফাংশন বিন্দুতে ধারাবাহিকতার বৈশিষ্ট্য হারায়।

একটি ব্যবধানে একটি ফাংশনের ধারাবাহিকতাবুদ্ধিমত্তার সাথে এবং খুব সহজভাবে প্রণয়ন করা হয়: একটি ফাংশন ব্যবধানে অবিচ্ছিন্ন থাকে যদি এটি প্রদত্ত ব্যবধানের প্রতিটি বিন্দুতে অবিচ্ছিন্ন থাকে।

বিশেষ করে, অনেক ফাংশন একটি অসীম ব্যবধানে, অর্থাৎ বাস্তব সংখ্যার সেটে একটানা থাকে। এটি একটি রৈখিক ফাংশন, বহুপদ, সূচকীয়, সাইন, কোসাইন ইত্যাদি। এবং সাধারণভাবে, যেকোনো প্রাথমিক ফাংশনতার উপর অবিরত সংজ্ঞার ডোমেইন, উদাহরণস্বরূপ, একটি লগারিদমিক ফাংশন ব্যবধানে অবিচ্ছিন্ন থাকে। আমি আশা করি এই মুহূর্তেপ্রধান ফাংশনগুলির গ্রাফগুলি কেমন তা আপনার কাছে বেশ ভাল ধারণা রয়েছে। আরও বিস্তারিত তথ্যতাদের ধারাবাহিকতা থেকে সংগ্রহ করা যেতে পারে সদয় ব্যক্তিফিচটেনগোল্টস উপাধি দ্বারা।

একটি সেগমেন্ট এবং অর্ধ-ব্যবধানে একটি ফাংশনের ধারাবাহিকতার সাথে, সবকিছু কঠিন নয়, তবে ক্লাসে এটি সম্পর্কে কথা বলা আরও উপযুক্ত। একটি সেগমেন্টে একটি ফাংশনের সর্বনিম্ন এবং সর্বোচ্চ মান খুঁজে বের করার বিষয়ে, কিন্তু আপাতত এটা নিয়ে চিন্তা না করা যাক।

বিরতি পয়েন্টের শ্রেণীবিভাগ

ফাংশনগুলির আকর্ষণীয় জীবন সমস্ত ধরণের বিশেষ পয়েন্টে সমৃদ্ধ, এবং বিরতি পয়েন্টগুলি তাদের জীবনীর পৃষ্ঠাগুলির মধ্যে একটি মাত্র।

বিঃদ্রঃ : শুধু ক্ষেত্রে, আমি একটি প্রাথমিক বিন্দুতে বাস করব: ব্রেকিং পয়েন্ট সর্বদা একক বিন্দু- সেখানে "এক সারিতে বেশ কয়েকটি বিরতি পয়েন্ট" নেই, অর্থাৎ, "ব্রেক ব্যবধান" বলে কিছু নেই।

এই পয়েন্টগুলি ঘুরে দুই ভাগে বিভক্ত বড় দল: প্রথম ধরনের ফেটে যাওয়াএবং দ্বিতীয় ধরনের ফেটে যাওয়া. প্রতিটি ধরণের ফাঁকের নিজস্ব আছে বৈশিষ্ট্যযা আমরা এখনই দেখব:

প্রথম ধরনের বিচ্ছিন্নতা বিন্দু

যদি ধারাবাহিকতার শর্ত একটি বিন্দুতে লঙ্ঘন করা হয় এবং একতরফা সীমা সসীম , তারপর এটা বলা হয় প্রথম ধরনের বিচ্ছিন্নতা বিন্দু.

সবচেয়ে আশাবাদী কেস দিয়ে শুরু করা যাক। পাঠের মূল ধারণা অনুসারে, আমি তত্ত্বটি বলতে চেয়েছিলাম "ইন সাধারণ দৃষ্টিকোণ”, তবে উপাদানটির বাস্তবতা প্রদর্শন করার জন্য, আমি নির্দিষ্ট অক্ষরগুলির সাথে বিকল্পটি স্থির করেছি।

এটি দুঃখজনক, শাশ্বত শিখার পটভূমিতে নবদম্পতির ছবির মতো, তবে নিম্নলিখিত শটটি সাধারণত গৃহীত হয়। আসুন অঙ্কনে ফাংশনের গ্রাফটি চিত্রিত করি:

এই ফাংশনটি বিন্দু ব্যতীত সমগ্র সংখ্যারেখায় অবিচ্ছিন্ন। এবং প্রকৃতপক্ষে, হর শূন্যের সমান হতে পারে না। তবে সীমার অর্থের সাথে মিল রেখে আমরা পারি অসীম বন্ধবাম এবং ডান দিক থেকে "শূন্য" এ যান, অর্থাৎ, একতরফা সীমা বিদ্যমান এবং স্পষ্টতই, মিলে যায়:
(ধারাবাহিকতার শর্ত নং 2 সন্তুষ্ট)।

কিন্তু ফাংশন বিন্দুতে সংজ্ঞায়িত করা হয় না, তাই, ধারাবাহিকতার শর্ত নং 1 লঙ্ঘন করা হয়, এবং ফাংশনটি এই সময়ে একটি বিচ্ছিন্নতার শিকার হয়।

এই ধরণের একটি বিরতি (বিদ্যমান সহ সাধারণ সীমা) ডাকল মেরামতযোগ্য ফাঁক. কেন অপসারণযোগ্য? কারণ ফাংশন পারে পুনরায় সংজ্ঞায়িত করাব্রেকিং পয়েন্টে:

এটা অদ্ভুত দেখায়? হতে পারে. কিন্তু এই ধরনের একটি ফাংশন স্বরলিপি কিছু বিরোধিতা করে না! এখন ব্যবধান বন্ধ এবং সবাই খুশি:

আসুন একটি আনুষ্ঠানিক চেক সঞ্চালন করা যাক:

2) - একটি সাধারণ সীমা আছে;
3)

সুতরাং, তিনটি শর্তই সন্তুষ্ট, এবং একটি বিন্দুতে একটি ফাংশনের ধারাবাহিকতার সংজ্ঞা দ্বারা ফাংশনটি একটি বিন্দুতে অবিচ্ছিন্ন।

যাইহোক, মাতান বিদ্বেষীরা ফাংশনটিকে একটি খারাপ উপায়ে সংজ্ঞায়িত করতে পারে, উদাহরণস্বরূপ :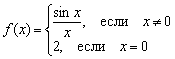

এটি আকর্ষণীয় যে প্রথম দুটি ধারাবাহিকতা শর্ত এখানে সন্তুষ্ট:
1) - ফাংশন একটি নির্দিষ্ট বিন্দুতে সংজ্ঞায়িত করা হয়;
2) - একটি সাধারণ সীমা আছে।

কিন্তু তৃতীয় সীমানাটি পাস করা হয়নি: , অর্থাৎ বিন্দুতে ফাংশনের সীমা সমান নাএকটি নির্দিষ্ট পয়েন্টে একটি প্রদত্ত ফাংশনের মান।

এইভাবে, এক পর্যায়ে ফাংশন একটি বিচ্ছিন্নতা ভোগ করে।

দ্বিতীয়, স্যাডার কেস বলা হয় প্রথম ধরনের ফেটে যাওয়া একটি লাফ দিয়ে. এবং দুঃখ একতরফা সীমা দ্বারা উদ্ভূত হয় যে সসীম এবং ভিন্ন. একটি উদাহরণ পাঠের দ্বিতীয় অঙ্কনে দেখানো হয়েছে। এই ধরনের একটি ফাঁক সাধারণত ঘটে piecewise সংজ্ঞায়িত ফাংশন, যা ইতিমধ্যে নিবন্ধে উল্লেখ করা হয়েছে গ্রাফ রূপান্তর সম্পর্কে.

piecewise ফাংশন বিবেচনা করুন এবং আমরা এর অঙ্কন সম্পূর্ণ করব। কিভাবে একটি গ্রাফ নির্মাণ? খুব সহজ. অর্ধ-ব্যবধানে আমরা একটি প্যারাবোলার একটি টুকরো আঁকি ( সবুজ রং), ব্যবধানে - একটি সরল রেখার অংশ (লাল) এবং অর্ধ-ব্যবধানে - একটি সরল রেখা ( নীল রং).

তদুপরি, অসমতার কারণে মূল্য নির্ধারণ করা হয় দ্বিঘাত ফাংশন(সবুজ বিন্দু), এবং অসমতার কারণে, এর জন্য মান নির্ধারণ করা হয় লিনিয়ার ফাংশন(নীল বিন্দু):

সবচেয়ে কঠিন ক্ষেত্রে, আপনাকে গ্রাফের প্রতিটি অংশের পয়েন্ট-বাই-পয়েন্ট নির্মাণ অবলম্বন করা উচিত (প্রথম দেখুন ফাংশন গ্রাফ সম্পর্কে পাঠ).

এখন আমরা কেবল বিন্দুতে আগ্রহী হব। এর ধারাবাহিকতার জন্য এটি পরীক্ষা করা যাক:

2) আসুন একতরফা সীমা গণনা করা যাক।

বাম দিকে আমাদের একটি লাল রেখার অংশ আছে, তাই বাম দিকের সীমা হল:

ডানদিকে নীল সরল রেখা, এবং ডান হাতের সীমা:

ফলস্বরূপ, আমরা পেয়েছি সসীম সংখ্যা, এবং তারা সমান না. যেহেতু একতরফা সীমাবদ্ধতা সসীম এবং ভিন্ন: , তারপর আমাদের ফাংশন সহ্য করে একটি লাফ দিয়ে প্রথম ধরনের বিচ্ছিন্নতা.

এটা যৌক্তিক যে ফাঁকটি দূর করা যাবে না - ফাংশনটিকে আসলেই আরও সংজ্ঞায়িত করা যাবে না এবং "একসাথে আঠালো" করা যাবে না, আগের উদাহরণের মতো।

দ্বিতীয় ধরনের বিচ্ছিন্নতা পয়েন্ট

সাধারণত, ফেটে যাওয়ার অন্যান্য সমস্ত ক্ষেত্রে চতুরতার সাথে এই বিভাগে শ্রেণীবদ্ধ করা হয়। আমি সবকিছু তালিকাভুক্ত করব না, কারণ অনুশীলনে, 99% সমস্যার মধ্যে আপনি সম্মুখীন হবেন অন্তহীন ফাঁক– যখন বাম-হাতি বা ডান-হাতি, এবং আরও প্রায়ই, উভয় সীমা অসীম।

এবং, অবশ্যই, সবচেয়ে সুস্পষ্ট ছবি হল বিন্দু শূন্যের হাইপারবোলা। এখানে উভয় একতরফা সীমা অসীম: , অতএব, বিন্দুতে ফাংশনটি দ্বিতীয় ধরণের বিচ্ছিন্নতা ভোগ করে।

আমি আমার নিবন্ধগুলি যতটা সম্ভব বৈচিত্র্যময় সামগ্রী দিয়ে পূরণ করার চেষ্টা করি, তাই আসুন এমন একটি ফাংশনের গ্রাফটি দেখি যা এখনও সম্মুখীন হয়নি:

স্ট্যান্ডার্ড স্কিম অনুযায়ী:

1) ফাংশনটি এই সময়ে সংজ্ঞায়িত করা হয় না কারণ হরটি শূন্যে যায়।

অবশ্যই, আমরা অবিলম্বে উপসংহারে পৌঁছাতে পারি যে ফাংশনটি পয়েন্টে একটি বিচ্ছিন্নতা ভোগ করে, তবে বিচ্ছিন্নতার প্রকৃতিকে শ্রেণীবদ্ধ করা ভাল হবে, যা প্রায়শই শর্ত দ্বারা প্রয়োজন হয়। এই জন্য:

আমি আপনাকে মনে করিয়ে দিই যে রেকর্ডিং দ্বারা আমরা বোঝাতে চাইছি অসীম একটি নেতিবাচক সংখ্যা , এবং প্রবেশের অধীনে - অসীম ধনাত্মক সংখ্যা.

একতরফা সীমা অসীম, যার মানে হল যে ফাংশনটি বিন্দুতে 2য় ধরণের বিচ্ছিন্নতা ভোগ করে। y-অক্ষ হল উল্লম্ব অ্যাসিম্পটোটগ্রাফের জন্য।

উভয় একতরফা সীমার অস্তিত্ব থাকা অস্বাভাবিক নয়, তবে তাদের মধ্যে শুধুমাত্র একটি অসীম, উদাহরণস্বরূপ:

এটি ফাংশনের গ্রাফ।

আমরা ধারাবাহিকতার জন্য পয়েন্টটি পরীক্ষা করি:

1) ফাংশন এই সময়ে সংজ্ঞায়িত করা হয় না.

2) আসুন একতরফা সীমা গণনা করি:

আমরা বক্তৃতার শেষ দুটি উদাহরণে এই ধরনের একতরফা সীমা গণনা করার পদ্ধতি সম্পর্কে কথা বলব, যদিও অনেক পাঠক ইতিমধ্যে সবকিছু দেখেছেন এবং অনুমান করেছেন।

বাম-হাতের সীমাটি সসীম এবং শূন্যের সমান (আমরা "বিন্দুতে যাই না"), তবে ডান-হাতের সীমা অসীম এবং গ্রাফের কমলা শাখাটি অসীমভাবে তার কাছাকাছি আসে উল্লম্ব অ্যাসিম্পটোট, সমীকরণ দ্বারা প্রদত্ত (কালো ডটেড লাইন)।

তাই ফাংশন ক্ষতিগ্রস্ত হয় দ্বিতীয় ধরনের বিরতিবিন্দুতে

1ম ধরণের বিচ্ছিন্নতার জন্য, ফাংশনটি বিচ্ছিন্নতা বিন্দুতেই সংজ্ঞায়িত করা যেতে পারে। উদাহরণস্বরূপ, একটি piecewise ফাংশন জন্য স্থানাঙ্কের উৎপত্তিস্থলে একটি কালো বোল্ড ডট লাগাতে দ্বিধা বোধ করুন। ডানদিকে একটি হাইপারবোলার একটি শাখা, এবং ডান হাতের সীমা অসীম। আমি মনে করি প্রায় প্রত্যেকেরই ধারণা আছে যে এই গ্রাফটি কেমন দেখাচ্ছে।

সবাই যা অপেক্ষা করছিল:

ধারাবাহিকতার জন্য একটি ফাংশন কিভাবে পরীক্ষা করবেন?

একটি বিন্দুতে ধারাবাহিকতার জন্য একটি ফাংশনের অধ্যয়ন একটি ইতিমধ্যে প্রতিষ্ঠিত রুটিন স্কিম অনুযায়ী পরিচালিত হয়, যা ধারাবাহিকতার তিনটি শর্ত পরীক্ষা করে থাকে:

উদাহরণ 1

এক্সপ্লোর ফাংশন

সমাধান:

1) সুযোগের মধ্যে একমাত্র বিন্দু যেখানে ফাংশন সংজ্ঞায়িত করা হয় না।

2) আসুন একতরফা সীমা গণনা করি:

একতরফা সীমা সসীম এবং সমান।

এইভাবে, বিন্দুতে ফাংশনটি একটি অপসারণযোগ্য বিচ্ছিন্নতা ভোগ করে।

এই ফাংশনের গ্রাফ দেখতে কেমন?

আমি সরলীকরণ করতে চাই , এবং এটি একটি সাধারণ প্যারাবোলা প্রাপ্ত হয় বলে মনে হয়. কিন্তুমূল ফাংশন পয়েন্ট এ সংজ্ঞায়িত করা হয় না, তাই নিম্নলিখিত ধারা প্রয়োজন:

চলুন অঙ্কন করা যাক:

উত্তর: যে বিন্দুতে এটি একটি অপসারণযোগ্য বিচ্ছিন্নতা ভোগ করে তা ব্যতীত ফাংশনটি সম্পূর্ণ সংখ্যারেখায় অবিচ্ছিন্ন।

ফাংশনটি আরও ভাল বা এত ভাল উপায়ে সংজ্ঞায়িত করা যেতে পারে, তবে শর্ত অনুসারে এটির প্রয়োজন নেই।

আপনি কি বলেন এটা একটা সুদূরপ্রসারী উদাহরণ? একদমই না. এটি অনুশীলনে কয়েক ডজন বার ঘটেছে। সাইটের প্রায় সব কাজই প্রকৃত স্বাধীন কাজ এবং পরীক্ষা থেকে আসে।

আসুন আমাদের প্রিয় মডিউলগুলি থেকে মুক্তি পান:

উদাহরণ 2

এক্সপ্লোর ফাংশন ধারাবাহিকতার জন্য। ফাংশন বিচ্ছিন্নতার প্রকৃতি নির্ধারণ করুন, যদি তারা বিদ্যমান থাকে। অঙ্কন কার্যকর করুন।

সমাধান: কিছু কারণে, শিক্ষার্থীরা ভয় পায় এবং একটি মডিউল সহ ফাংশন পছন্দ করে না, যদিও তাদের সম্পর্কে জটিল কিছু নেই। আমরা ইতিমধ্যে পাঠে এই জাতীয় জিনিসগুলিকে কিছুটা স্পর্শ করেছি। গ্রাফের জ্যামিতিক রূপান্তর. যেহেতু মডিউলটি অ-নেতিবাচক, এটি নিম্নরূপ প্রসারিত হয়েছে: , যেখানে "আলফা" কিছু অভিব্যক্তি। ভিতরে এক্ষেত্রে, এবং আমাদের ফাংশন টুকরো টুকরো লেখা উচিত: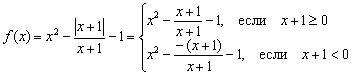

কিন্তু উভয় অংশের ভগ্নাংশ অবশ্যই দ্বারা হ্রাস করা উচিত। হ্রাস, আগের উদাহরণের মতো, পরিণতি ছাড়াই ঘটবে না। মূল ফাংশন বিন্দুতে সংজ্ঞায়িত করা হয় না যেহেতু হর শূন্যে যায়। অতএব, সিস্টেমের অতিরিক্ত শর্তটি নির্দিষ্ট করা উচিত এবং প্রথম অসমতা কঠোর করা উচিত:

এখন খুব সম্পর্কে দরকারী অভ্যর্থনাসমাধান: একটি খসড়াতে কাজটি চূড়ান্ত করার আগে, একটি অঙ্কন তৈরি করা সুবিধাজনক (এটি শর্ত দ্বারা প্রয়োজনীয় কিনা তা নির্বিশেষে)। এটি সাহায্য করবে, প্রথমত, অবিলম্বে ধারাবাহিকতা এবং বিচ্ছিন্নতার পয়েন্টগুলি দেখতে, এবং দ্বিতীয়ত, এটি আপনাকে একতরফা সীমা খুঁজে বের করার সময় ত্রুটি থেকে 100% রক্ষা করবে।

এর অঙ্কন করা যাক. আমাদের গণনা অনুসারে, বিন্দুর বাম দিকে প্যারাবোলার একটি টুকরো আঁকতে হবে (নীল রঙ), এবং ডানদিকে - একটি প্যারাবোলার একটি টুকরো (লাল রঙ), যখন ফাংশনটি সংজ্ঞায়িত করা হয়নি নিজেই পয়েন্ট:

সন্দেহ হলে, কয়েকটি x মান নিন এবং সেগুলিকে ফাংশনে প্লাগ করুন (মনে রাখা যে মডিউল সম্ভাব্য বিয়োগ চিহ্নকে ধ্বংস করে) এবং গ্রাফটি পরীক্ষা করুন।

আসুন বিশ্লেষণাত্মকভাবে ধারাবাহিকতার জন্য ফাংশনটি পরীক্ষা করি:

1) ফাংশন বিন্দুতে সংজ্ঞায়িত করা হয় না, তাই আমরা অবিলম্বে বলতে পারি যে এটি অবিচ্ছিন্ন নয়।

2) চলুন বিচ্ছিন্নতার প্রকৃতি স্থাপন করি; এটি করার জন্য, আমরা একতরফা সীমা গণনা করি:

একতরফা সীমাগুলি সসীম এবং ভিন্ন, যার অর্থ হল বিন্দুতে একটি লাফ দিয়ে ফাংশনটি 1ম ধরণের বিচ্ছিন্নতা ভোগ করে। আবার নোট করুন যে সীমা খুঁজে বের করার সময়, বিরতি পয়েন্টে ফাংশনটি সংজ্ঞায়িত করা হয়েছে কিনা তা বিবেচ্য নয়।

এখন যা বাকি আছে তা হল খসড়া থেকে অঙ্কনটি স্থানান্তর করা (এটি গবেষণার সাহায্যে তৈরি করা হয়েছিল ;-)) এবং কাজটি সম্পূর্ণ করুন:

উত্তর: ফাংশনটি একটি লাফ দিয়ে প্রথম ধরণের বিচ্ছিন্নতা ভোগ করে এমন বিন্দু ব্যতীত সমগ্র সংখ্যারেখায় অবিচ্ছিন্ন।

কখনও কখনও তাদের বিরতি জাম্পের অতিরিক্ত ইঙ্গিত প্রয়োজন। এটি সহজভাবে গণনা করা হয় - ডান সীমা থেকে আপনাকে বাম সীমাটি বিয়োগ করতে হবে: , অর্থাৎ, বিরতি পয়েন্টে আমাদের ফাংশনটি 2 ইউনিট নিচে নেমে গেছে (যেমন বিয়োগ চিহ্ন আমাদের বলে)।

উদাহরণ 3

এক্সপ্লোর ফাংশন ধারাবাহিকতার জন্য। ফাংশন বিচ্ছিন্নতার প্রকৃতি নির্ধারণ করুন, যদি তারা বিদ্যমান থাকে। একটি অঙ্কন তৈরি করুন।

এটি আপনার নিজের সমাধান করার জন্য একটি উদাহরণ, পাঠের শেষে একটি নমুনা সমাধান।

চলুন টাস্কটির সবচেয়ে জনপ্রিয় এবং বিস্তৃত সংস্করণে এগিয়ে যাই, যখন ফাংশনটি তিনটি অংশ নিয়ে গঠিত:

উদাহরণ 4

ধারাবাহিকতার জন্য একটি ফাংশন পরীক্ষা করুন এবং ফাংশনের একটি গ্রাফ প্লট করুন .

সমাধান: এটা স্পষ্ট যে ফাংশনের তিনটি অংশই সংশ্লিষ্ট ব্যবধানে অবিচ্ছিন্ন, তাই এটি টুকরোগুলির মধ্যে "জাংশন" এর শুধুমাত্র দুটি বিন্দু পরীক্ষা করতে থাকে। প্রথমে, আসুন একটি খসড়া অঙ্কন করি; আমি নিবন্ধের প্রথম অংশে পর্যাপ্ত বিশদে নির্মাণ কৌশল সম্পর্কে মন্তব্য করেছি। একমাত্র জিনিসটি হল আমাদের সাবধানে আমাদের একক পয়েন্টগুলি অনুসরণ করতে হবে: অসমতার কারণে, মানটি সরলরেখার (সবুজ বিন্দু) অন্তর্গত এবং অসমতার কারণে, মানটি প্যারাবোলা (লাল বিন্দু) এর অন্তর্গত:

ঠিক আছে, নীতিগতভাবে, সবকিছু পরিষ্কার =) যা বাকি থাকে তা হল সিদ্ধান্তকে আনুষ্ঠানিক করা। দুটি "যোগদান" পয়েন্টগুলির প্রতিটির জন্য, আমরা স্ট্যান্ডার্ডভাবে 3টি ধারাবাহিকতা শর্তগুলি পরীক্ষা করি:

আমি)আমরা ধারাবাহিকতার জন্য বিন্দু পরীক্ষা

একতরফা সীমাগুলি সসীম এবং ভিন্ন, যার অর্থ হল বিন্দুতে একটি লাফ দিয়ে ফাংশনটি 1ম ধরণের বিচ্ছিন্নতা ভোগ করে।

আসুন ডান এবং বাম সীমার মধ্যে পার্থক্য হিসাবে বিচ্ছিন্নতা জাম্প গণনা করি:
, অর্থাৎ, গ্রাফটি একটি ইউনিটকে ঝাঁকুনি দিয়েছে।

II)আমরা ধারাবাহিকতার জন্য বিন্দু পরীক্ষা

1) - ফাংশন একটি নির্দিষ্ট পয়েন্টে সংজ্ঞায়িত করা হয়।

2) একতরফা সীমা খুঁজুন:

– একতরফা সীমা সীমিত এবং সমান, যার মানে একটি সাধারণ সীমা আছে।

3) - একটি বিন্দুতে একটি ফাংশনের সীমা একটি নির্দিষ্ট বিন্দুতে এই ফাংশনের মানের সমান।

চূড়ান্ত পর্যায়ে, আমরা অঙ্কনটিকে চূড়ান্ত সংস্করণে স্থানান্তর করি, তারপরে আমরা চূড়ান্ত জ্যা রাখি:

উত্তর: ফাংশনটি সম্পূর্ণ সংখ্যারেখার উপর অবিচ্ছিন্ন থাকে, সেই বিন্দু ব্যতীত যেখানে এটি একটি লাফ দিয়ে প্রথম ধরণের বিচ্ছিন্নতা ভোগ করে।

উদাহরণ 5

ধারাবাহিকতার জন্য একটি ফাংশন পরীক্ষা করুন এবং এর গ্রাফ তৈরি করুন .

এটি আপনার নিজের সমাধান করার জন্য একটি উদাহরণ, সংক্ষিপ্ত সমাধানএবং পাঠের শেষে টাস্কের একটি আনুমানিক নমুনা।

আপনি ধারণা পেতে পারেন যে এক পর্যায়ে ফাংশনটি অবিচ্ছিন্ন হতে হবে এবং অন্য সময়ে অবশ্যই একটি বিচ্ছিন্নতা থাকতে হবে। অনুশীলনে, এটি সর্বদা হয় না। অবশিষ্ট উদাহরণগুলিকে অবহেলা না করার চেষ্টা করুন - বেশ কয়েকটি আকর্ষণীয় এবং গুরুত্বপূর্ণ বৈশিষ্ট্য থাকবে:

উদাহরণ 6

একটি ফাংশন দেওয়া . পয়েন্টে ধারাবাহিকতার জন্য ফাংশনটি তদন্ত করুন। একটি গ্রাফ তৈরি করুন।

সমাধান: এবং আবার অবিলম্বে খসড়াটিতে অঙ্কনটি সম্পাদন করুন:

এই গ্রাফের বিশেষত্ব হল পিসওয়াইজ ফাংশনটি অ্যাবসিসা অক্ষের সমীকরণ দ্বারা দেওয়া হয়। এই এলাকা এখানে আঁকা হয় সবুজ, এবং একটি নোটবুকে এটি সাধারণত একটি সাধারণ পেন্সিল দিয়ে গাঢ়ভাবে হাইলাইট করা হয়। এবং, অবশ্যই, আমাদের রামগুলি সম্পর্কে ভুলবেন না: মানটি স্পর্শক শাখার (লাল বিন্দু) অন্তর্গত এবং মানটি সরলরেখার অন্তর্গত।

অঙ্কন থেকে সবকিছু পরিষ্কার - ফাংশনটি সম্পূর্ণ সংখ্যারেখা বরাবর অবিচ্ছিন্ন, যা অবশিষ্ট থাকে তা হল সমাধানটিকে আনুষ্ঠানিক করা, যা 3-4টি অনুরূপ উদাহরণের পরে আক্ষরিক অর্থে সম্পূর্ণ অটোমেশনে আনা হয়:

আমি)আমরা ধারাবাহিকতার জন্য বিন্দু পরীক্ষা

1) - ফাংশন একটি নির্দিষ্ট বিন্দুতে সংজ্ঞায়িত করা হয়।

2) আসুন একতরফা সীমা গণনা করি:

, যার মানে একটি সাধারণ সীমা আছে।

ঠিক সেই ক্ষেত্রে, আমি আপনাকে একটি তুচ্ছ সত্যের কথা মনে করিয়ে দিই: একটি ধ্রুবকের সীমা ধ্রুবকের সমান। এই ক্ষেত্রে, শূন্যের সীমা নিজেই শূন্যের সমান (বাম-হাতের সীমা)।

সুতরাং, একটি বিন্দুতে একটি ফাংশনের ধারাবাহিকতার সংজ্ঞা দ্বারা একটি বিন্দুতে একটি ফাংশন অবিচ্ছিন্ন।

II)আমরা ধারাবাহিকতার জন্য বিন্দু পরীক্ষা

1) - ফাংশন একটি নির্দিষ্ট বিন্দুতে সংজ্ঞায়িত করা হয়।

2) একতরফা সীমা খুঁজুন:

এবং এখানে - একের সীমা নিজেই ইউনিটের সমান।

- একটি সাধারণ সীমা আছে।

যথারীতি, গবেষণার পরে আমরা আমাদের অঙ্কন চূড়ান্ত সংস্করণে স্থানান্তর করি।

উত্তর: ফাংশনটি বিন্দুতে অবিচ্ছিন্ন।

অনুগ্রহ করে মনে রাখবেন যে শর্তে আমাদের ধারাবাহিকতার জন্য সম্পূর্ণ ফাংশন অধ্যয়ন করার বিষয়ে কিছু জিজ্ঞাসা করা হয়নি, এবং এটি তৈরি করা ভাল গাণিতিক ফর্ম হিসাবে বিবেচিত হয়। সুনির্দিষ্ট এবং পরিষ্কারউত্থাপিত প্রশ্নের উত্তর। যাইহোক, যদি শর্তটি আপনাকে একটি গ্রাফ তৈরি করার প্রয়োজন না করে, তাহলে আপনার আছে প্রতিটি অধিকারএটি তৈরি করবেন না (যদিও শিক্ষক আপনাকে পরে এটি করতে বাধ্য করতে পারেন)।

এটি নিজেই সমাধান করার জন্য একটি ছোট গাণিতিক "টং টুইস্টার":

উদাহরণ 7

একটি ফাংশন দেওয়া . পয়েন্টে ধারাবাহিকতার জন্য ফাংশনটি তদন্ত করুন। ব্রেকপয়েন্ট শ্রেণীবদ্ধ করুন, যদি থাকে। অঙ্কন কার্যকর করুন।

সমস্ত "শব্দ" সঠিকভাবে "উচ্চারণ" করার চেষ্টা করুন =) এবং গ্রাফটি আরও সুনির্দিষ্টভাবে আঁকুন, নির্ভুলতা, এটি সর্বত্র অতিরিক্ত হবে না;-)

আপনার মনে আছে, আমি অবিলম্বে একটি খসড়া হিসাবে অঙ্কনটি সম্পূর্ণ করার পরামর্শ দিয়েছি, কিন্তু সময়ে সময়ে আপনি এমন উদাহরণগুলি দেখতে পাবেন যেখানে আপনি অবিলম্বে গ্রাফটি কেমন দেখাচ্ছে তা খুঁজে বের করতে পারবেন না। অতএব, কিছু ক্ষেত্রে, প্রথমে একতরফা সীমা খুঁজে বের করা সুবিধাজনক এবং শুধুমাত্র তারপর, অধ্যয়নের উপর ভিত্তি করে, শাখাগুলিকে চিত্রিত করা। চূড়ান্ত দুটি উদাহরণে আমরা কিছু একতরফা সীমা গণনা করার জন্য একটি কৌশলও শিখব:

উদাহরণ 8

ধারাবাহিকতার জন্য ফাংশনটি পরীক্ষা করুন এবং এর পরিকল্পিত গ্রাফ তৈরি করুন।

সমাধান: খারাপ পয়েন্টগুলি স্পষ্ট: (সূচকের হরকে শূন্যে কমিয়ে দেয়) এবং (সম্পূর্ণ ভগ্নাংশের হরকে শূন্যে হ্রাস করে)। এই ফাংশনের গ্রাফটি দেখতে কেমন তা স্পষ্ট নয়, যার মানে প্রথমে কিছু গবেষণা করা ভাল।