We will consider expressions of the Fourier series in trigonometric and complex form, and also pay attention to the Dirichlet conditions for the convergence of the Fourier series. In addition, we will dwell in detail on the explanation of such a concept as the negative frequency of the signal spectrum, which often causes difficulty when becoming familiar with the theory of spectral analysis.
Periodic signal. Trigonometric Fourier series
Let there be a periodic signal of continuous time that repeats with a period c, i.e. , where is an arbitrary integer.
As an example, Figure 1 shows a sequence of rectangular pulses of duration c, repeated with a period of c.
Figure 1. Periodic sequence
rectangular pulses
From the course of mathematical analysis it is known that the system of trigonometric functions
With multiple frequencies, where rad/s is an integer, it forms an orthonormal basis for the decomposition of periodic signals with a period satisfying the Dirichlet conditions. The Dirichlet conditions for the convergence of the Fourier series require that a periodic signal be specified on the segment and satisfy the following conditions:
For example, the periodic function 
does not satisfy the Dirichlet conditions because the function has discontinuities of the second kind and takes infinite values at , where is an arbitrary integer. So the function cannot be represented near Fourier. You can also give an example of the function 
, which is limited, but also does not satisfy the Dirichlet conditions, since it has an infinite number of extremum points as it approaches zero. Graph of a function shown in Figure 2.
Figure 2. Function graph :
a - two repetition periods; b - in the vicinity
Figure 2a shows two repetition periods of the function , and in Figure 2b - the area in the vicinity of . It can be seen that as it approaches zero, the oscillation frequency increases infinitely, and such a function cannot be represented by a Fourier series, because it is not piecewise monotonic.
It should be noted that in practice there are no signals with infinite current or voltage values. Functions with an infinite number of extrema of type also do not occur in applied problems.
All real periodic signals satisfy the Dirichlet conditions and can be represented by an infinite trigonometric Fourier series of the form:
In expression (2), the coefficient specifies the constant component of the periodic signal.
At all points where the signal is continuous, the Fourier series (2) converges to the values of the given signal, and at points of discontinuity of the first kind - to the average value , where and are the limits to the left and to the right of the discontinuity point, respectively.
It is also known from the course of mathematical analysis that the use of a truncated Fourier series, containing only the first terms instead of an infinite sum, leads to an approximate representation of the signal:
At which the minimum mean square error is ensured. Figure 3 illustrates the approximation of a periodic square wave train and a periodic ramp wave when using different numbers of Fourier series terms.
Figure 3. Approximation of signals using a truncated Fourier series:
a - rectangular pulses; b - sawtooth signal
Fourier series in complex form
In the previous section, we examined the trigonometric Fourier series for the expansion of an arbitrary periodic signal satisfying the Dirichlet conditions. Using Euler's formula, we can show:
Then the trigonometric Fourier series (2) taking into account (4):
Thus, a periodic signal can be represented by the sum of a constant component and complex exponentials rotating at frequencies with coefficients for positive frequencies, and for complex exponentials rotating at negative frequencies.
Let's consider the coefficients for complex exponentials rotating with positive frequencies:
Expressions (6) and (7) coincide; in addition, the constant component can also be written through a complex exponential at zero frequency:
Thus, (5) taking into account (6)-(8) can be represented as a single sum when indexed from minus infinity to infinity:
The subscript in the frequency designation indicates the number of the discrete harmonic, with negative subscripts corresponding to negative frequencies.
From expression (2) it follows that for a real signal the coefficients of series (2) are also real. However, (9) associates a real signal with a set of complex conjugate coefficients related to both positive and negative frequencies.
Some explanations of the Fourier series in complex form
In the previous section, we made the transition from the trigonometric Fourier series (2) to the Fourier series in complex form (9). As a result, instead of decomposing periodic signals in the basis of real trigonometric functions, we received an expansion in the basis of complex exponentials, with complex coefficients, and even negative frequencies appeared in the expansion! Since this issue is often misunderstood, some clarification is necessary.
First, working with complex exponents is in most cases easier than working with trigonometric functions. For example, when multiplying and dividing complex exponents, it is enough to just add (subtract) the exponents, while the formulas for multiplying and dividing trigonometric functions are more cumbersome.
If the signal is periodic and real, then the trigonometric Fourier series (2) seems more clear, because all expansion coefficients , and remain real. However, one often has to deal with complex periodic signals (for example, when modulating and demodulating, a quadrature representation of the complex envelope is used). In this case, when using the trigonometric Fourier series, all coefficients , and expansions (2) will become complex, while when using the Fourier series in complex form (9), the same expansion coefficients will be used for both real and complex inputs signals.
And finally, it is necessary to dwell on the explanation of the negative frequencies that appeared in (9). This question often causes misunderstanding. IN Everyday life
we do not encounter negative frequencies. For example, we never tune our radio to a negative frequency. Let's consider the following analogy from mechanics. Let there be a mechanical spring pendulum that oscillates freely with a certain frequency. Can a pendulum oscillate with a negative frequency? Of course not. Just as there are no radio stations broadcasting at negative frequencies, the frequency of oscillations of a pendulum cannot be negative.
But a spring pendulum is a one-dimensional object (the pendulum oscillates along one straight line).
We can also give another analogy from mechanics: a wheel rotating with a frequency of . The wheel, unlike the pendulum, rotates, i.e. a point on the surface of the wheel moves in a plane, and does not simply oscillate along one straight line. Therefore, to unambiguously set the rotation of the wheel, setting the rotation frequency is not enough, because it is also necessary to set the direction of rotation. This is precisely why we can use the frequency sign.
So, if the wheel rotates with an angular frequency rad/s counterclockwise, then we consider that the wheel rotates with a positive frequency, and if clockwise, then the rotation frequency will be negative. Thus, for a rotation command, a negative frequency ceases to be nonsense and indicates the direction of rotation.
And now the most important thing that we must understand. The oscillation of a one-dimensional object (for example, a spring pendulum) can be represented as the sum of the rotations of two vectors shown in Figure 4.
Figure 4. Oscillation of a spring pendulum
The pendulum oscillates along the real axis of the complex plane with a frequency according to the harmonic law. The movement of the pendulum is shown as a horizontal vector. The top vector rotates on the complex plane with a positive frequency (counterclockwise), and the bottom vector rotates with a negative frequency (clockwise). Figure 4 clearly illustrates the well-known relation from the trigonometry course:
Thus, the Fourier series in complex form (9) represents periodic one-dimensional signals as a sum of vectors on the complex plane rotating with positive and negative frequencies. At the same time, let us note that in the case of a real signal, according to (9), the expansion coefficients for negative frequencies are complex conjugate to the corresponding coefficients for positive frequencies. In the case of a complex signal, this property of the coefficients does not hold due to the fact that and are also complex.
Spectrum of periodic signals
The Fourier series in complex form is the decomposition of a periodic signal into a sum of complex exponentials rotating at positive and negative frequencies that are multiples of rad/c with corresponding complex coefficients that determine the spectrum of the signal. Complex coefficients can be represented using the Euler formula as , where is the amplitude spectrum, a is the phase spectrum.
Since periodic signals are laid out in a row only on a fixed frequency grid, the spectrum of periodic signals is lined (discrete).
Figure 5. Spectrum of a periodic sequence
rectangular pulses:
a - amplitude spectrum; b - phase spectrum
Figure 5 shows an example of the amplitude and phase spectrum of a periodic sequence of rectangular pulses (see Figure 1) at c, pulse duration c and pulse amplitude B.
Fourier series of periodic functions with period 2π.
The Fourier series allows us to study periodic functions by decomposing them into components. Alternating currents and voltages, displacements, speed and acceleration of crank mechanisms and acoustic waves are typical practical examples application of periodic functions in engineering calculations.
The Fourier series expansion is based on the assumption that all functions of practical significance in the interval -π ≤x≤ π can be expressed in the form of convergent trigonometric series (a series is considered convergent if the sequence of partial sums composed of its terms converges):
Standard (=ordinary) notation through the sum of sinx and cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
where a o, a 1,a 2,...,b 1,b 2,.. are real constants, i.e.
Where, for the range from -π to π, the coefficients of the Fourier series are calculated using the formulas:
The coefficients a o , a n and b n are called Fourier coefficients, and if they can be found, then series (1) is called next to Fourier, corresponding to the function f(x). For series (1), the term (a 1 cosx+b 1 sinx) is called the first or fundamental harmonic,
Another way to write a series is to use the relation acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Where a o is a constant, with 1 =(a 1 2 +b 1 2) 1/2, with n =(a n 2 +b n 2) 1/2 - the amplitudes of the various components, and is equal to a n =arctg a n /b n.
For series (1), the term (a 1 cosx+b 1 sinx) or c 1 sin(x+α 1) is called the first or fundamental harmonic,(a 2 cos2x+b 2 sin2x) or c 2 sin(2x+α 2) is called second harmonic and so on.
To accurately represent a complex signal typically requires an infinite number of terms. However, in many practical problems it is sufficient to consider only the first few terms.
Fourier series of non-periodic functions with period 2π.
Expansion of non-periodic functions.
If the function f(x) is non-periodic, it means that it cannot be expanded into a Fourier series for all values of x. However, it is possible to define a Fourier series representing a function over any range of width 2π.
Given a non-periodic function, a new function can be constructed by selecting values of f(x) within a certain range and repeating them outside that range at 2π intervals. Since the new function is periodic with period 2π, it can be expanded into a Fourier series for all values of x. For example, the function f(x)=x is not periodic. However, if it is necessary to expand it into a Fourier series in the interval from o to 2π, then outside this interval a periodic function with a period of 2π is constructed (as shown in the figure below).
For non-periodic functions such as f(x)=x, the sum of the Fourier series is equal to the value of f(x) at all points in a given range, but it is not equal to f(x) for points outside the range. To find the Fourier series of a non-periodic function in the 2π range, the same formula of Fourier coefficients is used.
Even and odd functions.
They say the function y=f(x) even, if f(-x)=f(x) for all values of x. Graphs of even functions are always symmetrical about the y-axis (that is, they are mirror images). Two examples of even functions: y=x2 and y=cosx.
They say that the function y=f(x) odd, if f(-x)=-f(x) for all values of x. Graphs of odd functions are always symmetrical about the origin.
Many functions are neither even nor odd.
Fourier series expansion in cosines.
The Fourier series of an even periodic function f(x) with period 2π contains only cosine terms (i.e., no sine terms) and may include a constant term. Hence,
where are the coefficients of the Fourier series,
The Fourier series of an odd periodic function f(x) with period 2π contains only terms with sines (that is, it does not contain terms with cosines).
Hence,
where are the coefficients of the Fourier series,
Fourier series at half cycle.
If a function is defined for a range, say from 0 to π, and not just from 0 to 2π, it can be expanded in a series only in sines or only in cosines. The resulting Fourier series is called near Fourier at half cycle.
If you want to get the decomposition Half-cycle Fourier by cosines functions f(x) in the range from 0 to π, then it is necessary to construct an even periodic function. In Fig. Below is the function f(x)=x, built on the interval from x=0 to x=π. Because the even function symmetrical about the f(x) axis, draw line AB, as shown in Fig. below. If we assume that outside the considered interval the obtained triangular shape is periodic with a period of 2π, then the final graph looks like, show. in Fig. below. Since we need to obtain the Fourier expansion in cosines, as before, we calculate the Fourier coefficients a o and a n
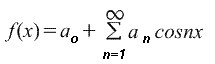
If you need to get Fourier half-cycle sine expansion functions f(x) in the range from 0 to π, then it is necessary to construct an odd periodic function. In Fig. Below is the function f(x)=x, built on the interval from x=0 to x=π. Since the odd function is symmetrical about the origin, we construct the line CD, as shown in Fig. If we assume that outside the considered interval the resulting sawtooth signal is periodic with a period of 2π, then the final graph has the form shown in Fig. Since we need to obtain the Fourier expansion of the half-cycle in terms of sines, as before, we calculate the Fourier coefficient. b
Fourier series for an arbitrary interval.
Expansion of a periodic function with period L.
Periodic function f(x) repeats as x increases by L, i.e. f(x+L)=f(x). The transition from the previously considered functions with a period of 2π to functions with a period of L is quite simple, since it can be done using a change of variable.
To find the Fourier series of the function f(x) in the range -L/2≤x≤L/2, we introduce a new variable u so that the function f(x) has a period of 2π relative to u. If u=2πx/L, then x=-L/2 for u=-π and x=L/2 for u=π. Also let f(x)=f(Lu/2π)=F(u). The Fourier series F(u) has the form
(The limits of integration can be replaced by any interval of length L, for example, from 0 to L)
Fourier series on a half-cycle for functions specified in the interval L≠2π.
For the substitution u=πх/L, the interval from x=0 to x=L corresponds to the interval from u=0 to u=π. Consequently, the function can be expanded into a series only in cosines or only in sines, i.e. V Fourier series at half cycle.
The cosine expansion in the range from 0 to L has the form
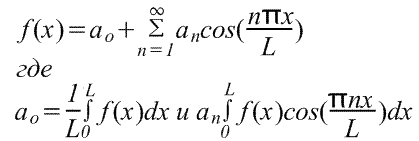
, Where
.
The Fourier series of a function f(x) on the interval (-l;l) is a trigonometric series of the form: 
, Where
.
Purpose. Online calculator is designed to expand the function f(x) into a Fourier Series.
For modulo functions (such as |x|), use cosine expansion.
Rules for entering functions:
For modulo functions, use cosine expansion. For example, for |x| it is necessary to enter a function without a module, i.e. x.Fourier series piecewise continuous, piecewise monotonic and bounded on the interval (- l;l) of the function converges on the entire number line.
Sum of Fourier series S(x) :
- is a periodic function with period 2 l. A function u(x) is called periodic with period T (or T-periodic) if for all x of the region R, u(x+T)=u(x).
- on the interval (- l;l) coincides with the function f(x), except for breakpoints
- at points of discontinuity (of the first kind, since the function is bounded) of the function f(x) and at the ends of the interval takes average values:
They say that the function expands into a Fourier series on the interval (- l;l):
.
If f(x) is an even function, then only even functions participate in its expansion, that is b n=0.
If f(x) is an odd function, then only odd functions participate in its expansion, that is and n=0
Near Fourier
functions f(x) on the interval (0; l) by cosines of multiple arcs
the row is called: 
, Where 
.
Near Fourier
functions f(x) on the interval (0; l) along the sines of multiple arcs
the row is called: 
, Where 
.
The sum of the Fourier series over the cosines of multiple arcs is an even periodic function with period 2 l, coinciding with f(x) on the interval (0; l) at points of continuity.
The sum of the Fourier series over the sines of multiple arcs is an odd periodic function with period 2 l, coinciding with f(x) on the interval (0; l) at points of continuity.
The Fourier series for a given function on a given interval has the property of uniqueness, that is, if the expansion is obtained in some other way than using formulas, for example, by selecting coefficients, then these coefficients coincide with those calculated from the formulas.
Example No. 1. Expand function f(x)=1:
a) in a complete Fourier series on the interval(-π ;π);
b) in a series along the sines of multiple arcs on the interval(0;π); plot the resulting Fourier series
Solution:
a) The Fourier series expansion on the interval (-π;π) has the form: 
,
and all coefficients b n=0, because this function is even; Thus,
Obviously, the equality will be satisfied if we accept
A 0 =2, A 1 =A 2 =A 3 =…=0
Due to the uniqueness property, these are the required coefficients. Thus, the required decomposition: 
or just 1=1.
In this case, when a series identically coincides with its function, the graph of the Fourier series coincides with the graph of the function on the entire number line.
b) The expansion on the interval (0;π) in terms of the sines of multiple arcs has the form:
It is obviously impossible to select the coefficients so that equality holds identically. Let's use the formula to calculate the coefficients:
Thus, for even n (n=2k) we have b n=0, for odd ( n=2k-1) - 
Finally, 
.
Let's plot the resulting Fourier series using its properties (see above).
First of all, we build a graph of this function on a given interval. Next, taking advantage of the oddness of the sum of the series, we continue the graph symmetrically to the origin: 
We continue in a periodic manner along the entire number line: 
And finally, at the break points we fill in the average (between the right and left limits) values: 
Example No. 2. Expand a function 
on the interval (0;6) along the sines of multiple arcs.
Solution: The required expansion has the form:
Since both the left and right sides of the equality contain only functions sin from different arguments, you should check whether, for any values of n (natural!), the arguments of the sines in the left and right parts equality:
or , from which n =18. This means that such a term is contained on the right side and its coefficient must coincide with the coefficient on the left side: b 18 =1;
or , from which n =4. Means, b 4 =-5.
Thus, by selecting the coefficients, it was possible to obtain the desired expansion:
Federal state budget educational institution higher education
"VOLGA STATE UNIVERSITY
TELECOMMUNICATIONS AND INFORMATICS"
Department of Higher Mathematics
O.V.STAROZHILOVA
SPECIAL CHAPTERS OF MATHEMATICS
protocol No. 45, dated March 10, 2017
Starozhilova, O.V.
C Special chapters of mathematics: textbook //Starozhilova O.V.. – Samara: PGUTI, 2017. –221 p.
Tutorial touches upon special branches of mathematics: mathematical logic and automata theory, propositional algebra, propositional calculus, elements of the theory of algorithms, regression analysis, optimization methods.
For university students and masters studying in the direction 03/09/02 " Information systems and technologies", who want to study special chapters of mathematics on their own.
Each section ends with control questions that will help check the theoretical mastery of the course, contains a large number of tasks for independent decision and answers to check.
The manual contains a laboratory complex and a number of engineering problems with an emphasis on software implementation of computational mathematics methods.
Starozhilova O.V., 2017
Chapter 1 Harmonic Analysis 6
1.1 Sounding string problem 7
1.2 Orthogonal systems of functions 8
1.3 Fourier series for the trigonometric system of functions 10
1.4 Sufficient conditions expansion of a function in a Fourier series 13
1.5 Fourier series expansion of a non-periodic function 17
1.6 Fourier series for even and odd functions 18
1.7 Fourier series for functions of any period 21
1.8 Fourier integral 27
1.9 Fourier integral for even and odd functions 29
1.10 Complex form Fourier integral 30
1.11 Fourier transform 32
Chapter 2 Mathematical logic and IV 33
2.1 Stages of logic development 34
2.2 Propositional logic 38
2.3Logical connectives 40
2.4Logical operations 41
2.5 Alphabet of propositional calculus 42
2.6 Formulas. Tautology 42
2.7 Laws of propositional logic 44
2.8 Formal theories. Hatchability. Interpretation 46
2.9 Axiomatic method 47
2.10 System of axioms of propositional calculus (PS) 52
2.11 Conclusion rules 53
2.12 Derived inference rules 56
2.13 Constructing a conclusion in propositional logic 62
2.14 Relationship between algebra and propositional calculus 66
Chapter 3 Regression Analysis Problems 70
3.1 Method least squares 74
3.2 Linear regression analysis 76
3.3 Estimation of the regression model 79
3.4 Problems in applying the linear regression method 83
3.5 Prerequisites of the statistical model LR 85
3.6 Problems of regression analysis 86
3.7 Multivariate normal regression model 90
3.8 Variation of the dependent variable 92
Test questions 94
Chapter 4 General formulation and types of decision-making problems 95
4.1 Mathematical formulation of the optimization problem 97
4.2 Local and global minimum TF 99
4.3 Methods unconditional optimization 102
4.4 Coordinate descent method 102
4.5 Rosenbrock method 105
4.6 Configuration method 105
4.7 Random search methods 108
4.8 Newton's method 112
Chapter 5 Fourier Transform 114
5.1 Fourier function approximation 114
5.2 Fourier transform 117
5.3 Fast Fourier transform 120
LABORATORY COMPLEX 123
Harmonic and spectral analysis 123
Topic 1. “Propositional logic” 131
Variants of individual assignments for the topic LP 133
Topic 2. Linear pairwise regression 140
Laboratory work № 1 141
Calculation of coefficients of the LR equation 141
Laboratory work No. 2 144
Calculating the sample correlation coefficient 144
Laboratory work No. 3 145
Calculation of estimates of variances of paired LR 145
Laboratory work No. 4 147
Excel functions for paired LR coefficients 147
Laboratory work No. 5 149
Construction of an interval estimate for the paired LR function 149
Laboratory work No. 6 151
Checking the significance of the LR equation using the Fisher criterion 151
Topic 3 Nonlinear pairwise regression 153
Laboratory work No. 7 153
Building a nonlinear regression using 153
Add Trendline Commands 153
Laboratory work No. 8 158
Selecting the best nonlinear regression 158
Topic 4. Linear multiple regression 161
Laboratory work No. 9 162
Calculation of LMR coefficients 162
Laboratory work No. 10 166
Significance testing in Regression mode 166
Topic 5. Nonlinear multiple regression 175
Laboratory work No. 11 175
Calculation for the Cobb-Douglas function 175
Test № 1 179
Paired regression 179
Test No. 2 181
Plural linear regression 181
Numerical methods for searching for an unconditional extremum 185
Graphical analysis of function 185
One-dimensional search problem 187
Svenn's algorithm 190
Brute force method 193
Bitwise search method 195
Dichotomy method. 198
Fibonacci method 201
Golden ratio method 205
Midpoint method 210
Newton's method 214
Literature 218
Chapter 1 Harmonic Analysis
DefinitionHarmonic analysis- branch of mathematics associated with the decomposition of vibrations into harmonic vibrations.
When studying periodic (i.e., repeating in time) phenomena, we consider periodic functions.
For example, a harmonic oscillation is described by a periodic function of time t:
Ø DefinitionPeriodic function- a function whose value does not change when a certain non-zero number called period functions.
Since the sum and difference of two periods is again a period and, therefore, any multiple of a period is also a period, then every periodic function has an infinite number of periods.
If a periodic function has a real period, is continuous and different from a constant, then it has the smallest positive period T; any other real period of the same function will have the form kT, Where k =±1, ±2,....
The sum, product and quotient of periodic functions with the same period are periodic functions with the same period.
Periodic functions play an extremely important role in the theory of oscillations and in mathematical physics in general. In the course of mathematical analysis, we became acquainted with the concept of a functional series, worked with its important special case - power series. Let's consider another very important one (including for physical applications) special case functional series - trigonometric series.
Ø Definition Functional range – series of the form
where are functions depending on one variable or several variables.
For each fixed value, the functional series turns into a numerical series
which may converge or may diverge.
Ø Definition Functional series convergence point- the point at which the functional series converges.
Ø Definition The set of all points of convergence is called convergence region of the series.
Is it possible this function represent in the form of a trigonometric series, i.e. is it possible to find the coefficients? a n And b n such that there is equality for everyone
The sum of the series is obviously a periodic function. This means that only periodic functions can be expanded into a trigonometric series f.
In addition, it is clear that if two periodic functions coincide on an interval whose length is equal to the period, then they coincide everywhere. Therefore, it is enough to check on a certain interval of length, for example, .
1.1 Sounding string problem
The study of trigonometric series was led to by the sounding string problem posed in the 18th century.
Given a function, is it possible to find a trigonometric series that converges and has as its sum the function. It is necessary to impose restrictions on it so that one can search for a trigonometric series converging to it.
A similar task was for power series, if it is solvable, then such a series is a Taylor series.
1.2 Orthogonal systems of functions
The systematic study of orthogonal systems of functions was begun in connection with the Fourier method for solving boundary value problems of equations of mathematical physics. One of the main problems in the theory of orthogonal systems of functions is the problem of decomposing a function f(x) in a series of the form , where is an orthogonal system of functions.
Ø Definition The functions are called orthogonal on , if fulfilled:
q Example , 
- the functions are orthogonal to , because 
q Example on is orthogonal to any function defined on.
Ø Definition An infinite system of functions is called orthogonal on if
q Example An infinite system of functions does not form an orthogonal system of functions
q Example -trigonometric function system forms a system of functions orthogonal to it.
, 
, 
.
Ø Definition Let an arbitrary system of functions orthogonal to . Row
where are arbitrary numerical coefficients, called next to each other according to an orthogonal system of functions.
Ø Definition Series according to the trigonometric system of functions
called trigonometric series.
ü Comment If is the sum of a trigonometric series converging at each point, then it is periodic, since , are periodic functions with period, then in the equality 
nothing will change, hence periodic.
ü Comment If is given on the segment, but not , then by shifting the origin of coordinates it can be reduced to the case studied.
ü Comment If a periodic function with period is not , then it is expanded into a trigonometric series
q Theorem If a number series converges, then the trigonometric series
converges absolutely and uniformly along the entire axis.
Proof
Hence,
series - majorizes a given trigonometric series, and according to Weierstrass’s test, converges uniformly.
Absolute convergence is obvious.
1.3 Fourier series for the trigonometric system of functions
Jean Baptiste Joseph Fourier 1768 – 1830 – French mathematician.
To calculate the coefficients of the Fourier series, we calculate the integrals
, 
, 
, 
,
q Theorem If there is equality for everyone
and the trigonometric series converges uniformly on the entire axis, then the coefficients of this series are determined
, 
,
Proof
The series converges uniformly on the entire number line, its terms are continuous functions, then its sum is also continuous and term-by-term integration of the series is possible within
Each integral is equal to zero, because trigonometric system of functions is orthogonal to , and then
To prove it, multiply both sides by
This will not disrupt the uniform convergence of the series.
Due to the uniform convergence of the series
and this means uniform convergence of the series.
Integrating on , we have
Due to the orthogonality of the trigonometric system of functions on
, 
, and from 
the integral at ,
, that, etc.
Let's remember that
The validity of these equalities follows from the application of trigonometric formulas to the integrand.
The formula for is proven in a similar way.
ü Comment The theorem remains valid on any interval, and the limits of integration are replaced by and respectively.
Ø Definition Trigonometric series
,
whose coefficients are determined by the formulas
, ,
,
called near Fourier for the function, and the coefficients are called Fourier coefficients.
If the Fourier series of a function f(x) converges at all its points of continuity, then we say that the function f(x) is expanded into a Fourier series.
ü Comment Not every trigonometric series is a Fourier series, even if it converges on the entire number line.
The sum of a non-uniformly convergent series may be discontinuous and not integrable, so determining the Fourier coefficients is impossible.
ü Comment The Fourier series is a special case of functional series.
1.4 Sufficient conditions for the expansion of a function in a Fourier series
Ø Definition The function is called piecewise monotonic on the segment, if this segment can be divided by a finite number of points x 1 , x 2 , ..., x n-1 into intervals ( a,x 1), (x 1,x 2), ..., (xn-1,b) so that on each of the intervals the function is monotonic, that is, it either does not increase or does not decrease.
ü Comment From the definition it follows that if a function is piecewise monotonic and bounded to [ a,b], then it has only discontinuities of the first kind.
Ø Definition The function is called piecewise smooth, if on each finite interval it and its derivative have at most a finite number of discontinuity points of the 1st kind.
q Theorem (Dirichlet condition sufficient condition for the decomposability of a function in a Fourier series): If a periodic function with a period satisfies one of the conditions:
then the Fourier series constructed for this function converges at all points
and converges to the number 
at each point of its discontinuity.
The sum of the resulting series is equal to the value of the function at the points of continuity of the function
Functions, decomposing them into components. Alternating currents and voltages, displacements, speed and acceleration of crank mechanisms and acoustic waves are typical practical examples of the use of periodic functions in engineering calculations.
The Fourier series expansion is based on the assumption that all functions of practical significance in the interval -π ≤x≤ π can be expressed in the form of convergent trigonometric series (a series is considered convergent if the sequence of partial sums composed of its terms converges):
Standard (=ordinary) notation through the sum of sinx and cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
where a o, a 1,a 2,...,b 1,b 2,.. are real constants, i.e.
Where, for the range from -π to π, the coefficients of the Fourier series are calculated using the formulas:
The coefficients a o , a n and b n are called Fourier coefficients, and if they can be found, then series (1) is called next to Fourier, corresponding to the function f(x). For series (1), the term (a 1 cosx+b 1 sinx) is called the first or fundamental harmonic,
Another way to write a series is to use the relation acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Where a o is a constant, with 1 =(a 1 2 +b 1 2) 1/2, with n =(a n 2 +b n 2) 1/2 - the amplitudes of the various components, and is equal to a n =arctg a n /b n.
For series (1), the term (a 1 cosx+b 1 sinx) or c 1 sin(x+α 1) is called the first or fundamental harmonic,(a 2 cos2x+b 2 sin2x) or c 2 sin(2x+α 2) is called second harmonic and so on.
To accurately represent a complex signal typically requires an infinite number of terms. However, in many practical problems it is sufficient to consider only the first few terms.
Fourier series of non-periodic functions with period 2π.
Expansion of non-periodic functions into Fourier series.
If the function f(x) is non-periodic, it means that it cannot be expanded into a Fourier series for all values of x. However, it is possible to define a Fourier series representing a function over any range of width 2π.
Given a non-periodic function, a new function can be constructed by selecting values of f(x) within a certain range and repeating them outside that range at 2π intervals. Since the new function is periodic with period 2π, it can be expanded into a Fourier series for all values of x. For example, the function f(x)=x is not periodic. However, if it is necessary to expand it into a Fourier series in the interval from o to 2π, then outside this interval a periodic function with a period of 2π is constructed (as shown in the figure below).
For non-periodic functions such as f(x)=x, the sum of the Fourier series is equal to the value of f(x) at all points in a given range, but it is not equal to f(x) for points outside the range. To find the Fourier series of a non-periodic function in the 2π range, the same formula of Fourier coefficients is used.
Even and odd functions.
They say the function y=f(x) even, if f(-x)=f(x) for all values of x. Graphs of even functions are always symmetrical about the y-axis (that is, they are mirror images). Two examples of even functions: y=x2 and y=cosx.
They say that the function y=f(x) odd, if f(-x)=-f(x) for all values of x. Graphs of odd functions are always symmetrical about the origin.
Many functions are neither even nor odd.
Fourier series expansion in cosines.
The Fourier series of an even periodic function f(x) with period 2π contains only cosine terms (i.e., no sine terms) and may include a constant term. Hence,
where are the coefficients of the Fourier series,
The Fourier series of an odd periodic function f(x) with period 2π contains only terms with sines (that is, it does not contain terms with cosines).
Hence,
where are the coefficients of the Fourier series,
Fourier series at half cycle.
If a function is defined for a range, say from 0 to π, and not just from 0 to 2π, it can be expanded in a series only in sines or only in cosines. The resulting Fourier series is called near Fourier at half cycle.
If you want to get the decomposition Half-cycle Fourier by cosines functions f(x) in the range from 0 to π, then it is necessary to construct an even periodic function. In Fig. Below is the function f(x)=x, built on the interval from x=0 to x=π. Since the even function is symmetrical about the f(x) axis, we draw line AB, as shown in Fig. below. If we assume that outside the considered interval the resulting triangular shape is periodic with a period of 2π, then the final graph looks like this: in Fig. below. Since we need to obtain the Fourier expansion in cosines, as before, we calculate the Fourier coefficients a o and a n
If you want to get functions f(x) in the range from 0 to π, then you need to construct an odd periodic function. In Fig. Below is the function f(x)=x, built on the interval from x=0 to x=π. Since the odd function is symmetrical about the origin, we construct the line CD, as shown in Fig. If we assume that outside the considered interval the resulting sawtooth signal is periodic with a period of 2π, then the final graph has the form shown in Fig. Since we need to obtain the Fourier expansion of the half-cycle in terms of sines, as before, we calculate the Fourier coefficient. b
Fourier series for an arbitrary interval.
Expansion of a periodic function with period L.
The periodic function f(x) repeats as x increases by L, i.e. f(x+L)=f(x). The transition from the previously considered functions with a period of 2π to functions with a period of L is quite simple, since it can be done using a change of variable.
To find the Fourier series of the function f(x) in the range -L/2≤x≤L/2, we introduce a new variable u so that the function f(x) has a period of 2π relative to u. If u=2πx/L, then x=-L/2 for u=-π and x=L/2 for u=π. Also let f(x)=f(Lu/2π)=F(u). The Fourier series F(u) has the form
Where are the coefficients of the Fourier series,
However, more often the above formula results in a dependence on x. Since u=2πx/L, it means du=(2π/L)dx, and the limits of integration are from -L/2 to L/2 instead of - π to π. Consequently, the Fourier series for the dependence on x has the form
where in the range from -L/2 to L/2 are the coefficients of the Fourier series,
(The limits of integration can be replaced by any interval of length L, for example, from 0 to L)
Fourier series on a half-cycle for functions specified in the interval L≠2π.
For the substitution u=πх/L, the interval from x=0 to x=L corresponds to the interval from u=0 to u=π. Consequently, the function can be expanded into a series only in cosines or only in sines, i.e. V Fourier series at half cycle.
The cosine expansion in the range from 0 to L has the form
