Konuyla ilgili ders ve sunum: "Güç fonksiyonları. Özellikler. Grafikler"
Ek materyaller
Sevgili kullanıcılar, yorumlarınızı, yorumlarınızı, dileklerinizi bırakmayı unutmayın! Tüm materyaller antivirüs programı ile kontrol edilmiştir.
11. sınıf için Integral çevrimiçi mağazasında öğretim yardımcıları ve simülatörler
9-11. Sınıflar için etkileşimli el kitabı "Trigonometri"
10-11. Sınıflar için etkileşimli el kitabı "Logarithms"
Güç fonksiyonları, tanım alanı.
Arkadaşlar, son dersimizde rasyonel üslü sayılarla çalışmayı öğrendik. Bu derste kuvvet fonksiyonlarına bakacağız ve kendimizi üssün rasyonel olduğu durumla sınırlayacağız.Şu formdaki fonksiyonları ele alacağız: $y=x^(\frac(m)(n))$.
Öncelikle üssü $\frac(m)(n)>1$ olan fonksiyonları ele alalım.
Bize belirli bir $y=x^2*5$ fonksiyonu verilsin.
Geçen derste verdiğimiz tanıma göre: eğer $x≥0$ ise fonksiyonumuzun tanım tanım kümesi $(x)$ ışınıdır. Fonksiyon grafiğimizi şematik olarak gösterelim.

Fonksiyonun özellikleri $y=x^(\frac(m)(n))$, $0 2. Ne çift ne de tektir.
3. $$ artar,
b) $(2,10)$,
c) ray $$'da.
Çözüm.
Arkadaşlar, 10. sınıfta bir segmentteki bir fonksiyonun en büyük ve en küçük değerini nasıl bulduğumuzu hatırlıyor musunuz?
Doğru, türevi kullandık. Örneğimizi çözelim ve en küçük ve en küçük değeri bulmak için algoritmayı tekrarlayalım. en yüksek değer.
1. Verilen fonksiyonun türevini bulun:
$y"=\frac(16)(5)*\frac(5)(2)x^(\frac(3)(2))-x^3=8x^(\frac(3)(2)) -x^3=8\sqrt(x^3)-x^3$.
2. Türev, orijinal fonksiyonun tüm tanım alanı boyunca mevcuttur, bu durumda kritik noktalar yoktur. Durağan noktaları bulalım:
$y"=8\sqrt(x^3)-x^3=0$.
$8*\sqrt(x^3)=x^3$.
64$x^3=x^6$.
$x^6-64x^3=0$.
$x^3(x^3-64)=0$.
$x_1=0$ ve $x_2=\sqrt(64)=4$.
Belirli bir segment yalnızca bir çözüm içerir: $x_2=4$.
Segmentin uçlarında ve ekstremum noktasında fonksiyonumuzun değerlerinin bir tablosunu oluşturalım:
Cevap: $y_(name)=-862.65$ at $x=9$; $y_(maks.)=38,4$, $x=4$'da.
Örnek. Denklemi çözün: $x^(\frac(4)(3))=24-x$.
Çözüm. $y=x^(\frac(4)(3))$ fonksiyonunun grafiği artar ve $y=24-x$ fonksiyonunun grafiği azalır. Arkadaşlar, siz ve ben biliyoruz: eğer bir fonksiyon artarken diğeri azalırsa, o zaman bunlar yalnızca bir noktada kesişir, yani tek bir çözümümüz olur.
Not:
$8^(\frac(4)(3))=\sqrt(8^4)=(\sqrt(8))^4=2^4=16$.
$24-8=16$.
Yani, $x=8$ ile $16=16$ doğru eşitliğini elde ettik, denklemimizin çözümü budur.
Cevap: $x=8$.
Örnek.
Fonksiyonun grafiğini çizin: $y=(x-3)^\frac(3)(4)+2$.
Çözüm.
Fonksiyonumuzun grafiği, $y=x^(\frac(3)(4))$ fonksiyonunun grafiğinden 3 birim sağa ve 2 birim yukarı kaydırılarak elde edilir. 
Örnek. $y=x^(-\frac(4)(5))$ doğrusuna $x=1$ noktasındaki teğet için bir denklem yazın.
Çözüm. Teğet denklemi bildiğimiz formülle belirlenir:
$y=f(a)+f"(a)(x-a)$.
Bizim durumumuzda $a=1$.
$f(a)=f(1)=1^(-\frac(4)(5))=1$.
Türevini bulalım:
$y"=-\frac(4)(5)x^(-\frac(9)(5))$.
Hesaplayalım:
$f"(a)=-\frac(4)(5)*1^(-\frac(9)(5))=-\frac(4)(5)$.
Teğet denklemini bulalım:
$y=1-\frac(4)(5)(x-1)=-\frac(4)(5)x+1\frac(4)(5)$.
Cevap: $y=-\frac(4)(5)x+1\frac(4)(5)$.
Bağımsız olarak çözülmesi gereken sorunlar
1. Segmentte fonksiyonun en büyük ve en küçük değerini bulun: $y=x^\frac(4)(3)$:a) $$.
b) $(4.50)$.
c) ray $$'da.
3. Denklemi çözün: $x^(\frac(1)(4))=18-x$.
4. Fonksiyonun grafiğini oluşturun: $y=(x+1)^(\frac(3)(2))-1$.
5. $x=1$ noktasındaki $y=x^(-\frac(3)(7))$ düz çizgisine teğet için bir denklem oluşturun.
İşlev nerede X– değişken miktar, A– belirli bir numara aranır Güç fonksiyonu .
Eğer o doğrusal bir fonksiyonsa, grafiği de düz bir çizgidir (bkz. paragraf 4.3, Şekil 4.7).
Eğer o zaman - ikinci dereceden fonksiyon grafiği bir paraboldür (bkz. paragraf 4.3, Şekil 4.8).
O halde grafiği kübik bir parabol ise (bkz. paragraf 4.3, Şekil 4.9).
Bu ters fonksiyondur
1. İhtisas: ![]()
2. Çoklu anlamlar:![]()
3. Çift ve tek: fonksiyon tuhaftır.
4. Fonksiyon frekansı: düzenli olmayan.
5. Fonksiyon sıfırları: X= 0 – tek sıfır.
6. Fonksiyonun maksimum veya minimum değeri yoktur.
7.
8. Bir fonksiyonun grafiği Düz bir çizgiye göre kübik bir parabolün grafiğine simetrik Y=X ve Şekil 2'de gösterilmektedir. 5.1.
 |
Güç fonksiyonu
1. İhtisas: ![]()
2. Çoklu anlamlar:
3. Çift ve tek: fonksiyon eşittir.
4. Fonksiyon frekansı: düzenli olmayan.
5. Fonksiyon sıfırları: tek sıfır X = 0.
6. Fonksiyonun en büyük ve en küçük değerleri: için en küçük değeri alır X= 0, 0'a eşittir.
7. Aralıkları artırın ve azaltın: fonksiyon aralıkta azalıyor ve aralıkta artıyor
8. Bir fonksiyonun grafiği(her biri için N Î N) ikinci dereceden bir parabolün grafiğine “benzerdir” (fonksiyon grafikleri Şekil 5.2'de gösterilmiştir).

Güç fonksiyonu
1. İhtisas: ![]()
2. Çoklu anlamlar: ![]()
3. Çift ve tek: fonksiyon tuhaftır.
4. Fonksiyon frekansı: düzenli olmayan.
5. Fonksiyon sıfırları: X= 0 – tek sıfır.
6. En yüksek ve en düşük değerler:
7. Aralıkları artırın ve azaltın: fonksiyon tanımın tüm alanı boyunca artmaktadır.
8. Bir fonksiyonun grafiği(her biri için ) kübik bir parabolün grafiğine “benzerdir” (fonksiyon grafikleri Şekil 5.3'te gösterilmiştir).
 |
Güç fonksiyonu![]()
1. İhtisas:
2. Çoklu anlamlar:
3. Çift ve tek: fonksiyon tuhaftır.
4. Fonksiyon frekansı: düzenli olmayan.
5. Fonksiyon sıfırları: sıfırları yoktur.
6. Fonksiyonun en büyük ve en küçük değerleri: fonksiyon herhangi biri için en büyük ve en küçük değerlere sahip değildir
7. Aralıkları artırın ve azaltın: fonksiyon tanım alanında azalıyor.
8. Asimptotlar:(eksen kuruluş birimi) – dikey asimptot;
(eksen Ah) - Yatay asimptot.
9. Bir fonksiyonun grafiği(herkes için N) bir hiperbol grafiğine “benzerdir” (fonksiyon grafikleri Şekil 5.4'te gösterilmiştir).
 |
Güç fonksiyonu
1. İhtisas:
2. Çoklu anlamlar:
3. Çift ve tek: fonksiyon eşittir.
4. Fonksiyon frekansı: düzenli olmayan.
5. Fonksiyonun en büyük ve en küçük değerleri: fonksiyon herhangi biri için en büyük ve en küçük değerlere sahip değildir
6. Aralıkları artırın ve azaltın: fonksiyon azalıyor ve artıyor
7. Asimptotlar: X= 0 (eksen kuruluş birimi) – dikey asimptot;
e= 0 (eksen Ah) - Yatay asimptot.
8. Fonksiyon grafikleri Bunlar ikinci dereceden hiperbollerdir (Şekil 5.5).
 |
Güç fonksiyonu
1. İhtisas:
2. Çoklu anlamlar:
3. Çift ve tek: fonksiyonun çift ve tek özelliği yoktur.
4. Fonksiyon frekansı: düzenli olmayan.
5. Fonksiyon sıfırları: X= 0 – tek sıfır.
6. Fonksiyonun en büyük ve en küçük değerleri: fonksiyon o noktada 0'a eşit en küçük değeri alır X= 0; pek önemli değil.
7. Aralıkları artırın ve azaltın: fonksiyon tanımın tüm alanı boyunca artmaktadır.
8. Belirli bir üs için bu tür fonksiyonların her biri, sağlanan fonksiyonun tersidir
9. Bir fonksiyonun grafiği herhangi bir fonksiyonun grafiğine "benzer" N ve Şekil 2'de gösterilmektedir. 5.6.

Güç fonksiyonu
1. İhtisas: ![]()
2. Çoklu anlamlar:![]()
3. Çift ve tek: fonksiyon tuhaftır.
4. Fonksiyon frekansı: düzenli olmayan.
5. Fonksiyon sıfırları: X= 0 – tek sıfır.
6. Fonksiyonun en büyük ve en küçük değerleri: fonksiyon herhangi biri için en büyük ve en küçük değerlere sahip değildir
7. Aralıkları artırın ve azaltın: fonksiyon tanımın tüm alanı boyunca artmaktadır.
8. Bir fonksiyonun grafiğiŞekil 2'de gösterilmiştir. 5.7.
 |
Tamsayılı kuvvet fonksiyonlarının özelliklerini ve grafiklerini hatırlayalım. negatif gösterge.
Çift n için:
Örnek fonksiyon:
Bu tür fonksiyonların tüm grafikleri iki sabit noktadan geçer: (1;1), (-1;1). Bu tür fonksiyonların özelliği eşlikleridir; grafikler op-amp eksenine göre simetriktir.

Pirinç. 1. Bir fonksiyonun grafiği
Tek n için:
Örnek fonksiyon:
Bu tür fonksiyonların tüm grafikleri iki sabit noktadan geçer: (1;1), (-1;-1). Bu tür fonksiyonların özelliği tek olmalarıdır; grafikler orijine göre simetriktir.

Pirinç. 2. Bir fonksiyonun grafiği
Temel tanımı hatırlayalım.
Rasyonel pozitif üssü olan negatif olmayan bir a sayısının kuvvetine sayı denir.
Rasyonel negatif üssü olan pozitif bir a sayısının kuvvetine sayı denir.
Eşitlik için:
![]()
![]()
Örneğin: ![]() ; - tanımı gereği negatif rasyonel üssü olan bir derecenin ifadesi mevcut değildir; Üs tamsayı olduğu için var,
; - tanımı gereği negatif rasyonel üssü olan bir derecenin ifadesi mevcut değildir; Üs tamsayı olduğu için var, ![]()
Rasyonel negatif üslü güç fonksiyonlarını ele almaya geçelim.
![]()
Örneğin:
Bu fonksiyonun grafiğini çizmek için bir tablo oluşturabilirsiniz. Bunu farklı bir şekilde yapacağız: önce paydanın grafiğini oluşturup inceleyeceğiz - bu bizim tarafımızdan biliniyor (Şekil 3).

Pirinç. 3. Bir fonksiyonun grafiği
Payda fonksiyonunun grafiği sabit bir noktadan (1;1) geçer. Orijinal fonksiyonu çizerken verilen nokta kalır, kök de sıfıra yaklaştığında fonksiyon sonsuza doğru yönelir. Ve tam tersine, x sonsuza doğru yöneldikçe fonksiyon da sıfıra doğru yönelir (Şekil 4).

Pirinç. 4. Fonksiyon grafiği
İncelenen işlevler ailesinden başka bir işlevi ele alalım.
![]()
Tanım gereği önemlidir
Paydadaki fonksiyonun grafiğini ele alalım: Bu fonksiyonun grafiği tarafımızdan bilinmektedir, tanım bölgesinde artar ve (1;1) noktasından geçer (Şekil 5).

Pirinç. 5. Bir fonksiyonun grafiği
Orijinal fonksiyonun grafiğini çizerken (1;1) noktası kalır, kök de sıfıra doğru yönelirken fonksiyon da sonsuza doğru yönelir. Ve tam tersine, x sonsuza doğru yöneldikçe fonksiyon da sıfıra doğru yönelir (Şekil 6).

Pirinç. 6. Bir fonksiyonun grafiği
Ele alınan örnekler, grafiğin nasıl aktığını ve incelenen fonksiyonun (negatif rasyonel üssü olan bir fonksiyon) özelliklerinin neler olduğunu anlamaya yardımcı olur.
Bu ailenin fonksiyonlarının grafikleri (1;1) noktasından geçer, fonksiyon tüm tanım bölgesi boyunca azalır.
İşlev kapsamı: ![]()
İşlev yukarıdan sınırlı değildir, ancak aşağıdan sınırlıdır. Fonksiyonun ne en büyüğü ne de en düşük değer.
Fonksiyon süreklidir ve sıfırdan artı sonsuza kadar tüm pozitif değerleri alır.
Fonksiyon aşağı doğru dışbükeydir (Şekil 15.7)
Eğri üzerinde A ve B noktaları alınır, içinden bir doğru çizilir, eğrinin tamamı doğru parçasının altındadır, bu durum eğri üzerindeki keyfi iki nokta için sağlanır, bu nedenle fonksiyon aşağı doğru dışbükeydir. Pirinç. 7.

Pirinç. 7. Fonksiyonun dışbükeyliği
Bu ailenin fonksiyonlarının aşağıdan sıfırla sınırlandığını ancak en küçük değere sahip olmadığını anlamak önemlidir.
Örnek 1 - \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \] aralığındaki bir fonksiyonun maksimum ve minimumunu bulun
Grafik (Şekil 2).

Şekil 2. $f\left(x\right)=x^(2n)$ fonksiyonunun grafiği
Doğal tek üssü olan bir kuvvet fonksiyonunun özellikleri
Tanım alanı tüm gerçek sayılardır.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- fonksiyon tektir.
$f(x)$ tüm tanım alanı boyunca süreklidir.
Aralığın tamamı gerçek sayılardır.
$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Fonksiyon, tanımın tüm alanı boyunca artar.
$f\left(x\right)0$, $x\in (0,+\infty)$ için.
$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$
\ \
Fonksiyon $x\in (-\infty ,0)$ için içbükeydir ve $x\in (0,+\infty)$ için dışbükeydir.
Grafik (Şekil 3).
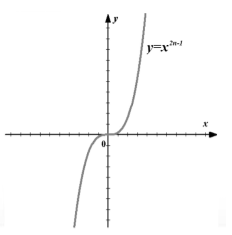
Şekil 3. $f\left(x\right)=x^(2n-1)$ fonksiyonunun grafiği
Tamsayı üssüyle kuvvet fonksiyonu
Öncelikle tam sayı üssü olan derece kavramını tanıtalım.
Tanım 3
$n$ tamsayı üssüne sahip bir $a$ gerçek sayısının kuvveti aşağıdaki formülle belirlenir:

Şekil 4.
Şimdi tamsayı üssü olan bir kuvvet fonksiyonunu, özelliklerini ve grafiğini ele alalım.
Tanım 4
$f\left(x\right)=x^n$ ($n\in Z)$, tamsayı üssü olan bir kuvvet fonksiyonu olarak adlandırılır.
Derece sıfırdan büyükse, doğal üssü olan bir kuvvet fonksiyonu durumuna geliriz. Yukarıda zaten tartışmıştık. $n=0$ için şunu elde ederiz doğrusal fonksiyon$y=1$. Değerlendirmesini okuyucuya bırakıyoruz. Geriye negatif tam sayı üssü olan bir kuvvet fonksiyonunun özelliklerini dikkate almak kalıyor.
Negatif tamsayı üssü olan bir kuvvet fonksiyonunun özellikleri
Tanımın etki alanı $\left(-\infty ,0\right)(0,+\infty)$'dır.
Üs çift ise fonksiyon çifttir, tek ise fonksiyon tektir.
$f(x)$ tüm tanım alanı boyunca süreklidir.
Kapsam:
Üs çift ise $(0,+\infty)$; tek ise $\left(-\infty ,0\right)(0,+\infty)$.
Tek bir üs için fonksiyon $x\in \left(-\infty ,0\right)(0,+\infty)$ olarak azalır. Üs çift ise fonksiyon $x\in (0,+\infty)$ olarak azalır. ve $x\in \left(-\infty ,0\right)$ olarak artar.
Tanımın tüm alanı boyunca $f(x)\ge 0$








