Да намеря производна на тригонометрична функция необходимост от използване таблица с производни, а именно производни 6-13.
Когато намерите първични производни тригонометрични функции За да избегнете често срещани грешки, трябва да обърнете внимание на следните точки:
- в израз на функция един от термините е често синус, косинус или друга тригонометрична функцияне от аргумента на функцията, а от числото (константата), следователно производната на този член е равна на нула;
- почти винаги трябва да опростите израза, получен в резултат на диференциране, и за това трябва уверено да използвате знания за операции с дроби;
- За да опростите израз, почти винаги трябва да знаете тригонометричните идентичности, например формулата двоен ъгъли формулата за единица като сбор от квадратите на синус и косинус.
Пример 1.Намерете производната на функция
Решение. Да кажем с производна на косинусвсичко е ясно, ще кажат много, които започват да изучават производни. Какво относно производна на синусдванадесет делено на pi? Отговор: приемете го за нула! Тук синусът (все пак функция!) е капан, защото аргументът не е променливата X или друга променлива, а просто число. Тоест синусът на това число също е число. А производната на число (константата), както знаем от таблицата с производните, е равна на нула. Така че оставяме само минус синуса на X и намираме неговата производна, без да забравяме за знака:
![]() .
.
Пример 2.Намерете производната на функция
![]() .
.
Решение. Вторият член е същия случай като първия член в предишния пример. Тоест това е число и производната на числото е нула. Намираме производната на втория член като производна на частното:
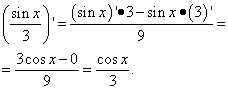
Пример 3.Намерете производната на функция
Решение. Това е друг проблем: тук в първия член няма арксинус или друга тригонометична функция, но има x, което означава, че е функция на x. Следователно, ние го разграничаваме като термин в сумата от функции:

Тук бяха необходими умения за работа с дроби, а именно за премахване на триетажната структура на фракцията.
Пример 4.Намерете производната на функция
![]() .
.
Решение. Тук буквата "phi" играе същата роля като "x" в предишните случаи (и в повечето други, но не всички) - независимата променлива. Следователно, когато търсим производната на произведение от функции, няма да бързаме да обявим производната на корена на „фи“ за нула. Така:
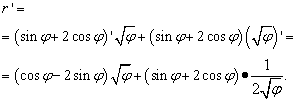
Но решението не свършва дотук. Тъй като подобни термини са събрани в две скоби, все още трябва да трансформираме (опростим) израза. Следователно, ние умножаваме скобите по факторите зад тях и след това привеждаме термините към общ знаменател и извършваме други елементарни трансформации:

Пример 5.Намерете производната на функция
Решение. В този пример ще трябва да знаем факта, че има такава тригонометрична функция - секанс - и нейните формули през косинуса. Нека разграничим:

Пример 6.Намерете производната на функция
![]() .
.
Решение. В този пример ще трябва да запомним формулата за двоен ъгъл от училище. Но първо нека разграничим:

![]() ,
,
(това е формулата за двоен ъгъл)
Представени са производните на обратни тригонометрични функции и извеждането на техните формули. Дадени са и изрази за производни от по-висок порядък. Връзки към страници с по-подробно описание на извеждането на формули.
Първо, извеждаме формулата за производната на арксинуса. Позволявам
y = arcsin x.
Тъй като арксинус е обратната функция на синуса, тогава
.
Тук y е функция на x. Диференцирайте по отношение на променливата x:
.
Прилагаме:
.
Така открихме:
.
Защото тогава. Тогава
.
И предишната формула приема формата:
. Оттук
.
Точно по този начин можете да получите формулата за производната на аркосинус. Въпреки това е по-лесно да се използва формула, свързваща обратни тригонометрични функции:
.
Тогава
.
По-подробно описание е представено на страницата „Извеждане на производните на арксинус и аркосинус“. Там се дава извеждане на производни по два начина- разгледани по-горе и съгласно формулата за производната на обратната функция.
Извеждане на производни на арктангенс и арккотангенс
По същия начин ще намерим производните на арктангенс и арккотангенс.
Позволявам
y = арктан х.
Арктангенсът е обратната функция на тангенса:
.
Диференцирайте по отношение на променливата x:
.
Прилагаме формулата за производна на сложна функция:
.
Така открихме:
.
Производна на аркотангенс:
.
Арксинус производни
Позволявам
.
Вече намерихме производната от първи ред на арксинуса:
.
Чрез диференциране намираме производната от втори ред:
;
.
Може да се напише и в следната форма:
.
От тук получаваме диференциално уравнение, което се удовлетворява от производните на арксинус от първи и втори ред:
.
Чрез диференциране на това уравнение можем да намерим производни от по-висок порядък.
Производна на арксинус от n-ти ред
Производната на арксинуса от n-ти ред има следната форма:
,
където е полином от степен . Определя се по формулите:
;
.
Тук .
Полиномът удовлетворява диференциалното уравнение:
.
Производна на аркосинус от n-ти ред
Производните за аркосинус се получават от производните за аркс синус, като се използва тригонометричната формула:
.
Следователно производните на тези функции се различават само по знак:
.
Производни на арктангенса
Позволявам . Намерихме производната на аркотангенса от първи ред:
.
Нека разбием фракцията в нейната най-проста форма:
.
Ето въображаемата единица, .
Диференцираме веднъж и привеждаме дробта към общ знаменател:
.
Замествайки , получаваме:
.
Производна на арктангенс от n-ти ред
По този начин производната на арктангенса от n-ти ред може да бъде представена по няколко начина:
;
.
Производни на аркотангенса
Нека бъде сега. Нека приложим формулата, свързваща обратни тригонометрични функции:
.
Тогава производната от n-ти ред на аркутангенса се различава само по знак от производната на аркутангенса:
.
Замествайки , намираме:
.
Препратки:
Н.М. Гюнтер, Р.О. Кузмин, Сборник задачи по висша математика, “Лан”, 2003 г.
Когато извеждаме първата формула от таблицата, ще продължим от дефиницията на производната функция в точка. Да вземем къде х– всяко реално число, т.е. х– всяко число от областта на дефиниране на функцията. Нека запишем границата на съотношението на нарастването на функцията към увеличението на аргумента при: ![]()
Трябва да се отбележи, че под граничния знак се получава изразът, който не е несигурността на нула, разделена на нула, тъй като числителят не съдържа безкрайно малка стойност, а точно нула. С други думи, увеличението на константна функция винаги е нула.
По този начин, производна на постоянна функцияе равно на нула в цялата област на дефиниране.
Производна на степенна функция.
Производна формула степенна функцияизглежда като ![]() , където степента стр– всяко реално число.
, където степента стр– всяко реално число.
Нека първо докажем формулата за естествения показател, т.е p = 1, 2, 3, …
Ще използваме определението за производна. Нека запишем границата на съотношението на увеличението на степенна функция към увеличението на аргумента: 
За да опростим израза в числителя, се обръщаме към биномната формула на Нютон: 
следователно 
Това доказва формулата за производната на степенна функция за естествен показател.
Производна на експоненциална функция.
Представяме извеждането на формулата за производна въз основа на определението:
Стигнахме до несигурност. За да го разширим, въвеждаме нова променлива и в . Тогава . При последния преход използвахме формулата за преход към нова логаритмична основа.
Нека заместим в първоначалния лимит: 
Ако си припомним втората забележителна граница, стигаме до формулата за производната на експоненциалната функция: 
Производна на логаритмична функция.
Нека докажем формулата за производната на логаритмична функция за всички хот домейна на дефиницията и всички валидни стойности на основата алогаритъм По дефиниция на производна имаме: 
Както забелязахте, по време на доказателството трансформациите бяха извършени с помощта на свойствата на логаритъма. Равенство  е вярно поради втората забележителна граница.
е вярно поради втората забележителна граница.
Производни на тригонометрични функции.
За да изведем формули за производни на тригонометрични функции, ще трябва да си припомним някои тригонометрични формули, както и първото забележително ограничение.
По дефиниция на производната за функцията синус имаме ![]() .
.
Нека използваме формулата за разликата на синусите: 
Остава да се обърнем към първата забележителна граница: 
По този начин, производната на функцията грях хИма cos x.
Формулата за производната на косинуса се доказва по абсолютно същия начин. 
Следователно, производната на функцията cos xИма – грях х.
Ще изведем формули за таблицата с производни за тангенс и котангенс, използвайки доказани правила за диференциране (производна на дроб). 
Производни на хиперболични функции.
Правилата за диференциране и формулата за производната на експоненциалната функция от таблицата с производни ни позволяват да изведем формули за производните на хиперболичния синус, косинус, тангенс и котангенс. 
Производна на обратната функция.
За да избегнем объркване по време на представяне, нека обозначим с долен индекс аргумента на функцията, чрез която се извършва диференцирането, тоест това е производната на функцията f(x)от х.
Сега нека формулираме правило за намиране на производната на обратна функция.
Нека функциите y = f(x)И x = g(y)взаимно обратни, определени на интервалите и съответно. Ако в точка има крайна ненулева производна на функцията f(x), тогава в точката има крайна производна на обратната функция g(y), и ![]() . В друга публикация
. В друга публикация ![]() .
.
Това правило може да бъде преформулирано за всеки хот интервала , тогава получаваме  .
.
Нека проверим валидността на тези формули.
Нека намерим обратната функция за натурален логаритъм ![]() (Тук ге функция и х- аргумент). След като решихме това уравнение за х, получаваме (тук хе функция и г– нейният аргумент). Това е,
(Тук ге функция и х- аргумент). След като решихме това уравнение за х, получаваме (тук хе функция и г– нейният аргумент). Това е, ![]() и взаимно обратни функции.
и взаимно обратни функции.
От таблицата на производните виждаме това ![]() И
И ![]() .
.
Нека се уверим, че формулите за намиране на производните на обратната функция ни водят до същите резултати: 
От курса на геометрията и математиката учениците са свикнали с факта, че концепцията за производна им се предава чрез областта на фигура, диференциали, граници на функции, както и граници. Нека се опитаме да разгледаме понятието производна от различен ъгъл и да определим как могат да бъдат свързани производната и тригонометричните функции.
И така, нека разгледаме произволна крива, която се описва от абстрактната функция y = f(x).
Нека си представим, че разписанието е карта на туристически маршрут. Увеличението ∆x (делта x) на фигурата е определено разстояние от пътя, а ∆y е промяната във височината на пътя над морското равнище.
Тогава се оказва, че отношението ∆x/∆y ще характеризира сложността на маршрута на всеки сегмент от маршрута. След като сте научили тази стойност, можете уверено да кажете дали изкачването/слизането е стръмно, дали ще ви трябва оборудване за катерене и дали туристите се нуждаят от определена физическа тренировка. Но този индикатор ще бъде валиден само за един малък интервал ∆x.
Ако организаторът на пътуването вземе стойностите за началната и крайната точка на маршрута, т.е. ∆x е равно на дължината на маршрута, тогава той няма да може да получи обективни данни за степента на трудност на пътуването. Следователно е необходимо да се изгради друга графика, която ще характеризира скоростта и „качеството“ на промените в пътя, с други думи, определя съотношението ∆x/∆y за всеки „метър“ от маршрута.
Тази графика ще бъде визуална производна за конкретен път и обективно ще описва неговите промени на всеки интервал от интерес. Много е лесно да се провери това; стойността ∆x/∆y не е нищо повече от разлика, взета за конкретна стойност на x и y. Нека приложим диференциране не към конкретни координати, а към функцията като цяло:

Производна и тригонометрични функции
Тригонометричните функции са неразривно свързани с производните. Това може да се разбере от следния чертеж. Фигурата на координатната ос показва функцията Y = f (x) - синята крива.
K (x0; f (x0)) е произволна точка, x0 + ∆x е увеличението по оста OX, а f (x0 + ∆x) е увеличението по оста OY в определена точка L.

Нека начертаем права линия през точките K и L и да построим правоъгълен триъгълник KLN. Ако мислено преместите сегмента LN по графиката Y = f (x), тогава точките L и N ще се стремят към стойностите K (x0; f (x0)). Нека наречем тази точка условно начало на графиката - граница; ако функцията е безкрайна, поне на един от интервалите, тази тенденция също ще бъде безкрайна и нейната гранична стойност е близка до 0.
Естеството на тази тенденция може да се опише чрез допирателна към избраната точка y = kx + b или чрез графика на производната на оригиналната функция dy - зелената права линия.
Но къде е тук тригонометрията?! Всичко е много просто, помислете за правилния триъгълник KLN. Диференциалната стойност за конкретна точка K е тангенса на ъгъла α или ∠K:

По този начин можем да опишем геометричния смисъл на производната и нейната връзка с тригонометричните функции.
Формули за производни на тригонометрични функции
Трансформациите на синус, косинус, тангенс и котангенс при определяне на производната трябва да се запомнят.

Последните две формули не са грешка, въпросът е, че има разлика между дефинирането на производната на прост аргумент и функция в същото качество.
Нека да разгледаме сравнителна таблица с формули за производните на синус, косинус, тангенс и котангенс:

Изведени са и формули за производните на арксинус, арккосинус, арктангенс и арккотангенс, въпреки че те се използват изключително рядко:

Струва си да се отбележи, че горните формули очевидно не са достатъчни за успешно решаване на типични USE задачи, което ще бъде демонстрирано при решаването на конкретен пример за намиране на производната на тригонометричен израз.
Упражнение: Необходимо е да се намери производната на функцията и да се намери нейната стойност за π/4:

Решение: За да намерим y’ е необходимо да си припомним основните формули за преобразуване на оригиналната функция в производна, а именно.
Предмет:„Производна на тригонометрични функции”.
Тип урок– урок за затвърдяване на знанията.
Форма на урока– интегриран урок.
Място на урока в урочната система за този раздел- общ урок.
Целите са поставени комплексно:
- образователен:да познава правилата за диференциране, да умее да прилага правилата за пресмятане на производни при решаване на уравнения и неравенства; подобряване на предметните, включително изчислителните умения и способности; Компютърни умения;
- развитие:развитие на интелектуални и логически умения и познавателни интереси;
- образователен:култивирайте адаптивност към съвременни условияобучение.
Методи:
- репродуктивни и продуктивни;
- практически и словесно;
- самостоятелна работа;
- програмирано обучение, T.S.O.;
- комбинация от фронтална, групова и индивидуална работа;
- диференцирано обучение;
- индуктивно-дедуктивен.
Форми на контрол:
- устно проучване,
- програмиран контрол,
- самостоятелна работа,
- индивидуални задачи на компютъра,
- партньорска проверка с помощта на диагностичната карта на ученика.
ПО ВРЕМЕ НА ЗАНЯТИЯТА
I. Организационен момент
II. Актуализиране на справочните знания
а) Комуникация на цели и задачи:
- да познава правилата за диференциране, да умее да прилага правилата за пресмятане на производни при решаване на задачи, уравнения и неравенства;
- подобряване на предметните, включително изчислителните умения и способности; Компютърни умения;
- развиват интелектуални и логически умения и познавателни интереси;
- култивиране на адаптивност към съвременните условия на обучение.
б) Повторение на учебен материал
Правила за изчисляване на производни (повторение на формули на компютър със звук). док.7.
- Каква е производната на синус?
- Каква е производната на косинус?
- Каква е производната на тангенса?
- Каква е производната на котангенса?
III. Устна работа
Намерете производната. |
|||
Опция 1. |
Вариант 2. |
||
при = 2х + 5. |
при = 2х – 5. |
||
при= 4cos х. |
при= 3sin х. |
||
при= tg х+ctg х. |
при= tg х-ctg х. |
||
при= грях 3 х. |
при= cos 4 х. |
||
Опции за отговор. |
|||
– 4син х |
– 3cos х |
||
1/cos 2 х+ 1/грех 2 х |
1/cos 2 х–1/грех 2 х |
1/грях 2 х–1/cos 2 х |
|
– 4sin4 х |
– 3cos3 х |
||
Размяна на тетрадки. В диагностичните карти правилно изпълнените задачи отбелязвайте със знак +, а неправилно изпълнените задачи със знак –.
IV. Решаване на уравнения с помощта на производна
– Как да намерим точките, в които производната е нула?
За да намерите точките, в които производната тази функцияе равно на нула, имате нужда от:
– определя естеството на функцията,
– намерете област дефиниции на функции,
– намерете производната на тази функция,
– решаване на уравнението f "(х) = 0,
- Изберете верният отговор.
Задача 1.
дадени: при
= х– грях х.
Намирам:точки, в които производната е нула.
Решение.Функцията е дефинирана и диференцируема върху множеството от всички реални числа, тъй като функциите са дефинирани и диференцируеми върху множеството от всички реални числа ж(х) = хИ T(х) = – грях х.
Използвайки правилата за диференциране, получаваме f
"(х) = (х– грях х)" = (х)" – (грех х)" = 1 – cos х.
Ако f "(х) = 0, тогава 1 – cos х = 0.
cos х= 1/; нека се отървем от ирационалността в знаменателя, получаваме cos х
= /2.
Според формулата T= ± arccos а+ 2n, n Z, получаваме: х= ± arccos /2 + 2n, n Z.
Отговор: x = ± /4 + 2n, n Z.
V. Решаване на уравнения с помощта на алгоритъм
Намерете в кои точки производната изчезва.
f(х) = грях х+cos х |
f(х) = грях 2 х – х |
f(х) = 2х+cos(4 х – ) |
Студентът може да избере всеки от трите примера. Първият пример е оценен " 3 ", второ - " 4 ", трето - " 5 " Решение в тетрадки с последваща взаимна проверка. Един ученик решава на дъската. Ако решението се окаже неправилно, ученикът трябва да се върне към алгоритъма и да опита да реши отново.
Програмирано управление.
Опция 1 |
Вариант 2 |
|||
г = 2х 3 |
г = 3х 2 |
|||
г = 1/4 х 4 + 2х 2 – 7 |
г = 1/2 х 4 + 4х + 5 |
|||
г = х 3 + 4х 2
– 3х. |
г = 2х 3 – 9х 2
+ 12х + 7. |
|||
г= грях 2 х– cos 3 х. |
г= cos 2 х– грях 3 х. |
|||
г= tg х–ctg( х + /4). |
г=ctg х+ tg( х – /4). |
|||
г= грях 2 х. |
г= cos 2 х. |
|||
Опции за отговор. |
||||
|
| ||||








