পাওয়ার ফাংশন এর বৈশিষ্ট্য এবং গ্রাফ টেবিল। পাওয়ার ফাংশন, এর বৈশিষ্ট্য এবং গ্রাফ

বিষয়ের উপর পাঠ এবং উপস্থাপনা: "পাওয়ার ফাংশন। বৈশিষ্ট্য। গ্রাফ"

অতিরিক্ত উপকরণ
প্রিয় ব্যবহারকারী, আপনার মন্তব্য, পর্যালোচনা, শুভেচ্ছা ছেড়ে ভুলবেন না! সমস্ত উপকরণ একটি অ্যান্টিভাইরাস প্রোগ্রাম দ্বারা চেক করা হয়েছে.

11 তম গ্রেডের জন্য ইন্টিগ্রাল অনলাইন স্টোরে শিক্ষণ সহায়ক এবং সিমুলেটর
9-11 গ্রেডের জন্য ইন্টারেক্টিভ ম্যানুয়াল "ত্রিকোণমিতি"
গ্রেড 10-11 "লগারিদম" এর জন্য ইন্টারেক্টিভ ম্যানুয়াল

পাওয়ার ফাংশন, সংজ্ঞার ডোমেইন।

বন্ধুরা, গত পাঠে আমরা শিখেছি কিভাবে মূলদ সূচক সহ সংখ্যার সাথে কাজ করতে হয়। এই পাঠে আমরা পাওয়ার ফাংশনগুলি দেখব এবং নিজেদেরকে সীমাবদ্ধ রাখব যেখানে সূচকটি যুক্তিযুক্ত।
আমরা ফর্মের ফাংশন বিবেচনা করব: $y=x^(\frac(m)(n))$।
আসুন প্রথমে ফাংশন বিবেচনা করি যার সূচক $\frac(m)(n)>1$।
আমাদের একটি নির্দিষ্ট ফাংশন দেওয়া যাক $y=x^2*5$।
আমরা শেষ পাঠে যে সংজ্ঞা দিয়েছিলাম তা অনুসারে: যদি $x≥0$, তাহলে আমাদের ফাংশনের সংজ্ঞার ডোমেন হল রে $(x)$। আসুন আমাদের ফাংশনের গ্রাফটি পরিকল্পিতভাবে চিত্রিত করি।

ফাংশনের বৈশিষ্ট্য $y=x^(\frac(m)(n))$, $0 2. এটি জোড় বা বিজোড়ও নয়।
3. $$ দ্বারা বৃদ্ধি পায়,
খ) $(2,10)$,
গ) রশ্মির উপর $$।
সমাধান।
বন্ধুরা, আপনার কি মনে আছে কিভাবে আমরা 10 তম গ্রেডে একটি বিভাগে একটি ফাংশনের সবচেয়ে বড় এবং ক্ষুদ্রতম মান খুঁজে পেয়েছি?
এটা ঠিক, আমরা ডেরিভেটিভ ব্যবহার করেছি। আসুন আমাদের উদাহরণটি সমাধান করি এবং ক্ষুদ্রতম এবং খুঁজে বের করার জন্য অ্যালগরিদম পুনরাবৃত্তি করি সর্বোচ্চ মান.
1. প্রদত্ত ফাংশনের ডেরিভেটিভ খুঁজুন:
$y"=\frac(16)(5)*\frac(5)(2)x^(\frac(3)(2))-x^3=8x^(\frac(3)(2)) -x^3=8\sqrt(x^3)-x^3$।
2. ডেরিভেটিভটি মূল ফাংশনের সংজ্ঞার পুরো ডোমেন জুড়ে বিদ্যমান, তারপরে কোন সমালোচনামূলক পয়েন্ট নেই। চলুন স্থির বিন্দু খুঁজে বের করা যাক:
$y"=8\sqrt(x^3)-x^3=0$।
$8*\sqrt(x^3)=x^3$।
$64x^3=x^6$।
$x^6-64x^3=0$।
$x^3(x^3-64)=0$।
$x_1=0$ এবং $x_2=\sqrt(64)=4$।
একটি প্রদত্ত সেগমেন্টে শুধুমাত্র একটি সমাধান রয়েছে $x_2=4$।
আসুন সেগমেন্টের শেষে এবং চরম বিন্দুতে আমাদের ফাংশনের মানগুলির একটি টেবিল তৈরি করি:
উত্তর: $y_(নাম)=-862.65$ এ $x=9$; $y_(সর্বোচ্চ।)=38.4$ এ $x=4$।

উদাহরণ। সমীকরণটি সমাধান করুন: $x^(\frac(4)(3))=24-x$।
সমাধান। $y=x^(\frac(4)(3))$ ফাংশনের গ্রাফ বাড়ে, এবং $y=24-x$ ফাংশনের গ্রাফ হ্রাস পায়। বন্ধুরা, আপনি এবং আমি জানি: যদি একটি ফাংশন বৃদ্ধি পায় এবং অন্যটি হ্রাস পায়, তবে তারা শুধুমাত্র একটি বিন্দুতে ছেদ করে, অর্থাৎ, আমাদের কাছে শুধুমাত্র একটি সমাধান আছে।
বিঃদ্রঃ:
$8^(\frac(4)(3))=\sqrt(8^4)=(\sqrt(8))^4=2^4=16$।
$24-8=16$.
অর্থাৎ, $x=8$ দিয়ে আমরা সঠিক সমতা পেয়েছি $16=16$, এটি হল আমাদের সমীকরণের সমাধান।
উত্তর: $x=8$।

উদাহরণ।
ফাংশন গ্রাফ করুন: $y=(x-3)^\frac(3)(4)+2$।
সমাধান।
আমাদের ফাংশনের গ্রাফটি $y=x^(\frac(3)(4))$ ফাংশনের গ্রাফ থেকে প্রাপ্ত হয়, এটিকে 3 ইউনিট ডানে এবং 2 ইউনিট উপরে স্থানান্তরিত করে।

উদাহরণ। $x=1$ বিন্দুতে $y=x^(-\frac(4)(5))$ রেখার স্পর্শকের জন্য একটি সমীকরণ লিখ।
সমাধান। স্পর্শক সমীকরণ আমরা জানি সূত্র দ্বারা নির্ধারিত হয়:
$y=f(a)+f"(a)(x-a)$।
আমাদের ক্ষেত্রে $a=1$।
$f(a)=f(1)=1^(-\frac(4)(5))=1$।
আসুন ডেরিভেটিভ খুঁজে বের করা যাক:
$y"=-\frac(4)(5)x^(-\frac(9)(5))$।
আসুন গণনা করা যাক:
$f"(a)=-\frac(4)(5)*1^(-\frac(9)(5))=-\frac(4)(5)$।
আসুন স্পর্শক সমীকরণটি খুঁজে বের করা যাক:
$y=1-\frac(4)(5)(x-1)=-\frac(4)(5)x+1\frac(4)(5)$।
উত্তর: $y=-\frac(4)(5)x+1\frac(4)(5)$।

স্বাধীনভাবে সমাধান করতে সমস্যা

1. ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মান খুঁজুন: $y=x^\frac(4)(3)$ অংশে:
ক) $$।
খ) $(4.50)$।
গ) রশ্মির উপর $$।
3. সমীকরণটি সমাধান করুন: $x^(\frac(1)(4))=18-x$।
4. ফাংশনের একটি গ্রাফ তৈরি করুন: $y=(x+1)^(\frac(3)(2))-1$।
5. $x=1$ বিন্দুতে $y=x^(-\frac(3)(7))$ সরলরেখার স্পর্শকের জন্য একটি সমীকরণ তৈরি করুন।

ফাংশন যেখানে এক্স- পরিবর্তনশীল পরিমাণ, ক- একটি প্রদত্ত নম্বর বলা হয় পাওয়ার ফাংশন .

যদি একটি রৈখিক ফাংশন হয়, তবে এর গ্রাফটি একটি সরল রেখা (অনুচ্ছেদ 4.3, চিত্র 4.7 দেখুন)।

তাহলে - দ্বিঘাত ফাংশন, এর গ্রাফ একটি প্যারাবোলা (অনুচ্ছেদ 4.3, চিত্র 4.8 দেখুন)।

যদি তাহলে এর গ্রাফ একটি ঘনক প্যারাবোলা হয় (অনুচ্ছেদ 4.3, চিত্র 4.9 দেখুন)।

পাওয়ার ফাংশন

এই জন্য বিপরীত ফাংশন

1. ডোমেইন:

2. একাধিক অর্থ:

3. এমনকি বিজোড়:ফাংশন অদ্ভুত।

4. ফাংশন ফ্রিকোয়েন্সি:অ-পর্যায়ক্রমিক

5. ফাংশন শূন্য: এক্স= 0 - একমাত্র শূন্য।

6. ফাংশনের সর্বোচ্চ বা সর্বনিম্ন মান নেই।

7.

8. একটি ফাংশনের গ্রাফএকটি সরলরেখার সাপেক্ষে একটি ঘনক প্যারাবোলার গ্রাফের প্রতিসম Y=এক্সএবং চিত্রে দেখানো হয়েছে। 5.1।

পাওয়ার ফাংশন

1. ডোমেইন:

2. একাধিক অর্থ:

3. এমনকি বিজোড়:ফাংশন সমান.

4. ফাংশন ফ্রিকোয়েন্সি:অ-পর্যায়ক্রমিক

5. ফাংশন শূন্য:একক শূন্য এক্স = 0.

6. ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মান:জন্য ক্ষুদ্রতম মান নেয় এক্স= 0, এটি 0 এর সমান।

7. বৃদ্ধি এবং হ্রাসের ব্যবধান:ফাংশন ব্যবধানে কমছে এবং ব্যবধানে বাড়ছে

8. একটি ফাংশনের গ্রাফ(প্রতিটির জন্য এন Î এন) একটি দ্বিঘাত প্যারাবোলার গ্রাফের সাথে "সদৃশ" (ফাংশন গ্রাফগুলি চিত্র 5.2 এ দেখানো হয়েছে)।

পাওয়ার ফাংশন

1. ডোমেইন:

2. একাধিক অর্থ:

3. এমনকি বিজোড়:ফাংশন অদ্ভুত।

4. ফাংশন ফ্রিকোয়েন্সি:অ-পর্যায়ক্রমিক

5. ফাংশন শূন্য: এক্স= 0 - একমাত্র শূন্য।

6. সর্বোচ্চ এবং সর্বনিম্ন মান:

7. বৃদ্ধি এবং হ্রাসের ব্যবধান:সংজ্ঞার পুরো ডোমেনে ফাংশনটি বাড়ছে।

8. একটি ফাংশনের গ্রাফ(প্রত্যেকটির জন্য) একটি কিউবিক প্যারাবোলার গ্রাফের সাথে "সদৃশ" (ফাংশন গ্রাফগুলি চিত্র 5.3 এ দেখানো হয়েছে)।

পাওয়ার ফাংশন

1. ডোমেইন:

2. একাধিক অর্থ:

3. এমনকি বিজোড়:ফাংশন অদ্ভুত।

4. ফাংশন ফ্রিকোয়েন্সি:অ-পর্যায়ক্রমিক

5. ফাংশন শূন্য:কোন শূন্য আছে.

6. ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মান:ফাংশনের কোনোটির জন্য সবচেয়ে বড় এবং ক্ষুদ্রতম মান নেই

7. বৃদ্ধি এবং হ্রাসের ব্যবধান:ফাংশন তার সংজ্ঞা ডোমেনে কমছে.

8. উপসর্গ:(অক্ষ OU) – উল্লম্ব অ্যাসিম্পটোট;

(অক্ষ উহু) - অনুভূমিক অ্যাসিম্পটোট।

9. একটি ফাংশনের গ্রাফ(যে কেউ জন্য এন) একটি হাইপারবোলার গ্রাফের সাথে "সদৃশ" (ফাংশন গ্রাফগুলি চিত্র 5.4 এ দেখানো হয়েছে)।

পাওয়ার ফাংশন

1. ডোমেইন:

2. একাধিক অর্থ:

3. এমনকি বিজোড়:ফাংশন সমান.

4. ফাংশন ফ্রিকোয়েন্সি:অ-পর্যায়ক্রমিক

5. ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মান:ফাংশনের কোনোটির জন্য সবচেয়ে বড় এবং ক্ষুদ্রতম মান নেই

6. বৃদ্ধি এবং হ্রাসের ব্যবধান:ফাংশন বাড়ছে এবং কমছে

7. উপসর্গ: এক্স= 0 (অক্ষ OU) – উল্লম্ব অ্যাসিম্পটোট;

Y= 0 (অক্ষ উহু) - অনুভূমিক অ্যাসিম্পটোট।

8. ফাংশন গ্রাফতারা দ্বিঘাত হাইপারবোলাস (চিত্র 5.5)।

পাওয়ার ফাংশন

1. ডোমেইন:

2. একাধিক অর্থ:

3. এমনকি বিজোড়:ফাংশনে জোড় এবং বিজোড়ের বৈশিষ্ট্য নেই।

4. ফাংশন ফ্রিকোয়েন্সি:অ-পর্যায়ক্রমিক

5. ফাংশন শূন্য: এক্স= 0 - একমাত্র শূন্য।

6. ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মান:ফাংশন বিন্দুতে 0 এর সমান ক্ষুদ্রতম মান নেয় এক্স= 0; সবচেয়ে গুরুত্বপূর্ণ নয়।

7. বৃদ্ধি এবং হ্রাসের ব্যবধান:সংজ্ঞার পুরো ডোমেনে ফাংশনটি বাড়ছে।

8. একটি নির্দিষ্ট সূচকের জন্য এই ধরনের প্রতিটি ফাংশন প্রদত্ত ফাংশনের বিপরীত

9. একটি ফাংশনের গ্রাফযেকোনো একটি ফাংশনের গ্রাফের সাথে "সদৃশ" এনএবং চিত্রে দেখানো হয়েছে। 5.6।

পাওয়ার ফাংশন

1. ডোমেইন:

2. একাধিক অর্থ:

3. এমনকি বিজোড়:ফাংশন অদ্ভুত।

4. ফাংশন ফ্রিকোয়েন্সি:অ-পর্যায়ক্রমিক

5. ফাংশন শূন্য: এক্স= 0 - একমাত্র শূন্য।

6. ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মান:ফাংশনের কোনোটির জন্য সবচেয়ে বড় এবং ক্ষুদ্রতম মান নেই

7. বৃদ্ধি এবং হ্রাসের ব্যবধান:সংজ্ঞার পুরো ডোমেনে ফাংশনটি বাড়ছে।

8. একটি ফাংশনের গ্রাফচিত্রে দেখানো হয়েছে। ৫.৭।

আসুন একটি পূর্ণসংখ্যা সহ পাওয়ার ফাংশনের বৈশিষ্ট্য এবং গ্রাফগুলি স্মরণ করি নেতিবাচক সূচক.

এমনকি n এর জন্য,:

উদাহরণ ফাংশন:

এই ধরনের ফাংশনের সমস্ত গ্রাফ দুটি নির্দিষ্ট বিন্দুর মধ্য দিয়ে যায়: (1;1), (-1;1)। এই ধরনের ফাংশনের বিশেষত্ব হল তাদের সমতা;

ভাত। 1. একটি ফাংশনের গ্রাফ

বিজোড় n এর জন্য,:

উদাহরণ ফাংশন:

এই ধরনের ফাংশনের সমস্ত গ্রাফ দুটি নির্দিষ্ট বিন্দুর মধ্য দিয়ে যায়: (1;1), (-1;-1)। এই ধরনের ফাংশনগুলির বিশেষত্ব হল যে তারা বিজোড় হয় গ্রাফগুলি উৎপত্তির সাথে প্রতিসম।

ভাত। 2. একটি ফাংশনের গ্রাফ

আসুন মৌলিক সংজ্ঞাটি স্মরণ করি।

একটি মূলদ ধনাত্মক সূচক সহ একটি অ-ঋণাত্মক সংখ্যা a এর শক্তিকে একটি সংখ্যা বলে।

একটি মূলদ ঋণাত্মক সূচক সহ একটি ধনাত্মক সংখ্যা a এর শক্তিকে একটি সংখ্যা বলে।

সমতার জন্য:

উদাহরণ স্বরূপ: ; - সংজ্ঞা অনুসারে, একটি নেতিবাচক যৌক্তিক সূচক সহ একটি ডিগ্রির অভিব্যক্তি বিদ্যমান নেই; বিদ্যমান কারণ সূচকটি পূর্ণসংখ্যা,

একটি যৌক্তিক ঋণাত্মক সূচকের সাথে পাওয়ার ফাংশন বিবেচনা করা যাক।

উদাহরণ স্বরূপ:

এই ফাংশনের একটি গ্রাফ প্লট করতে, আপনি একটি টেবিল তৈরি করতে পারেন। আমরা এটি ভিন্নভাবে করব: প্রথমে আমরা হরটির গ্রাফ তৈরি করব এবং অধ্যয়ন করব - এটি আমাদের জানা (চিত্র 3)।

ভাত। 3. একটি ফাংশনের গ্রাফ

ডিনোমিনেটর ফাংশনের গ্রাফ একটি নির্দিষ্ট বিন্দু (1;1) এর মধ্য দিয়ে যায়। মূল ফাংশন প্লট করার সময় প্রদত্ত বিন্দুঅবশিষ্ট থাকে, যখন মূলটিও শূন্যের দিকে ঝোঁক, ফাংশনটি অসীমের দিকে ঝোঁক। এবং, বিপরীতভাবে, x যেমন অনন্তের দিকে ঝোঁক, ফাংশনটি শূন্যের দিকে ঝোঁক (চিত্র 4)।

ভাত। 4. ফাংশন গ্রাফ

অধ্যয়ন করা ফাংশন পরিবার থেকে আরেকটি ফাংশন বিবেচনা করা যাক.

সংজ্ঞা দ্বারা এটি গুরুত্বপূর্ণ

হর-এ ফাংশনের গ্রাফটি বিবেচনা করা যাক: , এই ফাংশনের গ্রাফটি আমাদের কাছে পরিচিত, এটি তার সংজ্ঞার ডোমেনে বৃদ্ধি পায় এবং বিন্দু (1;1) (চিত্র 5) এর মধ্য দিয়ে যায়।

ভাত। 5. একটি ফাংশনের গ্রাফ

মূল ফাংশনের গ্রাফ প্লট করার সময়, বিন্দু (1;1) থেকে যায়, যখন রুটটিও শূন্যের দিকে থাকে, ফাংশনটি অনন্তের দিকে ঝোঁক দেয়। এবং, বিপরীতভাবে, x যেমন অনন্তের দিকে ঝোঁক, ফাংশনটি শূন্যের দিকে ঝোঁক (চিত্র 6)।

ভাত। 6. একটি ফাংশনের গ্রাফ

বিবেচিত উদাহরণগুলি বুঝতে সাহায্য করে কিভাবে গ্রাফ প্রবাহিত হয় এবং ফাংশনের বৈশিষ্ট্যগুলি কী কী অধ্যয়ন করা হচ্ছে - একটি নেতিবাচক যুক্তিযুক্ত সূচক সহ একটি ফাংশন।

এই পরিবারের ফাংশনের গ্রাফগুলি বিন্দু (1;1) এর মধ্য দিয়ে যায়, সংজ্ঞার পুরো ডোমেনে ফাংশনটি হ্রাস পায়।

ফাংশন সংজ্ঞা সুযোগ:

ফাংশনটি উপরে থেকে সীমাবদ্ধ নয়, তবে নীচে থেকে সীমাবদ্ধ। ফাংশন একটি মহান বা নেই সর্বনিম্ন মান.

ফাংশনটি ক্রমাগত এবং শূন্য থেকে প্লাস ইনফিনিটি পর্যন্ত সমস্ত ইতিবাচক মান নেয়।

ফাংশনটি নিচের দিকে উত্তল (চিত্র 15.7)

পয়েন্ট A এবং B বক্ররেখায় নেওয়া হয়, তাদের মাধ্যমে একটি সেগমেন্ট টানা হয়, পুরো বক্ররেখাটি সেগমেন্টের নীচে থাকে, এই অবস্থাবক্ররেখার দুইটি বিন্দুর জন্য সন্তুষ্ট, তাই ফাংশনটি নিচের দিকে উত্তল। ভাত। 7.

ভাত। 7. ফাংশনের উত্তলতা

এটা বোঝা গুরুত্বপূর্ণ যে এই পরিবারের ফাংশনগুলি নীচে থেকে শূন্য দ্বারা আবদ্ধ, কিন্তু ক্ষুদ্রতম মান নেই।

উদাহরণ 1 - ব্যবধানে একটি ফাংশনের সর্বাধিক এবং সর্বনিম্ন নির্ণয় করুন \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \]

গ্রাফ (চিত্র 2)।

চিত্র 2. ফাংশনের গ্রাফ $f\left(x\right)=x^(2n)$

একটি প্রাকৃতিক বিজোড় সূচক সহ একটি পাওয়ার ফাংশনের বৈশিষ্ট্য

সংজ্ঞার ডোমেইন হল সমস্ত বাস্তব সংখ্যা।

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- ফাংশনটি বিজোড়।

$f(x)$ সংজ্ঞার সমগ্র ডোমেনে ক্রমাগত।

পরিসীমা হল সব বাস্তব সংখ্যা।

$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$

সংজ্ঞার পুরো ডোমেনে ফাংশন বৃদ্ধি পায়।

$f\left(x\right)0$, $x\in (0,+\infty)$ এর জন্য।

$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\ডান)(n-1)\cdot x^(2n-3)$

\ \

ফাংশনটি $x\in (-\infty ,0)$ এর জন্য অবতল এবং $x\in (0,+\infty)$ এর জন্য উত্তল।

গ্রাফ (চিত্র 3)।

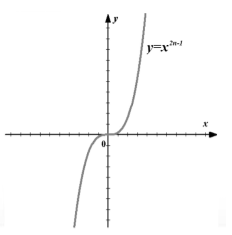
চিত্র 3. ফাংশনের গ্রাফ $f\left(x\right)=x^(2n-1)$

পূর্ণসংখ্যা সূচক সহ পাওয়ার ফাংশন

প্রথমে, একটি পূর্ণসংখ্যা সূচক সহ একটি ডিগ্রির ধারণাটি চালু করা যাক।

সংজ্ঞা 3

পূর্ণসংখ্যার সূচক $n$ সহ একটি বাস্তব সংখ্যা $a$ এর শক্তি সূত্র দ্বারা নির্ধারিত হয়:

চিত্র 4।

আসুন এখন একটি পূর্ণসংখ্যা সূচক, এর বৈশিষ্ট্য এবং গ্রাফ সহ একটি পাওয়ার ফাংশন বিবেচনা করি।

সংজ্ঞা 4

$f\left(x\right)=x^n$ ($n\in Z)$ কে একটি পূর্ণসংখ্যা সূচক সহ একটি পাওয়ার ফাংশন বলা হয়।

যদি ডিগ্রী শূন্যের চেয়ে বেশি হয়, তাহলে আমরা একটি প্রাকৃতিক সূচক সহ একটি পাওয়ার ফাংশনের ক্ষেত্রে আসি। আমরা ইতিমধ্যে উপরে এটি আলোচনা করা হয়েছে. $n=0$ এর জন্য আমরা পাই লিনিয়ার ফাংশন$y=1$। আমরা তার বিবেচনা পাঠকের উপর ছেড়ে দেব। এটি একটি ঋণাত্মক পূর্ণসংখ্যা সূচকের সাথে একটি পাওয়ার ফাংশনের বৈশিষ্ট্যগুলি বিবেচনা করে

একটি ঋণাত্মক পূর্ণসংখ্যা সূচক সহ একটি পাওয়ার ফাংশনের বৈশিষ্ট্য

সংজ্ঞার ডোমেন হল $\left(-\infty ,0\right)(0,+\infty)$।

যদি সূচক জোড় হয়, তাহলে ফাংশনটি জোড় হয়;

$f(x)$ সংজ্ঞার সমগ্র ডোমেনে ক্রমাগত।

সুযোগ:

যদি সূচকটি জোড় হয়, তাহলে $(0,+\infty)$; যদি এটি বিজোড় হয়, তাহলে $\left(-\infty ,0\right)(0,+\infty)$।

একটি বিজোড় সূচকের জন্য, ফাংশনটি $x\in \left(-\infty ,0\right)(0,+\infty)$ হিসাবে হ্রাস পায়। একটি সমান সূচকের জন্য, ফাংশনটি $x\in (0,+\infty)$ হিসাবে হ্রাস পায়। এবং $x\in \left(-\infty ,0\right)$ হিসাবে বৃদ্ধি পায়।

$f(x)\ge 0$ সংজ্ঞার সমগ্র ডোমেনে