ઉકેલ સાથે ત્રિકોણમિતિ વિધેયોના ઉદાહરણોના ડેરિવેટિવ્સને ઉકેલવા. સરળ ત્રિકોણમિતિ કાર્યોના વ્યુત્પન્ન

શોધવા માટે ત્રિકોણમિતિ કાર્યનું વ્યુત્પન્ન ઉપયોગ કરવાની જરૂર છે ડેરિવેટિવ્ઝનું કોષ્ટક, એટલે કે ડેરિવેટિવ્ઝ 6-13.

જ્યારે તમે શોધો પ્રાઇમ ડેરિવેટિવ્ઝ ત્રિકોણમિતિ કાર્યો સામાન્ય ભૂલો ટાળવા માટે, તમારે નીચેના મુદ્દાઓ પર ધ્યાન આપવું જોઈએ:

• વિધેય અભિવ્યક્તિમાં, એક શબ્દ વારંવાર હોય છે સાઈન, કોસાઈન અથવા અન્ય ત્રિકોણમિતિ કાર્યફંક્શનની દલીલમાંથી નહીં, પરંતુ સંખ્યા (સતત), તેથી આ શબ્દનું વ્યુત્પન્ન શૂન્ય બરાબર છે;
• લગભગ હંમેશા તમારે ભિન્નતાના પરિણામે મેળવેલા અભિવ્યક્તિને સરળ બનાવવાની જરૂર છે, અને આ માટે તમારે અપૂર્ણાંક સાથેની કામગીરીના જ્ઞાનનો વિશ્વાસપૂર્વક ઉપયોગ કરવાની જરૂર છે;
• અભિવ્યક્તિને સરળ બનાવવા માટે, તમારે લગભગ હંમેશા ત્રિકોણમિતિ ઓળખ જાણવાની જરૂર છે, ઉદાહરણ તરીકે, સૂત્ર ડબલ કોણઅને સાઈન અને કોસાઈનના વર્ગોના સરવાળા તરીકે એકતા માટેનું સૂત્ર.

ઉદાહરણ 1.ફંક્શનનું વ્યુત્પન્ન શોધો

ઉકેલ. ચાલો સાથે કહીએ કોસાઇનનું વ્યુત્પન્નબધું સ્પષ્ટ છે, ઘણા લોકો જે ડેરિવેટિવ્ઝનો અભ્યાસ કરવાનું શરૂ કરે છે તેઓ કહેશે. તે વિષે સાઈનનું વ્યુત્પન્નબાર ભાગ્યા pi? જવાબ: તેને શૂન્ય બરાબર ગણો! અહીં સાઈન (આખરે એક કાર્ય!) એક છટકું છે, કારણ કે દલીલ એ ચલ X અથવા અન્ય કોઈપણ ચલ નથી, પરંતુ માત્ર એક સંખ્યા છે. એટલે કે, આ સંખ્યાની સાઈન પણ એક સંખ્યા છે. અને સંખ્યાનું વ્યુત્પન્ન (સતત), જેમ કે આપણે ડેરિવેટિવ્ઝના કોષ્ટકમાંથી જાણીએ છીએ, તે શૂન્ય બરાબર છે. તેથી, અમે ફક્ત X ની માઈનસ સાઈન છોડીએ છીએ અને તેનું વ્યુત્પન્ન શોધીએ છીએ, ચિહ્ન વિશે ભૂલશો નહીં:

.

ઉદાહરણ 2.ફંક્શનનું વ્યુત્પન્ન શોધો

.

ઉકેલ. બીજી મુદત એ પાછલા ઉદાહરણમાં પ્રથમ ટર્મ જેવો જ કેસ છે. એટલે કે, તે એક સંખ્યા છે, અને સંખ્યાનું વ્યુત્પન્ન શૂન્ય છે. આપણે બીજા પદનું વ્યુત્પન્ન ભાગાંકના વ્યુત્પન્ન તરીકે શોધીએ છીએ:

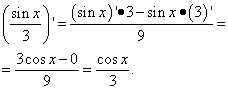
ઉદાહરણ 3.ફંક્શનનું વ્યુત્પન્ન શોધો

ઉકેલ. આ બીજી સમસ્યા છે: અહીં પ્રથમ ટર્મમાં કોઈ આર્ક્સીન અથવા અન્ય ત્રિકોણમિતિ ફંક્શન નથી, પરંતુ ત્યાં x છે, જેનો અર્થ એ છે કે તે x નું કાર્ય છે. તેથી, અમે તેને કાર્યોના સરવાળામાં શબ્દ તરીકે અલગ પાડીએ છીએ:

અહીં અપૂર્ણાંક સાથેની કામગીરીમાં કુશળતા જરૂરી હતી, એટલે કે, અપૂર્ણાંકની ત્રણ માળની રચનાને દૂર કરવામાં.

ઉદાહરણ 4.ફંક્શનનું વ્યુત્પન્ન શોધો

.

ઉકેલ. અહીં અક્ષર "ફી" અગાઉના કેસોમાં "x" ની સમાન ભૂમિકા ભજવે છે (અને મોટાભાગના અન્યમાં, પરંતુ બધા નહીં) - સ્વતંત્ર ચલ. તેથી, જ્યારે આપણે ફંક્શનના ઉત્પાદનનું વ્યુત્પન્ન શોધીએ છીએ, ત્યારે આપણે શૂન્ય સમાન “ફી” ના મૂળના વ્યુત્પન્નને જાહેર કરવા માટે ઉતાવળ નહીં કરીએ. તેથી:

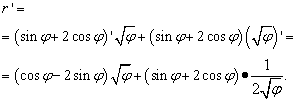
પરંતુ ઉકેલ ત્યાં સમાપ્ત થતો નથી. સમાન શબ્દો બે કૌંસમાં એકત્રિત કરવામાં આવ્યા હોવાથી, અમારે હજુ પણ અભિવ્યક્તિને રૂપાંતરિત (સરળ) કરવાની જરૂર છે. તેથી, અમે કૌંસને તેમની પાછળના પરિબળો દ્વારા ગુણાકાર કરીએ છીએ, અને પછી અમે શરતોને સામાન્ય છેદ પર લાવીએ છીએ અને અન્ય પ્રાથમિક પરિવર્તનો કરીએ છીએ:

ઉદાહરણ 5.ફંક્શનનું વ્યુત્પન્ન શોધો

ઉકેલ. આ ઉદાહરણમાં, આપણે એ હકીકત જાણવાની જરૂર પડશે કે આવા ત્રિકોણમિતિ કાર્ય છે - સેકન્ટ - અને કોસાઇન દ્વારા તેના સૂત્રો. ચાલો તફાવત કરીએ:

ઉદાહરણ 6.ફંક્શનનું વ્યુત્પન્ન શોધો

.

ઉકેલ. આ ઉદાહરણમાં, આપણે શાળામાંથી ડબલ એંગલ ફોર્મ્યુલા યાદ રાખવાની જરૂર પડશે. પરંતુ પ્રથમ ચાલો તફાવત કરીએ:

,

(આ ડબલ એંગલ ફોર્મ્યુલા છે)

વ્યસ્ત ત્રિકોણમિતિ કાર્યોના વ્યુત્પન્ન અને તેમના સૂત્રોના વ્યુત્પન્નતા રજૂ કરવામાં આવ્યા છે. ઉચ્ચ ક્રમના ડેરિવેટિવ્ઝ માટે અભિવ્યક્તિઓ પણ આપવામાં આવે છે. સૂત્રોના વ્યુત્પત્તિના વધુ વિગતવાર વર્ણન સાથે પૃષ્ઠોની લિંક્સ.

પ્રથમ, આપણે આર્ક્સીનના વ્યુત્પન્ન માટે સૂત્ર મેળવીએ છીએ. દો
y = આર્ક્સીન એક્સ.
ત્યારથી આર્ક્સીન એ સાઈનનું વ્યસ્ત કાર્ય છે, તો પછી
.
અહીં y એ x નું કાર્ય છે. ચલ x ના સંદર્ભમાં તફાવત કરો:
.
અમે અરજી કરીએ છીએ:
.
તેથી અમને મળ્યું:
.

કારણ કે, પછી. પછી
.
અને અગાઉનું સૂત્ર ફોર્મ લે છે:
. અહીંથી
.

બરાબર આ રીતે, તમે ચાપ કોસાઇનના વ્યુત્પન્ન માટેનું સૂત્ર મેળવી શકો છો. જો કે, વ્યસ્ત ત્રિકોણમિતિ કાર્યોને લગતા સૂત્રનો ઉપયોગ કરવો વધુ સરળ છે:
.
પછી
.

"આર્કસાઇન અને આર્કોસાઇનના ડેરિવેટિવ્ઝનું વ્યુત્પત્તિ" પૃષ્ઠ પર વધુ વિગતવાર વર્ણન રજૂ કરવામાં આવ્યું છે. ત્યાં આપવામાં આવે છે બે રીતે ડેરિવેટિવ્ઝની વ્યુત્પત્તિ- ઉપર ચર્ચા કરેલ અને વ્યસ્ત કાર્યના વ્યુત્પન્ન માટેના સૂત્ર અનુસાર.

આર્કટેન્જેન્ટ અને આર્કોટેન્જેન્ટના ડેરિવેટિવ્સની વ્યુત્પત્તિ

એ જ રીતે આપણે આર્કટેન્જેન્ટ અને આર્કોટેન્જેન્ટના ડેરિવેટિવ્સ શોધીશું.

દો
y = આર્ક્ટન એક્સ.
આર્કટેંજન્ટ એ સ્પર્શકનું વ્યસ્ત કાર્ય છે:
.
ચલ x ના સંદર્ભમાં તફાવત કરો:
.
અમે જટિલ કાર્યના વ્યુત્પન્ન માટે સૂત્ર લાગુ કરીએ છીએ:
.
તેથી અમને મળ્યું:
.

આર્ક કોટેન્જેન્ટનું વ્યુત્પન્ન:
.

આર્ક્સીન ડેરિવેટિવ્ઝ

દો
.
અમને આર્ક્સીનનું પ્રથમ-ક્રમનું વ્યુત્પન્ન પહેલેથી જ મળ્યું છે:
.
તફાવત કરીને, અમે બીજા-ક્રમનું વ્યુત્પન્ન શોધીએ છીએ:
;
.
તે નીચેના સ્વરૂપમાં પણ લખી શકાય છે:
.
અહીંથી આપણને મળે છે વિભેદક સમીકરણ, જે પ્રથમ અને બીજા ઓર્ડરના આર્ક્સીન ડેરિવેટિવ્ઝ દ્વારા સંતુષ્ટ છે:
.

આ સમીકરણને અલગ કરીને, આપણે ઉચ્ચ ક્રમના ડેરિવેટિવ્ઝ શોધી શકીએ છીએ.

nth ક્રમના આર્કસાઇનનું વ્યુત્પન્ન

nમા ક્રમના આર્કસાઇનનું વ્યુત્પન્ન નીચેનું સ્વરૂપ ધરાવે છે:
,
ડિગ્રીની બહુપદી ક્યાં છે. તે સૂત્રો દ્વારા નક્કી કરવામાં આવે છે:
;
.
અહીં .

બહુપદી વિભેદક સમીકરણને સંતોષે છે:
.

nth ક્રમના આર્કોસાઇનનું વ્યુત્પન્ન

ત્રિકોણમિતિ સૂત્રનો ઉપયોગ કરીને આર્ક કોસાઇન માટેના ડેરિવેટિવ્સ આર્ક સાઇન માટેના ડેરિવેટિવ્સમાંથી મેળવવામાં આવે છે:
.
તેથી, આ કાર્યોના ડેરિવેટિવ્ઝ ફક્ત ચિહ્નમાં અલગ પડે છે:
.

આર્કટેન્જેન્ટના વ્યુત્પન્ન

દો . અમને પ્રથમ ક્રમના આર્ક કોટેન્જેન્ટનું વ્યુત્પન્ન મળ્યું:
.

ચાલો અપૂર્ણાંકને તેના સૌથી સરળ સ્વરૂપમાં તોડીએ:

.
અહીં કાલ્પનિક એકમ છે, .

અમે એકવાર ભેદ કરીએ છીએ અને અપૂર્ણાંકને સામાન્ય છેદ પર લાવીએ છીએ:

.

અવેજીમાં, અમને મળે છે:
.

nમા ક્રમના આર્ક્ટેંજેન્ટનું વ્યુત્પન્ન

આમ, nમા ક્રમના આર્કટેન્જેન્ટના વ્યુત્પન્નને ઘણી રીતે રજૂ કરી શકાય છે:
;
.

આર્ક કોટેન્જેન્ટના વ્યુત્પન્ન

હવે રહેવા દો. ચાલો વ્યસ્ત ત્રિકોણમિતિ કાર્યોને જોડતા સૂત્રને લાગુ કરીએ:
.
પછી ચાપ સ્પર્શકનો nમો ક્રમ વ્યુત્પન્ન માત્ર ચાપ સ્પર્શકના વ્યુત્પન્ન ચિહ્નથી અલગ પડે છે:
.

અવેજીમાં, અમે શોધીએ છીએ:
.

સંદર્ભ:
એન.એમ. ગુંથર, આર.ઓ. કુઝમિન, ઉચ્ચ ગણિતમાં સમસ્યાઓનો સંગ્રહ, "લેન", 2003.

કોષ્ટકનું પ્રથમ સૂત્ર મેળવતી વખતે, આપણે એક બિંદુ પર વ્યુત્પન્ન કાર્યની વ્યાખ્યાથી આગળ વધીશું. ચાલો ક્યાં લઈએ x- કોઈપણ વાસ્તવિક સંખ્યા, એટલે કે, x- કાર્યની વ્યાખ્યાના ડોમેનમાંથી કોઈપણ સંખ્યા. ચાલો ફંક્શનના ઇન્ક્રીમેન્ટના ગુણોત્તરની મર્યાદા અને દલીલના ઇન્ક્રીમેન્ટની મર્યાદા અહીં લખીએ:

એ નોંધવું જોઈએ કે મર્યાદા ચિહ્ન હેઠળ અભિવ્યક્તિ પ્રાપ્ત થાય છે, જે શૂન્ય દ્વારા શૂન્ય ભાગ્યાની અનિશ્ચિતતા નથી, કારણ કે અંશમાં અનંત મૂલ્ય નથી, પરંતુ ચોક્કસપણે શૂન્ય છે. બીજા શબ્દોમાં કહીએ તો, સ્થિર કાર્યની વૃદ્ધિ હંમેશા શૂન્ય હોય છે.

આમ, સતત કાર્યનું વ્યુત્પન્નવ્યાખ્યાના સમગ્ર ડોમેનમાં શૂન્ય બરાબર છે.

પાવર ફંક્શનનું વ્યુત્પન્ન.

વ્યુત્પન્ન સૂત્ર પાવર કાર્યજેવો દેખાય છે , જ્યાં ઘાતાંક પી- કોઈપણ વાસ્તવિક સંખ્યા.

ચાલો સૌ પ્રથમ પ્રાકૃતિક ઘાતાંક માટેનું સૂત્ર સાબિત કરીએ, એટલે કે, માટે p = 1, 2, 3, …

આપણે ડેરિવેટિવની વ્યાખ્યાનો ઉપયોગ કરીશું. ચાલો પાવર ફંક્શનના ઇન્ક્રીમેન્ટ અને દલીલના ઇન્ક્રીમેન્ટના ગુણોત્તરની મર્યાદા લખીએ:

અંશમાં અભિવ્યક્તિને સરળ બનાવવા માટે, અમે ન્યૂટન દ્વિપદી સૂત્ર તરફ વળીએ છીએ:

આથી,

આ કુદરતી ઘાતાંક માટે પાવર ફંક્શનના વ્યુત્પન્ન માટેનું સૂત્ર સાબિત કરે છે.

ઘાતાંકીય કાર્યનું વ્યુત્પન્ન.

અમે વ્યાખ્યાના આધારે વ્યુત્પન્ન સૂત્રની વ્યુત્પત્તિ રજૂ કરીએ છીએ:

અમે અનિશ્ચિતતા પર પહોંચ્યા છીએ. તેને વિસ્તૃત કરવા માટે, અમે એક નવું ચલ રજૂ કરીએ છીએ, અને પર. પછી . છેલ્લા સંક્રમણમાં, અમે નવા લઘુગણક આધાર પર સંક્રમણ માટે સૂત્રનો ઉપયોગ કર્યો.

ચાલો મૂળ મર્યાદામાં બદલીએ:

જો આપણે બીજી નોંધપાત્ર મર્યાદાને યાદ કરીએ, તો આપણે ઘાતાંકીય કાર્યના વ્યુત્પન્ન માટેના સૂત્ર પર પહોંચીએ છીએ:

લઘુગણક કાર્યનું વ્યુત્પન્ન.

ચાલો બધા માટે લઘુગણક ફંક્શનના વ્યુત્પન્ન માટેના સૂત્રને સાબિત કરીએ xવ્યાખ્યાના ડોમેન અને આધારના તમામ માન્ય મૂલ્યોમાંથી aલઘુગણક વ્યુત્પન્નની વ્યાખ્યા દ્વારા અમારી પાસે છે:

તમે નોંધ્યું છે તેમ, પુરાવા દરમિયાન લઘુગણકના ગુણધર્મોનો ઉપયોગ કરીને પરિવર્તનો હાથ ધરવામાં આવ્યા હતા. સમાનતા બીજી નોંધપાત્ર મર્યાદાને કારણે સાચું છે.

ત્રિકોણમિતિ કાર્યોના વ્યુત્પન્ન.

ત્રિકોણમિતિ કાર્યોના વ્યુત્પન્ન માટેના સૂત્રો મેળવવા માટે, આપણે કેટલાક ત્રિકોણમિતિ સૂત્રો તેમજ પ્રથમ નોંધપાત્ર મર્યાદાને યાદ કરવી પડશે.

આપણી પાસે સાઈન ફંક્શન માટે વ્યુત્પન્નની વ્યાખ્યા દ્વારા .

ચાલો સાઈન ફોર્મ્યુલાના તફાવતનો ઉપયોગ કરીએ:

તે પ્રથમ નોંધપાત્ર મર્યાદા તરફ વળવાનું બાકી છે:

આમ, કાર્યનું વ્યુત્પન્ન પાપ xત્યાં છે cos x.

કોસાઇનના વ્યુત્પન્ન માટેનું સૂત્ર બરાબર એ જ રીતે સાબિત થયું છે.

તેથી, કાર્યનું વ્યુત્પન્ન cos xત્યાં છે -પાપ એક્સ.

અમે ભેદભાવના સાબિત નિયમો (અપૂર્ણાંકનું વ્યુત્પન્ન) નો ઉપયોગ કરીને સ્પર્શક અને કોટેન્જેન્ટ માટેના ડેરિવેટિવ્ઝના કોષ્ટક માટે સૂત્રો મેળવીશું.

હાઇપરબોલિક કાર્યોના વ્યુત્પન્ન.

ભેદભાવના નિયમો અને ડેરિવેટિવ્ઝના કોષ્ટકમાંથી ઘાતાંકીય કાર્યના વ્યુત્પન્ન માટેના સૂત્ર અમને હાયપરબોલિક સાઈન, કોસાઈન, ટેન્જેન્ટ અને કોટેન્જેન્ટના ડેરિવેટિવ્ઝ માટેના સૂત્રો મેળવવાની મંજૂરી આપે છે.

વ્યસ્ત કાર્યનું વ્યુત્પન્ન.

પ્રસ્તુતિ દરમિયાન મૂંઝવણ ટાળવા માટે, ચાલો સબસ્ક્રિપ્ટમાં ફંક્શનની દલીલને સૂચવીએ કે જેના દ્વારા ભિન્નતા કરવામાં આવે છે, એટલે કે, તે ફંક્શનનું વ્યુત્પન્ન છે. f(x)દ્વારા x.

હવે ઘડીએ વ્યસ્ત કાર્યનું વ્યુત્પન્ન શોધવા માટેનો નિયમ.

કાર્યો કરવા દો y = f(x)અને x = g(y)પરસ્પર વ્યુત્ક્રમ, અંતરાલ પર અને અનુક્રમે વ્યાખ્યાયિત. જો કોઈ બિંદુ પર ફંક્શનનું મર્યાદિત બિન-શૂન્ય વ્યુત્પન્ન હોય f(x), પછી બિંદુ પર વ્યસ્ત કાર્યનું મર્યાદિત વ્યુત્પન્ન છે g(y), અને . બીજી પોસ્ટમાં .

આ નિયમ કોઈપણ માટે સુધારી શકાય છે xઅંતરાલમાંથી, પછી આપણને મળે છે .

ચાલો આ સૂત્રોની માન્યતા તપાસીએ.

ચાલો કુદરતી લઘુગણક માટે વ્યસ્ત કાર્ય શોધીએ (અહીં yએક કાર્ય છે, અને x- દલીલ). માટે આ સમીકરણ ઉકેલ્યા x, અમે મેળવીએ છીએ (અહીં xએક કાર્ય છે, અને y- તેણીની દલીલ). તે જ, અને પરસ્પર વ્યસ્ત કાર્યો.

ડેરિવેટિવ્ઝના કોષ્ટકમાંથી આપણે તે જોઈએ છીએ અને .

ચાલો ખાતરી કરીએ કે વ્યસ્ત કાર્યના ડેરિવેટિવ્ઝ શોધવા માટેના સૂત્રો આપણને સમાન પરિણામો તરફ દોરી જાય છે:

ભૂમિતિ અને ગણિતના અભ્યાસક્રમથી, શાળાના બાળકો એ હકીકત માટે ટેવાયેલા છે કે વ્યુત્પન્નની વિભાવના તેમને આકૃતિના ક્ષેત્ર, તફાવતો, કાર્યોની મર્યાદાઓ તેમજ મર્યાદાઓ દ્વારા આપવામાં આવે છે. ચાલો વ્યુત્પન્નની વિભાવનાને એક અલગ ખૂણાથી જોવાનો પ્રયાસ કરીએ, અને નિર્ધારિત કરીએ કે વ્યુત્પન્ન અને ત્રિકોણમિતિ કાર્યોને કેવી રીતે જોડી શકાય.

તેથી, ચાલો કેટલાક મનસ્વી વળાંકને ધ્યાનમાં લઈએ જે અમૂર્ત કાર્ય y = f(x) દ્વારા વર્ણવવામાં આવે છે.

ચાલો કલ્પના કરીએ કે સમયપત્રક એ પ્રવાસી માર્ગનો નકશો છે. આકૃતિમાં વધારો ∆x (ડેલ્ટા x) એ પાથનું ચોક્કસ અંતર છે, અને ∆y એ સમુદ્ર સપાટીથી ઉપરના માર્ગની ઊંચાઈમાં ફેરફાર છે.
પછી તે તારણ આપે છે કે ગુણોત્તર ∆x/∆y રૂટના દરેક સેગમેન્ટ પર રૂટની જટિલતાને દર્શાવશે. આ મૂલ્ય શીખ્યા પછી, તમે આત્મવિશ્વાસપૂર્વક કહી શકો છો કે ચઢાણ/અવરોહણ ઊભો છે કે કેમ, તમારે ચડતા સાધનોની જરૂર પડશે કે કેમ અને પ્રવાસીઓને ચોક્કસની જરૂર છે કે કેમ? શારીરિક તાલીમ. પરંતુ આ સૂચક માત્ર એક નાના અંતરાલ ∆x માટે માન્ય રહેશે.

જો ટ્રિપનો આયોજક ટ્રાયલના પ્રારંભિક અને અંતિમ બિંદુઓ માટે મૂલ્યો લે છે, એટલે કે, ∆x રૂટની લંબાઈ જેટલી છે, તો તે મુશ્કેલીની ડિગ્રી પર ઉદ્દેશ્ય ડેટા પ્રાપ્ત કરી શકશે નહીં. સફરની. તેથી, અન્ય ગ્રાફનું નિર્માણ કરવું જરૂરી છે જે પાથમાં ફેરફારોની ગતિ અને "ગુણવત્તા" ને દર્શાવશે, બીજા શબ્દોમાં કહીએ તો, માર્ગના દરેક "મીટર" માટે ગુણોત્તર ∆x/∆y નક્કી કરે છે.

આ ગ્રાફ ચોક્કસ પાથ માટે વિઝ્યુઅલ ડેરિવેટિવ હશે અને રસના દરેક અંતરાલ પર તેના ફેરફારોનું નિરપેક્ષપણે વર્ણન કરશે. આને ચકાસવું ખૂબ જ સરળ છે; મૂલ્ય ∆x/∆y એ x અને y ના ચોક્કસ મૂલ્ય માટે લેવામાં આવેલા વિભેદક સિવાય બીજું કંઈ નથી. ચાલો વિશિષ્ટ કોઓર્ડિનેટ્સ માટે નહીં, પરંતુ સમગ્ર કાર્ય માટે ભિન્નતા લાગુ કરીએ:

વ્યુત્પન્ન અને ત્રિકોણમિતિ કાર્યો

ત્રિકોણમિતિ કાર્યો ડેરિવેટિવ્ઝ સાથે અસ્પષ્ટ રીતે જોડાયેલા છે. આ નીચેના ચિત્ર પરથી સમજી શકાય છે. કોઓર્ડિનેટ અક્ષની આકૃતિ Y = f (x) - વાદળી વળાંક દર્શાવે છે.

K (x0; f (x0)) એક મનસ્વી બિંદુ છે, x0 + ∆x એ OX અક્ષ સાથેનો વધારો છે, અને f (x0 + ∆x) એ ચોક્કસ બિંદુ L પર OY અક્ષ સાથેનો વધારો છે.

ચાલો K અને L બિંદુઓ દ્વારા સીધી રેખા દોરીએ અને બાંધીએ જમણો ત્રિકોણકેએલએન. જો તમે માનસિક રીતે સેગમેન્ટ LN ને ગ્રાફ Y = f (x) સાથે ખસેડો છો, તો પછી પોઈન્ટ L અને N મૂલ્યો K (x0; f (x0)) તરફ વળશે. ચાલો આ બિંદુને ગ્રાફની શરતી શરૂઆત કહીએ - મર્યાદા; જો કાર્ય અનંત છે, ઓછામાં ઓછા એક અંતરાલ પર, આ વલણ પણ અનંત હશે, અને તેનું મર્યાદિત મૂલ્ય 0 ની નજીક છે.

આ વલણની પ્રકૃતિ પસંદ કરેલ બિંદુ y = kx + b માટે સ્પર્શક દ્વારા અથવા મૂળ કાર્ય dy - લીલી સીધી રેખાના વ્યુત્પન્નના ગ્રાફ દ્વારા વર્ણવી શકાય છે.

પણ અહીં ત્રિકોણમિતિ ક્યાં છે ?! બધું ખૂબ જ સરળ છે, કાટકોણ ત્રિકોણ KLN ને ધ્યાનમાં લો. ચોક્કસ બિંદુ K માટે વિભેદક મૂલ્ય એ કોણ α અથવા ∠K ની સ્પર્શક છે:

આ રીતે, આપણે વ્યુત્પન્નનો ભૌમિતિક અર્થ અને ત્રિકોણમિતિ કાર્યો સાથેના તેના સંબંધનું વર્ણન કરી શકીએ છીએ.

ત્રિકોણમિતિ કાર્યો માટે વ્યુત્પન્ન સૂત્રો

ડેરિવેટિવ નક્કી કરતી વખતે સાઈન, કોસાઈન, ટેન્જેન્ટ અને કોટેન્જેન્ટનું રૂપાંતરણ યાદ રાખવું જોઈએ.

છેલ્લા બે સૂત્રો ભૂલ નથી, મુદ્દો એ છે કે સાદી દલીલના વ્યુત્પન્નને વ્યાખ્યાયિત કરવા અને સમાન ક્ષમતામાં કાર્ય વચ્ચે તફાવત છે.

ચાલો સાઇનસ, કોસાઇન, ટેન્જેન્ટ અને કોટેન્જેન્ટના ડેરિવેટિવ્ઝ માટેના સૂત્રો સાથે તુલનાત્મક કોષ્ટક જોઈએ:

આર્ક્સીન, આર્કોસિન, આર્ક્ટેન્જેન્ટ અને આર્કોટેન્જેન્ટના ડેરિવેટિવ્ઝ માટે પણ ફોર્મ્યુલા લેવામાં આવ્યા છે, જો કે તેનો ઉપયોગ ખૂબ જ ભાગ્યે જ થાય છે:

તે નોંધવું યોગ્ય છે કે ઉપરોક્ત સૂત્રો સ્પષ્ટપણે વિશિષ્ટ USE કાર્યોને સફળતાપૂર્વક ઉકેલવા માટે પૂરતા નથી, જે ત્રિકોણમિતિ અભિવ્યક્તિના વ્યુત્પન્નને શોધવાના વિશિષ્ટ ઉદાહરણને ઉકેલતી વખતે દર્શાવવામાં આવશે.

કસરત: ફંક્શનનું વ્યુત્પન્ન શોધવું અને π/4 માટે તેનું મૂલ્ય શોધવું જરૂરી છે:

ઉકેલ: y’ શોધવા માટે મૂળ ફંક્શનને ડેરિવેટિવમાં રૂપાંતરિત કરવા માટેના મૂળભૂત સૂત્રોને યાદ કરવા જરૂરી છે, એટલે કે.

વિષય:"ત્રિકોણમિતિ કાર્યોનું વ્યુત્પન્ન".
પાઠનો પ્રકાર- જ્ઞાનને એકીકૃત કરવાનો પાઠ.
પાઠ ફોર્મ- સંકલિત પાઠ.
આ વિભાગ માટે પાઠ સિસ્ટમમાં પાઠનું સ્થાન- સામાન્ય પાઠ.
લક્ષ્યો વ્યાપક રીતે સેટ કરવામાં આવ્યા છે:

• શૈક્ષણિક:ભિન્નતાના નિયમો જાણો, સમીકરણો અને અસમાનતાઓને ઉકેલતી વખતે ડેરિવેટિવ્ઝની ગણતરી માટેના નિયમો લાગુ કરવામાં સક્ષમ બનો; કોમ્પ્યુટેશનલ, કૌશલ્યો અને ક્ષમતાઓ સહિત વિષયમાં સુધારો કરવો; કોમ્પ્યુટર કૌશલ્ય;
• વિકાસશીલ:બૌદ્ધિક અને તાર્કિક કુશળતા અને જ્ઞાનાત્મક રુચિઓનો વિકાસ;
• શૈક્ષણિક:માટે અનુકૂલનક્ષમતા કેળવો આધુનિક પરિસ્થિતિઓતાલીમ

પદ્ધતિઓ:

• પ્રજનન અને ઉત્પાદક;
• વ્યવહારુ અને મૌખિક;
• સ્વતંત્ર કાર્ય;
• પ્રોગ્રામ કરેલ શિક્ષણ, T.S.O.;
• ફ્રન્ટલ, જૂથ અને સંયોજન વ્યક્તિગત કાર્ય;
• વિભિન્ન શિક્ષણ;
• પ્રેરક-કપાતાત્મક.

નિયંત્રણના સ્વરૂપો:

• મૌખિક સર્વેક્ષણ,
• પ્રોગ્રામ કરેલ નિયંત્રણ,
• સ્વતંત્ર કાર્ય,
• કમ્પ્યુટર પર વ્યક્તિગત કાર્યો,
• વિદ્યાર્થીના ડાયગ્નોસ્ટિક કાર્ડનો ઉપયોગ કરીને પીઅર સમીક્ષા.

વર્ગો દરમિયાન

I. સંસ્થાકીય ક્ષણ

II. સંદર્ભ જ્ઞાન અપડેટ કરવું

a) ધ્યેયો અને ઉદ્દેશ્યોની વાતચીત:

• ભિન્નતાના નિયમો જાણો, સમસ્યાઓ, સમીકરણો અને અસમાનતાઓને ઉકેલતી વખતે ડેરિવેટિવ્ઝની ગણતરી માટેના નિયમો લાગુ કરવામાં સક્ષમ બનો;
• કોમ્પ્યુટેશનલ, કૌશલ્યો અને ક્ષમતાઓ સહિત વિષયમાં સુધારો કરવો; કોમ્પ્યુટર કૌશલ્ય;
• બૌદ્ધિક અને તાર્કિક કુશળતા અને જ્ઞાનાત્મક રુચિઓ વિકસાવવા;
• આધુનિક શિક્ષણની પરિસ્થિતિઓમાં અનુકૂલનક્ષમતા કેળવો.

b) શૈક્ષણિક સામગ્રીનું પુનરાવર્તન

ડેરિવેટિવ્ઝની ગણતરી માટેના નિયમો (ધ્વનિ સાથે કમ્પ્યુટર પર સૂત્રોનું પુનરાવર્તન). દસ્તાવેજ.7.

1. સાઈનનું વ્યુત્પન્ન શું છે?
2. કોસાઇનનું વ્યુત્પન્ન શું છે?
3. સ્પર્શકનું વ્યુત્પન્ન શું છે?
4. કોટેન્જેન્ટનું વ્યુત્પન્ન શું છે?

III. મૌખિક કાર્ય

નોટબુક બદલી. ડાયગ્નોસ્ટિક કાર્ડ્સમાં, યોગ્ય રીતે પૂર્ણ થયેલ કાર્યોને + ચિહ્ન વડે ચિહ્નિત કરો અને ખોટી રીતે પૂર્ણ થયેલ કાર્યોને – ચિહ્ન વડે ચિહ્નિત કરો.

IV. વ્યુત્પન્નનો ઉપયોગ કરીને સમીકરણો ઉકેલવા

- જે બિંદુઓ પર વ્યુત્પન્ન શૂન્ય છે તે કેવી રીતે શોધી શકાય?

જે બિંદુઓ પર વ્યુત્પન્ન છે તે શોધવા માટે આ કાર્યશૂન્ય બરાબર છે, તમારે જરૂર છે:

- કાર્યની પ્રકૃતિ નક્કી કરો,
- વિસ્તાર શોધો કાર્ય વ્યાખ્યાઓ,
- આ કાર્યનું વ્યુત્પન્ન શોધો,
- સમીકરણ ઉકેલો f "(x) = 0,
- સાચો જવાબ પસંદ કરો.

કાર્ય 1.

આપેલ: ખાતે = એક્સ-પાપ x.
શોધો:બિંદુઓ કે જેના પર વ્યુત્પન્ન શૂન્ય છે.
ઉકેલ.તમામ વાસ્તવિક સંખ્યાઓના સેટ પર ફંક્શન વ્યાખ્યાયિત અને અલગ કરી શકાય તેવું છે, કારણ કે તમામ વાસ્તવિક સંખ્યાઓના સેટ પર ફંક્શન વ્યાખ્યાયિત અને ભિન્નતાપાત્ર છે g(x) = xઅને t(x) = – પાપ x.
ભિન્નતાના નિયમોનો ઉપયોગ કરીને, આપણે મેળવીએ છીએ f "(x) = (x-પાપ x)" = (x)" - (પાપ x)" = 1 – cos x.
જો f "(x) = 0, પછી 1 – cos x = 0.
cos x= 1/; ચાલો છેદમાં અતાર્કિકતાથી છુટકારો મેળવીએ, આપણને cos મળે છે x = /2.
સૂત્ર મુજબ t= ± આર્કોસ a+ 2n, n Z, આપણને મળે છે: એક્સ= ± આર્કોસ /2 + 2n, n Z.
જવાબ: x = ± /4 + 2n, n Z.

V. અલ્ગોરિધમનો ઉપયોગ કરીને સમીકરણો ઉકેલવા

વ્યુત્પન્ન કયા બિંદુઓ પર અદૃશ્ય થઈ જાય છે તે શોધો.

વિદ્યાર્થી ત્રણમાંથી કોઈપણ દાખલા પસંદ કરી શકે છે. પ્રથમ ઉદાહરણ રેટ કરેલ છે " 3 ", બીજું -" 4 ", ત્રીજું -" 5 " નોટબુકમાં સોલ્યુશન પછી પરસ્પર ચકાસણી. એક વિદ્યાર્થી બોર્ડમાં નિર્ણય લે છે. જો ઉકેલ ખોટો હોવાનું બહાર આવે છે, તો વિદ્યાર્થીએ અલ્ગોરિધમ પર પાછા ફરવાની અને ફરીથી ઉકેલવાનો પ્રયાસ કરવાની જરૂર છે.

પ્રોગ્રામ કરેલ નિયંત્રણ.

વિકલ્પ 1		વિકલ્પ 2
y = 2એક્સ 3		y = 3એક્સ 2
y = 1/4 એક્સ 4 + 2એક્સ 2 – 7		y = 1/2 એક્સ 4 + 4એક્સ + 5
y = એક્સ 3 + 4એક્સ 2 – 3એક્સ. સમીકરણ ઉકેલો y " = 0		y = 2એક્સ 3 – 9એક્સ 2 + 12એક્સ + 7. સમીકરણ ઉકેલો y " = 0.
y= પાપ 2 એક્સ- કારણ 3 એક્સ.		y= cos 2 એક્સ- પાપ 3 એક્સ.
y= tg એક્સ-ctg( એક્સ + /4).		y=સીટીજી એક્સ+ tg( એક્સ – /4).
y= પાપ 2 એક્સ.		y= cos 2 એક્સ.
જવાબ વિકલ્પો.
કોટેડ જીભ એલેક્ઝાંડર નેવઝોરોવે યુરી ડુડ્યા વિશે વ્લાદિમીર સોલોવ્યોવના નિવેદનોને ન્યાય આપવાનું હાથ ધર્યું ડહાપણની દાઢ એવજેનિયા મેદવેદેવે યુલિયા લિપનિટ્સકાયા એવજેનિયા મેદવેદેવ વીકેની સ્થિતિ પર ટિપ્પણી કરવાનો ઇનકાર કર્યો હતો ડહાપણની દાઢ બોરિસ નોટકિન વ્યક્તિગત. બોરિસ નોટકિન. પ્રસ્તુતકર્તાનું સંક્ષિપ્ત જીવનચરિત્ર સાઇટ પર નવું ઘંટડી મરી lecho ચેરી અને કુટીર ચીઝ સાથે ચોક્સ પેસ્ટ્રીમાંથી ડમ્પલિંગ - અન્ના ઉવારોવા પ્રોટીન ક્રીમ સાથે સ્તરવાળી ટ્યુબ નોખરુ (ઔષધિઓ સાથે બેખમીર પાઇ) સફરજન અને લીંબુના રસ સાથે પૅનકૅક્સ > સૌથી વધુ લોકપ્રિય શા માટે ચિકન લીવર કડવું છે? સ્વાદિષ્ટ સૅલ્મોન દૂધ કેવી રીતે બનાવવું દુશ્મનોથી રક્ષણ માટે ધાર્મિક વિધિઓ અને કાવતરાં માછલીના દૂધમાંથી શું રાંધવું એલેક્સી નેવલનીએ "રશિયન કૂચ" માં ભાગ લેવાનો ઇનકાર કર્યો © 2024. ડેન્ટલ કન્સલ્ટેશન પોર્ટલ. લોકપ્રિય વિભાગો ઓર્થોપેડિક્સ કોટેડ જીભ મોઢામાંથી દુર્ગંધ આવે છે ડહાપણની દાઢ પેઢાં સ્ટેમેટીટીસ દૂર કરવું