De particular importancia para caracterizar la distribución de una variable aleatoria son las características numéricas llamadas momentos inicial y central.
El momento inicial k-ésimo orden α k(X) variable aleatoria X k-ésima potencia de esta cantidad, es decir
α k(X) = METRO(X k) (6.8)
Fórmula (6.8) debido a la definición de expectativa matemática para varios variables aleatorias tiene su propia forma, es decir, para una variable aleatoria discreta con un conjunto finito de valores
para una variable aleatoria continua
 , (6.10)
, (6.10)
Dónde F(X) - densidad de distribución de una variable aleatoria X.
Integral impropia en la fórmula (6.10) se convierte en integral definida durante un intervalo finito, si los valores de una variable aleatoria continua existen solo en este intervalo.
Una de las características numéricas introducidas anteriormente es valor esperado- no es más que el momento inicial de primer orden, o, como dicen, el primer momento inicial:
METRO(X) = α 1 (X).
En el párrafo anterior se introdujo el concepto de variable aleatoria centrada. HM(X). Si esta cantidad se considera la principal, entonces también se pueden encontrar sus momentos iniciales. Por la magnitud misma X Estos momentos se llamarán centrales.
Momento central k-ésimo orden mk(X) variable aleatoria X llamada expectativa matemática k-ésima potencia de la variable aleatoria centrada, es decir
mk(X) = METRO[(HM(X))k] (6.11)
En otras palabras, el punto central k-ésimo orden es la expectativa matemática k grado de desviación.
Momento central k El orden de una variable aleatoria discreta con un conjunto finito de valores se encuentra mediante la fórmula:
![]() , (6.12)
, (6.12)
para una variable aleatoria continua usando la fórmula:
 (6.13)
(6.13)
En el futuro, cuando quede claro de qué tipo de variable aleatoria estamos hablando, no la escribiremos en la notación de los momentos inicial y central, es decir, en lugar de α k(X) Y mk(X) simplemente escribiremos α k Y mk .
Es obvio que el momento central de primer orden es igual a cero, ya que éste no es más que la expectativa matemática de la desviación, la cual es igual a cero según lo previamente demostrado, es decir .
No es difícil entender que el momento central de segundo orden de una variable aleatoria X coincide con la varianza de la misma variable aleatoria, es decir
Además, existen las siguientes fórmulas que conectan los momentos inicial y central:

Así, los momentos de primer y segundo orden (esperanza matemática y dispersión) caracterizan las características más importantes de la distribución: su posición y el grado de dispersión de los valores. Para más Descripción detallada Las distribuciones son momentos de órdenes superiores. Mostrémoslo.
Supongamos que la distribución de una variable aleatoria es simétrica con respecto a su expectativa matemática. Entonces todos los momentos centrales de orden impar, si existen, son iguales a cero. Esto se explica por el hecho de que, debido a la simetría de la distribución, para cada valor positivo de la cantidad X − METRO(X) hay un valor negativo de igual magnitud y las probabilidades de estos valores son iguales. En consecuencia, la suma de la fórmula (6.12) consta de varios pares de términos iguales en magnitud pero de diferente signo, que se cancelan entre sí al realizar la suma. Por tanto, el importe total, es decir el momento central de cualquier variable aleatoria discreta de orden impar es cero. De manera similar, el momento central de cualquier orden impar de una variable aleatoria continua es igual a cero, al igual que la integral en límites simétricos de una función impar.
Es natural suponer que si el momento central de un orden impar es diferente de cero, entonces la distribución en sí no será simétrica con respecto a su expectativa matemática. Además, cuanto más difiere el momento central de cero, mayor es la asimetría en la distribución. Tomemos el momento central del orden impar más pequeño como una característica de la asimetría. Dado que el momento central de primer orden es cero para variables aleatorias que tienen cualquier distribución, es mejor utilizar el momento central de tercer orden para este propósito. Sin embargo, este momento tiene la dimensión de un cubo de una variable aleatoria. Para deshacerse de este inconveniente y pasar a una variable aleatoria adimensional, divida el valor del momento central por el cubo de la desviación estándar.
Coeficiente de asimetría Como o simplemente asimetría se llama relación entre el momento central de tercer orden y el cubo de la desviación estándar, es decir
A veces la asimetría se llama "asimetría" y se designa S k de que viene palabra inglesa sesgado - "oblicuo".
Si el coeficiente de asimetría es negativo, entonces su valor está fuertemente influenciado por términos negativos (desviaciones) y la distribución tendrá asimetría izquierda, y el gráfico de distribución (curva) es más plano a la izquierda de la expectativa matemática. Si el coeficiente es positivo, entonces asimetría derecha, y la curva es más plana a la derecha de la expectativa matemática (figura 6.1).
 |
Como se ha mostrado, para caracterizar la dispersión de los valores de una variable aleatoria en torno a su expectativa matemática, se utiliza el segundo momento central, es decir dispersión. Si este momento es de gran importancia. valor numérico, entonces esta variable aleatoria tiene una gran dispersión de valores y la curva de distribución correspondiente tiene una forma más plana que la curva para la cual el segundo momento central tiene un valor menor. Por lo tanto, el segundo momento central caracteriza, en cierta medida, la curva de distribución de “parte superior plana” o “de parte superior aguda”. Sin embargo, esta característica no es muy conveniente. El momento central de segundo orden tiene la dimensión igual al cuadrado Dimensiones de una variable aleatoria. Si intentamos obtener una cantidad adimensional dividiendo el valor del momento por el cuadrado de la desviación estándar, entonces para cualquier variable aleatoria obtenemos: ![]() . Por tanto, este coeficiente no puede ser ninguna característica de la distribución de una variable aleatoria. Es lo mismo para todas las distribuciones. En este caso, se puede utilizar el momento central de cuarto orden.
. Por tanto, este coeficiente no puede ser ninguna característica de la distribución de una variable aleatoria. Es lo mismo para todas las distribuciones. En este caso, se puede utilizar el momento central de cuarto orden.
Exceso Ek es la cantidad determinada por la fórmula
![]() (6.15)
(6.15)
La curtosis se utiliza principalmente para variables aleatorias continuas y sirve para caracterizar la llamada "inclinación" de la curva de distribución o, como ya se mencionó, para caracterizar la curva de distribución de "parte superior plana" o "de parte superior afilada". Se considera que la curva de distribución de referencia es la curva distribución normal(Esto se discutirá en detalle en el próximo capítulo). Para una variable aleatoria distribuida según una ley normal, se cumple la igualdad. Por tanto, la curtosis dada por la fórmula (6.15) sirve para comparar esta distribución con una normal, para la cual la curtosis es igual a cero.
Si se obtiene una curtosis positiva para alguna variable aleatoria, entonces la curva de distribución de este valor tiene más picos que la curva de distribución normal. Si la curtosis es negativa, entonces la curva tiene una parte superior más plana en comparación con la curva de distribución normal (Fig. 6.2).
 |
Pasemos ahora a tipos específicos de leyes de distribución para variables aleatorias discretas y continuas.
Además de las características de posición (valores promedio y típicos de una variable aleatoria), se utilizan una serie de características, cada una de las cuales describe una u otra propiedad de la distribución. Como tales características se utilizan con mayor frecuencia los llamados momentos.
El concepto de momento es muy utilizado en mecánica para describir la distribución de masas (momentos estáticos, momentos de inercia, etc.). En la teoría de la probabilidad se utilizan exactamente las mismas técnicas para describir las propiedades básicas de la distribución de una variable aleatoria. Muy a menudo, en la práctica se utilizan dos tipos de momentos: inicial y central.
El momento inicial de orden sésimo de una variable aleatoria discontinua es una suma de la forma:
 . (5.7.1)
. (5.7.1)
Obviamente, esta definición coincide con la definición del momento inicial de orden s en mecánica, si las masas se concentran en los puntos en el eje de abscisas.
Para una variable aleatoria continua X, el momento inicial de orden s se llama integral
 . (5.7.2)
. (5.7.2)
Es fácil ver que la característica principal de la posición introducida en el n° anterior - la expectativa matemática - no es más que el primer momento inicial de la variable aleatoria.
Usando el signo de expectativa matemática, puedes combinar dos fórmulas (5.7.1) y (5.7.2) en una. De hecho, las fórmulas (5.7.1) y (5.7.2) son completamente similares en estructura a las fórmulas (5.6.1) y (5.6.2), con la diferencia de que en lugar de y hay, respectivamente, y . Por lo tanto, podemos escribir una definición general del momento inicial de orden ésimo, válida tanto para discontinuos como para cantidades continuas:
![]() , (5.7.3)
, (5.7.3)
aquellos. El momento inicial del décimo orden de una variable aleatoria es la expectativa matemática del décimo grado de esta variable aleatoria.
Antes de definir el momento central, introducimos un nuevo concepto de "variable aleatoria centrada".
Sea una variable aleatoria con expectativa matemática. Una variable aleatoria centrada correspondiente al valor es la desviación de la variable aleatoria de su expectativa matemática:
En el futuro, acordaremos denotar en todas partes la variable aleatoria centrada correspondiente a una variable aleatoria dada con la misma letra con un símbolo en la parte superior.
Es fácil verificar que la expectativa matemática de una variable aleatoria centrada es igual a cero. De hecho, para una cantidad discontinua
de manera similar para una cantidad continua.
Centrar una variable aleatoria es obviamente equivalente a mover el origen de las coordenadas al punto medio, "central", cuya abscisa es igual a la expectativa matemática.
Los momentos de una variable aleatoria centrada se denominan momentos centrales. Son análogos a los momentos con respecto al centro de gravedad en mecánica.
Por tanto, el momento central de orden s de una variable aleatoria es la expectativa matemática de la potencia ésima de la variable aleatoria centrada correspondiente:
![]() , (5.7.6)
, (5.7.6)
y para continuo – por la integral
 . (5.7.8)
. (5.7.8)
En lo que sigue, en los casos en los que no haya dudas sobre a qué variable aleatoria pertenece un momento dado, por brevedad escribiremos simplemente y en lugar de y.
Evidentemente, para cualquier variable aleatoria el momento central de primer orden es igual a cero:
![]() , (5.7.9)
, (5.7.9)
ya que la expectativa matemática de una variable aleatoria centrada es siempre igual a cero.
Derivemos relaciones que conectan los momentos central e inicial de varios órdenes. Realizaremos la conclusión sólo para cantidades discontinuas; es fácil comprobar que exactamente las mismas relaciones son válidas para cantidades continuas si reemplazamos sumas finitas por integrales y probabilidades por elementos de probabilidad.
Consideremos el segundo punto central:

De manera similar para el tercer momento central obtenemos:
Expresiones para etc. se puede obtener de manera similar.
Así, para los momentos centrales de cualquier variable aleatoria son válidas las fórmulas:
 (5.7.10)
(5.7.10)
En términos generales, los momentos pueden considerarse no sólo relativos al origen (momentos iniciales) o expectativa matemática (momentos centrales), sino también relativos a un punto arbitrario:
![]() . (5.7.11)
. (5.7.11)
Sin embargo, los momentos centrales tienen una ventaja sobre todos los demás: el primer momento central, como hemos visto, siempre es igual a cero, y el siguiente, el segundo momento central, con este sistema de referencia tiene un valor mínimo. Demostrémoslo. Para una variable aleatoria discontinua en, la fórmula (5.7.11) tiene la forma:
 . (5.7.12)
. (5.7.12)
Transformemos esta expresión:
Obviamente, este valor alcanza su mínimo cuando , es decir cuando se toma el momento relativo al punto.
De todos los momentos, el primer momento inicial (expectativa matemática) y el segundo momento central se utilizan con mayor frecuencia como características de una variable aleatoria.
El segundo momento central se llama varianza de la variable aleatoria. Dada la extrema importancia de esta característica, entre otros puntos, le introducimos una denominación especial:
Según la definición del momento central.
aquellos. la varianza de una variable aleatoria X es la expectativa matemática del cuadrado de la variable centrada correspondiente.
Reemplazando la cantidad en la expresión (5.7.13) por su expresión, también tenemos:
![]() . (5.7.14)
. (5.7.14)
Para calcular directamente la varianza, utilice las siguientes fórmulas:
 , (5.7.15)
, (5.7.15)
 (5.7.16)
(5.7.16)
En consecuencia, para cantidades discontinuas y continuas.
La dispersión de una variable aleatoria es una característica de la dispersión, la dispersión de los valores de una variable aleatoria alrededor de su expectativa matemática. La palabra "dispersión" en sí misma significa "dispersión".
Si recurrimos a la interpretación mecánica de la distribución, entonces la dispersión no es más que el momento de inercia de una determinada distribución de masa con respecto al centro de gravedad (expectativa matemática).
La varianza de una variable aleatoria tiene la dimensión del cuadrado de la variable aleatoria; Para caracterizar visualmente la dispersión, es más conveniente utilizar una cantidad cuya dimensión coincida con la dimensión de la variable aleatoria. Para hacer esto, toma la raíz cuadrada de la varianza. El valor resultante se llama desviación estándar (de lo contrario, "estándar") de la variable aleatoria. Denotaremos la desviación estándar:
![]() , (5.7.17)
, (5.7.17)
Para simplificar las notaciones, a menudo usaremos las abreviaturas de desviación estándar y dispersión: y. En el caso de que no haya duda de a qué variable aleatoria se relacionan estas características, a veces omitiremos el símbolo x y y escribiremos simplemente y . Las palabras “desviación estándar” a veces se abreviarán y se sustituirán por las letras r.s.o.
En la práctica, se suele utilizar una fórmula que expresa la dispersión de una variable aleatoria a través de su segundo momento inicial (la segunda de las fórmulas (5.7.10)). En la nueva notación se verá así:
La expectativa y la varianza (o desviación estándar) son las características más utilizadas de una variable aleatoria. Caracterizan las características más importantes de la distribución: su posición y grado de dispersión. Para una descripción más detallada de la distribución se utilizan momentos de órdenes superiores.
El tercer punto central sirve para caracterizar la asimetría (o “asimetría”) de la distribución. Si la distribución es simétrica con respecto a la expectativa matemática (o, en una interpretación mecánica, la masa se distribuye simétricamente con respecto al centro de gravedad), entonces todos los momentos de orden impar (si existen) son iguales a cero. De hecho, en total

cuando la ley de distribución es simétrica respecto de la ley e impar, a cada término positivo le corresponde un término negativo igual en valor absoluto, de modo que toda la suma es igual a cero. Obviamente lo mismo es cierto para la integral
 ,
,
que es igual a cero como integral en los límites simétricos de una función impar.
Por lo tanto, es natural elegir uno de los momentos impares como característica de la asimetría de la distribución. El más simple de ellos es el tercer momento central. Tiene la dimensión del cubo de una variable aleatoria: para obtener una característica adimensional, el tercer momento se divide por el cubo de la desviación estándar. El valor resultante se denomina “coeficiente de asimetría” o simplemente “asimetría”; lo denotaremos:
En la Fig. 5.7.1 muestra dos distribuciones asimétricas; una de ellas (curva I) tiene asimetría positiva (); la otra (curva II) es negativa ().

El cuarto punto central sirve para caracterizar la llamada “frialdad”, es decir Distribución puntiaguda o plana. Estas propiedades de distribución se describen mediante la denominada curtosis. La curtosis de una variable aleatoria es la cantidad
El número 3 se resta de la relación porque es muy importante y está muy extendida en la naturaleza ley de distribución normal (que conoceremos en detalle más adelante). Por tanto, para una distribución normal la curtosis es cero; las curvas que tienen más picos en comparación con la curva normal tienen una curtosis positiva; Las curvas que tienen una parte superior más plana tienen curtosis negativa.
En la Fig. 5.7.2 muestra: distribución normal (curva I), distribución con curtosis positiva (curva II) y distribución con curtosis negativa (curva III).

Además de los momentos iniciales y centrales comentados anteriormente, en la práctica a veces se utilizan los llamados momentos absolutos (inicial y central), determinados por las fórmulas
Evidentemente, los momentos absolutos de orden par coinciden con los momentos ordinarios.
De los momentos absolutos, el más utilizado es el primer momento central absoluto.
![]() , (5.7.21)
, (5.7.21)
llamada desviación media aritmética. Junto con la dispersión y la desviación estándar, la desviación media aritmética a veces se utiliza como característica de la dispersión.
La expectativa, la moda, la mediana, los momentos inicial y central y, en particular, la dispersión, la desviación estándar, la asimetría y la curtosis son las características numéricas más utilizadas de las variables aleatorias. En muchos problemas de práctica características completas La variable aleatoria (la ley de distribución) no es necesaria o no puede obtenerse. En estos casos, uno se limita a una descripción aproximada de la variable aleatoria utilizando ayuda. Características numéricas, cada una de las cuales expresa alguna propiedad característica de la distribución.
Muy a menudo, se utilizan características numéricas para reemplazar aproximadamente una distribución por otra, y generalmente se intenta realizar este reemplazo de tal manera que varios puntos importantes permanezcan sin cambios.
Ejemplo 1. Se lleva a cabo un experimento, como resultado del cual puede aparecer o no un evento, cuya probabilidad es igual a . Se considera una variable aleatoria: el número de ocurrencias de un evento (variable aleatoria característica de un evento). Determinar sus características: expectativa matemática, dispersión, desviación estándar.
Solución. La serie de distribución de valor tiene la forma:

donde es la probabilidad de que el evento no ocurra.
Usando la fórmula (5.6.1) encontramos la expectativa matemática del valor:
La dispersión del valor está determinada por la fórmula (5.7.15):
(Sugerimos que el lector obtenga el mismo resultado expresando la dispersión en términos del segundo momento inicial).
Ejemplo 2. Se realizan tres tiros independientes a un objetivo; La probabilidad de acertar en cada tiro es 0,4. variable aleatoria: número de aciertos. Determinar las características de una cantidad: expectativa matemática, dispersión, r.s.d., asimetría.
Solución. La serie de distribución de valor tiene la forma:

Calculamos las características numéricas de la cantidad.
El momento inicial k th orden variable aleatoriaX X k :
En particular,
Momento central k th orden variable aleatoriaXse llama esperanza matemática de la cantidad k :
 .
(5.11)
.
(5.11)
En particular,
Usando las definiciones y propiedades de la expectativa matemática y la dispersión, podemos obtener que
 ,
,
 ,
,
Rara vez se utilizan momentos de orden superior.
Supongamos que la distribución de la variable aleatoria es simétrica con respecto a la expectativa matemática. Entonces todas las centrales de orden impar son iguales a cero. Esto puede explicarse por el hecho de que para cada valor positivo de la desviación X–M[X] hay (debido a la simetría de la distribución) un valor negativo igual en valor absoluto, y sus probabilidades serán las mismas. Si el momento central es de orden impar y distinto de cero, entonces esto indica una asimetría de la distribución y cuanto mayor es el momento, mayor es la asimetría. Por lo tanto, lo más razonable es tomar algún momento central extraño como característica de la asimetría de la distribución. Dado que el momento central de primer orden siempre es igual a cero, es aconsejable utilizar para este fin el momento central de tercer orden. Sin embargo, es inconveniente aceptar este punto para evaluar la asimetría porque su valor depende de las unidades en las que se mide la variable aleatoria. Para eliminar este inconveniente, se divide 3 entre 3 y así obtener una característica.
Coeficiente de asimetría A se llama cantidad
 .
(5.12)
.
(5.12)

Arroz. 5.1
Si el coeficiente de asimetría es negativo, esto indica una gran influencia en el valor de 3 desviaciones negativas. En este caso, las curvas de distribución son más planas a la izquierda de M[X]. Si el coeficiente A es positivo, entonces la curva es más plana hacia la derecha.Como se sabe, la dispersión (segundo momento central) sirve para caracterizar la dispersión de los valores de una variable aleatoria en torno a la expectativa matemática. Cuanto mayor sea la dispersión, más plana será la curva de distribución correspondiente. Sin embargo, el momento normalizado de segundo orden 2 / 2 no puede servir como característica de la distribución de “parte superior plana” o “de parte superior afilada” porque para cualquier distribución D[ X]/ 2 =1. En este caso se utiliza el momento central de cuarto orden.
Exceso mi se llama cantidad
 .
(5.13)
.
(5.13)
h
Arroz. 5.2
Ejemplo 5.6. DSV X viene dado por la siguiente ley de distribución:
Encuentre el coeficiente de asimetría y la curtosis.
 Arroz. 5.4
Arroz. 5.4




Ahora calculemos los momentos centrales:

Encontremos la expectativa matemática. X 2 :
METRO(X 2) = 1* 0, 6 + 4* 0, 2 + 25* 0, 19+ 10000* 0, 01 = 106, 15.
Vemos eso METRO(X 2) mucho más METRO(X). Esto se debe a que después de elevar al cuadrado posible significado cantidades X 2 correspondiente al valor X=100 magnitud X, llegó a ser igual a 10.000, es decir aumentó significativamente; la probabilidad de este valor es baja (0,01).
Así, la transición de METRO(X)A METRO(X 2) permitió tener mejor en cuenta la influencia en la expectativa matemática de ese valor posible, que es grande y tiene una probabilidad baja. Por supuesto, si el valor X tenía varios valores grandes e improbables, entonces la transición al valor X 2, y más aún a las cantidades X 3 , X 4, etc., nos permitirían “fortalecer aún más el papel” de estos valores importantes, pero poco probables, posibles. Por eso resulta aconsejable considerar la expectativa matemática de una potencia entera positiva de una variable aleatoria (no solo discreta, sino también continua).
Momento inicial de orden k variable aleatoria X se llama expectativa matemática de una cantidad Xk:
v k = M(X).
En particular,
v 1 = METRO(X),v 2 = METRO(X 2).
Usando estos puntos, la fórmula para calcular la varianza D(X)= METRO(X 2)- [METRO(X)] 2 se puede escribir así:
D(X)=v 2 – . (*)
Además de los momentos de la variable aleatoria. X es aconsejable considerar momentos de desviación XM(X).
El momento central de orden k de una variable aleatoria X es la esperanza matemática de la cantidad(HM(X))k:
En particular,
Las relaciones que conectan los momentos inicial y central se derivan fácilmente. Por ejemplo, comparando (*) y (***), obtenemos
metro 2 = v 2 – .
No es difícil, a partir de la definición del momento central y utilizando las propiedades de la expectativa matemática, obtener las fórmulas:
metro 3 = v 3 – 3v 2 v 1 + 2 ,
metro 4 = v 4 – 4v 3 v 1 + 6v 2 + 3 .
Rara vez se utilizan momentos de orden superior.
Comentario. Los puntos aquí discutidos se denominan teórico. A diferencia de los momentos teóricos, los momentos que se calculan a partir de datos de observación se denominan empírico. A continuación se dan definiciones de momentos empíricos (véase el capítulo XVII, § 2).
Tareas
1. Se conocen las varianzas de dos variables aleatorias independientes: D(X) = 4, D(Y)=3. Encuentra la varianza de la suma de estas cantidades.
Reps. 7.
2. Varianza de una variable aleatoria X es igual a 5. Encuentre la varianza de las siguientes cantidades: a) X-1; segundo) -2 X; V) Z H + 6.
Reps. a) 5; segundo) 20; c) 45.
3. Valor aleatorio X toma sólo dos valores: +C y -C, cada uno con una probabilidad de 0,5. Encuentra la varianza de esta cantidad.
Reps. CON 2 .
4. , conociendo la ley de su distribución
| X | 0, 1 | |||
| PAG | 0, 4 | 0, 2 | 0, 15 | 0, 25 |
Reps. 67,6404.
5. Valor aleatorio X puede tomar dos valores posibles: X 1 con probabilidad 0,3 y X 2 con probabilidad 0,7, y X 2 >x 1 . Encontrar X 1 y X 2, sabiendo que METRO(X) = 2, 7i D(X) =0,21.
Reps. X 1 = 2, X 2 = 3.
6. Encuentra la varianza de una variable aleatoria. X-número de ocurrencias de eventos A en dos pruebas independientes, Si METRO(X) = 0, 8.
Nota. Escribe la ley binomial de la distribución de probabilidad del número de ocurrencias de un evento. A en dos ensayos independientes.
Reps. 0, 48.
7. Se está probando un dispositivo que consta de cuatro dispositivos que funcionan de forma independiente. Las probabilidades de falla del dispositivo son las siguientes: R 1 = 0,3; R 2 = 0,4; pag 3 = 0,5; R 4 = 0,6. Encuentre la expectativa matemática y la varianza del número de dispositivos fallidos.
Reps. 1,8; 0,94.
8. Encuentra la varianza de una variable aleatoria. X- el número de ocurrencias del evento en 100 ensayos independientes, en cada uno de los cuales la probabilidad de que ocurra el evento es 0,7.
Reps. 21.
9. Varianza de una variable aleatoria D(X) = 6,25. Encuentre la desviación estándar s( X).
Reps. 2, 5.
10. La variable aleatoria está especificada por la ley de distribución.
| X | |||
| PAG | 0, 1 | 0, 5 | 0, 4 |
Encuentre la desviación estándar de este valor.
Reps. 2, 2.
11. La varianza de cada una de las 9 variables aleatorias mutuamente independientes distribuidas idénticamente es igual a 36. Encuentre la varianza de la media aritmética de estas variables.
Reps. 4.
12. La desviación estándar de cada una de las 16 variables aleatorias mutuamente independientes distribuidas idénticamente es 10. Encuentre la desviación estándar de la media aritmética de estas variables.
Reps. 2,5.
Capítulo Nueve
LEY DE LOS GRANDES NÚMEROS
Observaciones preliminares
Como ya se sabe, es imposible predecir con seguridad de antemano cuál de los posibles valores tomará una variable aleatoria como resultado de la prueba; depende de muchos razones aleatorias, que no se puede tener en cuenta. Parecería que, dado que disponemos de información muy modesta sobre cada variable aleatoria en este sentido, es casi imposible establecer patrones de comportamiento y la suma de un número suficientemente grande de variables aleatorias. Actualmente, esto no es verdad. Resulta que para algunos relativamente condiciones amplias el comportamiento global de un número suficientemente grande de variables aleatorias casi pierde su carácter aleatorio y se vuelve natural.
Para la práctica, es muy importante conocer las condiciones en las que la acción combinada de muchas causas aleatorias conduce a un resultado casi independiente del azar, ya que permite prever el curso de los fenómenos. Estas condiciones se indican en los teoremas que llevan nombre común ley números grandes. Estos incluyen los teoremas de Chebyshev y Bernoulli (hay otros teoremas que no se analizan aquí). El teorema de Chebyshev es la ley más general de los grandes números, el teorema de Bernoulli es el más simple. Para demostrar estos teoremas usaremos la desigualdad de Chebyshev.
La desigualdad de Chebyshev
La desigualdad de Chebyshev es válida para variables aleatorias discretas y continuas. Por simplicidad, nos limitamos a demostrar esta desigualdad para cantidades discretas.
Considere una variable aleatoria discreta X, especificado por la tabla de distribución:
| X | X 1 | X 2 | … | xn |
| pag | pag 1 | PAG 2 | … | pn |
Plantémonos la tarea de estimar la probabilidad de que la desviación de una variable aleatoria de su expectativa matemática no exceda el valor absoluto del número positivo e. Si e es lo suficientemente pequeño, entonces estimaremos la probabilidad de que X tomará valores bastante cercanos a su expectativa matemática. P. L. Chebyshev demostró una desigualdad que nos permite dar la estimación que nos interesa.
La desigualdad de Chebyshev. La probabilidad de que la desviación de una variable aleatoria X de su expectativa matemática en valor absoluto sea menor que un número positivo e no sea menor que 1-D(X)/mi 2 :
R(|X-M(X)|< e ) 1-D(X)/mi 2 .
Prueba. Desde eventos que consisten en la implementación de desigualdades. |X-M(X)|
R(|X-M(X)|< e )+R(|X-M(X)| mi)= 1.
De ahí la probabilidad que nos interesa
R(|X-M(X)|< e )= 1-R(|X-M(X)| mi). (*)
Por tanto, el problema se reduce a calcular la probabilidad. R(| HM(X)| mi).
Escribamos la expresión para la varianza de la variable aleatoria. X:
D(X)= [X 1 -METRO(X)] 2 pag 1 + [X 2 -METRO(X)] 2 pag 2 +…+ [xn -M(X)]2p.n.
Obviamente, todos los términos de esta suma no son negativos.
Descartemos aquellos términos para los cuales | xyo-METRO(X)|<mi(para los términos restantes | xj-METRO(X)| mi), Como resultado, la cantidad sólo puede disminuir. Aceptemos asumir, para mayor certeza, que el k los primeros términos (sin pérdida de generalidad, podemos suponer que en la tabla de distribución los valores posibles están numerados exactamente en este orden). De este modo,
D(X) [x k + 1 -METRO(X)] 2 p k + 1 + [x k + 2 -METRO(X)] 2 pag k + z + ... +[xn -M(X)] 2 p.n.
Tenga en cuenta que ambos lados de la desigualdad | xj - METRO(X)| mi (j = k+1, k+ 2, ..., PAG) son positivas, por lo tanto al elevarlas al cuadrado obtenemos la desigualdad equivalente | xj - METRO(X)| 2 mi 2 Usemos esta observación y, reemplazando cada uno de los factores en la suma restante | xj - METRO(X)| 2 en numero mi 2(en este caso la desigualdad sólo puede aumentar), obtenemos
D(X) mi 2 (rk+ 1 +pk+ 2 + … + r n). (**)
Según el teorema de la suma, la suma de las probabilidades rk+ 1 +pk+ 2 + … + r n existe la posibilidad de que X tomará uno, no importa cuál, valor x k + 1 , xk+ 2 ,....xp, y para cualquiera de ellos la desviación satisface la desigualdad | xj - METRO(X)| mi De ello se deduce que la cantidad rk+ 1 +pk+ 2 + … + r n expresa probabilidad
PAG(|X - METRO(X)| mi).
Esta consideración nos permite reescribir la desigualdad (**) de la siguiente manera:
D(X) mi 2 P(|X - METRO(X)| mi),
PAG(|X - METRO(X)| mi)D(X) /mi 2 (***)
Sustituyendo (***) en (*), finalmente obtenemos
PAG(|X - METRO(X)| <mi) 1- D(X) /mi 2 ,
Q.E.D.
Comentario. La desigualdad de Chebyshev tiene una importancia práctica limitada porque a menudo proporciona una estimación aproximada y a veces trivial (sin interés). Por ejemplo, si D(X)>e 2 y por lo tanto D(X)/mi 2 > 1 luego 1 - D(X)/mi 2 < 0; Así, en este caso, la desigualdad de Chebyshev sólo indica que la probabilidad de desviación no es negativa, y esto ya es obvio, ya que cualquier probabilidad se expresa mediante un número no negativo.
La importancia teórica de la desigualdad de Chebyshev es muy grande. A continuación usaremos esta desigualdad para derivar el teorema de Chebyshev.
teorema de chebyshev
El teorema de Chebyshev. Si X 1 , X 2 ,…, X n, ...-variables aleatorias independientes por pares, y sus varianzas están uniformemente acotadas(no exceda un número constante C), entonces no importa cuán pequeño sea el número positivo e, la probabilidad de desigualdad
En otras palabras, bajo las condiciones del teorema
Así, el teorema de Chebyshev establece que si se considera un número suficientemente grande de variables aleatorias independientes con varianzas limitadas, entonces se puede considerar casi confiable un evento que consiste en el hecho de que la desviación de la media aritmética de las variables aleatorias de la media aritmética de sus las expectativas matemáticas serán arbitrariamente grandes en valor absoluto pequeñas
Prueba. Introduzcamos una nueva variable aleatoria en consideración: la media aritmética de variables aleatorias.
=(X 1 +X 2 +…+X norte)/norte.
Encontremos la expectativa matemática. . Usando las propiedades de la expectativa matemática (el factor constante se puede sacar del signo de la expectativa matemática, la expectativa matemática de la suma es igual a la suma de las expectativas matemáticas de los términos), obtenemos
METRO ![]() =
=
![]() . (*)
. (*)
Aplicando la desigualdad de Chebyshev a la cantidad, tenemos
Sustituyendo el lado derecho (***) en la desigualdad (**) (razón por la cual esta última sólo puede fortalecerse), tenemos
De aquí, pasando al límite en , obtenemos
Finalmente, teniendo en cuenta que la probabilidad no puede exceder uno, finalmente podemos escribir
El teorema ha sido demostrado.
Arriba, al formular el teorema de Chebyshev, asumimos que las variables aleatorias tienen expectativas matemáticas diferentes. En la práctica, sucede a menudo que las variables aleatorias tienen la misma expectativa matemática. Obviamente, si volvemos a suponer que las dispersiones de estas cantidades son limitadas, entonces el teorema de Chebyshev será aplicable a ellas.
Denotemos la expectativa matemática de cada una de las variables aleatorias por A; En el caso que nos ocupa, la media aritmética de las expectativas matemáticas, como es fácil de ver, también es igual a A. Podemos formular el teorema de Chebyshev para el caso particular que estamos considerando.
Si X 1 , X 2 , ..., hp...-variables aleatorias independientes por pares que tienen la misma expectativa matemática a, y si las varianzas de estas variables son uniformemente limitadas, entonces no importa cuán pequeño sea el número e>Oh, probabilidad de desigualdad
![]()
será tan cercano a la unidad como se desee si el número de variables aleatorias es lo suficientemente grande.
En otras palabras, bajo las condiciones del teorema habrá igualdad.

La esencia del teorema de Chebyshev.
La esencia del teorema probado es la siguiente: aunque las variables aleatorias independientes individuales pueden tomar valores alejados de sus expectativas matemáticas, la media aritmética de un número suficientemente grande de variables aleatorias con una alta probabilidad toma valores cercanos a una determinada constante número, es decir, el número ( METRO(X 1)+ METRO(X 2)+...+M(Xp))/PAG(o al número A en un caso especial). En otras palabras, las variables aleatorias individuales pueden tener una dispersión significativa y su media aritmética es dispersamente pequeña.
Por lo tanto, no se puede predecir con seguridad qué valor posible tomará cada una de las variables aleatorias, pero sí se puede predecir qué valor tomará su media aritmética.
Entonces, media aritmética de un número suficientemente grande de variables aleatorias independientes(cuyas varianzas están uniformemente acotadas) pierde el carácter de variable aleatoria. Esto se explica por el hecho de que las desviaciones de cada valor de sus expectativas matemáticas pueden ser tanto positivas como negativas, y en la media aritmética se cancelan entre sí.
El teorema de Chebyshev es válido no sólo para variables aleatorias discretas, sino también continuas; ella resulta ser un brillante ejemplo, confirmando la validez de la doctrina del materialismo dialéctico sobre la conexión entre azar y necesidad.
Valor esperado. Expectativa matemática variable aleatoria discreta X, tomando un número finito de valores Xi con probabilidades Ri, la cantidad se llama:
Expectativa matemática variable aleatoria continua X se llama integral del producto de sus valores X sobre la densidad de distribución de probabilidad F(X):
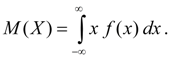 (6b)
(6b)
Integral impropia (6 b) se supone que es absolutamente convergente (de lo contrario, dicen que la expectativa matemática METRO(X) no existe). La expectativa matemática caracteriza valor promedio variable aleatoria X. Su dimensión coincide con la dimensión de la variable aleatoria.
Propiedades de la expectativa matemática:
Dispersión. Diferencia variable aleatoria X el numero se llama:
La varianza es característica de dispersión valores de variables aleatorias X en relación con su valor medio METRO(X). La dimensión de la varianza es igual a la dimensión de la variable aleatoria al cuadrado. Con base en las definiciones de varianza (8) y expectativa matemática (5) para una variable aleatoria discreta y (6) para una variable aleatoria continua, obtenemos expresiones similares para la varianza:
 (9)
(9)
Aquí metro = METRO(X).
Propiedades de dispersión:
Desviación Estándar:
![]() (11)
(11)
Dado que la dimensión del promedio desviación cuadrada Al igual que el de una variable aleatoria, se utiliza más a menudo como medida de dispersión que de varianza.
Momentos de distribución. Los conceptos de expectativa matemática y dispersión son casos especiales de más concepto general para características numéricas de variables aleatorias – momentos de distribución. Los momentos de distribución de una variable aleatoria se introducen como expectativas matemáticas de algunas funciones simples de una variable aleatoria. Entonces, momento de orden. k relativo al punto X 0 se llama expectativa matemática METRO(X–X 0 )k. Momentos sobre el origen. X= 0 se llaman momentos iniciales y están designados:
![]() (12)
(12)
El momento inicial de primer orden es el centro de la distribución de la variable aleatoria considerada:
![]() (13)
(13)
Momentos sobre el centro de distribución. X= metro son llamados puntos centrales y están designados:
![]() (14)
(14)
De (7) se deduce que el momento central de primer orden es siempre igual a cero:
Los momentos centrales no dependen del origen de los valores de la variable aleatoria, ya que cuando se desplazan por un valor constante CON su centro de distribución se desplaza en el mismo valor CON, y la desviación del centro no cambia: X – metro = (X – CON) – (metro – CON).
Ahora es obvio que dispersión- Este momento central de segundo orden:
Asimetría. Momento central de tercer orden:
![]() (17)
(17)
sirve para evaluación asimetrías de distribución. Si la distribución es simétrica con respecto al punto X= metro, entonces el momento central de tercer orden será igual a cero (como todos los momentos centrales de órdenes impares). Por tanto, si el momento central de tercer orden es distinto de cero, entonces la distribución no puede ser simétrica. La magnitud de la asimetría se evalúa utilizando un modelo adimensional. coeficiente de asimetría:
 (18)
(18)
El signo del coeficiente de asimetría (18) indica asimetría del lado derecho o del lado izquierdo (Fig. 2).

Arroz. 2. Tipos de asimetría de distribución.
Exceso. Momento central de cuarto orden:
![]() (19)
(19)
sirve para evaluar el llamado exceso, que determina el grado de inclinación (pico) de la curva de distribución cerca del centro de la distribución en relación con la curva de distribución normal. Ya que para una distribución normal, el valor tomado como curtosis es:
 (20)
(20)
En la Fig. La Figura 3 muestra ejemplos de curvas de distribución con diferentes valores de curtosis. Para distribución normal mi= 0. Las curvas que son más puntiagudas de lo normal tienen una curtosis positiva, las que son más planas tienen una curtosis negativa.

Arroz. 3. Curvas de distribución con grados variables frialdad (exceso).
Momentos de orden superior en aplicaciones de ingeniería. estadística matemática normalmente no se utiliza.
Moda
discreto una variable aleatoria es su valor más probable. Moda continuo una variable aleatoria es su valor en el que la densidad de probabilidad es máxima (Fig. 2). Si la curva de distribución tiene un máximo, entonces la distribución se llama unimodal. Si una curva de distribución tiene más de un máximo, entonces la distribución se llama multimodal. A veces hay distribuciones cuyas curvas tienen un mínimo en lugar de un máximo. Estas distribuciones se denominan antimodal. EN caso general la moda y la expectativa matemática de una variable aleatoria no coinciden. En el caso especial, para modal, es decir. teniendo una distribución moda, simétrica y siempre que exista una expectativa matemática, esta última coincide con la moda y centro de simetría de la distribución.
Mediana variable aleatoria X- este es su significado Bueno, para lo cual se cumple la igualdad: es decir es igualmente probable que la variable aleatoria X será menos o más Bueno. Geométricamente mediana es la abscisa del punto en el que el área bajo la curva de distribución se divide por la mitad (Fig. 2). En el caso de una distribución modal simétrica, la mediana, la moda y la expectativa matemática son las mismas.