Definisi. Misalkan suatu fungsi f(x) terdefinisi pada suatu interval dan x 0 menjadi sebuah titik dalam interval tersebut. Jika , maka f(x) dikatakan kontinu di titik x 0 .
Dari definisi tersebut dapat disimpulkan bahwa kita dapat berbicara tentang kontinuitas hanya dalam kaitannya dengan titik-titik di mana f(x) didefinisikan (ketika mendefinisikan limit suatu fungsi, kondisi seperti itu tidak ditetapkan). Untuk fungsi berkelanjutan , yaitu operasi f dan lim bersifat komutatif. Dengan demikian, dua definisi limit suatu fungsi pada suatu titik dapat diberikan dua definisi kontinuitas - "dalam bahasa barisan" dan "dalam bahasa pertidaksamaan" (dalam bahasa ε-δ). Disarankan agar Anda melakukannya sendiri.
Untuk penggunaan praktis, terkadang lebih mudah untuk mendefinisikan kontinuitas dalam bahasa pertambahan.
Nilai Δx=x-x 0 disebut pertambahan argumen, dan Δy=f(x)-f(x 0) adalah pertambahan fungsi ketika berpindah dari titik x 0 ke titik x.
Definisi. Misalkan f(x) terdefinisi di titik x 0 . Suatu fungsi f(x) disebut kontinu di suatu titik x 0 jika kenaikan argumen yang sangat kecil pada titik ini berhubungan dengan kenaikan fungsi yang sangat kecil, yaitu Δy→0 untuk Δx→0.

Contoh 1. Buktikan bahwa fungsi y=sinx kontinu untuk sembarang nilai x.
Larutan. Misalkan x 0 adalah titik sembarang. Dengan menambah Δx, kita mendapatkan intinya x=x 0 +Δx. Kemudian . Kita mendapatkan .
Definisi. Fungsi y=f(x) disebut kontinu di titik x 0 sebelah kanan (kiri) jika
.
Suatu fungsi yang kontinu pada suatu titik dalam akan kontinu kanan dan kiri. Hal sebaliknya juga berlaku: jika suatu fungsi kontinu di suatu titik di kiri dan kanan, maka fungsi tersebut kontinu di titik tersebut. Namun suatu fungsi hanya dapat kontinu pada satu sisi saja. Misalnya untuk , , f(1)=1, oleh karena itu, fungsi ini hanya kontinu di sebelah kiri (untuk grafik fungsi ini, lihat paragraf 5.7.2 di atas).
Definisi. Suatu fungsi disebut kontinu pada suatu interval jika fungsi tersebut kontinu pada setiap titik pada interval tersebut.
Khususnya, jika intervalnya adalah sebuah segmen, maka kontinuitas satu sisi tersirat di ujung-ujungnya.

Sifat-sifat fungsi kontinu

1. Semua fungsi dasar kontinu dalam domain definisinya.
2. Jika f(x) dan φ(x), yang diberikan pada interval tertentu, kontinu di titik x 0 interval tersebut, maka fungsinya juga kontinu di titik tersebut.
3. Jika y=f(x) kontinu di titik x 0 dari X, dan z=φ(y) kontinu di titik yang bersesuaian y 0 =f(x 0) dari Y, maka fungsi yang kompleks z=φ(f(x)) kontinu di titik x 0 .

Istirahat fungsi dan klasifikasinya

Tanda kontinuitas fungsi f(x) di titik x 0 adalah persamaan, yang menyiratkan adanya tiga kondisi:
1) f(x) didefinisikan pada titik x 0 ;
2) ;
3) .
Jika setidaknya salah satu dari persyaratan ini dilanggar, maka x 0 disebut titik putus fungsi. Dengan kata lain, break point adalah titik dimana fungsi tersebut tidak kontinu. Dari pengertian break point maka break point suatu fungsi adalah:
a) titik-titik yang termasuk dalam domain definisi fungsi di mana f(x) kehilangan sifat kontinuitas,
b) titik-titik yang tidak termasuk dalam domain definisi f(x), yaitu titik-titik yang berdekatan pada dua interval domain definisi fungsi.
Misalnya, untuk suatu fungsi, titik x=0 adalah titik putus, karena fungsi pada titik ini tidak terdefinisi, dan fungsinya mempunyai diskontinuitas di titik x=1 yang berbatasan dengan dua interval (-∞,1) dan (1,∞) dari domain definisi f(x) dan tidak ada.

Klasifikasi berikut diadopsi untuk break point.
1) Jika pada titik x 0 terdapat berhingga Dan , tetapi f(x 0 +0)≠f(x 0 -0), maka x 0 disebut titik diskontinuitas jenis pertama , dan dipanggil lompatan fungsi .

Contoh 2. Pertimbangkan fungsinya
Fungsi tersebut hanya dapat dipecah pada titik x=2 (di titik lain fungsi tersebut kontinu seperti polinomial lainnya).
Kami akan menemukannya , . Karena limit satu sisinya berhingga, tetapi tidak sama satu sama lain, maka pada titik x=2 fungsi tersebut mempunyai diskontinuitas jenis pertama. perhatikan itu , oleh karena itu fungsi pada titik ini kontinu di sebelah kanan (Gbr. 2).
2) Poin diskontinuitas jenis kedua disebut titik-titik yang paling sedikit salah satu batas satu sisinya sama dengan atau tidak ada.

Contoh 3. Fungsi y=2 1/ x kontinu untuk semua nilai x kecuali x=0. Mari kita cari limit satu sisi: , , oleh karena itu x=0 adalah titik diskontinuitas jenis kedua (Gbr. 3).
3) Titik x=x 0 disebut titik istirahat yang dapat dilepas , jika f(x 0 +0)=f(x 0 -0)≠f(x 0).
Kita akan “menghilangkan” gap tersebut dalam arti cukup dengan mengubah (mendefinisikan ulang atau mendefinisikan ulang) nilai fungsi pada titik ini dengan menetapkan , dan fungsi tersebut akan menjadi kontinu pada titik x 0 .
Contoh 4. Diketahui bahwa , dan limit ini tidak bergantung pada cara x cenderung nol. Namun fungsi di titik x=0 tidak terdefinisi. Jika kita mendefinisikan ulang fungsi tersebut dengan menetapkan f(0)=1, maka fungsi tersebut ternyata kontinu di titik ini (di titik lain kontinu sebagai hasil bagi fungsi kontinu sinx dan x).
Contoh 5. Periksa kontinuitas suatu fungsi .
Larutan. Fungsi y=x 3 dan y=2x terdefinisi dan kontinu di mana pun, termasuk di interval yang ditunjukkan. Mari kita periksa titik persimpangan interval x=0:
, , . Kita peroleh bahwa , yang menyiratkan bahwa pada titik x=0 fungsi tersebut kontinu.
Definisi. Suatu fungsi yang kontinu pada suatu interval kecuali sejumlah titik diskontinuitas jenis pertama yang terbatas atau diskontinuitas yang dapat dilepas disebut kontinu sepotong-sepotong pada interval ini.

Contoh fungsi diskontinu

Contoh 1. Fungsi tersebut terdefinisi dan kontinu pada (-∞,+∞) kecuali pada titik x=2. Mari kita tentukan jenis istirahatnya. Karena Dan , maka pada titik x=2 terdapat diskontinuitas jenis kedua (Gbr. 6).
Contoh 2. Fungsi tersebut terdefinisi dan kontinu untuk semua x kecuali x=0, yang penyebutnya nol. Mari kita cari limit satu sisi di titik x=0:
Batas satu sisi berhingga dan berbeda, oleh karena itu x=0 adalah titik diskontinuitas jenis pertama (Gbr. 7).
Contoh 3. Tentukan di titik mana dan diskontinuitas seperti apa yang dimiliki fungsi tersebut
Fungsi ini didefinisikan pada [-2,2]. Karena x 2 dan 1/x kontinu pada interval [-2,0] dan , maka diskontinuitas hanya dapat terjadi pada persimpangan interval, yaitu pada titik x=0. Karena , maka x=0 merupakan titik diskontinuitas jenis kedua.

Contoh 4. Apakah mungkin untuk menghilangkan kesenjangan fungsi:
A) di titik x=2;
B) di titik x=2;
V) di titik x=1?
Larutan. Mengenai contoh a) kita dapat langsung mengatakan bahwa diskontinuitas f(x) pada titik x=2 tidak dapat dihilangkan, karena pada titik ini terdapat batas satu sisi yang tak terhingga (lihat contoh 1).
b) Fungsi g(x) meskipun mempunyai limit satu sisi berhingga di titik x=2

(,),

tetapi keduanya tidak bersamaan, sehingga kesenjangan tersebut juga tidak dapat dihilangkan.
c) Fungsi φ(x) pada titik diskontinuitas x=1 mempunyai batas berhingga satu sisi yang sama: . Oleh karena itu, kesenjangan dapat dihilangkan dengan mendefinisikan ulang fungsi di x=1 dengan menempatkan f(1)=1 sebagai ganti f(1)=2.

Contoh 5. Tunjukkan bahwa fungsi Dirichlet

diskontinyu di setiap titik pada sumbu numerik.
Larutan. Misalkan x 0 adalah sembarang titik dari (-∞,+∞). Di setiap lingkungannya terdapat poin-poin rasional dan irasional. Artinya di sembarang lingkungan x 0 fungsi tersebut akan mempunyai nilai sama dengan 0 dan 1. Dalam hal ini, limit fungsi di titik x 0 tidak dapat ada baik di kiri maupun di kanan, yang berarti bahwa fungsi Dirichlet mempunyai diskontinuitas jenis kedua di setiap titik pada sumbu real.

Contoh 6. Temukan breakpoint fungsi

dan menentukan jenisnya.
Larutan. Titik yang diduga putus adalah titik x 1 =2, x 2 =5, x 3 =3.
Pada titik x 1 =2 f(x) mempunyai diskontinuitas jenis kedua, karena
.
Titik x 2 =5 merupakan titik kontinuitas, karena nilai fungsi pada titik ini dan sekitarnya ditentukan oleh garis kedua, dan bukan garis pertama: .
Mari kita periksa intinya x 3 =3: , , maka x=3 adalah titik diskontinuitas jenis pertama.

Untuk keputusan independen.
Periksa fungsi kontinuitas dan tentukan jenis titik diskontinuitas:
1) ; Jawaban: x=-1 – titik diskontinuitas lepasan;
2) ; Jawaban: Diskontinuitas jenis kedua di titik x=8;
3) ; Jawaban: Diskontinuitas jenis pertama pada x=1;
4)
Jawab: Pada titik x 1 =-5 terdapat celah yang dapat dilepas, pada x 2 =1 terdapat celah jenis kedua, dan pada titik x 3 =0 terdapat celah jenis pertama.
5) Bagaimana cara memilih bilangan A agar berfungsi

apakah kontinu di x=0?
Jawaban: SEBUAH=2.
6) Apakah mungkin memilih bilangan A agar berfungsi

apakah kontinu di x=2?
Jawaban: tidak.

Kontinuitas suatu fungsi pada suatu titik. Fungsi y = f(x ) disebut tidak pra-

dendeng di titik x 0 jika:

1) fungsi ini didefinisikan di beberapa lingkungan titik x 0 ;

2) ada batasnya f(x);

→ x 0

3) batas ini sama dengan nilainya fungsi di titik x 0, mis. limf (x )= f (x 0 ) .
		x→x0
Kondisi terakhir setara dengan kondisi lim		y = 0, dimana x = x − x 0 – kapan
	x→ 0
rotasi argumen, y = f (x 0 +	x )− f (x 0 ) – kenaikan fungsi, sesuai
menambah argumen	x, yaitu fungsi	f(x) kontinu di x 0

jika dan hanya jika pada titik ini kenaikan argumen yang sangat kecil berhubungan dengan kenaikan fungsi yang sangat kecil.

Kontinuitas satu arah. Fungsi y = f (x) disebut kontinu

di sebelah kiri pada titikx 0 jika didefinisikan pada beberapa setengah interval(a ;x 0 ]

dan lim f (x)= f (x 0).

x→ x0 − 0

Suatu fungsi y = f(x) dikatakan kontinu kanan di titik x 0 jika op-

didistribusikan pada setengah interval tertentu [ x 0 ;a ) dan limf (x )= f (x 0 ) .

x→ x0 + 0

Fungsi y = f(x)		kontinu di titik x 0			saat itu dan hanya ketika dia
kontinu
lim f (x)= limf (x)= limf (x)= f (x 0).
x→ x0 + 0	x→ x0 − 0	x→x0

Kontinuitas suatu fungsi pada suatu himpunan. Fungsi y = f (x) disebut

terus menerus di lokasi syuting X jika kontinu pada setiap titik himpunan ini. Apalagi jika suatu fungsi didefinisikan pada akhir suatu interval garis bilangan, maka kontinuitas pada titik tersebut dipahami sebagai kontinuitas di kanan atau kiri. Secara khusus, fungsi y = f (x) disebut non-

terputus-putus pada segmen [a; b] jika dia

1) kontinu pada setiap titik interval(a;b) ;

2) benar kontinu pada suatu titik A ;

3) dibiarkan kontinu pada suatu titik B.

Titik henti fungsi. Titik x 0 yang termasuk dalam domain definisi fungsi y = f(x) atau menjadi titik batas domain tersebut disebut

titik istirahat dari fungsi ini, iff(x) tidak kontinu pada titik tersebut.

Titik diskontinuitas dibagi menjadi titik diskontinuitas jenis pertama dan kedua:

1) Jika ada limit berhingga lim f (x )= f (x 0 − 0) dan

x→ x0 − 0

	f (x)= f (x 0 + 0), dan tidak ketiga bilangan tersebut adalah f (x 0 − 0), f (x 0 + 0),		f (x 0 ) sama
x→ x0 + 0
di antara mereka sendiri, lalu x 0		disebut titik diskontinuitas jenis pertama.
	Khususnya jika batas kiri dan kanan fungsi berada di titik x 0		sama antara
	dirimu sendiri, tapi	tidak sama dengan nilai fungsi pada saat ini:

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , maka x 0 disebut titik diskontinuitas lepasan.

Dalam hal ini, dengan menyetel f (x 0 )= A, Anda dapat mengubah fungsi di titik x 0

sehingga menjadi kontinu ( mendefinisikan kembali fungsi dengan kontinuitas). Selisih f (x 0 + 0)− f (x 0 − 0) disebut lompatan suatu fungsi pada suatu titik x 0 .

Lompatan fungsi pada titik diskontinuitas lepasan adalah nol.

2) Titik diskontinuitas yang bukan merupakan titik diskontinuitas jenis pertama disebut breakpoint jenis kedua. Pada titik diskontinuitas jenis kedua, paling sedikit salah satu batas satu sisi f (x 0 − 0) dan f (x 0 + 0) tidak ada atau tidak terhingga.

Sifat-sifat fungsi kontinu di suatu titik.

		f(x)	dan g (x) kontinu di titik x 0, maka fungsinya
f(x)±g(x),	f(x)g(x) dan	f(x)	(di mana g (x)≠ 0) juga kontinu di titik x.
		g(x)

2) Jika fungsi u(x) kontinu di titik x 0, dan fungsi f(u) kontinu

di titik u 0 = u (x 0), maka fungsi kompleks f (u (x)) kontinu di titik x 0.

3) Semua fungsi dasar dasar (c, xa, a x, loga x, sinx, cosx, tgx, ctgx, secx, cosecx, arcsinx, arccosx, arctgx, arcctgx) kontinu di setiap fungsi dasar

ke titik domain definisi mereka.

Dari sifat 1)–3) dapat disimpulkan bahwa semua fungsi dasar (fungsi yang diperoleh dari fungsi dasar dasar menggunakan sejumlah operasi aritmatika dan operasi komposisi yang terbatas) juga kontinu di setiap titik domain definisinya.

Sifat-sifat fungsi kontinu pada suatu interval.

1) (teorema nilai antara) Biarkan fungsi f(x) terdefinisi

aktif dan kontinu pada ruas [a;b]. Kemudian untuk nomor C apa saja yang terlampir

antara bilangan f(a) dan f(b), (f(a)< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (Teorema Bolzano – Cauchy

terputus-putus pada segmen [a;b] dan mengambil nilai tanda yang berbeda di ujungnya.

Maka paling sedikit ada satu titik x 0 [ a ; b ] sehingga f (x 0 )= 0 .

3) (1st teorema Weierstrass) Biarkan fungsi f (x) didefinisikan dan

robek pada ruas [a;b]. Kemudian fungsi ini dibatasi pada segmen ini.

4) (2nd teorema Weierstrass) Biarkan fungsi f (x) didefinisikan dan

terburu-buru di segmen tersebut		[a;b] . Kemudian fungsi ini mencapai interval [ a ;
terbesar		paling sedikit	nilai-nilai, yaitu	ada
x1, x2 [sebuah; B] ,		untuk apa pun	poin x [a;b]	adil	kesenjangan

f (x 1 )≤ f (x )≤ f (x 2 ) .

Contoh 5.17. Dengan menggunakan definisi kontinuitas, buktikan bahwa fungsi y = 3x 2 + 2x − 5 kontinu di titik sembarang x 0 pada garis bilangan.

Solusi: Metode 1: Misalkan x 0 adalah titik sembarang pada sumbu bilangan. Anda-

Pertama-tama kita menghitung limit fungsi f (x) sebagai x → x 0, dengan menerapkan teorema limit jumlah dan hasil kali fungsi:

lim f (x )= lim(3x 2 + 2x − 5)= 3(limx )2 + 2 limx − 5= 3x 2							− 5.
x→x0	x→x0	x→x0	x→x0
Kemudian kita hitung nilai fungsinya di titik x:f (x)= 3x 2							− 5 .
Membandingkan hasil yang diperoleh, kita lihat				lim f (x )= f (x 0 ) , yang menurut
				x→x0

definisi dan berarti kontinuitas fungsi yang ditinjau di titik x 0.

Metode 2: Biarkan		x – pertambahan argumen pada titik x 0. Mari kita temukan korespondensinya
sesuai	kenaikan			kamu = f(x0 + x) − f(x0 ) =
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x − 5)
6 x x+ (x) 2	2x = (6x + 2)x + (x)2.
Sekarang mari kita hitung batas pertambahan fungsi ketika argumen bertambah
		berusaha

	y = lim (6x + 2)		x + (x )2 = (6x + 2) lim		x + (limx)2 = 0.
x→ 0	x→ 0			x→ 0	x→ 0

Jadi, lim y = 0, yang menurut definisinya kontinuitas

x→ 0

fungsi untuk setiap x 0 R .

Contoh 5.18. Temukan titik diskontinuitas fungsi f (x) dan tentukan tipenya. DI DALAM

Dalam kasus diskontinuitas lepasan, tentukan fungsi berdasarkan kontinuitas:

1) f (x) = 1− x 2 di x< 3;

5x bila x ≥ 3

2) f (x)= x 2 + 4 x + 3;

x+1

	f(x)=
		x4 (x− 2)
	f(x)= arctan
			(x − 5)

Penyelesaian: 1) Daerah definisi fungsi ini adalah bilangan bulat

sumbu y (−∞ ;+∞ ) . Pada interval (−∞ ;3) ,(3;+∞ ) fungsinya kontinu. Diskontinuitas hanya mungkin terjadi pada titik x = 3, di mana spesifikasi analitik fungsi tersebut berubah.

Mari kita cari limit satu sisi fungsi pada titik yang ditunjukkan:

f (3− 0)= lim (1− x 2 )= 1− 9= 8;

x →3 −0

f (3+ 0)= lim 5x = 15.

x →3 +0

Kita melihat limit kiri dan kanan berhingga, jadi x = 3
pecah I			f(x). Fungsi melompat ke
f (3+ 0)− f (3− 0)= 15− 8= 7 .
		f (3)= 5 3= 15= f (3+ 0) , maka pada intinya		x = 3

f(x) kontinu kanan.

2) Fungsi tersebut kontinu pada seluruh garis bilangan kecuali titik x = − 1, yang tidak terdefinisi. Mari kita ubah ekspresi f(x) dengan memperluas pembilangnya

pecahan menjadi faktor:		f(x)=			4x+3			(x + 1)(x + 3)	X + 3 untuk x ≠ − 1.
					x+1			x+1
Mari kita cari limit satu sisi fungsi di titik x = − 1:
	f(x)=batas	f (x )= lim(x + 3)= 2 .
x →−1−0	x →−1 +0		x →−1

Diketahui bahwa limit kiri dan kanan fungsi pada titik yang diteliti ada, berhingga dan sama besar, oleh karena itu x = − 1 adalah titik yang dapat dipindahkan

garis lurus y = x + 3 dengan titik “tertusuk” M (− 1;2) . Agar fungsinya menjadi permanen

terputus-putus, kita harus meletakkan f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 .

Jadi, setelah mendefinisikan lebih lanjut f (x) dengan kontinuitas di titik x = − 1, kita memperoleh fungsi f * (x)= x + 3 dengan domain definisi (−∞ ;+∞ ) .

3) Fungsi ini jelas dan berkesinambungan bagi semua orang x kecuali poin

x = 0,x = 2, yang penyebut pecahannya menjadi nol.

Perhatikan titik x = 0:

Karena di lingkungan nol yang cukup kecil, fungsi tersebut hanya mengambil

	untuk nilai negatif, maka f (− 0)= lim			= −∞ = f (+0)	Itu. dot
			(x − 2)
	x →−0
	x = 0 adalah titik diskontinuitas fungsi jenis kedua		f(x).

Perhatikan sekarang titik x = 2:

Fungsi tersebut mengambil nilai negatif mendekati kiri yang dipertimbangkan

	Oleh karena itu, titik dan yang positif ada di sebelah kanan				f (2− 0)=			= −∞,
							x4 (x− 2)
						x →2 −0
	f (2+ 0)= batas			= +∞ . Seperti pada kasus sebelumnya, pada titikx = 2
			(x − 2)
	x →2 +0

tion tidak memiliki batas berhingga kiri dan kanan, yaitu. menderita ruptur tipe II pada saat ini.

x = 5 .

f (5− 0)= lim arctan

π ,f (5+ 0)= lim arctan

x = 5

(x − 5)

(x − 5)

x →5 −0

x →5 +0

ka pecah

f (5+ 0)− f (5− 0)=

π − (−

π )= π (lihat Gambar 5.2).

Masalah untuk diselesaikan secara mandiri

5.174. Dengan menggunakan definisi saja, buktikan kontinuitas fungsi f(x) in

setiap titik x 0 R :

a) f(x) = c= konstanta;		b) f(x)= x;
c) f (x)= x 3;		d) f (x)= 5x 2 − 4x + 1;
e) f (x)= sinx.
5.175. Buktikan bahwa fungsinya	f(x) = x2	1 ketika x ≥ 0,	terus menerus menyala
		1 di x< 0
seluruh garis bilangan. Buatlah grafik fungsi ini.
5.176. Buktikan bahwa fungsinya	f(x) = x2	1 ketika x ≥ 0,	tidak berkelanjutan
		0 di x< 0

di titik x = 0, tetapi kontinu di titik tersebut. Gambarkan fungsi f(x).

dendeng di titik x =

Namun terus menerus di sebelah kiri pada saat ini. Buat grafik

fungsi f(x).

5.178. Fungsi grafik

a) kamu =

x+1

b) kamu= x+

x+1

x+1

x+1

Manakah dari kondisi kontinuitas pada titik putus dari fungsi-fungsi ini yang terpenuhi dan mana yang tidak terpenuhi?

5.179. Tentukan titik istirahat fungsi

dosa x		Untuk x ≠ 0
		pada x = 0

Kondisi kesinambungan manakah yang terpenuhi pada saat ini dan mana yang tidak terpenuhi?

Definisi titik istirahat fungsi dan jenisnya merupakan lanjutan dari tema kesinambungan fungsi. Penjelasan visual (grafis) tentang makna titik putus suatu fungsi juga diberikan berbeda dengan konsep kontinuitas. Mari pelajari cara mencari breakpoint suatu fungsi dan menentukan tipenya. Dan milik kami akan membantu kami dalam hal ini teman yang setia- batas kiri dan kanan, umumnya disebut batas satu sisi. Jika ada yang takut dengan batasan sepihak, kami akan segera menghilangkannya.

Titik-titik pada suatu grafik yang tidak saling terhubung disebut titik istirahat fungsi . Grafik fungsi yang mengalami diskontinuitas di titik x=2 - - pada gambar di bawah.

Generalisasi di atas adalah definisi berikut. Jika suatu fungsi tidak kontinu di suatu titik, maka fungsi tersebut mempunyai diskontinuitas di titik tersebut dan titik itu sendiri disebut titik istirahat . Ada jeda jenis pertama dan jenis kedua .

Untuk menentukan jenis (karakter) titik istirahat fungsi perlu ditemukan dengan percaya diri batas, jadi sebaiknya buka pelajaran terkait di jendela baru. Namun sehubungan dengan breakpoint, kami memiliki sesuatu yang baru dan penting - batasan satu sisi (kiri dan kanan). Secara umum ditulis (batas kanan) dan (batas kiri). Seperti halnya limit pada umumnya, untuk mencari limit suatu fungsi, Anda perlu mensubstitusi X ke dalam ekspresi fungsi dengan kecenderungan X. Tapi, mungkin Anda bertanya, apa bedanya limit kanan dan kiri, jika yang kanan ada yang ditambahkan ke X, tapi yang ini nol, dan yang kiri ada yang dikurangi X, tapi ini sesuatu - juga nol? Dan Anda akan benar. Umumnya.

Namun dalam praktik mencari titik diskontinuitas suatu fungsi dan menentukan tipenya, ada dua kasus umum dimana limit kanan dan limit kiri tidak sama:

• suatu fungsi mempunyai dua atau lebih ekspresi bergantung pada bagian garis bilangan yang memiliki x (ekspresi ini biasanya ditulis dalam tanda kurung kurawal setelahnya F(X)= );
• sebagai hasil dari mensubstitusikan apa yang cenderung ke X, kita mendapatkan pecahan yang penyebutnya tetap ditambah nol (+0) atau dikurangi nol (-0) dan oleh karena itu pecahan tersebut berarti plus tak terhingga atau minus tak terhingga, dan ini adalah hal yang sama sekali berbeda.

Poin diskontinuitas jenis pertama

Break point jenis pertama: suatu fungsi mempunyai batas kiri berhingga (yaitu tidak sama dengan tak terhingga) dan batas kanan berhingga, tetapi fungsi tersebut tidak terdefinisi pada suatu titik atau batas kiri dan kanan berbeda (tidak sama).

Titik diskontinuitas lepasan jenis pertama. Batas kiri dan kanan sama. Dalam hal ini, dimungkinkan untuk mendefinisikan lebih lanjut fungsi pada suatu titik. Mendefinisikan suatu fungsi pada suatu titik, secara sederhana, berarti menyediakan hubungan titik-titik yang diantara titik-titik tersebut terdapat suatu titik yang limit kiri dan limit kanannya sama satu sama lain. Dalam hal ini, koneksi harus mewakili hanya satu titik di mana nilai fungsi harus ditemukan.

Contoh 1. Tentukan titik putus fungsi dan jenis (karakter) titik putus tersebut.

Poin diskontinuitas jenis kedua

Break point jenis kedua: titik di mana setidaknya salah satu batasnya (kiri atau kanan) tidak terhingga (sama dengan tak terhingga).

Contoh 3.

Larutan. Dari ungkapan kekuatan di e jelas bahwa fungsinya tidak terdefinisi pada titik tersebut. Mari kita cari limit kiri dan kanan fungsi pada titik ini:

Salah satu limitnya sama dengan tak terhingga, sehingga titik tersebut merupakan titik diskontinuitas jenis kedua. Grafik suatu fungsi dengan titik putus ada di bawah contoh.

Menemukan breakpoint suatu fungsi dapat menjadi tugas independen atau bagian darinya Penelitian dan grafik fungsi penuh .

Contoh 4. Tentukan titik putus fungsi dan jenis (karakter) titik putus fungsi tersebut

Larutan. Dari ekspresi pangkat pada 2 jelas bahwa fungsi tersebut tidak terdefinisi pada suatu titik. Mari kita cari limit kiri dan kanan fungsi pada titik ini.

Kesenjangan yang bisa dilepas.

Definisi. Dot A disebut titik diskontinuitas lepasan dari fungsi tersebut kamu=f(x), jika limit fungsinya f(x) ada pada saat ini, tetapi pada saat ini A fungsi f(x) baik tidak didefinisikan atau memiliki arti pribadi f(a), berbeda dari batasnya f(x) pada saat ini.

Contoh. Misalnya saja fungsinya

sudah tepat sasaran x=0 celah yang dapat diperbaiki. Memang, nilai pembatas dari fungsi ini ada pada titik tersebut x=0 sama dengan 1. Nilai parsialnya sama dengan 2.

Jika fungsinya f(x) sudah tepat sasaran A celah yang dapat dihilangkan, maka celah tersebut dapat dihilangkan tanpa mengubah nilai fungsi pada titik selainnya A. Untuk melakukan ini, cukup dengan meletakkan nilai fungsi pada titik A sama dengan nilai batasnya pada titik ini. Jadi, dalam contoh di atas, cukup untuk menjelaskannya f(0)=1 kemudian , yaitu. fungsi f(x) akan menjadi kontinu pada titik tersebut x=0.

Gangguan jenis pertama.

Definisi. Dot A disebut titik diskontinuitas jenis pertama jika pada titik ini fungsinya f(x) mempunyai batas kanan dan kiri yang terbatas tetapi tidak sama

Mari kita berikan beberapa contoh.

Contoh. Fungsi y=sgnx sudah tepat sasaran x=0 pecahnya jenis pertama. Memang benar, dan dengan demikian batas-batas ini tidak sama satu sama lain.

Contoh. Fungsi , didefinisikan di mana saja kecuali intinya x=1, tepat sasaran x=1 pecahnya jenis pertama. Memang, .

Gangguan jenis kedua.

Definisi. Dot A disebut titik diskontinuitas jenis kedua jika pada titik ini fungsinya f(x) tidak mempunyai paling sedikit salah satu dari batas satu sisinya atau jika paling sedikit salah satu dari batas satu sisinya tidak terhingga.

Contoh. Fungsi f(x)=tan x, tentu saja, mempunyai diskontinuitas jenis kedua di setiap titik x k =π/2+π k, k=0, ± 1, ± 2,…, karena pada setiap titik tersebut

Contoh. Fungsi tersebut mempunyai diskontinuitas jenis kedua pada titiknya x=0, karena pada titik ini tidak ada batas kanan dan kiri.

Kontinuitas suatu fungsi pada suatu segmen

Definisi. Fungsi didefinisikan pada suatu interval dan kontinu pada setiap titiknya disebut kontinu pada ruas tersebut.

Apalagi di bawah kesinambungan pada intinya A dipahami sebagai kesinambungan di sebelah kanan, dan kesinambungan di suatu titik B- kontinuitas di sebelah kiri.

Kami akan mengatakan itu fungsinya kamu=f(x), ditentukan di set (X) mencapai tepi atas (bawah) di atasnya , jika hal seperti itu ada x 0 ∈(x), Apa f(x 0)=β (f(x 0)=α).

Teorema [Weierstrass].. Setiap fungsi yang kontinu pada suatu interval dibatasi dan mencapai batas atasnya dan batas bawahnya.

Teorema [Bolzano-Cauchy]. Jika fungsinya kamu=f(x) kontinu pada segmen tersebut Dan f(a)=SEBUAH, f(b)=B, lalu untuk apa pun C, menyimpulkan antara A Dan B, ada benarnya ξ∈ , Apa f(ξ)=C.

Dengan kata lain, suatu fungsi kontinu pada suatu interval, yang mengambil dua nilai apa pun, juga mengambil nilai apa pun yang terletak di antara keduanya.

Konsekuensi. Jika suatu fungsi kontinu pada suatu segmen dan mengambil nilai-nilai yang tandanya berbeda di ujung-ujungnya, maka paling sedikit ada satu titik pada segmen tersebut di mana fungsi tersebut hilang.

Konsekuensi. Biarkan fungsinya kamu=f(x) kontinu pada segmen tersebut Dan , . Lalu fungsinya f(x) mengambil semua nilai dari segmen tersebut dan hanya nilai-nilai ini.

Jadi, himpunan semua nilai suatu fungsi yang diberikan dan kontinu pada suatu segmen tertentu juga merupakan segmen.

Kontinuitas fungsi. Poin-poin penting.

Banteng berjalan, bergoyang, mendesah sambil berjalan:
- Oh, papannya hampir habis, sekarang aku akan jatuh!

Dalam pelajaran ini kita akan mempelajari konsep kontinuitas suatu fungsi, klasifikasi titik diskontinuitas dan masalah praktis yang umum studi kontinuitas fungsi. Dari nama topiknya saja, banyak yang secara intuitif menebak apa yang akan dibahas dan menganggap materinya cukup sederhana. Ini benar. Tetapi tugas-tugas sederhanalah yang paling sering dihukum karena kelalaian dan pendekatan yang dangkal untuk menyelesaikannya. Oleh karena itu, saya menyarankan Anda mempelajari artikel ini dengan sangat hati-hati dan memahami semua seluk-beluk dan tekniknya.

Apa yang perlu Anda ketahui dan dapat lakukan? Tidak banyak. Untuk mempelajari pelajaran dengan baik, Anda perlu memahami apa itu pelajaran batas suatu fungsi. Pembaca dengan level rendah persiapan sudah cukup untuk memahami artikel Batasan fungsi. Contoh solusi dan untuk melihat makna geometris batas dalam manual Grafik dan sifat-sifat fungsi dasar. Anda juga disarankan untuk membiasakan diri dengannya transformasi geometri grafik, karena latihan dalam banyak kasus melibatkan pembuatan gambar. Prospeknya optimis untuk semua orang, dan bahkan ketel penuh akan mampu mengatasi tugasnya sendiri dalam satu atau dua jam ke depan!

Kontinuitas fungsi. Breakpoint dan klasifikasinya

Konsep kontinuitas fungsi

Mari kita perhatikan beberapa fungsi yang kontinu pada seluruh garis bilangan:

Atau, lebih ringkasnya, fungsi kita kontinu (himpunan bilangan real).

Apa kriteria kontinuitas “filistin”? Jelas jadwalnya fungsi berkelanjutan dapat digambar tanpa mengangkat pensil dari kertas.

Dalam hal ini, dua konsep sederhana harus dibedakan dengan jelas: domain suatu fungsi Dan kelangsungan fungsi. DI DALAM kasus umum itu bukan hal yang sama. Misalnya:

Fungsi ini didefinisikan pada seluruh garis bilangan, yaitu untuk setiap orang Arti “x” mempunyai arti tersendiri bagi “y”. Khususnya, jika , maka . Perhatikan bahwa poin lainnya diselingi, karena menurut definisi suatu fungsi, nilai argumen harus sesuai satu-satunya nilai fungsi. Dengan demikian, domain fungsi kami: .

Namun fungsi ini tidak terus menerus aktif! Sangat jelas terlihat bahwa saat ini dia sedang menderita celah. Istilah ini juga cukup jelas dan visual, di sini pensil tetap harus disobek dari kertasnya. Nanti kita akan melihat klasifikasi breakpoint.

Kontinuitas suatu fungsi pada suatu titik dan suatu interval

Dalam suatu permasalahan matematika tertentu, kita dapat membicarakan tentang kontinuitas suatu fungsi pada suatu titik, kontinuitas suatu fungsi pada suatu interval, setengah interval, atau kontinuitas suatu fungsi pada suatu segmen. Itu adalah, tidak ada “hanya kesinambungan”– fungsinya dapat berkelanjutan DI MANA SAJA. Dan “bahan penyusun” mendasar dari segala hal lainnya adalah kelangsungan fungsi pada intinya .

Teori analisis matematis memberikan definisi kontinuitas suatu fungsi pada suatu titik menggunakan lingkungan “delta” dan “epsilon”, tetapi dalam praktiknya digunakan definisi lain, yang akan kita perhatikan baik-baik.

Pertama mari kita ingat batas sepihak yang menyerbu hidup kita di pelajaran pertama tentang grafik fungsi. Pertimbangkan situasi sehari-hari:

Jika kita mendekati sumbu ke titik kiri(panah merah), maka nilai "permainan" yang sesuai akan bergerak sepanjang sumbu ke titik (panah merah). Secara matematis, fakta ini diperbaiki dengan menggunakan batas kiri:

Perhatikan entri (berbaca “x cenderung ka di sebelah kiri”). Simbol "tambahan" "minus nol". , pada dasarnya ini berarti kita mendekati angka tersebut dari sisi kiri.

Begitu pula jika mendekati titik “ka” di sebelah kanan(panah biru), maka “permainan” akan memiliki nilai yang sama, tetapi sepanjang panah hijau, dan batas sebelah kanan akan diformat sebagai berikut:

"Aditif" melambangkan , dan entri tersebut berbunyi: “x cenderung ke ka di sebelah kanan.”

Jika limit satu sisi berhingga dan sama(seperti dalam kasus kami): , maka kita akan mengatakan bahwa ada batasan UMUM. Sederhana saja, batasan umumnya adalah “biasa” kita batas suatu fungsi, sama dengan bilangan berhingga.

Perhatikan bahwa jika fungsinya tidak ditentukan pada (tusukan titik hitam pada cabang grafik), maka perhitungan di atas tetap valid. Seperti yang telah disebutkan beberapa kali, khususnya dalam artikel pada fungsi yang sangat kecil, ekspresi berarti "x" sangat dekat mendekati intinya, sementara TIDAK PENTING, apakah fungsi itu sendiri terdefinisi pada suatu titik tertentu atau tidak. Contoh yang baik akan muncul di paragraf berikutnya, ketika fungsinya dianalisis.

Definisi: suatu fungsi kontinu di suatu titik jika limit fungsi di suatu titik sama dengan nilai fungsi di titik tersebut: .

Definisi tersebut dirinci dalam kondisi berikut:

1) Fungsi harus terdefinisi pada titik, yaitu nilai harus ada.

2) Harus ada limit umum dari fungsi tersebut. Seperti disebutkan di atas, ini menyiratkan adanya dan kesetaraan batas satu sisi: .

3) Limit fungsi pada suatu titik tertentu harus sama dengan nilai fungsi pada titik tersebut: .

Jika dilanggar setidaknya satu dari tiga kondisi, maka fungsi tersebut kehilangan sifat kontinuitas di titik tersebut.

Kontinuitas suatu fungsi dalam suatu interval dirumuskan dengan cerdik dan sangat sederhana: suatu fungsi kontinu pada interval jika kontinu di setiap titik pada interval tertentu.

Secara khusus, banyak fungsi yang kontinu pada interval tak terhingga, yaitu pada himpunan bilangan real. Ini adalah fungsi linier, polinomial, eksponensial, sinus, kosinus, dll. Dan secara umum, apa saja fungsi dasar terus menerus pada nya domain definisi, misalnya, fungsi logaritma kontinu pada interval . saya berharap untuk saat ini Anda memiliki gambaran yang cukup bagus tentang seperti apa grafik fungsi utama. Lagi Informasi rinci tentang kesinambungannya dapat dipelajari orang baik dengan nama keluarga Fichtengolts.

Dengan kontinuitas suatu fungsi pada suatu segmen dan setengah interval, semuanya juga tidak sulit, tetapi lebih tepat membicarakan hal ini di kelas tentang mencari nilai minimum dan maksimum suatu fungsi pada suatu segmen, tapi untuk saat ini jangan khawatir.

Klasifikasi titik istirahat

Kehidupan fungsi yang menakjubkan kaya akan segala macam poin khusus, dan break point hanyalah salah satu halaman biografi mereka.

Catatan : untuk berjaga-jaga, saya akan membahas satu hal mendasar: titik puncaknya selalu satu titik– tidak ada “beberapa break point berturut-turut”, yaitu tidak ada yang namanya “interval break”.

Poin-poin ini pada gilirannya dibagi menjadi dua kelompok besar: pecahnya jenis pertama Dan pecahnya jenis kedua. Setiap jenis celah mempunyai perbedaannya masing-masing karakteristik yang akan kita lihat sekarang:

Titik diskontinuitas jenis pertama

Jika kondisi kontinuitas dilanggar pada suatu titik dan batas sepihak terbatas , lalu disebut titik diskontinuitas jenis pertama.

Mari kita mulai dengan kasus yang paling optimis. Sesuai dengan ide awal pembelajaran, saya ingin menyampaikan teori “in pandangan umum”, tetapi untuk menunjukkan realitas materi, saya memilih opsi dengan karakter tertentu.

Sedih sekali, seperti foto pengantin baru dengan latar belakang Api Abadi, namun bidikan berikut ini diterima secara umum. Mari kita gambarkan grafik fungsi pada gambar:


Fungsi ini kontinu pada seluruh garis bilangan, kecuali titik. Faktanya, penyebutnya tidak boleh sama dengan nol. Namun sesuai dengan pengertian batasannya, kita bisa sangat dekat mendekati “nol” baik dari kiri maupun dari kanan, yaitu, batas satu sisi ada dan, tentu saja, bertepatan:
(Kondisi kontinuitas No. 2 terpenuhi).

Tetapi fungsinya tidak terdefinisi pada titik tersebut, oleh karena itu, Kondisi kontinuitas No. 1 dilanggar, dan fungsi tersebut mengalami diskontinuitas pada titik ini.

Istirahat jenis ini (dengan yang sudah ada batas umum) disebut celah yang dapat diperbaiki. Mengapa bisa dilepas? Karena fungsinya bisa mendefinisikan ulang pada titik puncaknya:

Apakah ini terlihat aneh? Mungkin. Namun notasi fungsi seperti itu tidak bertentangan dengan apapun! Sekarang kesenjangan telah tertutup dan semua orang senang:


Mari kita lakukan pemeriksaan formal:

2) – ada batasan umum;
3)

Jadi, ketiga syarat terpenuhi, dan fungsi tersebut kontinu di suatu titik menurut definisi kontinuitas suatu fungsi di suatu titik.

Namun, pembenci matan bisa mendefinisikan fungsinya dengan cara yang buruk, misalnya :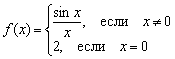


Menariknya, dua kondisi kontinuitas pertama terpenuhi di sini:
1) – fungsi didefinisikan pada suatu titik tertentu;
2) – ada batasan umum.

Namun batas ketiga belum terlampaui: , yaitu limit fungsi pada titik tersebut tidak sama nilai fungsi tertentu pada suatu titik tertentu.

Dengan demikian, pada suatu titik fungsi tersebut mengalami diskontinuitas.

Kasus kedua yang lebih menyedihkan disebut pecahnya jenis pertama dengan lompatan. Dan kesedihan ditimbulkan oleh batasan sepihak itu terbatas dan berbeda. Contohnya ditunjukkan pada gambar kedua pelajaran. Kesenjangan seperti itu biasanya terjadi ketika fungsi yang ditentukan sedikit demi sedikit, yang telah disebutkan dalam artikel tentang transformasi grafik.

Pertimbangkan fungsi sepotong-sepotong dan kami akan menyelesaikan gambarnya. Bagaimana cara membuat grafik? Sangat sederhana. Pada setengah interval kita menggambar pecahan parabola ( warna hijau), pada interval – ruas garis lurus (merah) dan pada setengah interval – garis lurus ( Warna biru).

Apalagi karena ketimpangan, nilainya ditentukan fungsi kuadrat(titik hijau), dan karena pertidaksamaan, maka ditentukan nilainya fungsi linear(titik biru):

Dalam kasus yang paling sulit, Anda harus menggunakan konstruksi titik demi titik pada setiap bagian grafik (lihat yang pertama pelajaran tentang grafik fungsi).

Sekarang kita hanya akan tertarik pada intinya. Mari kita periksa kontinuitasnya:

2) Mari kita hitung limit satu sisi.

Di sebelah kiri kita ada ruas garis merah, jadi batas sisi kirinya adalah:

Di sebelah kanan adalah garis lurus berwarna biru, dan batas sebelah kanan:

Hasilnya, kami menerima angka yang terbatas, dan mereka tidak sama. Karena batasnya sepihak terbatas dan berbeda: , maka fungsi kita akan menoleransi diskontinuitas jenis pertama dengan lompatan.

Adalah logis bahwa kesenjangan tersebut tidak dapat dihilangkan - fungsinya sebenarnya tidak dapat didefinisikan lebih lanjut dan “direkatkan”, seperti pada contoh sebelumnya.

Poin diskontinuitas jenis kedua

Biasanya, semua kasus pecah lainnya secara cerdik diklasifikasikan ke dalam kategori ini. Saya tidak akan mencantumkan semuanya, karena dalam praktiknya, dalam 99% masalah yang akan Anda temui kesenjangan yang tak ada habisnya– ketika kidal atau tidak kidal, dan lebih sering lagi, kedua batas tersebut tidak terbatas.

Dan tentu saja gambaran yang paling jelas adalah hiperbola di titik nol. Di sini kedua limit satu sisi tidak terhingga: , oleh karena itu, fungsi tersebut mengalami diskontinuitas jenis kedua di titik .

Saya mencoba mengisi artikel saya dengan konten yang beragam, jadi mari kita lihat grafik fungsi yang belum terlihat:

sesuai dengan skema standar:

1) Fungsi tersebut tidak terdefinisi pada saat ini karena penyebutnya menjadi nol.

Tentu saja, kita dapat langsung menyimpulkan bahwa fungsi tersebut mengalami diskontinuitas pada titik , namun sebaiknya kita mengklasifikasikan sifat diskontinuitas, yang sering kali diperlukan oleh kondisi tersebut. Untuk ini:

Izinkan saya mengingatkan Anda bahwa yang kami maksud dengan rekaman adalah kecil sekali angka negatif , dan di bawah entri - bilangan positif yang sangat kecil.

Batas satu sisi tidak terhingga, artinya fungsi tersebut mengalami diskontinuitas jenis ke-2 di titik tersebut. Sumbu y adalah asimtot vertikal untuk grafik.

Tidak jarang kedua limit satu sisi tersebut ada, namun hanya satu saja yang tidak terhingga, misalnya:

Ini adalah grafik fungsinya.

Kami memeriksa poin kontinuitas:

1) Fungsinya belum terdefinisi pada saat ini.

2) Mari kita hitung batas satu sisi:

Kita akan membicarakan metode penghitungan batas satu sisi seperti itu dalam dua contoh terakhir kuliah, meskipun banyak pembaca sudah melihat dan menebak semuanya.

Limit sebelah kirinya berhingga dan sama dengan nol (kita “tidak menuju ke titik itu sendiri”), tetapi limit sebelah kanannya tidak terhingga dan cabang jingga pada grafik mendekati tak terhingga mendekati batasnya. asimtot vertikal, diberikan oleh persamaan (garis putus-putus hitam).

Jadi fungsinya terganggu diskontinuitas jenis kedua pada titik.

Sedangkan untuk diskontinuitas jenis ke-1, fungsinya dapat didefinisikan pada titik diskontinuitas itu sendiri. Misalnya saja untuk fungsi sepotong-sepotong Jangan ragu untuk memberi titik hitam tebal di titik asal koordinat. Di sebelah kanan adalah cabang hiperbola, dan limit di sebelah kanannya tidak terhingga. Saya rasa hampir semua orang memiliki gambaran seperti apa grafik ini.

Apa yang dinantikan semua orang:

Bagaimana cara memeriksa suatu fungsi untuk kontinuitas?

Kajian suatu fungsi kontinuitas pada suatu titik dilakukan menurut skema rutin yang telah ditetapkan, yang terdiri dari pemeriksaan tiga kondisi kontinuitas:

Contoh 1

Jelajahi fungsi

Larutan:

1) Satu-satunya titik dalam ruang lingkup adalah ketika fungsinya tidak didefinisikan.

2) Mari kita hitung batas satu sisi:

Batas satu sisi terbatas dan sama.

Jadi, pada titik tersebut fungsi tersebut mengalami diskontinuitas yang dapat dilepas.

Seperti apa grafik fungsi ini?

Saya ingin menyederhanakan , dan sepertinya diperoleh parabola biasa. TETAPI fungsi aslinya tidak didefinisikan pada titik , sehingga diperlukan klausa berikut:

Mari kita membuat gambarnya:

Menjawab: fungsi tersebut kontinu pada seluruh garis bilangan kecuali titik di mana fungsi tersebut mengalami diskontinuitas yang dapat dilepas.

Fungsi tersebut dapat didefinisikan lebih lanjut baik atau buruk, tetapi menurut kondisi hal ini tidak diperlukan.

Anda bilang ini contoh yang tidak masuk akal? Sama sekali tidak. Hal ini telah terjadi puluhan kali dalam praktiknya. Hampir semua tugas situs ini berasal dari kerja dan tes independen yang nyata.

Mari kita singkirkan modul favorit kita:

Contoh 2

Jelajahi fungsi untuk kontinuitas. Tentukan sifat diskontinuitas fungsi, jika memang ada. Jalankan gambarnya.

Larutan: Entah kenapa, siswa takut dan tidak menyukai fungsi-fungsi yang ada pada modul, padahal tidak ada yang rumit tentangnya. Kita telah sedikit menyinggung hal-hal seperti itu dalam pelajaran. Transformasi geometri grafik. Karena modulnya non-negatif, maka modul diperluas sebagai berikut: , di mana “alpha” adalah suatu ekspresi. DI DALAM pada kasus ini, dan fungsi kita harus ditulis sepotong demi sepotong: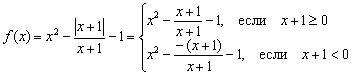

Namun pecahan kedua pecahan tersebut harus dikurangi sebesar . Pengurangan, seperti contoh sebelumnya, tidak akan terjadi tanpa konsekuensi. Fungsi aslinya tidak terdefinisi pada titik tersebut karena penyebutnya menjadi nol. Oleh karena itu, sistem juga harus menentukan kondisinya , dan membuat pertidaksamaan pertama menjadi ketat:

Sekarang tentang SANGAT Penerimaan yang BERMANFAAT solusi: sebelum menyelesaikan tugas pada suatu rancangan, ada baiknya membuat gambar (terlepas dari apakah diperlukan oleh kondisi atau tidak). Ini akan membantu, pertama, untuk segera melihat titik kontinuitas dan titik diskontinuitas, dan kedua, 100% melindungi Anda dari kesalahan saat menemukan batas satu sisi.

Mari kita menggambar. Sesuai dengan perhitungan kami, di sebelah kiri titik perlu menggambar pecahan parabola (warna biru), dan di sebelah kanan - sepotong parabola (warna merah), sedangkan fungsinya tidak ditentukan di titik itu sendiri:

Jika ragu, ambil beberapa nilai x dan masukkan ke dalam fungsinya (mengingat bahwa modul menghancurkan kemungkinan tanda minus) dan periksa grafiknya.

Mari kita periksa fungsi kontinuitas secara analitis:

1) Fungsi tersebut tidak terdefinisi pada suatu titik, sehingga dapat langsung dikatakan bahwa fungsi tersebut tidak kontinu pada suatu titik.

2) Mari kita tentukan sifat diskontinuitas; untuk melakukan ini, kita menghitung batas satu sisi:

Batas satu sisinya berhingga dan berbeda, artinya fungsi tersebut mengalami diskontinuitas jenis pertama dengan lompatan pada titik tersebut. Perhatikan lagi bahwa ketika mencari limit, tidak masalah apakah fungsi pada titik break point terdefinisi atau tidak.

Sekarang yang tersisa hanyalah mentransfer gambar dari draft (dibuat seolah-olah dengan bantuan penelitian ;-)) dan menyelesaikan tugas:

Menjawab: fungsi tersebut kontinu pada seluruh garis bilangan kecuali pada titik yang mengalami diskontinuitas jenis pertama akibat lompatan.

Terkadang mereka memerlukan indikasi tambahan tentang lompatan diskontinuitas. Ini dihitung secara sederhana - dari batas kanan Anda perlu mengurangi batas kiri: , yaitu, pada titik istirahat fungsi kita melonjak 2 unit ke bawah (seperti yang ditunjukkan oleh tanda minus).

Contoh 3

Jelajahi fungsi untuk kontinuitas. Tentukan sifat diskontinuitas fungsi tersebut, jika memang ada. Buatlah gambar.

Ini adalah contoh untuk Anda pecahkan sendiri, contoh solusi di akhir pelajaran.

Mari kita beralih ke versi tugas yang paling populer dan tersebar luas, ketika fungsinya terdiri dari tiga bagian:

Contoh 4

Periksa suatu fungsi untuk kontinuitas dan buat grafik fungsinya .

Larutan: Jelas bahwa ketiga bagian fungsi tersebut kontinu pada interval yang bersesuaian, sehingga yang tersisa hanyalah memeriksa dua titik “persimpangan” di antara bagian-bagian tersebut. Pertama, mari kita membuat rancangan gambar; saya mengomentari teknik konstruksi dengan cukup detail di bagian pertama artikel. Satu-satunya hal adalah kita perlu hati-hati mengikuti titik tunggal kita: karena pertidaksamaan, nilainya termasuk dalam garis lurus (titik hijau), dan karena pertidaksamaan, nilainya termasuk dalam parabola (titik merah):


Ya prinsipnya semuanya jelas =) Tinggal meresmikan keputusan. Untuk masing-masing dari dua titik “penggabungan”, kami secara standar memeriksa 3 kondisi kontinuitas:

SAYA) Kami memeriksa poin kontinuitas

1)

Batas satu sisinya berhingga dan berbeda, artinya fungsi tersebut mengalami diskontinuitas jenis pertama dengan lompatan pada titik tersebut.

Mari kita hitung lompatan diskontinuitas sebagai selisih antara batas kanan dan batas kiri:
, yaitu grafiknya tersentak naik satu satuan.

II) Kami memeriksa poin kontinuitas

1) – fungsi didefinisikan pada titik tertentu.

2) Temukan batas satu sisi:

– limit satu sisi berhingga dan sama, artinya ada limit umum.

3) – limit suatu fungsi di suatu titik sama dengan nilai fungsi tersebut di suatu titik tertentu.

Pada tahap akhir, kami mentransfer gambar ke versi final, setelah itu kami memasang akord terakhir:

Menjawab: fungsi tersebut kontinu di sepanjang garis bilangan, kecuali pada titik yang mengalami diskontinuitas jenis pertama dengan lompatan.

Contoh 5

Periksa suatu fungsi untuk kontinuitas dan buat grafiknya .

Ini adalah contoh untuk Anda pecahkan sendiri, solusi singkat dan contoh perkiraan tugas di akhir pelajaran.

Anda mungkin mendapat kesan bahwa pada satu titik fungsinya harus kontinu, dan pada titik lain harus ada diskontinuitas. Dalam praktiknya, hal ini tidak selalu terjadi. Cobalah untuk tidak mengabaikan contoh lainnya - akan ada beberapa fitur menarik dan penting:

Contoh 6

Diberikan suatu fungsi . Selidiki fungsi kontinuitas pada titik-titik. Buat grafik.

Larutan: dan sekali lagi segera jalankan gambar pada draft:

Keunikan grafik ini adalah fungsi sepotong-sepotong diberikan oleh persamaan sumbu absis. Area ini digambar di sini hijau, dan di buku catatan biasanya dicetak tebal dengan pensil sederhana. Dan, tentu saja, jangan lupakan domba jantan kita: nilainya milik cabang singgung (titik merah), dan nilainya milik garis lurus.

Semuanya jelas dari gambar - fungsinya kontinu di sepanjang garis bilangan, yang tersisa hanyalah memformalkan solusi, yang dibawa ke otomatisasi penuh secara harfiah setelah 3-4 contoh serupa:

SAYA) Kami memeriksa poin kontinuitas

1) – fungsi didefinisikan pada suatu titik tertentu.

2) Mari kita hitung batas satu sisi:

, yang berarti ada batasan umum.

Untuk berjaga-jaga, izinkan saya mengingatkan Anda tentang fakta sepele: limit suatu konstanta sama dengan konstanta itu sendiri. Dalam hal ini, limit dari nol sama dengan nol itu sendiri (limit kidal).

3) – limit suatu fungsi di suatu titik sama dengan nilai fungsi tersebut di suatu titik tertentu.

Jadi, suatu fungsi kontinu di suatu titik menurut definisi kontinuitas suatu fungsi di suatu titik.

II) Kami memeriksa poin kontinuitas

1) – fungsi didefinisikan pada suatu titik tertentu.

2) Temukan batas satu sisi:

Dan di sini – limit satu sama dengan satuan itu sendiri.

– ada batasan umum.

3) – limit suatu fungsi di suatu titik sama dengan nilai fungsi tersebut di suatu titik tertentu.

Jadi, suatu fungsi kontinu di suatu titik menurut definisi kontinuitas suatu fungsi di suatu titik.

Seperti biasa, setelah penelitian kami mentransfer gambar kami ke versi final.

Menjawab: fungsi tersebut kontinu di titik-titiknya.

Perlu diketahui bahwa dalam kondisi tersebut kita tidak ditanya apapun tentang mempelajari seluruh fungsi untuk kontinuitas, dan itu dianggap sebagai bentuk matematika yang baik untuk dirumuskan tepat dan jelas jawaban atas pertanyaan yang diajukan. Omong-omong, jika kondisinya tidak mengharuskan Anda membuat grafik, maka Anda sudah melakukannya benar jangan membangunnya (walaupun guru bisa memaksamu melakukannya nanti).

Sebuah "twister lidah" ​​matematika kecil untuk menyelesaikannya sendiri:

Contoh 7

Diberikan suatu fungsi . Selidiki fungsi kontinuitas pada titik-titik. Klasifikasikan breakpoint, jika ada. Jalankan gambarnya.

Cobalah untuk "mengucapkan" semua "kata" dengan benar =) Dan gambar grafiknya dengan lebih tepat, akurat, tidak akan berlebihan di mana-mana ;-)

Seperti yang Anda ingat, saya merekomendasikan untuk segera menyelesaikan gambar sebagai draf, tetapi dari waktu ke waktu Anda menemukan contoh di mana Anda tidak dapat langsung mengetahui seperti apa grafiknya. Oleh karena itu, dalam beberapa kasus, akan bermanfaat untuk terlebih dahulu menemukan batas satu sisi dan baru kemudian, berdasarkan penelitian, menggambarkan cabang-cabangnya. Dalam dua contoh terakhir kita juga akan mempelajari teknik menghitung beberapa limit satu sisi:

Contoh 8

Periksa fungsi kontinuitas dan buat grafik skemanya.

Larutan: poin buruknya jelas: (mengurangi penyebut eksponen menjadi nol) dan (mengurangi penyebut seluruh pecahan menjadi nol). Grafik fungsi ini tidak jelas seperti apa, jadi sebaiknya lakukan riset terlebih dahulu.