ഈജൻവാല്യൂസും ഈജൻ വെക്ടറും. ഒരു മാട്രിക്സിൻ്റെ ഈജൻ മൂല്യങ്ങളും ഈജൻ വെക്ടറുകളും

ഏകതാനമായ രേഖീയ സമവാക്യങ്ങളുടെ സിസ്റ്റം

ഏകതാനമായ സംവിധാനം രേഖീയ സമവാക്യങ്ങൾരൂപത്തിൻ്റെ ഒരു സിസ്റ്റം എന്ന് വിളിക്കുന്നു

ഈ സാഹചര്യത്തിൽ അത് വ്യക്തമാണ് , കാരണം ഈ ഡിറ്റർമിനൻ്റുകളിലെ ഒരു നിരയിലെ എല്ലാ ഘടകങ്ങളും പൂജ്യത്തിന് തുല്യമാണ്.

അജ്ഞാതരെ സൂത്രവാക്യങ്ങൾക്കനുസൃതമായി കണ്ടെത്തിയതിനാൽ , Δ ≠ 0 ആയിരിക്കുമ്പോൾ, സിസ്റ്റത്തിന് ഒരു അദ്വിതീയ പൂജ്യം പരിഹാരമുണ്ട് x = വൈ = z= 0. എന്നിരുന്നാലും, പല പ്രശ്നങ്ങളിലും രസകരമായ ചോദ്യം ഉണ്ടോ എന്നതാണ് ഏകതാനമായ സംവിധാനംപൂജ്യം ഒഴികെയുള്ള പരിഹാരങ്ങൾ.

സിദ്ധാന്തം.ലീനിയർ സിസ്റ്റത്തിന് വേണ്ടി ഏകതാനമായ സമവാക്യങ്ങൾപൂജ്യമല്ലാത്ത ഒരു പരിഹാരം ഉണ്ടായിരുന്നു, അത് Δ ≠ 0 ആണ്.

അതിനാൽ, ഡിറ്റർമിനൻ്റ് Δ ≠ 0 ആണെങ്കിൽ, സിസ്റ്റത്തിന് ഒരു അദ്വിതീയ പരിഹാരമുണ്ട്. Δ ≠ 0 ആണെങ്കിൽ, രേഖീയ ഏകതാനമായ സമവാക്യങ്ങളുടെ സിസ്റ്റത്തിന് അനന്തമായ പരിഹാരങ്ങളുണ്ട്.

ഉദാഹരണങ്ങൾ.

ഒരു മാട്രിക്സിൻ്റെ ഈജൻ വെക്റ്ററുകളും ഈജൻ മൂല്യങ്ങളും

ഒരു ചതുര മാട്രിക്സ് നൽകട്ടെ , എക്സ്- ചില മാട്രിക്സ് കോളം, അതിൻ്റെ ഉയരം മാട്രിക്സിൻ്റെ ക്രമവുമായി പൊരുത്തപ്പെടുന്നു എ. .

പല പ്രശ്നങ്ങളിലും നമ്മൾ സമവാക്യം പരിഗണിക്കേണ്ടതുണ്ട് എക്സ്

ഇവിടെ λ ഒരു നിശ്ചിത സംഖ്യയാണ്. ഏതെങ്കിലും λ ഈ സമവാക്യത്തിന് പൂജ്യം പരിഹാരമുണ്ടെന്ന് വ്യക്തമാണ്.

ഈ സമവാക്യത്തിന് പൂജ്യമല്ലാത്ത പരിഹാരങ്ങളുള്ള സംഖ്യയെ വിളിക്കുന്നു ഈജൻ മൂല്യംമെട്രിക്സ് എ, എ എക്സ്അത്തരം λ എന്ന് വിളിക്കപ്പെടുന്നു ഈജൻ വെക്റ്റർമെട്രിക്സ് എ.

നമുക്ക് മാട്രിക്സിൻ്റെ ഈജൻ വെക്റ്റർ കണ്ടെത്താം എ. എന്തുകൊണ്ടെന്നാല് ഇ∙X = X, അപ്പോൾ മാട്രിക്സ് സമവാക്യം ഇങ്ങനെ മാറ്റിയെഴുതാം അഥവാ . വിപുലീകരിച്ച രൂപത്തിൽ, ഈ സമവാക്യം രേഖീയ സമവാക്യങ്ങളുടെ ഒരു സിസ്റ്റമായി മാറ്റിയെഴുതാം. ശരിക്കും .

അതിനാൽ

അതിനാൽ, കോർഡിനേറ്റുകൾ നിർണ്ണയിക്കുന്നതിനുള്ള ഏകതാനമായ രേഖീയ സമവാക്യങ്ങളുടെ ഒരു സിസ്റ്റം ഞങ്ങൾ നേടിയിട്ടുണ്ട്. x 1, x 2, x 3വെക്റ്റർ എക്സ്. ഒരു സിസ്റ്റത്തിന് പൂജ്യമല്ലാത്ത സൊല്യൂഷനുകൾ ഉണ്ടാകണമെങ്കിൽ, സിസ്റ്റത്തിൻ്റെ ഡിറ്റർമിനൻ്റ് പൂജ്യത്തിന് തുല്യമായിരിക്കേണ്ടത് ആവശ്യമാണ്, അതായത്.

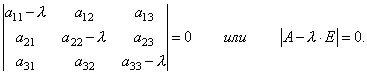
ഇത് λ യുടെ മൂന്നാം ഡിഗ്രി സമവാക്യമാണ്. അതിനെ വിളിക്കുന്നു സ്വഭാവ സമവാക്യംമെട്രിക്സ് എλ യുടെ ഈജൻ മൂല്യങ്ങൾ നിർണ്ണയിക്കാൻ സഹായിക്കുന്നു.

ഓരോ ഐജൻവാല്യൂവും λ ഒരു ഈജൻ വെക്‌ടറുമായി യോജിക്കുന്നു എക്സ്, അതിൻ്റെ കോർഡിനേറ്റുകൾ സിസ്റ്റത്തിൽ നിന്ന് λ യുടെ അനുബന്ധ മൂല്യത്തിൽ നിർണ്ണയിക്കപ്പെടുന്നു.

ഉദാഹരണങ്ങൾ.

വെക്‌റ്റർ ബീജഗണിതം. വെക്‌ടറിൻ്റെ ആശയം

ഭൗതികശാസ്ത്രത്തിൻ്റെ വിവിധ ശാഖകൾ പഠിക്കുമ്പോൾ, അവയുടെ സംഖ്യാ മൂല്യങ്ങൾ വ്യക്തമാക്കിക്കൊണ്ട് പൂർണ്ണമായും നിർണ്ണയിക്കപ്പെടുന്ന അളവുകൾ ഉണ്ട്, ഉദാഹരണത്തിന്, നീളം, വിസ്തീർണ്ണം, പിണ്ഡം, താപനില മുതലായവ. അത്തരം അളവുകളെ സ്കെയിലർ എന്ന് വിളിക്കുന്നു. എന്നിരുന്നാലും, അവയ്‌ക്ക് പുറമേ, അളവുകളും ഉണ്ട്, ഏത് സംഖ്യാ മൂല്യത്തിന് പുറമേ, ബഹിരാകാശത്ത് അവയുടെ ദിശയും അറിയേണ്ടത് ആവശ്യമാണ്, ഉദാഹരണത്തിന്, ശരീരത്തിൽ പ്രവർത്തിക്കുന്ന ശക്തി, വേഗതയും ത്വരിതവും ശരീരം ബഹിരാകാശത്ത് നീങ്ങുമ്പോൾ, പിരിമുറുക്കം കാന്തികക്ഷേത്രംബഹിരാകാശത്ത് ഒരു നിശ്ചിത പോയിൻ്റിൽ മുതലായവ. അത്തരം അളവുകളെ വെക്റ്റർ അളവുകൾ എന്ന് വിളിക്കുന്നു.

നമുക്ക് കർശനമായ ഒരു നിർവചനം അവതരിപ്പിക്കാം.

സംവിധാനം ചെയ്ത വിഭാഗംഅവയിൽ ഏതാണ് ആദ്യത്തേത്, രണ്ടാമത്തേത് എന്ന് അറിയാവുന്ന അറ്റങ്ങളുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ നമുക്ക് ഒരു സെഗ്മെൻ്റിനെ വിളിക്കാം.

വെക്റ്റർഒരു നിശ്ചിത ദൈർഘ്യമുള്ള ഒരു ഡയറക്റ്റ് സെഗ്മെൻ്റിനെ വിളിക്കുന്നു, അതായത്. ഇത് ഒരു നിശ്ചിത ദൈർഘ്യത്തിൻ്റെ ഒരു വിഭാഗമാണ്, അതിൽ പരിമിതപ്പെടുത്തുന്ന പോയിൻ്റുകളിലൊന്ന് തുടക്കമായും രണ്ടാമത്തേത് അവസാനമായും എടുക്കുന്നു. എങ്കിൽ എ- വെക്റ്ററിൻ്റെ ആരംഭം, ബിഅതിൻ്റെ അവസാനമാണ്, പിന്നെ വെക്‌ടറിനെ ചിഹ്നത്താൽ സൂചിപ്പിക്കും, കൂടാതെ, വെക്‌ടറിനെ പലപ്പോഴും ഒരു അക്ഷരം സൂചിപ്പിക്കുന്നു. ചിത്രത്തിൽ, വെക്റ്റർ ഒരു സെഗ്മെൻ്റും അതിൻ്റെ ദിശയും ഒരു അമ്പടയാളവും സൂചിപ്പിക്കുന്നു.

മൊഡ്യൂൾഅഥവാ നീളംഒരു വെക്‌ടറിനെ അതിനെ നിർവചിക്കുന്ന ഡയറക്‌ട് സെഗ്‌മെൻ്റിൻ്റെ ദൈർഘ്യം എന്ന് വിളിക്കുന്നു. സൂചിപ്പിക്കുന്നത് || അല്ലെങ്കിൽ ||.

സീറോ വെക്റ്റർ എന്ന് വിളിക്കപ്പെടുന്നതും ഞങ്ങൾ ഉൾപ്പെടുത്തും, അതിൻ്റെ തുടക്കവും അവസാനവും ഒത്തുചേരുന്നു, വെക്റ്ററുകളായി. അത് നിയുക്തമാക്കിയിരിക്കുന്നു. പൂജ്യം വെക്റ്ററിന് ഒരു പ്രത്യേക ദിശ ഇല്ല, അതിൻ്റെ മോഡുലസ് പൂജ്യം ||=0 ആണ്.

വെക്റ്ററുകൾ എന്ന് വിളിക്കുന്നു കോളിനിയർ, അവ ഒരേ വരിയിലോ സമാന്തര ലൈനുകളിലോ ആണെങ്കിൽ. മാത്രമല്ല, വെക്റ്ററുകളും ഒരേ ദിശയിലാണെങ്കിൽ, നമ്മൾ എഴുതും , വിപരീതം.

ഒരേ തലത്തിന് സമാന്തരമായി നേർരേഖയിൽ സ്ഥിതി ചെയ്യുന്ന വെക്റ്ററുകൾ എന്ന് വിളിക്കുന്നു കോപ്ലനാർ.

രണ്ട് വെക്റ്ററുകളെ വിളിക്കുന്നു തുല്യമായ, അവ കോളിനിയറാണെങ്കിൽ, ഒരേ ദിശയും നീളത്തിൽ തുല്യവുമാണ്. ഈ സാഹചര്യത്തിൽ അവർ എഴുതുന്നു.

വെക്‌ടറുകളുടെ സമത്വത്തിൻ്റെ നിർവചനത്തിൽ നിന്ന്, ഒരു വെക്‌ടറിനെ സമാന്തരമായി കൊണ്ടുപോകാൻ കഴിയുമെന്നും അതിൻ്റെ ഉത്ഭവം ബഹിരാകാശത്ത് ഏത് സ്ഥലത്തും സ്ഥാപിക്കാമെന്നും പിന്തുടരുന്നു.

ഉദാഹരണത്തിന്.

വെക്‌റ്ററുകളിലെ രേഖീയ പ്രവർത്തനങ്ങൾ

1. വെക്‌ടറിനെ ഒരു സംഖ്യ കൊണ്ട് ഗുണിക്കുക.

   വെക്‌ടറിൻ്റെയും സംഖ്യ λ എന്നതിൻ്റെയും ഗുണനം ഒരു പുതിയ വെക്‌ടറാണ്:

   ഒരു വെക്‌ടറിൻ്റെയും ഒരു സംഖ്യയുടെയും λ എന്നതിൻ്റെ ഗുണനഫലം സൂചിപ്പിക്കുന്നു.

   

   ഉദാഹരണത്തിന്,വെക്‌ടറിൻ്റെ അതേ ദിശയിൽ ഒരു വെക്‌റ്റർ ഉണ്ട്, വെക്‌ടറിൻ്റെ പകുതി നീളമുണ്ട്.

   അവതരിപ്പിച്ച പ്രവർത്തനത്തിന് ഇനിപ്പറയുന്നവയുണ്ട് പ്രോപ്പർട്ടികൾ:

2. വെക്റ്റർ കൂട്ടിച്ചേർക്കൽ.

   രണ്ട് അനിയന്ത്രിതമായ വെക്‌ടറുകൾ ആകട്ടെ. നമുക്ക് ഒരു ഏകപക്ഷീയമായ പോയിൻ്റ് എടുക്കാം ഒഒരു വെക്റ്റർ നിർമ്മിക്കുക. അതിനുശേഷം പോയിൻ്റിൽ നിന്ന് എനമുക്ക് വെക്റ്റർ മാറ്റിവെക്കാം. ആദ്യത്തെ വെക്‌ടറിൻ്റെ തുടക്കത്തെ രണ്ടാമത്തേതിൻ്റെ അവസാനവുമായി ബന്ധിപ്പിക്കുന്ന വെക്‌ടറിനെ വിളിക്കുന്നു തുകഈ വെക്‌ടറുകളിൽ നിന്ന് സൂചിപ്പിച്ചിരിക്കുന്നു .

   

   വെക്റ്റർ കൂട്ടിച്ചേർക്കലിൻ്റെ രൂപപ്പെടുത്തിയ നിർവചനത്തെ വിളിക്കുന്നു സമാന്തരരേഖാ നിയമം, വെക്‌ടറുകളുടെ അതേ തുക ഇനിപ്പറയുന്ന രീതിയിൽ ലഭിക്കും. പോയിൻ്റിൽ നിന്ന് മാറ്റിവയ്ക്കാം ഒവെക്റ്ററുകൾ കൂടാതെ. ഈ വെക്റ്ററുകളിൽ നമുക്ക് ഒരു സമാന്തരരേഖ നിർമ്മിക്കാം ഒഎബിസി. വെക്‌ടറുകൾ മുതൽ, പിന്നെ വെക്‌റ്റർ, ഇത് ശീർഷത്തിൽ നിന്ന് വരച്ച ഒരു സമാന്തരരേഖയുടെ ഡയഗണൽ ആണ്. ഒ, വ്യക്തമായും വെക്റ്ററുകളുടെ ആകെത്തുക ആയിരിക്കും.

   

   ഇനിപ്പറയുന്നവ പരിശോധിക്കുന്നത് എളുപ്പമാണ് വെക്റ്റർ കൂട്ടിച്ചേർക്കലിൻ്റെ സവിശേഷതകൾ.

3. വെക്റ്റർ വ്യത്യാസം.

   നൽകിയിരിക്കുന്ന വെക്‌ടറിലേക്കുള്ള വെക്‌റ്റർ കോളിനിയർ, നീളത്തിൽ തുല്യവും വിപരീത ദിശയിലുള്ളതുമായ, വിളിക്കുന്നു എതിർവശത്ത്ഒരു വെക്‌ടറിനുള്ള വെക്‌റ്റർ, ഇത് സൂചിപ്പിക്കുന്നത്. വെക്‌ടറിനെ λ = –1: എന്ന സംഖ്യ കൊണ്ട് ഗുണിച്ചതിൻ്റെ ഫലമായി വിപരീത വെക്‌ടറിനെ കണക്കാക്കാം.

നിർവ്വചനം 9.3.വെക്റ്റർ എക്സ് വിളിച്ചു ഈജൻ വെക്റ്റർമെട്രിക്സ് എ, അങ്ങനെ ഒരു നമ്പർ ഉണ്ടെങ്കിൽ λ, സമത്വം നിലനിർത്തുന്നത്: എ എക്സ്= λ എക്സ്, അതായത് അപേക്ഷിച്ചതിൻ്റെ ഫലം എക്സ് മാട്രിക്സ് വ്യക്തമാക്കിയ രേഖീയ പരിവർത്തനം എ, ഈ വെക്‌ടറിൻ്റെ സംഖ്യ കൊണ്ട് ഗുണിക്കുന്നതാണ് λ . നമ്പർ തന്നെ λ വിളിച്ചു ഈജൻ മൂല്യംമെട്രിക്സ് എ.

ഫോർമുലകളിലേക്ക് മാറ്റിസ്ഥാപിക്കുന്നു (9.3) x` j = λx j ,ഐജൻ വെക്‌ടറിൻ്റെ കോർഡിനേറ്റുകൾ നിർണയിക്കുന്നതിനുള്ള സമവാക്യങ്ങളുടെ ഒരു സംവിധാനം നമുക്ക് ലഭിക്കും:

. (9.5)

ഈ ലീനിയർ ഹോമോജീനിയസ് സിസ്റ്റത്തിന് അതിൻ്റെ പ്രധാന ഡിറ്റർമിനൻ്റ് 0 ആണെങ്കിൽ മാത്രമേ നിസ്സാരമായ ഒരു പരിഹാരം ഉണ്ടാകൂ (ക്രാമർ നിയമം). ഈ അവസ്ഥ ഫോമിൽ എഴുതുന്നതിലൂടെ:

ഈജൻമൂല്യങ്ങൾ നിർണ്ണയിക്കുന്നതിനുള്ള ഒരു സമവാക്യം നമുക്ക് ലഭിക്കും λ , വിളിച്ചു സ്വഭാവ സമവാക്യം. ചുരുക്കത്തിൽ ഇത് ഇനിപ്പറയുന്ന രീതിയിൽ പ്രതിനിധീകരിക്കാം:

| A - λE | = 0, (9.6)

അതിൻ്റെ ഇടതുവശത്ത് മാട്രിക്സിൻ്റെ ഡിറ്റർമിനൻ്റ് അടങ്ങിയിരിക്കുന്നതിനാൽ A-λE. ബഹുപദ ബന്ധു λ | A - λE| വിളിച്ചു സ്വഭാവ ബഹുപദംമെട്രിക്സ് എ.

സ്വഭാവ ബഹുപദത്തിൻ്റെ ഗുണങ്ങൾ:

1) ഒരു രേഖീയ പരിവർത്തനത്തിൻ്റെ സ്വഭാവ ബഹുപദം അടിസ്ഥാനത്തിൻ്റെ തിരഞ്ഞെടുപ്പിനെ ആശ്രയിക്കുന്നില്ല. തെളിവ്. (കാണുക (9.4)), പക്ഷേ അതിനാൽ, . അതിനാൽ, അടിസ്ഥാനം തിരഞ്ഞെടുക്കുന്നതിനെ ആശ്രയിക്കുന്നില്ല. ഇതിനർത്ഥം | A-λE| ഒരു പുതിയ അടിസ്ഥാനത്തിലേക്ക് മാറുമ്പോൾ മാറില്ല.

2) മാട്രിക്സ് ആണെങ്കിൽ എരേഖീയ പരിവർത്തനമാണ് സമമിതി(ആ. ഒപ്പം ij =a ji), അപ്പോൾ സ്വഭാവസമവാക്യത്തിൻ്റെ (9.6) എല്ലാ വേരുകളും യഥാർത്ഥ സംഖ്യകളാണ്.

ഈജൻ മൂല്യങ്ങളുടെയും ഈജൻ വെക്റ്ററുകളുടെയും ഗുണങ്ങൾ:

1) നിങ്ങൾ ഈജൻ വെക്ടറുകളിൽ നിന്ന് ഒരു അടിസ്ഥാനം തിരഞ്ഞെടുക്കുകയാണെങ്കിൽ x 1, x 2, x 3 , ഈജൻവാല്യൂസുമായി പൊരുത്തപ്പെടുന്നു λ 1, λ 2, λ 3മെട്രിക്സ് എ, ഈ അടിസ്ഥാനത്തിൽ രേഖീയ പരിവർത്തനം A ന് ഡയഗണൽ രൂപത്തിൻ്റെ ഒരു മാട്രിക്സ് ഉണ്ട്:

(9.7) ഈ വസ്തുവിൻ്റെ തെളിവ് ഈജൻ വെക്റ്ററുകളുടെ നിർവചനത്തിൽ നിന്ന് പിന്തുടരുന്നു.

2) പരിവർത്തനത്തിൻ്റെ മൂല്യങ്ങൾ ആണെങ്കിൽ എവ്യത്യസ്തമാണ്, അപ്പോൾ അവയുടെ അനുബന്ധ ഈജൻ വെക്‌ടറുകൾ രേഖീയമായി സ്വതന്ത്രമാണ്.

3) മാട്രിക്സിൻ്റെ സ്വഭാവ ബഹുപദമാണെങ്കിൽ എമൂന്ന് ഉണ്ട് വിവിധ വേരുകൾ, പിന്നെ ചില അടിസ്ഥാനത്തിൽ മാട്രിക്സ് എഒരു ഡയഗണൽ രൂപമുണ്ട്.

നമുക്ക് മാട്രിക്സിൻ്റെ ഈജൻ മൂല്യങ്ങളും ഈജൻ വെക്റ്ററുകളും കണ്ടെത്താം നമുക്ക് രചിക്കാം സ്വഭാവ സമവാക്യം: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

കണ്ടെത്തിയ ഓരോ മൂല്യത്തിനും അനുയോജ്യമായ ഈജൻ വെക്റ്ററുകളുടെ കോർഡിനേറ്റുകൾ നമുക്ക് കണ്ടെത്താം λ. (9.5) എന്നതിൽ നിന്ന്, എങ്കിൽ അത് പിന്തുടരുന്നു എക്സ് (1) ={x 1 ,x 2 ,x 3) - ഈജൻ വെക്റ്റർ അനുബന്ധം λ 1 =-2, പിന്നെ

- ഒരു സഹകരണ സംവിധാനവും എന്നാൽ അനിശ്ചിതത്വവും. അതിൻ്റെ പരിഹാരം ഫോമിൽ എഴുതാം എക്സ് (1) ={എ,0,-എ), ഇവിടെ a എന്നത് ഏതെങ്കിലും സംഖ്യയാണ്. പ്രത്യേകിച്ചും, നമുക്ക് അത് ആവശ്യമുണ്ടെങ്കിൽ | x (1) |=1, എക്സ് (1) =

സിസ്റ്റത്തിലേക്ക് മാറ്റിസ്ഥാപിക്കുന്നു (9.5) λ 2 =3, രണ്ടാമത്തെ ഈജൻ വെക്‌ടറിൻ്റെ കോർഡിനേറ്റുകൾ നിർണയിക്കുന്നതിനുള്ള ഒരു സംവിധാനം നമുക്ക് ലഭിക്കും - x (2) ={y 1,y 2,y 3}:

, എവിടെ എക്സ് (2) ={b,-b,b) അല്ലെങ്കിൽ, നൽകിയിരിക്കുന്നു | x (2) |=1, x (2) =

വേണ്ടി λ 3 = 6 ഈജൻ വെക്റ്റർ കണ്ടെത്തുക x (3) ={z 1, z 2, z 3}:

, x (3) ={സി,2c,c) അല്ലെങ്കിൽ സാധാരണ പതിപ്പിൽ

x (3) = എന്നത് ശ്രദ്ധിക്കാവുന്നതാണ് എക്സ് (1) എക്സ് (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = ബിസി- 2bc + bc= 0. അങ്ങനെ, ഈ മാട്രിക്സിൻ്റെ ഈജൻ വെക്‌ടറുകൾ ജോടിയായി ഓർത്തോഗണൽ ആണ്.

പ്രഭാഷണം 10.

ചതുരാകൃതിയിലുള്ള രൂപങ്ങളും സമമിതി മെട്രിക്സുകളുമായുള്ള അവയുടെ ബന്ധവും. ഒരു സമമിതി മാട്രിക്സിൻ്റെ ഈജൻ വെക്റ്ററുകളുടെയും ഈജൻ മൂല്യങ്ങളുടെയും ഗുണങ്ങൾ. ഒരു ക്വാഡ്രാറ്റിക് രൂപത്തെ കാനോനിക്കൽ രൂപത്തിലേക്ക് ചുരുക്കുന്നു.

നിർവ്വചനം 10.1.ചതുരാകൃതിയിലുള്ള രൂപംയഥാർത്ഥ വേരിയബിളുകൾ x 1, x 2,…, x nഈ വേരിയബിളുകളിൽ രണ്ടാം ഡിഗ്രിയുടെ പോളിനോമിയൽ എന്ന് വിളിക്കുന്നു, അതിൽ ഒരു സ്വതന്ത്ര പദവും ഒന്നാം ഡിഗ്രിയുടെ നിബന്ധനകളും അടങ്ങിയിട്ടില്ല.

ചതുരാകൃതിയിലുള്ള രൂപങ്ങളുടെ ഉദാഹരണങ്ങൾ:

(എൻ = 2),

(എൻ = 3). (10.1)

കഴിഞ്ഞ പ്രഭാഷണത്തിൽ നൽകിയ ഒരു സമമിതി മാട്രിക്സിൻ്റെ നിർവചനം നമുക്ക് ഓർക്കാം:

നിർവ്വചനം 10.2.സ്ക്വയർ മാട്രിക്സ് എന്ന് വിളിക്കുന്നു സമമിതി, എങ്കിൽ, അതായത്, പ്രധാന ഡയഗണലിനെക്കുറിച്ച് സമമിതിയുള്ള മാട്രിക്സ് ഘടകങ്ങൾ തുല്യമാണെങ്കിൽ.

ഒരു സമമിതി മാട്രിക്സിൻ്റെ ഈജൻ മൂല്യങ്ങളുടെയും ഈജൻ വെക്റ്ററുകളുടെയും ഗുണങ്ങൾ:

1) ഒരു സമമിതി മാട്രിക്സിൻ്റെ എല്ലാ ഐജൻമൂല്യങ്ങളും യഥാർത്ഥമാണ്.

തെളിവ് (ഇതിനായി എൻ = 2).

മാട്രിക്സ് അനുവദിക്കുക എഫോം ഉണ്ട്: . നമുക്ക് ഒരു സ്വഭാവ സമവാക്യം ഉണ്ടാക്കാം:

(10.2) നമുക്ക് വിവേചനം കണ്ടെത്താം:

അതിനാൽ, സമവാക്യത്തിന് യഥാർത്ഥ വേരുകൾ മാത്രമേയുള്ളൂ.

2) ഈജൻ വെക്‌ടറുകൾസമമിതി മാട്രിക്സ് ഓർത്തോഗണൽ ആണ്.

തെളിവ് (ഇതിനായി എൻ= 2).

ഈജൻ വെക്‌ടറുകളുടെ കോർഡിനേറ്റുകളും സമവാക്യങ്ങളെ തൃപ്തിപ്പെടുത്തേണ്ടതുമാണ്.

www.siteകണ്ടെത്താൻ നിങ്ങളെ അനുവദിക്കുന്നു. സൈറ്റ് കണക്കുകൂട്ടൽ നടത്തുന്നു. കുറച്ച് നിമിഷങ്ങൾക്കുള്ളിൽ സെർവർ ശരിയായ പരിഹാരം നൽകും. മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംആയിരിക്കും ബീജഗണിത പദപ്രയോഗം, ഡിറ്റർമിനൻ്റ് കണക്കാക്കുന്നതിനുള്ള നിയമം കണ്ടെത്തി മെട്രിക്സ് മെട്രിക്സ്, പ്രധാന ഡയഗണലിനൊപ്പം ഡയഗണൽ മൂലകങ്ങളുടെയും വേരിയബിളിൻ്റെയും മൂല്യങ്ങളിൽ വ്യത്യാസങ്ങൾ ഉണ്ടാകും. കണക്കാക്കുമ്പോൾ ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യം, ഓരോ മൂലകവും മെട്രിക്സ്അനുബന്ധ മറ്റ് മൂലകങ്ങൾക്കൊപ്പം ഗുണിക്കും മെട്രിക്സ്. മോഡിൽ കണ്ടെത്തുക ഓൺലൈൻചതുരത്തിന് മാത്രമേ സാധ്യമാകൂ മെട്രിക്സ്. പ്രവർത്തനം കണ്ടെത്തുന്നു ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംമൂലകങ്ങളുടെ ഉൽപന്നത്തിൻ്റെ ബീജഗണിത തുക കണക്കാക്കുന്നതിലേക്ക് കുറയ്ക്കുന്നു മെട്രിക്സ്ഡിറ്റർമിനൻ്റ് കണ്ടെത്തുന്നതിൻ്റെ ഫലമായി മെട്രിക്സ്, നിർണ്ണയിക്കാൻ വേണ്ടി മാത്രം ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യം. ഈ പ്രവർത്തനംസിദ്ധാന്തത്തിൽ ഒരു പ്രത്യേക സ്ഥാനം വഹിക്കുന്നു മെട്രിക്സ്, വേരുകൾ ഉപയോഗിച്ച് ഐജൻവാല്യൂകളും വെക്റ്ററുകളും കണ്ടെത്താൻ നിങ്ങളെ അനുവദിക്കുന്നു. കണ്ടെത്താനുള്ള ചുമതല ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംഗുണന ഘടകങ്ങൾ ഉൾക്കൊള്ളുന്നു മെട്രിക്സ്ഒരു നിശ്ചിത നിയമം അനുസരിച്ച് ഈ ഉൽപ്പന്നങ്ങൾ സംഗ്രഹിച്ചുകൊണ്ട് പിന്തുടരുന്നു. www.siteകണ്ടെത്തുന്നു മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംമോഡിൽ നൽകിയിരിക്കുന്ന അളവ് ഓൺലൈൻ. കണക്കുകൂട്ടല് ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംഅതിൻ്റെ അളവ് കണക്കിലെടുക്കുമ്പോൾ, ഇത് സംഖ്യാപരമായ അല്ലെങ്കിൽ പ്രതീകാത്മക ഗുണകങ്ങളുള്ള ഒരു ബഹുപദം കണ്ടെത്തുന്നു, ഡിറ്റർമിനൻ്റ് കണക്കാക്കുന്നതിനുള്ള നിയമമനുസരിച്ച് ഇത് കണ്ടെത്തുന്നു. മെട്രിക്സ്- അനുബന്ധ മൂലകങ്ങളുടെ ഉൽപ്പന്നങ്ങളുടെ ആകെത്തുക മെട്രിക്സ്, നിർണ്ണയിക്കാൻ വേണ്ടി മാത്രം ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യം. ഒരു ക്വാഡ്രാറ്റിക് വേരിയബിളുമായി ബന്ധപ്പെട്ട് ഒരു ബഹുപദം കണ്ടെത്തുന്നു മെട്രിക്സ്, ഒരു നിർവചനം പോലെ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യം, സിദ്ധാന്തത്തിൽ സാധാരണ മെട്രിക്സ്. ഒരു ബഹുപദത്തിൻ്റെ വേരുകളുടെ അർത്ഥം ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംഈജൻ വെക്റ്ററുകളും ഈജൻ മൂല്യങ്ങളും നിർണ്ണയിക്കാൻ ഉപയോഗിക്കുന്നു മെട്രിക്സ്. മാത്രമല്ല, ഡിറ്റർമിനൻ്റ് ആണെങ്കിൽ മെട്രിക്സ്അപ്പോൾ പൂജ്യത്തിന് തുല്യമായിരിക്കും മാട്രിക്സിൻ്റെ സ്വഭാവ സമവാക്യംവിപരീതത്തിൽ നിന്ന് വ്യത്യസ്തമായി ഇപ്പോഴും നിലനിൽക്കും മെട്രിക്സ്. കണക്കാക്കാൻ വേണ്ടി മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംഅല്ലെങ്കിൽ ഒരേസമയം നിരവധി കണ്ടെത്തുക മെട്രിക്സ് സ്വഭാവ സമവാക്യങ്ങൾ, നിങ്ങൾ ധാരാളം സമയവും പരിശ്രമവും ചെലവഴിക്കേണ്ടതുണ്ട്, അതേസമയം ഞങ്ങളുടെ സെർവർ നിമിഷങ്ങൾക്കുള്ളിൽ കണ്ടെത്തും ഓൺലൈൻ മാട്രിക്‌സിനുള്ള സ്വഭാവ സമവാക്യം. ഈ സാഹചര്യത്തിൽ, കണ്ടെത്താനുള്ള ഉത്തരം ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംകണ്ടെത്തുമ്പോൾ അക്കങ്ങൾ ഉണ്ടെങ്കിലും, ശരിയായതും മതിയായ കൃത്യതയോടെയും ആയിരിക്കും ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംയുക്തിരഹിതമായിരിക്കും. സൈറ്റിൽ www.siteഘടകങ്ങളിൽ പ്രതീക എൻട്രികൾ അനുവദനീയമാണ് മെട്രിക്സ്, അതാണ് ഓൺലൈൻ മാട്രിക്‌സിനുള്ള സ്വഭാവ സമവാക്യംകണക്കാക്കുമ്പോൾ പൊതുവായ പ്രതീകാത്മക രൂപത്തിൽ പ്രതിനിധീകരിക്കാം ഓൺലൈൻ മാട്രിക്സിൻ്റെ സ്വഭാവ സമവാക്യം. കണ്ടെത്തുന്നതിനുള്ള പ്രശ്നം പരിഹരിക്കുമ്പോൾ ലഭിച്ച ഉത്തരം പരിശോധിക്കുന്നത് ഉപയോഗപ്രദമാണ് ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യംസൈറ്റ് ഉപയോഗിച്ച് www.site. ഒരു പോളിനോമിയൽ കണക്കുകൂട്ടുന്ന പ്രവർത്തനം നടത്തുമ്പോൾ - മാട്രിക്സിൻ്റെ സ്വഭാവ സമവാക്യം, ഈ പ്രശ്നം പരിഹരിക്കുമ്പോൾ നിങ്ങൾ ശ്രദ്ധയും അതീവ ശ്രദ്ധയും പുലർത്തേണ്ടതുണ്ട്. അതാകട്ടെ, വിഷയത്തെക്കുറിച്ചുള്ള നിങ്ങളുടെ തീരുമാനം പരിശോധിക്കാൻ ഞങ്ങളുടെ സൈറ്റ് നിങ്ങളെ സഹായിക്കും ഓൺലൈൻ മാട്രിക്സിൻ്റെ സ്വഭാവ സമവാക്യം. പരിഹരിച്ച പ്രശ്നങ്ങളുടെ നീണ്ട പരിശോധനകൾക്ക് നിങ്ങൾക്ക് സമയമില്ലെങ്കിൽ, പിന്നെ www.siteകണ്ടെത്തുമ്പോഴും കണക്കാക്കുമ്പോഴും പരിശോധിക്കുന്നതിനുള്ള ഒരു സൗകര്യപ്രദമായ ഉപകരണമായിരിക്കും ഇത് ഓൺലൈൻ മാട്രിക്സിനുള്ള സ്വഭാവ സമവാക്യം.

ഒരു ചതുര മാട്രിക്സിൻ്റെ ഒരു ഐജൻ വെക്റ്റർ, തന്നിരിക്കുന്ന മാട്രിക്സ് കൊണ്ട് ഗുണിക്കുമ്പോൾ, ഒരു കോളിനിയർ വെക്റ്റർ ഉണ്ടാകുന്നു. ലളിതമായ വാക്കുകളിൽ, ഒരു മാട്രിക്സിനെ ഒരു ഈജൻ വെക്റ്റർ കൊണ്ട് ഗുണിക്കുമ്പോൾ, രണ്ടാമത്തേത് അതേപടി നിലനിൽക്കും, എന്നാൽ ഒരു നിശ്ചിത സംഖ്യ കൊണ്ട് ഗുണിച്ചാൽ.

നിർവ്വചനം

ഒരു eigenvector പൂജ്യമല്ലാത്ത വെക്റ്റർ V ആണ്, ഇത് ഒരു ചതുര മാട്രിക്സ് M കൊണ്ട് ഗുണിക്കുമ്പോൾ, ചില സംഖ്യകൾ λ കൊണ്ട് വർദ്ധിക്കുന്നു. ബീജഗണിത നൊട്ടേഷനിൽ ഇത് ഇതുപോലെ കാണപ്പെടുന്നു:

M × V = λ × V,

ഇവിടെ λ എന്നത് M എന്ന മാട്രിക്സിൻ്റെ ഈജൻവാല്യൂ ആണ്.

നമുക്ക് പരിഗണിക്കാം സംഖ്യാ ഉദാഹരണം. റെക്കോർഡിംഗ് എളുപ്പത്തിനായി, മാട്രിക്സിലെ സംഖ്യകളെ ഒരു അർദ്ധവിരാമം കൊണ്ട് വേർതിരിക്കും. നമുക്ക് ഒരു മാട്രിക്സ് എടുക്കാം:

• M = 0; 4;
• 6; 10.

നമുക്ക് അതിനെ ഒരു കോളം വെക്റ്റർ കൊണ്ട് ഗുണിക്കാം:

• വി = -2;

ഒരു മാട്രിക്സിനെ ഒരു കോളം വെക്റ്റർ കൊണ്ട് ഗുണിക്കുമ്പോൾ, നമുക്ക് ഒരു കോളം വെക്റ്ററും ലഭിക്കും. കണിശമായ ഗണിത ഭാഷഒരു കോളം വെക്റ്റർ കൊണ്ട് 2 × 2 മാട്രിക്സ് ഗുണിക്കുന്നതിനുള്ള ഫോർമുല ഇതുപോലെ കാണപ്പെടും:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 എന്നാൽ ആദ്യ വരിയിലും ആദ്യ നിരയിലും സ്ഥിതി ചെയ്യുന്ന മാട്രിക്സ് M ൻ്റെ മൂലകം എന്നാണ് അർത്ഥമാക്കുന്നത്, M22 എന്നാൽ രണ്ടാമത്തെ വരിയിലും രണ്ടാമത്തെ നിരയിലും സ്ഥിതി ചെയ്യുന്ന ഘടകം എന്നാണ് അർത്ഥമാക്കുന്നത്. ഞങ്ങളുടെ മാട്രിക്സിന്, ഈ ഘടകങ്ങൾ M11 = 0, M12 = 4, M21 = 6, M22 10 ന് തുല്യമാണ്. ഒരു കോളം വെക്റ്ററിന്, ഈ മൂല്യങ്ങൾ V11 = –2, V21 = 1. ഈ ഫോർമുല അനുസരിച്ച്, ഒരു വെക്റ്റർ മുഖേന ഒരു ചതുര മാട്രിക്സിൻ്റെ ഉൽപ്പന്നത്തിൻ്റെ ഇനിപ്പറയുന്ന ഫലം നമുക്ക് ലഭിക്കും:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

സൗകര്യത്തിനായി, നിര വെക്റ്റർ ഒരു വരിയിൽ എഴുതാം. അതിനാൽ, ഞങ്ങൾ ചതുര മാട്രിക്സിനെ വെക്റ്റർ (-2; 1) കൊണ്ട് ഗുണിച്ചു, അതിൻ്റെ ഫലമായി വെക്റ്റർ (4; -2). വ്യക്തമായും, ഇത് λ = -2 കൊണ്ട് ഗുണിച്ച അതേ വെക്റ്റർ ആണ്. ലാംഡ ഇൻ ഈ സാഹചര്യത്തിൽമാട്രിക്സിൻ്റെ ഈജൻ മൂല്യത്തെ സൂചിപ്പിക്കുന്നു.

ഒരു മാട്രിക്സിൻ്റെ ഈജൻ വെക്റ്റർ ഒരു കോളിനിയർ വെക്റ്റർ ആണ്, അതായത്, ഒരു മാട്രിക്സ് കൊണ്ട് ഗുണിച്ചാൽ ബഹിരാകാശത്ത് അതിൻ്റെ സ്ഥാനം മാറാത്ത ഒരു വസ്തു. വെക്റ്റർ ബീജഗണിതത്തിലെ കോളിനാരിറ്റി എന്ന ആശയം ജ്യാമിതിയിലെ സമാന്തരത എന്ന പദത്തിന് സമാനമാണ്. ഒരു ജ്യാമിതീയ വ്യാഖ്യാനത്തിൽ, കോളിനിയർ വെക്റ്ററുകൾ വ്യത്യസ്ത ദൈർഘ്യമുള്ള സമാന്തര വിഭാഗങ്ങളാണ്. യൂക്ലിഡിൻ്റെ കാലം മുതൽ, ഒരു വരിയ്ക്ക് സമാന്തരമായി അനന്തമായ വരികൾ ഉണ്ടെന്ന് നമുക്കറിയാം, അതിനാൽ ഓരോ മാട്രിക്സിനും അനന്തമായ ഈജൻ വെക്റ്ററുകൾ ഉണ്ടെന്ന് അനുമാനിക്കുന്നത് യുക്തിസഹമാണ്.

മുമ്പത്തെ ഉദാഹരണത്തിൽ നിന്ന്, ഈജൻ വെക്‌ടറുകൾ (-8; 4), (16; -8), (32, -16) എന്നിവയാകാമെന്ന് വ്യക്തമാണ്. ഇവയെല്ലാം ഈജൻവാല്യൂ λ = -2 ന് അനുയോജ്യമായ കോളിനിയർ വെക്റ്ററുകളാണ്. ഈ വെക്‌ടറുകൾ ഉപയോഗിച്ച് ഒറിജിനൽ മാട്രിക്‌സ് ഗുണിക്കുമ്പോൾ, ഒറിജിനലിൽ നിന്ന് 2 മടങ്ങ് വ്യത്യാസമുള്ള ഒരു വെക്‌ടറിൽ നമ്മൾ അവസാനിക്കും. അതുകൊണ്ടാണ്, ഒരു ഈജൻ വെക്റ്റർ കണ്ടെത്തുന്നതിനുള്ള പ്രശ്നങ്ങൾ പരിഹരിക്കുമ്പോൾ, രേഖീയമായി സ്വതന്ത്രമായ വെക്റ്റർ വസ്തുക്കൾ മാത്രം കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. മിക്കപ്പോഴും, ഒരു n × n മാട്രിക്‌സിന്, ഒരു n എണ്ണം ഈജൻ വെക്‌ടറുകൾ ഉണ്ട്. ഞങ്ങളുടെ കാൽക്കുലേറ്റർ രൂപകൽപ്പന ചെയ്‌തിരിക്കുന്നത് സെക്കൻഡ്-ഓർഡർ സ്‌ക്വയർ മെട്രിക്‌സുകളുടെ വിശകലനത്തിനായാണ്, അതിനാൽ മിക്കവാറും എല്ലായ്‌പ്പോഴും ഫലം രണ്ട് ഈജൻ വെക്‌ടറുകൾ കണ്ടെത്തും, അവ പൊരുത്തപ്പെടുന്ന സന്ദർഭങ്ങൾ ഒഴികെ.

മുകളിലുള്ള ഉദാഹരണത്തിൽ, ഒറിജിനൽ മാട്രിക്സിൻ്റെ ഐജൻവെക്റ്റർ ഞങ്ങൾ മുൻകൂട്ടി അറിയുകയും ലാംഡ നമ്പർ വ്യക്തമായി നിർണ്ണയിക്കുകയും ചെയ്തു. എന്നിരുന്നാലും, പ്രായോഗികമായി, എല്ലാം നേരെ വിപരീതമായി സംഭവിക്കുന്നു: ഈജൻ മൂല്യങ്ങൾ ആദ്യം കണ്ടെത്തുന്നു, അതിനുശേഷം മാത്രമേ ഈജൻ വെക്റ്ററുകൾ കണ്ടെത്തൂ.

പരിഹാര അൽഗോരിതം

ഒറിജിനൽ മാട്രിക്സ് എം വീണ്ടും നോക്കാം, അതിൻ്റെ രണ്ട് ഐജൻ വെക്റ്ററുകളും കണ്ടെത്താൻ ശ്രമിക്കാം. അതിനാൽ, മാട്രിക്സ് ഇതുപോലെ കാണപ്പെടുന്നു:

• M = 0; 4;
• 6; 10.

ആദ്യം നമ്മൾ eigenvalue λ നിർണ്ണയിക്കേണ്ടതുണ്ട്, ഇതിന് ഇനിപ്പറയുന്ന മാട്രിക്സിൻ്റെ ഡിറ്റർമിനൻ്റ് കണക്കാക്കേണ്ടതുണ്ട്:

• (0 - λ); 4;
• 6; (10 - λ).

പ്രധാന ഡയഗണലിലെ മൂലകങ്ങളിൽ നിന്ന് അജ്ഞാതമായ λ കുറച്ചാണ് ഈ മാട്രിക്സ് ലഭിക്കുന്നത്. സ്റ്റാൻഡേർഡ് ഫോർമുല ഉപയോഗിച്ചാണ് ഡിറ്റർമിനൻ്റ് നിർണ്ണയിക്കുന്നത്:

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

ഞങ്ങളുടെ വെക്റ്റർ പൂജ്യമല്ലാത്തതായിരിക്കണം എന്നതിനാൽ, തത്ഫലമായുണ്ടാകുന്ന സമവാക്യം രേഖീയമായി ആശ്രിതമായി ഞങ്ങൾ അംഗീകരിക്കുകയും ഞങ്ങളുടെ ഡിറ്റർമിനൻ്റ് detA പൂജ്യത്തിന് തുല്യമാക്കുകയും ചെയ്യുന്നു.

(0 - λ) × (10 - λ) - 24 = 0

നമുക്ക് ബ്രാക്കറ്റുകൾ തുറന്ന് മാട്രിക്സിൻ്റെ സ്വഭാവ സമവാക്യം നേടാം:

λ 2 - 10λ - 24 = 0

ഇത് സ്റ്റാൻഡേർഡ് ആണ് ക്വാഡ്രാറ്റിക് സമവാക്യം, അത് വിവേചനത്തിലൂടെ പരിഹരിക്കേണ്ടതുണ്ട്.

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

വിവേചനത്തിൻ്റെ റൂട്ട് sqrt(D) = 14 ആണ്, അതിനാൽ λ1 = -2, λ2 = 12. ഇപ്പോൾ ഓരോ ലാംഡ മൂല്യത്തിനും നമ്മൾ eigenvector കണ്ടെത്തേണ്ടതുണ്ട്. λ = -2 എന്നതിനായുള്ള സിസ്റ്റം ഗുണകങ്ങൾ നമുക്ക് പ്രകടിപ്പിക്കാം.

• M - λ × E = 2; 4;
• 6; 12.

ഈ ഫോർമുലയിൽ, E എന്നത് ഐഡൻ്റിറ്റി മാട്രിക്സ് ആണ്. തത്ഫലമായുണ്ടാകുന്ന മാട്രിക്സിനെ അടിസ്ഥാനമാക്കി, ഞങ്ങൾ ലീനിയർ സമവാക്യങ്ങളുടെ ഒരു സിസ്റ്റം സൃഷ്ടിക്കുന്നു:

2x + 4y = 6x + 12y,

ഇവിടെ x ഉം y ഉം ഈജൻ വെക്റ്റർ മൂലകങ്ങളാണ്.

ഇടതുവശത്തുള്ള എല്ലാ X-കളും വലതുവശത്തുള്ള എല്ലാ Y-കളും ശേഖരിക്കാം. വ്യക്തമായും - 4x = 8y. പദപ്രയോഗം - 4 കൊണ്ട് ഹരിച്ചാൽ x = –2y നേടുക. ഇപ്പോൾ നമുക്ക് മാട്രിക്സിൻ്റെ ആദ്യ ഈജൻ വെക്റ്റർ നിർണ്ണയിക്കാൻ കഴിയും, അജ്ഞാതരുടെ ഏതെങ്കിലും മൂല്യങ്ങൾ എടുക്കുക (രേഖീയമായി ആശ്രയിക്കുന്ന ഈജൻ വെക്റ്ററുകളുടെ അനന്തത ഓർക്കുക). നമുക്ക് y = 1 എടുക്കാം, തുടർന്ന് x = –2. അതിനാൽ, ആദ്യത്തെ ഈജൻ വെക്റ്റർ V1 = (–2; 1) പോലെ കാണപ്പെടുന്നു. ലേഖനത്തിൻ്റെ തുടക്കത്തിലേക്ക് മടങ്ങുക. ഈ വെക്‌റ്റർ ഒബ്‌ജക്‌റ്റിനെയാണ് ഈജൻ വെക്‌ടർ എന്ന ആശയം തെളിയിക്കാൻ ഞങ്ങൾ മാട്രിക്‌സിനെ ഗുണിച്ചത്.

ഇനി നമുക്ക് λ = 12 ൻ്റെ ഈജൻ വെക്റ്റർ കണ്ടെത്താം.

• M - λ × E = -12; 4
• 6; -2.

നമുക്ക് രേഖീയ സമവാക്യങ്ങളുടെ അതേ സംവിധാനം ഉണ്ടാക്കാം;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x = y.

ഇപ്പോൾ നമ്മൾ x = 1 എടുക്കുന്നു, അതിനാൽ y = 3. അങ്ങനെ, രണ്ടാമത്തെ ഈജൻ വെക്റ്റർ V2 = (1; 3) പോലെ കാണപ്പെടുന്നു. തന്നിരിക്കുന്ന വെക്‌ടറുകൊണ്ട് ഒറിജിനൽ മാട്രിക്‌സിനെ ഗുണിക്കുമ്പോൾ, ഫലം എപ്പോഴും ഒരേ വെക്‌ടറിനെ 12 കൊണ്ട് ഗുണിച്ചാൽ ലഭിക്കും. ഇവിടെയാണ് പരിഹാര അൽഗോരിതം അവസാനിക്കുന്നത്. ഒരു മാട്രിക്സിൻ്റെ ഐജൻ വെക്റ്റർ എങ്ങനെ സ്വമേധയാ നിർണ്ണയിക്കാമെന്ന് ഇപ്പോൾ നിങ്ങൾക്കറിയാം.

• ഡിറ്റർമിനൻ്റ്;
• ട്രെയ്സ്, അതായത്, പ്രധാന ഡയഗണലിലെ മൂലകങ്ങളുടെ ആകെത്തുക;
• റാങ്ക്, അതായത്, രേഖീയ സ്വതന്ത്ര വരികൾ/നിരകളുടെ പരമാവധി എണ്ണം.

മേൽപ്പറഞ്ഞ അൽഗോരിതം അനുസരിച്ച് പ്രോഗ്രാം പ്രവർത്തിക്കുന്നു, പരിഹാര പ്രക്രിയ കഴിയുന്നത്ര ചെറുതാക്കുന്നു. പ്രോഗ്രാമിൽ ലാംഡയെ "സി" എന്ന അക്ഷരത്താൽ നിയുക്തമാക്കിയിരിക്കുന്നത് ചൂണ്ടിക്കാണിക്കേണ്ടത് പ്രധാനമാണ്. ഒരു സംഖ്യാ ഉദാഹരണം നോക്കാം.

പ്രോഗ്രാം എങ്ങനെ പ്രവർത്തിക്കുന്നു എന്നതിൻ്റെ ഉദാഹരണം

ഇനിപ്പറയുന്ന മാട്രിക്സിനായി ഈജൻ വെക്റ്ററുകൾ നിർണ്ണയിക്കാൻ ശ്രമിക്കാം:

• M = 5; 13;
• 4; 14.

നമുക്ക് ഈ മൂല്യങ്ങൾ കാൽക്കുലേറ്ററിൻ്റെ സെല്ലുകളിലേക്ക് നൽകുകയും ഇനിപ്പറയുന്ന രൂപത്തിൽ ഉത്തരം നേടുകയും ചെയ്യാം:

• മാട്രിക്സ് റാങ്ക്: 2;
• മാട്രിക്സ് ഡിറ്റർമിനൻ്റ്: 18;
• മാട്രിക്സ് ട്രെയ്സ്: 19;
• ഈജൻ വെക്‌ടറിൻ്റെ കണക്കുകൂട്ടൽ: c 2 - 19.00c + 18.00 (സ്വഭാവ സമവാക്യം);
• Eigenvector കണക്കുകൂട്ടൽ: 18 (ആദ്യത്തെ ലാംഡ മൂല്യം);
• Eigenvector കണക്കുകൂട്ടൽ: 1 (രണ്ടാമത്തെ ലാംഡ മൂല്യം);
• വെക്റ്റർ 1 നുള്ള സമവാക്യങ്ങളുടെ സിസ്റ്റം: -13x1 + 13y1 = 4x1 - 4y1;
• വെക്റ്റർ 2 നുള്ള സമവാക്യങ്ങളുടെ സിസ്റ്റം: 4x1 + 13y1 = 4x1 + 13y1;
• ഈജൻ വെക്റ്റർ 1: (1; 1);
• ഈജൻ വെക്റ്റർ 2: (-3.25; 1).

അങ്ങനെ, നമുക്ക് രണ്ട് രേഖീയ സ്വതന്ത്ര ഈജൻ വെക്ടറുകൾ ലഭിച്ചു.

ഉപസംഹാരം

ലീനിയർ ബീജഗണിതവും അനലിറ്റിക്കൽ ജ്യാമിതിയും ഏതൊരു പുതുമുഖ എഞ്ചിനീയറിംഗ് മേജർക്കും അടിസ്ഥാന വിഷയങ്ങളാണ്. വലിയ അളവിലുള്ള വെക്റ്ററുകളും മെട്രിക്സുകളും ഭയാനകമാണ്, മാത്രമല്ല അത്തരം ബുദ്ധിമുട്ടുള്ള കണക്കുകൂട്ടലുകളിൽ തെറ്റുകൾ വരുത്തുന്നത് എളുപ്പമാണ്. ഞങ്ങളുടെ പ്രോഗ്രാം വിദ്യാർത്ഥികളെ അവരുടെ കണക്കുകൂട്ടലുകൾ പരിശോധിക്കാൻ അനുവദിക്കും അല്ലെങ്കിൽ ഒരു ഐജൻവെക്റ്റർ കണ്ടെത്തുന്നതിനുള്ള പ്രശ്നം യാന്ത്രികമായി പരിഹരിക്കും. ഞങ്ങളുടെ കാറ്റലോഗിൽ മറ്റ് ലീനിയർ ആൾജിബ്ര കാൽക്കുലേറ്ററുകൾ ഉണ്ട്, അവ നിങ്ങളുടെ പഠനത്തിലോ ജോലിയിലോ ഉപയോഗിക്കുക.