Олох тригонометрийн функцийн дериватив ашиглах хэрэгтэй деривативын хүснэгт, тухайлбал дериватив 6-13.
Та олох үед анхны деривативууд тригонометрийн функцууд Нийтлэг алдаанаас зайлсхийхийн тулд та дараахь зүйлийг анхаарч үзэх хэрэгтэй.
- функцийн илэрхийлэлд нэг нэр томъёо нь ихэвчлэн байдаг синус, косинус эсвэл бусад тригонометрийн функцфункцийн аргументаас биш, харин тооноос (тогтмол), тиймээс энэ нэр томъёоны дериватив нь тэгтэй тэнцүү байна;
- бараг үргэлж та ялгах үр дүнд олж авсан илэрхийллийг хялбарчлах хэрэгтэй бөгөөд үүний тулд та бутархайтай үйлдлийн талаархи мэдлэгээ итгэлтэйгээр ашиглах хэрэгтэй;
- Илэрхийллийг хялбарчлахын тулд та бараг үргэлж тригонометрийн таних тэмдэг, жишээлбэл, томъёог мэддэг байх хэрэгтэй давхар өнцөгмөн нэгдмэл байдлын томьёо нь синус ба косинусын квадратуудын нийлбэр юм.
Жишээ 1.Функцийн деривативыг ол
Шийдэл. -тай хэлье косинусын деривативБүх зүйл тодорхой, деривативыг судалж эхэлсэн олон хүн хэлэх болно. Яах вэ синусын деривативарван хоёрыг пи-д хуваах уу? Хариулт: үүнийг тэгтэй тэнцүү гэж үзнэ үү! Энд синус (эцсийн эцэст функц!) нь занга юм, учир нь аргумент нь X хувьсагч эсвэл бусад хувьсагч биш, харин зүгээр л тоо юм. Өөрөөр хэлбэл, энэ тооны синус нь бас тоо юм. Мөн деривативын хүснэгтээс бидний мэдэж байгаагаар тооны дериватив (тогтмол) нь тэгтэй тэнцүү байна. Тиймээс бид зөвхөн X-ийн хасах синусыг үлдээж, түүний деривативыг олохын тулд тэмдгийн талаар мартаж болохгүй.
![]() .
.
Жишээ 2.Функцийн деривативыг ол
![]() .
.
Шийдэл. Хоёрдахь нэр томьёо нь өмнөх жишээний эхний гишүүнтэй ижил тохиолдол юм. Энэ нь тоо бөгөөд уг тооны дериватив нь тэг юм. Бид хоёр дахь гишүүний деривативыг хуваалтын дериватив гэж олно.
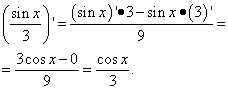
Жишээ 3.Функцийн деривативыг ол
Шийдэл. Энэ бол өөр нэг асуудал юм: энд эхний гишүүнд арксинус эсвэл өөр тригонометик функц байхгүй, харин х байдаг бөгөөд энэ нь х-ийн функц гэсэн үг юм. Тиймээс бид үүнийг функцүүдийн нийлбэр дэх нэр томъёо гэж ялгадаг.

Энд бутархайтай ажиллах ур чадвар, тухайлбал бутархайн гурван давхар бүтцийг арилгах шаардлагатай байв.
Жишээ 4.Функцийн деривативыг ол
![]() .
.
Шийдэл. Энд "phi" үсэг нь өмнөх тохиолдлуудад "x" -тэй ижил үүрэг гүйцэтгэдэг (мөн бусад ихэнх тохиолдолд, гэхдээ бүгд биш) - бие даасан хувьсагч. Тиймээс бид функцүүдийн үржвэрийн деривативыг хайхдаа “phi” язгуурын деривативыг тэгтэй тэнцүү гэж зарлах гэж яарахгүй. Тэгэхээр:
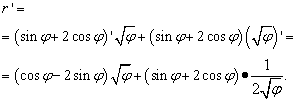
Гэхдээ шийдэл үүгээр дуусахгүй. Ижил төстэй нэр томъёог хоёр хаалтанд цуглуулсан тул бид илэрхийллийг хувиргах (хялбаршуулах) шаардлагатай хэвээр байна. Тиймээс бид хаалтуудыг тэдгээрийн ард байгаа хүчин зүйлүүдээр үржүүлж, дараа нь нэр томъёог нийтлэг хуваагч руу авчирч, бусад энгийн хувиргалтыг хийдэг.

Жишээ 5.Функцийн деривативыг ол
Шийдэл. Энэ жишээнд бид ийм тригонометрийн функц байдаг - секант - косинусаар дамжуулан түүний томъёог мэдэх шаардлагатай болно. Ялгаж үзье:

Жишээ 6.Функцийн деривативыг ол
![]() .
.
Шийдэл. Энэ жишээнд бид сургуулиасаа давхар өнцгийн томъёог санаж байхыг шаардах болно. Гэхдээ эхлээд ялгаж үзье:

![]() ,
,
(энэ бол давхар өнцгийн томьёо)
Урвуу тригонометрийн функцүүдийн деривативууд ба тэдгээрийн томъёоны гарал үүслийг үзүүлэв. Дээд эрэмбийн деривативуудын илэрхийлэл мөн өгөгдсөн. Томъёоны гарал үүслийн талаар илүү нарийвчилсан тайлбар бүхий хуудасны холбоосууд.
Эхлээд бид арксинусын деривативын томъёог гаргаж авдаг. Болъё
у = arcsin x.
Арксинус нь синусын урвуу функц учраас
.
Энд y нь x-ийн функц юм. x хувьсагчаар ялгах:
.
Бид өргөдөл гаргана:
.
Тиймээс бид олсон:
.
Учир нь . Дараа нь
.
Мөн өмнөх томъёо нь дараах хэлбэртэй байна.
. Эндээс
.
Яг ийм байдлаар та нумын косинусын деривативын томъёог олж авах боломжтой. Гэсэн хэдий ч урвуу тригонометрийн функцуудтай холбоотой томъёог ашиглах нь илүү хялбар байдаг.
.
Дараа нь
.
Илүү нарийвчилсан тайлбарыг "Арксин ба арккосины деривативын гарал үүсэл" хуудсанд оруулсан болно. Тэнд өгч байна деривативыг хоёр аргаар гаргаж авах- урвуу функцийн деривативын томъёоны дагуу дээр хэлэлцсэн.
Арктангенс ба арккотангенсийн деривативын гарал үүсэл
Үүнтэй адилаар бид арктангенс ба арккотангенсийн деривативуудыг олох болно.
Болъё
у = арктан х.
Арктангенс нь тангенсийн урвуу функц юм:
.
x хувьсагчаар ялгах:
.
Бид нарийн төвөгтэй функцийн деривативын томъёог ашигладаг.
.
Тиймээс бид олсон:
.
Нумын котангенсын дериватив:
.
Арксины деривативууд
Болъё
.
Бид арксинусын нэгдүгээр эрэмбийн деривативыг аль хэдийн олсон.
.
Ялгах замаар бид хоёр дахь эрэмбийн деривативыг олно.
;
.
Үүнийг мөн дараах хэлбэрээр бичиж болно.
.
Эндээс бид авдаг дифференциал тэгшитгэл, энэ нь эхний болон хоёрдугаар эрэмбийн арксин деривативуудаар хангагдсан:
.
Энэ тэгшитгэлийг ялгах замаар бид дээд эрэмбийн деривативуудыг олж чадна.
n-р эрэмбийн арксинусын дериватив
n-р эрэмбийн арксинусын дериватив нь дараах хэлбэртэй байна.
,
градусын олон гишүүнт хаана байна . Үүнийг дараах томъёогоор тодорхойлно.
;
.
Энд.
Олон гишүүнт нь дифференциал тэгшитгэлийг хангана:
.
n-р эрэмбийн арккосинын дериватив
Нумын косинусын деривативыг нумын синусын деривативаас тригонометрийн томъёогоор гаргаж авна.
.
Тиймээс эдгээр функцүүдийн деривативууд нь зөвхөн тэмдгээр ялгаатай байдаг.
.
Арктангенсын деривативууд
Let . Бид эхний дарааллын нумын котангенсийн деривативыг олсон.
.
Бутархайг хамгийн энгийн хэлбэрт нь задалъя:
.
Энд төсөөллийн нэгж, .
Бид нэг удаа ялгаж, бутархайг нийтлэг хуваагч руу авчирдаг.
.
Орлуулснаар бид дараахь зүйлийг авна.
.
n-р эрэмбийн артангенсийн дериватив
Тиймээс n-р эрэмбийн артангенсийн деривативыг хэд хэдэн аргаар илэрхийлж болно.
;
.
Нумын котангенсын деривативууд
Одоо байг. Урвуу тригонометрийн функцуудыг холбох томъёог ашиглацгаая.
.
Дараа нь нумын шүргэгчийн n-р эрэмбийн дериватив нь нумын шүргэгчийн деривативаас зөвхөн тэмдгээр ялгаатай байна.
.
Орлуулснаар бид дараахь зүйлийг олно.
.
Лавлагаа:
Н.М. Гүнтер, Р.О. Кузьмин, Дээд математикийн асуудлын цуглуулга, "Лан", 2003 он.
Хүснэгтийн хамгийн эхний томьёог гаргаж авахдаа бид тухайн цэгийн дериватив функцийн тодорхойлолтоос эхэлнэ. Хаашаа авцгаая x- дурын бодит тоо, өөрөөр хэлбэл, x– функцийн тодорхойлолтын мужаас дурын тоо. Функцийн өсөлтийн аргументийн өсөлтийн харьцааны хязгаарыг дараах байдлаар бичье. ![]()
Хязгаарын тэмдгийн дор илэрхийлэл гарч ирснийг тэмдэглэх нь зүйтэй бөгөөд энэ нь тэгийг тэгээр хуваасан тодорхой бус байдал биш, учир нь тоологч нь хязгааргүй жижиг утгыг агуулдаггүй, харин яг тэг байдаг. Өөрөөр хэлбэл, тогтмол функцийн өсөлт үргэлж тэг байна.
Тиймээс, тогтмол функцийн деривативтодорхойлолтын бүх домайн даяар тэгтэй тэнцүү байна.
Хүчин чадлын функцийн дериватив.
Дериватив томъёо эрчим хүчний функцшиг харагдаж байна ![]() , илтгэгч хаана байна х- дурын бодит тоо.
, илтгэгч хаана байна х- дурын бодит тоо.
Эхлээд натурал илтгэгчийн томъёог баталъя, өөрөөр хэлбэл for p = 1, 2, 3, …
Бид деривативын тодорхойлолтыг ашиглах болно. Хүчин чадлын функцийн өсөлтийн аргументийн өсөлтийн харьцааны хязгаарыг бичье. 
Тоолуур дахь илэрхийллийг хялбарчлахын тулд бид Ньютоны бином томъёо руу шилждэг. 
Тиймээс, 
Энэ нь натурал илтгэгчийн чадлын функцийн деривативын томъёог баталж байна.
Экспоненциал функцийн дериватив.
Бид дараах тодорхойлолт дээр үндэслэн дериватив томъёоны гарал үүслийг танилцуулж байна.
Бид тодорхойгүй байдалд ирлээ. Үүнийг өргөжүүлэхийн тулд бид шинэ хувьсагчийг нэвтрүүлж, . Дараа нь . Сүүлийн шилжилтийн үед бид шинэ логарифмын суурь руу шилжих томъёог ашигласан.
Анхны хязгаарыг орлуулъя: 
Хэрэв бид хоёр дахь гайхалтай хязгаарыг эргэн санавал экспоненциал функцийн деривативын томъёонд хүрнэ. 
Логарифм функцийн дериватив.
Бүгдэд зориулсан логарифм функцийн деривативын томъёог баталъя xтодорхойлолтын домэйн болон суурийн бүх хүчинтэй утгуудаас алогарифм Деривативын тодорхойлолтоор бид: 
Таны анзаарсанчлан нотолгооны явцад логарифмын шинж чанарыг ашиглан хувиргалтыг хийсэн. Тэгш байдал  хоёр дахь гайхалтай хязгаарын улмаас үнэн юм.
хоёр дахь гайхалтай хязгаарын улмаас үнэн юм.
Тригонометрийн функцүүдийн деривативууд.
Тригонометрийн функцүүдийн деривативын томъёог гаргахын тулд бид тригонометрийн зарим томьёо, мөн эхний гайхалтай хязгаарыг эргэн санах хэрэгтэй болно.
Синусын функцийн деривативын тодорхойлолтоор бид байна ![]() .
.
Синусын зөрүүний томъёог ашиглая: 
Эхний гайхалтай хязгаарт шилжих хэвээр байна: 
Тиймээс функцийн дериватив гэм хБайна cos x.
Косинусын деривативын томъёог яг ижил аргаар нотолсон. 
Тиймээс функцийн дериватив cos xБайна – нүгэл х.
Бид шүргэгч ба котангенсийн деривативын хүснэгтийн томъёог ялгах батлагдсан дүрмийг (бутархайн дериватив) ашиглан гаргана. 
Гиперболын функцүүдийн деривативууд.
Ялгах дүрэм ба деривативын хүснэгтээс экспоненциал функцийн деривативын томъёо нь гиперболын синус, косинус, тангенс, котангенсийн деривативуудын томъёог гаргаж авах боломжийг олгодог. 
Урвуу функцийн дериватив.
Илтгэлийн явцад төөрөгдөл гаргахгүйн тулд ялгах функцийн аргументыг, өөрөөр хэлбэл функцийн дериватив гэдгийг дэд тэмдэгтээр тэмдэглэе. f(x) By x.
Одоо томъёолъё урвуу функцийн деривативыг олох дүрэм.
Функцуудыг зөвшөөр у = f(x)Тэгээд x = g(y)харилцан урвуу, интервалууд болон тус тусад нь тодорхойлогддог. Хэрэв тухайн цэг дээр функцийн төгсгөлтэй тэгээс бус дериватив байвал f(x), тэгвэл тухайн цэг дээр урвуу функцийн төгсгөлөг дериватив байна g(y), ба ![]() . Өөр нэг бичлэгт
. Өөр нэг бичлэгт ![]() .
.
Энэ дүрмийг хэнд ч өөрчилж болно xинтервалаас , дараа нь бид авна  .
.
Эдгээр томъёоны үнэн зөвийг шалгацгаая.
Натурал логарифмын урвуу функцийг олъё ![]() (Энд yфункц мөн x- маргаан). Энэ тэгшитгэлийг шийдсэний дараа x, бид (энд xфункц мөн y- түүний аргумент). Тэр бол,
(Энд yфункц мөн x- маргаан). Энэ тэгшитгэлийг шийдсэний дараа x, бид (энд xфункц мөн y- түүний аргумент). Тэр бол, ![]() ба харилцан урвуу функцууд.
ба харилцан урвуу функцууд.
Деривативын хүснэгтээс бид үүнийг харж байна ![]() Тэгээд
Тэгээд ![]() .
.
Урвуу функцийн деривативыг олох томъёо нь ижил үр дүнд хүргэж байгаа эсэхийг шалгацгаая. 
Сургуулийн сурагчид геометр, математикийн хичээлээс эхлэн үүсмэл ойлголтыг дүрс, дифференциал, функцын хязгаар, хязгаар зэргээр дамжуулан тэдэнд дамжуулдаг гэдэгт дассан байдаг. Дериватив гэдэг ойлголтыг өөр өнцгөөс харж, дериватив болон тригонометрийн функцийг хэрхэн холбож болохыг тодорхойлъё.
Тиймээс y = f(x) хийсвэр функцээр дүрслэгдсэн дурын муруйг авч үзье.
Хуваарь нь аялал жуулчлалын маршрутын зураг гэж төсөөлөөд үз дээ. Зураг дээрх ∆x (дельта x) өсөлт нь замын тодорхой зай, ∆y нь далайн түвшнээс дээш замын өндрийн өөрчлөлт юм.
Дараа нь ∆x/∆y харьцаа нь маршрутын сегмент тус бүрийн замын нарийн төвөгтэй байдлыг тодорхойлох болно. Энэ үнэ цэнийг мэдсэнийхээ дараа та өгсөх/уруу эгц байх эсэх, танд авирах хэрэгсэл хэрэгтэй эсэх, жуулчдад тодорхой авиралт хэрэгтэй эсэхийг итгэлтэйгээр хэлж чадна. биеийн тамирын дасгал. Гэхдээ энэ үзүүлэлт зөвхөн нэг жижиг ∆x интервалд хүчинтэй байх болно.
Хэрэв аяллыг зохион байгуулагч нь замын эхлэл ба төгсгөлийн утгыг авдаг, өөрөөр хэлбэл ∆x нь маршрутын урттай тэнцүү бол тэрээр хүндрэлийн зэрэгтэй холбоотой бодит мэдээллийг олж авах боломжгүй болно. аяллын тухай. Тиймээс зам дахь өөрчлөлтийн хурд, "чанар" -ыг тодорхойлох өөр график байгуулах, өөрөөр хэлбэл, маршрутын "метр" бүрийн ∆x/∆y харьцааг тодорхойлох шаардлагатай.
Энэ график нь тодорхой замд зориулсан харааны дериватив байх бөгөөд сонирхлын интервал бүрт түүний өөрчлөлтийг бодитойгоор тайлбарлах болно. Үүнийг шалгах нь маш энгийн бөгөөд ∆x/∆y утга нь x ба y-ийн тодорхой утгад авсан дифференциалаас өөр зүйл биш юм. Ялгааг тодорхой координатуудад биш, харин бүхэлд нь функцэд хэрэглэцгээе.

Дериватив ба тригонометрийн функцууд
Тригонометрийн функцууд нь деривативтай салшгүй холбоотой байдаг. Үүнийг дараах зургаас ойлгож болно. Координатын тэнхлэгийн зураг нь Y = f (x) функцийг харуулж байна - цэнхэр муруй.
K (x0; f (x0)) нь дурын цэг, x0 + ∆x нь OX тэнхлэгийн дагуух өсөлт, f (x0 + ∆x) нь тодорхой L цэг дэх OY тэнхлэгийн дагуух өсөлт юм.

K, L цэгүүдээр шулуун шугам татаад байгуулъя зөв гурвалжин KLN. Хэрэв та LN сегментийг Y = f (x) графикийн дагуу оюун ухаанаараа хөдөлгөвөл L ба N цэгүүд нь K (x0; f (x0)) утга руу чиглэнэ. Энэ цэгийг графикийн нөхцөлт эхлэл - хязгаар гэж нэрлэе; хэрэв функц нь ядаж аль нэг интервал дээр хязгааргүй байвал энэ хандлага нь бас хязгааргүй байх бөгөөд түүний хязгаарлах утга нь 0-тэй ойролцоо байна.
Энэ хандлагын мөн чанарыг сонгосон цэгт шүргэгч y = kx + b эсвэл анхны функцийн dy - ногоон шулуун шугамын деривативын графикаар дүрсэлж болно.
Гэхдээ энд тригонометр хаана байна?! Бүх зүйл маш энгийн, зөв гурвалжин KLN-ийг авч үзье. Тодорхой K цэгийн дифференциал утга нь α эсвэл ∠K өнцгийн тангенс юм.

Ийм байдлаар бид деривативын геометрийн утга, түүний тригонометрийн функцтэй хамаарлыг тодорхойлж чадна.
Тригонометрийн функцүүдийн дериватив томъёо
Деривативыг тодорхойлохдоо синус, косинус, тангенс, котангенсийн хувиргалтыг цээжлэх ёстой.

Сүүлийн хоёр томьёо нь алдаа биш бөгөөд гол нь энгийн аргументын дериватив болон ижил хүчин чадалтай функцийг тодорхойлоход ялгаа байгаа явдал юм.
Синус, косинус, тангенс, котангенсийн деривативуудын томъёо бүхий харьцуулсан хүснэгтийг харцгаая.

Арксин, арккосин, арктангенс, арккотангенсийн деривативын хувьд томьёог гаргаж авсан боловч маш ховор хэрэглэгддэг:

Дээрх томьёо нь тригонометрийн илэрхийлэлийн деривативыг олох тодорхой жишээг шийдвэрлэхдээ харуулах ердийн USE даалгавруудыг амжилттай шийдвэрлэхэд хангалтгүй гэдгийг тэмдэглэх нь зүйтэй.
Дасгал хийх: Функцийн деривативыг олж π/4-ийн утгыг олох шаардлагатай:

Шийдэл: Y'-ийг олохын тулд анхны функцийг дериватив болгон хувиргах үндсэн томъёог эргэн санах хэрэгтэй.
Сэдэв:"Тригонометрийн функцүүдийн дериватив".
Хичээлийн төрөл- мэдлэгийг нэгтгэх хичээл.
Хичээлийн маягт- нэгдсэн хичээл.
Энэ хэсгийн хичээлийн систем дэх хичээлийн байр- ерөнхий хичээл.
Зорилтууд нь дараахь зүйлийг цогцоор нь тодорхойлсон болно.
- боловсролын:ялгах дүрмийг мэдэх, тэгшитгэл, тэгш бус байдлыг шийдвэрлэхдээ деривативыг тооцоолох дүрмийг хэрэглэх чадвартай байх; хичээл, түүний дотор тооцоолол, ур чадвар, чадварыг сайжруулах; Компьютер дээр ажиллах чадвар;
- хөгжиж буй:оюуны болон логик ур чадвар, танин мэдэхүйн сонирхлыг хөгжүүлэх;
- боловсролын:дасан зохицох чадварыг төлөвшүүлэх орчин үеийн нөхцөлсургалт.
Арга:
- нөхөн үржихүй, үржил шим;
- практик ба аман яриа;
- бие даасан ажил;
- програмчлагдсан сургалт, T.S.O.;
- урд талын, бүлэг ба хослол бие даасан ажил;
- ялгавартай сургалт;
- индуктив-дедуктив.
Хяналтын хэлбэрүүд:
- аман судалгаа,
- програмчлагдсан удирдлага,
- бие даасан ажил,
- компьютер дээрх бие даасан ажил,
- оюутны оношилгооны картыг ашиглан үе тэнгийн үзлэг.
ХИЧЭЭЛИЙН ҮЕД
I. Зохион байгуулалтын мөч
II. Лавлах мэдлэгийг шинэчлэх
a) Зорилго, зорилтуудыг илэрхийлэх:
- ялгах дүрмийг мэдэх, бодлого, тэгшитгэл, тэгш бус байдлыг шийдвэрлэхдээ деривативыг тооцоолох дүрмийг хэрэглэх чадвартай байх;
- хичээл, түүний дотор тооцоолол, ур чадвар, чадварыг сайжруулах; Компьютер дээр ажиллах чадвар;
- оюуны болон логик ур чадвар, танин мэдэхүйн сонирхлыг хөгжүүлэх;
- орчин үеийн сургалтын нөхцөлд дасан зохицох чадварыг төлөвшүүлэх.
б) Боловсролын материалыг давтах
Деривативыг тооцоолох дүрэм (компьютер дээрх томьёог дуу авиагаар давтах). doc.7.
- Синусын дериватив нь юу вэ?
- Косинусын дериватив гэж юу вэ?
- Шүргэгчийн дериватив нь юу вэ?
- Котангентын дериватив нь юу вэ?
III. Аман ажил
Деривативыг ол. |
|||
Сонголт 1. |
Сонголт 2. |
||
цагт = 2X + 5. |
цагт = 2X – 5. |
||
цагт= 4cos X. |
цагт= 3 нүгэл X. |
||
цагт= тг X+ctg X. |
цагт= тг X-ctg X. |
||
цагт= нүгэл 3 X. |
цагт= cos 4 X. |
||
Хариултын сонголтууд. |
|||
– 4 нүгэл X |
- 3 cos X |
||
1/cos 2 X+ 1/нүгэл 2 X |
1/cos 2 X-1/нүгэл 2 X |
1/нүгэл 2 X–1/cos 2 X |
|
– 4sin4 X |
– 3cos3 X |
||
Тэмдэглэлийн дэвтэр солилцох. Оношлогооны картуудад зөв гүйцэтгэсэн ажлыг + тэмдгээр, буруу гүйцэтгэсэн ажлыг - тэмдгээр тэмдэглэнэ.
IV. Дериватив ашиглан тэгшитгэлийг шийдвэрлэх
– Дериватив тэг байх цэгүүдийг хэрхэн олох вэ?
Дериватив байгаа цэгүүдийг олох энэ функцтэгтэй тэнцүү, танд хэрэгтэй:
- функцийн мөн чанарыг тодорхойлох;
- талбайг олох функцийн тодорхойлолтууд,
- энэ функцийн деривативыг олох;
- тэгшитгэлийг шийднэ е "(x) = 0,
- зөв хариултыг сонго.
Даалгавар 1.
Өгөгдсөн: цагт
= X- нүгэл x.
Олно:дериватив нь тэг байх цэгүүд.
Шийдэл.Функц нь бүх бодит тоонуудын олонлог дээр тодорхойлогдож, ялгагдах боломжтой тул функц нь бүх бодит тоонуудын олонлог дээр тодорхойлогдож, ялгагдах боломжтой байдаг. g(x) = xТэгээд т(x) = – гэм x.
Ялгах дүрмийг ашиглан бид олж авна е
"(x) = (x- нүгэл x)" = (x)" - (нүгэл x)" = 1 – cos x.
Хэрэв е "(x) = 0, дараа нь 1 – cos x = 0.
cos x= 1/; хуваагч дахь иррациональ байдлаас салцгаая, бид cos авна x
= /2.
Томъёоны дагуу т= ± arccos а+ 2n, n Z, бид дараахь зүйлийг авна. X= ± arccos /2 + 2n, n Z.
Хариулт: x = ± /4 + 2n, n Z.
V. Алгоритм ашиглан тэгшитгэлийг шийдвэрлэх
Дериватив аль цэгт алга болохыг ол.
е(x) = нүгэл x+cos x |
е(x) = нүгэл 2 x – x |
е(x) = 2x+cos(4 x – ) |
Оюутан гурван жишээний аль нэгийг сонгож болно. Эхний жишээг "үнэлсэн" 3 ", хоёрдугаарт -" 4 ", гурав дахь -" 5 " Шийдвэрийг дэвтэрт оруулаад дараа нь харилцан шалгах. Нэг оюутан самбар дээр шийдвэр гаргадаг. Хэрэв шийдэл буруу болбол оюутан алгоритм руу буцаж очоод дахин шийдэхийг оролдох хэрэгтэй.
Програмчлагдсан удирдлага.
Сонголт 1 |
Сонголт 2 |
|||
y = 2X 3 |
y = 3X 2 |
|||
y = 1/4 X 4 + 2X 2 – 7 |
y = 1/2 X 4 + 4X + 5 |
|||
y = X 3 + 4X 2
– 3X. |
y = 2X 3 – 9X 2
+ 12X + 7. |
|||
y= нүгэл 2 X- учир нь 3 X. |
y= cos 2 X- нүгэл 3 X. |
|||
y= тг X–ctg( X + /4). |
y=ctg X+ тг( X – /4). |
|||
y= нүгэл 2 X. |
y= cos 2 X. |
|||
Хариултын сонголтууд. |
||||
|
| ||||








